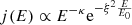| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 9 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202243449 | |
| Published online | 17 August 2022 | |
The properties of 0.11 keV–344 MeV ion spectra in the inner heliosheath using regularized κ-distributions
1
Institut für Theoretische Physik, Lehrstuhl IV: Plasma-Astroteilchenphysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
e-mail: kls@tp4.rub.de
2
Research Department, Plasmas with Complex Interactions, Ruhr-Universität Bochum, 44780 Bochum, Germany
3
Office of Space Research & Technology, Academy of Athens, 10679 Athens, Greece
e-mail: kdialynas@phys.uoa.gr
4
Physics Institute, University of Bern, Bern, Switzerland
5
Max Planck Institute for Solar System Research, Justus-von-Liebig-Weg 3, 37077 Goettingen, Germany
Received:
2
March
2022
Accepted:
2
June
2022
Context. The shape of the ion energy spectra plays a critical role in determining the ion energetics, the acceleration mechanisms, and the possible sources of different plasma and suprathermal ion populations. The determination of the exact shape of the total particle spectrum provides the necessary means to address the inner heliosheath dynamics. Apart from various modelling efforts, a direct fit to the measured ion spectra for an extended energy range of ∼0.11–344 MeV has not been performed to date.
Aims. We use an extended set of combined 0.11–55 keV remotely sensed energetic neutral atoms (ENA) measurements from the Interstellar Boundary Explorer (IBEX-Lo and IBEX-Hi) and the Cassini/Ion and Neutral Camera (INCA), converted to protons, together with ∼28 keV–344 MeV in situ ion measurements from the low-energy charged particle (LECP) and cosmic ray subsystem (CRS) experiments on Voyager 2, over the declining phase of solar cycle 23 (SC23) and the ascending phase of solar cycle 24 (SC24) to study the characteristics of the particle energy spectrum.
Methods. We fitted the 0.11 keV–344 MeV composite ion spectra with a set of regularized isotropic κ-distribution functions (RKDs), which allowed us to determine the macroscopic physical properties.
Results. We demonstrate that the 2009–2012 composite spectrum that corresponds to the declining phase of SC23 is well fitted by three different RKDs, while the 2013–2016 spectrum, associated with the rise of SC24, can only be approximated with six different κ-distribution functions.
Conclusions. Our results are generally consistent with shock accelerated particles that undergo additional acceleration inside the inner heliosheath. We identify a low-energy transmitted population of particles, a suprathermal reflected population and a very-high-energy component that is modulated by galactic cosmic rays. The 2013–2016 time period is most likely associated with a mixture of particles from SC23 and SC24, which is reflected by the need to employ six RDKs.
Key words: plasmas / Sun: heliosphere / solar wind / methods: data analysis
© K. Scherer et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
The solar wind (SW) interacts directly with the very local interstellar medium (VLISM), forming the heliosphere (Parker 1961). The neutral interstellar atoms that enter the heliosphere become ionized by various processes, namely photo-ionization, electron-impact ionization, and charge-exchange (see e.g., Scherer et al. 2014), and get ‘picked up’ by the SW where they are accelerated to higher energies, forming a unique distribution of ions with a cutoff at roughly twice the SW bulk speed, called ‘pickup ions’ (PUIs). For example, observations from the New Horizons spacecraft at ∼38 AU (McComas et al. 2017) show that the PUI distribution is heated in the frame of the SW with increasing distance, before reaching the inner boundary of our solar bubble, called termination shock (TS). The region between the TS and the heliopause (HP) has traditionally been referred to as the ‘inner heliosheath’ (IHS), and the region upstream of the HP has been called the ‘outer heliosheath’ (OHS). Recent studies (e.g., Dialynas et al. 2021; McComas et al. 2020) call these regions the ‘heliosheath’ (HS) and the ‘very local interstellar medium’ (VLISM; Holzer 1989; Zank 2015), respectively. The existence of an OHS (and consequently an IHS) does not depend on the existence of a bow shock or a bow wave in front of the heliosphere, a subject that is debated in the literature (e.g., McComas et al. 2012; Scherer & Fichtner 2014), because the pristine interstellar medium (ISM) has to flow around the heliopause, and will eventually build a hydrogen wall and influence the transport of low-energy cosmic rays. We choose to use the terms IHS and OHS in the present study.
The TS crossings of the Voyager 1 (V1) and Voyager 2 (V2) missions in 2004 (∼94 AU; Decker et al. 2005; Stone et al. 2005) and 2007 (∼84 AU; Decker et al. 2008; Stone et al. 2008), respectively, led to the discovery of the reservoir of ions and electrons that constitutes the IHS, where the particle pressure substantially exceeds the magnetic field pressure (β = Pparticle/PMAG ≫ 1; Decker et al. 2015; Dialynas et al. 2019, 2020). The IHS extends out to the HP (which serves as the interface between the SW plasma and the VLISM), which was measured in situ by V1 in 2012 (∼122 AU; Burlaga et al. 2013; Gurnett et al. 2013; Krimigis et al. 2013; Stone et al. 2013) and by V2 in 2019 (∼119 AU; Burlaga et al. 2019; Gurnett & Kurth 2019; Krimigis et al. 2019; Richardson et al. 2019; Stone et al. 2019). These measurements reveal the dynamic nature of the boundary, showing an increase in galactic cosmic rays (GCRs), magnetic field, and temperature, and a simultaneous decrease in suprathermal particles and invading of interstellar flux tubes into the IHS, pointing to the possibility of flux tube interchange instability at the boundary (e.g., Krimigis et al. 2013; Florinski 2015) and an outflow of suprathermal ions upstream of the HP out to ∼28 AU, originating from inside the IHS (Dialynas et al. 2021). The activity upstream of the HP is summarized in Gurnett et al. (2021), whereas a summary of the effects of the solar activity to the particle dynamics in interplanetary space, the IHS, and the OHS is presented in Hill et al. (2020).
The crossings of both Voyagers from the TS proved that the shocked thermal plasma in the region downstream of the TS remained supersonic. The bulk of the upstream energy density of the SW went into heating the PUIs, whereas a substantial amount (∼15%) was transferred to suprathermal (> 28 keV) particles (Richardson et al. 2008; Decker et al. 2008). The potential role played by electrons was studied by Chalov & Fahr (2013). Moreover, despite previous expectations (e.g., Pesses et al. 1981) that date back to the 1980’s, the ∼10–100 MeV intensities in both V1 and V2 did not peak at the TS, inferring that the anomalous cosmic rays (ACRs) are not accelerated at the TS, but most likely in the IHS by various mechanisms (e.g., Langner et al. 2006; Ferreira et al. 2007; Lazarian & Opher 2009; Drake et al. 2010; Strauss et al. 2010; Fisk & Gloeckler 2013; Zieger et al. 2015).
The contribution of remotely sensed observations of energetic neutral atoms (ENAs) from the Interstellar Boundary Explorer (IBEX; McComas et al. 2009) and particularly the Cassini/Ion and Neutral Camera (INCA; Krimigis et al. 2009) that covers the > 5.2 to ∼28 keV part of the PUI distribution that was not measured in situ by the Voyagers, was unequaled (see also Sect. 2). These observations further corroborate the complexity of the ∼10 eV to ∼344 MeV energy spectra inside the IHS (Dialynas et al. 2020), revealing a number of softening and/or hardening breaks that possibly correspond to acceleration mechanisms inside the IHS that are not currently described by recent sophisticated models (e.g., Gkioulidou et al. 2022). A recent model from Zirnstein et al. (2021) shows that a proton distribution that is consistent with the IBEX measurements requires a turbulence power ratio at the TS that is ten times higher than that observed by Voyager (Burlaga et al. 2008). Overall, the shape of the ion energy spectra plays a critical role in determining the ion energetics, the acceleration mechanisms, and the possible sources of different plasma and suprathermal ion populations.
Heliospheric plasmas, such as the SW or the plasma in the IHS, involve non-thermal acceleration processes. Their distributions no longer exhibit a Maxwellian (i.e., exponential) cutoff, but often a (decreasing) power law, which can be parameterized by κ-distributions, introduced empirically by Olbert (1968), and published for the first time by Vasyliunas (1968) as a global fitting model. More rigorous analyses involve a combination of multiple (anisotropic) distribution functions, including Maxwellian and κ distributions (Maksimovic et al. 2005; Štverák et al. 2008). The standard κ distributions (SKDs) are a powerful tool for modelling non-thermal distributions, but have a critical limitation in defining the velocity moments of order l (e.g., the macroscopic physical properties), which diverge for low values of κ < (l + 1)/2 (Lazar & Fichtner 2021). To overcome this behaviour, Scherer et al. (2017) introduced a generalization of the isotropic standard κ distribution: the regularized κ distribution, for which all velocity moments converge (see also Scherer et al. 2020, for a more general discussion). We briefly recall its definition in Sect. 3. Despite their limitations, κ-distributions were used to model the evolution of PUIs in the IHS (e.g., Fahr et al. 2016) and electrons (e.g., Fahr et al. 2017). They are also used to model the interaction of protons with neutral hydrogen in the IHS (Heerikhuisen et al. 2008; Livadiotis et al. 2011). For further reading we recommend Lazar & Fichtner (2021) and Livadiotis (2017).
In the present study we model the 0.11 keV–344 MeV composite ion spectra in the IHS, presented in Dialynas et al. (2020), with regularized κ distributions, following the method of Scherer et al. (2020). Section 2 provides a brief overview of the measurements employed in our analysis, and our model is thoroughly explained in Sect. 3. The results are presented in Sect. 4, and are subsequently discussed in Sect. 5, in accordance with various studies published in the literature. Finally, Sect. 6 provides a brief summary of our findings.
2. Measurement details and instrumentation
The energy spectra used in the present study (Fig. 1) are taken from Dialynas et al. (2020) and represent a combination of remotely sensed 0.11 keV to 55 MeV HENA (converted to protons) from IBEX and Cassini/INCA, and ∼28 keV–344 MeV in situ ions from the Voyager 2 (V2) mission, over the time period from the beginning of 2009 to the end of 2016. These energy spectra can be thought of as representative of the IHS conditions during the declining phase of solar cycle 23 (SC23) and the rise of solar cycle 24 (SC24) in the direction of V2.
 |
Fig. 1. Upper left panel: fit with three RKD distribution functions for the period 2009–2012. The yellow dotted line is the fit to the yellow data points, the blue dotted line the fit to the blue marked data points, and the green dotted line the fit to green data points. The red line is the sum of the total distribution |
The ENAs created by the proton-neutral gas interactions through the charge-exchange (CE) process (e.g., Lindsay & Stebbings 2005; Fahr et al. 2007; Scherer et al. 2014), are remotely detected by IBEX (located at ∼1 AU) and Cassini/INCA (at ∼10 AU; end of mission 15 Sep. 2017) that provide full sky images of the heliosphere (e.g., McComas et al. 2009; Krimigis et al. 2009).
Specifically, the IBEX mission includes two single-pixel ENA cameras, namely the IBEX-Lo (Fuselier et al. 2009) taking measurements from ∼10 eV to ∼2 keV (Galli et al. 2016, a new data release can be found in Galli et al. 2022), and the IBEX-Hi (Funsten et al. 2009) that measures ENAs from ∼520 eV to ∼6 keV (e.g., McComas et al. 2014). The INCA instrument on Cassini (Krimigis et al. 2009), part of the Magnetospheric Imaging Instrument (MIMI; Krimigis et al. 2004) utilized a large geometry factor (G ∼ 2.4 cm2 sr) and a broad field of view (FOV; 90° ×120°), possessing a high sensitivity to detect very-low-ENA intensity events in the heliosphere and image large parts of the sky sphere over the energy range of ∼5.2–55 keV (e.g., Dialynas et al. 2017b).
The first images of the IBEX mission at < 6 keV showed the existence of a bright and narrow stripe of ENA emissions that cuts through the region between the V1 and V2 positions towards the upwind hemisphere and roughly encircles the global heliosphere (McComas et al. 2009; Schwadron et al. 2009). This unexpected feature, called the ‘ribbon’ is thought to lie beyond the HP, formed through a secondary ENA process (Heerikhuisen et al. 2010). The ribbon is superimposed over the so-called globally distributed flux (GDF), a ‘background’ ENA emission that exhibits different characteristics from the ribbon (Livadiotis et al. 2011; Schwadron et al. 2011) and is thought to be formed from within the IHS (e.g., Dayeh et al. 2011; Schwadron et al. 2014; McComas et al. 2009, 2017, 2020). The < 6 keV IBEX/ENA measurements in Dialynas et al. (2020; also shown in Fig. 1, converted to ions) do not take contributions from the ribbon.
At higher energies, the > 5.2 keV ENAs measured by Cassini/INCA have shown the existence of a ‘belt’ of varying ENA intensities, identified as a relatively wide and nearly energy-independent ENA region that wraps around the celestial sphere and two ‘basins’ where the ENA minima occur (Krimigis et al. 2009; Dialynas et al. 2013). Both these features have been proven undeniably to be of IHS origin (e.g., Krimigis et al. 2009, 2011; Dialynas et al. 2013, 2017a,b, 2019, 2020).
The ENAs from 0.11 to 55 keV (from IBEX-Lo, IBEX-Hi, and INCA) are sampled in the pixels enclosing the position of V2, and are converted to protons (shown in Fig. 1) using an interstellar neutral hydrogen distribution of nH ∼ 0.12 cm−3 (Dialynas et al. 2019; Swaczyna et al. 2020) and a line of sight (LOS) of LHS ∼ 35 AU (as measured by V2; e.g., Decker et al. 2008; Krimigis et al. 2019), meaning they are assumed to form through CE interactions from inside the IHS. For thorough information concerning the combination of the measurements shown in Fig. 1, the reader should refer to Dialynas et al. (2020) and references therein.
The ∼28–3.5 MeV data shown in Fig. 1 are in situ ions from the low-energy charged particle (LECP) detector on V2 (Krimigis et al. 1977), which measures the differential intensities of ions within the 28 keV to ∼60 MeV/Nuc energy range, together with an integral ion measurement > 211 MeV (e.g., Decker et al. 2015). The ∼3–344 MeV part of the energy spectra in Fig. 1 is taken from the cosmic ray subsystem (CRS) instrument (Stone et al. 1977) that resolves the energy spectra and elemental composition of all cosmic-ray nuclei from hydrogen through iron over the energy range from ∼1–500 MeV/nuc (e.g., Cummings et al. 2016).
The shape and properties of the energy spectra shown here, together with specific details about the measurement techniques and analyses concerning the IBEX, INCA, LECP and CRS capabilities and data, are thoroughly explained in Dialynas et al. (2020, 2022), Galli (2022) and references therein.
3. The model
Past modelling efforts (e.g., Zirnstein & McComas 2015) used a single κ-distribution over an energy range of ∼0.1–100 keV to characterize the PUI spectrum downstream of the TS, and examined the change in this proton distribution due to the charge exchange losses inside the IHS, showing that the IHS spectra do not retain their initial shape. Dialynas et al. (2019) further showed that the use of a single κ-distribution downstream of the TS may fit the several hundred kilo-electron-volt part of the ion distribution, but it would substantially underestimate the particle fluxes in (at least) the ∼5.2–24 keV energy range. Clearly, the description of the proton spectra inside the IHS and (perhaps) even at the TS, especially when considering an extended energy range of ∼0.11 keV–344 MeV, requires the use of multiple κ-distributions.
We model the particle energy spectra shown in Fig. 1 with a combination of isotropic regularized κ-distributions (RKDs). Through visual inspection we identify a couple of ‘cutoffs’, that is to say energies where a power law is ‘cut off’ by the corresponding distribution function. Our analysis reveals the need for three RKD distributions to fit the period 2009–2012, and six RKDs for the period 2013–2016. Before we go into the discussion of the ‘fitting’ (see Sect. 3.2 below), we present the RKDs and the corresponding differential fluxes in the next section.
3.1. The regularized distribution
The isotropic regularized RKD was discussed in detail in Scherer et al. (2020). For the convenience of the reader, we repeat it here. The RKD is given by:
where v is the speed, Θ the normalization speed, n0 the number density, κ > 0 a real number, 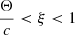 a cutoff parameter, and U(a, b, z) is the Kummer-U function (e.g., Abramowitz & Stegun 1970). The pressure is a trace of the second-order moment tensor, which for the isotrpic RKD yields:
a cutoff parameter, and U(a, b, z) is the Kummer-U function (e.g., Abramowitz & Stegun 1970). The pressure is a trace of the second-order moment tensor, which for the isotrpic RKD yields:
We define the total RKD ft as:
with, in our cases, n = 3 or n = 6. Thus, we have to put an index to n0, Θ, κ, and ξ in Eqs. (1) and (2). The total pressure is the sum all partial pressures 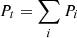 , as well as the total number density
, as well as the total number density 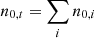 .
.
The temperature for the partial pressures is given by the ideal gas law Ti = Pi/n0, i/kBol, with the corresponding number density n0, i and the Boltzmann constant kBol. The total temperature is then:
To get the differential flux, we replace the velocity by 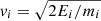 , where Ei and mi are the energy and mass for the ith RKD. To save writing we omit the indices and get:
, where Ei and mi are the energy and mass for the ith RKD. To save writing we omit the indices and get:
With E0 = mpΘ2/2 and E = mpv2/2 we find for the differential flux 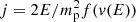 in SI units (Formula‘6 from Fahr et al. 2017; replacing the electron mass by the proton mass me → mp ≡ m):
in SI units (Formula‘6 from Fahr et al. 2017; replacing the electron mass by the proton mass me → mp ≡ m):
When we measure E, E0 in keV and n in cm−3
where j is now in [1/(keV s cm2 sr)].
As will be discussed in this study, while the SKD would not provide an adequate approximation, we introduce the differential flux of the SKD by Fahr et al. (2017) as:
Here U⊥ corresponds to the normalization speed and Γ(z) is the Gamma-function (e.g., Abramowitz & Stegun 1970). In both cases (RKD and SKD), for large E, the distribution function follows a power law form in energy of ≈E−κ. For energies E > E0, we can approximate the κ part of the RKD:
(for the SKD without the exponential term). The exponential term approximates unity as long as the argument is (much) less than one (ξ2E/E0 < 1).
For the total distribution function, we thus get a piecewise power law for the distributions fi. For the RKD, we have a cutoff, which allows us to plot the differential flux for the total distribution, but not for the SKD because there the power law of the first partial distribution dominates (see Fig. 2 and discussion below).
 |
Fig. 2. Fit with three SDK distribution functions. Same structure as in Fig. 1. The red line is the sum of all the fitted distributions, which is nearly identically to the yellow line (covered by the red). See the text for further detail. |
3.2. The ‘fit’ procedure
The measurements shown in Fig. 1 contain a total of 38 data points representing the differential flux as a function of energy, for both time periods considered. We need to fit four parameters for each partial distribution function fi. Thus, a fit with three distributions results in a total of 12 free parameters, whereas a six distribution fit results in 24 free parameters. Especially in the latter case, we have partial distributions, which can be ‘fitted’ only for four points. Therefore, we refrain from naming it a ‘fit’ to the data, but rather the optimum solution of the corresponding equation system. Thus the errors for the fit procedures are not well defined, or may be large because of the small number of points. Nevertheless, we approximated the differential fluxes for both periods.
The period 2009–2012, shown in the upper left panel of Fig. 1 and in Table 1, requires the use of three distribution functions. The total fitted curve is given by the red line, while the partial fits are colour coded (f1 in gold, f2 in blue, and f3 in green). The differential flux for the total distribution fits the entire spectrum quite well. The numbers given in Table 1 also show that the κ-value is always below 1.5, which is the lower limit for the SKD.
Parameter for the three fitted RKD distributions and the total number density, pressure, and temperature.
Nevertheless, we fitted three SKD’s to the differential flux, as shown in Fig. 2 and Table 3. Because there is no cutoff, the spectrum is dominated by the first SKD (gold). Moreover, it can be seen that the cutoffs are not well fitted and that the κ-value is always 1.51, which is the lower boundary for the fitting procedure. Comparing the results between Tables 1 and 3, we notice that the total pressure and temperature for the SKD fit is larger by a factor of ∼100. This is caused by the fact that the pressure close to the lower boundary for the SKD is not well defined (it increases quickly to infinity). The other reason for that behaviour can be seen in Fig. 2, where the fit to the first distribution function f1 covers the entire spectrum, and the area under this curve is much larger than the area under the RKD f1 curve for the same spectrum. Thus, one has to cut the distribution function artificially at the cutoff points in the spectra as discussed in Scherer et al. (2018, 2019). Then, the points around the cutoff still remain, which cannot be fitted with a truncated SKD. Thus, one needs to apply an RKD to get the observed cutoffs correctly, and to get more reliable pressures (temperatures). Hence we no longer discuss the SKD.
The energy spectra for the second period (2013–2016) could not be fitted with three κ-distributions, but required the use of six RKDs. The result is shown in the lower left panel of Fig. 1 and in Table 2. One can see from Table 2 that the κ-values scatter between κ = 0.34 and κ = 1.73. Also, the differential spectrum for the total fit is somewhat higher than the data, which can be accounted for by multiplying the sum of all RKDs by a factor of 0.6. The result is shown in the lower left panel of Fig. 1 together with the error bars of the data points. Thus, we have to multiply all the number densities by a factor of 0.6, as well as the pressure. The temperatures remain unchanged because T ∝ P/n. Interestingly, the particle pressure that results from our analysis (∼0.308 pPa) is only somewhat higher than the overall (isotropic) pressure in the IHS that was calculated directly from these measurements for the same time period (Dialynas et al. 2020, ∼0.251 pPa), further supporting the relative success of our model and the need for the multiplying factor of 0.6. The overestimation of the particle pressure in our model by ∼20% is a result of a slight overestimation of the particle fluxes in the ∼0.5–100 keV part of the energy spectra that carry a substantial amount of the total particle pressure inside the IHS. A multiplying factor of 0.5 provides a better representation of this part of the distribution (blue dotted line in the lower right panel of Fig. 1) and corresponds to a total pressure of ∼0.256 pPa, which is in agreement with the pressure calculated by Dialynas et al. (2020). Furthermore, a total effective pressure of ∼0.267 ± 0.55 pPa was calculated by Rankin et al. (2019) using data-driven models and observations from IBEX.
Parameters for the three fitted SKD distributions, and the total number density, pressure and temperature.
The choice of the factor is quite arbitrary and it is also possible that, for different parts of the adaption, different factors can be used. Because these factors cannot be accessed by the fit, we have only given the number densities and pressures in Table 2 multiplied by a factor of 0.6. One can easily change these values using the original number densities and pressures. The number densities are directly proportional to the distribution functions, and therefore also the pressure. The temperatures, the fitted energies E0 (or corresponding normalization speeds Θ), the κ-values, and the cutoff parameters are not affected by such a factor.
4. Results
The results for the RKD fit are shown in Fig 1, Tables 1 and 2. In the tables, the fitted values for the number densities n0, i, the characteristic energies E0, i, the kappa value κi, and the cutoff parameter ξi are shown for the distributions in question, that is to say three RKDs fi, i ∈ {1, 2, 3} for the period 2009–2012 (Table 1) and six RKDs fi, i ∈ {1, …, 6} for the period 2013–2016. In the tables, the derived parameter for the pressure, the temperature, and the characteristic speeds 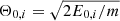 are also shown. Additionally, in Table 2 the values for the number densities and pressures reduce by a factor of 0.6 (0.5) are shown (see detail above).
are also shown. Additionally, in Table 2 the values for the number densities and pressures reduce by a factor of 0.6 (0.5) are shown (see detail above).
4.1. The period from 2009 to 2012
We concentrate the discussion first on the period 2009–2012 shown in Fig. 1 and Table 1. From the table, we immediately see that the κ-value is always below 1.5, and thus can only be fitted by an RKD, not an SKD. We also acknowledge that this time period corresponds roughly to the solar minimum of SC24, where the sunspot numbers on the sun and the SW pressure at ∼1 AU bottomed out at around 2010, presenting a maximum between 2014 and 2015 (see also the discussion in Dialynas et al. 2020). We note that the slow SW needs about one year to reach the TS, while the fast SW takes only 0.5 years. Beyond the TS, the SW ions are transported through the IHS with radial velocities of < 100 km s−1 that progressively decrease to zero, especially close to the HP (e.g., Decker et al. 2012). We note that the general morphology of the HP between the two voyager crossings was very similar, but there is a dramatic contrast between the plasma flow regime between the V1 encounter north of the heliographic equatorial plane (stagnation region with tangential flow in the −T direction Krimigis et al. 2011) and V2 in the south (Krimigis et al. 2019, transition region with the tangential flow in the +T direction).
When we concentrate on the characteristic speeds (energies), we see that the three distinct RKDs have characteristic speeds that differ by orders of magnitude. The first RKD with the highest number density (n1 ≈ 0.01 cm−3) has a characteristic speed of 35 km s−1, which can be attributed to lie within the IHS. The measurements from the plasma science experiment (PLS) on Voyager 2 beyond the TS (Richardson & Decker 2014) over the 2009–2013 time period, are consistent with convected Maxwellian distributions with typical thermal speeds of ∼30 km s−1 (with a spread between ∼20 and 50 km s−1). In addition, the measured plasma temperature from V2/PLS over the 2009–2013 time period varies within ∼40−90 kK (Richardson & Decker 2015), which implies that the derived temperatures of T1 ≈ 85 kK fit in to that scenario.
For the second RKD, we have a characteristic speed of ≈650 km s−1 and a temperature of ≈100 kK, which can be attributed to the termination shock particles and accelerated PUIs (Chalov & Fahr 2000). These authors modelled the shock drift acceleration at the TS and found two populations of PUIs: a transmitted component, where the PUIs are transported through the TS and have a cuttoff around 10 keV; and a multiple reflected population with a cutoff around 500 keV (they called it valley). These cutoffs coincide with the one found in the data and fitted by the RKD. The corresponding number density for the higher energetic particles (the transmitted PUIs) are quite low: n1 ≈ 4 × 10−6 cm−3.
Although highly sophisticated models that consider the heating and acceleration of PUIs at the TS (e.g., Giacalone et al. 2021) are constrained by the Voyager/LECP measurements, their inability to account for the measured fluxes of ENAs over the ∼0.5 to ∼55 keV energies (e.g., Gkioulidou et al. 2022) implies that this population of particles is consistent with PUIs that are accelerated (or accelerated additionally) inside the IHS, that is to say downstream of the TS, and not necessarily at the TS. A recent analysis by Zirnstein et al. (2021) shows that the measured IBEX spectrum cannot be obtained with protons being accelerated at the TS, unless using a turbulence power ratio at the shock foot that is ten times larger than what was observed by Voyager (e.g., Burlaga et al. 2008).
The third RKD has even lower number densities (n3 ≈ 1 × 10−8 cm−3), characteristic speeds (4440 km s−1), and temperatures (T3 ≈ 1 MK). A close inspection of the data points at the highest energies, show that they start to increase, presenting a noticeable ‘hardening break’, at ∼10 MeV (Fig. 1), which is an indication of a contribution of galactic (GCR) and/or anomalous cosmic rays (ACR; see e.g., Cummings et al. 2016; Stone et al. 2019; Bisschoff et al. 2019). Earlier analyses attributed this feature in the spectra to a local disturbance at V2, which was most likely caused by a global merged interaction region (GMIR) passing through the IHS (Rankin et al. 2019). However, as explained in Dialynas et al. (2020), this is a result of the unfolding of the ACR spectrum inside the IHS (up to at least the year 2011), which was not the expected power law at the TS during the V2 crossing.
The sources of ACRs, generated from SW PUIs (that are the dominant energy source in the IHS) are different from those of GCRs. Previous analyses comparing the ACR energy spectra with the estimated flux of PUIs at the TS revealed a mass-dependent acceleration that favours heavier ions (Cummings & Stone 2007, and references therein), and the analysis of Cummings et al. (2019) supports the idea of ACRs being accelerated back towards the flank or tail of the TS. However, other analyses show that different processes, such as magnetic reconnection (Drake et al. 2010; Zank et al. 2015; Zhao et al. 2019) or the so-called pump mechanism (Fisk & Gloeckler 2012) can also potentially accelerate ACRs inside the IHS, whereas these particles are influenced by interstellar PUIs (Hill et al. 2020).
At higher energies, the spectra beyond about 100 MeV most likely have contributions from GCR (Dialynas et al. 2020) and, as shown in our analysis, they cannot be fitted with a power law or a κ-distribution. This is indicated by the very low κ = 0.76 value, which is consistent with the fact that the interstellar GCR spectrum at low energies is almost flat (e.g., Stone et al. 2019; Bisschoff et al. 2019). While the RKD does not capture the high-energy tail that is modulated by GCRs, we note that a sufficient approximation of the > 300 MeV GCR spectra in interplanetary space was based on a force field approximation (e.g., Roussos et al. 2020, and references therein), whereas the measured GCR spectra upstream at the HP together with estimated spectra in the VLISM using a variety of different models (e.g., Engelmann et al. 1990; leaky-box model and Vladimirov et al. 2011; GALPROP model Bisschoff et al. 2019) are shown in Cummings et al. (2016).
4.2. The period from 2013 to 2016
The upper right panel of Fig. 1 provides a fit with three distribution functions, which is clearly inadequate to describe the measured spectra, and substantially undershoots the proton fluxes, especially within the energy range of ∼1–55 keV. We thus consider an adaption with six RKDs, shown in the lower left panel of Fig. 1. Because the sum of the adaptions (red dotted line shown in the lower right panel of Fig. 1) is too large by a factor of ∼0.6 (or ∼0.5; see discussion in Sect. 3), we multiply the number densities by this number, to produce a better approximation of the measurements (green dotted line for the factor of 0.6, and blue dotted line for the factor of 0.5). As explained earlier, the approach of using a set of six distribution functions cannot be called a fit to the data, but rather a solution of the corresponding equation system. Thus, this is an adaption to the data with six distribution functions, rather than a fit.
The reason for this behaviour is not surprising, but is due to the fact that the ascending phase of SC24 (2013–2016) has not yet filled the entire IHS, and thus we have a combination of the proton fluxes from the previous cycle 23 and the ascending cycle 24. This can be seen in the first three distribution functions, which have slightly different characteristic speeds (Θ1, 2, 3 ≈ [14, 22, 95] km s−1). The same holds true for the fourth and fifth distributions (Θ4, 5 ≈ (1.6, 9.8) Mm s−1), while the sixth distribution has a characteristic speed of Θ ≈ 14 Mm s−1 and resembles most probably a mixture of ACRs and GCRs.
Notably, the < 28 keV measurements in the spectra shown in Fig. 1 present the largest discrepancy with the three κ-distribution approach and correspond to measured ENAs (IBEX-Hi and INCA) that have been converted to protons. The ENA fluxes at the IBEX energies generally respond somewhat slower to the SW pressure changes over the SC than the ENAs corresponding to the energies covered by INCA. For example, unlike the > 5.2 keV ENA measurements from INCA and in situ ions from LECP (Dialynas et al. 2017b), the < 6 keV ENAs do not present a local minimum within the year 2013, and require more time to respond to the min-to-max pressure changes over the SC than higher energy ENAs and in situ ions (e.g., McComas et al. 2020). However, it should be noted that the response of the ∼4.29 keV ENA IBEX channel exhibits the shortest time delay and largest flux variation (Reisenfeld et al. 2016; Zirnstein et al. 2018; McComas et al. 2020), in concert with the > 5.2 keV ENAs from INCA (Dialynas et al. 2017b, 2019) that respond within ∼2–3 yr, on average. A response to a large SW intensification in the upwind hemisphere (but not downwind), with a time delay of ∼2–3 yr, especially of the higher energy (∼4.29 keV) ENAs, has been previously reported in McComas et al. (2018).
The differences between the two periods under discussion can be identified via the recorded ICME/CME/SSS events at about 1 au, considering the lists compiled by the George Mason University, Space Weather Lab1. Because these disturbances usually need 1–3 yr to reach the IHS, we can count the number of disturbances in the time period from 2007 to 2010 (or going only one year back between 2009 and 2011) to be about 31 (61). In the later period, from 2011 to 2014 (2012–2015), there are more than 100 (100) events. From those numbers we assume that the state of the IHS between 2009 and 2011 is quite calm, as the SW was quite calm at 1 au, while it is highly dynamic in the latter period. Thus, although it is possible to fit the state of the IHS in the first period (2009–2012), the latter time period (2013–2016, where the maximum conditions of SC24 reach the IHS), presents further complications that render such an attempt rather challenging, as explained in this section (see also Sect. 5).
5. Discussion
Chalov & Fahr (2000) studied the particle energy spectra downstream of the TS, focusing on an energy range of 10−1–104 keV, while recent analyses have simulated only parts of the ion spectrum. For example, Baliukin et al. (2022) provide a good approximation to the corresponding part of the spectrum (IBEX-Hi), whereas other authors compare the different types of shock acceleration (diffusive shock versus shock drift acceleration), see Zirnstein et al. (2021), or simulate it locally (Lembège & Yang 2018; Giacalone et al. 2021; Wu et al. 2016). A recent simulation of most parts of the ENA and PUI-spectrum can be found in Czechowski et al. (2020), which is based on the model of PUI acceleration at the TS proposed by Zank et al. (2010).
Other authors concentrate more on simulating ENA spectra (Galli et al. 2019; Zirnstein et al. 2021), which show similar behaviour as the fitted spectra, discussed above.
A common problem among most of these sophisticated modelling efforts that simulate the proton energy spectra, especially within the critical part of the distribution that corresponds to the > 0.5–55 keV energies (which provides a significant amount of pressure inside the IHS), is that they substantially underestimate the measured fluxes. Zirnstein et al. (2017) discuss the persistent discrepancy between their model and the 0.71–4.29 keV IBEX measurements of a factor of ∼2–3, as a possible result of a misestimation of the IHS thickness (a common issue among most of the advanced heliosphere models, e.g., Kleimann et al. 2022), and/or a less constrained velocity diffusion of ions inside the IHS, and/or as a result of adopting a less precise ion distribution function downstream of the TS. The model of Baliukin et al. (2022) employs a kinetic treatment of PUIs and produces simulated spectra that differ by a factor of only ∼1.5 from the measured data.
At higher energies, the ENA simulations from Czechowski et al. (2020) are lower by a factor of > 4 from the > 5.2 keV measured ENAs (Dialynas et al. 2017a) for both solar minimum and maximum conditions. Moreover, the simulated energy spectra in Czechowski et al. (2020) are substantially harder than the measured spectra. As explained in Dialynas et al. (2019), underestimating the flux and spectral slope of this part of the proton distribution leads to a considerable underestimation of the partial particle pressure inside the IHS, thus preventing realistic numbers from being obtained for the pressure balance that forms our solar bubble. Recently, Gkioulidou et al. (2022) has provided hybrid simulations of ions downstream of the TS using the sophisticated Giacalone et al. (2021) model, showing an energy-depended discrepancy between the 0.52 and 55 keV measured (IBEX-Hi and INCA) and simulated ENA fluxes, with the observations being persistently higher than the model, suggesting that further acceleration of PUIs occurs within the IHS.
There has also been an attempt to model the PUI flux in the IHS by Fahr et al. (2016) using a SKD. Some of these models have the problem that using a SKD limits the power index κ to values above 1.5, while our fit shows that the best values of κ are below that value for all three fitted distributions: κ1, 2, 3 ≈ 1.3, 1.3, 1.1, see Table 1.
The advantage of the RKD fit to the spectra is that we can estimate the macroscopic velocity moments (density and pressure) and, assuming that the ideal gas law holds, we can estimate the temperatures. We point out that the higher order velocity moments l of the RKD increase with κ → 0 as 1/([l + 1]ξl) (Husidic et al. 2022), and thus even the small κ values, such as κ = 0.34 for the second adapted distribution in the period 2013–2016, have a finite pressure (temperature).
When we look at the total number densities, we recognize that they agree quite well with the standard assumption of the interstellar neutral gas densities (Dialynas et al. 2019, 2020; Swaczyna et al. 2020) in 2009–2012, while those in 2013–2016 are slightly larger when we use the factor of 0.6 for the adaption of the distribution functions to the spectra. Nevertheless, the latter period should be handled with care because we do not have a quasi-stationary state; the SW speed is strongly varying between high- and low-speed streams (McComas et al. 2008), whereas during the first period (approximately solar minimum) we have a quasi-stationary state of the heliosphere because the high-speed winds are now located above 35°, while the low speed wind is located below 35° and the entire SW is quite smooth. During the latter period, we then also have a quasi-stationary TS for which the shock drift acceleration (e.g., Chalov & Fahr 2000) applies, while during the period 2013–2016, the TS moves in and out (Strumik & Ratkiewicz 2022, and references therein). Thus, the TS moves over the declining phase of each SC with some time delay because of the finite travel time of the SW. That is the difference between the two periods; in fact SC24 has the weakest conditions among all known SCs. The minimum of SC23 was deep and very prolonged, which can account for a ‘quasi-stationary’ condition inside the IHS (McComas et al. 2013). Thus the dynamics of the change between SC23 and SC24 explain the differences between the 2009–2013 and the 2013–2016 time periods.
For the adaption of the spectrum in 2013–2016, the sum of the distribution functions is a little bit higher than that of the adapted single distributions. The reason is that adaption fits the required points quite well, but the sum is slightly too large. The multiplication of all number densities by a factor of 0.6 (0.5) gives better results. These values (number densities and pressures) are indicated in Table 2 by the factor of 0.6. Furthermore, we have calculated the total number densities, pressures, and temperatures without the contribution of f6, because that will give values that are too high. The reason is that it continues to high energies, where one has to take into account the modulation of ACRs and GCRs, which will increase towards 1 MeV or 1 GeV and then fall off exponentially as ∼E−2.3 (Bisschoff et al. 2019) to ∼E−2.7 (Fisk & Gloeckler 2012) towards the knee of the GCRs that occurs at ∼8 × 106 GeV.
6. Summary and conclusion
We have demonstrated that the 0.11 keV–344 MeV composite proton spectra during the solar minimum period from 2009 to the end of 2012 can be fitted with three RKDs, namely for the lowest energy range (RKD f1, the transmitted PUIs), and the middle energy range (RKD f2, the multiply reflected PUIs), and the highest energies (RKD f3, which are most probably a mixture of the highest transmitted PUIs and modulated ACRs/GRCs).
For the subsequent period 2013–2016 (i.e., a period of solar maximum), a fit needs six (rather than three) distributions. The reason may be the highly dynamic IHS during that period. Our approach indicates that there seems to be a mixture of transmitted particles from the minimum of cycle 23 and from the maximum of solar cycle 24 in the lowest and middle energy ranges. The highest energy range splits into high-energetic transmitted particles or pre-accelerated ACRs, and a high-energy component of GCRs, which should not be represented by an RKD. Overall, as discussed in Sect. 5, our results are consistent with PUI and ACR shock accelerated particles that undergo additional acceleration inside the IHS.
Although the description of the dynamic state of the IHS with ion spectra that are averaged over three to four years can be potentially problematic, we stress that during the first period (2009–2012) the state of the SW was quite calm when it reached the TS, and thus we could fit the average ion spectrum quite adequately, attributing it to the transmitted and reflected PUI populations. In contrast, the highly dynamic state of the IHS during the ascending phase of SC24 towards solar maximum made the task of fitting the ion measurements during the second time period (2013–2016) challenging. During that time, the state in the IHS seems to be quite chaotic. Nevertheless, our analysis for the subject time period resulted in a total pressure for the IHS that is comparable to the pressures provided by Dialynas et al. (2020), who accurately obtained the magnitude of the magnetic field upstream at the HP by performing a pressure balance at the boundary. This indicates that our approach does in fact capture part of the dynamics of the IHS, as discussed in Sect. 4.
Besides the fact that these data have been fitted with physics-based distribution functions for the first time, the results are another demonstration of the usefulness of RKDs, because equivalent fits with standard κ-distributions would not be possible.
Acknowledgments
KD acknowledges the support from the NASA contracts NAS597271, NNX07AJ69G, and NNN06AA01C and subcontract at the Office of Space Research and Technology (Academy of Athens), together with useful discussions and collaboration with all SHIELD team members (NASA grant 18-DRIVE18_2-0029, Our Heliospheric Shield, 80NSSC20K0603: http://sites.bu.edu/shield-drive/) that made this work possible. KS, KD, HF and AG are grateful to join the ISSI workshop “The Heliosphere in the Local Interstellar Medium” and the useful discussions therein.
References
- Abramowitz, M., & Stegun, I. 1970, Handbook of Mathematical Functions (New York: Dover Publications) [Google Scholar]
- Baliukin, I. I., Izmodenov, V. V., & Alexashov, D. B. 2022, MNRAS, 509, 5437 [Google Scholar]
- Bisschoff, D., Potgieter, M. S., & Aslam, O. P. M. 2019, ApJ, 878, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., Ness, N. F., Acuña, M. H., et al. 2008, Nature, 454, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., Ness, N. F., & Stone, E. C. 2013, Science, 341, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., Ness, N. F., Berdichevsky, D. B., et al. 2019, Nat. Astron., 3, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Chalov, S. V., & Fahr, H. J. 2000, A&A, 360, 381 [NASA ADS] [Google Scholar]
- Chalov, S. V., & Fahr, H. J. 2013, MNRAS, 433, L40 [NASA ADS] [Google Scholar]
- Cummings, A. C., & Stone, E. C. 2007, Space Sci. Rev., 130, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Cummings, A. C., Stone, E. C., Heikkila, B. C., et al. 2016, ApJ, 831, 18 [CrossRef] [Google Scholar]
- Cummings, A., Stone, E., Heikkila, B. C., Lal, N., & Richardson, J. 2019, Int. Cosmic Ray Conf., 36, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Czechowski, A., Bzowski, M., Sokół, J. M., et al. 2020, ApJ, 888, 1 [NASA ADS] [Google Scholar]
- Dayeh, M. A., McComas, D. J., Livadiotis, G., et al. 2011, ApJ, 734, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B., Krimigis, S. M., Roelof, E. C., et al. 2005, Science, 309, 2020 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B., Krimigis, S. M., Roelof, E. C., et al. 2008, Nature, 454, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B., Krimigis, S. M., Roelof, E. C., & Hill, M. E. 2012, Nature, 489, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B., Krimigis, S. M., Roelof, E. C., & Hill, M. E. 2015, J. Phys. Conf. Ser., 577, 012006 [NASA ADS] [CrossRef] [Google Scholar]
- Dialynas, K., Krimigis, S. M., Mitchell, D. G., Roelof, E. C., & Decker, R. B. 2013, ApJ, 778, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Dialynas, K., Krimigis, S. M., Mitchell, D. G., Decker, R. B., & Roelof, E. C. 2017a, J. Phys. Conf. Ser., 900, 012005 [NASA ADS] [CrossRef] [Google Scholar]
- Dialynas, K., Krimigis, S. M., Mitchell, D. G., Decker, R. B., & Roelof, E. C. 2017b, Nat. Astron., 1, 0115 [NASA ADS] [CrossRef] [Google Scholar]
- Dialynas, K., Krimigis, S. M., Decker, R. B., & Mitchell, D. G. 2019, Geophys. Res. Lett., 46, 7911 [NASA ADS] [CrossRef] [Google Scholar]
- Dialynas, K., Galli, A., Dayeh, M. A., et al. 2020, ApJ, 905, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Dialynas, K., Krimigis, S. M., Decker, R. B., & Hill, M. E. 2021, ApJ, 917, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Dialynas, K., Krimigis, S. M., Decker, R. B., et al. 2022, Space Sci. Rev., 218, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. F., Opher, M., Swisdak, M., & Chamoun, J. N. 2010, ApJ, 709, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Engelmann, J. J., Ferrando, P., Soutoul, A., et al. 1990, A&A, 233, 96 [NASA ADS] [Google Scholar]
- Fahr, H.-J., Fichtner, H., & Scherer, K. 2007, Rev. Geophys., 45, RG4003 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H.-J., Sylla, A., Fichtner, H., & Scherer, K. 2016, J. Geophys. Res.: Space Phys., 121, 8203 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H.-J., Krimigis, S. M., Fichtner, H., et al. 2017, ApJ, 848, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, S. E. S., Potgieter, M. S., & Scherer, K. 2007, J. Geophys. Res. (Space Phys.), 112, A11101 [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2012, Space Sci. Rev., 173, 433 [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2013, ApJ, 776, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Florinski, V. 2015, ApJ, 813, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Funsten, H. O., Allegrini, F., Bochsler, P., et al. 2009, Space Sci. Rev., 146, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Fuselier, S. A., Bochsler, P., Chornay, D., et al. 2009, Space Sci. Rev., 146, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, A., Baliukin, I., Bzowski, M., et al. 2022, Space Sci. Rev., 218, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, A., Wurz, P., Schwadron, N. A., et al. 2016, ApJ, 821, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, A., Wurz, P., Fichtner, H., Futaana, Y., & Barabash, S. 2019, ApJ, 886, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, A., Wurz, P., Schwadron, N. A., et al. 2022, ApJS, submitted [Google Scholar]
- Giacalone, J., Nakanotani, M., Zank, G. P., et al. 2021, ApJ, 911, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Gkioulidou, M., Opher, M., Kornbleuth, M., et al. 2022, ApJ, 931, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., & Kurth, W. S. 2019, Nat. Astron., 3, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., Kurth, W. S., Burlaga, L. F., & Ness, N. F. 2013, Science, 341, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., Kurth, W. S., Stone, E. C., et al. 2021, AJ, 161, 11 [Google Scholar]
- Heerikhuisen, J., Pogorelov, N. V., Florinski, V., Zank, G. P., & le Roux, J. A. 2008, ApJ, 682, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Heerikhuisen, J., Pogorelov, N. V., Zank, G. P., et al. 2010, ApJ, 708, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, M. E., Allen, R. C., Kollmann, P., et al. 2020, ApJ, 905, 69 [Google Scholar]
- Holzer, T. E. 1989, ARA&A, 27, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Husidic, E., Scherer, K., Lazar, M., Fichtner, H., & Poedts, S. 2022, ApJ, 927, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Kleimann, J., Dialynas, K., Fratenale, F., et al. 2022, Space Sci. Rev., in press [Google Scholar]
- Krimigis, S. M., Armstrong, T. P., Axford, W. I., et al. 1977, Space Sci. Rev., 21, 329 [Google Scholar]
- Krimigis, S. M., Mitchell, D. G., Hamilton, D. C., et al. 2004, Space Sci. Rev., 114, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Krimigis, S. M., Mitchell, D. G., Roelof, E. C., Hsieh, K. C., & McComas, D. J. 2009, Science, 326, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Krimigis, S. M., Roelof, E. C., Decker, R. B., & Hill, M. E. 2011, Nature, 474, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Krimigis, S. M., Decker, R. B., Roelof, E. C., et al. 2013, Science, 341, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Krimigis, S. M., Decker, R. B., Roelof, E. C., et al. 2019, Nat. Astron., 3, 997 [Google Scholar]
- Langner, U. W., Potgieter, M. S., Fichtner, H., & Borrmann, T. 2006, J. Geophys. Res. (Space Phys.), 111, A01106 [NASA ADS] [CrossRef] [Google Scholar]
- Lazar, M., & Fichtner, H. 2021, Kappa Distributions, in Astrophysics and Space Science Library, 464 [CrossRef] [Google Scholar]
- Lazarian, A., & Opher, M. 2009, ApJ, 703, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lembège, B., & Yang, Z. 2018, ApJ, 860, 84 [CrossRef] [Google Scholar]
- Lindsay, B. G., & Stebbings, R. F. 2005, J. Geophys. Res. (Space Phys.), 110, A12213 [NASA ADS] [CrossRef] [Google Scholar]
- Livadiotis, G. 2017, Kappa Distributions (Elesevier) [Google Scholar]
- Livadiotis, G., McComas, D. J., Dayeh, M. A., Funsten, H. O., & Schwadron, N. A. 2011, ApJ, 734, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., et al. 2005, J. Geophys. Res. (Space Phys.), 110, A09104 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Ebert, R. W., Elliott, H. A., et al. 2008, Geophys. Res. Lett., 35, 18103 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Allegrini, F., Bochsler, P., et al. 2009, Science, 326, 959 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Alexashov, D., Bzowski, M., et al. 2012, Science, 336, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Angold, N., Elliott, H. A., et al. 2013, ApJ, 779, 2 [Google Scholar]
- McComas, D. J., Allegrini, F., Bzowski, M., et al. 2014, ApJ, 213, 20 [NASA ADS] [Google Scholar]
- McComas, D. J., Zirnstein, E. J., Bzowski, M., et al. 2017, ApJ, 233, 8 [NASA ADS] [Google Scholar]
- McComas, D. J., Dayeh, M. A., Funsten, H. O., et al. 2018, ApJ, 856, L10 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Bzowski, M., Dayeh, M. A., et al. 2020, ApJ, 248, 26 [NASA ADS] [Google Scholar]
- Olbert, S. 1968, in Physics of the Magnetosphere, eds. R. D. L. Carovillano, & J. F. McClay, Astrophys. Space Sci. Lib., 10, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1961, ApJ, 134, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Pesses, M. E., Jokipii, J. R., & Eichler, D. 1981, ApJ, 246, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Rankin, J. S., McComas, D. J., Richardson, J. D., & Schwadron, N. A. 2019, ApJ, 883, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenfeld, D. B., Bzowski, M., Funsten, H. O., et al. 2016, ApJ, 833, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, J. D., & Decker, R. B. 2014, ApJ, 792, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, J. D., & Decker, R. B. 2015, J. Phys. Conf. Ser., 577 [Google Scholar]
- Richardson, J. D., Kasper, J. C., Wang, C., Belcher, J. W., & Lazarus, A. J. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, J. D., Belcher, J. W., Garcia-Galindo, P., & Burlaga, L. F. 2019, Nat. Astron., 3, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Roussos, E., Dialynas, K., Krupp, N., et al. 2020, ApJ, 904, 165 [Google Scholar]
- Scherer, K., & Fichtner, H. 2014, ApJ, 782, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Scherer, K., Fichtner, H., Fahr, H.-J., Bzowski, M., & Ferreira, S. 2014, A&A, 563, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scherer, K., Fichtner, H., & Lazar, M. 2017, Europhys. Lett., 120, 50002 [NASA ADS] [CrossRef] [Google Scholar]
- Scherer, K., Jörg Fahr, H., Fichtner, H., et al. 2018, Ann. Geophys., 36, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Scherer, K., Fichtner, H., Fahr, H. J., & Lazar, M. 2019, ApJ, 881, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Scherer, K., Husidic, E., Lazar, M., & Fichtner, H. 2020, MNRAS, 497, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Schwadron, N. A., Bzowski, M., Crew, G. B., et al. 2009, Science, 326, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Schwadron, N. A., Allegrini, F., Bzowski, M., et al. 2011, ApJ, 731, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Schwadron, N. A., Moebius, E., Fuselier, S. A., et al. 2014, ApJS, 215, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Vogt, R. E., McDonald, F. B., et al. 1977, Space Sci. Rev., 21, 355 [NASA ADS] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2005, Science, 309, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2008, Nature, 454, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2013, Science, 341, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Cummings, A. C., Heikkila, B. C., & Lal, N. 2019, Nat. Astron., 3, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, R. D., Potgieter, M. S., Ferreira, S. E. S., & Hill, M. E. 2010, A&A, 522, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strumik, M., & Ratkiewicz, R. 2022, A&A, 657, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Štverák, Š., Trávníček, P., Maksimovic, M., et al. 2008, J. Geophys. Res. (Space Phys.), 113, A03103 [Google Scholar]
- Swaczyna, P., McComas, D. J., Zirnstein, E. J., et al. 2020, ApJ, 903, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyliunas, V. M. 1968, in Physics of the Magnetosphere, eds. R. D. L. Carovillano, & J. F. McClay, Astrophys. Space Sci. Lib., 10, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Vladimirov, A. E., Digel, S. W., Jóhannesson, G., et al. 2011, Comput. Phys. Commun., 182, 1156 [Google Scholar]
- Wu, Y., Florinski, V., & Guo, X. 2016, ApJ, 832, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P. 2015, ARA&A, 53, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Heerikhuisen, J., Pogorelov, N. V., Burrows, R., & McComas, D. 2010, ApJ, 708, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Hunana, P., Mostafavi, P., et al. 2015, ApJ, 814, 137 [Google Scholar]
- Zhao, L. L., Zank, G. P., Hu, Q., et al. 2019, ApJ, 886, 144 [Google Scholar]
- Zieger, B., Opher, M., Tóth, G., Decker, R. B., & Richardson, J. D. 2015, J. Geophys. Res. (Space Phys.), 120, 7130 [NASA ADS] [CrossRef] [Google Scholar]
- Zirnstein, E. J., & McComas, D. J. 2015, ApJ, 815, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Zirnstein, E. J., Heerikhuisen, J., Zank, G. P., et al. 2017, ApJ, 836, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Zirnstein, E. J., Heerikhuisen, J., McComas, D. J., et al. 2018, ApJ, 859, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Zirnstein, E. J., Kumar, R., Bandyopadhyay, R., et al. 2021, ApJ, 916, L21 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameter for the three fitted RKD distributions and the total number density, pressure, and temperature.
Parameters for the three fitted SKD distributions, and the total number density, pressure and temperature.
All Figures
 |
Fig. 1. Upper left panel: fit with three RKD distribution functions for the period 2009–2012. The yellow dotted line is the fit to the yellow data points, the blue dotted line the fit to the blue marked data points, and the green dotted line the fit to green data points. The red line is the sum of the total distribution |
| In the text | |
 |
Fig. 2. Fit with three SDK distribution functions. Same structure as in Fig. 1. The red line is the sum of all the fitted distributions, which is nearly identically to the yellow line (covered by the red). See the text for further detail. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



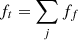
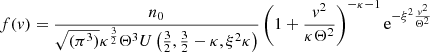
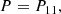
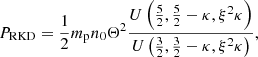
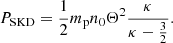
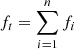
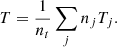
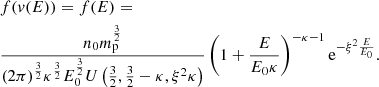
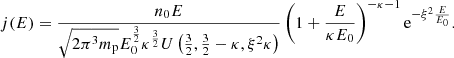
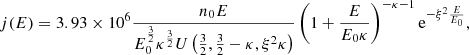
![$$ \begin{aligned} j(E) = \frac{2 n_{\rm e} E}{\pi ^{3/2} m_{\rm e}^2 U_\perp ^3} \frac{\Gamma (\kappa +1)}{\kappa ^{3/2}\Gamma (\kappa -1/2)} \left[ 1+\frac{2 E}{\kappa E_0}\right]^{-\kappa -1}\!. \end{aligned} $$](/articles/aa/full_html/2022/08/aa43449-22/aa43449-22-eq16.gif)