EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 546 (October 2012) A&A, 546 (2012) A36 Full HTML
Free Access
Issue
A&A
Volume 546, October 2012
Article Number A36
Number of page(s) 12
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201219015
Published online 02 October 2012

© ESO, 2012

1. Introduction

Low-mass X-ray binaries (LMXBs) are accreting systems consisting of a low-mass star (≲1 M⊙) transferring mass onto a neutron star or black hole through Roche-lobe overflow. Extensive studies of nearby galaxies with Chandra have confirmed the long-suspected fact that their contribution to X-ray emission in early-type galaxies is substantial (e.g., Irwin et al. 2003; Kim & Fabbiano 2004). Their collective luminosity was found to closely follow the near-infrared light as well as the scaling relation of the LMXB population with the stellar mass obtained (Gilfanov 2004). However, a moderate scatter exists in these relations, suggesting that the specific number (per unit stellar mass) of X-ray binaries is not universally constant among galaxies and that secondary correlations may play a role.

Table 1

The galaxy sample.

Obviously, one of the main candidates for the second-order correlation is the LMXBs with the age of the stellar population. Unlike high-mass X-ray binaries, LMXBs are found both in young and old galaxies. Given that the characteristic time scale for the stellar evolution of the donor star and for the orbital evolution of the binary are both in the Gyrs range, it is not surprising that younger and older galaxies differ in their LMXB content. For example, Kim & Fabbiano (2010) recently reported evidence that younger galaxies may have a higher fraction of bright sources than older ones. On the theoretical side, the population synthesis calculations by Fragos et al. (2008) predict that the formation rate of LMXBs steadily decreases with time after 1 Gyr from the star formation event. This conclusion seems to have been supported by observations: based on the analysis of galaxies detected in the extended Chandra Deep Field South, Lehmer et al. (2007) found that for optically faint early-type galaxies (where LMXBs dominate the X-ray emission), LX/LB increases moderately with redshift over z ~ 0.0−0.5 range. Furthermore, Fragos et al. (2012) calculated the evolution of the specific LMXB luminosity through cosmic time. Their results suggest that the specific luminosity density of LMXBs peaks at z ~ 2.5 and declines towards redshift z = 0. However, there are observational facts that appear to challenge these conclusions. In a S0 galaxy NGC 5102, whose stellar population is younger than 1 Gyr, Kraft et al. (2005) found only two sources brighter than 1037 erg/s, which is three times less than the predicted number of six LMXBs. Bogdán & Gilfanov (2010) reported similar results for two young elliptical galaxies, NGC 3377 and NGC 3585. Admittedly, both studies suffered from relatively low statistical significance of the results and therefore cannot be considered as a final argument. Similarly, the result of Lehmer et al. (2007) was not based on a direct determination of the age of the stellar environment (which was rather inferred from the redshift) and could have been contaminated by other effects (e.g., the rate of galaxy mergers).

It is obvious that more observational effort is needed in order to clarify this issue. The progress in this direction is hampered by the difficulty in reliably determining the age of stellar populations. In addition, a significant fraction of LMXBs in elliptical galaxies reside in globular clusters (GCs) that are dynamically formed in two-body stellar interactions, rather than having a primordial origin. In order to investigate the age effects on the primordial population of LMXBs, GC sources need to be identified and excluded completely from the analysis. To this end, clean and reliable lists of GCs are needed, which are not available for the large number of galaxies required for a statistically meaningful study.

By now, Chandra has observed a large number of galaxies with different morphological types and ages. On the other hand, significant progress has been achieved in the accuracy of age-determination techniques and advanced spectroscopical methods have been applied to a large number of galaxies. This motivated us to undertake a systematic study of the dependence of properties of LMXB populations on stellar age. Among such properties, we consider the specific (per unit stellar mass) number and X-ray luminosity of LMXBs and their luminosity distributions. In our analysis, we will take into account possible contamination by the GC sources to the degree allowed by the available GC data.

The paper is structured as follows: in Sect. 2 we describe our selection criteria and the resulting sample. In Sect. 3 we describe the X-ray and near-infrared data preparation and analysis. In Sect. 4 we discuss average scaling relations for LMXBs and their average XLFs. Dependence of the LMXB numbers and luminosity distribution on stellar age is discussed in Sect. 5. In Sect. 6 we consider the origin of the luminous X-ray sources in early-type galaxies and their dependence on age. In Sect. 8 we discuss caveats and implications of our results. Finally, our results are summarized in Sect. 9.

2. The sample

Our goal was to build the largest possible sample covering the widest possible range of stellar ages. The size of the sample, however, was limited by the content of the Chandra archive and by the published age determinations. Our selection criteria were the following. Firstly we selected all early-type (E/S0) galaxies available in the Chandra archive. We cross-correlated this list with publications on stellar age determinations, leaving only galaxies for which reliable age determinations are available (see below). From the remaining galaxies, we selected only the ones located within the distance of  ~25 Mpc, which ensures a source detection sensitivity of better than 5 × 1037 erg/s in less than 150 ks of Chandra observation. Then we chose massive systems with LK > 5 × 1010 LK, ⊙ to guarantee the presence of a statistically meaningful number of LMXBs ( ≳ 20) above the Chandra sensitivity limit. Finally, we excluded galaxies with ongoing or very recent star formation since the stellar content in such galaxies is likely to be inhomogeneous.

In total, we selected 20 galaxies with the integrated KS-band luminosity in the relatively narrow range from  ~8 × 1010 to 4 × 1011 LK,⊙. The main properties of these galaxies are listed in Table 1. Chandra detection sensitivity (Llim), which is defined as 60% completeness level (Sect. 3.3) of LMXBs in the study field (Sect. 3.1), ranges from  ~4 × 1036 to 1038 erg/s (Table 3). This ensures that there is a statistically meaningful number of compact sources in each galaxy.

Table 2

Stellar age measurements.

2.1. The stellar age

The most accurate and widely used method of age determination of elliptical galaxies is the spectroscopic estimator, which compares observed strength of absorption lines of age-sensitive elements with predictions from the simple stellar population (SSP) synthesis models. A number of such measurements for different galaxy samples are published in the literature, e.g., Trager et al. (2000); Kuntschner et al. (2001); Terlevich & Forbes (2002); Caldwell et al. (2003); Thomas et al. (2005); Denicoló et al. (2005); Sánchez-Blázquez et al. (2006); Annibali et al. (2007); Gallagher et al. (2008). It is known that contamination by gas emission is one of the most important factors affecting the accuracy of age determination. Therefore, for galaxies with more than one measurement, we chose those correcting gas emission in a more rigorous way, and prioritized the age-determination studies in the following order: 1) Annibali et al. (2007); 2) Sánchez-Blázquez et al. (2006); and 3) Terlevich & Forbes (2002). These three papers contain ages for 18 galaxies in our sample. They are summarized in Table 2, where for each galaxy we also list the adopted age. Two galaxies (NGC 3923 and NGC 4125) are not covered by these measurements. We adopted their ages from Thomas et al. (2005) for NGC 3923 and from Schweizer & Seitzer (1992) for NGC 4125.

The accuracy and limitations of age determination and its impact on our results are discussed in Sect. 7.1.

2.2. The GC content

To characterize the GC content of a galaxy, we use the GC specific frequency (SN), which is conventionally defined by the relation SN = NGC100.4(MV + 15) (Harris 1991). As this parameter is sensitive to the assumed distance to the galaxy, the sensitivity limit, and the completeness of the optical data, we collected the most accurate measurements of the total number of GCs (NGC) in our galaxies and then computed SN with the distances used in this paper. For two galaxies, NGC 3585 and NGC 4125, NGC were not available, and we used the local SN from Humphrey (2009) as an approximation of its global value. All values of SN are listed in Table 1, and caveats are discussed in Sect. 7.2.

Table 3

Chandra observations.

3. Data analysis

3.1. Data preparation and source detection

Chandra observations of our sample galaxies are listed in Table 3. We reduced the data following the standard CIAO threads (CIAO version 4.2; CALDB version 4.2.1). We did not exclude time intervals for background flares since the benefit of the increased exposure time outweighs the increased background. The energy range was limited to 0.5 − 8.0 keV. We made exposure maps in this energy range, assuming the single power-law model with Γ = 1.7 under the galactic absorption for each galaxy. To detect point sources, we used CIAO task wavdetect with the parameters adopted from Voss & Gilfanov (2006, 2007). Thresholds were set to 10-6, yielding on average one false detection per 8.2′ × 8.2′ area (106 ACIS pixels).

We corrected the offsets of galaxies with multiple observations following Voss & Gilfanov (2007), by using the point sources detected in each observation within the 4′ radius of the telescope axis. The observations were then shifted using CIAO task reproject_events to match the coordinate system of the reference (marked with an asterisk in Table 3). The images were combined and re-analyzed. We performed wavdetect again on the combined images to finalize the point sources in each galaxy. To avoid the source crowding problem and the bias of the incompleteness of LMXBs in the galaxy center, we excluded the central a = 5″ ellipse region (with the eccentricity and position angle following D25). We define the region outside the central 5″ inside D25 as the study field throughout this paper. The total number of point sources detected in the study field is listed in Table 4.

Table 4

Statistics of point sources in the study field.

To estimate the source counts, we applied circular aperture centered on the central coordinates (output of wavdetect) of each source. We defined the source region as including 85% of the local point spread function (PSF) value. The PSF file was extracted by CIAO task mkpsf from each image, then combined together for multiple observations. The background region was defined as three times the radius of the source region. We excluded the source regions from background regions with overlapping neighboring sources. The source net counts (with the majority in the source region and minority in the background region), and errors were then computed by the Eqs. (1) and (2) in Voss & Gilfanov (2007). To convert the absorbed source count rates into unabsorbed luminosities in 0.5 − 8 keV, we assumed a power-law spectrum (Γ = 1.7) with galactic absorption. We listed the faintest source detected in each galaxy in Table 3 and the total number of point sources above Llim in Table 4.

3.2. Cosmic X-ray background sources

We estimated the cosmic X-ray background (CXB) sources (most of which are background active galactic nucleus (AGN)), using the full band (0.5−10 keV) log(N) − log(S) distribution of CXB sources from Georgakakis et al. (2008) and converted the flux to the 0.5 − 8 keV band, assuming a power-law spectrum with a photon index of 1.4. The total number of CXB sources among all detected point sources and point sources above Llim in the study field are listed in Table 4 (the model was corrected by the incompleteness function of CXB sources derived in Sect. 3.3). In most galaxies, CXB sources contribute less than 15% of the total X-ray population, except for NGC 3379 and NGC 4382, where the contribution is somewhat higher (25−30%), however, essential statistics sustain for the LMXB study. As well known, CXB source density is subject to field-to-field variations due to the cosmic variance. These variations limit the accuracy of the CXB level predictions based on the source counts in selected extragalactic fields to  ~10−30% of the predicted CXB value, depending on the solid angle. As the CXB contribution to the total number of sources is rather small, these uncertainties are relatively unimportant in most of the luminosity range. The situation changes in the bright end of the XLF, where the cosmic variance becomes the major limiting factor in our analysis.

3.3. X-ray incompleteness correction

The detection sensitivity of point sources varies throughout the Chandra images. Reasons include the inhomogeneous level of the diffuse X-ray emission in the galaxy, the deterioration of the PSF at large off-axis angles, and the nonuniform exposure of an image in which observations with different pointings are combined. To calculate the point source detection sensitivity, we used the method and code from Voss & Gilfanov (2006), in which the detection method was inverted using the local PSF, background, and exposure. The incompleteness function K(L) is computed as the fraction of pixels weighted by the assumed spatial distribution of sources, in which detection sensitivity is better (lower value) than the given luminosity. We calculated K(L) separately for the CXB sources and LMXBs, since the CXB sources have a flat distribution, while the field LMXBs are expected to follow the KS-band light (for which we used the 2MASS Large Galaxy Atlas data (Jarrett et al. 2003) – see Sect. 3.4).

To estimate the incompleteness-corrected number of LMXBs in the study field in each galaxy, we did incompleteness correction for the number of all resolved point sources, assuming K(L) for the field LMXBs, and then subtracted the corresponding number of CXB sources. This procedure is described by the equation (1)where 4πD2dNCXB/dL equals dNCXB/dS, which is the log (N) − log (S) distribution of the CXB sources. We listed the total number of LMXBs above Llim, CXB subtracted and incompleteness corrected, in Table 4.

3.4. Near-infrared data analysis

We calculated the stellar mass in the study field from near-infrared data, using the KS (2.16 μm) images from the 2MASS Large Galaxy Atlas (Jarrett et al. 2003) provided by the NASA/IPAC Infrared Science archive. Most images are background subtracted, except for NGC 821, for which we obtained the background from adjacent regions. We also removed the contamination of bright fore/background point sources from images visually. The integrated, point source- and background-subtracted count rate (S) was converted into calibrated magnitudes with mK(mag) = KMAGZP-2.5log (S), where KMAGZP is the zero point magnitude for the KS-band given in the image header. Thus the integrated KS-band luminosity was calculated and then converted to stellar mass with the KS-band mass-to-light ratios (Table 1) derived from Bell & de Jong (2001) and with B − V colors from RC3 catalog (de Vaucouleurs et al. 1991). We list the results in the Table 4.

thumbnail Fig. 1

Observed cumulative distribution of all resolved point sources in all galaxies. The distribution is not corrected for incompleteness or the contribution of CXB sources. The shaded area shows 1σ Poissonian uncertainty. The thick solid and dotted lines show the predicted distribution of CXB sources based on the log (N) − log (S) from Georgakakis et al. (2008) and Moretti et al. (2003), respectively.

4. Average XLF and scaling relations for LMXBs

4.1. XLF of compact sources and the CXB contribution

Figure 1 presents the combined luminosity distribution of all X-ray compact sources detected within the study fields of galaxies and the predicted distribution of the CXB sources. It shows that the CXB contribution is relatively unimportant below log (LX) = 39, where it accounts for approximately 10% of the observed compact sources.

Due to quick declining of the LMXB XLF in the log (LX) ~ 38.5−39 range, an accurate account of the CXB contribution becomes crucial at log (LX) ≳ 39. There is an apparent tail of the observed source counts in this luminosity range, whose slope is similar to the slope of the predicted distribution of CXB sources. Its normalization, however, is somewhat higher than predicted by the CXB log (N) − log (S) from Georgakakis et al. (2008). Quantitatively, we detected 24 sources above 1039 erg/s, while 11.8 background AGN in these fields is predicted, based on Georgakakis et al. (2008). The Poissonian distribution predicts a low probability of  ~1.2 × 10-3 for such a deviation solely due to random fluctuations. We also checked the predictions of the CXB log (N) − log (S) determined by Moretti et al. (2003) and found that they can fully account for the observed bright sources, as shown by the dotted line in Fig. 1. In computing this prediction, we used the soft band (0.5 − 2 keV) counts and converted them to the 0.5−8 keV band, as described in Zhang et al. (2011).

Comparing the two predictions, the following remarks should be made. The more recent work of Georgakakis et al. (2008) is based on a larger sample of sources detected in a larger number of Chandra surveys, and its results are in good agreement with another recent study by Kim et al. (2007). Moreover, converting the soft band flux from Moretti et al. (2003) into 0.5 − 8 keV highly depends on the assumed spectrum of CXB sources, for example, changing the photon index from 1.4 to 1.9 makes  ~1.5 times difference. In addition, the numbers of bright sources detected outside the D25 region of galaxies tends to be in agreement with the prediction of the log (N) − log (S) by Georgakakis et al. (2008) (see below). For these reasons, we decided to accept Georgakakis et al. (2008) as our default CXB model.

thumbnail Fig. 2

Cumulative XLFs of LMXBs in galaxies of our sample. They are CXB subtracted, incompleteness corrected, and normalized to the stellar mass of the host galaxy. They are plotted above corresponding Llim of each galaxy. The solid line is the average XLF of LMXBs in nearby galaxies from Gilfanov (2004).

4.2. Average XLF of LMXBs

The CXB-subtracted and incompleteness-corrected cumulative XLFs of compact X-ray sources in each galaxy are plotted in Fig. 2. As LMXBs are almost the only type of compact X-ray source in early-type galaxies capable of emitting at the log (LX) ≳ 36 luminosity level, the distributions shown in Fig. 2 can be regarded as luminosity functions of LMXBs in these galaxies. The XLFs have been normalized to unit stellar mass in the study field. It is clear that all the XLFs have a similar shape, which is broadly consistent with the average XLF of LMXBs in nearby galaxies obtained by Gilfanov (2004) (plotted with the thick line in the figure). On the other hand, a notable scatter of more than a factor of two exists for the normalization, which is a manifestation of the scatter in the LMXB-stellar mass relation, as discussed below.

To construct combined XLF of all galaxies with different detection sensitivity, we followed the method described in Zhang et al. (2011). The cumulative and differential forms of our XLF are plotted in Fig. 3. We fitted the combined XLF with the template introduced in Gilfanov (2004): (2)where L36 = LX/1036 erg/s and normalizations K1,2,3 are related by: 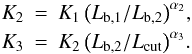The value of the high-luminosity cut-off was fixed at Lcut = 5 × 104. We performed maximum-likelihood fitting to the unbinned data. Our best-fit parameters with 1σ errors are: 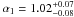, , 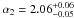, 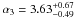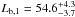and 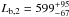. The normalization is K1 = 1.01 ± 0.28 per 1011 M⊙.

thumbnail Fig. 3

Combined luminosity distribution of LMXBs in our sample in cumulative (upper panel) and differential (lower panel) forms. The distributions are CXB subtracted and incompleteness corrected, as described in the text. The shaded area in the upper panel indicates the 1σ Poissonian uncertainty. The solid lines show the best-fit model with two breaks, the dotted lines show the average LMXB XLF from Gilfanov (2004). See Sect. 6 for discussion and caveats of the high-luminosity tail.

The combined XLF obtained in this study is broadly consistent with the average LMXB XLF obtained by Gilfanov (2004) (cf. dotted line in Fig. 3). The XLF of the sources in our sample appears to be somewhat flatter in the bright end of log (LX) ≳ 38.5, having more luminous sources. As evident in Sect. 5.2, this is related to the large fraction of younger galaxies in our sample. Additionally, there is a rather peculiar tail of luminous sources above log (LX) ≳ 39, which will be discussed in Sect. 6.

4.3. Scaling relations for LMXBs

By definition, the present sample is not designed for detailed analysis of scaling relations of LMXBs with stellar mass, since selected galaxies occupy a rather narrow range of masses (less than a factor of  ≲ 7). The XLF analysis presented above suggests that our data is generally consistent with the NX − M∗ and LX − M ∗  dependence obtained previously. This is analyzed below.

thumbnail Fig. 4

Relation of the total number (upper panel) and luminosity (lower panel) of LMXBs in the study field in each galaxy with the stellar mass. The solid lines show the best fittings.

The total numbers and collective luminosities of LMXBs that are more luminous than 5 × 1037 erg/s (after subtracting the CXB contribution and correcting for the incompleteness, Eq. (1)) for all the galaxies are plotted against stellar mass in Fig. 4. The combined XLF of our sample gives the values of NX/M ∗  = 54.3 and LX/M ∗  = 8.5 × 1039 erg/s per 1011 M⊙. The fit to the data of individual galaxies shown in the scatter plots in Fig. 4 gives NX/M ∗  = 66.0 and LX/M ∗  = 9.6 × 1039 erg/s per 1011 M⊙. These values are  ~ 1.4 − 1.7 times larger than those obtained by Gilfanov (2004) (37.8 and 5.8 × 1039 erg/s). This is caused by different age distributions and GC contents of the two samples. The best-fit relations are shown by the solid lines in the plot. The rms deviation of the points from best-fit relations are 0.19 dex for NX and 0.16 dex for LX. The observed scatter is likely caused by the large spread in the galaxy ages and (related to it) variation in the contribution of binaries formed dynamically in GCs. These effects are further discussed in the next section.

thumbnail Fig. 5

Correlation of the XLF normalization, fXLF (Eq. (3)), with stellar age (left) and SN (right). Circles mark galaxies with SN > 2.0 (left panel), and squares mark galaxies with the stellar age  > 6 Gyr (right panel).

5. Dependence on stellar age and GC content

5.1. Correlation of LMXBs with age and GC content of the host galaxy

To characterize the number of LMXBs per unit stellar mass in each galaxy, we used the following quantity 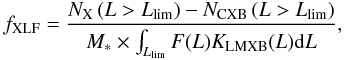(3)where NX(L > Llim) and NCXB(L > Llim) are the numbers of detected X-ray sources and predicted CXB sources (Table 4), F(L) is the best-fit differential XLF normalized to 1011 M⊙, M ∗  is the stellar mass in units of 1011 M⊙, and KLMXB(L) is the incompleteness function of LMXBs in the given galaxy. The so-defined fXLF is the specific (per 1011 M⊙) XLF normalization computed from the number of resolved LMXBs above Llim, assuming the average XLF shape of the resolved sources, modified by the point-source detection incompleteness. For the average XLF, we used the best-fit model from Sect. 4. With this definition, the fXLF equals 1 corresponds to 5.4 LMXBs with luminosity LX > 5 × 1037 erg/s per 1010 M⊙.

Obviously, fXLF has the advantage that all detected X-ray sources above 0.6 incompleteness level are involved in the calculation. The disadvantage is that it relies on the assumption that the XLF shape does not change from galaxy to galaxy. However, it is known that the XLFs of GC and field LMXBs are different (Zhang et al. 2011), as well as the LMXBs in young and old galaxies (Kim & Fabbiano 2010). The systematic bias can be further amplified by the fact that different galaxies have different values of Llim. To investigate the importance of these effects, we computed fXLF for several galaxies using the average XLFs for young and old galaxies (see the next section) and found that they differ by no more than  ~30%. This is insignificant given the scatter of the points and the amplitude of the correlations found below. As a further check, we recomputed fXLF in the luminosity range of 5 × 1037 to 5 × 1038 erg/s where both effects are minimal. We did not find any systematic changes in our results.

We plot fXLF versus stellar age and SN in Fig. 5. Both plots show moderate trends that the fXLF increases with the stellar age of the host galaxy and its GC content. Despite rather large scatter of the points, the Spearman rank-order correlation test gives the null hypothesis probability of p = 0.003 for the age- and much larger value of p = 0.017 for the SN-dependence. These numbers indicate a moderately significant correlation of  ~2.5−3σ.

The correlation of fXLF with SN is similar to the one found in previous studies (e.g., Humphrey & Buote 2008; Boroson et al. 2011). The presence of such correlation was interpreted as evidence suggesting that a significant part (if not all) of the LMXB population, including the field sources, was formed in GCs and subsequently expelled into the field. The existence of the equally strong correlation of the specific LMXB frequency with the age of the stellar population suggests that this interpretation is not unique and the more important correlation may be with the stellar age.

In order to investigate this further, we fit the data with a two-parameter linear model in the form fXLF = a × t + b × SN + c. Using χ2 minimization, we found the following values of best-fit parameters: a = 0.044 ± 0.008, b = 0.049 ± 0.012, c = 0.385 ± 0.047, with a very large value of χ2 = 129.7 for 17 d.o.f. With these best-fit values the contribution of the age term is about two times larger than the contribution of the SN term, suggesting that the more important parameter is the age, rather than the GC content of the host galaxy. However, because of the rather large dispersion of the points and correspondingly large value of χ2, any firm conclusion is premature.

The average values of fXLF for galaxies younger and older than 6 Gyr are 0.75 ± 0.08 and 1.08 ± 0.06, respectively. The statistical significance of the difference between these two values is  ≈ 3.3σ, in agreement with the Spearman test results. The total number of LMXBs per unit stellar mass above 5 × 1037 erg/s in the young galaxy sample is 4.17 ± 0.27, which is  ~2/3 of that in the old (6.27 ± 0.26). The prediction from the average XLF is 5.4.

thumbnail Fig. 6

XLFs of LMXBs in young and old galaxies in cumulative (upper panel) and differential (lower panel) forms. The data for old galaxies (red in the color version of the plot) is marked by circles in the lower panel and is surrounded by the shaded area showing the 1σ Poissonian uncertainty in the upper panel. Statistical uncertainty for young galaxies has comparable amplitude.

thumbnail Fig. 7

XLFs of LMXBs in galaxies with high and low SN (see text for details) in cumulative (upper panel) and differential (lower panel) forms. The data for high-SN galaxies (red in the color version of the plot) is marked by squares in the lower panel and is surrounded by the shaded area showing the 1σ Poissonian uncertainty in the upper panel. Statistical uncertainty for low-SN galaxies has comparable amplitude.

5.2. XLFs of young and old galaxies

In order to investigate the age dependence of the LMXB XLFs, we divided galaxies into young and old groups using their median age (6 Gyr) as a boundary. Each group contains ten galaxies, which are marked correspondingly in Table 2. The study regions in young and old galaxies cover a total solid angle of 125.9 and 251.6 arcmin2 respectively, with a total stellar mass of 1.28 and 1.32 × 1012 M⊙.

We constructed combined XLF of each group and plotted them in Fig. 6. In general, older galaxies have deeper Chandra observations that have reached a sensitivity of  ~5 × 1036 erg/s, while the young group has a sensitivity of  ~3 × 1037 erg/s. The overall shape of the XLF for young galaxies is flatter than that of the old ones. This behavior is in agreement with findings of Kim & Fabbiano (2010).

Similarly, we use the median value of the SN distribution (SN = 2.0) to divide galaxies into GC-rich and GC-poor subgroups. The resulting XLFs are shown in Fig. 7. As expected from the age dependence of the XLF and the general correlation between age and SN, the combined XLF of GC-rich galaxies is steeper than that of the GC-poor ones. However, unlike XLFs of young and old galaxies, they appear to be similar in the bright end log (LX) ≳ 38.5−39.

6. Nature of (ultra-) luminous X-ray sources

After subtracting the contribution of background sources, a rather peculiar tail of luminous sources with log (LX) ≳ 39 remains (Fig. 3). Although the CXB contribution is insignificant throughout most of the luminosity range, its correct subtraction is critical for establishing the nature of bright sources. In total, we detected 24 compact sources with luminosity exceeding 1039 erg/s. Subtracting from this number the 11.8 background AGN predicted from the Georgakakis et al. (2008) CXB log (N) − log (S), we obtain that  ~ 12−13 sources should be associated with galaxies from our sample. Similarly, among sources with LX > 2 × 1039 erg/s (7 sources observed, 4.3 background AGN predicted),  ~2−3 sources are expected to be associated with galaxies. Assuming Poissonian distribution, these numbers correspond to moderately low probabilities of being a result of pure statistical fluctuations:  ~1.2 × 10-3 and 0.14 for the two luminosity ranges, suggesting that the luminous sources may indeed be X-ray binaries.

Table 5

Sources brighter than 1039 erg/s.

On the other hand, it is well known that the CXB source counts produce somewhat different results in different sky fields due to cosmic variance. Moreover, the slope of the bright tail of the luminosity distribution of all compact sources in Fig. 1 is similar to the slope of the CXB log (N) − log (S). It is therefore possible that the tail of bright sources in Fig. 3 is due to background AGN, which is unaccounted for due to cosmic variance. The amplitude of CXB source density variations depends primarily on the considered angular scales and decreases as the solid angle increases. Because we combined data from 20 galaxies distributed over the extragalactic sky, we do not expect cosmic variance to be particularly strong in the combined LMXB XLFs shown in Figs. 3 and 6. In order to investigate this further, we checked the source numbers outside the D25 but within  ~10′ × 10′ around the aim point of the Chandra observation. In total 41 sources with log (LX) > 39 were detected, while the CXB log (N) − log (S) of Georgakakis et al. (2008) predicts 49.8 background AGN. These two numbers are consistent within  ~1.4σ, which suggests that the effect of cosmic variance is not very strong. Moreover, the observed local CXB source density is  ~20% lower than predicted, i.e., in computing the LMXB XLF shown in Fig. 3, the CXB contribution may be somewhat over-subtracted.

Furthermore, we checked the luminous, LX > 1039 erg/s sources individually. In particular, we looked up their identifications in the NASA Extragalactic Database and checked their location relative to the D25 radius of the host galaxy. The results are presented in Table 5. In the table, we list young and old galaxies separately, using as before the median age of 6 Gyr as the boundary. Among the 24 luminous sources, 17 are detected in the young galaxies and 7 in the old ones, with the CXB source predictions being 5.8 and 6.0, respectively. Taken at face value, these numbers suggest that all luminous sources are located in young galaxies. On the other hand, the luminous sources are evenly distributed between GC-rich (12 sources detected, 7.2 background AGN expected) and GC-poor galaxies (12 sources detected, 4.6 background AGN expected).

According to the NED, four of the luminous sources are confirmed background AGN, including the brightest sources with LX ~ 1040 erg/s located in NGC 4374. As expected, this number is significantly smaller than the predicted number of  ≈ 12 AGN, due to incompleteness of the NED. Interestingly, six luminous sources are located in GCs, two of which are in the old galaxy sample. All six sources have luminosities  ~1−2 × 1039 erg/s, which makes them plausible black hole candidates. Both GC sources in NGC 720 were found by Jeltema et al. (2003). Both sources in NGC 4472, (+12:29:42.33, +08:00:07.96) and (+12:29:41.00, +07:57:44.46) were previously reported by Maccarone et al. (2003, 2011), respectively. Of the two sources in NGC 4552, one (+12:35:45.77, +12:33:02.46) was previously known (Xu et al. 2005), while the other (+12:35:41.22, +12:34:51.43) is, to our knowledge, a new identification.

The above analysis suggests that the XLF of compact sources in young galaxy sample extends significantly beyond 1039 erg/s, with the specific frequency of luminous sources  ≈ 8.8 ± 3.2 sources per 1012 M⊙. Although the numbers of detected sources and uncertainties of the CXB subtraction do not allow us to constrain its shape, it appears to be a smooth extension of the LMXB XLF observed at lower luminosities. The luminosities of these sources, up to  ~3−7 × 1039 erg/s, are compatible with, or exceed only slightly, the Eddington limit for a  ~10 M⊙ black hole. We therefore believe that most likely these sources are stellar mass black holes accreting from a low or intermediate mass companion. In the case of an evolved companion, such systems may be transient sources (King et al. 1997; Piro & Bildsten 2002). In order to check this possibility, we investigated the variability of those luminous sources for which multiple observations were available. Although bright sources show significant variability, we did not find any evidence for transient behavior up to a factor of  ~5.

7. Caveats and uncertainties

The accuracy of our conclusions obviously depends on the accuracy of the quantities used to characterize stellar ages and GC content of galaxies. However, both quantities are subject to several, currently unavoidable, uncertainties. In the following subsections, we discuss these uncertainties in detail.

7.1. Stellar age determinations

Stellar age determinations are based on the comparison of the strengths of the absorption lines of age-sensitive elements with predictions from the stellar synthesis models. In the core of their algorithms lies the assumption of SSP. The SSP assumption is an obviously oversimplified picture of the stellar populations in early-type galaxies. This is especially true when the entire galaxy is characterized by a single value of the stellar age. In this case, the problem can be addressed considering the spatially resolved stellar age maps, as discussed below. It is more complicated when a small fraction of the young population is mixed with the older underlying population, thus biasing the SSP-equivalent age towards younger ages (e.g., Salim & Rich 2010; Marino et al. 2011). In this case, more sophisticated assumptions regarding the stellar population content have to be made. At present, such analysis is not available for a sufficiently large number of galaxies for statistically meaningful study. Also, the complexity of the answer obtained in this case would not allow an analysis in terms of simple age-fXLF plots.

More “technical” issues also affect the outcome of age determination in each particular galaxy. These include, for example, differences in the correction for the ionized gas emission, in the selection of absorption lines used for fitting the spectral population models, and in the choice of libraries of stellar population synthesis models (see, e.g., Annibali et al. 2007). As a result, there is a spread of values obtained by different authors that is sometimes rather large. We tried to minimize the effect of these issues by assigning priorities to different age determinations, as described in the Sect. 2.1.

Many of the age measurements analyze the spectrum of the very small central region of the galaxy, usually corresponding to re/8, where re is the effective radius of the galaxy with a typical size of 30′′. As LMXBs are rare objects, their numbers inside re/8 detected in a typical Chandra observation of a typical galaxy are by far too insufficient for any statistically meaningful analysis. On the contrary, to increase their numbers, LMXBs are collected from a region whose size is comparable with the D25 diameter. Moreover, the central region of the size of  ~few arcsec is usually excluded from the X-ray point source analysis in order to exclude from the analysis the central (weak) AGN, peaked diffuse emission, and source confusion. Thus, the LMXBs and age measurements are inevitably performed in geometrically different, sometimes barely overlapping regions of the galaxy. Obviously, such analysis requires an assumption of the homogeneity of the stellar population, which may not be fulfilled in all cases. The statistical study of Tortora et al. (2010) investigated a sample of  ~50 000 nearby galaxies with the Sloan Digital Sky Survey data. Their results show no age gradient for massive early-type galaxies (>1010 M⊙) with a central age older than 6 Gyr, while for the ones with a central age younger than 6 Gyr, age gradients can be as big as ∇age ~ 0.4 (2.5 times difference). Based on the spatially resolved age maps delivered by the SAURON project, Kuntschner et al. (2010) came to a similar conclusion. This result suggests that the ages of old galaxies in our sample should be on average sufficiently reliable, whereas an additional scatter of a factor of  ~2 along the age axis may be possible for younger galaxies. Evidence for such behavior can possibly be seen in Fig. 5.

To investigate this further, we searched for individual studies of the age gradients galaxy by galaxy. The six galaxies included in the SAURON sample (NGC 821, NGC 3379, NGC 4278, NGC 4374, NGC 4382, and NGC 4552) do not have significant age gradients. Based on the long-slit spectroscopy results, we found evidence for complicated age structure in the following galaxies. NGC 720 was suggested to have been formed by a merger of an old (5−13 Gyr) small-scale spheroid and a younger (2.5−5 Gyr) large-scale disk component (Rembold et al. 2005), meaning that the average stellar age of NGC 720 should be older than 3 Gyr value adopted in this paper. NGC 4125 was found to have experienced a recent merger event: thus young stellar components likely exist in this galaxy (Pu et al. 2010). NGC 4365 is likely to be older than 7.9 Gyr, as the results of Davies et al. (2001) suggest that the decoupled core and the main body of the galaxy have the same age of  ~14 Gyr. With these numbers, the data points for NGC 720 and NGC 4365 should shift to the right in the left-hand panel of Fig. 5, while NGC 4125 may shift to the left. Such a correction will reduce the scatter on this plot. No such detailed studies could be found for other galaxies from our sample. This analysis confirms that at least a part of the scatter on the age – fXLF plot is due to complexities of the age structure of the early-type galaxies.

The above discussion suggests a promising venue for future studies, based on the comparison of the spatial distribution of compact sources with spatially resolved stellar age maps. This is similar to the analysis conducted by Shtykovskiy & Gilfanov (2007) for high-mass X-ray binaries, based on the comparison of their spatial distribution with spatially resolved star-formation history in the Small Magellanic Cloud. The outcome of such an analysis would be the full-time dependence of the LMXB population passed from the star-formation event.

7.2. Specific frequency of GCs SN

The main complication in determining the GC content is the lack of uniform optical data suitable for this purpose, in particular individual GC lists for all galaxies. For this reason, we had to rely on the published total numbers of GC candidates detected in each galaxy to calculate the SN. Since LMXBs are collected from the D25 region of each galaxy, GCs in the same region should be counted. However, published numbers often referred to different regions. For example, the HST data typically covered regions smaller than D25, while the data from ground-based telescopes often had a larger field of view. Because we compute V-band luminosity for the same region where GCs are counted, this would not matter if the spatial distribution of GCs followed that of stellar light. However, GCs are known to have a broader distribution than stars (Bassino et al. 2006), so the value of SN depends on the spatial region over which it was computed. For example, the SN values measured from the HST data (e.g., Humphrey 2009; Peng et al. 2008) is on average smaller than the ones determined by the ground-based telescopes (see references in Table 1).

The picture is further complicated by the fact that red (metal-rich) GCs are more concentrated toward the galaxy centers, more accurately tracing the stellar population, while the blue (metal-poor) GCs are often more extended (e.g., Bassino et al. 2006). Since there are approximately three times as many LMXBs in red GCs as in blue GCs (e.g., Bellazzini et al. 1995), an accurate selection of the spatial regions and, ideally, a separation of the red and blue GCs are important.

thumbnail Fig. 8

Correlation of SN with stellar age. Filled circles mark galaxies with larger fXLF.

Our ability to take these complications into account is limited due to the lack of uniform optical data for the GC systems in the galaxies in our sample. These complications introduce scatter in our data, which currently cannot be eliminated.

7.3. Correlation between stellar age and SN

In our sample, there is a strong correlation between stellar age and SN, as illustrated by Fig. 8. Although we did not find any report about such a correlation in the literature, its existence is not surprising because more GCs are expected to be found in older galaxies as a result of more massive GCs being formed in larger star bursts at larger redshifts (Bastian 2008). A significant fraction of these GCs will survive through the following evolution of the galaxy (Fall & Zhang 2001). A detailed investigation of the behavior of SN and its dependence on the environment and formation history of the host galaxy is beyond the scope of this paper. However, presence of the SN-age correlation (at least in our sample) significantly complicates the separation of the effects of these two factors on the LMXB population.

7.4. Conclusion

There are a number of uncertainties associated with measurements of stellar age and SN. Many of these, for example, age gradients, can be alleviated in principle with more sophisticated analysis of the optical data, e.g., with spatially resolved stellar age maps. On the other hand, proper use of the improved optical data would require better statistics in the X-ray data. Indeed, as one can see from Fig. 5, the vertical error bars, which are determined by the accuracy of the X-ray data, are often nearly as big as the uncertainties in the stellar ages. This requires dedicated effort in collecting optical and X-ray data of adequate quality for sufficiently large numbers of galaxies to allow statistically meaningful analysis. Further progress may be possible by comparing the spatial distributions of X-ray sources with the SAURON stellar age maps (cf. Shtykovskiy & Gilfanov 2007). Other deficiencies, for example, the failure of the SSP assumption in regions with complex age content, require different data analysis approaches to be considered.

In the present paper, we used the currently available data and a somewhat simplistic approach, in the spirit of the SSP assumption, to investigate for the first time the sign and the amplitude of the secular evolution of LMXB populations with cosmic time. Obviously, the age and SN uncertainties affect the appearance of the data points in the age-fXLF and SN–fXLF planes and contribute to their dispersion. However, the fact that we detect statistically significant correlations between parameters of interest suggests that the uncertainties do not completely wash out the effects of the age and GC content on the population of LMXBs in galaxies. This is further supported by the correlation between SN and stellar age, as the errors in these quantities are uncorrelated.

8. Discussion

8.1. GCs vs. stellar age

The dependence of the LMXB population on stellar age and GC content cannot be easily separated due to the existence of a strong correlation between these two parameters in our sample. Results of the linear regression analysis suggest that about  ~2/3 of the amplitude of the fXLF variation is due to stellar age dependence and  ~1/3 is caused by changing GC content. However, because of the large scatter of the points and corresponding very large value of the χ2, this result should be interpreted with caution and any firm conclusion would be premature.

The X-ray binaries dynamically formed in GCs can reside in their parent clusters or be expelled into the field, either due to kicks and/or tidal interactions or during the destruction of the parent cluster. The former could in principle be identified and removed from the sample, provided that clean and complete GC lists are available. This, however, is not possible due to limitations of the GC data. A significant part of which was obtained by the ground-based facilities and suffers from incompleteness and foreground star contamination. Although HST data is available for a number of galaxies, it also has limited completeness. Besides, in the luminosity range of interest, X-ray sources in GCs do not account for more than  ~30−40% of the LMXB population (Zhang et al. 2011), which is hardly sufficient to explain the amplitude of the observed dependence (right-hand panel in Fig. 5). The contribution of binaries that are dynamically formed in GCs and expelled into the field is unclear. Based on the correlations of the specific frequency of LMXBs with that of GCs, it has been argued that the entire population of LMXBs has been formed dynamically in GCs (e.g., White et al. 2002). Our results, however, suggest that an important factor is the evolution of the LMXB population with time. Part of the correlation of the specific frequency of LMXBs with that of GCs is real, due to the contribution of sources formed dynamically (and mostly retained) in GC. Another part is, however, an artifact of the dependence of the GC content on the age of the galaxy.

The importance of age dependence is further supported by the comparison of the XLF of young and old galaxies (Fig. 6). Zhang et al. (2011) have shown that the XLF of GC sources in the log (LX) ≳ 37 luminosity range is flatter than that of the field sources (see, e.g., their Fig. 7). Therefore, as older galaxies have larger GC content, i.e., a larger fraction of dynamically formed binaries, their XLF should be expected to be flatter than the XLF of the young galaxy sample, if the main increase is due to the dynamically formed sources. This prediction is at odds with our observations: the XLF of old galaxies is steeper than that of the young galaxies (see also Kim & Fabbiano 2010). This suggests that the effects of the evolution of the LMXB population are at least comparable to the effect of the increased GC content, if not stronger.

8.2. Comparison with Fragos et al. calculations

Our results appear to be at odds with the population synthesis calculations of Fragos et al. (2008), who predicted a significant decrease of the LMXB population with time. In particular, they predict more than an order of magnitude decrease of the number of LMXBs in the age interval from 5.5 Gyr to 9.5 Gyr. Their prediction includes the log (LX) ≳ 37.5 luminosity range, well covered by the Chandra data used here, so that such a significant change in the specific number of sources would clearly reveal itself in our analysis. This is illustrated, for example, by the comparison of our Fig. 6 with the Fig. 3 in Fragos et al. (2008). Along the same lines, in more recent calculations Fragos et al. (2012) considered the overall evolution of the X-ray binary populations with cosmic time and came to a similar conclusion: that the specific luminosity of LMXBs per unit stellar mass in the Universe is decreasing by about an order of magnitude between the redshift z = 1 and z = 0.

The reason for this discrepancy is not clear. On the one hand, the Fragos et al. calculations consider primordial binaries only and do not include dynamically formed systems in GCs. Therefore, their results could be reconciled with our observations if one assumed that the absolute majority of LMXBs are of dynamical origin. Quantitatively, in order to allow more than a ten-fold decrease in the numbers of primordial LMXBs between 5.5 and 9.5 Gyr and still be compatible with our observations, the contribution of primordial systems should be less than a few per cent in the  ~ 10 Gyr old galaxies. This would also imply that, on average, dynamically formed LMXBs contribute  ≳ 95 − 99% to the LMXB population at the redshift z = 0. We consider this possibility unlikely because it would contradict the evidence presented in this paper and in other studies (e.g., Juett 2005; Kundu et al. 2007; Voss et al. 2009; Zhang et al. 2011).

Another important caveat is that Fragos et al. (2008) considered coeval stellar populations. Similar considerations complicate stellar age determinations, so the discussion of Sect. 7.1 applies here fully. Quantitatively, however, significant deviations from the SSP assumption in galaxies with young SSP ages would be required in order to account for the observed discrepancy between theory and our observations. Indeed, the single-starburst calculations by Fragos et al. (2012, in Fig. 2) predict a  ≈ 100-fold decrease in the specific LMXB luminosity between 2 and 10 Gyr. Such a drop in the LMXB populations can be reconciled with our results only by assuming that the fraction of young stars in galaxies with the youngest SSP ages (e.g., NGC 4382 − 1.6 Gyr and NGC 5866 − 1.8 Gyr) is actually rather small,  ≲ 10-2. Detailed data about the star-formation history and stellar age structure of galaxies with young SSP ages is needed in order to see if this possibility is feasible.

9. Summary

The main goal of this paper was to study the dependence of the population of LMXBs on stellar age. To this end, we collected 20 nearby early-type galaxies, which were observed by Chandra to sufficient depth, and had the stellar age measured.

  • 1.

    We found that older galaxies tend to hostmore LMXBs per unit stellar mass than youngerones (Fig. 5). The correlation has large scatter,with the points occupying the dynamical range by a factorof 4. When averaged over young (t < 6 Gyr) and old (t > 6 Gyr) subsamples, the specific frequency of LMXBs with LX > 5 × 1037 erg/s varies from 4.17 ± 0.27 to 6.27 ± 0.26 per 1010 M⊙. Interpretation of this dependence is complicated by the rather strong correlation between the GC content of the galaxy and its stellar age. We presented evidence suggesting that an important factor is the intrinsic evolution of the populations of LMXBs with time. Its effect is enhanced by the larger GC content of older galaxies, resulting in larger numbers of dynamically formed binaries in them.

  • 2.

    Our results appear to challenge recent population synthesis calculations by Fragos et al. (2008, 2012), predicting a more than  ~ten-fold decrease of the primordial LMXB population between  ~5.5 and 9.5 Gyr (a hundred-fold decrease between 2 and 10 Gyr). This discrepancy can be understood under rather extreme assumptions about the contribution of the dynamically formed LMXBs and/or the fraction of truly young stellar populations in the galaxies with young SSP ages. The caveats to the comparison of our data with calculations of Fragos et al. (2008, 2012) are discussed in Sect. 8.2.

  • 3.

    There is clear evolution of the XLF with age: the one of older galaxies is steeper in the entire studied luminosity range, log (LX) ≳ 37.5, than the one of younger galaxies (Fig. 6). A similar result was also reported by Kim & Fabbiano (2010).

  • 4.

    Young galaxies host a significant population of (ultra-) luminous X-ray sources with luminosity exceeding 1039 erg/s. We estimate their specific frequency of  ≈8.8 ± 3.2 sources per 1012 M⊙ in the young subsample. Such sources are significantly less frequent in the old subsample (≈1 source against  ≈ 7), with the 90% upper limit of  ≈ 2.9 sources per 1012 M⊙

  • 5.

    As a byproduct of this study, we compiled a list of six black hole candidates in GCs, of which five were previously known and one is identified for the first time (Table 5).

Acknowledgments

This research made use of Chandra archival data provided by Chandra X-ray Center and the 2MASS Large Galaxy Atlas data provided by NASA/IPAC infrared science archive. Ákos Bogdán acknowledges support provided by NASA through Einstein Postdoctoral Fellowship grant number PF1-120081 awarded by the Chandra X-ray Center, which is operated by the Smithsonian Astrophysical Observatory for NASA under contract NAS8-03060. We also wish to thank Rasmus Voss, Andrew Cooper, Diederik Kruijssen, Junhua Gu, and Jingying Wang for the discussions which have greatly improved the quality of this paper.

References

  1. Annibali, F., Bressan, A., Rampazzo, R., Zeilinger, W. W., & Danese, L. 2007, A&A, 463, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bassino, L. P., Faifer, F. R., Forte, J. C., et al. 2006, A&A, 451, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bastian, N. 2008, MNRAS, 390, 759 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bellazzini, M., Pasquali, A., Federici, L., Ferraro, F. R., & Pecci, F. F. 1995, ApJ, 439, 687 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bogdán, Á., & Gilfanov, M. 2010, A&A, 512, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Boroson, B., Kim, D.-W., & Fabbiano, G. 2011, ApJ, 729, 12 [NASA ADS] [CrossRef] [Google Scholar]
  8. Caldwell, N., Rose, J. A., & Concannon, K. D. 2003, AJ, 125, 2891 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cantiello, M., Blakeslee, J. P., & Raimondo, G. 2007, ApJ, 668, 209 [NASA ADS] [CrossRef] [Google Scholar]
  10. Davies, R. L., Kuntschner, H., Emsellem, E., et al. 2001, ApJ, 548, L33 [NASA ADS] [CrossRef] [Google Scholar]
  11. de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (Springer) [Google Scholar]
  12. Denicoló, G., Terlevich, R., Terlevich, E., Forbes, D. A., & Terlevich, A. 2005, MNRAS, 358, 813 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  14. Dirsch, B. 1996, Master’s Thesis, Master Thesis, University of Bonn [Google Scholar]
  15. Dirsch, B., Schuberth, Y., & Richtler, T. 2005, A&A, 433, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Fall, S. M., & Zhang, Q. 2001, ApJ, 561, 751 [NASA ADS] [CrossRef] [Google Scholar]
  17. Forbes, D. A. 1996, AJ, 112, 954 [NASA ADS] [CrossRef] [Google Scholar]
  18. Forbes, D. A., Grillmair, C. J., Williger, G. M., Elson, R. A. W., & Brodie, J. P. 1998, MNRAS, 293, 325 [NASA ADS] [CrossRef] [Google Scholar]
  19. Forbes, D. A., Georgakakis, A. E., & Brodie, J. P. 2001, MNRAS, 325, 1431 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fragos, T., Kalogera, V., Belczynski, K., et al. 2008, ApJ, 683, 346 [NASA ADS] [CrossRef] [Google Scholar]
  21. Fragos, T., Lehmer, B., Tremmel, M., et al. 2012, ApJ, submitted [arXiv:1206.2395] [Google Scholar]
  22. Gallagher, J. S., Garnavich, P. M., Caldwell, N., et al. 2008, ApJ, 685, 752 [NASA ADS] [CrossRef] [Google Scholar]
  23. Georgakakis, A., Nandra, K., Laird, E. S., Aird, J., & Trichas, M. 2008, MNRAS, 388, 1205 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gilfanov, M. 2004, MNRAS, 349, 146 [NASA ADS] [CrossRef] [Google Scholar]
  25. Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef] [Google Scholar]
  26. Humphrey, P. J. 2009, ApJ, 690, 512 [NASA ADS] [CrossRef] [Google Scholar]
  27. Humphrey, P. J., & Buote, D. A. 2008, ApJ, 689, 983 [NASA ADS] [CrossRef] [Google Scholar]
  28. Irwin, J. A., Athey, A. E., & Bregman, J. N. 2003, ApJ, 587, 356 [NASA ADS] [CrossRef] [Google Scholar]
  29. Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
  30. Jeltema, T. E., Canizares, C. R., Buote, D. A., & Garmire, G. P. 2003, ApJ, 585, 756 [NASA ADS] [CrossRef] [Google Scholar]
  31. Juett, A. M. 2005, ApJ, 621, L25 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kim, D.-W., & Fabbiano, G. 2004, in BAAS, Amer. Astron. Soc. Meeting Abstracts #204, 36, 751 [Google Scholar]
  33. Kim, D.-W., & Fabbiano, G. 2010, ApJ, 721, 1523 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kim, M., Wilkes, B. J., Kim, D.-W., et al. 2007, ApJ, 659, 29 [Google Scholar]
  35. King, A. R., Frank, J., Kolb, U., & Ritter, H. 1997, ApJ, 484, 844 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kissler-Patig, M., Richtler, T., & Hilker, M. 1996, A&A, 308, 704 [NASA ADS] [Google Scholar]
  37. Kissler-Patig, M., Richtler, T., Storm, J., & della Valle, M. 1997, A&A, 327, 503 [NASA ADS] [Google Scholar]
  38. Kraft, R. P., Nolan, L. A., Ponman, T. J., Jones, C., & Raychaudhury, S. 2005, ApJ, 625, 785 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kundu, A., Maccarone, T. J., & Zepf, S. E. 2007, ApJ, 662, 525 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kuntschner, H., Lucey, J. R., Smith, R. J., Hudson, M. J., & Davies, R. L. 2001, MNRAS, 323, 615 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kuntschner, H., Emsellem, E., Bacon, R., et al. 2010, MNRAS, 408, 97 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lehmer, B. D., Brandt, W. N., Alexander, D. M., et al. 2007, ApJ, 657, 681 [NASA ADS] [CrossRef] [Google Scholar]
  43. Maccarone, T. J., Kundu, A., & Zepf, S. E. 2003, ApJ, 586, 814 [NASA ADS] [CrossRef] [Google Scholar]
  44. Maccarone, T. J., Kundu, A., Zepf, S. E., & Rhode, K. L. 2011, MNRAS, 410, 1655 [NASA ADS] [Google Scholar]
  45. Marino, A., Rampazzo, R., Bianchi, L., et al. 2011, MNRAS, 411, 311 [NASA ADS] [CrossRef] [Google Scholar]
  46. Moretti, A., Campana, S., Lazzati, D., & Tagliaferri, G. 2003, ApJ, 588, 696 [NASA ADS] [CrossRef] [Google Scholar]
  47. Peng, E. W., Jordán, A., Côté, P., et al. 2008, ApJ, 681, 197 [NASA ADS] [CrossRef] [Google Scholar]
  48. Piro, A. L., & Bildsten, L. 2002, ApJ, 571, L103 [NASA ADS] [CrossRef] [Google Scholar]
  49. Pu, S. B., Saglia, R. P., Fabricius, M. H., et al. 2010, A&A, 516, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Rembold, S. B., Pastoriza, M. G., & Bruzual, G. 2005, A&A, 436, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Rhode, K. L., & Zepf, S. E. 2004, AJ, 127, 302 [NASA ADS] [CrossRef] [Google Scholar]
  52. Salim, S., & Rich, R. M. 2010, ApJ, 714, L290 [NASA ADS] [CrossRef] [Google Scholar]
  53. Sánchez-Blázquez, P., Gorgas, J., Cardiel, N., & González, J. J. 2006, A&A, 457, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Schweizer, F., & Seitzer, P. 1992, AJ, 104, 1039 [NASA ADS] [CrossRef] [Google Scholar]
  55. Shtykovskiy, P. E., & Gilfanov, M. R. 2007, Astron. Lett., 33, 437 [NASA ADS] [CrossRef] [Google Scholar]
  56. Sikkema, G., Peletier, R. F., Carter, D., Valentijn, E. A., & Balcells, M. 2006, A&A, 458, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Spitler, L. R., Forbes, D. A., Strader, J., Brodie, J. P., & Gallagher, J. S. 2008, MNRAS, 385, 361 [NASA ADS] [CrossRef] [Google Scholar]
  58. Terlevich, A. I., & Forbes, D. A. 2002, MNRAS, 330, 547 [NASA ADS] [CrossRef] [Google Scholar]
  59. Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
  60. Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [NASA ADS] [CrossRef] [Google Scholar]
  61. Tortora, C., Napolitano, N. R., Cardone, V. F., et al. 2010, MNRAS, 407, 144 [NASA ADS] [CrossRef] [Google Scholar]
  62. Trager, S. C., Faber, S. M., Worthey, G., & González, J. J. 2000, AJ, 119, 1645 [NASA ADS] [CrossRef] [Google Scholar]
  63. Voss, R., & Gilfanov, M. 2006, A&A, 447, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Voss, R., & Gilfanov, M. 2007, A&A, 468, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Voss, R., Gilfanov, M., Sivakoff, G. R., et al. 2009, ApJ, 701, 471 [Google Scholar]
  66. White, III, R. E., Sarazin, C. L., & Kulkarni, S. R. 2002, ApJ, 571, L23 [NASA ADS] [CrossRef] [Google Scholar]
  67. Xu, Y., Xu, H., Zhang, Z., et al. 2005, ApJ, 631, 809 [NASA ADS] [CrossRef] [Google Scholar]
  68. Zhang, Z., Gilfanov, M., Voss, R., et al. 2011, A&A, 533, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

The galaxy sample.

In the text
Table 2

Stellar age measurements.

In the text
Table 3

Chandra observations.

In the text
Table 4

Statistics of point sources in the study field.

In the text
Table 5

Sources brighter than 1039 erg/s.

In the text

All Figures

thumbnail Fig. 1

Observed cumulative distribution of all resolved point sources in all galaxies. The distribution is not corrected for incompleteness or the contribution of CXB sources. The shaded area shows 1σ Poissonian uncertainty. The thick solid and dotted lines show the predicted distribution of CXB sources based on the log (N) − log (S) from Georgakakis et al. (2008) and Moretti et al. (2003), respectively.
In the text
thumbnail Fig. 2

Cumulative XLFs of LMXBs in galaxies of our sample. They are CXB subtracted, incompleteness corrected, and normalized to the stellar mass of the host galaxy. They are plotted above corresponding Llim of each galaxy. The solid line is the average XLF of LMXBs in nearby galaxies from Gilfanov (2004).
In the text
thumbnail Fig. 3

Combined luminosity distribution of LMXBs in our sample in cumulative (upper panel) and differential (lower panel) forms. The distributions are CXB subtracted and incompleteness corrected, as described in the text. The shaded area in the upper panel indicates the 1σ Poissonian uncertainty. The solid lines show the best-fit model with two breaks, the dotted lines show the average LMXB XLF from Gilfanov (2004). See Sect. 6 for discussion and caveats of the high-luminosity tail.
In the text
thumbnail Fig. 4

Relation of the total number (upper panel) and luminosity (lower panel) of LMXBs in the study field in each galaxy with the stellar mass. The solid lines show the best fittings.
In the text
thumbnail Fig. 5

Correlation of the XLF normalization, fXLF (Eq. (3)), with stellar age (left) and SN (right). Circles mark galaxies with SN > 2.0 (left panel), and squares mark galaxies with the stellar age  > 6 Gyr (right panel).
In the text
thumbnail Fig. 6

XLFs of LMXBs in young and old galaxies in cumulative (upper panel) and differential (lower panel) forms. The data for old galaxies (red in the color version of the plot) is marked by circles in the lower panel and is surrounded by the shaded area showing the 1σ Poissonian uncertainty in the upper panel. Statistical uncertainty for young galaxies has comparable amplitude.
In the text
thumbnail Fig. 7

XLFs of LMXBs in galaxies with high and low SN (see text for details) in cumulative (upper panel) and differential (lower panel) forms. The data for high-SN galaxies (red in the color version of the plot) is marked by squares in the lower panel and is surrounded by the shaded area showing the 1σ Poissonian uncertainty in the upper panel. Statistical uncertainty for low-SN galaxies has comparable amplitude.
In the text
thumbnail Fig. 8

Correlation of SN with stellar age. Filled circles mark galaxies with larger fXLF.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.