| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219006 | |
| Published online | 05 October 2012 | |
Impact of orbital motion on the structure and stability of adiabatic shocks in colliding wind binaries⋆
1
UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de
Grenoble (IPAG) UMR 5274,
38041
Grenoble,
France
e-mail: astrid.lamberts@obs.ujf-grenoble.fr
2
Laboratoire AIM, CEA/DSM – CNRS – Université Paris 7, Irfu/Service
d’Astrophysique, CEA-Saclay, 91191
Gif-sur-Yvette,
France
Received:
9
February
2012
Accepted:
26
June
2012
Context. The collision of winds from massive stars in binaries results in the formation of a double-shock structure with observed signatures from radio to X-rays.
Aims. We study the structure and stability of the colliding wind region as it turns into a spiral owing to the orbital motion. We focus on adiabatic winds, where mixing between the two winds is expected to be restricted to the Kelvin-Helmholtz instability. Mixing of the Wolf-Rayet wind with hydrogen-rich material is important for dust formation in pinwheel nebulae such as WR 104, where the spiral structure has been resolved in infrared.
Methods. We use the hydrodynamical code RAMSES to solve the equations of hydrodynamics on an adaptive grid. A wide range of binary systems with different wind velocities and mass-loss rates are studied with two-dimensional simulations. A specific three-dimensional simulation is performed to model WR 104.
Results. Orbital motion leads to the formation of two distinct spiral arms where the Kelvin-Helmholtz instability develops differently. We find that the spiral structure is destroyed when there is a large velocity gradient between the winds, unless the collimated wind is much faster. We argue that the Kelvin-Helmholtz instability plays a major role in determining whether the structure is maintained. We discuss the consequences for various colliding-wind binaries. When their spiral structure is stable, there is no straightforward relationship between the spatial step of the spiral, the wind velocities, and the orbital period. Our 3D simulation of WR 104 indicates that the colder, well-mixed trailing arm has more favourable conditions for dust formation than the leading arm. The single-arm infrared spiral follows more closely the mixing map than the density map, suggesting that the dust-to-gas ratio may vary between the leading and trailing density spirals. However, the density is much lower than what dust formation models require. Including radiative cooling would lead to higher densities, and also to thin shell instabilities whose impact on the large-scale structure remains unknown.
Key words: instabilities / binaries: general / stars: individual: WR 104 / stars: winds, outflows / hydrodynamics
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
During the main-sequence and Wolf-Rayet (WR) phase, massive stars possess highly supersonic
winds due to radiation pressure on atomic lines. Wind mass-loss rates range from
Ṁ ≃ 10-8 M⊙ yr-1
for O or B type stars to
Ṁ ≃ 10-4 M⊙ yr-1
for Wolf-Rayet stars (Puls et al. 2008). Many massive
stars lie in binary systems, although the binary fraction differs from one stellar cluster
to another: Kobulnicky & Fryer (2007) give a
binary fraction of 70% for the OB2 cluster, while Ritchie
et al. (2009) give a binary fraction of at least 30% in the Westerlund I cluster.
In binary systems, the interaction of the two supersonic stellar winds creates two strong
shocks separated by a contact discontinuity. First of all, the geometry of the colliding
wind region depends on the momentum-flux ratio of the winds (Lebedev & Myasnikov 1990) 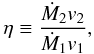 (1)where v is
the wind velocity. The subscript 1 usually stands for the stronger wind, and the subscript 2
for the weaker one so that η ≤ 1. There are several important observational
signatures of the colliding wind region. The shock-heated gas generates observable thermal
X-ray emission (e.g. Cherepashchuk 1976; Luo et al. 1990; Usov
1992; Stevens et al. 1992). The presence of
intra-binary structures causes variations in the emission line profiles with orbital phase
(e.g. Shore & Brown 1988; Wiggs & Gies 1993). The high densities reached in
the colliding wind region are thought to enable the formation of dust, explaining the large
infrared emission from binary systems with WR stars (Williams et al. 1987; Usov 1991), and the
formation of spiral structures extending to distances of up to 300 times the binary
separation (“pinwheel nebulae”, Tuthill et al. 1999).
In some systems, the diffusive shock acceleration of particles leads to non-thermal radio
emission (Dougherty & Williams 2000; see
De Becker 2007, for a review). The radio emission
has been resolved by long-baseline interferometry and shown to have a morphology changing
with orbital phase (e.g. Dougherty et al. 2005). A
new exotic class of colliding wind binaries is gamma-ray binaries, where the non-thermal
emission is thought to arise from the interaction of a pulsar relativistic wind with the
wind of its massive stellar companion (Dubus 2006).
Interpreting all these observational data requires increasingly detailed knowledge of the
physics of colliding winds, hence numerical simulations, notably of the large-scale regions
that can be resolved in radio or infrared.
(1)where v is
the wind velocity. The subscript 1 usually stands for the stronger wind, and the subscript 2
for the weaker one so that η ≤ 1. There are several important observational
signatures of the colliding wind region. The shock-heated gas generates observable thermal
X-ray emission (e.g. Cherepashchuk 1976; Luo et al. 1990; Usov
1992; Stevens et al. 1992). The presence of
intra-binary structures causes variations in the emission line profiles with orbital phase
(e.g. Shore & Brown 1988; Wiggs & Gies 1993). The high densities reached in
the colliding wind region are thought to enable the formation of dust, explaining the large
infrared emission from binary systems with WR stars (Williams et al. 1987; Usov 1991), and the
formation of spiral structures extending to distances of up to 300 times the binary
separation (“pinwheel nebulae”, Tuthill et al. 1999).
In some systems, the diffusive shock acceleration of particles leads to non-thermal radio
emission (Dougherty & Williams 2000; see
De Becker 2007, for a review). The radio emission
has been resolved by long-baseline interferometry and shown to have a morphology changing
with orbital phase (e.g. Dougherty et al. 2005). A
new exotic class of colliding wind binaries is gamma-ray binaries, where the non-thermal
emission is thought to arise from the interaction of a pulsar relativistic wind with the
wind of its massive stellar companion (Dubus 2006).
Interpreting all these observational data requires increasingly detailed knowledge of the
physics of colliding winds, hence numerical simulations, notably of the large-scale regions
that can be resolved in radio or infrared.
On large scales, orbital motion is expected to turn the shock structure into a spiral,
although we show that this is not always true. Orbital motion breaks the symmetry with
respect to the binary axis and no analytic solution predicts the detailed structure of the
colliding wind region. Material in the spiral is generally assumed to behave ballistically,
so that the step of the spiral is the wind velocity v times the orbital
period Porb. The wind velocity to use is unclear. Tuthill et al. (2008) took the speed of the dominant wind
v1 (dominant in the sense that
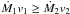 ),
whereas Parkin & Pittard (2008) assumed that
it is the slower wind that determines the step of the spiral but focus their study on
binaries with equal wind velocities. Simple dynamical models of the shocked layer have been
developed for use with radiative transfer codes, assuming that the double shock structure is
infinitely thin (thin shell hypothesis) and that the material is ballistic (Harries et al. 2004; Parkin & Pittard 2008). The spiral structure is then reproduced at small
computational cost but this neglects the impact of the pressure, which creates a distinction
between both arms of the spiral (Lemaster et al.
2007; Pittard 2009; van Marle et al. 2011), the influence of the reconfinement of the weaker
wind for small η (Lamberts et al.
2011), and the large-scale evolution of instabilities in the colliding wind region
(see below). Walder & Folini (2003) provide
the first large-scale three-dimensional simulation showing a few spiral steps. The
resolution in the simulation is too low to model instabilities. Okazaki et al. (2008) and Parkin et al.
(2011) both present a three-dimensional simulation of η Carinae
showing instabilities at the wind interface, using respectively a SPH method and a
grid-based method. Up to now, neither a two-dimensional nor three-dimensional hydrodynamical
simulation has modelled a complete step of the spiral at high resolution. We achieve this by
using the hydrodynamical code RAMSES (Teyssier 2002)
with adaptive mesh refinement (AMR). Adaptive mesh refinement allows large scale simulations
to be performed while keeping a high enough resolution close to the binary in order to form
the shocks properly (Sect. 2).
),
whereas Parkin & Pittard (2008) assumed that
it is the slower wind that determines the step of the spiral but focus their study on
binaries with equal wind velocities. Simple dynamical models of the shocked layer have been
developed for use with radiative transfer codes, assuming that the double shock structure is
infinitely thin (thin shell hypothesis) and that the material is ballistic (Harries et al. 2004; Parkin & Pittard 2008). The spiral structure is then reproduced at small
computational cost but this neglects the impact of the pressure, which creates a distinction
between both arms of the spiral (Lemaster et al.
2007; Pittard 2009; van Marle et al. 2011), the influence of the reconfinement of the weaker
wind for small η (Lamberts et al.
2011), and the large-scale evolution of instabilities in the colliding wind region
(see below). Walder & Folini (2003) provide
the first large-scale three-dimensional simulation showing a few spiral steps. The
resolution in the simulation is too low to model instabilities. Okazaki et al. (2008) and Parkin et al.
(2011) both present a three-dimensional simulation of η Carinae
showing instabilities at the wind interface, using respectively a SPH method and a
grid-based method. Up to now, neither a two-dimensional nor three-dimensional hydrodynamical
simulation has modelled a complete step of the spiral at high resolution. We achieve this by
using the hydrodynamical code RAMSES (Teyssier 2002)
with adaptive mesh refinement (AMR). Adaptive mesh refinement allows large scale simulations
to be performed while keeping a high enough resolution close to the binary in order to form
the shocks properly (Sect. 2).
Small-scale simulations without orbital motion (see Stevens et al. 1992; and references in Lamberts et al. 2011, hereafter Paper I) have shown that several instabilities are at work in colliding wind binaries. Thin shell instabilities occur when cooling is important so that the shocked zone narrows to a thin layer, which is easily perturbed (Vishniac 1994). They provoke strong distortions of the whole colliding region (Pittard 2009; van Marle et al. 2011). However, these instabilities are unlikely to be dominant in wide binary systems where cooling is inefficient, the shocks adiabatic, and the colliding wind region wider (Stevens et al. 1992). In this case, the velocity difference between both winds triggers the Kelvin-Helmholtz instability (KHI) at the contact discontinuity (Paper I). The inlusion of orbital motion has led to contradictory results. Lemaster et al. (2007) found that eddies develop even when the winds are completely identical, because orbital motion introduces a velocity difference. Pittard (2009) found no eddies in a simulation with a similar setup. van Marle et al. (2011) also found no eddies, although their simulation has an initial non-period binary system where the collision between the winds of the WR and its early-type companion is expected to be close to adiabatic (see Sect. 5). The infrared emission is very well-matched by an Archimedean spiral, although its brightest point is shifted by 13 milli-arcsec from its centre, possibly because dust formation is inhibited at smaller radii (Tuthill et al. 2008, hereafter T2008). The WR wind is hostile to dust formation owing to its high temperature, low density, and absence of hydrogen (Cherchneff et al. 2000). The wind collision region is more favourable, providing high densities, shielding from the ultraviolet radiation of the WR star, and the possibility of mixing with hydrogen from the companion star (Marchenko & Moffat 2007). We carried out 2D and 3D hydrodynamical simulations using the parameters of WR 104 to investigate these questions (Sect. 5). We then relate all our results to observations (Sect. 6).
2. Numerical simulations
2.1. Equations
We use the hydrodynamical code RAMSES for our simulations (Teyssier 2002). This code uses a second-order Godunov method to solve
the equations of hydrodynamics ![\begin{eqnarray} &&\frac{\partial\rho}{\partial t}+\nabla \cdot(\rho \vec{v}) = 0\\ &&\frac{\partial(\rho \vec{v})}{\partial t}+\nabla (\rho \vec{v}\vec{v})+\nabla P = 0 \\ &&\frac{\partial E }{\partial t}+\nabla \cdot[\vec{v}(E+P)] = 0, \end{eqnarray}](/articles/aa/full_html/2012/10/aa19006-12/aa19006-12-eq12.png) where
ρ is the density, v the velocity, and
P the pressure of the gas. The total energy density E
is given by
where
ρ is the density, v the velocity, and
P the pressure of the gas. The total energy density E
is given by 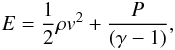 (5)where γ
is the adiabatic index, which we set to 5/3 to model adiabatic flows.
(5)where γ
is the adiabatic index, which we set to 5/3 to model adiabatic flows.
 |
Fig. 1 2D simulation of WR104. Left panel: AMR map, the coarse level is lmin = 7 (yellow grid in outer regions), the highest resolution is lmax = 16 (pale yellow at the very center of the grid). Right panel: the density map shows refinement happens at the shocks. |
2.2. Numerical parameters
We use the MinMod slope limiter together with the exact Riemann solver (Sects. 3, 4) or the HLLC (Sect. 5) Riemann solver to avoid numerical quenching of instabilities. We perform 2D and 3D simulations on a Cartesian grid with outflow boundary conditions. We use AMR, which enables to locally increase the spatial resolution according to the properties of the flow. We base the refinement criterion on velocity gradients. Figure 1 shows the AMR mesh of the central part of the simulation of WR 104 and the corresponding density map. Refinement occurs very close to the stars and at the discontinuities. In Sect. 3 we perform small-scale simulations where the size of the computational domain is lbox = 40a, with a the binary separation. We have nx = 64 for the resolution of the coarse (unrefined) grid and use seven levels of refinement. This gives an equivalent resolution that is at least two times higher than in former studies (Lemaster et al. 2007; Pittard 2009; van Marle et al. 2011). In Sect. 4, we perform larger-scale simulations where lbox = 400a and the coarse grid also has nx = 64 although we use up to nine levels of refinement. In some cases, we adapt the size of our grid to larger or smaller values to model a complete step of the spiral.
2.3. Generation of the winds
To simulate the winds, we keep the same method as used in Paper I, which was largely
inspired by Lemaster et al. (2007). Around each
star, we create a wind by imposing a given density, pressure, and velocity profile in a
spherical zone called a mask. The masks are reset to their initial values at each time
step to create steady winds. We add two passive scalars s1 and
s2 to distinguish both winds and to quantify mixing. We
initialise the passive scalars in the masks; their evolution is determined by
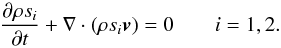 (6)In the free wind
of the first star, s1 = 1
and s2 = 0, whereas in the second wind it is the other way
round. In the shocked zone, both scalars have an intermediate value which accounts for the
mixing of the winds. The rotation of the stars is clockwise in the figures, their
positions are updated using a leapfrog method. For each simulation, the input parameters
are the mass M, mass-loss rate Ṁ, wind
velocity v (which we assume to be constant), and Mach number ℳ
at r = a for each star. The exact value of the Mach
number does not matter for the colliding wind region, as long as it is high enough for
pressure terms to be neglected (Paper I), which is the case for massive-star winds. Here,
the Mach numbers of both winds are set to 30. In all our simulations, the star with the
highest momentum flux is considered as the first star. We refer to its wind as the
stronger wind. The values of the parameters of the winds in the simulations are given in
the table in Appendix B. Both stars have a mass of 15 M⊙ and
the binary separation a is 1 AU. The corresponding orbital period
Porb is 0.18 yr (67 days). The orbital velocity of the stars
is vorb = 81 km s-1. The winds are isotropic in
the workframe of the simulation. As the orbital velocity is negligible with respect to the
speed of the winds, each wind can also be considered isotropic in the frame corotating
with the corresponding star. We neglect stellar rotation and the wind acceleration. We
only study circular orbits.
(6)In the free wind
of the first star, s1 = 1
and s2 = 0, whereas in the second wind it is the other way
round. In the shocked zone, both scalars have an intermediate value which accounts for the
mixing of the winds. The rotation of the stars is clockwise in the figures, their
positions are updated using a leapfrog method. For each simulation, the input parameters
are the mass M, mass-loss rate Ṁ, wind
velocity v (which we assume to be constant), and Mach number ℳ
at r = a for each star. The exact value of the Mach
number does not matter for the colliding wind region, as long as it is high enough for
pressure terms to be neglected (Paper I), which is the case for massive-star winds. Here,
the Mach numbers of both winds are set to 30. In all our simulations, the star with the
highest momentum flux is considered as the first star. We refer to its wind as the
stronger wind. The values of the parameters of the winds in the simulations are given in
the table in Appendix B. Both stars have a mass of 15 M⊙ and
the binary separation a is 1 AU. The corresponding orbital period
Porb is 0.18 yr (67 days). The orbital velocity of the stars
is vorb = 81 km s-1. The winds are isotropic in
the workframe of the simulation. As the orbital velocity is negligible with respect to the
speed of the winds, each wind can also be considered isotropic in the frame corotating
with the corresponding star. We neglect stellar rotation and the wind acceleration. We
only study circular orbits.
2.4. 2D and 3D simulations
We perform our 2D simulations in the orbital plane of the binary. We thus model the
cylindrical (r,θ) plane instead of the (r,z) plane as
classically done (e.g. Stevens et al. 1992; Brighenti & D’Ercole 1995; Pittard et al. 2006). This implies that the density
evolves ∝ r-1 instead of ∝ r-2
in a spherical geometry. For a given η, the structure of the colliding
wind binary is thus different in 2D and 3D. However, as discussed in Paper I, the
mapping 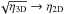 captures
most of the 3D structure in the 2D simulations. This point is re-discussed in Sect. 5,
where we compare the results of a 2D simulation of WR 104 with a full 3D simulation
including orbital motion. A major advantage of our 2D setup is the possibility of
implementing orbital motion for a modest computational cost, enabling the study of the
flow structure up to scales currently inaccessible to full 3D calculations.
captures
most of the 3D structure in the 2D simulations. This point is re-discussed in Sect. 5,
where we compare the results of a 2D simulation of WR 104 with a full 3D simulation
including orbital motion. A major advantage of our 2D setup is the possibility of
implementing orbital motion for a modest computational cost, enabling the study of the
flow structure up to scales currently inaccessible to full 3D calculations.
3. Impact of orbital motion on the shock arms
We carried out simulations of adiabatic colliding winds identical to those carried out in
Paper I, except that they now include orbital motion to study its impact on the shock
structure and development of the KHI. The simulations explore η = 1
and η = 0.0625 for different velocity
ratios β ≡ v1/ v2 = 1,2,20,
and all in a box of size 8a. Briefly, the results without orbital motion
were that (1) no instability is seen when β = 1;
(2) for 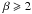 ,
the instabilities affect the position of the contact discontinuity, while for
β = 20 the KHI also affects the shock positions;
(3) for η = 0.0625 the instabilities remain confined to the weaker wind.
We present first the results of the simulations for β = 1, where the KHI
instability may be triggered (or not) by orbital shear (Sect. 3.1). We then discuss the
simulations with β ≠ 1. In these cases, the dominant wind is slower and
much denser than the weaker wind. For η = 1, there is no difference between
simulations where β = B
and β = 1/ B.
,
the instabilities affect the position of the contact discontinuity, while for
β = 20 the KHI also affects the shock positions;
(3) for η = 0.0625 the instabilities remain confined to the weaker wind.
We present first the results of the simulations for β = 1, where the KHI
instability may be triggered (or not) by orbital shear (Sect. 3.1). We then discuss the
simulations with β ≠ 1. In these cases, the dominant wind is slower and
much denser than the weaker wind. For η = 1, there is no difference between
simulations where β = B
and β = 1/ B.
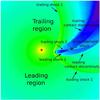 |
Fig. 2 Density map of a colliding wind binary including orbital motion ({η = 0.065, β = 0.5} ). The stars are shown by the black circles. The spiral structure has a leading and trailing arm. Each arm is composed of one shock from each wind and a contact discontinuity. In this case, both shocks from the wind of the second star intersect, totally confining the second wind. |
A view of the overall colliding-wind structure is given in Fig. 2. We define the leading arm as the arm preceding the second star, with respect to orbital motion (clockwise motion). The trailing arm is the second part of the spiral. We note that there is no dominant wind when η = 1 so that the definition of leading/trailing is degenerate in this case. (The definition also has no link with the definition commonly used in galactic dynamics.) In each arm, there is a shock in the wind from the first star and a shock in the wind from the second star, separated by a contact discontinuity. In 2D simulations, when η < 0.25 the second wind is confined by the intersection of the shocks. In a 3D simulation, this occurs for η ≃ 0.06 (Paper I).
Close to the binary, the relative motion of the stars creates an “aberration” (Parkin & Pittard 2008) of the shocked zone. Parkin & Pittard (2008) introduce the skew angle
μ, which measures the offset between the line of centres of the stars and
the symmetry axis of the shocked region. It is given by 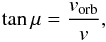 (7)where v is
taken as the speed of the slowest wind. This angle remains small unless the velocities of
the winds are strongly reduced or orbital motion becomes important We measured
μ in our simulations by finding the best fit of the analytic position of
the contact discontinuity derived by Canto et al.
(1996). An example is given in Fig. 3. We
measured μ ≃ 22° in the simulation
{η = 0.0625,β = 0.05} , while the theory predicts
μ = 21°. The simulation of WR 104 (see Sect. 5) gives
μ ≃ 9°, while the theory predicts
μ = 8°. We found that μ is too small in our
other simulations to allow correct measurements.
(7)where v is
taken as the speed of the slowest wind. This angle remains small unless the velocities of
the winds are strongly reduced or orbital motion becomes important We measured
μ in our simulations by finding the best fit of the analytic position of
the contact discontinuity derived by Canto et al.
(1996). An example is given in Fig. 3. We
measured μ ≃ 22° in the simulation
{η = 0.0625,β = 0.05} , while the theory predicts
μ = 21°. The simulation of WR 104 (see Sect. 5) gives
μ ≃ 9°, while the theory predicts
μ = 8°. We found that μ is too small in our
other simulations to allow correct measurements.
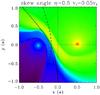 |
Fig. 3 Determination of the skew angle μ for {η = 0.5, β = 0.05} using a density map. The dashed line shows the theoretical position of the contact discontinuity for μ = 0 (no orbital motion). The solid line fits the contact discontinuity in the simulation. The length scale is set by the binary separation a. |
3.1. Simulations with β = 1
 |
Fig. 4 Small-scale simulation: density, velocity, and mixing for a simulation with identical winds (η = 1, β = 1). The density is given in g cm-2, the velocity is in km s-1 and the mixing of the winds is a dimensionless variable. The length scale is the binary separation a. |
Figure 4 shows the density, velocity, and mixing map for a simulation with identical winds {η = 1, β = 1} . We define the mixing to be the product of the passive scalars s1 × s2. The free (unshocked) winds correspond to the low density parts at the top and bottom. The denser parts are the shocked winds. The radial inhomogeneities visible in the unshocked wind region of the velocity map is a numerical artefact: it corresponds to minute anisotropies in the stellar wind due to the finite size of the masks. As shown in Appendix A, the orbital period is much longer than the local shear timescale. The Coriolis force does not impact the development of the KHI. However, the velocity map shows that a ≃ 20% velocity difference develops in each arm at a distance ≃ 20a from the binary. Orbital motion makes the shocked material leading the contact discontinuity (red region on the velocity map) accelerate in the lower-density free-wind region. Conversely, the shocked wind trailing the contact discontinuity (in green) moves into the denser, shocked material of the other wind. The resulting velocity difference is sufficient to trigger the KHI, even though the original wind speeds are equal. The instability is clearly present in the mixing map. We therefore confirm the results of Lemaster et al. (2007) that orbital motion triggers the KHI, even when the winds are identical. We also observe, as they do, an artificial enhancement of the instabilities when the shocks align with the grid. Our simulations contradict the results of van Marle et al. (2011), who find no KHI. Their simulations are performed with a Lax-Friedrichs Riemann solver. We ran a test simulation with the Lax-Friedrichs Riemann solver and observed no development of the KHI either, owing to the high numerical diffusivity.
Figure 5 shows the density, velocity, and mixing for {η = 0.0625, β = 1} . Because of the low value of η, there is a reconfinement shock (Paper I) behind the second star. The various discontinuities are indicated in the velocity map, which should be compared with the simpler geometry shown previously in Fig. 2. Our simulations without orbital motion showed no KHI because the initial velocities are identical. Here, as in the η = 1 case, orbital motion leads to velocity shear and mixing at the contact discontinuity. The KHI is confined to narrow regions close to the discontinuity because the velocity difference is small. We had found the same behaviour in the models explored in Paper I. We also see that complex velocity structures arise in the colliding wind region even in this a priori simple case where both winds have the same velocity, highlighting the possible difficulties in interpreting spectral line features arising from this region without any guidance from numerical simulations.
3.2. Simulations with β ≠ 1
 |
Fig. 6 Small scale simulation: density (left column) and mixing (right column) for simulations with {η = 1, β = 2,20} (two upper rows) and {η = 0.0625, β = 0.05,0.5,2,20} (lower rows). The length scale is the binary separation a. |
Figure 6 shows the density and mixing for simulations with {η = 1, β = 2,20} and {η = 0.0625, β = 0.05,0.5,2,20} . These maps show the impact of rotation on the arm geometry and the development of the instabilities.
The leading and trailing arms become markedly different when the velocity difference increases, even when η = 1. The shocked zone preceded by the unshocked wind with the high velocity and low density is larger than the zone preceded by the lower-velocity, higher-density wind. The latter shocked zone is compressed by the high velocity wind into a high density region (van Marle et al. 2011). We verified that, as expected if this explanation is correct, for β > 1 the compressed arm is the trailing arm, while for β < 1 the compressed arm is the leading arm (see Fig. 6). For β = 20, compression results in a rim of puffed-up matter where the density increases by two orders of magnitude with respect to the simulation with β = 1. The differentiation of both arms is independent of the instabilities in the winds but plays a role in their development.
The KHI starts similarly in both arms close to the binary major axis as the velocity difference and density jump across the contact discontinuity are the same in both arms. The symmetry between both arms is broken as the flow moves outwards. The compression of the shocked zone in the narrower arm results in a thin mixed zone with small-scale structures, whereas the eddies are stretched out in the wider arm. Mixing covers a larger area in the wider zone. This is not just a geometrical effect. We show in Appendix A that when media have different densities (α ≠ 0, see Eq. (A.10)) mixing by the KHI occurs preferentially in the least dense medium. This can be observed in Fig. 6, e.g. for η = 0.0625, β = 2) and indicates that the mixing we observe is results from the KHI. Both velocity and density profiles thus play a role in the development of the KHI in colliding wind binaries. They both impact the large-scale outcome of the spiral structure as we demonstrate in Sect. 4.
We checked that the mixing is physical and not numerical. If mixing results from numerical diffusion, the physical size of the mixed zone increases with decreasing resolution. If mixing follows from instabilities, the physical size of the mixed zone is constant with resolution. We measured the width of both mixed zone across the contact discontinuity at y = 6 for {η = 0.0625, β = 2} in a set of simulations with different resolutions. In all cases, nx = 64 and we successively added levels of refinement. The limit of the zone was determined to be s1 × s2 = 0.05. The successive widths of the mixed layer are for the wider arm: 22 a, 17a, 12a, 8.6a, 6.3a, 5.8a, 5.7a, and 5.6a. For the narrower arm we measure 8.8a, 5.0a,3.7a, 2.3a, 1.9a, 1.4a, 1.1a and 0.67a. In the wider arm, the width is almost constant for the three highest resolutions, which enables mixing to be resolved. In the narrower arm, the difference between simulations decreases with resolution, but the width is not constant. The narrower arm is only marginally resolved.
4. Formation of a spiral structure
We now consider the large-scale evolution of the previous simulations (Sect. 3) in a box of size lbox = 400a. Density and mixing maps are shown for η = 1 in Fig. 7 and for η = 0.0625 in Fig. 8, with β increasing from top to bottom in both figures. The spatial scale is the same in all plots except for the top two panels of Fig. 8, where we reduced the size of the domain to avoid unnecessary computational costs. The different behaviour of mixing in both arms discussed in Sect. 3 persists on the larger scales, eventually causing both contact discontinuities to merge into one single spiral in simulations with η = 0.0625 (Fig. 8). We cannot exclude that this merger results from numerical artefacts owing to the use of a Cartesian grid to describe an inherently spherical phenomenon. Merging should still occur naturally from inhomogeneities in the winds. Figures 7, 8 also show that the colliding wind region does not always turn into a stable spiral and that, for a given η the appearance depends strongly on the velocity ratio β. We discuss below the step size that we measure when a steady spiral forms before addressing the issue of the stability of the pattern.
 |
Fig. 7 Large-scale simulation: density (left column) and mixing (right column) for simulations with {η = 1, β = 1,2,20} (from top to bottom) in the large boxes. The length scale is the binary separation a. The mixing of the winds is a dimensionless variable. |
4.1. The step of the spiral
We found that, when a stable spiral structure is formed, an Archimedean spiral with a step size S provides a good fit to the results of our simulations. We measured S by overplotting an Archimedian spiral to the mixing maps and finding the best fit of the spiral arms, by eye. We checked our result by measuring the mean size of the steps in the same maps. As in Pittard (2009), we found that the fit with an Archimedean spiral is imperfect at the apex. However, the deviation is small and limited to a region ≃ 10a. Mixing closely follows the contact discontinuities in the arms so we used the mixing maps to trace the spiral. The spiral is not always clearly apparent in the density maps (e.g. {η = 0.0625,β = 1} in Fig. 8), especially when a complex flow is established by the presence of a reconfinement shock behind the weaker star (Fig. 1). The fitted S for various values of η and β is compared to the theoretical estimate S1 in Fig. 9, S1 is based on the assumption that the velocity of the stronger wind controls the structure scale so that S1 = Porbv1 (e.g. T2008). When v1 = v2, there is no ambiguity in the velocity that sets the step size, and we verify that, in this case, S = S1 for all η. This also rules out any significant numerical issue with the way in which the spiral develops. There are significant deviations from S1 in all the other cases, except when η ≪ 1 i.e. when the first wind largely dominates the momentum balance. For more balanced ratios η, the spiral step is smaller than expected when the weaker wind is slower than the stronger wind, and vice-versa when the weaker wind is the fastest. The use of the slowest wind speed instead of v1 (e.g. Parkin & Pittard 2008) does not provide a better agreement with our simulations. The results do not provide a straightforward analytical correction using η and β that could be used to interpret observations of pinwheel nebulae without requiring hydrodynamical simulations.
 |
Fig. 9 Step of the spiral S/ S1 as a function of β for η =1 (diamonds), 0.5 (diagonal crosses), and 0.0625 (crosses). The symbols are respectively joined by a solid, dashed, and dash-dotted line for easier identification. |
4.2. Stability of the spiral structure
The complete disruption of the spiral structure for large velocity ratios (Figs. 7, 8) was
unexpected. The breakdown can be traced to the KHI: we found that the structure was
stabilised when we tested a setup with a Lax-Friedrichs Riemann solver and a smaller
resolution, in which case the KHI is artificially suppressed (Paper I). The amplitude of
the KHI appears to destroy the spiral when strong velocity gradients are present,
resulting in widespread turbulence and important mixing throughout the domain. Curiously,
for η = 0.625, the structure is unstable
when v1 = 20v2, while it is
stable for the opposite velocity
gradient v1 = 0.05v2: the strong
density gradient (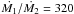 ) is also likely to play a role
in the stability. We indeed measure α ≃ 0.95 in the mixed region at
r ≃ 50a, which implies there has been a strong
reduction in the KHI growth rate.
) is also likely to play a role
in the stability. We indeed measure α ≃ 0.95 in the mixed region at
r ≃ 50a, which implies there has been a strong
reduction in the KHI growth rate.
Presence (S) or absence (X) of a spiral structure in simulations for various wind-momentum (η) and velocity (β) ratio.
Table 1 summarises the presence or absence of spiral structures, for all the simulations we performed. We compared these results with the KHI growth rate, normalised by the rate at which eddies propagate (see Appendix A for details). Although the growth rate gives no indication of the saturation in the non-linear regime, we suspect that the spiral is destabilized most easily when the eddies grow quickly before propagating further away.
 |
Fig. 10 Theoretical 2D growth rate of the KHI in colliding wind binaries as a function of the velocity ratio β = v1/ v2 of the winds. The solid, dashed, and dash-dotted lines correspond to η = 1,0.5, 0.0625 respectively. |
Figure 10 shows the normalised growth rate (see Eq. (A.12)) as a function of β for η = 1,0.5, and 0.0625. For η = 1, the curve is symmetric. The KHI does not develop when there is no velocity difference, peaks at βmax ≃ 2, and drops for higher values of β because the density gradient dampens the growth rate. The symmetry with respect to β = 1 is broken when η < 1: the normalised growth rate is weaker for β < 1 and stronger for β > 1. The lower the value of η, the stronger this asymmetry. Hence, stable structures are expected near β = 1, for β ≫ 1, and for β ≪ 1. In addition, when η ≠ 1, structures with β < 1 should be more stable than with β > 1.
The results of the simulations are in qualitative agreement with these expectations. When
η = 1, there is a spiral
for β = 1,2,4 but not for
β = 8,20 (Table 1), which is consistent with the
faster growth of the KHI when β increases from 1. However, the transition
from stable to unstable spirals occurs further away than expected from Fig. 10 (βmax ≃ 2). In addition,
we were unable to recover a stable final structure for very high β (or,
equivalently in the case η = 1, very low β), up to
β = 200 (Fig. 10). Tests at
higher β are computationally too expensive (and may not have much
astrophysical relevance). For η = 0.5, we found that the spiral is
maintained for values close to β = 1 but is quickly destroyed for
higher/lower values of β. In this case, a stable spiral is recovered when
β ≤ 0.01, which is consistent with the lower growth rate, while the
spiral remains destroyed for the symmetric value of β = 20 (higher growth
rate). We observe a similar behaviour for η = 0.0625. Stabilisation is
possible for a higher β = 0.05, which is consistent with the lower growth
rate of the instability for β < 1 as
η decreases. We conclude that the presence of a spiral depends on
η and β in a way that is consistent with having stable
structures for near-equal velocity
winds (v1 ≃ v2) or when the
weaker wind is much faster (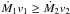 and v2 ≫ v1).
and v2 ≫ v1).
5. The pinwheel nebula WR 104
WR 104 is a binary composed of an early-type star and a WR star. The system shows an excess of infrared (IR) emission related to dust production. The IR emission has been resolved into a spiral structure with several steps imaged (T2008). The high temperatures and low densities in WR winds are difficult to reconcile with dust formation, which requires a temperature of around 1000 K and a number density of between 106 cm-3 and 1013 cm-3 (Cherchneff & Tielens 1995). An additional constraint for dust formation arises from the absence of hydrogen in the WR wind, leading to uncommon chemical processes (Cherchneff et al. 2000). Dust production appears to be closely-related to binarity and the presence of dense colliding-wind structures: in eccentric systems, such as WR 48 or WR 112, dust production is limited to orbital phases close to periastron, while it is continuous in systems with circular orbits. Systems viewed pole-on show an extended spiral structure in IR. WR 104 is the prototype system of these pinwheel nebulae. Pioneering work on the large-scale spiral structure of WR +O binaries led Walder & Folini (2002, 2003) to expect dust formation only at the very centre of the binary. Our aim is to determine whether a hydrodynamical model with adiabatic winds reproduces the observed large-scale structure of WR 104, study mixing, and identify regions where dust production may be possible. Detailed modelling of dust formation and growth in colliding wind binaries is beyond the scope of this study.
5.1. Simulation parameters
System parameters for WR 104.
Table 2 has the wind parameters of the binary system WR 104. The characteristics of the companion to the WR star are poorly constrained (van der Hucht 2001) and, like T2008, we refer to the companion star as the “OB” star. An orbital period (241.5 ± 0.5 days), eccentricity e < 0.06, inclination (i < 16°), and angular outflow-velocity of the spiral 0.28 mas day-1 in WR 104 were found by fitting an Archimedean spiral to the IR maps (T2008). The orbital separation a is about 2.1−2.8 AU for a total mass of 20–50 M⊙. We took e = 0 and a = 2.34 AU. Given the uncertainties in both the mass-loss rate and velocities, η varies between 0.0125 = 1/ 80 and 0.0033 = 1/ 300. Assuming a constant velocity for the OB wind and ROB = 10 R⊙ (Harries et al. 2004), the second shock forms at 2.7 ROB < r < 5.1 ROB, depending on η.
The shock position can be influenced by additional physical processes. The OB wind is accelerated within distances of ≃ 2–3 stellar radii and has not necessarily reached its final velocity at the shock, which modifies the effective momentum-flux ratio of the collision. The shock position moves to 2.2 ROB < r < 4.7 ROB, if acceleration is taken into account by using the velocity law v = v∞(1 − ROB/ r). Radiative braking of the WR wind by the OB radiation field (Gayley et al. 1997) can also play a role in WR 104 (T2008). A slower WR wind moves the shock away from the OB star (up to 12 ROB if radiative braking is able to stop the WR wind completely, which is only marginally possible in WR 104, see T2008). The magnitude of both effects, their compensating influence, and the uncertainties in the wind parameters did not justify including these processes. We adopted constant velocity winds and η = 0.0033 to ease comparison with T2008.
Radiative cooling can significantly change the shock structure. The ratio
χ of the cooling timescale tcool to the
dynamical timescale tesc provides an estimate of its
importance (Stevens et al. 1992) 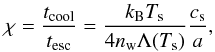 (8)where
Λ ≈ 2 × 10-23 erg cm3 s-1 is the emission rate for
solar abundances, nw the number density of the unshocked wind,
(8)where
Λ ≈ 2 × 10-23 erg cm3 s-1 is the emission rate for
solar abundances, nw the number density of the unshocked wind,
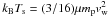 the shock
temperature, and cs the associated sound speed. The system is
adiabatic if χ > 1 and isothermal if
χ ≪ 1. According to the value of η, we found that
1.5 < χOB < 5
for the OB star and
0.4 < χWR < 1.4.
for the WR star. The system is at the transition between the two regimes. The emission
rate is of the same order of magnitude for the chemical composition of a WO star (St-Louis et al. 2005). Although chemical abundances are
different in oxygen-rich in oxygen-rich WO stars and carbon rich WC stars, their cooling
curves are similar, especially in the bremsstrahlung regime (beyond 106.5 K),
as the winds are mostly composed of helium. Inverse Compton (IC) cooling is important for
temperatures ≥ 106.5 K. The luminosities of both stars and electron
temperatures in the winds are roughly equal. The corresponding cooling rate for the OB
star is ≃ 6.3 × 10-23 erg cm3 s-1 and
2.4 × 10-25 erg cm3 s-1 for the WR star, as it scales
as Ṁ-1. Inverse Compton cooling of electrons on the OB stellar
photons can thus be expected to contribute significantly to cooling and help drive the WR
wind into the radiative regime. The acceleration of non-thermal particles also allows for
cooling in the system (Pittard 2010). The exact
impact can only be determined by proper modelling of particle distributions and the
corresponding energy losses, which is beyond the scope of this paper. In Eq. (8), the escape timescale is assumed to be
≃ a/ cs but could be as
short 2.7–5.1 ROB/ cs
(increasing χ by a factor of 10–20) if one takes the distance from the OB
star (~shock curvature radius, Stevens et al.
1992). In the following, we neglect cooling in the energy equation and assume
adiabatic winds.
the shock
temperature, and cs the associated sound speed. The system is
adiabatic if χ > 1 and isothermal if
χ ≪ 1. According to the value of η, we found that
1.5 < χOB < 5
for the OB star and
0.4 < χWR < 1.4.
for the WR star. The system is at the transition between the two regimes. The emission
rate is of the same order of magnitude for the chemical composition of a WO star (St-Louis et al. 2005). Although chemical abundances are
different in oxygen-rich in oxygen-rich WO stars and carbon rich WC stars, their cooling
curves are similar, especially in the bremsstrahlung regime (beyond 106.5 K),
as the winds are mostly composed of helium. Inverse Compton (IC) cooling is important for
temperatures ≥ 106.5 K. The luminosities of both stars and electron
temperatures in the winds are roughly equal. The corresponding cooling rate for the OB
star is ≃ 6.3 × 10-23 erg cm3 s-1 and
2.4 × 10-25 erg cm3 s-1 for the WR star, as it scales
as Ṁ-1. Inverse Compton cooling of electrons on the OB stellar
photons can thus be expected to contribute significantly to cooling and help drive the WR
wind into the radiative regime. The acceleration of non-thermal particles also allows for
cooling in the system (Pittard 2010). The exact
impact can only be determined by proper modelling of particle distributions and the
corresponding energy losses, which is beyond the scope of this paper. In Eq. (8), the escape timescale is assumed to be
≃ a/ cs but could be as
short 2.7–5.1 ROB/ cs
(increasing χ by a factor of 10–20) if one takes the distance from the OB
star (~shock curvature radius, Stevens et al.
1992). In the following, we neglect cooling in the energy equation and assume
adiabatic winds.
 |
Fig. 11 Density (g cm-3), mixing, velocity (km s-1), and temperature (K) in the orbital plane of the 3D simulation of WR 104 (top row). Corresponding 2D maps on the same scale (bottom row). The length scale is the binary separation a. |
The low value of η is challenging for numerical simulations (see discussion in Paper I). The mask of the star needs to be as small as possible so that the shocks can form properly. A minimum length of eight computational cells per direction is needed to obtain the spherical symmetry of the winds. Numerical resolution on scales much smaller than a stellar radius (0.05 AU) is thus required close to the binary. Further away, we need to maintain a high resolution in order to properly study the instabilities, while following a spiral step requires a box size ≥ 200 AU. We carried out two complementary simulations: a 3D simulation covering scales up to 12a and a 2D simulation to model a whole step of the spiral structure.
We used the large-scale 2D simulation to determine the step of the spiral and the impact
of mixing. As explained in Sect. 2.4, we used the mapping
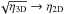 to obtain
comparable 2D and 3D results. We took η2D = 0.0625 to help
comparisons with the results in Sects. 3, 4, which is close enough to
η2DWR104 ≃ 0.057 derived from a straight application of the
mapping. It is important to have the right velocity difference for the Kelvin-Helmholtz
instability. We thus adapted ṀWR in order to
have η2D = 0.0625 for the 2D simulation. We used a
200a ≈ 500 AU simulation box with
nx = 128 and 12 levels of refinement.
This gives an equivalent resolution equal to 219 ≃ 5 × 105 cells. We
used nested grids to slowly decrease the maximum allowed resolution away from the binary.
to obtain
comparable 2D and 3D results. We took η2D = 0.0625 to help
comparisons with the results in Sects. 3, 4, which is close enough to
η2DWR104 ≃ 0.057 derived from a straight application of the
mapping. It is important to have the right velocity difference for the Kelvin-Helmholtz
instability. We thus adapted ṀWR in order to
have η2D = 0.0625 for the 2D simulation. We used a
200a ≈ 500 AU simulation box with
nx = 128 and 12 levels of refinement.
This gives an equivalent resolution equal to 219 ≃ 5 × 105 cells. We
used nested grids to slowly decrease the maximum allowed resolution away from the binary.
We used the smaller-scale 3D simulations to obtain quantitative results on the density and temperature in the winds. The 3D simulation follows one-eight of an orbit of WR 104 in a 12a ≈ 30 AU simulation box, which is large enough to see the impact of orbital motion. The orbital plane is the mid-plane of the box and the centre of mass of the binary is placed in a corner of the box to maximise the use of the simulated volume. We used AMR with a maximal equivalent resolution of 40963. We limited the high resolution to a narrow zone of 3a close to the binary where the instabilities develop. This corresponds to the same equivalent resolution as in our 2D model. We modelled only ≃ 20 layers at this high resolution in the z direction and we gradually reduced the resolution when going away from the orbital plane.
5.2. Global structure
 |
Fig. 12 Density (g cm-2), mixing and velocity (km s-1) in 2D simulations of WR 104. The length scale is the binary separation. |
Figure 11 shows the density, velocity, mixing, and temperature in the binary orbital plane of the 3D simulation (top row). The bottom row displays the corresponding 2D map on the same scale. The comparison confirms that the mapping in η captures adequately the 3D structure in the 2D simulation. The positions of the shocks and contact discontinuity along the line of centres are similar in both the 2D and 3D simulations and match the analytic solutions (Paper I). The opening angle defined by the contact discontinuities, which are well traced in the mixing map, is 15 ± 1°. This angle is consistent with the analytical estimates that have been used (Harries et al. 2004, T2008). However, the opening angle defined by the location of the shocks is wider in 2D than in 3D, which may have some influence on the density structure on larger scales (see Sect. 5.3). Because of the low η, there is a reconfinement shock behind the OB wind at a distance ≃ 0.75a in the 3D simulation (1.5a in the 2D simulation). All of the OB wind is involved in the collision and no fraction escapes freely to infinity.
Material piles up in both arms of the spiral. T2008 suggest that different strengths of the shock can change the conditions for dust formation in each arm. In the 3D simulation, the Mach number of the trailing arm at r ≃ 12a is 13% higher than in the leading arm, in agreement with the results of Lemaster et al. (2007). The small temperature difference is unlikely to affect dust formation. A more significant effect is that compression leads to a hotter temperature in the leading arm than in the trailing arm. Material in the mixing zone of the trailing arm experiences a temperature an order-of-magnitude cooler than in the mixing zone of the leading arm. Dust formation may be favoured in this arm, seeding the spiral structure when the contact discontinuities merge farther out (see below).
The amount of mixing increases with the distance to the binary. Integrating in spheres of increasing radii, the ratio of mixed material to the total amount of material in the spiral within r increases from ≲ 0.1% at r = a to ≃ 5% at r = 10a. These values are constant during the last stages of the simulation (lasting ≃ 0.1Porb), indicating the development of the instabilities has reached a steady state. As can be seen in Fig. 11 and expected from theory (Appendix A), mixing occurs mostly in the lower density regions of the colliding wind zone. The velocity map shows that the velocity is mostly radial and that matter is accelerated on a distance of a few times the binary separation. After substraction of the radial component, we have found the velocity of the flow along the spiral in the 3D simulation reaches a maximal value of ≃ 800 km s-1. This corresponds to the low density region in the centre of the spiral. In the outer regions of the spiral, the velocity along the spiral reaches ≃ 500 km s-1.
Figure 12 shows the 2D simulation on the largest scale (200a or about 470 AU). A stable spiral structure forms as expected for β = 0.6 and η = 0.0625 (Table 1). The collimated OB wind generates a low density spiral bounded on each side by walls of material where the density is ~100 times higher. The initially different mixing in both arms blurs at a distance of ≃ 50a. The mixing zones more or less merge and follow the leading arm, overlapping slightly with the density enhancement of the arm. The step of the spiral is 1.05SWR where SWR = vWR × Porb = 170 AU = 77a. T2008 assumed SWR to determine a distance of 2.6 kpc from the observed step size. The 5% correction to this distance required owing to the intrinsically larger spiral step is smaller than the uncertainties in the measured WR velocity and observed angular step size.
The single-armed spiral observed in the IR is more reminiscent of the mixing region than the double spiral in the density map. A double-armed spiral structure, separated by a very under-dense region of angular size ≃ 27 mas (at 2.6 kpc), would have been resolved if the IR emission correlated with density (i.e. for a constant gas-to-dust ratio). However, we caution that the width of the low density zone may be overestimated in this 2D simulation since it is likely to be related to the opening angle of the shocks, which Fig. 11 shows to be wider in 2D than in 3D. Whether one observes this tube as one or two pieces depends on the optical depth of the material. If it is optically thin, one likely observes two spirals. However, if the material is opaque, one observes only one spiral. The inclusion of dust radiative transfer would be required for a closer comparison of the observations with the hydrodynamical simulation.
5.3. Conditions for dust formation
One criterion for dust formation is a high enough density. Cherchneff & Tielens (1995) indicate different paths towards the formation of amorphous carbon for number densities n ranging from 106 to 1013 cm-3 and present a detailed study for n = 1010 cm-3. This gives ρ = 1.4 × 10-14 g cm-3 assuming a mean molecular weight μ = 1.4, which is typical of a ionized WC wind (Stevens et al. 1992). Such a density is only present in our 3D simulation at the edge of the spiral, up to a distance ≃ 2a from the WR star. In the 2D simulation, along the walls we find that the density drops as ρ ∝ r-1. Using this as guidance, we expect ρ ∝ r-2 in 3D on large scales. The minimum value n = 106 cm-3 considered by Cherchneff & Tielens (1995) is reached at r ≃ 25 a at the inner wall of the spiral. This is equivalent to one-third of a turn along the spiral. The density is too low for dust formation beyond this distance so that any dust present far away has been advected out.
We also expect the temperature to drop beyond 6000 K at roughly half a turn of the spiral by extrapolating the temperatures close to the binary. This is the limit for dust condensation (Cherchneff et al. 2000). It is consistent with the IR observations of a quarter-orbit shift between the maximum IR emission and the binary centre. Both the radiative cooling and photoionization heating of the wind would have to be included to permit an accurate determination of the temperature and the impact of shielding from the stellar radiation fields.
6. Discussion
6.1. Asymmetries due to orbital motion
Orbital motion breaks the symmetry around the binary axis and introduces significant differences from the stationary case with adiabatic winds. It causes a velocity difference that triggers the KHI even when both winds are strictly identical. It results in differentiation of the two arms flanking the weaker star. The arm moving into the densest unshocked wind is compressed, dampening the KHI, while the other arm expands and sees Kelvin-Helmholtz eddies of larger size. The density difference between the inner cavity and the bracketing walls can reach two orders of magnitude. According to Parkin et al. (2011), radiation pressure can have a similar effect, either enhancing or reducing the initial difference. Varricatt et al. (2004) modelled the variations in the emission-line profiles of WR 140 by using a rotating cone with dense edges, allowing them to constrain the opening angle of the colliding wind region. They found a wider opening angle than expected using the analytic formula for the opening angle of the contact discontinuity (Canto et al. 1996) with the standard value of η for this system. Our simulations also show that matter accumulates at the shock rather than the contact discontinuity. The observed opening angle thus corresponds to the opening angle of the shocks, which is wider than the opening angle of the contact discontinuity. This also increases the fraction of the WR wind involved in the collision compared to estimates using the contact discontinuity. Some of the spectral line features that are not explained by models where both arms have equal emission (absorption) could be due to differences between the leading and trailing arm (Stevens & Howarth 1999). The skew angle that we measured in the simulations matches the theoretical value given by Eq. (7). However, as we found that the step of the spiral is mostly determined by the speed of the stronger wind (and not the speed of the slower wind), we wonder whether this could also be the case for the skew angle. This is implicitly assumed by Kenny & Taylor (2007). Our simulations do not allow us to answer this question.
6.2. To spiral or not to spiral
The simulations presented here are the first including at least one step of the spiral. We have shown that a structure is maintained on these scales when the two winds have nearly equal velocities (β ≃ 1). This is consistent with the observations of pinwheel nebulae in several WR + O star binaries (Tuthill et al. 2006; Monnier et al. 2007; Millour et al. 2009), since their winds do have comparable velocities. The spiral is destabilised when the stronger wind has a velocity between 10–50% of the weaker wind (Table 1). For example, the episodic ejection of large amounts of (initially) slow-moving material could have temporarily destabilised any spiral structure in the luminous blue variable (LBV)/WR binary HD 5980 (Nazé et al. 2007; Georgiev et al. 2011). Eta Carina may be a case where any large-scale structure generated near apastron (when the system is closer to being adiabatic) is destroyed because of the destabilising velocity ratio β ≃ 1/ 6 – although this would have to be examinated in order to assess the effects of the high orbital eccentricity (Parkin et al. 2011). We expect our results to hold for eccentric orbits if the system stays adiabatic. If the system moves from adiabatic to radiative along its orbit then thin-shell instabilities develop with unknown consequences for the large-scale structure.
The spiral is stabilised again when the velocity ratio β ≪ 1. This situation may occur in gamma-ray binaries composed of a young non-accreting pulsar and an early-type star (Dubus 2006). In this case, the stellar wind interacts with the tenuous, relativistic pulsar wind. Bosch-Ramon & Barkov (2011) argued that the KHI would destroy any large-scale structure. Assuming our results hold in the relativistic regime, we find that a stable spiral can form on large scales if the stellar wind dominates, because β ≪ 1 in this situation. The structure is unstable if the pulsar wind dominates, pointing to the intriguing possibility that the interaction may switch from one regime to another in gamma-ray binaries with Be companions such as PSR B1259-63. The highly eccentric orbit takes the pulsar close to the equatorial disc where the slow-moving stellar outflow dominates momentum balance (Tavani & Arons 1997), leading to a stable colliding-wind region. However, at apastron, the pulsar wind may dominate over the radiatively-driven stellar wind and be unable to form a stable structure. Strong mixing of the two winds leads to rapid Coulomb or bremsstrahlung losses for the high energy particles, which has an impact on the gamma-ray emission (Zdziarski et al. 2010). Extended radio emission was detected around PSR B1259-63 near periastron (Moldón et al. 2011a). Regular changes in the radio morphology with orbital phase have been observed in other gamma-ray binaries that are compatible with non-thermal synchrotron emission from a stable collimated pulsar wind structure on scales ≤ vwPorb (Dhawan et al. 2006; Ribó et al. 2008; Moldón et al. 2011b). The luminosity and frequency of the radiation are probably too low to be able to detect the spiral structure on larger scales.
An example of colliding winds with β ≫ 1 also involves pulsars, this time with a low-mass companion (Roberts 2011). The weak stellar wind is overwhelmed by the relativistic wind of the recycled millisecond pulsar. No stable spiral is expected in this case. Another possible case is eruptive symbiotics such as AG Peg, HM Sge, or V1016 Cyg. These systems are composed of a red giant, with a very slow wind (≃ 20 km s-1) and a hot companion, a white dwarf in nova outburst at the origin of a fast outflow of several 1000 km s-1 (Girard & Willson 1987). We expect the spiral structure to be destroyed if the hot companion dominates. The radio maps of HM Sge (which has a possible 90 year orbit) show a more fragmented emission-region than expected from colliding wind models (Kenny & Taylor 2005), possibly because of thin shell instabilities triggered by radiative losses. The radio maps of AG Peg have been interpreted by assuming a stable spiral structure and a reversal in with time (Kenny & Taylor 2007). However, the application to symbiotics is not straightforward. For AG Peg, the comparable orbital and wind speeds may significantly change the dynamics of the interaction (e.g. Folini & Walder 2000). For HM Sge, there is probably no time to form a spiral because of the long orbital period.
Finally, we note that the KHI also intervenes in the bow shock structure created by the adiabatic interaction of the wind of a fast-moving star with the interstellar medium (e.g. Mira). The controlling parameter is the ratio of wind speed to star velocity. Much like with spirals, fast growth of the KHI may strongly disturb the cometary structure at large distances, as seen in some hydrodynamical simulations (Wareing et al. 2006, 2007).
6.3. Dust formation in pinwheel nebulae
Dust formation in WR 104 and other pinwheel nebulae should be helped by the mixing with hydrogen-rich material from the early-type star that we observe in the 2D and 3D simulations. Williams et al. (2009) argued that stronger dust emission in the trailing arm would explain better the IR high-resolution images of WR 140, and attributed this to density variations. The winds have nearly identical velocities but the WR has a mass-loss rate ten times higher than its O companion. The O wind is therefore in-between two high-density regions. Our simulations do not suggest very different densities. However, larger amplitude mixing is expected in the trailing arm because it propagates in the more tenuous O wind, possibly enhancing dust formation in this arm. The lower temperature in the trailing arm also helps, both effects being enhanced by IC cooling in the OB wind. Hence, a different dust-to-gas ratio between both arms could be an alternative explanation. High density eddies triggered by the KHI in the arms could also be responsible for the observation of IR obscuration events by dust clouds in other WR+O star systems (Veen et al. 1998).
The offset of the peak IR emission in WR 104 is consistent with the distance at which we estimated the temperature to fall below the dust sublimation temperature. This estimate is based on an adiabatic computation and neglects the impact of photoionisation by the stars and cooling by either radiative losses or particle acceleration. It assumes there is no thermal conduction that creates a pre-heated zone around the shocks and widens the region with the highest temperature (Myasnikov & Zhekov 1998). It also results in a higher density, and thus enhanced cooling in the shocked region (see Fig. 5 Myasnikov & Zhekov 1998). It may be important at the contact discontinuity if one of the winds is radiative and the other adiabatic. The determination of the limit of the ionised region and the exact temperature within the spiral requires a radiative transfer computation, which is beyond the scope of this paper. The densities in the colliding wind region are on the low side compared to what dust formation models require. Adiabatic shocks only enhance the density by a factor of four so cooling is required. Close to the binary, the winds are likely to display evidence of some cooling due to bremsstrahlung in the WR wind but even more due to IC losses in the OB wind. This results in a thinner and denser shocked layer. Pittard (2009) show the post-shock density is about 100 times higher in their model cwb1, which has strong cooling, than in their adiabatic model cwb3. Radiative cooling also decreases the temperature, bringing the region where dust condensation is possible closer to the binary. Thin-shell instabilities can develop when cooling is strong, enhancing the mixing of the winds. Given the impact of the (weaker) KHI in adiabatic colliding winds, thin shell instabilities can also be expected to significantly influence the large-scale structure. Pittard (2009) showed that the differentiation of the arms remains when thin-shell instabilities are present but the large-scale outcome has not yet been studied. Mixing is probably enhanced by the presence of clumps in the winds (Moffat et al. 1988). Walder & Folini (2003) argued that clumps of sizes comparable to the stellar radii survive in the shocked region and can strongly increase cooling. Smaller clumps are destroyed when passing the shocks and do not affect the temperature distribution in the winds (Pittard 2007).
Strong cooling is not necessarily present in all WR binaries. Williams et al. (2012) present evidence from long-term IR observations of WR 48 for dust production throughout the orbit. The stellar winds in this system have similar characteristics to those of WR 104 but the (tentative) orbital period is much longer at 32 years. Williams et al. (2012) estimate the system to be adiabatic with an average χ ≃ 11. The value will be even higher at apoastron in the eccentric orbit (e = 0.6), still dust formation is present. High densities will be much more difficult to reach than in WR 104, requiring dust formation at hitherto lower densities than have been considered possible.
7. Conclusion
We have studied the large-scale impact of orbital motion and the Kelvin-Helmholtz instability on adiabatic shocks in colliding wind binaries. We have used hydrodynamical simulations with AMR to perform the first high-resolution simulations of complete spiral steps. Orbital motion induces differentiation between both arms of the spiral. The arm propagating in the higher density wind gets compressed, while the arm propagating in the lower density wind expands. We explained that this is due to a stronger growth of the KHI in the wider arm and discuss possible observational signatures in spectral lines. We confirmed that the KHI arises even when both winds have identical speeds. We computed the step of the spiral and caution that there can be large differences from the standard estimates. We discovered that the large-scale spiral structure is destroyed when the velocity gradient between the winds is sufficiently steep. Strong density gradients have a stabilizing effect. According to our simulations, we are able to predict whether certain types of binaries display an extended spiral. Systems with stable spirals are those with near-equal velocity winds and those where the weaker wind is much faster. Performing high-resolution simulations of the pinwheel nebula WR 104, we demonstrated that in an adiabatic model, significant mixing of the WR wind occurs with the hydrogen-rich wind of the companion. We found the temperature drops beyond the limit of dust formation at roughly half a step of the spiral. However, we cautioned that this is based on simplified assumptions that neglect the effects of ionisation, and cooling through either radiative processes or the acceleration of non-thermal particles. Nonetheless, the density in those regions falls short of the critical density for dust condensation. Including radiative cooling would lead to higher densities, and also to thin shell instabilities. The impact of these instabilities both on the differentiation of the two arms and the spiral structure is unknown: resolving the thin shock layer in a large-scale simulation remains a very challenging numerical problem.
Online material
Appendix A: The Kelvin Helmholtz instability in stratified flows
A.1. Linear theory (Chandrasekhar 1961)
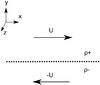 |
Fig. A.1 Configuration of the stratified flow. |
A flow can be considered as incompressible with respect to the
Kelvin-Helmholtz-instability if the Mach number of the velocity discontinuity
ℳcd = Δv/ cs ≲ .3
where Δv is the velocity difference at the interface and
cs the sound speed. At the centre of the binary system,
the winds are subsonic and the flow is incompressible as the two winds collide
head-on. We use the incompressible approximation in the following computations.
However, this may not be fully applicable further away from the binary as the winds
re-accelerate. That said, the interface remains marginally sonic
(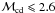 in all our simulations). In this case, the evolution of the KHI is complex to
determine as it depends on the binary parameters (η,
β) but also on the development of the KHI closer to the binary. We
have a system with a mean profile
U = ± Uex.
Above y = 0, the flow has a density ρ+
and ρ− for
y < 0 (see Fig. A.1). We neglect the Coriolis force since the local shear timescale
τS = Δx/ ΔU ~ 10-6 yr
is much shorter than the orbital period
τΩ ~ 10-1 yr. In this approximation, the
linearised equation of motion is:
in all our simulations). In this case, the evolution of the KHI is complex to
determine as it depends on the binary parameters (η,
β) but also on the development of the KHI closer to the binary. We
have a system with a mean profile
U = ± Uex.
Above y = 0, the flow has a density ρ+
and ρ− for
y < 0 (see Fig. A.1). We neglect the Coriolis force since the local shear timescale
τS = Δx/ ΔU ~ 10-6 yr
is much shorter than the orbital period
τΩ ~ 10-1 yr. In this approximation, the
linearised equation of motion is:  In
the following, each quantity is Fourier transformed in x
and t thanks to homogeneity:
Q = Qexp [i(ωt − kx)].
Rewriting the equation of motions and combining them leads to
In
the following, each quantity is Fourier transformed in x
and t thanks to homogeneity:
Q = Qexp [i(ωt − kx)].
Rewriting the equation of motions and combining them leads to 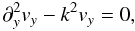 (A.3)which is solved
with two decaying solutions
(A.3)which is solved
with two decaying solutions 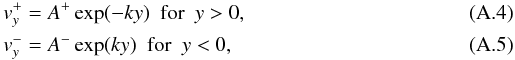 A+
and A− being two arbitrarily chosen constants that are
adjusted by jump conditions at the interface y = 0: pressure should
be continuous and fluid particles should stick to the interface on both sides. The
pressure condition is given by:
A+
and A− being two arbitrarily chosen constants that are
adjusted by jump conditions at the interface y = 0: pressure should
be continuous and fluid particles should stick to the interface on both sides. The
pressure condition is given by: 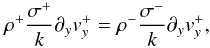 (A.6)where
σ ± = ω ± U. The
second condition is obtained defining a displacement vector
ξ(x) that follows the interface. By definition, a
fluid particle located at
(x,ξ(x) − ϵ) satisfies
(A.6)where
σ ± = ω ± U. The
second condition is obtained defining a displacement vector
ξ(x) that follows the interface. By definition, a
fluid particle located at
(x,ξ(x) − ϵ) satisfies
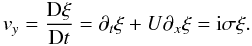 (A.7)Applying this
to both side of interface (± ϵ) leads to the jump condition
(A.7)Applying this
to both side of interface (± ϵ) leads to the jump condition
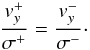 (A.8)Combining (A.6) and (A.8) and looking for non trivial solutions gives
(A.8)Combining (A.6) and (A.8) and looking for non trivial solutions gives 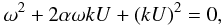 (A.9)where
α = (ρ+ − ρ−)/ (ρ+ + ρ−).
An instability arises whenever
(A.9)where
α = (ρ+ − ρ−)/ (ρ+ + ρ−).
An instability arises whenever
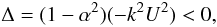 (A.10)which is always
true since −1 ≤ α ≤ 1. The growth rate
is
(A.10)which is always
true since −1 ≤ α ≤ 1. The growth rate
is 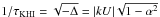 .
Hence, a density contrast |α| close to 1 strongly dampens the
growth rate of the KHI.
.
Hence, a density contrast |α| close to 1 strongly dampens the
growth rate of the KHI.
In colliding wind binaries, the density and the velocity of both winds are related
through the momentum-flux ratio η. Using Eq. (1) and mass conservation for both winds
then and assuming the interaction occurs far enough from the binary (so that
r1 ≃ r2), the density ratio
is roughly ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:mass_cons} && \frac{\rho_2}{\rho_{1}}\simeq \eta \beta^{2}, \\[1mm] \label{eq:growth_khi} && \frac{\tau_{\rm adv}}{\tau_{\rm KHI}}=\frac{|\beta-1|\sqrt{1-\alpha^2}}{-\alpha(\beta-1)+(\beta+1)}=\frac{\eta^{1/2}\beta |\beta-1|}{1+\eta \beta^3}\cdot \end{eqnarray}](/articles/aa/full_html/2012/10/aa19006-12/aa19006-12-eq238.png)
A.2. Nonlinear evolution
A.2.1. Two-dimensional evolution
 |
Fig. A.2 Snapshot of the mixing at t = 21 (in dimensionless units) for α = 0.5. |
To investigate the evolution of the KHI in the nonlinear regime, we performed numerical simulations for increasing α. The 2D setup is as follows: box size (lx = 8,ly = 4), resolution (1024 × 256), code PLUTO (Mignone et al. 2007), adiabatic equation of state P ∝ ρ5/ 3, background pressure P = 1 in the initial state (using units scaled to the box length, density, and velocity shear). Reflective boundary conditions are enforced in y to confine the instability in the simulation box. We always have ρ+ > ρ− i.e. the densest medium is found where y > 0.
In addition to that, we follow the mixing using a passive scalar as explained in
Sect. 2.3. We performed simulations for
{α = 0,0.5,0.9,0.99} .
Kelvin-Helmholtz eddies are clearly present in the density snapshot shown in
Fig. A.2 for model α = 0.5.
To show the diffusion of the passive scalar as a function of time, we plot the
evolution of 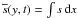 as a function of y and t in Fig. A.3. These results demonstrate that when
α ≠ 0, the scalar diffusion propagates much less in the denser
medium (y > 0) and that diffusion looks
less efficient when |α| increases, in the sense that the region
with intermediate values of the scalar s becomes smaller when
α increases.
as a function of y and t in Fig. A.3. These results demonstrate that when
α ≠ 0, the scalar diffusion propagates much less in the denser
medium (y > 0) and that diffusion looks
less efficient when |α| increases, in the sense that the region
with intermediate values of the scalar s becomes smaller when
α increases.
 |
Fig. A.3 Mixing due to the KHI. From left to right, top to bottom: α = 0,0.5,0.9,0.99. |
A.3. Three-dimensional evolution
We performed simulations for α = 0 and 0.9 in 3D to compared them to
the 2D ones. They are very similar to the 2D configuration, except for the resolution,
which was reduced to 500 × 100 × 100 in order to reduce computational costs. We set
lz = lx = 4.0,
where 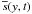 is shown in Fig. A.4. The direct comparison with the 2D cases
indicates that faster diffusion into the more tenuous region still occurs in the 3D
simulation.
is shown in Fig. A.4. The direct comparison with the 2D cases
indicates that faster diffusion into the more tenuous region still occurs in the 3D
simulation.
Figure A.5 shows the mixing at different times in the 2D and 3D simulations, for α = 0.,0.9. It confirms that both in the 2D and 3D case, the KHI behaves similarly with respect to the velocity gradient.
 |
Fig. A.4 Mixing in the 3D simulations with α = 0 (left) and α = 0.9 (right). |
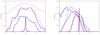 |
Fig. A.5 Mixing in 2D simulations (blue solid line) and 3D simulations (red dashed line) for α = 0 (left panel) and α = 0.9 (right panel). The different curves show different timesteps separated by Δt = 5. |
Appendix B: Parameters of the simulations
Parameters of the simulations.
Acknowledgments
The authors thank the anonymous referee for pointing out the importance of inverse Compton cooling. A.L. and G.D. are supported by the European Community via contract ERC-StG-200911. Calculations have been performed at CEA on the DAPHPC cluster and using HPC resources from GENCI- [CINES] (Grant 2011046391).
References
- Bosch-Ramon, V., & Barkov, M. V. 2011, A&A, 535, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brighenti, F., & D’Ercole, A. 1995, MNRAS, 277, 53 [NASA ADS] [Google Scholar]
- Canto, J., Raga, A. C., & Wilkin, F. P. 1996, ApJ, 469, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and hydromagnetic stability [Google Scholar]
- Cherchneff, I., & Tielens, A. G. G. M. 1995, in Wolf-Rayet Stars: Binaries; Colliding Winds, Evolution, eds. K. A. van der Hucht, & P. M. Williams, IAU Symp., 163, 346 [Google Scholar]
- Cherchneff, I., Le Teuff, Y. H., Williams, P. M., & Tielens, A. G. G. M. 2000, A&A, 357, 572 [NASA ADS] [Google Scholar]
- Cherepashchuk, A. M. 1976, Pis ma Astronomich. Z., 2, 356 [Google Scholar]
- Crowther, P. A. 1997, MNRAS, 290, L59 [NASA ADS] [CrossRef] [Google Scholar]
- De Becker, M. 2007, A&ARv, 14, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Dhawan, V., Mioduszewski, A., & Rupen, M. 2006, in VI Microquasar Workshop: Microquasars and Beyond [Google Scholar]
- Dougherty, S. M., & Williams, P. M. 2000, MNRAS, 319, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Dougherty, S. M., Beasley, A. J., Claussen, M. J., Zauderer, B. A., & Bolingbroke, N. J. 2005, ApJ, 623, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G. 2006, A&A, 456, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Folini, D., & Walder, R. 2000, Ap&SS, 274, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Gayley, K. G., Owocki, S. P., & Cranmer, S. R. 1997, ApJ, 475, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Georgiev, L., Koenigsberger, G., Hillier, D. J., et al. 2011, AJ, 142, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Girard, T., & Willson, L. A. 1987, A&A, 183, 247 [NASA ADS] [Google Scholar]
- Harries, T. J., Monnier, J. D., Symington, N. H., & Kurosawa, R. 2004, MNRAS, 350, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., & Prinja, R. K. 1989, ApJS, 69, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., & Schmutz, W. 1992, A&A, 261, 503 [NASA ADS] [Google Scholar]
- Kenny, H. T., & Taylor, A. R. 2005, ApJ, 619, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Kenny, H. T., & Taylor, A. R. 2007, ApJ, 662, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Lamberts, A., Fromang, S., & Dubus, G. 2011, MNRAS, 418, 2618 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Lebedev, M. G., & Myasnikov, A. V. 1990, Fluid Dynamics, 25, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Lemaster, M. N., Stone, J. M., & Gardiner, T. A. 2007, ApJ, 662, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, D., McCray, R., & Mac Low, M. 1990, ApJ, 362, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Marchenko, S. V., & Moffat, A. F. J. 2007, in Massive Stars in Interactive Binaries, eds. N. St.-Louis, & A. F. J. Moffat, ASP Conf. Ser., 367, 213 [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Millour, F., Driebe, T., Chesneau, O., et al. 2009, A&A, 506, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffat, A. F. J., Drissen, L., Lamontagne, R., & Robert, C. 1988, ApJ, 334, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Moldón, J., Johnston, S., Ribó, M., Paredes, J. M., & Deller, A. T. 2011a, ApJ, 732, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Moldón, J., Ribó, M., & Paredes, J. M. 2011b, A&A, 533, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monnier, J. D., Tuthill, P. G., Danchi, W. C., Murphy, N., & Harries, T. J. 2007, ApJ, 655, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Myasnikov, A. V., & Zhekov, S. A. 1998, MNRAS, 300, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Nazé, Y., Corcoran, M. F., Koenigsberger, G., & Moffat, A. F. J. 2007, ApJ, 658, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, A. T., Owocki, S. P., Russell, C. M. P., & Corcoran, M. F. 2008, MNRAS, 388, L39 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Parkin, E. R., & Pittard, J. M. 2008, MNRAS, 388, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Parkin, E. R., Pittard, J. M., Corcoran, M. F., & Hamaguchi, K. 2011, ApJ, 726, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. M. 2007, ApJ, 660, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. M. 2009, MNRAS, 396, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. M. 2010, in High Energy Phenomena in Massive Stars, eds. J. Martí, P. L. Luque-Escamilla, & J. A. Combi, ASP Conf. Ser., 422, 145 [Google Scholar]
- Pittard, J. M., Dougherty, S. M., Coker, R. F., O’Connor, E., & Bolingbroke, N. J. 2006, A&A, 446, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribó, M., Paredes, J. M., Moldón, J., Martí, J., & Massi, M. 2008, A&A, 481, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ritchie, B. W., Clark, J. S., Negueruela, I., & Crowther, P. A. 2009, A&A, 507, 1585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, M. S. E. 2011, in AIP Conf. Ser. 1357, eds. M. Burgay, N. D’Amico, P. Esposito, A. Pellizzoni, & A. Possenti, 127 [Google Scholar]
- Shore, S. N., & Brown, D. N. 1988, ApJ, 334, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- St-Louis, N., Moffat, A. F. J., Marchenko, S., & Pittard, J. M. 2005, ApJ, 628, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., & Howarth, I. D. 1999, MNRAS, 302, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., Blondin, J. M., & Pollock, A. M. T. 1992, ApJ, 386, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Tavani, M., & Arons, J. 1997, ApJ, 477, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuthill, P. G., Monnier, J. D., & Danchi, W. C. 1999, Nature, 398, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Tuthill, P., Monnier, J., Tanner, A., et al. 2006, Science, 313, 935 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tuthill, P. G., Monnier, J. D., Lawrance, N., et al. 2008, ApJ, 675, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Usov, V. V. 1991, MNRAS, 252, 49 [NASA ADS] [Google Scholar]
- Usov, V. V. 1992, ApJ, 389, 635 [NASA ADS] [CrossRef] [Google Scholar]
- van der Hucht, K. A. 2001, New Astron. Rev., 45, 135 [NASA ADS] [CrossRef] [Google Scholar]
- van Marle, A. J., Keppens, R., & Meliani, Z. 2011, A&A, 527, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varricatt, W. P., Williams, P. M., & Ashok, N. M. 2004, MNRAS, 351, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Veen, P. M., van Genderen, A. M., van der Hucht, K. A., et al. 1998, A&A, 329, 199 [NASA ADS] [Google Scholar]
- Vishniac, E. T. 1994, ApJ, 428, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Walder, R., & Folini, D. 2002, in Interacting Winds from Massive Stars, eds. A. F. J. Moffat, & N. St-Louis, ASP Conf. Ser., 260, 595 [Google Scholar]
- Walder, R., & Folini, D. 2003, in A Massive Star Odyssey: From Main Sequence to Supernova, eds. K. van der Hucht, A. Herrero, & C. Esteban, IAU Symp., 212, 139 [Google Scholar]
- Wareing, C. J., Zijlstra, A. A., Speck, A. K., et al. 2006, MNRAS, 372, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J., Zijlstra, A. A., & O’Brien, T. J. 2007, ApJ, 660, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Wiggs, M. S., & Gies, D. R. 1993, ApJ, 407, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, P. M., van der Hucht, K. A., & The, P. S. 1987, A&A, 182, 91 [NASA ADS] [Google Scholar]
- Williams, P. M., Marchenko, S. V., Marston, A. P., et al. 2009, MNRAS, 395, 1749 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, P. M., van der Hucht, K. A., van Wyk, F., et al. 2012, MNRAS, 420, 2526 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Neronov, A., & Chernyakova, M. 2010, MNRAS, 403, 1873 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Presence (S) or absence (X) of a spiral structure in simulations for various wind-momentum (η) and velocity (β) ratio.
All Figures
 |
Fig. 1 2D simulation of WR104. Left panel: AMR map, the coarse level is lmin = 7 (yellow grid in outer regions), the highest resolution is lmax = 16 (pale yellow at the very center of the grid). Right panel: the density map shows refinement happens at the shocks. |
| In the text | |
 |
Fig. 2 Density map of a colliding wind binary including orbital motion ({η = 0.065, β = 0.5} ). The stars are shown by the black circles. The spiral structure has a leading and trailing arm. Each arm is composed of one shock from each wind and a contact discontinuity. In this case, both shocks from the wind of the second star intersect, totally confining the second wind. |
| In the text | |
 |
Fig. 3 Determination of the skew angle μ for {η = 0.5, β = 0.05} using a density map. The dashed line shows the theoretical position of the contact discontinuity for μ = 0 (no orbital motion). The solid line fits the contact discontinuity in the simulation. The length scale is set by the binary separation a. |
| In the text | |
 |
Fig. 4 Small-scale simulation: density, velocity, and mixing for a simulation with identical winds (η = 1, β = 1). The density is given in g cm-2, the velocity is in km s-1 and the mixing of the winds is a dimensionless variable. The length scale is the binary separation a. |
| In the text | |
 |
Fig. 5 Small-scale simulation: same as Fig. 4 for {η = 0.0625, β = 1} . |
| In the text | |
 |
Fig. 6 Small scale simulation: density (left column) and mixing (right column) for simulations with {η = 1, β = 2,20} (two upper rows) and {η = 0.0625, β = 0.05,0.5,2,20} (lower rows). The length scale is the binary separation a. |
| In the text | |
 |
Fig. 7 Large-scale simulation: density (left column) and mixing (right column) for simulations with {η = 1, β = 1,2,20} (from top to bottom) in the large boxes. The length scale is the binary separation a. The mixing of the winds is a dimensionless variable. |
| In the text | |
 |
Fig. 8 Large-scale simulation: same as Fig. 7 for {η = 0.0625, β = 0.05,0.5,0.1,1,2,20} . |
| In the text | |
 |
Fig. 9 Step of the spiral S/ S1 as a function of β for η =1 (diamonds), 0.5 (diagonal crosses), and 0.0625 (crosses). The symbols are respectively joined by a solid, dashed, and dash-dotted line for easier identification. |
| In the text | |
 |
Fig. 10 Theoretical 2D growth rate of the KHI in colliding wind binaries as a function of the velocity ratio β = v1/ v2 of the winds. The solid, dashed, and dash-dotted lines correspond to η = 1,0.5, 0.0625 respectively. |
| In the text | |
 |
Fig. 11 Density (g cm-3), mixing, velocity (km s-1), and temperature (K) in the orbital plane of the 3D simulation of WR 104 (top row). Corresponding 2D maps on the same scale (bottom row). The length scale is the binary separation a. |
| In the text | |
 |
Fig. 12 Density (g cm-2), mixing and velocity (km s-1) in 2D simulations of WR 104. The length scale is the binary separation. |
| In the text | |
 |
Fig. A.1 Configuration of the stratified flow. |
| In the text | |
 |
Fig. A.2 Snapshot of the mixing at t = 21 (in dimensionless units) for α = 0.5. |
| In the text | |
 |
Fig. A.3 Mixing due to the KHI. From left to right, top to bottom: α = 0,0.5,0.9,0.99. |
| In the text | |
 |
Fig. A.4 Mixing in the 3D simulations with α = 0 (left) and α = 0.9 (right). |
| In the text | |
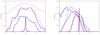 |
Fig. A.5 Mixing in 2D simulations (blue solid line) and 3D simulations (red dashed line) for α = 0 (left panel) and α = 0.9 (right panel). The different curves show different timesteps separated by Δt = 5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


