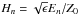| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 12 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201219707 | |
| Published online | 31 August 2012 | |
New high-density deformable mirrors for high-contrast imaging
1
60 rue des bergers,
75015
Paris,
France
e-mail: riaud.pierre@gmail.com
2
Université de Liège, 17 Allée du 6 Août, 4000
Sart Tilman,
Belgium
Received:
29
May
2012
Accepted:
25
July
2012
This paper presents a new architecture for deformable mirrors, suitable for adaptive optics (AO) observations. The performance of these systems directly depends on the density of actuators, which correct for wavefront errors. Therefore, deformable mirrors of large sizes are difficult to build because of the required number of actuators. Moreover, these actuators use either piezoelectric, magnetic, or electrostatic systems, which all suffer from nonlinear behavior (hysteresis). To solve these problems, we propose to use addressable vertical-cavity surface-emitting laser (VCSELs) systems, which move, through radiation pressure, a CVD-diamond membrane coated with an aluminum/gold thin film. The advantage of such a system is the high actuator density (16 384 on 41 mm2) without hysteresis problems. This technology is therefore well-suited for the next generation of AO systems.
Key words: instrumentation: high angular resolution / instrumentation: adaptive optics / methods: numerical
© ESO, 2012
1. Introduction
Deformable mirrors (DM), coupled with wavefront-sensing systems, are used in adaptive optics to correct in real time for the atmospheric turbulence. They are also used in high-contrast imaging optical workbenches such as HCIT (Trauger 2009) to correct for some residual speckles after some coronagraphics systems. Indeed, phase and intensity errors introduced in the pupil plane create residual speckles in the final imaging plane after the coronagraphic effect. All coronagraphs suppress the coherent part of the light and leave some residual non-coherent speckles.
Extreme AO (ExAO) can be used to correct these phase residuals at the 0.1 nm level. In these cases, using high-density deformable mirrors with a small footprint (active area) is essential to correct for the high number of Zernike polynomials, without hysteresis. Nowadays, the performance of state-of-the-art high-density DMs are still limited by their relatively significant footprint (>9 cm2). Despite the technological advances, new techniques that use piezoelectric, magnetic, or electrostatic systems generate undesirable hysteresis responses.
In this paper, we present a new concept that solves most of these drawbacks (density, footprint, hysteresis). The solution we propose makes use of high-density vertical-cavity surface-emitting laser (VCSELs) that move a thin CVD-diamond membrane (e.g., synthetic diamond, produced using chemical vapor deposition technique) with an aluminum coating through radiation pressure. Thanks to present progress in the microsystem manufacturing, a 128 × 128 fully matrix-addressable VCSELs array is under study today. This configuration allows high actuator density (16 384), small footprint (0.41 cm2 with 50 μm array pitch) and no hysteresis due to the free-mechanical movement induced by each laser radiation pressure.
The DM concept is explained in detail in Sect. 2, while the radiation pressure theory on a clamped membrane is presented in Sect. 3. Because the device uses a VCSELs array (Kasten et al. 2007; Seurin et al. 2008; Bardinal et al. 2011) to exercise pressure on the thick membrane via laser beams, it is essential to take into account any possible diffraction effects; these calculations are given in Sect. 4. The optical propagation of light allows one to calculate (a) the “waffle” effect and (b) the inter-actuator crossing effect, because the laser beam size is larger than the actuator pitch (see the Gaussian convolution in Appendix E). The first stage of the numerical simulation of the membrane deflection can be performed with a simple linear model, which is presented in Sect. 5. However, due to the very thick (1–2 μm) multi-layer membrane, the deformation level can be higher than the thickness and a nonlinear model must also be investigated to perform better numerical simulations of the deformation constraint (i.e. laser power vs. dynamic). These calculations are presented in Sect. 5.5. The temporal response of the device is also investigated in Sect. 7 by directly calculating the resonance frequencies. Finally, an estimation of the thermal deformation of the membrane, due to the high laser power, is proposed in Sect. 8.
2. Principle
This paper introduces the concept of using radiation pressure to distort a thin CVD-diamond membrane. The pressure is produced by a fully addressable VCSELs array, which consists of spatially monomode (TEM 00) laser diodes. This new optical MEMS architecture creates a high-density actuator on a very small footprint. The impressive performance of VCSELs, such as (a) high-power laser-diode emission (several mW per diode), (b) circular monomode beam, and (c) efficient high-frequency modulation, is providing the motivation for using light for a possible non-mechanical movement of the thin membrane with radiation pressure (Mansuripur 2004; Labeyrie et al. 2010).
2.1. VCSELs array manufacturing
Up to 128 × 128 VCSELs array are under study in the near-infrared (808−1064 nm) and this high number of laser-diodes (16 384) constitutes a possibility to obtain the largest high-density deformable mirror ever made. We propose to use laser-diodes working around 808−1064 nm because this technology allows a high-power emission (up to 1 KW for an entire array, see for example the commercially available Lasertel product V1 QCW for high-power VCSEL at 808 nm). The actuator pitch is a free parameter, but with the present nanotechnology the number of laser-diodes varies inversely with the pitch dimension, and a value between 25–100 μm should be feasible. The main problem in manufacturing a fully-addressable VCSELs array is the number of metal connections or wires that is required to operate the array. Matrix-addressable arrays greatly reduce the number of required metal connections. As a comparison, for a 128 × 128 array, 16 384 metal wires are required for the individually addressed array, but only 256 metal wires are required for the matrix-addressable array (Conk 2002). If we chose the distance between each laser diode to be 50 μm, the effective size of the deformable mirror will only be 6.5 mm × 6.5 mm. This footprint is perfectly adapted to classical optical workbenches used for high-contrast imaging. Indeed, in this type of workbench, the size of the pupil must remain small in diameter (with 0.25 to 3 cm) to ensure a relatively small size of the overall optical system (2 m to 3 m).
Each laser-diode can be driven in intensity with high-frequency modulation (several KHz),
to allow a proper distortion of a small part of the thin membrane. Before that, the
Gaussian monomode beam provided by each microlaser must be collimated with an array of
square fused silica microlenses.
Let Λx,Λy be the distance
between each laser diode in the x and y direction,
respectively,
and Nd = nx × ny
the total number of laser-diodes. These parameters are important to define the actuator
pitch and the full effective size of the deformable mirror. The focal length
FL needed for a good collimation is given directly by the
beam divergence (1/e2): 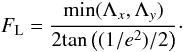 (1)We obtain 15 to 20
degrees of the total beam divergence for the commercial VCSELs array, the focal length of
the microlens array needs to
be FL > 142 μm
for a 50 μm array pitch. This value is the minimum focal length to
achieve a complete illumination of the microlens by the full width at half maximum of the
Gaussian beam. To know the full laser field given by the entire array, we must simulate
the propagation until the membrane is reached with Fresnel diffraction. The gap between
microlens and a limited precision alignment must be taken into account to properly
evaluate the diffraction field on the membrane, which produces some correlation problems
between actuators. In classical mirror theory, this correlation is generally known as
“waffle” effect.
(1)We obtain 15 to 20
degrees of the total beam divergence for the commercial VCSELs array, the focal length of
the microlens array needs to
be FL > 142 μm
for a 50 μm array pitch. This value is the minimum focal length to
achieve a complete illumination of the microlens by the full width at half maximum of the
Gaussian beam. To know the full laser field given by the entire array, we must simulate
the propagation until the membrane is reached with Fresnel diffraction. The gap between
microlens and a limited precision alignment must be taken into account to properly
evaluate the diffraction field on the membrane, which produces some correlation problems
between actuators. In classical mirror theory, this correlation is generally known as
“waffle” effect.
Figure 1 presents the optical scheme that uses polarized light (provided directly by the VCSELs array or by a linear polarizing system) to separate the input laser beam (Ein, Hin) from the output (Eout, Hout) after reflection on the thin coated membrane. The proposed optical device can either be a Faraday rotator or a polarizing cube, necessary to achieve a perfect separation of the output beam and dramatically decrease a possible interference process between the two laser fields.
 |
Fig. 1 Key functional elements of a high-density actuator deformable mirror, driven by radiation pressure from a VCSELs array. Bottom to top: fully addressable VCSELs array of laser diodes in the near-infrared (808−1064 nm). The emitting region of the laser diode is around 9 μm (the laser size), and the actuator pitch is given by the laser diode spacing. Each Gaussian beam (provided by laser diodes) is collimated by a square microlens array in fused silica with a proper anti-reflection coating (transmission >99.5%). The microlens array must be very well aligned (<0.5 μm) with the VCSEL array. If the VCSELs array is not in polarized emission, a linear polarizer is needed. The light passes through an optical polarizing device and arrives on a thin CVD-diamond membrane (≈1 μm of thickness) with aluminum coating (100 nm of thickness) on each face. The linear polarizer and the optical polarizing device management can have the same component as a polarizing cube with high polarization purity (>104). The radiation pressure produced by each laser diode locally distorts the membrane with a Gaussian shape, which definies the actuator response of the system. |
2.2. Membrane manufacturing
Finally, we decided to take a 1 μm thick CVD-diamond membrane (see Espinosa et al. 2003; Koizumi et al. 2008) with a 100 nm aluminum and 60 nm gold coating. The thickness of the membrane must be (a) as low as possible to allow a sufficient displacement (i.e. dynamic range) due to the radiation pressure and (b) thin enough not to break during movement. The CVD-diamond material constitutes the best possible choice, due to its high Young’s modulus (greater than 1000 GPa). The mechanical resonance frequency must be high compared to the maximum frequency (10KHz) used in the deformable mirror (200 KHz for a 50 μm length).
To manufacture a diamond membrane of 1–10 μm thickness range, we must use nanocrystalline or ultra-nanocrystalline CVD diamond (Hess 2012). Membranes as thin as 100 nm already exist (Espinosa et al. 2003) and clearly demonstrate the feasibility of the DM concept. The choice of reflection coating for the laser beams can be a simple aluminum, because it directly provides a low-density membrane (3.51 g/cm3 for CVD-diamond material and 2.7 g/cm3 for aluminum coating), but gold (19.3 g/cm3) provides a better reflectivity at 980 nm than aluminum also with low-roughness and low-depolarization issue. The gold coating must be greater than 60 nm of thickness. Concerning the reflecting surface used for the phase corrections, the metallic coating can also be aluminum because it provides low roughness and small mass at the other face.
In the following section we present the fundamental equations that describe the radiation pressure (the Lorentz law), using as a starting point Maxwell’s electromagnetic field equations.
3. Radiation pressure simulation
3.1. The Lorentz law
Following Mansuripur (2004), we calculated the
electromagnetic radiation force and its associated acceleration for a thin suspended
membrane, produced by a direct application of the Lorentz law of classical
electrodynamics. We used Maxwell’s equations to determine the distributions of the two
fields, E and H, present in the electromagnetic
radiation both inside and outside the considered medium. The Lorentz law describes the
electromagnetic force F on a particle of charge q and
velocity 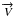 :
:
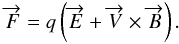 (2)The magnetic field
(2)The magnetic field
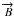 is related to the H-field via the permeability of free space
μ0,
is related to the H-field via the permeability of free space
μ0,  (3)All three
(3)All three
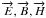 fields are classical time harmonic fields, written for the electric field as
fields are classical time harmonic fields, written for the electric field as
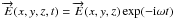 with
ω the angular frequency.
with
ω the angular frequency.
The next step is to calculate the interaction of laser light in the considered medium.
For this purpose we introduce two new vectors that take into account some of the
properties of the interacting medium:
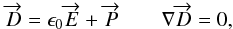 (4)where
(4)where
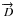 is the electric displacement vector,
is the electric displacement vector, 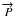 is the local polarization density within the considered medium, and
ϵ0 is the permittivity of free space. The divergence of
is the local polarization density within the considered medium, and
ϵ0 is the permittivity of free space. The divergence of
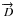 is generally equal to zero and occurs when there are no free charges in the system.
is generally equal to zero and occurs when there are no free charges in the system.
In a linear medium with a relative permittivity ϵ , the two vectors
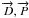 become
become 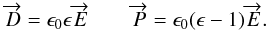 (5)The complex refractive
index of the medium is given by
(5)The complex refractive
index of the medium is given by 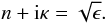 When the light interacts
with the medium, the perpendicular H-field at the interface between
adjacent media must remain continuous. Nevertheless, this is not the case for a tangential
H-field at such interfaces. Maxwell’s equation
When the light interacts
with the medium, the perpendicular H-field at the interface between
adjacent media must remain continuous. Nevertheless, this is not the case for a tangential
H-field at such interfaces. Maxwell’s equation
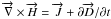 can be used to create an
interfacial current density,
can be used to create an
interfacial current density, 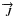 .
The high conductance of aluminum or gold permits the flow of the surface current. Using
the charge conservation principle for this specific medium, we obtain
.
The high conductance of aluminum or gold permits the flow of the surface current. Using
the charge conservation principle for this specific medium, we obtain
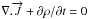 , where ρ is
the surface charge density. The motion of the conduction electrons corresponds to a
surface current density
, where ρ is
the surface charge density. The motion of the conduction electrons corresponds to a
surface current density 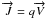 and the only source of electrical currents are bound charges, with a current
density,
and the only source of electrical currents are bound charges, with a current
density, 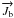 ,
of
,
of 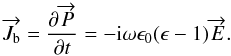 (6)The
H-field of the electromagnetic wave will create a force on the bound
current, which, according to the Lorentz law, will be
(6)The
H-field of the electromagnetic wave will create a force on the bound
current, which, according to the Lorentz law, will be
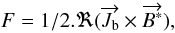 (7)where ℜ is the real
part of the vectorial product between the bound current density,
(7)where ℜ is the real
part of the vectorial product between the bound current density,
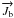 ,
and the magnetic field
,
and the magnetic field 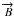 .
.
3.2. Forces on a homogeneous membrane with clamped edge
 |
Fig. 2 Composition of the thin membrane and how the light from the laser interacts in its
interior. The membrane consists of three films: (a) an aluminum coating of width
h1, (b) a CVD-diamond substrate of width
h2, and (c) an aluminum or gold coating, of width
h3. Left: the shape of the
clamped-edge membrane, hm(r), is only
depending on r, and in the classical adaptive optics
implementations, the gravity vector is vertical. Right: a linearly
polarized plane wave (Ein,
Hin) is normally incident on the surface of a medium
of complex dielectric constant ϵ1.
E1t, E1r are the electric
fields inside the first reflective medium for, the transmitted and reflected waves
respectively. For a good reflection of light with aluminum or gold, the thickness of
the coating must be greater than 50 nm and the two electric fields inside with
medium will be strongly attenuated. In this case, E2t,
E2r,Et
inside and outside the CVD-diamond will be equal to zero.
|
In the vacuum, the amplitude of the H-field of the electromagnetic wave
is proportional to the E-field
(H0 = E0/Z0)
with 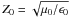 being the free-space impedance. In a dielectric medium with a relative permittivity
ϵn this relation
becomes
being the free-space impedance. In a dielectric medium with a relative permittivity
ϵn this relation
becomes 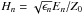 .
.
As shown in Fig. 2, the membrane is illuminated at a
normal incidence, the complex reflection and transmission coefficients are denoted by
r1 and t1 respectively, and the
absorption coefficient is A1 (see Table 1). The counter-propagating beams within the first aluminum coating have
an E-field amplitude E1t and
E1r and the total field distribution is given by
![\begin{eqnarray} &&\label{efield1} E_x=E_{\rm 1t}{\rm e}^{{\rm i}\Gamma z}+E_{\rm 1r}{\rm e}^{-{\rm i}\Gamma z} \nonumber \\[1mm] && H_y=(\sqrt{\epsilon_1}E_{\rm 1t}/Z_0){\rm e}^{{\rm i}\Gamma z}-(\sqrt{\epsilon_1}E_{\rm 1r}/Z_0){\rm e}^{-{\rm i}\Gamma z} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq71.png) (8)
(8) ![\begin{eqnarray} \label{efield2} &&E_{\rm 1t}=2E_{\rm in} /\left((1+\rho) +\sqrt{\epsilon_1}(1-\rho)\right) \qquad E_{\rm 1r}=\rho E_{\rm 1t}\\ &&\Gamma=2\pi\sqrt{\epsilon_1}/\lambda \qquad \rho=\left(\sqrt{\epsilon_1}-1\right) / \left(\sqrt{\epsilon_1}+1\right){\rm e}^{{\rm i}2\Gamma h_1} \\[1mm] \label{efield3} &&r_1=\frac{\rho - \left(\left(\sqrt{\epsilon_1}-1\right)/\left(\sqrt{\epsilon_1}+1\right) \right)} {1-\rho\left(\left(\sqrt{\epsilon_1}-1\right)/\left(\sqrt{\epsilon_1}+1\right) \right)} \\ &&t_1= \frac{4\sqrt{\epsilon_1}} {\left(\sqrt{\epsilon_1}+1\right)^2 {\rm e}^{-{\rm i}\Gamma h_1} -\left(\sqrt{\epsilon_1}-1\right)^2 {\rm e}^{{\rm i}\Gamma h_1}}\\ &&|r_1|^2 + |t_1|^2 = 1+A_1 \qquad A_1>0 . \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq72.png) Therefore,
the radiation pressure force, Fz, becomes
Therefore,
the radiation pressure force, Fz, becomes
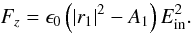 (14)
(14)
Parameters used for the reflection coating.
4. Optical simulation
This section presents a complete analytical simulation of the electromagnetic field due to the VCSEL’s array on the membrane. The VCSEL array is composed of nx × ny lasers. Each laser monomode diode creates a Gaussian illumination on the microlens array. The proposed optical system propagates this laser mode onto the membrane with the same shape. Nevertheless, in the classical micro lens array, the Fresnel diffraction pattern between the lenses sets a limitation on their filling factor. Indeed, it is currently impossible to manufacture lenselet arrays with 100% of filling factor (it is usually around 99%). If the lens pitch in the x and y directions are 50 μm, the diffractive zone is ≈0.5 μm. All lens boundaries create Fresnel diffraction is called a waffle effect.
The entrance amplitude light field in each microlens is considered Gaussian with the
following definition: 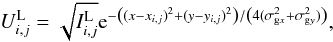 (15)where
(15)where
 is the intensity of
the laser (i,j), and
xi,j,yi,j
are the cartesian coordinates of the beam center for the laser (i,j).
The 4 factor on the beam width in amplitude corresponds to a classical Gaussian distribution
beam (with the factor of 2 in the denominator) for the intensity laser,
is the intensity of
the laser (i,j), and
xi,j,yi,j
are the cartesian coordinates of the beam center for the laser (i,j).
The 4 factor on the beam width in amplitude corresponds to a classical Gaussian distribution
beam (with the factor of 2 in the denominator) for the intensity laser, 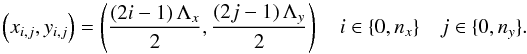 (16)Finally, we assume
that each Gaussian is symmetric, with
σgx = σgy,
although this will not be the case if the laser diode presents beam astigmatism.
(16)Finally, we assume
that each Gaussian is symmetric, with
σgx = σgy,
although this will not be the case if the laser diode presents beam astigmatism.
Now, we calculate the Fresnel diffraction caused by the imperfect filling factor on the square array of laser diodes. The array pitch is set by the previously defined Λx and Λy distances. Fx and Fy are the filling factors in the cartesian coordinates, with Fx = 0.99Λx and Fy = 0.99Λy.
The entire demonstration is given in appendix A and the results are presented in Fig. 3.
 |
Fig. 3 Numerical simulation of the illuminated field Pz obtained by the proposed VCSEL array (128 × 128, pitch of 50 μm). We chose a circular clamped membrane of rm = 7 mm (circle limit). Our simulation considers a random wavefront error of 0.1 wave rms and includes the Fresnel propagation. To enhance the last effect in the image, the brightness scale is not linear (|I|0.25). |
For z = 2 cm and λ = 0.98 μm, all Fresnel numbers are ≪ 1 (Fraunhofer diffraction mode). A numerical calculation shows that UFr < 10-4Ug, which means that the waffle effect caused by the imperfect filling factor seems to be very low. The total illuminated laser field on the membrane can be considered continuous. The membrane mechanical deformation with nx × ny actuators will be modelled as a single, large actuator. The full analytical development is the scope of the following section.
Material properties.
5. Modeling the membrane deformation w
5.1. Equation of motion for a membrane in cartesian coordinates
Let w = w(x,y,t) be the mechanical
membrane deformation, and
Pz = Pz(x,y,t)
the radiative pressure given by the VCSEL array. The full dynamical mechanical deformation
is ![\begin{eqnarray} \label{mcc1} &&-\frac{1} {ab} \left[\bar{\rho} h \frac{\partial^2 w}{\partial t^2} + \zeta\frac{\partial w}{\partial t} + K w \right]\nonumber\\ &&\quad + \left[ D \bigtriangledown^4 w -\frac{P_{t}} {ab} \bigtriangledown^2 w - \frac{h} {ab} G\left( \phi_s,\sigma \right) \right]= P_z(x,y,t) . \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq108.png) (17) Assuming
that the temporal part of the radiation pressure is equal to the membrane deformation, the
the solution to Eq. (17) can be decomposed
into a spatial and temporal component as follows:
(17) Assuming
that the temporal part of the radiation pressure is equal to the membrane deformation, the
the solution to Eq. (17) can be decomposed
into a spatial and temporal component as follows: 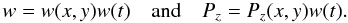 (18)Plugging
Eqs. (18) into (17) yields the temporal and spatial equations
as follows:
(18)Plugging
Eqs. (18) into (17) yields the temporal and spatial equations
as follows: 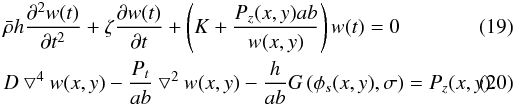 Details
about each of the terms the temporal and spatial equations consist of will be provided in
the following sections. Appendix B gives static
solutions in the Fourier plane for the linear model. These solutions are needed to enable
the numerical simulations of the membrane deformation.
Details
about each of the terms the temporal and spatial equations consist of will be provided in
the following sections. Appendix B gives static
solutions in the Fourier plane for the linear model. These solutions are needed to enable
the numerical simulations of the membrane deformation.
5.2. Numerical calculation: the Galerkin method
Prior to the development of the finite element method (FEM), there existed an approximation and recursive technique to solve differential equations, known as the Galerkin method (Galerkin 1915). The basic idea of this technique is to use the Fourier development given by Eq. (B.3) with Wn,m as unknown parameters to approximate the solution iteratively. For more information concerning this method see Dubey (2005), and Kerrour & Hobar (2006). The Galerkin method is also a method of weighted residuals, where over the interior and boundary an appropriate function is set to zero. Now, we carefully explain the calculation to obtain de radiation pressure Pz(x,y) and the membrane deformation w(x,y) (the final wavefront).
We define the weighted residuals R(x,y) as
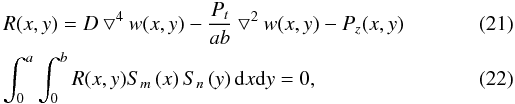 where
w(x,y) is the solution on the DM array:
where
w(x,y) is the solution on the DM array: ![\begin{eqnarray} \label{gm2} R(x,y)&=& \sum_{m'=1}^{n_y} \sum_{n'=1}^{n_x} W_{m',n'} \left(D \bigtriangledown^4\left[S_{m'}\left(x\right) S_{n'}\left(y\right)\right]\right)\nonumber \\[1mm] &&-\sum_{m'=1}^{n_y} \sum_{n'=1}^{n_x} W_{m',n'} \left( \frac{P_{t}} {ab}\bigtriangledown^2\left[S_{m'}\left(x\right)S_{n'}\left(y\right)\right] \right)\nonumber \\[1mm] &&- \frac{4}{ab}\int_0^a \int_0^b P_z(x,y) S_m\left(x\right) S_n\left(y\right){\rm d}x{\rm d}y . \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq116.png) (23)After
some calculations, Eq. (23) gives
(23)After
some calculations, Eq. (23) gives
![\begin{eqnarray} \label{gm3} && \sum_{m=1}^{n_x} \sum_{n=1}^{n_y} W_{m,n} \left[D \left( \left( \frac{m \pi}{a}\right)^2 + \left( \frac{n \pi}{b}\right)^2\right)^2 -\frac{P_{t}} {ab}\left( \left(\frac{m \pi}{a}\right)^2 + \left( \frac{n \pi}{b}\right)^2\right)\right]=\nonumber \\[1mm] &&\frac{4}{ab}\int_0^a \int_0^b \left[\frac{1}{c}\frac{(|r_1|^2 - A_1)}{ab} U_{\rm f}(x,y)U^*_{\rm f}(x,y) \right] S_m\left(x\right) S_n\left(y\right) {\rm d}x , {\rm d}y\nonumber \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq117.png) where
c is the speed of light in the vacuum. The total illuminated laser
field is
Uf = Ug + UFr ≈ Ug.
This is because, as we previously calculated, the Fresnel propagation is negligible,
with UFr < 10-4Ug,
where
c is the speed of light in the vacuum. The total illuminated laser
field is
Uf = Ug + UFr ≈ Ug.
This is because, as we previously calculated, the Fresnel propagation is negligible,
with UFr < 10-4Ug,
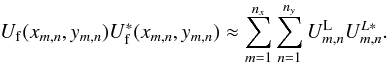 (24)
(24)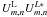 is the influence function of actuator m,n, and
(xm,n,ym,n)
are the cartesian coordinates of the actuator center (see Eq. (15)). However, the final shape of the mirror
surface depends on the positions of the neighbor actuators. The two matrixes
Wm,n and
Iz,m,n are not diagonals. Solving this
linear system allows us to fully characterize this influence function.
is the influence function of actuator m,n, and
(xm,n,ym,n)
are the cartesian coordinates of the actuator center (see Eq. (15)). However, the final shape of the mirror
surface depends on the positions of the neighbor actuators. The two matrixes
Wm,n and
Iz,m,n are not diagonals. Solving this
linear system allows us to fully characterize this influence function.
The membrane deformation linear model, presented in this section, is the first approximation to retrieve the relationship between w(x,y) and Pz(x,y). However, two corrections must be applied on this model:
-
because the membrane is a multi-layer system, itsmechanical properties must be corrected for;
-
the deformation w(x,y) becomes nonlinear when the amplitude is larger than the membrane thickness. Therefore a nonlinear model that includes an Airy stress function is preferable to obtain a better evaluation of membrane deformation amplitude w(x,y).
Parameters used for the composite membrane.
5.3. Multi-element membrane
The mechanical properties of a multi-layer system differ from a single-layer homogenous
membrane. Because the Poisson’s ratios differ for diamond/aluminum, there will be a change
in the length of the lines that are parallel to the lower material (Al) due to an in-plane
strain ϵz. An equivalent single-material
approach, Myers et al. (2006), can be used for this
study if 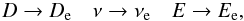 (25)where
De,νe,Ee
are the equivalent mechanical properties of the proposed structure. Our model is composed
of four layers of different materials. The top layers are considered as one bi-material
layer (Al 100 nm/diamond 500 nm) and the bottom one as well (diamond 500 nm/Al 100 nm or
diamond 500 nm/Au 60 nm). Some mechanical properties of these materials are summarized in
Table 2. The mathematical expressions of
De,νe,Ee
are given in Appendix C.
(25)where
De,νe,Ee
are the equivalent mechanical properties of the proposed structure. Our model is composed
of four layers of different materials. The top layers are considered as one bi-material
layer (Al 100 nm/diamond 500 nm) and the bottom one as well (diamond 500 nm/Al 100 nm or
diamond 500 nm/Au 60 nm). Some mechanical properties of these materials are summarized in
Table 2. The mathematical expressions of
De,νe,Ee
are given in Appendix C.
For the layer combination Al/Au we chose an average Young’s modulus of 70 GPa with a Poisson’s ratio of 0.33 and 0.44, respectively. Concerning the Stress coefficient σ, we chose the conservative value of 20 MPa. A coating optimization of the Al/diamond/Au system can decrease near the zero value the stress coefficient.
5.4. Deflection of the membrane
The deflection of a circular clamped membrane is given by Sheplak & Seiner (1999):
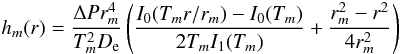 (26)
(26)![\begin{eqnarray} \nonumber \\[-0.7cm] T_m=\frac{r_m} {h} \sqrt{\frac{12(1-\nu^2_{\rm e}) \sigma} {E_{\rm e}}} , \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq133.png) (27)where
ΔP is differential pressure,
Tm is a tension parameter due to the
residual stress σ in the membrane,
I0(Tm) and
I1(Tm) are
modified Bessel function on the order of 0 and 1 respectively. The maximum deflection of
the membrane is given for r = 0,
(27)where
ΔP is differential pressure,
Tm is a tension parameter due to the
residual stress σ in the membrane,
I0(Tm) and
I1(Tm) are
modified Bessel function on the order of 0 and 1 respectively. The maximum deflection of
the membrane is given for r = 0,
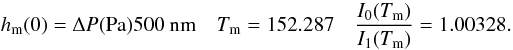 (28)We notice
that the deformation memory will be very low for diamond material because this effect
occurs only on the elasticity deformation region (>95 GPa) and
diamond has the highest elastic moduli and fracture strength of any known material. In the
real world, the membrane breaks with the cleavage process before non-reversible
deformation. For cubic materials, the crack occurs around
E/10 ≈ 110 GPa (Hess
2012).
(28)We notice
that the deformation memory will be very low for diamond material because this effect
occurs only on the elasticity deformation region (>95 GPa) and
diamond has the highest elastic moduli and fracture strength of any known material. In the
real world, the membrane breaks with the cleavage process before non-reversible
deformation. For cubic materials, the crack occurs around
E/10 ≈ 110 GPa (Hess
2012).
5.5. Nonlinear model for the static solutions
Our surface deflection amplitude can be more than the membrane thickness. In this case,
the vertical deflections are accompanied by stretching of the mirror surface. The
stretching is a nonlinear process that causes the mirror layer to increase its
load-carrying capabilities. To include this nonlinear stretching of the membrane into our
model the plate equation must modified as 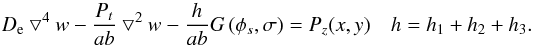 (29)The complete
evaluation of this equation using the same Galerkin method as the linear model in
Appendix B is given in Appendix D.
(29)The complete
evaluation of this equation using the same Galerkin method as the linear model in
Appendix B is given in Appendix D.
6. DM: the spatial response
Using the methods describe above, we simulated our 128 × 128 DM. First, we used the linear
model with the membrane composite stiffness De to estimate the
deformation function wL(x,y). Equation (24) can be put into matrix form:
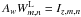 .
.
Second, we used Eq. (D.17) to estimate the Airy stress function with the linear solution of the deformation function wL(x,y). We calculated the new deflection function wNL(x,y) using the nonlinear model Eq. (D.18). Finally, to increase the precision of the w(x,y) result, we repeated the two last processes until the desired relative error was achieved.
6.1. Direct evaluation
For our study, we needed to obtain the input laser field for a known membrane deformation. In this context, this is not necessary to resolve the system of equations.
The laser intensity was evaluated directly using the nonlinear model (Eq. (D.18)). First of all, we assumed that the
final membrane deformation w(x,y) is a pure Zernike
polynomial Zp. Using Eq. (B.7), we numerically projected the Zernike
polynomial Zp on the
Sm(x)/Sn(y)
Fourier basis, we obtained the Zm,n
coefficients as Wm,n. As we explain in the
following scheme, we evaluated the nonlinear function G and calculated
the input laser flux 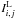 ,
,
![\begin{equation} \nonumber Z_p \longrightarrow Z_{m,n} \!\longrightarrow\! \left[\phi_{s,m,n}\, / \,G\left(0,\sigma\right)\right]_{\rm NL} \!\longrightarrow\! \left[G\left( \phi_s,\sigma\right)\right]_{\rm NL} \!\longrightarrow\! I_{z,m,n} . \end{equation}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq151.png) Using the
Iz,m,n function evaluation in Appendix
E for a purely Gaussian laser field (without the
Fresnel propagation), we obtain
Using the
Iz,m,n function evaluation in Appendix
E for a purely Gaussian laser field (without the
Fresnel propagation), we obtain 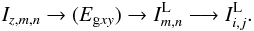 An example using
an input Zernike (Z55) in the pupil plane is presented in
Fig. 4.
An example using
an input Zernike (Z55) in the pupil plane is presented in
Fig. 4.
 |
Fig. 4 Example of the nonlinear simulation on Zernike 55. The projection of
Z55 in the Fourier plane gives the
Zm,n/Wm,n
coefficients. The Airy-type stress function
φs,m,n is evaluated by the
Wm,n coupling (see Eq. (D.17)). The nonlinear part of the
Eq. (29)
(G(φs,σ))
is calculated and the Iz,m,n is
directly obtained. A deconvolution by the Gaussian laser beam distribution
(Egxy) and the final projection on
the DM plane gives |
Cavity depth and damping coefficient for Al/diamond/Au membrane.
6.2. Positive vs. negative correction
Our proposed optical MEMS using the radiation pressure as actuator performs wavefront
deflection in the same way (always the positive values). Negative wavefront values are
also allowed but we need to add an input curvature as a defocus
∝ 4r2/a2 on
the membrane. The input wavefront Zp is
changed to 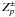 as
as
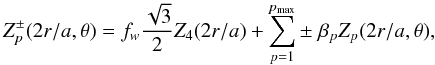 (30)where
(30)where
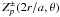 is the
desired entrance wavefront (here a sum of simple Zernike polynomials) in
the r,θ polar coordinate
basis, ±βp are the Zernike weight
coefficients, and fw is the level of membrane
defocus. We present the corrected wavefront as a finite sum of Zernikes
between p = 1 to pmax ≈ 10 000
for 128 × 128 actuators.
is the
desired entrance wavefront (here a sum of simple Zernike polynomials) in
the r,θ polar coordinate
basis, ±βp are the Zernike weight
coefficients, and fw is the level of membrane
defocus. We present the corrected wavefront as a finite sum of Zernikes
between p = 1 to pmax ≈ 10 000
for 128 × 128 actuators.
Under these conditions, the dynamic of the optical MEMS is decreased by a factor of about 2 to perform both positive and negative wavefront corrections. The maximum deflection is calculated according to our previous nonlinear model (see Sect. D), representing the full dynamic of the proposed architecture (i.e. 1 μm = ±500 nm).
7. DM: dynamical modeling
We notice that the spatial nonlinear equation (see Eq. (29)) is given in cartesian coordinates because of the square shape of the nx × ny actuators. The radiation pressure acts as forced vibration on a clamped circular membrane and we coupled the possible vibration effect of actuators with some natural modes of vibration of the circular membrane.
7.1. The DM frequency response
To properly calculate the coupling parameter, we write the spatial and temporal equations
in the following way. ![\begin{eqnarray} \label{eqwxyt} &&\bigtriangledown^4 w(x,y) \! -\! \frac{P_{t}} {D_{\rm e} ab} \bigtriangledown^2 w(x,y) \! -\! \frac{h} {D_{\rm e} ab} G\left( \phi_s(x,y),\sigma \right) \! -\! \lambda^4_m w(x,y) \! =\! 0 \nonumber\\[1.5mm] &&\frac{\partial^2 w(t)} {\partial t^2} + \frac{\zeta} {\bar{\rho} h} \frac{\partial w(t)} {\partial t} + \left(\omega^2_0 + \omega^2\right)w(t)= 0 \nonumber \\[1.5mm] && \lambda^4_m=\frac{P_z} {w D_{\rm e}} \qquad \omega^2=\frac{P_z} {w} \frac{ab}{\bar{\rho} h} \qquad \omega^2_0=\frac{K} {\bar{\rho} h} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq177.png) (31)
(31)
-
where
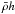 is the main dynamical
coefficient proportional to the mass of the membrane;
is the main dynamical
coefficient proportional to the mass of the membrane; -
ζ is the damping coefficient (including air viscous damping);
-
K + Pz(x,y)ab/w(x,y) is the stiffness coefficient of the proposed system (including the air stiffness K inside a cavity).
The resolution of the temporal equation gives ![\begin{eqnarray} \label{eqwt} &&w(t)={\rm e}^{\frac{-t\zeta}{2\rho h}} \left(\frac{1}{C_{\zeta}} {\rm sinh}\left(\frac{-t}{2\rho h}C_{\zeta}\right) + {\rm cosh}\left(\frac{-t}{2\rho h}C_{\zeta} \right)\right) \\[1.5mm] &&C_{\zeta} = \sqrt{\zeta^2-4\bar{\rho}^2h^2\left(\omega^2_0 + \omega^2\right)} . \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq181.png)
7.2. Resonance frequencies calculation for a circular clamped membrane
In the previous analysis, the membrane temporal motion was not governed by resonance
frequencies. Indeed, the
Pz/w
parameter is not a modal function of a circular clamped membrane. If we are interested in
the effect of resonance frequencies on the membrane dynamic, we need to perform a modal
analysis for a circular clamped membrane in polar coordinates (see Mehta 2009), which gives ![\begin{eqnarray} \label{eqrf1} && w(r,\theta) \propto \left(J_{m}(\lambda_c r)I_m(\lambda_c r_m)-J_m(\lambda_c r_m)I_m(\lambda_c r)\right) \left(\cos(m \theta\right) \nonumber \\[1.5mm] &&\quad \left. + \sin(m \theta)\right) . \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq183.png) (34) The
frequency equation with infinitely many solutions for each value of m is
(34) The
frequency equation with infinitely many solutions for each value of m is
![\begin{eqnarray} \label{eqrf2} &&\left[\frac{\partial J_{m}(\lambda_c r)} {\partial r} I_m(\lambda_c r_m)-J_m(\lambda_c r_m) \frac{\partial I_m(\lambda_{\rm c} r)} {\partial r}\right]_{r=r_m} =0 \\[1.5mm] &&J_{m-1}(\lambda_{{\rm c},m,n} r_m)I_m(\lambda_{{\rm c},m,n} r_m)-J_m(\lambda_{{\rm c},m,n} r_m)I_{m-1}(\lambda_{{\rm c},m,n} r_m)=0 . \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq185.png) Each
Bessel function also possesses n roots (nodes), therefore
λc is a function of the m and
n coefficients. We notice that these two parameters
n,m are not the same physical meaning as the previous Fourier analysis
for spatial solution. The values of resonance frequencies are given by
Each
Bessel function also possesses n roots (nodes), therefore
λc is a function of the m and
n coefficients. We notice that these two parameters
n,m are not the same physical meaning as the previous Fourier analysis
for spatial solution. The values of resonance frequencies are given by 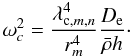 (37)We also point out
that the first frequency for an Al/diamond/Al membrane
is fc,0,1 = 116 Hz
compared to the Al/diamond/Au membrane,
where fc,0,1 = 105 Hz
(see Table 5).
(37)We also point out
that the first frequency for an Al/diamond/Al membrane
is fc,0,1 = 116 Hz
compared to the Al/diamond/Au membrane,
where fc,0,1 = 105 Hz
(see Table 5).
Some 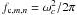 values in Hz for the free vibration of the Al/diamond/Au membrane.
values in Hz for the free vibration of the Al/diamond/Au membrane.
7.3. The modal decomposition by a modified Hankel transform
We previously calculated the temporal response of the membrane as a function of
Pz(x,y)/w(x,y)
(see Eq. (32)). The important question is
to know whether there exists natural resonance for a fixed value of wavefront correction
w(x,y) or not. For a membrane deflection
w = w(r,θ) (Eq. (34)), we propose to calculate the resonance
coefficients αc,m,n using a modified version
of the Hankel transform, 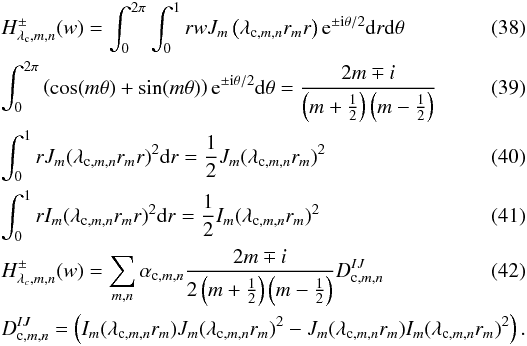 We
previously integrated the w function on the θ with a
modulation of e±iθ/2 as an azimuthally
averaged function to perform the correct modal analysis.
We
previously integrated the w function on the θ with a
modulation of e±iθ/2 as an azimuthally
averaged function to perform the correct modal analysis.
The imaginary and real part correspond to the cos and the sin modulation of the wavefront. This calculation is the modal decomposition of the deflection function w for cos/sin modes.
If the input wavefront is a direct sum of Zernike polynomials (Nijboer-Zernike
decomposition, see Magette 2010), the modal
decomposition is more straightforward and we have 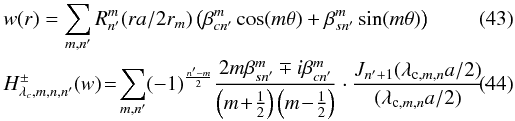 If
we equalize Eqs. (42) with (44), we obtain the resonance frequencies
αc,m,n as a function of Zernike
coefficients
If
we equalize Eqs. (42) with (44), we obtain the resonance frequencies
αc,m,n as a function of Zernike
coefficients 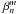 as
as
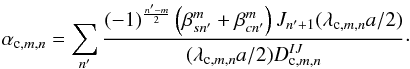 (45)In this case, if a
low-order Zernike polynomials have a larger amplitude with respect to each other, the
deformable mirror will present overshooting behavior for some resonance frequencies given
by our modal analysis.
(45)In this case, if a
low-order Zernike polynomials have a larger amplitude with respect to each other, the
deformable mirror will present overshooting behavior for some resonance frequencies given
by our modal analysis.
7.4. Passive vibration attenuation
The DM system possesses a small cavity between the moving membrane and the polarizing
optical system. This cavity can be open (pressure equilibrium) or closed. The cavity depth
can be adjusted for the DM optimization. If we assume that this cavity depth was
significantly smaller than the radius of the membrane, the ratio
Lcav/rm ≪ 1.
In this case, we can approximate the response of the air within the cavity as a
distribution of springs and dampers acting on each differential element of the membrane
(actuators). The cavity stiffness K can be defined as
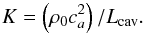 The resonance
frequencies and the cavity stiffness calculation show a useful frequency bandpass of
about 1–10 KHz. Indeed, with an attenuation of 1/f for
natural resonance frequencies (see Table 5), and
the Shannon theorem applied on the cavity stiffness frequency
(ω0/2π), the optimal
frequency response of our optical DM is in the KHz range.
The resonance
frequencies and the cavity stiffness calculation show a useful frequency bandpass of
about 1–10 KHz. Indeed, with an attenuation of 1/f for
natural resonance frequencies (see Table 5), and
the Shannon theorem applied on the cavity stiffness frequency
(ω0/2π), the optimal
frequency response of our optical DM is in the KHz range.
8. Laser membrane heating: cooling parameters
Under high-power laser irradiation, the mirror absorbs a small fraction of the incident light and is heated to temperatures much higher than those of the coating beneath it. The thermal degradation must be evaluated and minimized to prevent mechanical degradation or thermal shape deformation. A cooling mechanism overcomes this thermal effect.
We notice that the laser damage of a classical thin membrane is as low as 340 W/cm2 for polyimide material, and >100 KW/cm2 for silicon nitride.
It is important to understand the mechanisms of the thermally induced distortions. One possible explanation of the membrane distortion is that the high laser power creates a spatially varying temperature distribution, which may warp the surface. Another possible source of the thermally induced distortions is the differential thermal expansion of the membrane’s material.
Concerning the silicon nitride material used for multi-layer dielectric-coated deformable mirrors, Sinha et al. (2002) obtained a thermally induced wavefront distortion of 32.3 and 39.1 nm rms for an incident intensity of 140 and 212 W/cm2, respectively, with a cw 1064 nm laser on a gold coated membrane. These values are very pessimistic regarding our free-standing reflective diamond membrane architecture. Indeed, the DM device used in Sinha et al. (2002) is a complex dielectric structure with silicon pillars, which explains the localization of the deformations by differential thermal expansion. A simple gold-coated silicon mirror presents no distortion for an incident intensity of 300 W/cm2.
This last study must be compared with the present design, where the maximum incident laser
intensity is 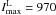 W/cm2 for 25 mW per
diode. In our case, the estimated membrane conductivity is about 1588 W/(mK) for a
gold-coated membrane and the thermal field distribution will be more uniform because the
laser heating is efficiently conducted over the membrane surface because of the high
conductivity of the materials (1800/318/237 W/(mK) for diamond, gold, and aluminum,
respectively).
W/cm2 for 25 mW per
diode. In our case, the estimated membrane conductivity is about 1588 W/(mK) for a
gold-coated membrane and the thermal field distribution will be more uniform because the
laser heating is efficiently conducted over the membrane surface because of the high
conductivity of the materials (1800/318/237 W/(mK) for diamond, gold, and aluminum,
respectively).
In our irradiation condition, a thermally induced wavefront distortion of less than 20 nm
rms seems to be achievable. The membrane cooling seems to be mandatory to perform high
wavefront precision corrections (residual <1 nm) with a maximum
absorbed laser power of 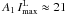 W/cm2 for gold-back
coating. Some studies that used silicon nitride material such as Morse et al. (2008) or Lee et al.
(2006), show a more experimental analysis of deformable mirrors under high-power
laser flux.
W/cm2 for gold-back
coating. Some studies that used silicon nitride material such as Morse et al. (2008) or Lee et al.
(2006), show a more experimental analysis of deformable mirrors under high-power
laser flux.
Another problem that occurs with laser heating is the mechanical thermal stress. Indeed,
changes in temperature produce expansion or contraction, resulting in thermal strains and
stress. For linear elastic materials, the thermal stress, σ, is governed by
the following expression: 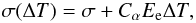 (46)where
Cα = 3.74 × 10-6 K-1
is the thermal expansion of Al/diamond/Au membrane dominated by the two metallic layers.
Indeed, the thermal expansion of diamond is only 1.18 × 10-6 K-1
compared with 23.1 and 14.2 × 10-6 K-1 for aluminum and gold,
respectively.
(46)where
Cα = 3.74 × 10-6 K-1
is the thermal expansion of Al/diamond/Au membrane dominated by the two metallic layers.
Indeed, the thermal expansion of diamond is only 1.18 × 10-6 K-1
compared with 23.1 and 14.2 × 10-6 K-1 for aluminum and gold,
respectively.
 |
Fig. 5 Non linear simulation of the w(x,y) maximum deflection with respect to the Zernike polynomial order. We present the deflection for two different membrane structures. The gold back-face coating shows a better dynamic than classical Al coating. A maximum deflection of 1 μm with ≈25 mW per laser diode seems to be possible. |
9. Optical cavity for high-power laser?
The optical scheme presented in Fig. 1 permits using of a high-reflectivity (R > 99.9%) cavity mirror to increase the laser power inside the cavity. This configuration could be used with a thicker membrane (2–10 μm) on the linear mechanical deformation region (see Fig. 5 for the low-amplitude deformation range). Owing to the cooling process, to ensure a high wavefront precision correction, this configuration seems to be limited to increasing the wavefront dynamic of our proposed DM.
10. Discussion
We now discuss the practical aspects of the proposed DM concept. The very thin CVD-diamond membrane must be manufactured using nanocrystalline or ultra-nanocrystalline grown to ensure the best mechanical properties near the single diamond crystal with a low roughness (1–3 nm rms). Some laboratories and industries routinely manufacture such membranes for micro-optical components such as MEMS.
The Au/Al coating can be optimized to minimize the stress coefficient σ. Concerning the aluminum coating σ = 20 MPa is generally obtained with classical sputtering system while for chromium-gold coating σ = −20 MPa can be reached after optimizing thermodynamical conditions.
Microlens arrays in fused silica with a very good wavefront error (<λ/20 rms in the visible) and very accurate centering (<0.5 μm) are commercially available, but a dedicated micro-optical lens manufacturing can be achieved for each VCSELs laser (see Bardinal et al. 2011) to allow the best possible lens centering, with high-precision microelectronic technology.
Finally, the main challenge is the VCSELs array manufacturing, not for the near-infrared laser technology (micro-cavity with Bragg mirrors), but for the properties of the metal wires on the matrix-addressable array for a high-power system. Indeed, for a high-power laser system, where the overall laser conversion efficiency is between 35% to 50%, the metal wire resistivity is an important limitation regarding the thermal management.
11. Conclusion
We showed the simulations of a new high-density deformable mirror using the VSCEL radiation pressure as actuators on a thin diamond membrane. A complete analysis with the nonlinear plate equation shows a dynamic of ±0.5 μm attainable with 25 mW per laser diode. Large array actuators (here 128 × 128 actuators) allowed us to correct the first 10 000 Zernike polynomials without segmentation effect.
The VCSEL array is modulated up to 1 GHz, but the temporal limitation response of the DM is mechanical because of the membrane response and its sufficient dampening. The dynamical analysis showed a possible use of the DM in 1 to 10 KHz. In theses cases, our proposed DM (considered as an optical MEMS) is well-suited for eXterm Adaptive Optics architecture as a “tweeter” correction (i.e. high-order correction with small dynamic). Indeed, low-order wavefront correction (up to Z36) with f < 1 KHz with a classical piezoelectric DM as a “boomer” deformable mirror is needed to desaturate the wavefront correction. This configruation can be applied for the E-ELT AO system (Hubin et al. 2006).
Acknowledgments
This work received the support of the University of Liège. The author is grateful to T. Nakos (ESO) for the manuscript corrections. The author also thank Antoine Labeyrie, for helpful discussions concerning the cavity optimization. The author wishes to thank the anonymous referee for useful comments and corrections.
References
- Azucena, O., Fernandez, B., & Kubby, J. 2008, in MEMS Adaptive Optics II, eds. S. S. Olivier, T. G. Bifano, & J. A. Kubby, Proc. SPIE, 6888, 68880Q [Google Scholar]
- Bardinal, V., Camps, T., Reig, B., et al. 2011, Adv. Opt. Tech., 2011, ID 609643 [Google Scholar]
- Barron, L. 2005, High-Reflectance, Sputter-Deposited Aluminum Alloy Thin Films for Micro-Electro-Mechanical Systems, Master Thesis [Google Scholar]
- Bass, M., DeCusatis, C., Enoch, J., et al. 2009, Handbook of Optics, Vol. IV, Optical Properties of Materials, Nonlinear Optics, Quantum Optics (McGraw-Hill), 1152 [Google Scholar]
- Conan, J.-M., Mugnier, L. M., Fusco, T., Michau, V., & Rousset, G. 1998, Appl. Opt., 37, 4614 [NASA ADS] [CrossRef] [Google Scholar]
- Conk, R. 2002, Fabrication techniques for micro-optical device arrays, Master Thesis [Google Scholar]
- Daughton, D. R., MacDonald, J., & Mulders, N. 2003, J. Non-Cryst. Sol., 319, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Dubey, Y. 2005, An approximate solution to buckling of plates by the galerkin method, Master Thesis [Google Scholar]
- Espinosa, H., Peng, B., Prorok, B., et al. 2003, J. Appl. Phys., 94, 6076 [NASA ADS] [CrossRef] [Google Scholar]
- Galerkin, B. 1915, Vestnik inzhenerov i tekhnikov, 19, 897 [Google Scholar]
- Hess, P. 2012, J. Appl. Phys., 111, 051101 [NASA ADS] [CrossRef] [Google Scholar]
- Hubin, N., Ellerbroek, B. L., Arsenault, R., et al. 2006, in The Scientific Requirements for Extremely Large Telescopes, eds. P. Whitelock, M. Dennefeld, & B. Leibundgut, IAU Symp., 232, 60 [Google Scholar]
- Kasten, A., Giannopoulos, A., Long, C., C., C., & Choquette, K. 2007, in Proc. SPIE, 6484, 64840C [Google Scholar]
- Kerrour, F., & Hobar, F. 2006, Semiconductor Physics, Quant. Electron. & Optoelectron., 9, 52 [Google Scholar]
- Koizumi, S., Nebel, C., & Nesládek, M. 2008, Physics and Applications of CVD Diamond (Wiley-VCH), 374 [Google Scholar]
- Labeyrie, A., Coroller, H. L., Residori, S., et al. 2010, in Pathways Towards Habitable Planets, eds. V. Coudé Du Foresto, D. M. Gelino, & I. Ribas, ASP Conf. Ser., 430, 239 [Google Scholar]
- Lee, J.-H., Lee, Y.-C., & Kang, E.-C. 2006, J. Opt. Soc. Korea, 10, 57 [CrossRef] [Google Scholar]
- Magette, A. 2010, Ph.D. Thesis: The International Liquid Mirror Telescope: optical testing and alignment using a Nijboer-Zernike aberration retrieval approch, IAGL, University of Liège, 1 [Google Scholar]
- Mansuripur, M. 2004, Opt. Expr., 12, 5375 [NASA ADS] [CrossRef] [Google Scholar]
- Mearini, G. 1992, Ph.D. Thesis, Case Western Reserve University [Google Scholar]
- Mehta, P. 2009, Vibrations of thin plate with piezoelectric actuator: theory and experiments, Master Thesis [Google Scholar]
- Morse, K. A., McHugh, S. L., & Fixler, J. 2008, Appl. Opt., 47, 5325 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, O., Anjanappa, M., & Freidhoff, C. 2006, COMSOL Users Conference, Boston, MA, October, 1 [Google Scholar]
- Pandey, A. K., Venkatesh, K., & Pratap, R. 2009, Sādhanāa, 34, 651 [Google Scholar]
- Salvadori, M. C., Brown, I. G., Vaz, A. R., Melo, L. L., & Cattani, M. 2003, Phys. Rev. B, 67, 153404 [NASA ADS] [CrossRef] [Google Scholar]
- Seurin, J., Ghosh, C., Khalfin, V., et al. 2008, in Vertical-Cavity Surface-Emitting Lasers XII, eds. C. Lei, & J. K. Guenter, Proc. SPIE, 6908, 69080 [Google Scholar]
- Sheplak, M., & Seiner, J. 1999, in 37th AIAA Aerospace Sciences Meeting, Reno [Google Scholar]
- Sinha, S., Mansell, J. D., & Byer, R. L. 2002, in Proc. SPIE, 4493, 55 [Google Scholar]
- Thornell, G., Ericson, F., Hedlund, C., et al. 1999, in Am. Phys. Soc., 981 [Google Scholar]
- Timoshenko, S. P., & Woinowsky-Krieger, S. 1959, Theory of Plates and Shells 2nd edition (McGraw-Hill), 594 [Google Scholar]
- Trauger, J. T. 2009, in BAAS, 41, AAS Meeting Abstracts, 213, 234.04 [Google Scholar]
- Zimmermann, A., Gross, J., & Fricke, J. 1995, J. Non-Cryst. Sol., 186, 238, proceedings of the Fourth International Symposium on AEROGELS [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Waffle effect: the Fresnel propagation
If the Fresnel diffraction pattern of a simple slit is well-defined, we obtain
![\appendix \setcounter{section}{1} \begin{eqnarray} \label{lensf} && U_{i,j}\left(\xi,x',y'\right)=\frac{{\rm e}^{{\rm i}2\pi z/\lambda}}{2i}\left[\left(C(\xi_{x2})+iS(\xi_{x2})-C(\xi_{x1})-iS(\xi_{x1})\right)\right]\nonumber\\ &&\quad \times\left[\left(C(\xi_{y2})+iS(\xi_{y2})-C(\xi_{y1})-iS(\xi_{y1}\right) \right] , \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq221.png) (A.1) where
z is the propagation distance between the microlens array and the
membrane, λ is the laser wavelength,
x′,y′ is the
cartesian coordinate of the diffracted field.
C(ξ)/S(ξ)
are the classical Fresnel integrals defined by
(A.1) where
z is the propagation distance between the microlens array and the
membrane, λ is the laser wavelength,
x′,y′ is the
cartesian coordinate of the diffracted field.
C(ξ)/S(ξ)
are the classical Fresnel integrals defined by 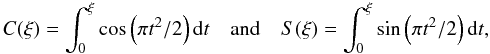 (A.2)where ξ
are the diffraction parameters for each laser diode, given by
(A.2)where ξ
are the diffraction parameters for each laser diode, given by 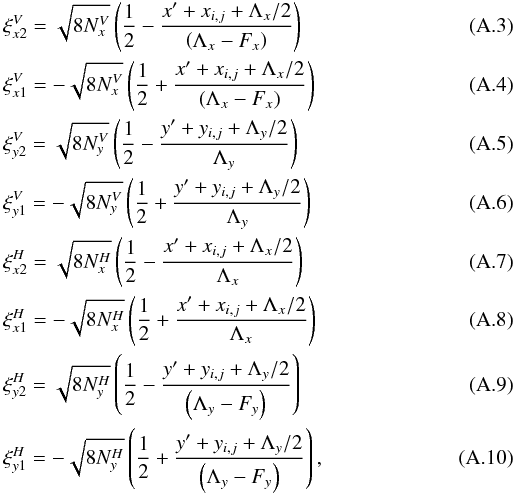 where
where
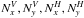 are the four
Fresnel numbers
are the four
Fresnel numbers 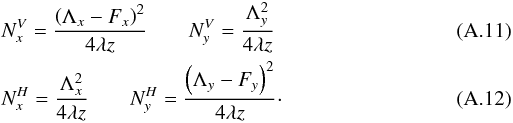 The
total illuminated Fresnel field has an amplitude of
Uf = Ug + UFr,
where Ug is the direct field and
UFr the diffracted field. Each term must be calculated as
follows:
The
total illuminated Fresnel field has an amplitude of
Uf = Ug + UFr,
where Ug is the direct field and
UFr the diffracted field. Each term must be calculated as
follows: 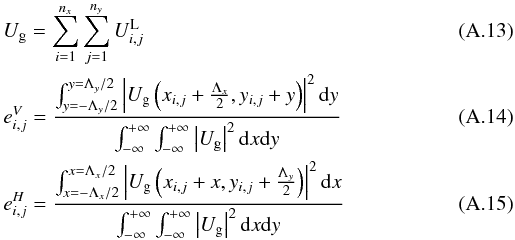 and
and
![\appendix \setcounter{section}{1} \begin{eqnarray} \label{lensf5} U_{\rm Fr}&=&\sum_{i=1}^{n_x-1}\sum_{j=1}^{n_y-1} \left[ U_{i,j}\left(\xi^V\right)\, e^V_{i,j}+ U_{i,j}\left(\xi^H\right)\, e^H_{i,j} \right] \\ &&+ \sum_{j=1}^{n_y} \left[U_{0,j}\left(\xi^V\right)\, e^V_{0,j}+ U_{n_x,j}\left(\xi^V\right)\, e^V_{n_x,j}\right] \nonumber\\ &&+ \sum_{i=1}^{n_x} \left[U_{i,0}\left(\xi^H\right)\, e^H_{i,0}+ U_{i,n_y}\left(\xi^H\right)\, e^H_{i,n_y}\right] , \nonumber \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq235.png) (A.16)where
(A.16)where
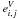 and
and
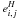 are the light
intensity values (energy) inside the vertical and horizontal slits, respectively.
are the light
intensity values (energy) inside the vertical and horizontal slits, respectively.
Appendix B: Linear model for the static solutions
In the first approximation (linear model), the deformable mirror can be well modeled by
the plate equation of Timoshenko &
Woinowsky-Krieger (1959): 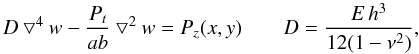 (B.1)where
▽ 4 and ▽ 2 are the biharmonic and the nabla operators on the
deformation w(x,y), respectively.
Pz(x,y) is the radiation
pressure, and Pt is the membrane tension. For
the numerical simulation, we chose a value of
Pt = 0.25 N/m (low mechanical tension). The
flexural rigidity D depends on the Young’s modulus E,
the Poisson’s ratio ν and the membrane thickness h. We
saw in Sect. 5.3 how the full membrane structure
(Al/diamond/Al or Al/diamond/Au) can be taken into account.
(B.1)where
▽ 4 and ▽ 2 are the biharmonic and the nabla operators on the
deformation w(x,y), respectively.
Pz(x,y) is the radiation
pressure, and Pt is the membrane tension. For
the numerical simulation, we chose a value of
Pt = 0.25 N/m (low mechanical tension). The
flexural rigidity D depends on the Young’s modulus E,
the Poisson’s ratio ν and the membrane thickness h. We
saw in Sect. 5.3 how the full membrane structure
(Al/diamond/Al or Al/diamond/Au) can be taken into account.
Using Navier’s method, the plate Eq. (B.1) can be transformed into a set of two linear partial differential equations:
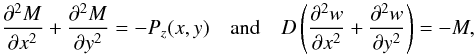 (B.2)where M
is the moment sum.
(B.2)where M
is the moment sum.
B.1. Boundary conditions and periodic solutions
Owing to the actuator influence function given by the microlens array focal ratio, the
wavefront correction shape w(x,y) is generally greater
than
nx·Λx × ny·Λy
in surface (see Fig. 3).The general boundary
condition reads 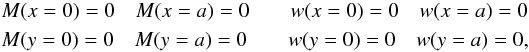 where
a and b are the geometrical extensions in the x and
y axis of the single large actuator used in this mechanical simulation, respectively.
Because of the intrinsic influence actuator function, the DM active surface extension
a > nxΛx
and
b > nyΛy.
To include in the w deformation function the
nx × ny
actuators, we chose a sinusoidal periodic orthogonal set of functions that satisfies
these boundary conditions (Fourier decomposition):
where
a and b are the geometrical extensions in the x and
y axis of the single large actuator used in this mechanical simulation, respectively.
Because of the intrinsic influence actuator function, the DM active surface extension
a > nxΛx
and
b > nyΛy.
To include in the w deformation function the
nx × ny
actuators, we chose a sinusoidal periodic orthogonal set of functions that satisfies
these boundary conditions (Fourier decomposition): 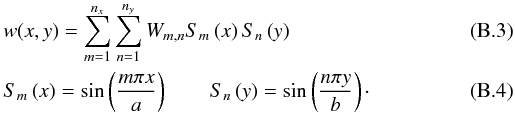 The
orthogonal set of functions possess the following properties:
The
orthogonal set of functions possess the following properties: 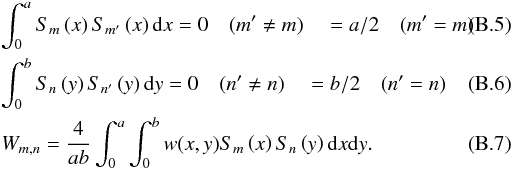
Appendix C: Multi-material mechanical transformations
The following equations show the different transformations applied on the
D,ν,E coefficients for two materials: ![\appendix \setcounter{section}{3} \begin{eqnarray} \label{multm2} &&D_{\rm e} = \frac{E_1 h^3_1} {12(1-\nu^2_1)} K_{\beta} \quad \nu_{\rm e} = \nu_1 \frac{K_{\gamma}}{K_{\beta}} \quad E_{\rm e}= \frac{D_{\rm e} \left(1-\nu^2_{\rm e}\right)}{\left(h_1 + h_2 \right)^3} \\[2mm] &&K_{\beta}= 1+ \frac{E_2 h^2_2 (1-\nu^2_1)}{E_1 h^2_1 (1-\nu^2_2)}+ \frac{3 \left(1-\nu^2_1 \right)\left(1+ \frac{h_2}{h_1}\right)^2 \left(1+ \frac{E_1 h_1}{E_2 h_2}\right)}{\left(1+ \frac{E_1 h_1}{E_2 h_2}\right)^2-\left(\nu_1+\nu_2 \frac{E_1 h_1}{E_2 h_2}\right)^2} \\[2mm] &&K_{\gamma}=1\! +\! \frac{\nu_2 E_2 h^3_2 (1-\nu^2_1) } {\nu_1 E_1 h^3_1 (1-\nu^2_2)} \! +\! \frac{3 \left(1-\nu^2_1 \right)\left(1+\frac{h_2}{h_1}\right)^2 \left(1+ \frac{\nu_2 E_1 h_1}{\nu_1 E_2 h_2}\right)} {\left(1+ \frac{E_1 h_1}{E_2 h_2}\right)^2-\left(\nu_1+\nu_2 \frac{E_1 h_1}{E_2 h_2}\right)^2}\cdot \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq257.png) The
Kγ coefficient is equivalent to
K3p in Myers et al. (2006) but with an error correction.
The
Kγ coefficient is equivalent to
K3p in Myers et al. (2006) but with an error correction.
Appendix D: Nonlinear model for the static solutions
Our surface deflection amplitude can be more than the membrane thickness. In this case,
the vertical deflections are accompanied by stretching of the mirror surface. The
stretching is a nonlinear process that causes the mirror layer to increase its
load-carrying capabilities. Now, our model possesses a new stress function
G(φs,σ)
defined as ![\appendix \setcounter{section}{4} \begin{eqnarray} \label{nlm1b} &&\bigtriangledown^4 \phi_s = -\frac{E_{\rm e}} {2} G\left( w,0 \right)\\[1mm] &&G\left( \phi_s,\sigma \right)= \frac{\partial^2 w} {\partial x^2} \left(\frac{\partial^2 \phi_s} {\partial y^2} +\sigma_x\right) + \frac{\partial^2 w} {\partial y^2} \left(\frac{\partial^2 \phi_s} {\partial x^2} +\sigma_y\right) \nonumber \\[1mm] &&\qquad\qquad\; - 2 \frac{\partial^2 w} {\partial x\partial y} \left(\frac{\partial^2 \phi_s} {\partial x\partial y} +\sigma_{xy}\right) \\[1mm] &&\frac{G\left( w,0 \right)} {2}=\left[\left(\frac{\partial^2 w} {\partial x^2} \frac{\partial^2 w} {\partial y^2}-\frac{\partial^2 w} {\partial x\partial y} \frac{\partial^2 w} {\partial x\partial y}\right) \right] , \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq261.png) where
φs is an Airy-type stress function and
σ = σx = σy = σxy
is a stress constant. We used the value equal to 20 MPa for this application (see
Table 3). Therefore, this term can be moved to
the left hand side of Eq. (29). We notice
here that we used the stiffness and the Young’s modulus for a composite membrane.
where
φs is an Airy-type stress function and
σ = σx = σy = σxy
is a stress constant. We used the value equal to 20 MPa for this application (see
Table 3). Therefore, this term can be moved to
the left hand side of Eq. (29). We notice
here that we used the stiffness and the Young’s modulus for a composite membrane.
D.1. φs(x,y) Airy stress function
We express the φs stress function in the
same basis set as the w(x,y) function (Fourier
decomposition). ![\appendix \setcounter{section}{4} \begin{eqnarray} \label{nlm2} &&\phi_s(x,y)= \sum_{m=1}^{n_x} \sum_{n=1}^{n_y} \phi_{s,m,n} \, C_m\left(x\right) C_n\left(y\right)\\[1mm] &&C_m\left(x\right)=\cos\left(\frac{m\pi x}{a}\right) \qquad C_n\left(y\right)=\cos\left( \frac{n \pi y}{b}\right) \cdot \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq265.png) The
Airy-type stress function solves in the same manner as the
w(x,y) deflection function with the Galerkin method
(see Azucena et al. 2008; Timoshenko & Woinowsky-Krieger 1959, p. 425). We obtain the
following equations:
The
Airy-type stress function solves in the same manner as the
w(x,y) deflection function with the Galerkin method
(see Azucena et al. 2008; Timoshenko & Woinowsky-Krieger 1959, p. 425). We obtain the
following equations: ![\appendix \setcounter{section}{4} \begin{eqnarray} \label{nlm3a} &&\int_0^a \int_0^b {\left(\bigtriangledown^4 \phi_s + \frac{E_{\rm e}} {2} G\left( w,0 \right)\right) C_m\left(x\right) C_n\left(y\right) {\rm d}x{\rm d}y} =0 \\[1mm] &&\bigtriangledown^4 \phi_s = \sum_{m=1}^{n_x} \sum_{n=1}^{n_y} \left( \left( \frac{m \pi}{a}\right)^2 + \left( \frac{n \pi}{b}\right)^2\right)^2 \phi_{s,m,n} \, C_m\left(x\right) C_n\left(y\right) . \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq266.png) The
derivative of w(x,y) deflection function can be
expressed in the following form:
The
derivative of w(x,y) deflection function can be
expressed in the following form: 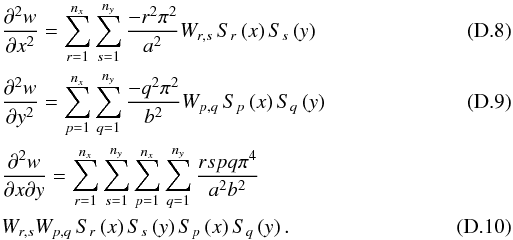 The
orthogonal set of functions
Cm/Cn
possess the same properties asn
Sm/Sn,
The
orthogonal set of functions
Cm/Cn
possess the same properties asn
Sm/Sn,
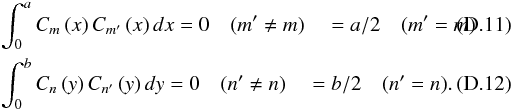 Now,
because of the compling coefficients
Wr,sWp,q
this is necessary to calculate during the final integration:
Now,
because of the compling coefficients
Wr,sWp,q
this is necessary to calculate during the final integration: ![\appendix \setcounter{section}{4} \begin{eqnarray} \label{nlm3d} &&\int_0^a C_m\left(x\right) S_r\left(x\right) S_p\left(x\right){\rm d}x =0 \quad(r\pm p \neq m) \\[1.5mm] &&\int_0^a C_m\left(x\right) S_r\left(x\right) S_p\left(x\right){\rm d}x =\mp\, a/4 \quad(r\pm p=m) \\[1.5mm] &&\int_0^a C_m\left(x\right) C_r\left(x\right) C_p\left(x\right){\rm d}x =0 \quad(r\pm p \neq m) \\[1.5mm] &&\int_0^a C_m\left(x\right) C_r\left(x\right) C_p\left(x\right){\rm d}x =a/4 \quad(r\pm p=m) . \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq272.png) We
obtain the same kinds of results (±b/4) with the
integation on the y axis on the s and
q variables as Eq. (D.13). After simplifications, the Airy stress function can be calculated by
correlating the input w(x,y) deformation fonction (see
Table D.1), and we obtain:
We
obtain the same kinds of results (±b/4) with the
integation on the y axis on the s and
q variables as Eq. (D.13). After simplifications, the Airy stress function can be calculated by
correlating the input w(x,y) deformation fonction (see
Table D.1), and we obtain: 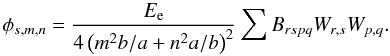 (D.17)The Airy stress
function presents a strong spatial frequency dependence: the most part of the Stress
function is in low frequency (see Fig. 4). This
result presents some limitations on the analytical evaluation of
φs,m,n. Indeed, the real area of the
membrane is
(D.17)The Airy stress
function presents a strong spatial frequency dependence: the most part of the Stress
function is in low frequency (see Fig. 4). This
result presents some limitations on the analytical evaluation of
φs,m,n. Indeed, the real area of the
membrane is  not only
ab that used in the previous calculation for the active area of the
DM. This physical characteristic changes the real value of the Airy stress function by
frequency filtering. The φs,m,n must be
evaluated on the entire circular membrane and then estimated on the active area of the
DM. The solution presented here seems to be pessimistic but a full analytical
development is beyond the scope of this paper. A global finite elements model (FEM) of
the DM seems to be more useful to know the dynamical response with respect to the
entrance VCSEL laser power.
not only
ab that used in the previous calculation for the active area of the
DM. This physical characteristic changes the real value of the Airy stress function by
frequency filtering. The φs,m,n must be
evaluated on the entire circular membrane and then estimated on the active area of the
DM. The solution presented here seems to be pessimistic but a full analytical
development is beyond the scope of this paper. A global finite elements model (FEM) of
the DM seems to be more useful to know the dynamical response with respect to the
entrance VCSEL laser power.
D.2. G(φs,σ) equation
The
G(φs,σ)
must be treated in the same manner,  (D.18)Equation
G(0,σ)
becomes
(D.18)Equation
G(0,σ)
becomes 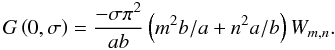 (D.19)Following the
mathematical development in the system of Eq. (D.17), the function
G(φs,0)
gives
(D.19)Following the
mathematical development in the system of Eq. (D.17), the function
G(φs,0)
gives ![\appendix \setcounter{section}{4} \begin{eqnarray} \label{nlm6} &&G\left( \phi_s,0\right) = \frac{\pi^4} {4 a^2b^2} \sum{ C_{rspq} \phi_{s,r,s} W_{p,q}} . \\[-0.5cm] && \nonumber \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq283.png) (D.20)
(D.20)
Brspq and Crspq coefficients.
Appendix E: Analytical evaluation of Iz,m,n
For a purely Gaussian laser field (without the Fresnel propagation), the integal
Iz,m,n can be evaluated analytically as a
convolution system (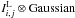 ):
): ![\appendix \setcounter{section}{5} \begin{eqnarray} \label{anI1} &&I_{z,m,n}\approx\frac{4(|r_1|^2 - A_1)}{c a^2b^2} \sum_{m=1}^{n_x} \sum_{n=1}^{n_y} I^{\rm L}_{m,n} \, E_{{\rm g}xy}(a,b,m,n) \\ && I^{\rm L}_{m,n}= \int_0^a \int_0^b I^{\rm L}_{i,j} \delta(x-x_{i,j})\delta(y-y_{i,j}) S_m\left(x\right)S_n\left(y\right) {\rm d}x{\rm d}y\nonumber\\ &&E_{{\rm g}xy}(a,b,m,n)=\int_0^a \int_0^b {\rm e}^{\frac{-{\left((x-a/2)^2+(y-b/2)^2\right)}} {2(\sigma_{{\rm g}x}^2+\sigma_{{\rm g}y}^2)}} S_m\left(x\right) S_n\left(y\right) {\rm d}x{\rm d}y \nonumber \\ \label{anI2} &&E_{{\rm g}xy}(a,b,m,n)= -\frac{\pi} {8} {\rm e}^{-\frac{\pi^2\left(\sigma_{{\rm g}x}^2+\sigma_{{\rm g}x}^2\right)\left(b^2m^2+a^2n^2\right)+ib^2\pi(m+n)} {2a^2b^2}} \\[1mm] &&\times\left( \sigma_{{\rm g}x}^2+\sigma_{{\rm g}x}^2 \right)\left( {\rm e}^{{\rm i}m\pi} -1 \right) \left( {\rm e}^{{\rm i}n\pi} -1 \right) \nonumber \\[1mm] &&\times \left(Erf\left(\frac{a^2+2{\rm i} m \pi (\sigma^2_{{\rm g}x}+\sigma^2_{{\rm g}y})}{2a\sqrt{2(\sigma_{{\rm g}x}^2+\sigma_{{\rm g}x}^2)}}\right) \! +\! Erf\left(\frac{a^2-2{\rm i} m \pi (\sigma^2_{{\rm g}x}+\sigma^2_{{\rm g}y})}{2a\sqrt{2(\sigma_{{\rm g}x}^2+\sigma_{{\rm g}x}^2)}}\right)\right)\nonumber \\[1mm] && \times \left(Erf\left(\frac{b^2+2{\rm i} n \pi (\sigma^2_{{\rm g}x}+\sigma^2_{{\rm g}y})}{2b\sqrt{2(\sigma_{{\rm g}x}^2+\sigma_{{\rm g}x}^2)}}\right) \! +\! Erf\left(\frac{b^2-2{\rm i} n \pi (\sigma^2_{{\rm g}x}+\sigma^2_{{\rm g}y})}{2b\sqrt{2(\sigma_{{\rm g}x}^2+\sigma_{{\rm g}x}^2)}}\right)\right), \nonumber \end{eqnarray}](/articles/aa/full_html/2012/09/aa19707-12/aa19707-12-eq297.png) where
Erf is the error function (the integral of the Gaussian distribution).
Numerically, we verify that Egxy ∈ ℜ.
where
Erf is the error function (the integral of the Gaussian distribution).
Numerically, we verify that Egxy ∈ ℜ.
To retrieve the exact value of the illuminated laser
field  , we must
deconvolve in the Fourier plane the Iz,m,n
illumination obtained by our model using the
Egxy function. Indeed,
, we must
deconvolve in the Fourier plane the Iz,m,n
illumination obtained by our model using the
Egxy function. Indeed,
 and this
operation is very similar to the myopic deconvolution given by Conan et al. (1998).
and this
operation is very similar to the myopic deconvolution given by Conan et al. (1998).
All Tables
All Figures
 |
Fig. 1 Key functional elements of a high-density actuator deformable mirror, driven by radiation pressure from a VCSELs array. Bottom to top: fully addressable VCSELs array of laser diodes in the near-infrared (808−1064 nm). The emitting region of the laser diode is around 9 μm (the laser size), and the actuator pitch is given by the laser diode spacing. Each Gaussian beam (provided by laser diodes) is collimated by a square microlens array in fused silica with a proper anti-reflection coating (transmission >99.5%). The microlens array must be very well aligned (<0.5 μm) with the VCSEL array. If the VCSELs array is not in polarized emission, a linear polarizer is needed. The light passes through an optical polarizing device and arrives on a thin CVD-diamond membrane (≈1 μm of thickness) with aluminum coating (100 nm of thickness) on each face. The linear polarizer and the optical polarizing device management can have the same component as a polarizing cube with high polarization purity (>104). The radiation pressure produced by each laser diode locally distorts the membrane with a Gaussian shape, which definies the actuator response of the system. |
| In the text | |
 |
Fig. 2 Composition of the thin membrane and how the light from the laser interacts in its
interior. The membrane consists of three films: (a) an aluminum coating of width
h1, (b) a CVD-diamond substrate of width
h2, and (c) an aluminum or gold coating, of width
h3. Left: the shape of the
clamped-edge membrane, hm(r), is only
depending on r, and in the classical adaptive optics
implementations, the gravity vector is vertical. Right: a linearly
polarized plane wave (Ein,
Hin) is normally incident on the surface of a medium
of complex dielectric constant ϵ1.
E1t, E1r are the electric
fields inside the first reflective medium for, the transmitted and reflected waves
respectively. For a good reflection of light with aluminum or gold, the thickness of
the coating must be greater than 50 nm and the two electric fields inside with
medium will be strongly attenuated. In this case, E2t,
E2r,Et
inside and outside the CVD-diamond will be equal to zero.
|
| In the text | |
 |
Fig. 3 Numerical simulation of the illuminated field Pz obtained by the proposed VCSEL array (128 × 128, pitch of 50 μm). We chose a circular clamped membrane of rm = 7 mm (circle limit). Our simulation considers a random wavefront error of 0.1 wave rms and includes the Fresnel propagation. To enhance the last effect in the image, the brightness scale is not linear (|I|0.25). |
| In the text | |
 |
Fig. 4 Example of the nonlinear simulation on Zernike 55. The projection of
Z55 in the Fourier plane gives the
Zm,n/Wm,n
coefficients. The Airy-type stress function
φs,m,n is evaluated by the
Wm,n coupling (see Eq. (D.17)). The nonlinear part of the
Eq. (29)
(G(φs,σ))
is calculated and the Iz,m,n is
directly obtained. A deconvolution by the Gaussian laser beam distribution
(Egxy) and the final projection on
the DM plane gives |
| In the text | |
 |
Fig. 5 Non linear simulation of the w(x,y) maximum deflection with respect to the Zernike polynomial order. We present the deflection for two different membrane structures. The gold back-face coating shows a better dynamic than classical Al coating. A maximum deflection of 1 μm with ≈25 mW per laser diode seems to be possible. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.