EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 545 (September 2012) A&A, 545 (2012) A82 Full HTML
Free Access
Issue
A&A
Volume 545, September 2012
Article Number A82
Number of page(s) 5
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201219340
Published online 11 September 2012

© ESO, 2012

1. Introduction

Amorphous solid water (ASW) is the main component of interstellar and cometary ices (Hagen et al. 1981; Tielens & Allamandola 1987). It provides a matrix environment for other species, sequentially accreted or formed via solid state astrochemical processes (Öberg et al. 2011). It has been experimentally verified that compact (non-porous) ASW is predominantly formed at low temperature through grain-surface reactions (Ioppolo et al. 2008; Dulieu et al. 2009; Oba et al. 2009; Ioppolo et al. 2010; Cuppen et al. 2010; Romanzin et al. 2010). Remote identification of its morphology and, more precisely its porosity is based on weak absorption features near 2.7 μm that are due to the O-H dangling mode of water on the surface of pores. Up to now, there is no astronomical detection of dangling absorption modes in the infrared spectra of interstellar ices (Keane et al. 2001). This has been taken as a proof that porous ASW is rare in space. However, this does not necessarily means that porous ASW is absent in space, given the diversity of astronomical ice environments (Kouchi & Yamamoto 1995; Gálvez et al. 2010). In shock regions and outflows, the sputtering of frozen water molecules from grain mantles redistributes ice on the remaining cold surfaces that may lead to the formation of a vapor-deposited ASW coating on grains. The main characteristic of vapor-deposited water ice is its porosity (Baragiola 2003). Porous ice is expected to be chemically more reactive as it provides large effective surface areas for catalysis, for the freeze-out of additional atoms and molecules, and for gas retention. Absorption areas can be hundreds of m2/g. As a consequence, a large amount of molecules can be stored inside pores at low temperatures affecting the efficiency of solid state astrochemical processes. In a later stage these species and eventual reaction products are thermally released (Collings et al. 2003).

In a laboratory setting, the morphology of ASW depends on experimental conditions such as temperature, deposition rate and deposition direction of water molecules onto the substrate (Stevenson et al. 1999; Kimmel et al. 2001; Dohnalek et al. 2003). Background deposition of water vapor onto a cold surface results in highly porous ASW (Stevenson et al. 1999; Kimmel et al. 2001). After deposition, the ice morphology may change depending on external influences. A disappearance of pores has been observed in ion and UV irradiation experiments (Palumbo 2006; Palumbo et al. 2010; Raut et al. 2008). Furthermore, thermal annealing triggers a phase transition between 38 and 68 K (Jenniskens & Blake 1994), and makes ASW more compact by closing pores thereby trapping other co-deposited gases (Mayer & Pletzer 1986; Bar-Nun et al. 1998; Collings et al. 2003). The mechanisms responsible for these morphology changes are not fully understood, particularly at low temperature, where diffusion of molecules is limited (Garrod et al. 2008). In previous studies a collapse of pores has also been concluded following X-ray and electron diffraction studies (Hallbrucker et al. 1989; Jenniskens et al. 1995), temperature-programmed desorption (Collings et al. 2003), infrared spectroscopy (Hagen et al. 1983; Rowland & Devlin 1991; Rowland et al. 1991), internal friction (Hessinger et al. 1996) and gas adsorption experiments (Bar-Nun et al. 1998; Kimmel et al. 2001; Horimoto et al. 2002).

In this paper, we present a new and generally applicable method yielding experimental results that directly demonstrate the thickness decrease of porous ASW upon heating. Section 2 describes details on experiment and data analysis. Section 3 presents the results obtained during deposition and thermal processing of different water ice morphologies. The discussion is given in Sect. 4, and includes a quantitative analysis of the experimental results followed by astrophysical implications. A summary and concluding remarks are given in the final section.

thumbnail Fig. 1

Exponential fit to subsequent interference fringes minima and maxima (m) and the corresponding thickness vs. deposition time.

2. Experimental methods

Experiments are performed in a high-vacuum chamber with a base pressure of 2 × 10-7 Torr at room temperature. The experimental set-up has been described in detail by Gerakines et al. (1995), and updated by Bouwman et al. 2007, and is therefore only briefly described here. Different water ices are grown either on a CsI window or on a silicon (Si) substrate at 15 and 140 K. The substrate is mounted on a closed-cycle helium cryostat that, in conjunction with resistive heating, allows an accurate temperature control from 15 to 300 K with a precision of 0.1 K. We use milli-Q grade water that is further purified by three freeze-pump-thaw cycles prior to deposition. Depending on the experimental conditions, water ices are grown with different morphologies, namely (i) porous amorphous; (ii) less-porous amorphous; and (iii) crystalline solid water. Less-porous ASW is obtained at 15 K by using a gas inlet (2 mm diameter) directed toward the substrate at normal incidence (Kimmel et al. 2001). Porous ASW and crystalline solid water are grown by background deposition at 15 and 140 K, respectively. In background deposition the gas inlet is directed away from the substrate, which allows the water molecules to impinge the surface with random trajectories (Stevenson et al. 1999; Dohnalek et al. 2003). The latter technique has the advantage that the ice growth is more uniform than in a directed deposition, but suffers from the possibility that gas is also deposited on the backside of the substrate.

The ice thickness is monitored during both deposition and thermal annealing by optical interference using a linearly polarized helium-neon (He-Ne) laser. The laser beam is s-polarized (perpendicular) with respect to the plane of incidence, and strikes the substrate surface at an incident angle θ0 =  35 ± 5°. The reflected light is thereafter converted to a digital signal by a photodiode. Another photodiode is used prior to the vacuum chamber to monitor any laser output fluctuations. The signal is recorded as a function of time using LabVIEW 8.6 (National Instruments). The ice thickness d can be expressed as a function of interference fringes (m): (1)where λ corresponds to the wavelength of the He-Ne laser (632.8 nm), n0 and n1 are the refractive indices of vacuum and ice, and θ1 is the angle of refraction. To exclude the influence of the gas deposited on the backside of the substrate, we use the Si substrate that is opaque to the laser wavelength. We use n0 = 1 for vacuum, n1 = 1.19 for porous ASW at 15 K (extrapolated from the data reported in Dohnalek et al. 2003), and n1 = 1.29 for less-porous ASW (Westley et al. 1998). A quantitative characterization of the ice thickness during deposition is possible by correlating the interference fringe pattern of subsequent minima and maxima (m) and the corresponding deposition time. An exponential fit to this data provides the best representation of the deposition rate as depicted in Fig. 1. This exponential behavior is expected as the pressure in the gas reservoir decreases with deposition time. The system is cycled through up to about 2.75 interference fringes, corresponding to an ice thickness of 837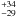 nm (~3000 MLs). The accuracy of the thickness determination is limited by the uncertainty in the literature values of the optical constants, and the incident angle of the laser beam (Baratta & Palumbo 1998). After deposition, the ice thickness is monitored as a function of temperature between 15 and 120 K using different heating rates from 1 to 4 K min-1.

Infrared spectra are obtained with a Fourier transform infrared spectrometer (Varian 670-IR FTIR) and recorded in transmission mode between 4000 and 400 cm-1 using the CsI window. An infrared spectrum has a 1 cm-1 resolution and is averaged over 256 interferograms. The spectrometer is flushed with dry air to minimize background fluctuations due to atmospheric absorptions. Background spectra are acquired at 15 K prior to deposition for each experiment.

thumbnail Fig. 2

Interference data for porous ASW grown on a Si substrate at 15 K following background deposition. The reflected intensity oscillates between constructive and destructive interference as the ice grows. The deposition is stopped at a point with maximum sensitivity to changes in ice thickness. The error in the thickness measured is about 4%.

thumbnail Fig. 3

Infrared transmission spectra of the O-H dangling mode of porous ASW, less-porous ASW, and crystalline solid water at 15 K. The absorption band related to the bulk O-H stretching modes has been subtracted for clarity.

3. Results

3.1. Interference data and infrared spectra during deposition

Figure 2 shows experimental interference data corresponding to the intensity of the reflected laser beam as a function of ice thickness, collected during a porous ASW growth on the Si substrate. The interference data exhibits a very small amplitude damping with ongoing deposition. This amplitude change can have different reasons; a loss of coherence of the reflected light because of surface roughness, cracks, and/or wide boundaries (Baragiola 2003; Howett et al. 2007; Romanescu et al. 2010). The distance between subsequent minima and maxima is constant within 1% indicating that the density of the porous ASW does not change significantly during deposition (Westley et al. 1998).

Because the He-Ne signal is fairly insensitive to changes in ice thickness near the fringe turning points, the water deposition is stopped when the signal is located at an upward slope, e.g., half-way between the third destructive interference (m = 2.5) and the third constructive interference (m = 3.0) in the fringe pattern. In this way, a variation of the He-Ne signal from m ≃ 2.75 onwards is interpreted as a variation of ice thickness, i.e., an increasing value corresponds to a thicker ice whereas a decreasing value corresponds to a thinner one.

The FTIR transmission spectra of porous ASW, less-porous ASW, and crystalline solid water grown on the CsI window are depicted in Fig. 3 in the 3760–3660 cm-1 range that covers the O-H dangling mode of water ice. This mode is used to visualize the level of porosity. To characterize the porosity of each water ice sample, all spectra are corrected with a baseline, and normalized to the bulk O-H stretching modes, located at lower wavenumbers (not shown here). For porous and less-porous ASW, two absorption bands are found at 3720 and 3696 cm-1 that correspond to the O-H dangling mode of the two- and three-coordinate surface-water molecules, respectively. These two bands have been taken as a typical porosity signature (Rowland & Devlin 1991; Rowland et al. 1991), and their intensities reflect the abundance of pores. For crystalline solid water, there is no O-H dangling mode. Therefore, we conclude that at fixed temperature (15 K), the porosity decreases from porous ASW to less-porous ASW, and from less-porous ASW to crystalline solid water. Theses results are in good agreement with earlier reports (Stevenson et al. 1999; Kimmel et al. 2001; Dohnalek et al. 2003; Palumbo 2006), and depict the different morphologies of the deposited samples.

thumbnail Fig. 4

Interference data from the end of deposition point onwards (Fig. 2), during the thermal annealing experiment on porous ASW, less-porous ASW, and crystalline solid water grown on a Si substrate, with a heating rate set to 2 K min-1. The gray lines represent the raw experimental data, and the black lines are the smoothed data.

thumbnail Fig. 5

Interference data during the thermal annealing experiment on porous ASW grown on a Si substrate, with different heating rates (1, 2, and 4 K min-1). The gray lines represent the raw experimental data, and the black lines are the smoothed data. The inset presents the evolution of the O-H dangling mode during the warm-up of porous ASW from 15 to 120 K.

3.2. Thermal processing of different water ice morphologies

Using optical interference, we can now monitor the thermal evolution of porous ASW, less-porous ASW, and non-porous crystalline solid water. The results are shown in Fig. 4. The corresponding interference data are scaled in order to get the same amplitude between the second constructive interference (m = 2.0) and the third destructive interference (m = 2.5) in the fringe patterns. The small offset is introduced for better visibility. At temperatures above 120 K, diffusion of water molecules becomes significant, and molecules rearrange to a thermodynamically favored crystalline structure (Raut et al. 2008). Hence, we exclude all data at temperatures higher than this threshold.

For crystalline solid water, the He-Ne signal is stable between 15 and 120 K, indicating that the ice thickness remains constant in this temperature range. The result is consistent with the lack of porosity of the sample deposited at 140 K, and then cooled down to 15 K, as confirmed by infrared spectroscopy in Fig. 3. For porous ASW, and less-porous ASW the He-Ne signal does not change between 15 and 20 K. Above 20 K, we observe a gradual drop in the interference signal, which reflects a structural change of the ices; the ices get thinner. Figure 4 shows that the decrease in the signal is stronger for the porous ASW, indicating that the magnitude of the thickness decrease is related to the initial porosity of the sample.

In order to check the temperature dependence of the observed thickness decrease, we monitor the He-Ne beam reflected from porous ASW samples that are warmed up with different heating rates (1, 2, and 4 K min-1). Before each measurement, we use the same background deposition protocol in order to allow accurate comparisons. Figure 5 shows the interference signal for different heating rates. The signal decay as function of temperature is comparable for the different thermal annealing experiments, indicating that the thickness decrease of porous ASW is a fully thermally determined process. The inset in Fig. 5 shows that the intensity of the O-H dangling feature decreases during the warm-up. This is consistent with the expected porosity loss as discussed in the literature (Baragiola 2003 and references therein); this porosity loss takes place together with the observed thickness decrease.

thumbnail Fig. 6

Schematic of the three-phase system layered structure.

4. Discussion

Previous work has shown a decrease in both porosity and gas-adsorption capacity of ASW with increasing temperature. We have directly demonstrated here that vapor deposited ASW undergoes a temperature-induced structural change upon heating. A quantitative analysis of the observed thickness decrease in porous ASW is possible by determining the ice thickness at different temperatures. This can be achieved by relating the reflected He-Ne laser intensity |R|2 to the ice thickness during thermal annealing. For layered structures (Fig. 6), the reflection coefficient R can be written as a function of the Fresnel reflection coefficients according to the relation (Westley et al. 1998; Dohnalek et al. 2003): 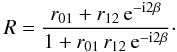(2)The Fresnel reflection coefficients r01 and r12 are associated to the vacuum/ice and ice/substrate interfaces, respectively, and are functions of the refractive indices of vacuum (n0), ice (n1), and substrate (n2). The values of the Fresnel reflection coefficients are given by the following equations and depend on the light polarization. For s-polarized light: 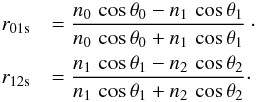(3)Snell’s law relates the angles of incidence (θ0, θ1, and θ2) with the complex indices of refraction (n0, n1, and n2). We use constant refractive indices n0 = 1 for vacuum, and n2 = 3.85 − 0.07i for the Si substrate (Mottier & Valette 1981).

thumbnail Fig. 7

Calculated thicknesses versus temperature during the thermal annealing experiment (2 K min-1) of porous ASW grown on a Si substrate. The vertical bars give the dispersion due to the resolution of the optical interference technique. The gray shaded area takes into account the dispersion due to the error in the initial thickness measured at 15 K.

The refractive index of porous ASW, however, is temperature dependent, and increases linearly from 22 to 120 K; n1(T) values are available from Dohnalek et al. 2003. We assume that the n1(T) values obtained depositing the sample at a given temperature are the same as those of the sample warmed up from 15 K to that temperature. The imaginary component, k, is very close to zero, and can be neglected (Warren 1984; Dohnalek et al. 2003). The exponential term β in Eq. (2) describes the phase change of the light as it passes through the ice with: (4)We assume that the amplitude of the reflected light at a given thickness and temperature is proportional to the photodiode signal (S), with a proportionality constant (A), calculated at 15 K with the initial ice thickness d0 (here d0 = 837 nm): 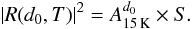(5)In order to measure the thickness of the ice for other temperatures, we need to take into account the variation of n1(T) with temperature, and to find the closest root (d) to the initial ice thickness that satisfies the following equation: 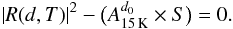(6)Figure 7 shows the calculated ice thickness versus temperature. We find a thickness change for porous ASW from ~833 nm at 20 K to ~733 nm at 120 K, which corresponds to a decrease of 12 ± 1%. The top and bottom edges of the gray shaded area delimit the error in the initial ice thickness measurement. We observe the same thickness decrease value of about 12% for both upper and lower d0 values, indicating that the accuracy of the derived thickness change is not strongly affected by the uncertainty of the initial thickness. This derived thickness change is a lower limit since the background accretion of the residual components remaining in the chamber is not explicitly taken into account. The results presented here are confirmed by recent theoretical work; molecular dynamics simulations performed on porous ASW show a thickness decrease of ~10% from 0 to 150 K) (Elkind & Fraser 2012, priv. comm.). For less-porous ASW the exact thickness decrease cannot be determined as the n1(T) values are unknown. Figure 4 indicates that the thickness change is less than for porous ASW, but definitely not zero as for crystalline solid water. The structural collapse of porous ASW is not large in terms of thickness but a decrease on the order of 12% may correspond to a substantial loss in terms of surface area; Bar-Nun et al. (1998) report an effective surface area loss as large as 90%. The physical mechanism involved during the collapse is poorly understood. It has been proposed that at 38 K, on average, the breaking of one hydrogen bond per molecule becomes possible, restructuring the ice (Jenniskens & Blake 1994; Jenniskens et al. 1995). This is in line with the results found here, with the exception that an onset of a structural change is already observed at 20 K.

The O-H dangling mode characteristic for porous ASW has not been observed in the infrared spectra of interstellar ices, reason why ASW in space is considered to be compact. Previous laboratory experiments are in line with this conclusion, and suggest that over the lifetime of a molecular cloud, pores in interstellar ices are lost upon cosmic ray bombardment (Palumbo 2006; Raut et al. 2008). The present study indicates that a structural change is also realized through heating, i.e., in a protoplanetary disk through radiation from the protostar. This also applies to less-porous ASW.

Upon heating the number of reaction sites becomes scarce, and a chemistry dominated by bulk processes may shift to a chemistry governed by surface processes. A decrease of reaction sites will naturally reduce the reaction efficiency. On the other hand, a low temperature structural collapse may facilitate reactions between adsorbates, and reaction efficiencies will increase with increasing temperature, as the mobility of reacting species gets larger. Gálvez et al. (2010) demonstrated that the thermal processing of porous ASW leads to a marked enhancement of low temperature acid-base reaction yields, in contrast to compact ASW. So far, a thermally induced ice collapse has not been taken explicitly into account in astrochemical models. The situation for mixed ices is likely even more complicated. How do CO or CO2 affect the water ice structure, morphology, and porosity loss upon heating? With the new technique discussed here, this question can be addressed, as soon as temperature dependent refraction indices have become available.

5. Conclusions

We have measured the thickness decrease of porous ASW upon heating for astronomically relevant temperatures, using a new experimental technique, based on optical interference and FTIR transmission spectroscopy.

  • 1.

    We find for porous ASW a thickness decrease of12 ± 1% upon heating from 20 to 120 K. For less-porous ASW this value is lower, and negligible for crystalline solid water.

  • 2.

    The thickness decrease observed by optical interference is accompanied by the compaction (porosity loss) observed by FTIR.

  • 3.

    Thermal compaction provides an additional explanation why porous ASW has not been observed in space so far.

  • 4.

    The observed structural collapse likely will influence the efficiency of the overall chemical solid state network in inter- and circumstellar ices.

Acknowledgments

Part of this work was supported by NOVA, the Netherlands Research School for Astronomy, a Vici grant from the Netherlands Organisation for ScientiÞc Research (NWO), and the European Community 7th Framework Programme (FP7/2007-2013) under grant agreement n.238258. We thank G. Strazzulla for many valuable comments to this study, and for providing the silicon substrate. We also thank X. Tielens, H. Fraser, and S. Cazaux for stimulating discussions. The referee is acknowledged for providing constructive comments and help in improving the contents of this paper.

References

  1. Baragiola, R. A. 2003, Planet. Space Sci., 51, 953 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baratta, G. A., & Palumbo, M. E. 1998, J. Opt. Soc. Am., 15, 3076 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bar-nun, A., & Owen, T. 1998, Solar System Ices, eds. B. Schmitt, C. De Bergh, M. Festou (Dordrecht: Kluwer), 353 [Google Scholar]
  4. Bouwman, J., Ludwig, W., Awad, Z., et al. 2007, A&A, 476, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Collings, M. P., Dever, J. W., Fraser, H. J., McCoustra, M. R. S., & Williams, D. A. 2003, ApJ, 583, 1058 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cuppen, H. M., Ioppolo, S., Romanzin, C., & Linnartz, H. 2010, PCCP, 12, 12077 [Google Scholar]
  7. Dohnalek, Z., Kimmel, G. A., Ayotte, P., Smith, S., & Kay, B. D. 2003, J. Chem. Phys., 118, 364 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dulieu, F., Amiaud, L., Congiu, E., et al. 2009, A&A, 512, A30 [Google Scholar]
  9. Gálvez, O., Maté, B., Herrero, V. J., & Escribano, R. 2010, ApJ, 724, 539 [NASA ADS] [CrossRef] [Google Scholar]
  10. Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gerakines, P. A., Schutte, W. A., Greenberg, J. M., & van Dishoeck, E. F. 1995, A&A, 296, 810 [NASA ADS] [Google Scholar]
  12. Hagen, W., Tielens, A. G. G. M., & Greenberg, J. M. 1981, Chem. Phys., 56, 367 [NASA ADS] [CrossRef] [Google Scholar]
  13. Hagen, W., Tielens, A. G. G. M., & Greenberg, J. M. 1983, A&A, 51, 389 [Google Scholar]
  14. Hallbrucker, A., Mayer, E., & Johari, G. P. 1989, J. Phys. Chem., 93, 4986 [CrossRef] [Google Scholar]
  15. Hessinger, J., White, Jr., & Pohl, R. O. 1996, Planet. Space Sci., 44, 937 [NASA ADS] [CrossRef] [Google Scholar]
  16. Horimoto, N., Kato, H. S., & Kawai, M. 2002, J. Chem. Phys., 116, 4375 [NASA ADS] [CrossRef] [Google Scholar]
  17. Howett, C. J. A., Carlson, R. W., Irwin, P. G. J., & Calcutt, S. B. 2007, J. Opt. Soc. Am. B, 24, 126 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ioppolo, S., Cuppen, H. M., Romanzin, C., van Dishoeck, E. F., & Linnartz, H. 2008, ApJ, 686, 1474 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ioppolo, S., Cuppen, H. M., Romanzin, C., van Dishoeck, E. F., & Linnartz, H. 2010, PCCP, 12, 12065 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jenniskens, P., & Blake, D. F. 1994, Science, 265, 753 [NASA ADS] [CrossRef] [Google Scholar]
  21. Jenniskens, P., Blake, D. F., Wilson, M. A., & Pohorille, A. 1995, ApJ, 455, 389 [NASA ADS] [CrossRef] [Google Scholar]
  22. Keane, J. V., Boogert, A. C. A., Tielens, A. G. G. M., Ehrenfreund, P., & Schutte, W. A. 2001, A&A, 375, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Kimmel, G. A., Stevenson, K. P., Dohnalek, Z., Smith, R. S., & Kay, B. D. 2001, J. Chem. Phys., 114, 5284 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kouchi, A., & Yamamoto, T. 1995, Prog. Cryst. Growth Charact. Mater., 30, 83 [Google Scholar]
  25. Mayer, E., & Pletzer, R. 1986, Nature, 319, 298 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mottier, P., & Valette, S. 1981, Appl. Opt., 20, 1630 [NASA ADS] [CrossRef] [Google Scholar]
  27. Oba, Y., Miyauchi, N., Hidaka, H., et al. 2009, ApJ, 701, 464 [NASA ADS] [CrossRef] [Google Scholar]
  28. Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
  29. Palumbo, M. E. 2006, A&A, 453, 903 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  30. Palumbo, M. E., Baratta, G. A., Leto, G., & Strazzulla, G. 2010, J. Mol. Struct., 972, 64 [NASA ADS] [CrossRef] [Google Scholar]
  31. Raut, U., Fama, M., Loeffler, M. J., & Baragiola, R. A. 2008, ApJ, 687, 1070 [NASA ADS] [CrossRef] [Google Scholar]
  32. Romanescu, C., Marschall, J., Kim, D., Khatiwada, A., & Kalogerakis, K. S. 2010, Icarus, 205, 695 [Google Scholar]
  33. Romanzin, C., Ioppolo, S., Cuppen, H. M., van Dishoeck, E. F., & Linnartz, H. 2010, J. Chem. Phys., 134, 084504 [Google Scholar]
  34. Rowland, B., & Devlin, J. P. 1991, J. Chem. Phys., 94, 812 [NASA ADS] [CrossRef] [Google Scholar]
  35. Rowland, B., Fisher, M., & Devlin, J. P. 1991, J. Chem. Phys., 95, 1378 [NASA ADS] [CrossRef] [Google Scholar]
  36. Stevenson, K. P., Kimmel, G. A., Dohnalek, Z., Smith, S., & Kay, B. D. 1999, Science, 283, 1505 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  37. Tielens, A. G. G. M., & Allamandola, L. J. 1987, in Physical Processes in Interstellar Clouds, eds. G. E. Morfill, & M. Scholer (Dordrecht: Reidel), 333 [Google Scholar]
  38. Warren, S. G. 1984, Appl. Opt., 23, 1206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  39. Westley, M. S., Baratta, G. A., & Baragiola, R. A. 1998, J. Chem. Phys., 108, 3321 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Exponential fit to subsequent interference fringes minima and maxima (m) and the corresponding thickness vs. deposition time.
In the text
thumbnail Fig. 2

Interference data for porous ASW grown on a Si substrate at 15 K following background deposition. The reflected intensity oscillates between constructive and destructive interference as the ice grows. The deposition is stopped at a point with maximum sensitivity to changes in ice thickness. The error in the thickness measured is about 4%.
In the text
thumbnail Fig. 3

Infrared transmission spectra of the O-H dangling mode of porous ASW, less-porous ASW, and crystalline solid water at 15 K. The absorption band related to the bulk O-H stretching modes has been subtracted for clarity.
In the text
thumbnail Fig. 4

Interference data from the end of deposition point onwards (Fig. 2), during the thermal annealing experiment on porous ASW, less-porous ASW, and crystalline solid water grown on a Si substrate, with a heating rate set to 2 K min-1. The gray lines represent the raw experimental data, and the black lines are the smoothed data.
In the text
thumbnail Fig. 5

Interference data during the thermal annealing experiment on porous ASW grown on a Si substrate, with different heating rates (1, 2, and 4 K min-1). The gray lines represent the raw experimental data, and the black lines are the smoothed data. The inset presents the evolution of the O-H dangling mode during the warm-up of porous ASW from 15 to 120 K.
In the text
thumbnail Fig. 6

Schematic of the three-phase system layered structure.
In the text
thumbnail Fig. 7

Calculated thicknesses versus temperature during the thermal annealing experiment (2 K min-1) of porous ASW grown on a Si substrate. The vertical bars give the dispersion due to the resolution of the optical interference technique. The gray shaded area takes into account the dispersion due to the error in the initial thickness measured at 15 K.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.