| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219100 | |
| Published online | 20 September 2012 | |
Thermal history modelling of the H chondrite parent body
1 Institut für Theoretische Astrophysik, Zentrum für Astronomie, Universität Heidelberg, Albert-Überle-Str. 2, 69120 Heidelberg, Germany
e-mail: gail@uni-heidelberg.de
2 Institut für Geowissenschaften, Universität Heidelberg, Im Neuenheimer Feld 236, 69120 Heidelberg, Germany
3 Institut für Planetologie, Universität Münster, Wilhelm-Klemm-Str. 10, 48149 Münster, Germany
Received: 23 February 2012
Accepted: 25 August 2012
Context. The cooling histories of individual meteorites can be empirically reconstructed by using ages obtained from different radioisotopic chronometers having distinct closure temperatures. For a given group of meteorites derived from a single parent body such data permit the detailed reconstruction of the cooling history of that body. Particularly suited for this purpose are H chondrites because (i) all of them are thought to derive from a single parent body (possibly asteroid (6) Hebe) and (ii) for several specimens precise radiometric ages over a wide range of closure temperatures are available.
Aims. A thermal evolution model for the H chondrite parent body is constructed by using the cooling histories of all H chondrites for which at least three different precise radiometric ages are available. The thermal model thus obtained is then used to constrain some important basic properties of the H chondrite parent body.
Methods. Thermal evolution models are calculated using our previously developed code, which incorporates the effects of sintering and uses new thermal conductivity data for porous materials. Several key parameters determining the thermal evolution of the H chondrite parent body are varied together with the unknown original location of the H chondrites within their parent body until an optimal fit between the radiometric age data and the properties of the model is obtained. The fit is performed in an automated way based on an “evolution algorithm” to allow for a simultaneous fit of a large number of data, which depend in a complex way on several parameters. Empirical data for the cooling history of H chondrites are taken from the literature and the thermal model is optimised for eight samples for which radiometric ages are available for at least three different closure temperatures.
Results. A set of parameters for the H chondrite parent body is found that yields excellent agreement (within error bounds) between the thermal evolution model and empirical data for the cooling histories of six of the examined eight H chondrites. For two of the samples significant discrepancies exist between model and empirical data, most likely reflecting inconsistencies in the empirical cooling data. The new thermal model constrains the radius and formation time of the H chondrite parent body, and the initial burial depths of the individual H chondrites. In addition, the model provides an estimate for the average surface temperature of the body, the average initial porosity of the material the body accreted from, and the initial 60Fe content of the H chondrite parent body.
Key words: meteorites, meteors, meteoroids / planets and satellites: physical evolution / minor planets, asteroids: general
© ESO, 2012
1. Introduction
Radiometric ages for chondritic meteorites and their components provide information on the accretion timescale of chondrite parent bodies, and on cooling paths within certain areas of these bodies. However, to utilize this age information for constraining the internal structure, and the accretion and cooling history of the chondrite parent bodies, the empirical cooling paths obtained by dating chondrites must be combined with theoretical models of the thermal evolution of planetesimals. Important parameters in such thermal models include the initial abundances of heat-producing short-lived radionuclides (26Al and 60Fe), which are determined by the accretion timescale, and the terminal size, chemical composition and physical properties of the chondritic planetesimals. Here we use our newly developed code for modelling the structure and thermal evolution of planetesimals of ≈ 100 km size (Henke et al. 2012, henceforth called Paper I) to constrain the properties and thermal evolution of the H chondrite parent body, and to evaluate the most important parameters that determined its thermal evolution. This is done by finding the optimal fit between a theoretical thermal model and empirical data for the cooling histories of H chondrites. The H chondrite parent body was chosen here as a test case, because it is the only body for which a comprehensive set of thermochronological data is available. For eight H chondrites in particular radiometric ages exist that were obtained using at least three distinct radioisotope chronometers characterised by different closure temperatures. The cooling history of these samples, therefore, is well constrained.
The well preserved and smooth cooling histories of many H chondrites were used to argue that the H chondrite parent body has not been subjected to catastrophic collisions during the first ≈100 Ma of its history. In that case an onion shell structure develops in which the degree of thermal metamorphism is a function of depth within the parent body; material of petrologic type H6 is found in the central part, while type H3 material is located at the surface. Based on the assumption of an onion shell structure, a number of thermal evolution models were constructed that used increasingly more complex physical input (Minster & Allegre 1979; Miyamoto et al. 1981; Bennett & McSween 1996; Akridge et al. 1998; Trieloff et al. 2003; Hevey & Sanders 2006; Sahijpal et al. 2007; Kleine et al. 2008; Harrison & Grimm 2010). All the previous thermal models of the H chondrite parent body found a radius of about 100 km and an accretion time of about 2 Ma after Ca-Al-rich inclusion (CAI) formation. The success of these models in reconstructing the empirical cooling histories of the H chondrites gave much support to the hypothesis that catastrophic collisions did not significantly disturb the initial thermal structure of the H chondrite parent body. It should be noted, however, that some hints exist for the occurrence of impacts (see Wittmann et al. 2010, and references therein), but these do not appear to have resulted in catastrophic disruption.
These previous thermal models, despite their success in reconstructing the observed empirical cooling rates for several H chondrites, fall short in providing insights into the physical processes occurring during the thermal history of a ≈ 100 km-sized planetesimals. This motivated us to use our new thermal evolution model (described in Paper I) to find the optimal fit between the empirical cooling history of the H chondrites and the thermal model. Our new thermal model applies recent data on the thermal conductivity of granular material (Krause et al. 2011a,b) and on the compaction by cold isostatic pressing before the onset of sintering (Güttler et al. 2009). The modelling of the sintering process is based on the same kind of theory (Rao & Chaklader 1972) as in Yomogida & Matsui (1984), but with some improvements. This theory does not consider more recent approaches for modelling hot pressing for technical processes (e.g. Arzt et al. 1983; Fischmeister & Arzt 1983; Larsson et al. 1996; Storåkers et al. 1999) but appears more appropriate for the lower pressure regime relevant for asteroids. The treatment of heat conduction of the chondritic material and its sintering under pressure and at high temperature still has to be considered as rather crude, but at least is based on physical concepts that are successfully applied in other fields and in some laboratory measurements.
We do not consider a possible melting of the body, because the H chondrite parent body is thought to have remained undifferentiated. Our results will show, however, that this assumption may not be entirely valid, because the calculated central temperature of the H chondrite parent body is only slightly below the solidus temperature of chondritic material (1200 K, Fei et al. 1997).
Our model considers more properties of the asteroidal body than traditional approaches, and so fitting of the model to the observed cooling histories is more difficult because of the much larger parameter space. Therefore we develop an automated method to perform such a fit that is based on the evolution algorithm that mimics the concepts that are thought to rule biological evolution in nature. This is some kind of intelligent trial-and-error method by which the optimum of some quality function can be found. Its advantage is that it does not require any kind of good behaviour of the quality function. It will be shown that this method (in the version described in Charbonneau 1995) can successfully be applied to our problem.
For fitting the model we exclusively use meteorites for which at least three age determinations at different closure temperatures are available. These meteorites do not only constrain the slope but also the curvature of an individual cooling path at a certain location within the parent body. Within the framework of the analytic model of Miyamoto et al. (1981), such a data set for a single meteorite would already completely determine the radius and the formation time of the body. However, in view of the presumably complex thermal evolution of meteorite parent bodies, a larger dataset for several meteorites is necessary for a reliable fit. For the H chondrites, 31 data from 8 meteorites (2 meteorites with 5 data, 3 with 4 data, 3 with 3 data) are available for this purpose. This allows determining all the important parameters of the H chondrite parent body by an optimization procedure.
Key data for cooling history of selected H chondrites.
The plan of this paper is as follows: in Sect. 2 we describe the available empirical data. In Sect. 3 we give a brief overview how we calculate thermal evolution models. Section 4 describes the optimisation method. Section 5 gives our results and conclusions. The paper closes with some final remarks in Sect. 6.
2. Data for cooling histories of H chondrites
Most ordinary chondrites were affected by thermal metamorphism in their parent bodies and exhibit a range of metamorphic conditions from type 3 (unequilibrated) to type 6 (equilibrated) (Dodd 1969). This range in metamorphic conditions probably reflects different heating and cooling histories, presumably caused by varying burial depths within the parent body (Miyamoto et al. 1981; McSween & Patchen 1989; Trieloff et al. 2003; Kleine et al. 2008). The heat source for the thermal metamorphism of ordinary chondrites most probably was heating by decay of 26Al and to a lesser extent also 60Fe.
Ordinary chondrites and their components have been dated by a variety of methods (Nyquist et al. 2009). Al-Mg ages for chondrules from L and LL chondrites indicate that chondrule formation occurred approximately 2 Myr after formation of CAIs, commonly regarded as the oldest objects formed in the solar system (Kita et al. 2000; Rudraswami & Goswami 2007; Rudraswami et al. 2008). The formation age of chondrules from H chondrites is less well known because no primitive H chondrite has yet been investigated with the Al-Mg system. However, a Hf-W age for the H4 chondrite Ste. Marguerite appears to date chondrule formation at 1.7 ± 0.7 Myr after CAI formation (Kleine et al. 2008, 2009), about contemporaneously to chondrule formation in L and LL chondrites.
The ages for chondrules from ordinary chondrites mainly constrain the timescale of parent body accretion (Alexander 2005; Kleine et al. 2008). In contrast, ages for equilibrated chondrites can be used to reconstruct the cooling history of ordinary chondrite parent bodies, by applying chronometers having different closure temperatures to a set of equilibrated chondrites of different metamorphic grade. By far the most comprehensive set of such age data exists for H chondrites (see Table 1), providing temporal information for cooling over almost the entire range of temperatures prevailing from the metamorphic peak down to ambient temperature. The closure temperatures for diffusive exchange of parent and daughter elements among the different minerals in a rock (Dodson 1973; Ganguly & Tirone 2001) for radiometric methods applied to H chondrites range from ≈ 1150 K (Hf-W) to ≈550 K (Ar-Ar). Additional information on the cooling history is provided by 244Pu fission tracks in orthopyroxene (corresponding to cooling below ≈550 K) and merrillite (corresponding to cooling below ≈390 K) (Pellas et al. 1997; Trieloff et al. 2003), and from metallographic cooling rates (corresponding to cooling between ≈800 and ≈600 K), which employ Fe-Ni diffusion profiles in metal grains consisting of kamacite and taenite (e.g., Herpfer et al. 1994; Hopfe & Goldstein 2001).
The age and thermochronological data available for H chondrites are summarised in Table 1, along with information on the closure temperatures of the different methods. These age data permit a detailed reconstruction of the cooling history of H chondrites, and form the basis for numerically simulating the accretion and cooling history of the H chondrite parent body (Sect. 5).
For calculating heating rates the difference between the formation time of CAIs and the ages from Table 1 has to be formed. This sets the zero-point of our time-scale and the instant for which the initial abundance of 26Al is prescribed. As reference time we take the value of 4568.5 ± 0.5 Ma from Bouvier et al. (2007).
3. Thermal evolution models
The temperature history of an undifferentiated meteoritic parent body is assumed to be determined by essentially three processes: (i) transient heating by decay of short-lived radioactive nuclei 26Al and 60Fe and long lasting heating by long-lived radioactives (40K, 232Th, 235U, 238U), (ii) transport of heat to the surface by heat conduction, and (iii) energy exchange with the environment by emission and absorption of radiation energy. The heat transport in the body is governed by the fact that the material is porous, that heat conductivity of chondritic material strongly depends on porosity (e.g. Krause et al. 2011b), and that the porosity changes by sintering as the body is heated up.
For the formation of the bodies we apply the “instantaneous formation” approximation, i.e., it is assumed that the bodies acquired most of their mass during a period short compared to the half-life τ1/2 = 7.2 × 105 a of the main heating source, 26Al. Present planetary formation scenarios suggest such rapid mass acquisition of 100 km sized and bigger bodies (e.g. Weidenschilling & Cuzzi 2006; Nagasawa et al. 2007). The rapid growth is approximated by the assumption that the bodies came into life at some instant tform and have constant mass over their subsequent evolution.
For reasons of computational economics the shape and internal structure of the body is assumed to be spherically symmetric, though this is certainly a strong simplification. In detail, the following equations are solved:
-
1.
The equation of hydrostatic equilibrium
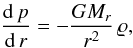 (1)for the pressure p, where
(1)for the pressure p, where  (2)and
(2)and 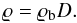 (3)The density ϱb is the mass-density of the consolidated material and D the fraction of volume filled with matter. The void fraction or porosity of the material is φ = 1 − D.
(3)The density ϱb is the mass-density of the consolidated material and D the fraction of volume filled with matter. The void fraction or porosity of the material is φ = 1 − D. -
The heat conduction equation for the evolution of the temperature
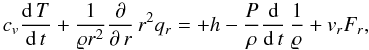 (4)where cv is the specific heat of material per unit mass, h the specific heating rate by decay of short living radioactives, Fr the local gravitational acceleration and vr the shrinking velocity during sintering. The heat current is
(4)where cv is the specific heat of material per unit mass, h the specific heating rate by decay of short living radioactives, Fr the local gravitational acceleration and vr the shrinking velocity during sintering. The heat current is 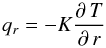 (5)with the heat-conduction coefficient K. The heat conductivity used in our model depends on the porosity φ = 1 − D of the material. We use the analytic fit
(5)with the heat-conduction coefficient K. The heat conductivity used in our model depends on the porosity φ = 1 − D of the material. We use the analytic fit 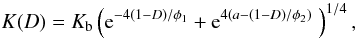 (6)to experimental data discussed in Krause et al. (2011a) and in Paper I, where φ1 = 0.08, φ2 = 0.167, and a = −1.1 are constants given in Paper I1. The pre-factor Kb corresponds to the heat conductivity of the bulk material (i.e., at D = 1). The average value of Kb is determined by extrapolating data obtained from a couple of ordinary chondrites (Yomogida & Matsui 1983) by means of Eq. (6) to zero porosity. Its value is K = 4 W m-1 s-1, but there is significant scatter.
(6)to experimental data discussed in Krause et al. (2011a) and in Paper I, where φ1 = 0.08, φ2 = 0.167, and a = −1.1 are constants given in Paper I1. The pre-factor Kb corresponds to the heat conductivity of the bulk material (i.e., at D = 1). The average value of Kb is determined by extrapolating data obtained from a couple of ordinary chondrites (Yomogida & Matsui 1983) by means of Eq. (6) to zero porosity. Its value is K = 4 W m-1 s-1, but there is significant scatter. -
3.
An equation for the sintering of the initially porous material under the influence of pressure
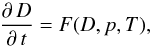 (7)where the right hand side is determined by solving a set of equations for the specific sintering model of Kakar & Chaklader (1967) and Rao & Chaklader (1972).
(7)where the right hand side is determined by solving a set of equations for the specific sintering model of Kakar & Chaklader (1967) and Rao & Chaklader (1972).
The internal structure and thermal evolution of parent bodies of planetesimals is calculated by the numerical method described in Paper I.
The radius of the body is not fixed but changes during the evolution by sintering of the initially porous material. If the body would be completely sintered the final radius would be R. This radius is related to the mass by M = (4π/3)ρb R3 with ρb being the bulk density of the completely consolidated material. Initially the material is porous and the radius is bigger because the density of the porous material ρ = Dρb is lower. The initial porosity is φsrf. This equals also the porosity of the outermost surface material which is too cool and under too low pressure for sintering.
The problem depends on a number of parameters, the most important of which are the bulk density ρb of the chondritic material, the mass M of the body or its radius R, the formation time tform (measured relative to the formation time of CAIs), the heat conduction properties of the material (Kb), the mass fractions XAl and XFe of Al and Fe, respectively, in the chondritic material, and the abundance ratios of short-lived radioactives, 26Al/ 27Al and 60Fe/ 56Fe, the porosity φsrf of the surface material, and the surface temperature Tsrf.
The surface temperature Tsrf depends during the initial phase of evolution on the properties of the ambient dusty accretion disk, after disk dispersal on the distance to the proto-sun. Since model properties depend only weakly on Tsrf, this quantity is held fixed over the whole evolution period in this study.
Some of the parameters are fixed by the properties of the H chondrite material and general properties of the solar system. They are given in Table 2 and their values are chosen as in Paper I. The remaining parameters M or R, tform, Tsrf, φsrf, and Kb are special properties of individual bodies and are varied in our model calculations.
Since there seem to be doubts that the 60Fe/ 56Fe ratio (at time of CAI formation) is the same for all bodies (see Quitté et al. 2010) we prefer to consider also this quantity as a free parameter (details are given in Sect. 5.1).
Fixed parameters of the H chondrite parent body models (taken from Paper I).
 |
Fig. 1 Schematic representation of the temperature evolution at two different depths (full lines) and at the centre (dotted line) of a planetesimal of the 100 km size class. The horizontal dashed lines correspond to fixed temperatures equal to the closure temperatures in Table 1. The circles indicate the instants at which at a given depth the temperature drops below a given temperature. These instants correspond to the closure ages of the different thermochronometers used for meteorites. |
4. The fitting procedure
4.1. Comparing thermochronological data with asteroid models
The data on the cooling history of meteorites described in Sect. 2 associate with a meteorite a number of temperature-time data pairs, corresponding to the instants where the temperature at the pristine location of the meteorite inside of its parent body fell below that temperature. The set of data pairs obtained for a meteorite corresponds to a set of intersection points between the temperature evolution curve of some mass-element with the lines of constant temperature on the descending part of the evolution curve. This requires, of course, that the temperature evolution at the location of the later meteorite proceeds without substantial disturbance by external influences (impacts, for instance).
Figure 1 demonstrates this for the four closure temperatures (1150 K, 720 K, 550 K, 390 K) of Table 1. The cooling curves are shown as full lines, the lines of constant temperature as dashed horizontal lines. The circles on a cooling curve correspond to the data for a hypothetical meteorite. Since the average slope of the curve connecting two neighbouring data points significantly varies for curves corresponding to different depth’s, it is obviously possible to reconstruct for a given model from only two data points the appropriate depth for which the temperature evolution curve runs through just these two data points.
If the properties of the body are not known and only two data points are available for a meteorite, such a fit would be possible for a whole range of model parameters. This does not allow any conclusion on the properties of the body. If, however, more than two data points are available for a meteorite this restricts the possible models since the overall shape of the temperature evolution curves depends on the model properties. The average slope of that part of the curve that connects neighbouring data points on the curve varies for different such pairs with model properties in a different way. This allows to reconstruct the properties of the body from cooling data on meteorites by looking for a set of model parameters for which for each of the meteorites an appropriate depth can be found such that the cooling curve runs through all data points.
Since for real meteorites, experimentally determined closure temperatures and ages are subject to considerable errors (cf. Table 1), data sets for an as big as possible number of meteorites (with at least three data points) are required and the task is to find a set of parameters that describe the properties of the parent body such that for each of the meteorites a depth below surface can be found such that the (somehow defined) minimum distance of all of the data points of a meteorite from the corresponding temperature evolution curve becomes as small as possible; and this should hold for all available meteorites. Hence one has to solve a minimisation problem, where some quality function has to be minimised with respect to a set of data and a set of parameters.
Parameter space of variable parameters for the meteoritic parent bodies.
In the past, this task has been solved mainly by trial and error. Formation times tform and parent body radii R for some bodies have been determined this way (Miyamoto et al. 1981; Bennett & McSween 1996; Akridge et al. 1998; Trieloff et al. 2003; Hevey & Sanders 2006; Sahijpal et al. 2007; Kleine et al. 2008; Harrison & Grimm 2010). However, the essential properties of an asteroidal body that determine its thermal evolution, are not merely R and tform but also some additional parameters, see Table 3. To these, one has to add the unknown depth’s for each meteorite as additional parameters of the optimisation problem. Here we aim to solve the problem by a general numerical algorithm that allows to treat the more extended parameter space (and possibly additional parameters in future calculations) and large data sets.
4.2. The data set
For reconstructing the parent body of a group of meteorites that are thought to derive from the same asteroidal body, we use all specimens for which at least three thermochronological data points are available. For the parent body of, e.g., the H chondrites, the eight meteorites given in Table 1 have sufficiently accurate determined data and the required minimum number of data points. Three of them have even four data points, the other five have three of them.
The burial depth of each of the J meteorites, enumerated by an index j (=1,...,J), in the parent body is characterised by the J mass-coordinates Mj in the theoretical model of the parent body, because the model calculation uses the mass-coordinate as independent variable (see Paper I). Then we have a list of I data quintuples 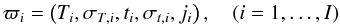 (8)with Ti being the closure temperature, ti the corresponding age, σT,i and σt,i the errors of Ti and ti, respectively, and ji a pointer to the appropriate member in the list (Mj,j ∈ { 1,...,J } ) of mass-coordinates corresponding to the different meteorites.
(8)with Ti being the closure temperature, ti the corresponding age, σT,i and σt,i the errors of Ti and ti, respectively, and ji a pointer to the appropriate member in the list (Mj,j ∈ { 1,...,J } ) of mass-coordinates corresponding to the different meteorites.
The mass-coordinates Mj are not known a priori. They have to be determined simultaneously with the parameter set given in Table 3 by the optimisation process.
4.3. The quality function
The quality function to be optimised can be defined in different ways. We construct in this paper one in the following way: For each of the mass-coordinates Mj it is known which of the data sets ϖi are associated with this Mj. During a model run, the instants when the temperature drops below the closing temperatures belonging to the data sets ϖi associated with j, are recorded. This defines for each i an age tmod,i on the temperature evolution curve j where it passes through the prescribed temperature Ti. Analogously, the temperature Tmod,i is recorded at instant ti for each of the data points.
As quality function for the optimisation process we choose the least squares deviation of the model age tmod,i from the empirically determined age ti, and of the model temperature Tmod,i from the closure temperature Ti: 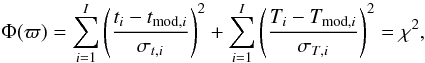 (9)this χ2 is to be minimised. The parameters (R, tform, 60Fe/56Fe, Tsrf, φsrf, Kb, Mj (j = 1,...,J)) are then determined such that each cooling curve corresponding to the burial depth of a certain meteorite in the model passes as close as possible to the empirically determined age-closure temperature pairs for all data points of that meteorite.
(9)this χ2 is to be minimised. The parameters (R, tform, 60Fe/56Fe, Tsrf, φsrf, Kb, Mj (j = 1,...,J)) are then determined such that each cooling curve corresponding to the burial depth of a certain meteorite in the model passes as close as possible to the empirically determined age-closure temperature pairs for all data points of that meteorite.
4.4. Choice of the optimisation algorithm
The basic problem is to determine the absolute minimum of the quality function Φ(ϖ) and possibly all other deep local potential minima with comparable depth. As is well known, such an optimisation problem with a large number of variables cannot be solved by analytical methods and the task of solving the problem by numerical methods becomes extremely difficult and time consuming if the surfaces Φ(ϖ) = const. have a complicated geometric structure, which is expected to be the case for our problem. No general method is known which allows to definitely
-
1.
find all local extremal values of an optimisation problem;
-
2.
and to decide if the real optimum indeed is contained within the set of extremal values found by the applied method.
Methods have been developed which allow one to find an in a certain sense best result, which means that for test cases with a known absolute minimum the algorithm always finds this minimum or at least a local minimum that is not much worse than the absolute one.
One method, that has successfully been applied to several difficult optimisation problems like that of the travelling salesman is the “evolution algorithm” developed by Rechenberg (1973, 1989). A detailed description of how this method can be applied to problems in astronomy and astrophysics and a code are given in Charbonneau (1995). We use this method to reconstruct the parent body’s properties of a suite of meteorites.
The basic idea is to imitate the concepts that are thought to rule the evolution of species in an algorithm to find the extremal values of some quality function. Evolution theory describes the change of the shape of creatures in a population during many generations due to the variability of the population and the dependence of the amount of the creature’s offspring on their conformity to the environment. The biologic term genotype means the whole heritable attributes of a creature, while phenotype denotes its appearance. During the development of the creature the phenotype forms according to the instructions of the genotype. The position in the genotype, where a certain property (e.g. eye colour) of the individual is encoded, is called gene. The value of the property (e.g. blue) is called allele. The amount of possible offspring (the reproduction outcome) depends on, how advantageous its alleles are. The reproduction outcome determines, how numerously certain alleles in a population are inherited compared to other respective alleles. Which processes are advantageous is determined by the environment. Thus after some generations advantageous alleles will accumulate in the population, while less advantageous ones will be depleted, such that after a certain number of generations only those alleles, the creature benefits most from, remain in the population in a noteworthy amount. This leads to a degeneration of the gene pool. But additionally mutations can cause random change of the genotype in a certain allele, which can cause change of the affected gene in a significant way and can create a completely different phenotype. Thus mutation adds novel alleles to the gene pool. These can be superior to the established alleles (even if they are destructive in most cases). So the mutations keep the variability of a population, and allow the population to adapt to changing environments.
An algorithm for finding parameters that works like evolution due to inheritance and natural selection is superior in finding of optimal parameters in ugly problems with many local minima compared to methods that, e.g., calculate in some way the derivative of the quality function and then go into the direction of downward slope and repeat calculating the derivative and so on. Those methods readily find the next local minimum which, however, might not be the absolute one. In the evolution algorithm mutations can produce extensive changes of the parameters to the parents’ ones. This can cause big jumps in the parameter space. Thus the population will not remain in a local minimum, but test remote regions again and again and perhaps find a deeper local minimum that is possibly a total one.
4.5. General implementation of an evolution algorithm
An evolution algorithm can be applied to every problem in which the variables to be optimised can be encoded to form a string of numbers (chromosome). This string then is the genotype. It is assumed in the following that for every individual the model is calculated and compared to the data by calculating a quality function, like Eq. (9), e.g., and ranked by this to other individuals. After determining which individuals are to get off-springs, their genotypes are cut at the same random digit(s) and the related parts are exchanged, so that, e.g., the initial part of parent 1 is connected to the end part of parent 2. The so generated string then represents the genotype of the new offspring individual. Mutation can be performed by giving every digit of the string of the genotype a certain possibility to take a random value.
An implementation of an evolution algorithm can be as follows:
-
1.
A random initial population is constructed with normally noreference to the problem.
-
2.
The fitness function of each individual is calculated by a user given algorithm which determines how well the individuals match the problem.
-
3.
A new generation is constructed by breeding of selected individuals of the old population. There the algorithm creates new parameters by exchange of information between the parameters of the two parent individuals. Also the mutation takes place in this step. In most cases the number of individuals in each generation will remain the same.
-
4.
The old population is replaced by the new one.
-
5.
Then back to 2.
4.6. Application to our problem
The particular implementation of a genetic algorithm that we use is that described in Charbonneau (1995). It uses a random number generator that generates numbers between 0 and 1 to derive a set of random parameter values for formation time, radius and all other parameters of the model. Each time the genetic algorithm requires a new value of Φ for some individual it provides a set of K random numbers 0 ≤ ξk ≤ 1 (k = 1,...,K) from which values for the corresponding physical parametres xk of the model are calculated as  (10)Here xk,min and xk,max are the minimum and maximum allowed values for xk according to Table 3. For this set of parameter values xk an evolution model is calculated and from its results the corresponding value of the quality function Φ.
(10)Here xk,min and xk,max are the minimum and maximum allowed values for xk according to Table 3. For this set of parameter values xk an evolution model is calculated and from its results the corresponding value of the quality function Φ.
The burial depth’s of the meteorites are treated as part of the parameter set of the model. Random values are assigned to the burial depths of each of the distinct H-chondrites. In this way for each of the individuals of the evolution algorithm, a certain depth is ascribed to every chondrite. Technically this is done by assigning to each meteorite a layer characterised by an index i and a position factor y that gives its relative position inside of the layer with respect to the edges of the layer, ri and ri − 1, so that the real position of the meteorite is 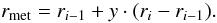 (11)Because the sintering behaviour is treated as the same everywhere within a single layer the factor y will not change during the thermal evolution. The temperature at the position of the meteorite is calculated by
(11)Because the sintering behaviour is treated as the same everywhere within a single layer the factor y will not change during the thermal evolution. The temperature at the position of the meteorite is calculated by  (12)and it is tested how good the temperature evolution of that Tmet matches the empirical data of the corresponding meteorite by means of Eq. (9).
(12)and it is tested how good the temperature evolution of that Tmet matches the empirical data of the corresponding meteorite by means of Eq. (9).
According to Charbonneau (1995) a fit achieved by a genetic algorithm is moderately good if I − K ∽ χ2, where I is the number of data points to be fitted and K the number of the optimised parameters. For example, for the six parameters given in Table 3, plus the eight layers of the eight meteorites (K = 6 + 8 = 14), and the 28 data points, one gets a desired value of χ2 < 14 for an acceptable fit.
5. Results for the parent body of H-chondrites
5.1. Parameters
Besides the physical parameters of the problem, that are not subject of the fitting procedure, we have a number of parameters that describe properties of the body and external quantities. These are given in Table 3, including the range of variation admitted during the optimisation process. The following parameters require some comments:
Radius: There are a number of reasons (Gaffey & Gilbert 1998; Morbidelli et al. 1994) why asteroid (6) Hebe is thought to be the parent body of the H chondrites and the IIE iron meteorites. Some general characteristics of (6) Hebe are listed in Table 4. If (6) Hebe is only a fragment of the original H chondrite parent body, then the size of (6) Hebe provides a firm lower limit for the size of the H chondrite parent body. Hebe is a somewhat irregular shaped body (Torppa et al. 2003) with dimensions 205 × 185 × 170 km corresponding to an average diameter of 186 km. Its high mass-density means that it is not a rubble pile as most other asteroids. It did not suffer catastrophic collisions that disrupted the whole body and where the debris later re-assembled to the present body. Nevertheless, a surface layer of unknown thickness has certainly been eroded over time by collisions with other bodies and the present size of Hebe defines only a lower limit to the size 4.56 Ga ago. But this lower limit should be observed in the model construction.
Some properties of asteroid (6) Hebe.
60Fe/ 56Fe-ratio: The decay of 60Fe may have contributed to the heating of the body, in particular since the recently re-determined half-life of τ1/2 = 2.62 ± 0.04 Ma (Rugel et al. 2009) significantly exceeds the half-life of 26Al of τ1/2 = 0.72 Ma. Though there is less 60Fe than 26Al, the heating period can be significantly prolonged in models with 60Fe compared to models with only 26Al included.
It has been questioned (cf. Dauphas et al. 2008; Quitté et al. 2010) that 60Fe was homogeneously distributed throughout the solar system. If true, this would mean that the initial 60Fe abundance in the parent body is not known a priori. On the other hand, a recent study by Tang & Dauphas (2012) argued for a homogeneous distribution of 60Fe on a relatively low level of 1.08 ± 0.21 × 10-8 for the initial 60Fe/ 56Fe abundance ratio at time of CAI formation. This is much lower than values previously reported, although the authors do no comment on the credibility of earlier studies.
At such a low abundance heating, by 60Fe is nearly negligible. Because of the presently unclear situation with respect to which value should be taken for the 60Fe/ 56Fe abundance ratio we treat this as an additional free parameter for the optimisation process. The range of 60Fe/ 56Fe ratios considered (see Table 3) is between no 60Fe and the maximum reported value (Birck & Lugmair 1988).
 |
Fig. 2 Results for the individual meteorites used in the model fit. The values of the free parameters and the burial depth’s of the meteorites found for the optimised model are given in Table 5. The full line shows the temperature evolution at the burial depth’s of the meteorites in the asteroid, as determined by the evolution algorithm. The dashed line shows the temperature evolution at the centre and the dotted line is the surface temperature. The square boxes indicate the individual data points and the error bars the uncertainty of closing temperature and age determinations. |
Surface temperature: This is determined by the unknown radius of the orbit, its eccentricity, by the rotation of the body, the surface albedo, and, during the first few million years, by the properties of the ambient accretion disc. All these factors are not known precisely. Therefore we think it best to include the surface temperature Tsrf as a free parameter in the optimisation process. The resulting temperature Tsrf then represents some kind of average temperature of the surface layers during the evolution period where the body first heats-up and then finally cools down below the lowest of the closure temperatures.
The resulting value for Tsrf has no bearing to the present surface temperature of a possible successor body, because in the meantime the body may have changed its properties by catastrophic collisions and it may have changed to some extent its orbit during the evolution of the asteroid belt. Surface temperatures in the present-day asteroid belt therefore cannot be considered as representative for the surface temperature during the phase where the essential metamorphic processes acted in the body, as it is assumed in some thermal evolution models.
The range of surface temperatures (see Table 3) is limited by the fact that Tsrf should be higher than the temperature where the body would contain ice ( ≈ 150 K) and lower than the lowest of the closing temperatures ( ≈ 400 K).
Surface porosity: During the (short) main growth phase of the body the structure of the surface layer is determined by the properties of the smaller planetesimals that form the body under consideration. Later the surface layer is gardened by continued impacts that produce a regolith surface layer for which theoretical calculations indicate a porosity in the range 20% to 30% (Richardson 2009; Warren 2011). Presently, too little is known on these processes as that they can be included in our model calculation. Therefore we include the porosity of the surface layer, φsrf, as a free parameter in the optimisation procedure. The resulting value then is some sort of average value of φsrf over the period where the metamorphic processes were active.
5.2. Data
The general optimisation method of the evolution algorithm is applied to the data for the set of H chondrites given in Table 1. For reasons that will become clear from the model results shown in the subsequent figures and are discussed later the two highest closing temperature data of Ste. Marguerite and the plutonium fission track datum of Nadiabondi are not used. Then we have totally 28 data points that have to be fitted. The problem depends on the 5 parameters given in Table 3 and the eight unknown burial depths of the meteorites.
The range of surface porosities (see Table 3) should in principle be restricted by the requirement, that the porosity should be higher than that of the most porous chondrites (about 20%, cf. Consolmagno et al. 2008). During the model calculations it was found that for an optimum fit values not much bigger than this minimum value are required and, therefore, no a priori restriction was imposed on φsrf during the final optimisation runs. The optimal set of parameters, indeed, satisfies the assumption.
Parameters and burial depths of the meteorites for the optimised H chondrite parent body model.
5.3. Model with fixed heat conductivity
An optimisation was run for the 5 + 8 = 13 parameter and the 28 given data points. The model used 250 mass-shells. The optimisation was run for about 5500 generations with hundred individuals per generation, i.e., totally a number of about 550 000 complete thermal evolution models were calculated for a complete optimisation run. This used about seven days on a normal desk-top computer equipped with a dual-core pentium processor operating with 2.6 GHz.
The finally accepted optimum fit had a value of χ2 = 3.1420. This value for χ2 can be considered as excellent in view of the fact that a good fit would require only χ2 ≲ 15 (cf. Sect. 4.6). The model parameters of the final optimum fit for the properties of the body and the burial depths of the meteoritic material are given in Table 5.
The central temperature at maximum, Tc = 1163 K, that results for the set of optimum parameters is below the Fe-FeS eutectic at 1220 K (Fei et al. 1997). For the optimum model the temperature in the centre therefore is below the border temperature where differentiation would just become possible. In so far the model is compatible with the basic assumption of the model calculation that melting can be neglected.
The cooling curves of the meteoritic materials at the resulting burial depths and the empirical age-temperature data points given by the radiometric ages are shown in Fig. 2 for the optimised model. The solution of the optimisation problem found here meets the data for the cooling history of the meteorites of Table 1 within their 1σ-error-boxes in all eight cases, though in a few cases only marginally. The fit between model and empirical data can be considered as excellent for the three meteorites with four data points: Kernouvé, Richardton, and Estacado. Also for three of the meteorites with three data points, Guareña, Allegan, and Forest Vale, the model fits the data-points rather well. Only for Nadiabondi and Ste. Marguerite the fit is of low quality. These two cases are discussed later.
The maximum temperature, Tmax, reached during the thermal history at each of the different depths are given in Table 5. For comparison, the table also gives the metamorphic temperature of the different petrologic types, Tmet (Slater-Reynolds & McSween 2005). The maximum temperatures of the different meteorites at their burial depth, Tmax, fit reasonably well with the requirement Tmax > Tmet, except for Ste. Marguerite.
The radius of 132 km required for the optimum model is significantly larger than the present day radius of (6) Hebe. If this asteroid is really the parent body of the H-chondrites this would mean, that a layer with an average thickness of about 40 km has been eroded over time from the surface of (6) Hebe. This is of the same size as the depth of the layer where the petrologic type changes from H5 to H6. The change from initial to present radius amounts to 29% or corresponds to a volume change of 64%, i.e., the body would have lost most of its initial mass. Consequently, all H3 and H4 chondrite material should have been removed, which is inconsistent with meteoritic record. Probably our optimised radius is too big and the most likely reason for this is that the treatment of heat conduction in the porous medium and of the sintering process is not yet realistic enough. The other possibility is that H-chondrites do not come from (6) Hebe, although the arguments favouring (6) Hebe as parent body are strong (Gaffey & Gilbert 1998).
The optimum value for the 60Fe abundance is compatible with the most recent abundance determination by Tang & Dauphas (2012). At this low abundance, heating by 60Fe contributes only marginally to the total heating of the parent body.
The thickness of the remaining porous outer layer is also given in Table 5. As lower boundary of this layer we define the radius where φ = 10%. At this degree of porosity usually the connections between pores start to close and the pore structure changes from a network of interconnected pores to isolated voids.
The low value of the surface porosity φsrf = 0.28 may either result from the fact, that planetesimals of the 100 km size-class gain most of their mass by collisions with smaller planetesimals that have already diameters of about 10 km and more and, therefore, are already largely compacted (see Fig. 10 of Paper I) if they are incorporated into the growing larger body. A second mechanism that may be responsible for the low value of φsrf is that our optimised value represents a mean value of the actual value of φsrf over the initial heating and the extended subsequent cooling period of 100 Ma. During that period impacts certainly continue with a decreasing rate that do not contribute to a significant further growth, but that form a regolith surface. According to model calculations this has a saturation porosity of 20% to 30% (Richardson 2009; Warren 2011) that would fit to the value of φsrf = 0.28 found by the optimisation process.
 |
Fig. 3 Results for a model fit where the heat conductivity at zero porosity, Kb, is included in the optimisation process. The values of the free parameters and the burial depth’s of the meteorites found for the optimised model are given in Table 6. For meaning of symbols see caption to Fig. 2. |
5.4. Model with optimised heat conductivity
The pre-factor Kb in our approximation for the porosity-dependent heat conductivity, Eq. (6), corresponds to the heat conductivity of the bulk material (i.e., at φ = 0 or D = 1), determined by extrapolating data obtained from a couple of ordinary chondrites (Yomogida & Matsui 1983) to zero porosity. Figure 6 in that paper and our Fig. 6 shows that there is considerable scatter in the data which results in some uncertainty of the value of Kb. The value for Kb used in the above model calculation (see Table 5) may therefore be an unfavourable choice from the allowed range of values compatible with experimental values. Additionally, there is the problem that the small suite of chondrites used for determining Kb may not be representative for the bulk of the material of the parent body.
Therefore we performed a model calculation where Kb was considered to be a free parameter of the problem for which an optimal value is determined by the optimisation procedure. The remaining number of data-points for closure times with which to compare is still big enough to allow for an additional parameter, because we now have 28 data points and 14 parameters (6 for the body and the 8 burial depth’s).
The model, again, used 250 mass-shells. The optimisation was run for about 5500 generations with hundred individuals per generation. The finally accepted optimum fit had a value of χ2 = 6.116 in generation 2945. With this value for χ2 the fit can also be considered as an excellent one in view of the fact that an acceptable fit would require only χ2 ≲ 14 (cf. Sect. 4.6). How the value of χ2 evolved during the optimisation process for this model is shown in Fig. 5. The somewhat “noisy” appearance of the evolution history reflects the permanent mutations and crossing of genes in the evolution algorithm that not always results in children that are as fit as their parents.
The model parameters of the final optimum fit for the properties of the body and the burial depth’s of the meteoritic material are given in Table 5 and the model results for the individual meteorites are shown in Fig. 3. The already good fit to the data points shown in Fig. 2 is once more slightly improved. The two meteorites Nadiabondi and Ste. Marguerite, however, drop out again and are not well fitted.
The thickness of the remaining porous outer layer is also given in Table 6. This layer is defined as that region where φ ≥ 0.1; its lower boarder is given by the radius where φ = 0.1. Around this border the heat conductivity K(φ) drops nearly discontinuously from the bulk value Kb to the low value K(φsrf). The blanketing effect of this layer is responsible for the shallow burial depths of the H4 and H5 chondrites found in the model, which are also found in other models (e.g Bennett & McSween 1996; Akridge et al. 1998; Harrison & Grimm 2010) that introduce an insulating outer regolith layer instead of modelling the sintering process.
In this model the radius of the body is smaller than in the model with prescribed Kb. With R = 111 km it is only 18 km bigger than the average radius of 93 km of (6) Hebe. If (6) Hebe really is the parent body, this would mean that material corresponding to 16% of the initial radius or 41% of the initial mass has been knocked-off by collisions. This model seems to be more plausible because the body then retained most of its mass and did not lose most of its mass as in the preceding model. This makes it more plausible that we still find H4 chondrites.
Parameter for the model with optimised K0, burial depths of the meteorites, and maximum temperature during their thermal history.
The optimum value for the 60Fe abundance agrees well with the most recent abundance determination of 1.08 ± 0.21 × 10-8 by Tang & Dauphas (2012).
The value for Kb required for an optimum fit is significantly lower than the average value for Kb obtained from the laboratory data but still inside the range of experimental values. This is shown in Fig. 6 where we plot the ratio Kexp/K(φ) for all chondrites from Yomogida & Matsui (1983). If one would have used only the experimental values for the H chondrites, the optimised value for Kb would be definitely too low. This may result from the fact that, as already mentioned, the H chondrites used by Yomogida & Matsui (1983) for measuring the heat conductivity and its dependence on φ are unfortunately not representative for the parent body as a whole. For instance could the material in the more central part of the body have for some reason different properties than the zones probed by the meteorites. Another probability could be that we neglected the temperature variation of the heat conductivity. If one looks at Fig. 6 this variation seems to be small, but in fact the heat conductivity drops with increasing temperature and may be significantly lower at 1000 K than the values seen in Fig. 6. Therefore the low value found in the optimisation may also simply mean that if we optimise Kb, the resulting value is kind of a “best average” between the lower conductivity of the hot core region of the parent body and of the higher conductivity in the cooler mantle region. The temperature dependence of the heat conductivity therefore should be considered in future model calculations.
5.5. Model with given Radius of (6) Hebe
We also tried a model fit with the present-day radius R = 93 km of (6) Hebe to check whether a somewhat sub-optimal but, nevertheless, acceptable fit could be obtained for this case. The value of Kb is included in the optimisation process, but R is now fixed. The model, again, used 250 mass-shells. The optimisation was run for about 5500 generations with hundred individuals per generation. The finally accepted optimum fit had a value of χ2 = 6.058 in generation 5461. With this value for χ2 the fit is not worse than the fit of the model with fixed K in view of the fact that an acceptable fit would require only χ2 ≲ 15 (cf. Sect. 4.6). The resulting set of parameters is given in Table 7 and the temperature variation at the burial depths of the meteorites is shown in Fig. 4.
The main difference between the models with optimised R and fixed R is that the resulting Tsrf in the first model is 178.2 and 250.4 K in the latter, all other things being very similar. The higher surface temperature is required to prevent a too rapid cooling of the outer layers of the smaller body. In practice this means that there is some ambiguity in the models with respect to the location of the body (surface temperature should decrease with increasing distance to the sun) and its radius. The optimisation process cannot really discriminate between the two cases considered here.
 |
Fig. 4 Results for a model fit where the radius is set equal to the observed radius of (6) Hebe. The burial depth’s of the meteorites found for the optimised model are given in Table 7. For meaning of symbols see caption to Fig. 2. |
 |
Fig. 5 Evolution history of the value of χ2 during the optimisation process with progressing number of generations, n, for the model where the heat conductivity at zero porosity, Kb, is included in the optimisation process. Shown is for each generation the particular individual with the lowest value of χ2 of all individuals of that generation, the formation time, tform, of this individual, and the radius of the body, R. For two representative meteorites, Kernouvé and Allegan, the evolution of the optimum value of the burial depth, d, is also shown. |
 |
Fig. 6 Data for thermal conductivity Kexp of ordinary chondrites (from Yomogida & Matsui 1983) divided by the analytical fit K(φ) given by Eq. (6) using a value of Kb = 1.75 obtained as optimum value for fitting the cooling history. Full black circles represent data for H chondrites, open circles data for L chondrites. The dashed line corresponds to the value of K = 4 used in model with fixed K. |
Parameter for the model assuming a radius equal to that of (6) Hebe, burial depths of the meteorites, and maximum temperature during their thermal history.
5.6. Nadiabondi and Ste. Marguerite
For Nadiabondi and Ste. Marguerite, some data points need to be discussed separately.
For Ste. Marguerite the temperature increase during metamorphism was insufficient for resetting some of the radioisotopic systems, making it difficult to constrain the cooling history of this meteorite. For instance, Kleine et al. (2008) argued that the closure temperature of the Hf-W system is much higher than the metamorphic peak temperature of Ste. Marguerite. The Hf-W age of 1.7 ± 0.7 Ma after CAI formation, therefore, must date a high-temperature event prior to the metamorphism. This event most likely was chondrule formation. This interpretation is consistent with our finding that the H chondrite parent body probably accreted at about 1.8 Ma after CAI formation.
Second, some data of relatively poor precision do not really constrain the fit procedure, e.g., in the case of Nadiabondi the low temperature datum of fission track retention of the phosphate merrillite. Nominally it yields an – impossible – negative cooling rate, and only within errors just relatively fast cooling can be inferred. Similarly, both fission track and Ar-Ar data of Ste. Marguerite have large uncertainties, precluding firm constraints on the cooling history, although the nominal values plot on the fitted cooling-curves.
5.7. A Miyamoto-like model
For comparison, the optimization was also done for a model where the porosity was set to a value of φsrf = 0.08. This is a typical value as it is observed for various H6 chondrites that have not been subject to strong shock modifications (Yomogida & Matsui 1983; Consolmagno et al. 2008). With this initial porosity the body is practically already compacted from the beginning on and sintering does not play any role. The heat conductivity then is practically constant throughout the body and for all times. The prefactor Kb of the heat conductivity was set to the same value as in Sect. 5.3 and was not included in the optimisation process. Such a model corresponds essentially to the kind of model considered originally by Miyamoto et al. (1981), the mayor difference being that heating by 60Fe is included.
The model, again, used 250 mass-shells. The optimisation was run for about 3260 generations with hundred individuals per generation. In generation 2299 an optimum value of χ2 = 5.94 was obtained that was considered as sufficiently good. The model parameters of the optimised model are shown in Table 8 and Fig. 7 shows the fit for the individual meteorites.
It is obviously possible to obtain also an acceptable fit to the observed cooling history of the meteorites with such kind of model. The parameters of such a model are somewhat different from the preceding cases because of the lack of an insulating porous outer layer and a higher heat conductivity during the initial warm-up phase. In particular a significant contribution of 60Fe decay to the heating is required to compensate for the more easy heat-loss in the present case. Though the model as a whole does not look worser than the model with optimised Kb, it is physically not acceptable since the lack of a porous outer layer is unrealistic.
 |
Fig. 7 Results for the individual meteorites if a Miyamoto-like model is used for the model fit. The burial depth’s of the meteorites found for this model are given in Table 8. For meaning of symbols see caption to Fig. 2. |
5.8. Comparison with earlier results
There are a number of previous attempts to reconstruct the properties of the H chondrite parent body using the empirically determined cooling rates of H chondrites derived from different depth within the parent body. Table 9 gives an overview on the results and the values of some key parameters of some of these models. The table lists all the models that attempted to obtain in some way a “best fit” between properties and cooling histories derived from laboratory studies and a thermal evolution model of the parent body. The results are generally the putative radius and formation time of the body, and the burial depths of the meteorites. All studies, including ours, showed, that the observed properties of the H chondrites are compatible with a parent body of about 100 km radius and an “onion shell” model. In this model the body is first heated within a period of ca. 3 Ma by decay of radioactive nuclei, mainly 26Al, and then cools down over an extended period of ca. 100 Ma, without suffering catastrophic collisions that would have disrupted the body, thereby disturbing its thermal evolution record.
Parameters and burial depths of the meteorites for the Miyamoto-like optimised H chondrite parent body model.
Despite the different assumptions made in the model calculations, from the rather simplistic model of a homogeneous body with constant material properties, that can be treated analytically (Miyamoto et al. 1981), to models with rather complex implemented physics like that of Harrison & Grimm (2010) and ours, the derived properties of the parent body are similar. These do not seem to depend very critical on the particular assumptions. The more strongly deviating results for the burial depths of the meteorites cannot be used to discriminate between models, because no independent information on this is presently available. This would require that methods are developed to determine the maximum pressure experienced by a meteorite.
The most important difference between our model and previous models is that we included sintering of the granular material in the modelling. This process is not considered in other models, except for Yomogida & Matsui (1984) and Benoit & Sears (1996). The model of Yomogida & Matsui (1984) unfortunately does not consider the important contribution of 26Al to the heating. Therefore this model cannot be compared to other models. Benoit & Sears (1996) gave only very few details on their model results such that one cannot make a comparison with our and other models also in this case. The models of Akridge et al. (1998) and Harrison & Grimm (2010) do not consider sintering, but simulate the insulating effect of a porous outer layer, that escaped sintering, over a consolidated body by introducing two outer layers with low filling factor, a “regolith” and a “mega-regolith” layer. The thickness’s of both layers were assumed by Akridge et al. (1998), but they were determined by an optimisation of the model by Harrison & Grimm (2010) and a thickness of 410 m was obtained for each of the layers. This compares well with a thickness of <1 km of a residual porous outer layer in our model. The thermal shielding of the consolidated interior of the body by a thin insulating outer layer of low thermal conductivity is obviously essential for obtaining a good fit between thermal evolution models to meteoritic data as it is obtained in the model by Harrison & Grimm (2010) and in ours.
Properties of the parent body of H chondrites derived by different thermal evolution models, and some key data used for the modelling. In some models an insulating outer regolith layer is assumed; in that cases a core radius and layer thickness are given.
A major difference between our model results and others is the earlier derived formation time, tform. This difference probably results from the lower mass-density used in other model calculations and the resulting lower mass of the body. Because of the resulting higher total heat capacity of the whole body (∫ρcpdV) in our model more heat from decay of radioactive nuclei is required to heat the body to the temperatures as witnessed by the observed cooling history of the various meteorites. Hence, an earlier formation time is required for our optimised model since the specific heating rate at zero time (equal to time of CAI formation) is almost the same in all models. The higher average density in our model is a result of the sintering process which results in very low or vanishing porosity over most of the volume of the body.
If (6) Hebe really is the parent body, the mass-density in our model fits well to that determined for Hebe (James & Chesley 2008; Baer et al. 2011). The densities used in other model calculations then would be too low and the earlier formation time found in the present model calculation therefore is probably more realistic than the later formation times found in other models.
The surface temperature, Tsrf, is determined in our model by the optimisation process, in the other model it seems to be chosen more or less arbitrary within the frame expected for bodies in the asteroid belt and in some cases adjusted to improve the model fit between closing temperatures and closing times observed for meteorites. The dependence of the thermal evolution model on the value of Tsrf is generally weak (e.g. Henke et al. 2012). The value determined by our optimisation procedure hinges mainly upon the fit to the two H4 chondrites that are most strongly affected by Tsrf because of the shallow burial depths required by their petrologic type.
There are a number of other model calculations (Bennett & McSween 1996; Hevey & Sanders 2006; Sahijpal et al. 2007; Warren 2011) that also studied the thermal evolution of asteroids and give important insight into their properties and the processes operating in them, but did not attempt to obtain definite results for the properties of the parent body of H chondrites from some kind of “best fit” to meteoritic data. Only the range of possible values is studied in these papers. This does not enable a direct comparison, but the range of possible values for radii and formation times given are in accord with the results shown in Table 9.
5.9. Orbit of parent body
If the number obtained for Tsrf from our optimisation process is taken seriously, it measures the average surface temperature for the first ≈20...30 Ma of evolution where the temperature for Forest Vale and Ste. Marguerite was above the closure temperature for Pu fission tracks. Since the observed lifetime of accretion disks is less than 10 Ma (Haisch et al. 2001) the surface temperature is determined by illumination by the young proto-sun and thermal emission from the surface, in particular during the most critical phase where the temperature at the burial depth evolved through the closing temperature for Pu fission tracks. Then we can estimate the average radius of the orbit of the parent body from the relation (for a rapidly rotating body)  (13)where σ is the Stefan-Boltzmann constant, A the albedo of the surface, a the distance to the protosun in AU, and S(1) the solar constant at 1 AU at this early evolution period.
(13)where σ is the Stefan-Boltzmann constant, A the albedo of the surface, a the distance to the protosun in AU, and S(1) the solar constant at 1 AU at this early evolution period.
For the solar constant S(1) we have to observe that the sun ignites at about 10 Ma hydrogen burning and has the luminosity of a 1 M⊙ star on the main sequence. Its luminosity during the first 100 Ma is by about 30% less than its present value (e.g. D’Antonia & Mazzitelli 1994). The typical surface albedo for S asteroids is 0.2 (Ryan & Woodward 2010). The surface albedo of (6) Hebe is particular high with 0.291 ± 0.029 (Ryan & Woodward 2010). The albedo found today is probably not typical for the material that covered the surfaces of the bodies 4.5 Ga ago, because highly processed material and the products of its grinding are presented at the surface. It must had contained a lot of more fine-grained material that only later matured by crystal growth at elevated temperatures and probably was darker.
We assume arbitrarily A = 0.1 and find a radius of the orbit of a = 1.96 AU (an albedo of A = 0.2 yields a = 1.85 AU). This is smaller than the present average radius of the orbit of 2.4 AU. If the temperature Tsrf found in optimisation is really representative for the average surface temperature during the essential phase of the thermal evolution, and if (6) Hebe is the parent body of the H chondrites, then our result means that (6) Hebe formed closer to sun than its present distance. However, a more detailed treatment of the processes determining the surface temperature is necessary, before any definite conclusions can be drawn.
6. Concluding remarks
We combined the code for modelling the internal structure and evolution of planetesimals of the 100 km size class (Henke et al. 2012) with a code for optimisation of a quality function that is based on an evolution algorithm. This allows finding a consistent set of parameters that describe the properties and evolution of a planetesimal and the burial depths of the meteorites. As such the thermal evolution of the model body reproduces very closely the empirically determined cooling history of all H chondrites with sufficient available data.
The results show, that the “onion shell” model successfully reproduces the thermal evolution history of all the meteorites used in this study. For six of the eight meteorites a burial depth can be found for which the empirical cooling data can be fitted in an excellent way with the local evolution of temperature at that burial depth. For the remaining two cases it is still possible to find a burial depth that results in a good fit if the Pu fission-track datum of Nadiabondi is rejected. This confirms earlier conclusions that the thermal evolution of the H chondrite parent body and its initial thermal structure has not been disturbed by catastrophic impacts.
The reconstructed properties of the parent body of the H chondrites are comparable to what has been found in other model calculations. The different published models treated the problem in different kinds of approximations, solving the heat conduction equation being almost the only feature common to all models, and used different values for the material properties. Our estimated size of 111 km of the parent body is somewhat bigger compared to the 100 km found in other models, and requires a slightly earlier formation time of 1.8 Ma compared to the 2.2–2.5 Ma found in other models. Such minor differences are certainly due to the different approaches used.
Our study shows, that the input physics of the models has to be improved, before more reliable data on the parent body can be obtained. Such improvements are currently underway in our group. In particular the heat conductivity has to be calculated from the specific properties of chondritic material. It will also be necessary to obtain more precise radiometric ages for a wider range of samples.
The advantage of our method is that it allows for a simultaneous and consistent fit of several model parameters to a big number of observational restrictions and is very flexible if the kind of data to be included in the optimization process is to be changed. A minor shortcoming of the optimisation method used is that a considerable number of complete evolution models has to be calculated during the course of the optimisation process, but our implicit solution method is fast enough that no restriction as to the applicability of the method to our problem results from this.
Acknowledgments
We thank the referee S. Sahijpal for a constructive and helpful referee report. This work was supported in part by “Forschergruppe 759” and in part by “Schwerpunktprogramm 1385”. Both are supported by the “Deutsche Forschungsgemeinschaft (DFG)”. S.H. is Member of the IMPRS for Astronomy & Cosmic Physics at the University of Heidelberg.
References
- Akridge, G., Benoit, P. H., & Sears, D. W. 1998, Icarus, 132, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, C. M. O. 2005, in Chondrites and the Protoplanetary Disk, eds. A. N. Krot, E. R. D. Scott, & B. Reipurth, ASP Conf. Ser., 341, 972 [Google Scholar]
- Arzt, E., Ashby, M. F., & Easterling, K. E. 1983, Metallurgical Transact. A, 14A, 211 [Google Scholar]
- Baer, J., Chesley, S., & Britt, D. 2011, Asteroid Masses V2.0, eAR-A-COMPIL-5-ASTMASS-V2.0, NASA Planetary Data System [Google Scholar]
- Bennett, M., & McSween, H. Y. 1996, Meteor. Planet. Sci., 31, 783 [Google Scholar]
- Benoit, P., & Sears, W. G. 1996, Lunar Planet. Sci. Conf. Lett., 28, 1178 [Google Scholar]
- Birck, J. L., & Lugmair, G. W. 1988, Earth Planet. Sci. Lett., 90, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, A., Blichert-Toft, J., Moynier, F., Vervoort, J., & Albarède, F. 2007, Geochim. Cosmochim. Acta, 71, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 1995, ApJS, 101, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Cherniak, D., Lanford, W. A., & Ryerson, F. J. 1991, Geochim. Cosmochim. Acta, 55, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- Consolmagno, G., Britt, D., & Macke, R. 2008, Chemie der Erde/Geochemistry, 68, 1 [Google Scholar]
- D’Antonia, F., & Mazzitelli, I. 1994, ApJS, 90, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Dauphas, N., Cook, D. L., Sacarabany, A., et al. 2008, ApJ, 686, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Dodd, R. 1969, Geochim. Cosmochim. Acta, 33, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson, M. H. 1973, Contributions to Mineralogy and Petrology, 40, 259 [Google Scholar]
- Fei, Y., Bertka, C. M., & Finger, L. W. 1997, Science, 275, 1621 [CrossRef] [Google Scholar]
- Fischmeister, H. F., & Arzt, E. 1983, Powder Metallurgy, 26, 82 [Google Scholar]
- Gaffey, M. J., & Gilbert, S. L. 1998, Meteor. Planet. Sci., 33, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Ganguly, J., & Tirone, M. 2001, Meteor. Planet. Sci., 36, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Göpel, C., Manhes, G., & Allegre, C. J. 1994, Earth Planet. Sci. Lett., 121, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Güttler, C., Krause, M., Geretshauser, R. J., Speith, R., & Blum, J. 2009, ApJ, 701, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, Jr., K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, K. P., & Grimm, R. E. 2010, Geochim. Cosmochim. Acta, 74, 5410 [NASA ADS] [CrossRef] [Google Scholar]
- Henke, S., Gail, H.-P., Trieloff, M., Schwarz, W. H., & Kleine, T. 2012, A&A, 537, A45 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herpfer, M., Larimer, J., & Goldstein, J. 1994, Geochim. Cosmochim. Acta, 58, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Hevey, P. J., & Sanders, I. S. 2006, Meteor. Planet. Sci., 41, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Hopfe, W., & Goldstein, J. 2001, Meteor. Planet. Sci., 36, 135 [NASA ADS] [CrossRef] [Google Scholar]
- James, B., & Chesley, S. R. 2008, Celestial. Mech. Dyn. Astr., 100, 27 [Google Scholar]
- Kakar, A. K., & Chaklader, A. C. D. 1967, J. Appl. Phys., 38, 3223 [NASA ADS] [CrossRef] [Google Scholar]
- Kita, N., Nagahara, H., Togashi, S., & Morishita, Y. 2000, Geochim. Cosmochim. Acta, 64, 3913 [NASA ADS] [CrossRef] [Google Scholar]
- Kleine, T., Touboul, M., Van Orman, J., et al. 2008, Earth Planet. Sci. Lett., 270, 106 [Google Scholar]
- Kleine, T., Touboul, M., Bourdon, B., et al. 2009, Geochim. Cosmochim. Acta, 73, 5150 [NASA ADS] [CrossRef] [Google Scholar]
- Kleine, T., Hans, U., Irving, A. J., & Bourdon, B. 2012, Geochim. Cosmochim. Acta, 84, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M., Blum, J., Skorov, Y., & Trieloff, M. 2011a, Icarus, 214, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M., Henke, S., Gail, H.-P., et al. 2011b, Lunar Planet. Sci. Conf. Lett., 42, 2696 [NASA ADS] [Google Scholar]
- Larsson, P. L., Biwa, S., & Storåkers, B. 1996, Acta Mater., 44, 3655 [CrossRef] [Google Scholar]
- McSween, H., & Patchen, A. 1989, Meteoritics, 24, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Minster, J. F., & Allegre, C. J. 1979, Earth Planet. Sci. Lett., 42, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Miyamoto, M., Fujii, N., & Takeda, H. 1981, Lunar Planet. Sci. Conf. Lett., 12B, 1145 [NASA ADS] [Google Scholar]
- Morbidelli, A., Gonczi, R., Froeschleé, C., & Farinella, P. 1994, A&A, 282, 955 [NASA ADS] [Google Scholar]
- Nagasawa, M., Thommes, E. W., Kenyon, S. J., Bromley, B. C., & Lin, D. N. C. 2007, in Protostars and Planets V, eds. B. Reipurt, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 639 [Google Scholar]
- Nyquist, L. E., Kleine, T., Shih, C.-Y., & Reese, Y. D. 2009, Geochim. Cosmochim. Acta, 73, 5115 [NASA ADS] [CrossRef] [Google Scholar]
- Pellas, P., Fiéni, C., Trieloff, M., & Jessberger, E. 1997, Geochim. Cosmochim. Acta, 61, 3477 [NASA ADS] [CrossRef] [Google Scholar]
- Quitté, G., Markowski, A., Latkoczy, C., Gabriel, A., & Pack, A. 2010, ApJ, 720, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, A. S., & Chaklader, A. C. D. 1972, J. Am. Ceram. Soc., 55, 596 [CrossRef] [Google Scholar]
- Rechenberg, I. 1973, Evolutionsstrategie – Optimierung technischer Systeme nach Prinzipien biologischer Evolution (Stuttgart: Frommann-Holzboog) [Google Scholar]
- Rechenberg, I. 1989, in Machine Learning: Principles and Techniques, ed. R. Forsyth (London: Chapman and Hall), 83 [Google Scholar]
- Richardson, J. E. 2009, Icarus, 204, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Rudraswami, N. G., & Goswami, J. N. 2007, Earth Planet. Sci. Lett., 257, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Rudraswami, N. G., Goswami, J. N., Chattopadhyay, B., Sengupta, S. K., & Thapliyal, A. P. 2008, Earth Planet. Sci. Lett., 274, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Rugel, G., Faestermann, T., Knie, K., et al. 2009, Phys. Rev. Lett., 103, 072502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ryan, E. L., & Woodward, C. E. 2010, AJ, 140, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Sahijpal, S., Soni, P., & Gupta, G. 2007, Meteor. Planet. Sci., 42, 1529 [Google Scholar]
- Slater-Reynolds, V., & McSween, J. 2005, Meteor. Planet. Sci., 40, 745 [Google Scholar]
- Storåkers, B., Fleck, N. A., & McMeeking, R. M. 1999, J. Mech. Phys. Solids, 47, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, H., & Dauphas, N. 2012, Lunar Planet. Sci. Conf. Lett., 43, 1703 [Google Scholar]
- Taylor, G. J., Maggiore, P., Scott, E. R. D., & Keil, A. E. 1987, Icarus, 69, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Torppa, J., Kaasalainen, M., Michałowski, T., et al. 2003, Icarus, 164, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Trieloff, M., Jessberger, E. K., Herrwerth, I., et al. 2003, Nature, 422, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, P. H. 2011, Meteor. Planet. Sci., 46, 53 [Google Scholar]
- Weidenschilling, S. J., & Cuzzi, J. N. 2006, in Meteorites and the Early Solar System II, eds. D. S. Lauretta, & H. Y. McSween (Tucson: University of Arizona Press), 473 [Google Scholar]
- Wittmann, A., Swindle, T. D., Cheek, L. C., Frank, E. A., & Kring, D. A. 2010, J. Geophys. Res., 115, E07009 [NASA ADS] [CrossRef] [Google Scholar]
- Yomogida, K., & Matsui, T. 1983, J. Geophys. Res., 88, 9513 [Google Scholar]
- Yomogida, K., & Matsui, T. 1984, Earth Planet. Sci. L., 68, 34 [Google Scholar]
All Tables
Parameters and burial depths of the meteorites for the optimised H chondrite parent body model.
Parameter for the model with optimised K0, burial depths of the meteorites, and maximum temperature during their thermal history.
Parameter for the model assuming a radius equal to that of (6) Hebe, burial depths of the meteorites, and maximum temperature during their thermal history.
Parameters and burial depths of the meteorites for the Miyamoto-like optimised H chondrite parent body model.
Properties of the parent body of H chondrites derived by different thermal evolution models, and some key data used for the modelling. In some models an insulating outer regolith layer is assumed; in that cases a core radius and layer thickness are given.
All Figures
 |
Fig. 1 Schematic representation of the temperature evolution at two different depths (full lines) and at the centre (dotted line) of a planetesimal of the 100 km size class. The horizontal dashed lines correspond to fixed temperatures equal to the closure temperatures in Table 1. The circles indicate the instants at which at a given depth the temperature drops below a given temperature. These instants correspond to the closure ages of the different thermochronometers used for meteorites. |
| In the text | |
 |
Fig. 2 Results for the individual meteorites used in the model fit. The values of the free parameters and the burial depth’s of the meteorites found for the optimised model are given in Table 5. The full line shows the temperature evolution at the burial depth’s of the meteorites in the asteroid, as determined by the evolution algorithm. The dashed line shows the temperature evolution at the centre and the dotted line is the surface temperature. The square boxes indicate the individual data points and the error bars the uncertainty of closing temperature and age determinations. |
| In the text | |
 |
Fig. 3 Results for a model fit where the heat conductivity at zero porosity, Kb, is included in the optimisation process. The values of the free parameters and the burial depth’s of the meteorites found for the optimised model are given in Table 6. For meaning of symbols see caption to Fig. 2. |
| In the text | |
 |
Fig. 4 Results for a model fit where the radius is set equal to the observed radius of (6) Hebe. The burial depth’s of the meteorites found for the optimised model are given in Table 7. For meaning of symbols see caption to Fig. 2. |
| In the text | |
 |
Fig. 5 Evolution history of the value of χ2 during the optimisation process with progressing number of generations, n, for the model where the heat conductivity at zero porosity, Kb, is included in the optimisation process. Shown is for each generation the particular individual with the lowest value of χ2 of all individuals of that generation, the formation time, tform, of this individual, and the radius of the body, R. For two representative meteorites, Kernouvé and Allegan, the evolution of the optimum value of the burial depth, d, is also shown. |
| In the text | |
 |
Fig. 6 Data for thermal conductivity Kexp of ordinary chondrites (from Yomogida & Matsui 1983) divided by the analytical fit K(φ) given by Eq. (6) using a value of Kb = 1.75 obtained as optimum value for fitting the cooling history. Full black circles represent data for H chondrites, open circles data for L chondrites. The dashed line corresponds to the value of K = 4 used in model with fixed K. |
| In the text | |
 |
Fig. 7 Results for the individual meteorites if a Miyamoto-like model is used for the model fit. The burial depth’s of the meteorites found for this model are given in Table 8. For meaning of symbols see caption to Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


