| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201218953 | |
| Published online | 20 September 2012 | |
Non-local radiative transfer of SiO masers in Miras
Implementation of the coupled escape probability method
1 Korea Astronomy and Space Science Institute, 776 Daedeokdae-ro, Yuseong-gu, 305-348 Daejeon, Korea
e-mail: yjyun@kasi.re.kr
2 Astronomy Program, Department of Physics and Astronomy, Seoul National University, 1 Gwanak-ro, Gwanak-gu, 151-742 Seoul, Korea
e-mail: yspark@astro.snu.ac.kr
Received: 3 February 2012
Accepted: 18 July 2012
Context. To properly understand the propagation of SiO masers within the shocked region of the circumstellar envelope of asymptotic giant branch stars, non-local radiative transfer calculations are required.
Aims. The present study focuses on investigating how the non-linear velocity field affects the amplification of SiO masers in the circumstellar envelope of a Mira variable.
Methods. We extend the capability of the coupled escape probability method to a spherical system and develop subroutines that are able to calculate the radiative transfer problems in an arbitrary velocity field. This method is applied to the model of a Mira variable that shows dramatic fluctuations in its physical conditions in the circumstellar envelope. We carry out the non-local calculations over the subset of whole epochs covering a complete stellar-pulsation cycle. We also include maser saturation in our calculations to properly treat the interaction of SiO maser radiation with the SiO molecules.
Results. We reproduce the typical features of SiO masers in Mira variables and compare our results with previous large velocity gradient (LVG) calculations and observations. The region of SiO masers is very confined, at a distance of about one stellar radius from the photosphere, which implies that there has been a tangential amplification process. The relative strengths and positions of SiO masers of v = 1, J = 1−0,2−1 and v = 2, J = 1−0 transitions are shown. The temporal variability of a SiO maser, which is driven by stellar pulsations, is also examined in this study, and our results show some differences from those of previous LVG calculations.
Key words: line: formation / masers / radiative transfer / stars: AGB and post-AGB / ISM: molecules / methods: numerical
© ESO, 2012
1. Introduction
Miras are late-type stars that evolve through the asymptotic giant branch late in their lives, as shown in the Hertzsprung-Russell diagram, and have masses of a few solar masses (Iben & Renzini 1983; Habing 1996). Miras are also pulsating variables with long periods and show periodic magnitude variations in the visual range (Habing 1996; Habing & Olofsson 2003). The large pulsations of Miras generate the extended stellar envelope and cause periodical structures of density, temperature, and velocity in the stellar envelope. The high mass-loss rates (10-7−10-4M⊙yr-1) of Miras (Knapp & Morris 1985) are also driven by the stellar pulsation and the wind generated by dust condensation. Thus, these stars play a crucial role in supplying heavy elements to the interstellar medium.
One of the observational tools for resolving the structure of the circumstellar envelope is to use a radio interferometer or its world-wide extension, called very long baseline interferometry (VLBI), in molecular maser transitions. Interferometers and VLBI systems provide the finest stellar images with angular resolutions better than one milli-arcseconds (Gonidakis et al. 2010). Several molecular masers, such as SiO, H2O, and OH masers, have been found in the extended envelopes of Miras. SiO masers appear within a few stellar radii from the photosphere of Miras (Greenhill et al. 1995; Desmurs et al. 2000; Diamond & Kemball 2003; Cotton et al. 2004), so they are very good tracers for studying the physical conditions and dynamics near late-type stars. Maser lines cannot be analyzed with the assumption of local thermodynamic equilibrium (TE). Masing conditions differ dramatically from those of local TE. Thus, a model of maser radiative transfer is indispensable and an important ingredient in the comprehensive understanding of the physical processes that occur in the circumstellar envelope. We present a radiative transfer model of SiO masers in late-type stars.
The most frequently used models for the calculation of SiO masers are based on the assumption of a large velocity gradient (LVG; Humphreys et al. 1996, 2002; Gray et al. 2009). Under this assumption, the radiative transfer problem becomes a local one (Mihalas 1978). Steep velocity gradients are produced in the extended atmosphere of late-type stars by stellar pulsation. However, there can be several pulses in the atmosphere at any instant, and the velocity field is complex, thus the same velocity in two or more zones can be traced by a ray of light, violating the premise of the LVG model. Accordingly, the applicability of the Sobolev assumption should be questioned. The validity of the LVG method may be strengthened by the fact that the physical conditions triggering SiO masers are very limited in the circumstellar envelope. For example, the molecular hydrogen number density is 108 − 1010cm-3, and the kinetic temperature is 700 − 1500K, and the regions that have these conditions are narrow in the circumstellar envelope according to the stellar pulsation model (Bowen 1988; Doel et al. 1995). This may explain the frequent usage of the LVG model. However, for serious study, one needs to test the validity of the LVG model and go further in performing a more rigorous treatment of radiative transfer for SiO masers in pulsating atmospheres. In this sense, a non-local model should be applied, although strangely non-local models with only static atmospheres have been developed to date (Bujarrabal 1994a,b). No SiO maser model has been developed for an envelope with a complicated velocity field. There have been several studies of the masers of OH and H2O molecules in stellar atmospheres, but these studies have all adopted static atmospheres or ones with moderate velocities within a few Doppler widths (Jones et al. 1994; Randell et al. 1995; Yates et al. 1997).
In reality, rigorously treating a velocity field wider than several Doppler widths, which is quite common in late-type stars, is very time-consuming. We devised a new method by applying and modifying the coupled escape probability (CEP) method (Elitzur & Asensio Ramos 2006; Yun et al. 2009). In this method, non-localness is explicitly treated through the coupled physical quantities of different zones, which is not the case for the most popular method of (accelerated) lambda iteration (ALI). In Yun et al. (2009, hereafter Paper I), this modified CEP method was applied to the calculation of the thermal lines in a spherical molecular cloud and good results were obtained, i.e., the results accorded with those of the ALI method and a faster calculation speed than the ALI method was achieved. In this present study, subroutines that can solve the radiative transfer problem in an arbitrary velocity field are added to the previously modified CEP method, thus the newly modified CEP method can be applied to maser lines affected by the complicated velocity fields of Mira variables. We solve the problems with a one-dimensional calculation, assuming spherical geometry, so that we are able to reproduce a ring-like maser distribution at best. One may question this decision because observations say that the maser distribution can be very patchy. However, it has been found from VLBI observations that there is missing flux amounting to 30 − 40% of the original emitted flux; this missing flux is attributed to the extended structure, which probably has a ring-like shape. This partly justifies our one-dimensional approach. Solving the problem by considering higher dimensions is currently prohibitively time-consuming.
An important characteristic of a maser is that the population inversion is largely affected by the degree of saturation owing to the response function of a molecule to the radiation (Field & Richardson 1984; Yariv 1989; Elitzur 1992). Thus, the resulting power of the maser radiation depends on whether the maser is saturated or unsaturated. Observations over a stellar cycle (Diamond & Kemball 2003; Cotton et al. 2004; Yi et al. 2005; Cotton et al. 2006; Wittkowski et al. 2007) have shown that the intensity of SiO masers varies considerably during the stellar pulsation period. In many epochs, the maser intensity becomes strong enough to be saturated, as was also shown in model calculations (Humphreys et al. 2002). Thus, maser saturation should be considered in the calculation of SiO masers in late-type stars, and we include the effects of maser saturation in our calculations to yield reliable maser intensities, which are needed to investigate the relative intensities of SiO masers and their temporal variability.
In Sect. 2, we introduce a pulsation model of Miras and describe the modification of the CEP method required to apply it to spherical systems with arbitrary velocity fields. In Sect. 3, we investigate the excitation conditions, paying attention to the population inversion that results in maser lines. Maser line profiles from several transitions, including v = 1,J = 1−0,2−1 and v = 2,J = 1−0, are calculated from various positions, and their distributions along the radial distance are derived. The result for the v = 2,J = 2−1 transition is not presented because it is thought that the transition probably overlaps with H2O lines, resulting in exceptionally low brightness (Oloffson et al. 1985). Because we do not take into account this line overlap, the results for this transition are unreliable. Our results are compared with those from models based on the LVG approximation and with single dish or VLBI observations. Representative studies of SiO masers in late-type stars, with the LVG-based models, were carried out by Humphreys et al. (1996) and Humphreys et al. (2002). Section 4 provides our summary and conclusion.
2. Mathematical formulation
2.1. The model of SiO masers in M-Miras
We use the same physical parameters that were used in Humphreys et al. (2002), which are based on the hydrodynamic solutions calculated by Bowen (1988). From the description of the physical conditions in the circumstellar envelope of M-type Miras in Bowen (1988), the spherically symmetric atmosphere is known to be periodically driven by a sinusoidally varying radial force. The sinusoidal motion of the boundary generates acoustic waves that propagate radially outwards and generate shocks as they encounter lower density regions. The successive impulses from the inner boundary induce oscillatory motions of the material and drive the mass loss from the star. Stellar rotation and magnetic fields are ignored, and dust is included in the model, such that dust contributes to the formation of the stellar wind. This hydrodynamic pulsation model for M-type Miras was also used to study SiO masers by Doel et al. (1995), Gray et al. (1995), and Humphreys et al. (1996). Humphreys et al. (1996) considered only a single phase of the stellar pulsation and showed that a ring-like structure of SiO masers was located at a distance of about one stellar radius from the photosphere. Humphreys et al. (2002) carried out their calculation for the 20 model phases of stellar pulsation that represent a complete stellar cycle. The stellar phase in the model is defined as zero when a new shock leaves the stellar photosphere. Thus, the sinusoidally varying inner boundary has its maximum outward velocity at zero stellar phase.
In this model, the period of stellar pulsation is 332 days, and the time interval between each phase is 16.6 days. Our calculations are performed for the 4 epochs shown in Fig. 1 of Humphreys et al. (2002), which are epochs 1, 6, 11, and 16. These four model epochs correspond to zero, 83 days, 166 days, and 249 days. The stellar radius, R∗, is 1.7 × 1013cm, and the effective temperature has a constant value of 3002.2K, which is independent of the stellar phase. The relative abundance of SiO to molecular hydrogen is fixed at 10-4, and the effect of dust is ignored in our calculations. The range of the circumstellar envelope used in this calculation extends from an inner boundary of R∗ = 1.7 × 1013cm ~ 1.1AU to an outer boundary of 5R∗ ~ 5.5AU. The important stellar parameters are listed in Table 1; Fig. 1 shows the physical conditions in the circumstellar envelope used in this study.
Parameters of the model M-Mira.
The basic assumption of our calculation is that all physical quantities are constant within a zone. The best way of realizing this assumption is to create as many zones as possible within the concerned region. However, the number of zones is restricted by the size of the memory installed in the computer, so we should determine a point of compromise between the number of zones and the precision of the result. The number of zones has a somewhat large effect on the results when the fluctuation of the physical parameters is very large within a small region. The circumstellar envelope of the M-Mira variable undergoes a remarkable change in the physical environments along the radial distance, i.e., the physical conditions close to the shock fronts change markedly over a typical Sobolev length. Thus, the equal spacing zones used in Paper I are inadequate for the circumstellar envelope of the M-Miras, and we adopt a new strategy to create the unequal spacing zones in this study. We first divide the whole range of the radius into several sections. In Fig. 1, we can easily identify some points at which the direction of the change in the physical parameters is reversed. The boundaries of the sections are determined by these points so as to make sure that the sign of the gradient of the physical parameters is unchanged within each section. Each section is subsequently divided into several subsections. The subsections are necessary to minimize the errors that arise from the interpolation of the physical parameters. The boundaries of the subsections are determined by the condition that the change in the physical parameters should be linear with distance within each subsection. Finally, we divide each subsection into zones, and the number of zones in each subsection is proportional to the gradient of each physical parameter. We effectively divide the system into many zones with the limited memory resources according to the above procedures.
As can be seen in Fig. 1, for example, the kinetic temperature shows a periodic fluctuation driven by the shock propagation, and it is somewhat difficult to divide the regions near the shock discontinuity into many zones according to the strict CEP condition. At epoch 1, the temperature changes by as much as ~8000 K over a radial range of 1.26−1.31AU, thus it is practically impossible to make zones in such a narrow region under the condition that the temperature can be assumed to be constant in each zone. This means that we cannot avoid breaking the basic assumption of the CEP method in this narrow region. We investigate the dependence of the calculated results on the number of zones to find a stable state in which consistent solutions are obtained regardless of the number of zones. It is found that the results largely depend on how the pulsating zones are divided when the number of zones is fewer than ~60. Only when the number of zones is larger than ~100 are the results guaranteed, and we use 200 zones in this calculation. Rays are also used to solve the radiative transfer problem in the circumstellar envelope, and the distribution of rays in the spherical system follows the method used in Paper I. The number of rays is 300 in this calculation.
 |
Fig. 1 Physical conditions in the circumstellar envelope of the model M-Mira. |
2.2. Radiative transfer in an arbitrary velocity field
We developed a numerical method to solve the radiative transfer problem in a spherical molecular cloud on the basis of the CEP methods. In this present study, we extend our method to deal with radiative transfer in an arbitrary velocity field. All mathematical formulations for radiative transfer in this study are basically the same as those of Paper I. The additional conditions are the stellar radiation and the complicated velocity field caused by stellar pulsation. It is a simple task to include the stellar radiation in the formulations described in Paper I. However, it is difficult to consider thoroughly the effect of the complicated velocity field for the radiative transfer. The LVG method has been widely used to solve radiative transfer problems in systems with a large velocity field and provided good results in many cases. The LVG method solves the radiative transfer problem locally so it cannot take into account the variation in physical parameters along the ray-paths. In addition, if the velocity field is not linear along the ray, the local radiation field is affected by the radiation emitted from distant places, thus the LVG method is no longer valid in this case.
We describe an elaborate treatment of a varying velocity field. First, we consider the radiative transfer in a zone in which the velocity field is linear with distance along the direction of the ray. The Doppler shift is caused by the velocity field, and the absorption profiles at the boundaries of the zone can be plotted, as shown in Fig. 2. The velocities at the boundaries in the direction of the ray are denoted by 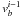 and
and 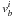 , and the velocity vector is defined in an observer’s frame. The
, and the velocity vector is defined in an observer’s frame. The 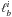 represents the distance passed by the ray from the starting point to the ith boundary. The specific intensity at the boundary of the zone is calculated along the ray-path
represents the distance passed by the ray from the starting point to the ith boundary. The specific intensity at the boundary of the zone is calculated along the ray-path 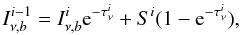 (1)where Si is the source function of the ith zone, and
(1)where Si is the source function of the ith zone, and 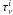 is the optical depth between the zone boundaries. The subscript b represents the quantity at the boundary of each zone, and the superscript i without the subscript b represents the quantity of the ith zone throughout this study. The intensity of incoming radiation
is the optical depth between the zone boundaries. The subscript b represents the quantity at the boundary of each zone, and the superscript i without the subscript b represents the quantity of the ith zone throughout this study. The intensity of incoming radiation 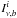 has been calculated in the previously passed zone, and the source function is assumed to be constant within a zone. In a static case, frequency does not vary along the ray, i.e.
has been calculated in the previously passed zone, and the source function is assumed to be constant within a zone. In a static case, frequency does not vary along the ray, i.e. 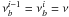 , thus the optical depth at a certain frequency over the path is simply
, thus the optical depth at a certain frequency over the path is simply
 |
Fig. 2 Radiative transfer in a zone with a velocity gradient. |
![\begin{equation} \label{eq20} \begin{array}{ll} \tau^{i}_{\nu} & = \kappa^i_0 \Phi^i (\nu) \ell^{i} \\[2mm] & =\displaystyle{\frac{1}{4\pi}}g_u B_{ul} E_{ul}(n^i_l - n^i_u) \Phi^i (\nu) \ell^{i}, \end{array} \end{equation}](/articles/aa/full_html/2012/09/aa18953-12/aa18953-12-eq35.png) (2)where ℓi is the path length along the ray within the ith zone, i.e.
(2)where ℓi is the path length along the ray within the ith zone, i.e. 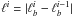 , gu is the statistical weight of the upper level, nl (nu) is the lower (upper) level population per state in the ith zone, Bul is the Einstein coefficient for the transition between the level u and l, and Eul is the energy separation between the levels. The absorption profile is
, gu is the statistical weight of the upper level, nl (nu) is the lower (upper) level population per state in the ith zone, Bul is the Einstein coefficient for the transition between the level u and l, and Eul is the energy separation between the levels. The absorption profile is 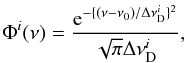 (3)where
(3)where 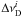 is the Doppler width in the ith zone, that is caused by thermal and turbulent motion, and ν0 is the rest frequency. We assume that the physical parameters, e.g., the kinetic temperature, are constant within a zone, thus the Doppler width and the shape of the absorption profile do not vary within a zone.
is the Doppler width in the ith zone, that is caused by thermal and turbulent motion, and ν0 is the rest frequency. We assume that the physical parameters, e.g., the kinetic temperature, are constant within a zone, thus the Doppler width and the shape of the absorption profile do not vary within a zone.
In a moving media, the frequency varies along the ray in an observer’s frame, i.e., the frequency ν in Eq. (3) is a function of location. Consequently, Eq. (2) should be expressed in an integral form along the path 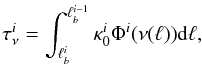 (4)which provides an exact description for the change of the absorption profile in the moving media. It is convenient to use the dimensionless absorption profile function
(4)which provides an exact description for the change of the absorption profile in the moving media. It is convenient to use the dimensionless absorption profile function 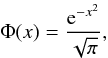 (5)where x ≡ (ν − ν0)/ΔνD. On the basis of the condition that the velocity changes linearly with distance in a zone, the frequency at an arbitrary location ℓ within the ith zone is
(5)where x ≡ (ν − ν0)/ΔνD. On the basis of the condition that the velocity changes linearly with distance in a zone, the frequency at an arbitrary location ℓ within the ith zone is 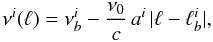 (6)where c is the speed of light, ai is the local velocity gradient of the ith zone, and
(6)where c is the speed of light, ai is the local velocity gradient of the ith zone, and 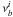 is the frequency at the ith boundary in frequency space (see Fig. 2). In this paper, the direction of the velocity is defined as positive when the molecules move away from the observer and as negative when they move in the opposite direction. The difference between the velocities at the two locations is always calculated by subtracting the velocity near the observer from that at another. Under this scheme, regardless of where the observer is located, the sign of ai becomes positive when the two points move away from each other and negative in the opposite case. Thus, Eq. (6) is entirely consistent with this scheme and valid in every case. Using Eqs. (5) and (6), we can rewrite Eq. (4) as
is the frequency at the ith boundary in frequency space (see Fig. 2). In this paper, the direction of the velocity is defined as positive when the molecules move away from the observer and as negative when they move in the opposite direction. The difference between the velocities at the two locations is always calculated by subtracting the velocity near the observer from that at another. Under this scheme, regardless of where the observer is located, the sign of ai becomes positive when the two points move away from each other and negative in the opposite case. Thus, Eq. (6) is entirely consistent with this scheme and valid in every case. Using Eqs. (5) and (6), we can rewrite Eq. (4) as 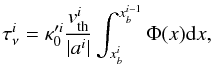 (7)where
(7)where 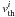 is the thermal velocity in the ith zone, and
is the thermal velocity in the ith zone, and 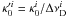 . The local velocity gradient ai in Eq. (7) is a constant within the zone, and
. The local velocity gradient ai in Eq. (7) is a constant within the zone, and 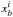 and
and 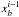 can easily be calculated as
can easily be calculated as 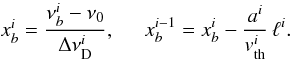 (8)We do not have to make any great effort to evaluate the integration in Eq. (7) because that integration is the definition of the error function
(8)We do not have to make any great effort to evaluate the integration in Eq. (7) because that integration is the definition of the error function 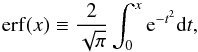 (9)and most computational languages provide it as an intrinsic math function. From Eqs. (8) and (9), the optical depth of Eq. (7) finally becomes
(9)and most computational languages provide it as an intrinsic math function. From Eqs. (8) and (9), the optical depth of Eq. (7) finally becomes 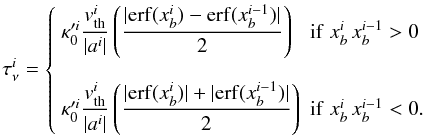 (10)We note that the sign of the optical depth is determined only by the sign of the absorption coefficient
(10)We note that the sign of the optical depth is determined only by the sign of the absorption coefficient 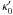 , as shown in Eq. (10), i.e., only population inversion can change the sign of the optical depth. We can trace the effect of the velocity field thoroughly with the optical depth derived in Eq. (10).
, as shown in Eq. (10), i.e., only population inversion can change the sign of the optical depth. We can trace the effect of the velocity field thoroughly with the optical depth derived in Eq. (10).
In contrast to the basic assumption of the CEP method, the specific intensity varies along the ray even within a zone. Thus, it is necessary to find a representative value for a zone, which we achieve by averaging the specific intensity over distance, as described in Paper I. As mentioned above, the frequency also varies along the ray within a zone in a moving media, so both the specific intensity and the absorption profile should be averaged together along the ray-path, and the result is given by ![\begin{equation} \label{eq110} \begin{array}{ll} \overline{ I^i_{\nu}\Phi^i(\nu) } &= \displaystyle{\frac{1}{\tau^i_{\nu}}} \int^{\tau^i_{\nu}}_0 I^i_{\nu}(t)\Phi^i(\nu,t) {\rm d}t \\ &=\displaystyle{\frac{1}{\ell^{i}}} \left[I^i_{\nu,b} \frac{1-\mathrm{e}^{-\tau^i_{\nu}}}{\kappa^i_0} +S^i \frac{\tau^i_{\nu}-(1-\mathrm{e}^{-\tau^i_{\nu}})}{\kappa^i_0} \right], \end{array} \end{equation}](/articles/aa/full_html/2012/09/aa18953-12/aa18953-12-eq66.png) (11)where ℓi is the path length of the ray in the ith zone, and
(11)where ℓi is the path length of the ray in the ith zone, and 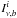 is the intensity of incoming radiation into the ith zone. The optical depth used in Eq. (11) is directly obtained from Eq. (10), where we note that κ0 is used instead of
is the intensity of incoming radiation into the ith zone. The optical depth used in Eq. (11) is directly obtained from Eq. (10), where we note that κ0 is used instead of 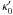 . To solve the equation of statistical equilibrium, we have to calculate the mean intensity averaged over both angles and frequencies and express it using Eq. (11) as
. To solve the equation of statistical equilibrium, we have to calculate the mean intensity averaged over both angles and frequencies and express it using Eq. (11) as 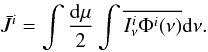 (12)The double integration in Eq. (12) was calculated numerically, and the detailed procedures were shown in Paper I, thus we describe the differences from them here. The range of frequency integration, i.e. the frequency bandwidth, was fixed for all the rays in the static media (Paper I), but in the moving media, each ray has its own frequency bandwidth owing to the velocity fluctuation along the ray. This means that the maximum frequency bandwidth differs from epoch to epoch because each epoch has a unique velocity field. We determined the maximum frequency bandwidth of each epoch by investigating the velocity fluctuations experienced by all the rays passing through the circumstellar envelope. This frequency bandwidth is divided into many bins to carry out the numerical integration in Eq. (12), and the number of the frequency bins is determined according to the way in which 31 points cover 8 Doppler widths, where 8 ΔνD is sufficient to cover the full frequency range of the normalized absorption profile. Thus, each epoch has a different number of frequency bins, and the numbers are 199, 109, 113, and 229 for 4 model epochs, i.e., epochs 1, 6, 11, and 16.
(12)The double integration in Eq. (12) was calculated numerically, and the detailed procedures were shown in Paper I, thus we describe the differences from them here. The range of frequency integration, i.e. the frequency bandwidth, was fixed for all the rays in the static media (Paper I), but in the moving media, each ray has its own frequency bandwidth owing to the velocity fluctuation along the ray. This means that the maximum frequency bandwidth differs from epoch to epoch because each epoch has a unique velocity field. We determined the maximum frequency bandwidth of each epoch by investigating the velocity fluctuations experienced by all the rays passing through the circumstellar envelope. This frequency bandwidth is divided into many bins to carry out the numerical integration in Eq. (12), and the number of the frequency bins is determined according to the way in which 31 points cover 8 Doppler widths, where 8 ΔνD is sufficient to cover the full frequency range of the normalized absorption profile. Thus, each epoch has a different number of frequency bins, and the numbers are 199, 109, 113, and 229 for 4 model epochs, i.e., epochs 1, 6, 11, and 16.
2.3. Statistical equilibrium
The formulation of the statistical process of the unsaturated maser is exactly the same as that of Paper I, and we give a simple description here. The steady-state rate equations for a molecule with L levels in the ith zone are 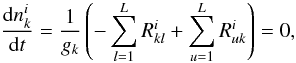 (13)where
(13)where 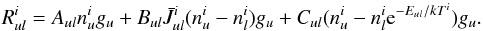 (14)Equation (13) gives L − 1 independent equations for the L unknown populations in each zone, and
(14)Equation (13) gives L − 1 independent equations for the L unknown populations in each zone, and 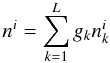 (15)for the overall density in each zone; Eq. (15) closes the system. Equations (13) and (15) form a set of non-linear algebraic equations, e.g., for the system with L levels and Z zones, the LZ equations are generated. This set of equations is solved by the Newton method, and the Jacobian is explicitly expressed manually with level populations before calculation to reduce the calculation time. This is possible because the dependencies of all terms in Eq. (12) on the level populations are explicit, thus we can easily see the dependencies of the mean intensity on the level populations between different zones. The essential philosophy of the CEP method is realized in this manner in the spherical system. The resultant Jacobian consists of Z × Z block matrices, and each block is an L × L matrix. The diagonal blocks of this Jacobian describe the radiative and the collisional interactions among the energy levels in the same zones, and non-diagonal blocks represent non-local radiative interactions between different zones. Thus, the process of non-local radiative transfer is explicitly controlled by the Jacobian. This method, which is performed with a manually prepared Jacobian, requires a much shorter calculation time than the numerical evaluation of the Jacobian, converging more rapidly into the solutions than the ALI method.
(15)for the overall density in each zone; Eq. (15) closes the system. Equations (13) and (15) form a set of non-linear algebraic equations, e.g., for the system with L levels and Z zones, the LZ equations are generated. This set of equations is solved by the Newton method, and the Jacobian is explicitly expressed manually with level populations before calculation to reduce the calculation time. This is possible because the dependencies of all terms in Eq. (12) on the level populations are explicit, thus we can easily see the dependencies of the mean intensity on the level populations between different zones. The essential philosophy of the CEP method is realized in this manner in the spherical system. The resultant Jacobian consists of Z × Z block matrices, and each block is an L × L matrix. The diagonal blocks of this Jacobian describe the radiative and the collisional interactions among the energy levels in the same zones, and non-diagonal blocks represent non-local radiative interactions between different zones. Thus, the process of non-local radiative transfer is explicitly controlled by the Jacobian. This method, which is performed with a manually prepared Jacobian, requires a much shorter calculation time than the numerical evaluation of the Jacobian, converging more rapidly into the solutions than the ALI method.
In this study, we use 5 vibrational energy levels of the SiO molecule from v = 0 to v = 4, and 20 rotational energy levels of the SiO molecule from J = 0 to J = 19. To obtain a more exact solution, we should have taken into account higher rotational energy levels, say, up to 240, over which the level populations are insignificant. It is practically very hard to include these higher levels in the model calculation, so we assume that the departure coefficients of the rotational energy levels above J = 19 are the same as that of J = 19 for each vibrational level (Langer & Watson 1984). The Einstein-A coefficients of the transitions involved are calculated with data from Drira et al. (1997). Collisional rate coefficients are taken from Bieniek & Green (1983) and extrapolated for large Δv transitions according to Lockett & Elitzur (1992). To calculate the energy levels and the transition frequencies, we use the formulae and Dunham constants of Campbell et al. (1995).
2.4. Maser saturation
When a maser is saturated, its intensity affects considerably the level populations from which the maser is generated (Field & Richardson 1984; Yariv 1989; Elitzur 1992). To treat maser saturation, we should modify the rate equations, i.e., Eqs. (13) and (14), according to the standard phenomenological maser model (Elitzur 1992), to 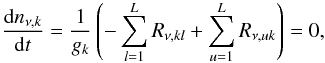 (16)where
(16)where 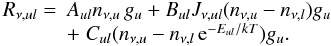 (17)The overall population satisfies the condition of
(17)The overall population satisfies the condition of 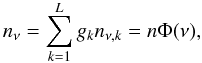 (18)where nν,k = nkΦ(ν), i.e., level populations are distributed according to the Doppler profile in an inhomogeneously broadened medium (Elitzur 1992; Field et al. 1994). As shown in Eqs. (16) and (17), the frequency dependence should be explicitly retained in both the level populations and the mean intensity because the level populations can be affected by the line radiation (Elitzur 1992). From the phenomenological equations, the pump and the loss rates (Elitzur 1992) for a certain maser transition are directly obtained, and the level populations also can be calculated together with the mean intensities.
(18)where nν,k = nkΦ(ν), i.e., level populations are distributed according to the Doppler profile in an inhomogeneously broadened medium (Elitzur 1992; Field et al. 1994). As shown in Eqs. (16) and (17), the frequency dependence should be explicitly retained in both the level populations and the mean intensity because the level populations can be affected by the line radiation (Elitzur 1992). From the phenomenological equations, the pump and the loss rates (Elitzur 1992) for a certain maser transition are directly obtained, and the level populations also can be calculated together with the mean intensities.
In Field & Gray (1988), the level populations were calculated from the density matrix formalism, and the diagonal elements were given by 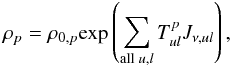 (19)where ρ0,p is an unsaturated population of level p,
(19)where ρ0,p is an unsaturated population of level p, 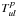 represents the coefficients that contain all the rate coefficients associated with collisions and non-maser radiative processes between the u and l levels, and Jν,ul is the mean intensity of the maser. Equation (19) describes all the effects in which masers, arising from the levels u and l, influence the population in level p via kinetic events coupling u and l to p. The population inversion was also derived in Field & Richardson (1984) as
represents the coefficients that contain all the rate coefficients associated with collisions and non-maser radiative processes between the u and l levels, and Jν,ul is the mean intensity of the maser. Equation (19) describes all the effects in which masers, arising from the levels u and l, influence the population in level p via kinetic events coupling u and l to p. The population inversion was also derived in Field & Richardson (1984) as 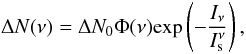 (20)where
(20)where 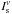 is the saturation intensity given by
is the saturation intensity given by 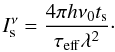 (21)In Eqs. (20) and (21), ΔN0 is the unsaturated population inversion that is defined as Nu − Nl(gu/gl), τeff is the inverse of the effective rate coefficient for the removal of a population from either masing level, and ts is the spontaneous lifetime of the maser transition. For the calculation of maser intensity, the gain coefficient (Yariv 1989) was used instead of the absorption coefficient and written as
(21)In Eqs. (20) and (21), ΔN0 is the unsaturated population inversion that is defined as Nu − Nl(gu/gl), τeff is the inverse of the effective rate coefficient for the removal of a population from either masing level, and ts is the spontaneous lifetime of the maser transition. For the calculation of maser intensity, the gain coefficient (Yariv 1989) was used instead of the absorption coefficient and written as 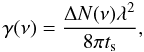 (22)where ΔN(ν) is obtained from Eq. (20) or can be calculated as gu(ρu − ρl) from Eq. (19). In masing zones, the propagation of the maser was described by above authors as
(22)where ΔN(ν) is obtained from Eq. (20) or can be calculated as gu(ρu − ρl) from Eq. (19). In masing zones, the propagation of the maser was described by above authors as 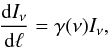 (23)where the spontaneous emission of the masing molecules is omitted, as is quite common in maser calculations, because its intensity is negligibly small compared to the maser intensity, and the explicit treatment of the spontaneous emission requires the reformulation of the maser theory using quantum electronics, which is clearly beyond the scope of this study. Equations (19) and (20) were derived for the molecules in the inhomogeneously broadened medium, thus we can use Eq. (23) to determine the maser intensity in the circumstellar envelope.
(23)where the spontaneous emission of the masing molecules is omitted, as is quite common in maser calculations, because its intensity is negligibly small compared to the maser intensity, and the explicit treatment of the spontaneous emission requires the reformulation of the maser theory using quantum electronics, which is clearly beyond the scope of this study. Equations (19) and (20) were derived for the molecules in the inhomogeneously broadened medium, thus we can use Eq. (23) to determine the maser intensity in the circumstellar envelope.
In this study, the strategy for calculating the emerging intensity of the maser is as follows. First, the unsaturated level populations are calculated by solving Eqs. (12), (13), and (15) under the basic assumption of the CEP method as described in previous sections. The maser propagations along the rays in each zone are then calculated by solving Eq. (23) coupled with Eq. (20). To solve Eq. (23), we use the Runge-Kutta method that is controlled by an adaptive step-size. At each propagation step, the frequency shifts are newly calculated for all the frequency bins to take account of the changes of the velocity field along the rays.
3. Results and discussion
3.1. Inversion of SiO maser transitions
 |
Fig. 3 Negative excitation temperatures of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 transitions. |
Figure 3 shows the negative excitation temperatures of three SiO maser transitions at four epochs. The transitions of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 have frequently been observed and calculated for SiO masers in many works so they are mainly investigated in this work to compare our results with other works. However, with Fig. 3, it is somewhat difficult to estimate the degree of population inversion with distance from the center of the star because the excitation temperature has an asymptotic behavior near the state at which the lower level population equals the upper one. Thus, we can infer the sketchy behavior of the inverted population of three transitions at each epoch from the excitation temperature.
Above all, it can be clearly seen that the population inversions occur in most parts of the circumstellar envelope for three transitions. This means that most zones can contribute to the amplification of the SiO masers, thus the importance of the non-local treatment is emphasized. The v = 2,J = 1−0 transition is inverted in a region at smaller radii than the other lines at epochs 1, 11, and 16. The displacement in the occurrence position of the two SiO masers of v = 1,J = 1−0 and v = 2,J = 1−0 has been observed in many studies, and the relative locations remain unclear. We can cautiously predict from Fig. 3 that the v = 2,J = 1−0 SiO maser occurs at a closer location to the star than the v = 1,J = 1−0 maser. At epochs 1 and 16, the v = 1,J = 1−0 transition suffers from the population inversion at a region slightly closer to the star than the v = 1,J = 2−1 transition. Interestingly, the inner boundaries of the inverted regions of the three transitions have almost the same radius at epoch 6. The excitation temperature of each transition also follows a different trend according to the epochs, which is strongly related to the varying physical conditions caused by the stellar pulsation.
3.2. Intensity and spatial distribution of SiO maser
 |
Fig. 4 Intensities integrated over frequency for SiO masers of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 transitions at epochs 1, 6, 11, and 16. The scale of intensity has been normalized to that of the peak value of the v = 1,J = 2−1 SiO maser at epoch 6. In panels with “ × 100”, this notation indicates that the intensity is multiplied by a factor of 100, in order to show this information clearly. |
 |
Fig. 5 Intensities integrated over frequency for SiO masers of v = 1,J = 3−2 and v = 2,J = 3−2 transitions at epochs 1, 6, 11, and 16. The scale of intensity has been normalized to that of the peak value of the v = 1,J = 2−1 SiO maser at epoch 6. In panels with “ × 10”, this notation indicates that the intensity is multiplied by a factor of 10, in order to show this information clearly. |
In Fig. 4, the emerging intensities of SiO maser, which are summed over frequency for each ray, are plotted with respect to distance from the center of the star at the epochs of 1, 6, 11, and 16. Figure 4 shows that masers occur at very confined regions, about one stellar radius from the photosphere, which agrees with the result of Humphreys et al. (1996, 2002). The SiO masers in late-type stars are commonly observed to have a ring-like morphology, which implies that there is a tangential amplification along the line of sight (Miyoshi et al. 1994; Diamond et al. 1994; Greenhill et al. 1995; Diamond & Kemball 1997; Boboltz & Marvel 2000; Cotton et al. 2004). Our results also show the very confined masing region surrounding the central star, and we can infer that SiO masers in this model also form a ring-like structure. Clumps formed by thermal instabilities may exist in the circumstellar envelope (Cuntz & Muchmore 1994) and cause inhomogeneities in the density and temperature structures of the circumstellar envelope. These clumps eventually form the patchy ring structure shown in the maps obtained from the VLBI observations. In Humphreys et al. (1996, 2002), the sites of maser action were chosen randomly to mimic this inhomogeneity. Those randomly distributed clumps caused the discrete ring structure of SiO masers, as in the results of observations (Humphreys et al. 1996, 2002).
In our result, the location of the peak and the width of the masing region for a transition also vary during the stellar cycle. Many observations show that the ring structures of SiO masers in late-type stars vary rapidly within a stellar cycle. In Humphreys et al. (2002), the mean radius of the ring of the v = 1,J = 1−0 SiO maser was found to vary across the range 1.93−2.3AU during the stellar cycle. In Fig. 4, the mean location of the v = 1,J = 1−0 SiO maser is always greater than 2 AU, and the location of the v = 1,J = 1−0 SiO maser peak moves inwards between epochs 1 and 6. Afterwards, the location of the v = 1,J = 1−0 SiO maser peak moves slightly outwards between epochs 6 and 16. This variation in the maser ring radius agrees with the results of Humphreys et al. (2002), in which the ring also contracts during epochs 1–6 and expands during epochs 6–18. As clearly seen in Fig. 1, a new large shock-driven expansion occurs in the inner region during the period of epochs 1–6, and the contraction of the maser ring also occurs when this shock sweeps the inner region during this period. The expansion of the ring is induced by the outer region where the temperature and density are enhanced by the post-shock conditions. The relation between the stellar pulsation and the ring radius of the maser in our calculation is in a good agreement with the results of Humphreys et al. (2002).
The v = 2,J = 1−0 SiO maser occurs at a site slightly closer to the photosphere than the v = 1,J = 1−0 SiO maser, as shown at epochs 1 and 16 in Fig. 4. It can be clearly seen that the v = 2,J = 1−0 SiO maser peak occurs at a more central region than the v = 1,J = 1−0 peak at epoch 16. We cannot compare our results with those of Humphreys et al. (2002) because they did not show their results for the v = 2,J = 1−0 SiO maser. High resolution observations, which were for a single epoch, using the VLBA (0.7 × 0.2 mas) by Desmurs et al. (2000), showed that the v = 2,J = 1−0 masers were found systematically to be on rings of smaller radius than the v = 1,J = 1−0 masers. Observations over the stellar cycle (Cotton et al. 2004; Yi et al. 2005; Cotton et al. 2006; Wittkowski et al. 2007) also showed smaller maser rings at v = 2,J = 1−0 than at v = 1,J = 1−0. The model calculations of Humphreys et al. (1996) also show v = 2,J = 1−0 masers lying a little inside the v = 1,J = 1−0 masers. Gray & Humphreys (2000) and Gray et al. (2009) predicted that the ring radii of the two masers and the displacements of the two maser rings vary during the stellar phase. Thus, our results for the displacements of the two SiO masers agree with previous studies.
The model calculation of Gray et al. (2009) predicted that the ring radius of the SiO masers in the v = 1,J = 2−1 line at 86 GHz should have a comparable or slightly larger radius than the ring formed by the v = 1,J = 1−0 masers. This small displacement between the rings of two masers was also found by Humphreys et al. (2002) throughout the stellar cycle, i.e., the v = 1,J = 2−1 SiO maser always occurs at an outer radius beyond the v = 1,J = 1−0 SiO maser. This also seems to agree with observations of Soria-Ruiz et al. (2004, 2007), in which they confirm that, in the star R Leo at least, the v = 1,J = 2−1 transition forms in a ring further from the star than the v = 1,J = 1−0 transition. However, we can hardly discern this displacement in Fig. 4. In Fig. 3, we can see that the population inversion in the transition v = 1,J = 1−0 occurs at a slightly more central region than the transition v = 1,J = 2−1 at epochs 1 and 16. Thus, this small displacement between the population inversions in the two transitions appears to have little effect on the relative locations of these two masers, i.e., the negative excitation temperature is inappropriate for investigating the maser propagation quantitatively.
At every epoch in our calculation, the amplitude of the v = 1,J = 2−1 maser is greater than that of the v = 1,J = 1−0 maser, as also shown by Humphreys et al. (2002), in which the v = 1,J = 2−1 maser is always stronger than the v = 1,J = 1−0 maser throughout the stellar cycle, except for epoch 9. This was also reported in previous observations (Schwartz et al. 1982; Cernicharo et al. 1993; Pardo et al. 1998). In our calculation, the v = 1,J = 1−0 SiO maser is stronger than the v = 2,J = 1−0 SiO maser at epochs 1 and 6, and the opposite case is true at epochs 11 and 16. The ratio of the v = 1,J = 1−0 to the v = 2,J = 1−0 maser intensity was reported to be nearly unity (Schwartz et al. 1979; Spencer et al. 1981; Nakada et al. 1993) for normal late-type stars. However, Kim et al. (2010) reported that this ratio varies from one source to another. The amplification factor of the v = 1,J = 1−0 maser is larger than that of the v = 2,J = 1−0 maser in the model calculation of Gray et al. (1995), but the opposite was found in the results of Humphreys et al. (1996). The intensity ratio of the v = 1,J = 1−0 SiO maser to the v = 2,J = 1−0 SiO maser seems to be very variable, thus it is unclear whether our results are consistent with the observational features of SiO masers in Miras.
We also investigated SiO masers in the transitions of v = 1, J = 3 − 2 and v = 2,J = 3 − 2, and display results for these in Fig. 5. First of all, we found that v = 1,J = 3 − 2 and v = 2,J = 3 − 2 masers occur every four epochs, while v = 1,J = 1−0 and v = 2,J = 1−0 masers have a non-masing epoch, as shown in Fig. 4. At epochs 1 and 16, the peak of the v = 1,J = 3 − 2 maser occurs at an outer radius, beyond the v = 1,J = 1−0,J = 2−1 maser peaks; the peak locations of these three masers are almost the same at epoch 6. At epochs 6 and 11, the amplitude of the v = 1,J = 3 − 2 maser is slightly greater than that of the v = 1,J = 2−1 maser, and the amplitudes of these two masers are nearly the same at epochs 1 and 16. This is somewhat different from the observational property of SiO masers in late-type stars. The v = 1,J = 3 − 2 maser is generally weaker than the v = 1,J = 2−1 maser in many observations (Schwartz et al. 1982; Cernicharo et al. 1993; Cho et al. 1998; Herpin et al. 1998; Pardo et al. 1998; Kang et al. 2006; Cho et al. 2009, 2010). The model calculations of Gray et al. (1995) and Humphreys et al. (1996) also showed that the v = 1,J = 3 − 2 maser has a lower amplification factor than the v = 1,J = 2−1 maser.
In our result, the amplitude of the v = 2,J = 3 − 2 maser increases remarkably compared to the v = 2,J = 1−0 maser at all epochs. This noticeable difference between the v = 2,J = 3−2 and the v = 2,J = 1−0 masers was also shown in the model calculation of Gray et al. (1995), in which the amplification factor of the v = 2,J = 3 − 2 maser is an order of magnitude greater than that of the v = 2,J = 1−0 maser. However, Humphreys et al. (1996) showed that the amplification factor of the v = 2,J = 3−2 maser is an order of magnitude smaller than that of the v = 2,J = 1−0 maser. Thus, the results of Gray et al. (1995) and Humphreys et al. (1996) are inconsistent with each other for the v = 2,J = 3−2 maser. In addition, the v = 2,J = 3−2 maser shows violent temporal variation compared with the v = 1,J = 2−1,3−2 masers, as shown in Figs. 4 and 5. This large variation in the amplitude of the v = 2,J = 3−2 maser, compared with those of the v = 1,J = 2−1,3−2 masers, was also reported by Cho et al. (2010). They observed Orion KL, which is not a late-type star, but Doeleman et al. (2004) suggested that the work of Humphreys et al. (2002) is relevant to the masers of Orion KL. They also argued that the v = 2,J = 3−2 maser can be a tracer of a turbulent region because this maser is sensitive to the variation in the physical parameters. In our model, the density and temperature change dramatically within a small distance owing to the shock, so this may cause the violent variation of the v = 2,J = 3 − 2 maser over the epochs. Thus, our result seems to agree with the observations.
In Figs. 4 and 5, we can see that the v = 2,J = 3−2 maser occurs closer to the photosphere than the v = 1,J = 3−2,J = 2−1, and J = 1−0 masers. Cho et al. (2010) also carried out radiative transfer calculations using the LVG model and the same input parameters of Goddi et al. (2009), reporting that the v = 2,J = 3−2 transition is more strongly inverted in a strong, hot radiation field than the v = 1 transition. They then argued that this may explain why the v = 2,J = 3−2 maser tends to lie closer to the photosphere than the v = 1,J = 3−2,J = 2−1, and J = 1−0 masers. Thus, our result is consistent with Cho et al. (2010).
3.3. Gain coefficient of SiO maser
To investigate the physical conditions for maser amplification, we calculated the unsaturated gain coefficients at the line center, using Eq. (22). To easily compare the resultant gain plots with the negative excitation temperature, we reversed the sign of the population inversion in the gain coefficient. The gain coefficient gives a better description of the population inversion than the excitation temperature, i.e., there is no asymptotic behavior in the gain coefficient. The gain coefficient is also closely related to the maser propagation, thus provides a more intuitive picture for estimating the physical parameters related to the masing action in the circumstellar envelope.
 |
Fig. 6 Unsaturated gain coefficients of the v = 1,J = 1−0,2−1 and v = 2,J = 1−0 transitions. |
As mentioned in Sect. 3.2, the relative intensity between the v = 1,J = 1−0 maser and the v = 2,J = 1−0 maser is somewhat controversial. Doel et al. (1995) reported that the v = 2,J = 1−0 transition is generally very weakly inverted, but yields a very strong maser intensity in the case of radiative propagation. They also found that the unsaturated inversion might be a poor guide to the strong masers, and ignored the velocity gradients in the direction of propagation. However, a rigorous investigation of the maser propagation should not consider only the physical conditions of local regions but also the global structure of the velocity field in the circumstellar envelope. Before we consider the velocity field, we use the gain coefficient as a guide to the basic study of the physical conditions needed for triggering the maser action in the local regions of the circumstellar envelope.
 |
Fig. 7 Calculated spectra for SiO masers of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 transitions. The scale of flux density has been normalized to that of the peak value of the v = 1,J = 2−1 SiO maser at epoch 1. In panels with “ × 100”, this notation indicates that the intensity is multiplied by a factor of 100, in order to show this information clearly. |
Figure 6 shows the unsaturated gain coefficients for the transitions of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 with respect to the distance from the center of the star. It can also be clearly seen that the v = 2,J = 1−0 maser is amplified more effectively at the most central radius than the v = 1,J = 1−0 maser at epochs 1, 11, and 16, shown in Fig. 6. At epoch 1, the v = 2,J = 1−0 transition undergoes considerable amplification in the inner regions, even to the radius of ~1.4 AU, and this causes the resultant maser intensity in the inner regions, as shown in Fig. 4. At epoch 6, the regions where the strong inversions occur are almost the same for all transitions, and the amount of amplification is greater than that of the other three epochs. As can be seen in Fig. 4, the maser peaks also occur at nearly the same location, and the integrated intensities in this epoch are greater than those in other epochs. The gain coefficient, at epoch 11, indicates that there is a very small amount of amplification for the v = 1,J = 1−0 transition, and the corresponding maser does not appear in this epoch, as shown in Fig. 4. At epoch 11, the v = 1,J = 2−1 transition undergoes strong inversion at the outer region compared with the other transitions, and the v = 1,J = 2−1 maser occurs at the location of ~2.7AU. The displacement between the locations at which the peak gain values occur is also seen at epoch 16, and the strong v = 2,J = 1−0 maser occurs at a more central region than the v = 1,J = 1−0 maser, as shown in Fig. 4.
We can also see that the location of the maximum amplification represented by the gain coefficient is very close to the region in which the masers occur. This enables us to investigate the physical conditions triggering the maser amplification in the circumstellar envelope of Miras. Thus, the physical conditions, such as density and kinetic temperature, triggering the maser can be investigated using Fig. 6. The typical conditions from Doel et al. (1995) and Humphreys et al. (1996) are n(H2) = 108 − 1010cm-3, and the kinetic temperature Tk = 700 − 1500K; these authors also reported that the zones with these physical conditions undergo substantial population inversion. These physical conditions are also found in our results as shown in Figs. 1, 4–6, and the situation may become complicated in a non-linear velocity field. As mentioned above, almost every zone in the circumstellar envelope undergoes population inversion, so the intensity is amplified continuously by these zones in the static system. However, if a linear velocity field exists with a large gradient, only very confined zones with the above physical conditions become important contributors to the maser. We have assumed that the velocity field is non-linear, in the same way to Humphreys et al. (1996, 2002), so several surfaces of equal velocity exist along the path of the ray. Thus, the zones on the same velocity surface can contribute to the amplification as long as these zones undergo the population inversion. The Sobolev approximation was generalized to deal with this situation by Rybicki & Hummer (1978), but Humphreys et al. (1996, 2002) could not use this development owing to the computational expense. In our present study, we include the effect of an arbitrary velocity field in the calculation of the optical depth, thus the contributions of the equal velocity surfaces can be rigorously considered.
3.4. Temporal variability of SiO maser in Miras
Several types of variability of SiO masers have been detected in many observations. These types of variability can be roughly placed into three categories (Humphreys et al. 2002). First, there is random variability where the SiO masers have quite different appearances from cycle to cycle. Second, there is long-term variability within a cycle in which SiO masers are correlated with the optical phase. The third type is rapid variability over a period of a few days, as shown in some observations (Balister et al. 1977; Pijpers et al. 1994). In this present study, we have considered only the long-term variability over the stellar cycle (of period 332.2 days). Only 4 epochs are used in our calculation, so it is impossible to make a complete comparison between our results and those of Humphreys et al. (2002). However, we can make a reasonable consideration about the long-term variability of SiO masers because the 4 epochs of 1, 6, 11, and 16 are distributed over an equal interval over a stellar cycle.
In Fig. 7, the calculated spectra of SiO masers in three transitions of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 are plotted for the 4 epochs. These spectra are calculated from the specific intensity of each ray weighted by the occupied area and are analogous to the spectral flux density. Figure 3 in Humphreys et al. (2002) shows the time series of the v = 1,J = 1−0 SiO maser spectra throughout the stellar cycle, consisting of 20 epochs. The temporal variability of this SiO maser was clearly shown in Humphreys et al. (2002), i.e., the maser intensity displays a sinusoidal variation over the stellar pulsation period. When we consider only the 4 epochs of 1, 6, 11, and 16, we find that the strongest v = 1,J = 1−0 maser occurs at epoch 1 in our results, and at epoch 16 in Humphreys et al. (2002). At epoch 6, the strength of the v = 1,J = 1−0 SiO maser is comparable with that at epoch 1 in our result, while there is no apparent maser peak at this epoch in Humphreys et al. (2002). At epoch 11, there is no distinguishable maser emission in both results. Thus, the temporal variation in the maser amplitudes in our calculation differs from that of Humphreys et al. (2002), the most distinguishable difference occurring at epoch 6.
The estimated stellar optical maximum occurs at a model phase of 0.78 in Humphreys et al. (2002), which corresponds to the time between epochs 16 and 17. In Humphreys et al. (2002), the v = 1,J = 1−0 SiO maser maximum interestingly occurs at epoch 17 (phase 0.85). Observations show that the periodic SiO variations are correlated with the optical light curve in many sources, and SiO masers lag in phase by ~0.2 behind the optical maximum (Clark et al. 1984; Martinez et al. 1988). Thus, the maximum of the maser may occur after the 0.2 model phase (about 4 epochs) of the optical maximum, which corresponds to approximately epoch 1 in this model. In our calculation, the v = 1,J = 1−0 SiO maser has a maximum intensity at epoch 1 and also undergoes a sinusoidal variation through four epochs which are distributed uniformly in one stellar cycle, as mentioned above. This seems to be more consistent with the observations, but we cannot be sure that our results are more reliable than those of Humphreys et al. (2002) because we did not perform the calculations for all the epochs, especially for epoch 17. In addition, as noted by Humphreys et al. (2002), the mean observed phase lag between the optical and maser maxima is very variable from star to star and among the cycles of the same star.
The typical conditions are such that n(H2) = 108−1010cm-3 and the kinetic temperature, Tk = 700−1500 K, as mentioned in the previous section. The most significant masing region seems to be close to a distance of 2 AU from the center of the star, as shown in Figs. 4 and 6. Thus, we can determine which epoch is more likely to have strong masers around 2 AU by investigating the physical parameters in this region for each epoch. At epochs 1 and 16, the kinetic temperatures at this location are nearly the same, but there is a large difference of molecular hydrogen densities at this location, as shown in Fig. 1. The density, n(H2), around 2 AU is about 1010cm-3 at epoch 1 and is an order of magnitude higher than this value at epoch 16. With only these conditions, we can say that epoch 1 has better conditions for the occurrence of SiO masers at around 2 AU than epoch 16. In addition to the density and the kinetic temperature, the non-linear velocity field can also affect the maser amplification. This means that the radiative coupling among the distant inversion regions at the same velocity may affect the epoch at which the maximum SiO maser intensity occurs. Although we included the non-linear velocity field in our calculation, the maximum intensity of the v = 1,J = 1−0 SiO maser still occurred at epoch 1, as we expected based on the density and kinetic temperature. This may imply that the remote coupled regions that have physical conditions that differ significantly from the above criteria do not contribute to the maser amplification as much as the regions of the suitable physical conditions.
In the previous section, we showed that the mean radius of the ring of the v = 1,J = 1−0 SiO maser varies over the stellar cycle, and that this spatial variation is driven by the stellar pulsation. The long-term variability of the SiO maser is also related to the stellar pulsation. Until a new strong shock passes the masing region, the intensity of the SiO maser continues to decrease, and the strong amplification of the SiO maser starts after the shock passes the masing region. During the period between epochs 1 and 6, a strong shock sweeps the location of ~2 AU radius, as shown in Fig. 1, and the intensity of the SiO maser becomes weak, as shown in Fig. 7. This location becomes a post-shock region during the epochs 11–16, and the intensity of the SiO maser increases, as shown in Fig. 7. During the same period, the intensity of the SiO maser is amplified by the physical parameters determined by the post-shock condition. Thus, the long-term variability of SiO masers seems to be closely related to the stellar pulsation of Miras in our results.
4. Concluding remarks
We have used the same physical parameters of a M-type Mira as Humphreys et al. (2002), with which our results were mainly compared. The main difference is that the LVG method was used in Humphreys et al. (2002), whereas the non-local method was used in our study. In the circumstellar envelope of late-type stars, the non-linear velocity field is driven by the stellar pulsation, so the non-local approach is almost certainly required to solve the radiative transfer problem rigorously. The naive LVG method was found to be inappropriate for a shocked region in the circumstellar envelope (Collison & Nedoluha 1995; Yates et al. 1997), i.e., the physical conditions change considerably on the distance scale of the Sobolev length. In this paper, we have shown that the excitation temperature and the gain coefficient indicate that the population inversion takes place across a wide area of the circumstellar envelope. Thus, the non-local treatment can yield a somewhat different maser intensity than the LVG method because the non-local method includes the contributions of all the separate regions to the maser amplification.
The results from our calculations have shown many typical features of SiO masers around late-type stars. We have found that the region of SiO masers is very confined at a distance of about one stellar radius from the photosphere, which is in good agreement with the observations (Miyoshi et al. 1994; Diamond et al. 1994; Greenhill et al. 1995; Diamond & Kemball 1997; Boboltz & Marvel 2000; Cotton et al. 2004; Yi et al. 2005) and the model calculations (Doel et al. 1995; Humphreys et al. 1996, 2002; Gray & Humphreys 2000; Gray et al. 2009). One of the most debated issues for SiO masers is whether the v = 2,J = 1−0 maser occurs in a more central location than the v = 1,J = 1−0 maser. We showed that the v = 2,J = 1−0 maser always occurs at a slightly smaller radii than the v = 1,J = 1−0 maser. Our results also showed that the v = 1,J = 2−1 maser is stronger than the v = 1,J = 1−0 maser, which agrees with the results of many of the previous studies mentioned above.
Our results also confirm that the size and the strength of each SiO maser ring vary throughout the stellar cycle, which has also been shown by multi-epoch, high-resolution observations. This indicates that the long-term variability of SiO masers is affected by the stellar pulsation, as previously reported by Humphreys et al. (2002). When a new strong shock sweeps the inner regions of the circumstellar envelope during the period between epochs 1 and 6, the radius of the v = 1,J = 1−0 SiO maser ring contracts, and the strength of the maser becomes weak. During the period between epochs 6 and 16, the expansion of the maser ring and the growth of its intensity are induced by the temperature and the density enhancements of the post-shock gas. Thus, the long-term variability of SiO masers seems to be closely related to the stellar pulsation of Miras in our results. We compared our results with those of Humphreys et al. (2002). The maximum spectral flux of the v = 1,J = 1−0 SiO maser occurs at epoch 1 in our calculations, but at epoch 17 in the calculations of Humphreys et al. (2002). Epoch 17 is near the optical maximum, so our result seems to be more consistent with previous observations in the sense that SiO masers lag in phase by ~0.2 behind the optical maximum (Clark et al. 1984; Martinez et al. 1988).
Our model is far from being complete because it does not take into account dust emission, polarization, and line overlap with other molecules. Tackling the line overlap could be done in the near future. However, one of the profound problems of our model is its inability to deal with a multi-dimensional system. Since, in our model, new level populations in all zones are derived at the same time during each iteration, evaluation of the model requires a huge amount of memory. The situation would be more problematic if we were to extend this method to two or three dimensions in order to consider the clumpy structure in the circumstellar envelope, an application that would be practically impossible. We may have to either develop or adopt a new method, such as the Gauss-Seidel algorithm (Trujillo Bueno & Fabiani Bendicho 1995; Asensio Ramos & Trujillo Bueno 2006; Daniel & Cernicharo 2008), in which the rate equation is solved zone by zone while updating level populations as a ray moves from one zone to another. However, we have proven in this study that the non-local radiative transfer method based on the CEP spirit is practical for treating the complicated velocity fields of late-type stars.
Acknowledgments
This work was supported by Basic Research Program (2011–2012) of the Korea Astronomy and Space Science Institute.
References
- Asensio Ramos, A., & Trujillo Bueno, J. 2006, EAS Publ. Ser., 18, 25 [CrossRef] [EDP Sciences] [Google Scholar]
- Balister, M., Batchelor, R. A., Haynes, R. F., et al. 1977, MNRAS, 180, 415 [NASA ADS] [Google Scholar]
- Bieniek, R. J., & Green, S. 1983, ApJ, 265, L29, erratum 270, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Boboltz, D. A., & Marvel, K. B. 2000, ApJ, 545, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Bowen, G. 1988, ApJ, 329, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Bujarrabal, V. 1994a, A&A, 285, 953 [NASA ADS] [Google Scholar]
- Bujarrabal, V. 1994b, A&A, 285, 971 [NASA ADS] [Google Scholar]
- Campbell, J. M., Klapstein, D., Dulick, M., Bernath, P. F., & Wallace, L. 1995, ApJS, 101, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Bujarrabal, V., & Santaren, J. L. 1993, ApJ, 407, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, S.-H., Chung, H.-S., Kim, H.-R., et al. 1998, ApJS, 115, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, S.-H., Chung, H.-S., Kim, H.-G., et al. 2009, ApJS, 181, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, S.-H., Kim, H.-G., Chung, H.-S., et al. 2010, AJ, 139, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, F. O., Troland, T. H., Pepper, G. H., & Johnson, D. R. 1984, ApJ, 283, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Collison, A. J., & Nedoluha, G. E. 1995, ApJ, 442, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Cotton, W. D., Mennesson, B., Diamond, P. J., et al. 2004, A&A, 414, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cotton, W. D., Vlemmings, W., Mennesson, B., et al. 2006, A&A, 456, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuntz, M., & Muchmore, D. O. 1994, ApJ, 433, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, F., & Cernicharo, J. 2008, A&A, 488, 1237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmurs, J. F., Bujarrabal, V., Colomer, F., & Alcolea, J. 2000, A&A, 360, 189 [NASA ADS] [Google Scholar]
- Diamond, P. J., & Kemball, A. J. 2003, ApJ, 599, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Diamond, P. J., Kemball, A. J., Junor, W., et al. 1994, ApJ, 430, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Diamond, P. J., Kemball, A. J., & Boboltz, D. A. 1997, Vistas Astron., 41, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Doel, R. C., Gray, M. D., Humphreys, E. M. L., Braithwaite, M. F., & Field, D. 1995, A&A, 302, 797 [NASA ADS] [Google Scholar]
- Doeleman, S. S., Lonsdale, C. J., Kondratko, P. T., & Predmore, C. R. 2004, ApJ, 607, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Drira, I., Hure, J. M., Spielfiedel, A., Feautrier, N., & Roueff, E. 1997, A&A, 319, 720 [NASA ADS] [Google Scholar]
- Elitzur, M. 1992, Astronomical Masers (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
- Elitzur, M., & Asensio Ramos, A. 2006, MNRAS, 365, 779 [Google Scholar]
- Field, D., & Gray, M. D. 1988, MNRAS, 234, 353 [NASA ADS] [Google Scholar]
- Field, D., & Richardson, I. M. 1984, MNRAS, 211, 799 [NASA ADS] [Google Scholar]
- Field, D., Gray, M. D., & de St. Paer, P. 1994, A&A, 282, 213 [NASA ADS] [Google Scholar]
- Goddi, C., Greenhill, L. J., Chandler, C. J., et al. 2009, ApJ, 698, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Gonidakis, I., Diamond, P. J., & Kemball, A. J. 2010, MNRAS, 406, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, M. D., & Humphreys, E. M. L. 2000, New Astron., 5, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, M. D., Humphreys, E. M. L., & Field, D. 1995, Ap&SS, 224, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, M. D., Wittkowski, M., Scholz, M., et al. 2009, MNRAS, 394, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Greenhill, L. J., Colomer, F., Moran, J. M., et al. 1995, ApJ, 449, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J. 1996, A&ARv, 7, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J., & Olofsson, H. 2003, Asymptotic Giant Branch Stars (Heidelberg: Springer) [Google Scholar]
- Herpin, F., Baudry, A., Alcolea, J., & Cernicharo, J. 1998, A&A, 334, 1037 [NASA ADS] [Google Scholar]
- Humphresy, E. M. L., Gray, M. D., Yates, J. A., et al. 1996, MNRAS, 282, 1359 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, E. M. L., Gray, M. D., Yates, J. A., et al. 2002, A&A, 386, 256 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, I., Jr., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, K. N., Field, D., Gray, M. D., & Walker, R. N. F. 1994, A&A, 288, 581 [NASA ADS] [Google Scholar]
- Kang, J., Cho, S.-H., Kim, H.-G., et al. 2006, ApJS, 165, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J., Cho, S.-H., Oh, C. S., & Byun, D.-Y. 2010, ApJS, 188, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Knapp, G. R., & Morris, M. 1985, ApJ, 292, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, S. H., & Watson, W. D. 1984, ApJ, 284, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Lockett, P., & Elitzur, M. 1992, ApJ, 399, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, A., Bujarrabal, V., & Alcolea, J. 1988, A&AS, 74, 273 [NASA ADS] [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres (San Francisco: W. H. Freeman and Company) [Google Scholar]
- Miyoshi, M., Matsumoto, K., Kameno, S., Takaba, H., & Iwata, T. 1994, Nature, 371, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Nakada, Y., Onaka, T., Yamamura, I., et al. 1993, PASJ, 45, 179 [NASA ADS] [Google Scholar]
- Oloffson, H., Rydbeck, O. E. H., & Nyman, L.-A. 1985, A&A, 150, 169 [NASA ADS] [Google Scholar]
- Pardo, J. R., Cernicharo, J., González-Alfonso, E., & Bujarrabal, V. 1998, A&A, 329, 219 [NASA ADS] [Google Scholar]
- Pijpers, F. P., Pardo, J. R., & Bujarrabal, V. 1994, A&A, 286, 501 [NASA ADS] [Google Scholar]
- Randell, J., Field, D., Jones, K. N., Yates, J. A., & Gray, M. D. 1995, A&A, 300, 659 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1978, ApJ, 219, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Schwartz, P. R., Waak, J. A., & Bologna, J. M. 1979, AJ, 84, 1349 [NASA ADS] [CrossRef] [Google Scholar]
- Schwartz, P. R., Zuckerman, B., & Bologna, J. M. 1982, ApJ, 256, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Soria-Ruiz, R., Alcolea, J., Colomer, F., et al. 2004, A&A, 426, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soria-Ruiz, R., Alcolea, J., Colomer, F., Bujarrabal, V., & Desmurs, J.-F. 2007, A&A, 468, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spencer, J. H., Winnberg, A., Olnon, F. M., et al. 1981, AJ, 86, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., & Fabiani Bendicho, P. 1995, ApJ, 455, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Ohnaka, K., Driebe, T., & Scholz, M. 2007, A&A, 470, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yariv, A. 1989, Quantum Electronics, 3rd edn. (London: Wiley) [Google Scholar]
- Yates, J. A., Field, D., & Gray, M. D. 1997, MNRAS, 285, 303 [NASA ADS] [Google Scholar]
- Yi, J., Booth, R. S., Conway, J., & Diamond, P. J. 2005, A&A, 432, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yun, Y. J., Park, Y.-S., & Lee, S. H. 2009, A&A, 507, 1785 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Physical conditions in the circumstellar envelope of the model M-Mira. |
| In the text | |
 |
Fig. 2 Radiative transfer in a zone with a velocity gradient. |
| In the text | |
 |
Fig. 3 Negative excitation temperatures of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 transitions. |
| In the text | |
 |
Fig. 4 Intensities integrated over frequency for SiO masers of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 transitions at epochs 1, 6, 11, and 16. The scale of intensity has been normalized to that of the peak value of the v = 1,J = 2−1 SiO maser at epoch 6. In panels with “ × 100”, this notation indicates that the intensity is multiplied by a factor of 100, in order to show this information clearly. |
| In the text | |
 |
Fig. 5 Intensities integrated over frequency for SiO masers of v = 1,J = 3−2 and v = 2,J = 3−2 transitions at epochs 1, 6, 11, and 16. The scale of intensity has been normalized to that of the peak value of the v = 1,J = 2−1 SiO maser at epoch 6. In panels with “ × 10”, this notation indicates that the intensity is multiplied by a factor of 10, in order to show this information clearly. |
| In the text | |
 |
Fig. 6 Unsaturated gain coefficients of the v = 1,J = 1−0,2−1 and v = 2,J = 1−0 transitions. |
| In the text | |
 |
Fig. 7 Calculated spectra for SiO masers of v = 1,J = 1−0,2−1 and v = 2,J = 1−0 transitions. The scale of flux density has been normalized to that of the peak value of the v = 1,J = 2−1 SiO maser at epoch 1. In panels with “ × 100”, this notation indicates that the intensity is multiplied by a factor of 100, in order to show this information clearly. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


