EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 545 (September 2012) A&A, 545 (2012) A100 Full HTML
Free Access
Issue
A&A
Volume 545, September 2012
Article Number A100
Number of page(s) 5
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201118578
Published online 13 September 2012

© ESO, 2012

1. Introduction

Galaxy clusters, the largest objects in the Universe, originate in the primordial density perturbations from cosmic gravitational collapse. They are used in a variety of ways to perform both cosmological and astrophysical studies. Modern astronomy satellites such as XMM-Newton and Chandra have high sensitivity and spatial resolution, and unprecedented results have been gained through detailed analysis of their data. However, there are discrepancies between the properties of galaxy clusters derived from Chandra and XMM-Newton data, such as gas temperature and total mass. Nevalainen et al. (2010) examined the cross-calibration of the energy dependence and normalization of the effective area of Chandra and XMM-Newton, finding that the discrepancies of the 0.5–7.0 keV band temperature measurements of galaxy clusters with EPIC/XMM-Newton and ACIS/Chandra could reach ~10–15% on average.

Abell 1835 is a classical bright cluster with a big cool core (Allen et al. 1996). Its X-ray morphology (Schmidt et al. 2001; Smith et al. 2005) shows that it is an undisturbed and relaxed cluster. It is also an optimal candidate for a triaxial joint analysis via X-ray, SZ, and lensing techniques (Morandi et al. 2012). The temperature difference between the Chandra and XMM-Newton analysis also exists in Abell 1835: ~12 keV from Chandra data (Schmidt et al. 2001) and ~7.6 keV from XMM-Newton data (Jia et al. 2004). After the point-spread function (PSF) correction of XMM-Newton data, Wang et al. (2010) derived a temperature profile similar to that of Jia et al. (2004). Therefore, the difference is not due to the PSF effect.

In addition, the masses of Abell 1835 derived from XMM-Newton and Chandra are different (Jia et al. 2004; Schmidt et al. 2001). Fortunately, the masses have been measured with the strong lensing method (Richard et al. 2010) as well as with the weak lensing method (Zhang et al. 2008). Since gravitational lensing directly probes the cluster total mass without any strong assumptions about the equilibrium state of the cluster, the lensing mass is generally more reliable.

Recently, the comparison of X-ray and gravitational lensing masses has been studied in detail by both observational and simulated analyses. Generally, the X-ray mass is consistent with or lower than the gravitational lensing mass. Richard et al. (2010) showed that the ratio of strong lensing mass and X-ray projected mass within r < 250 kpc, MSL/MX, was 1.3. It was also found that the mass derived from the X-ray measurement is about half of the strong lensing mass in some clusters (e.g., A1689, Andersson & Madejski 2004, Lemze et al. 2008; PKS 0745-191; Chen et al. 2003). Moreover, Zhang et al. (2008) showed that the average ratio of the weak lensing mass to X-ray mass was 1.09 ± 0.08, while Mahdavi et al. (2008) demonstrated that MX/MWL is 1.03 ± 0.07 and 0.78 ± 0.09 at r2500 and r500, respectively. N-body/hydrodynamical simulation work also estimated the ratio between X-ray and lensing masses, MX/MWL, which was 0.88 ± 0.02 and 0.75 ± 0.02 at r500 in Meneghetti et al. (2010a) and Rasia et al. (2012), respectively.

In this work, we reanalyse the Chandra data of Abell 1835 with the same deprojection technique as Jia et al. (2004) to ascertain if the differences in temperatures derived from Chandra and XMM-Newton data can be corrected by data analysis. Furthermore, we investigate the reasons for the temperature differences and establish which result is more reasonable.

This paper is organized as follows: the Chandra observations and data preparation are described in Sect. 2. Section 3 shows the basic spectra analysis, while Sect. 4 presents the deprojected electron density profile and the mass profile. In Sect. 5, we discuss the reasons for the temperature differences derived from Chandra and XMM-Newton data. We present our conclusions in Sect. 6.

Throughout this paper, we assume H0 = 70 km s-1 Mpc-1, ΩΛ = 0.7, Ωm = 0.3. One arcminute corresponds to 236.2 kpc at Abell 1835 redshift of 0.2523. The selected energy band is 0.5–7.0 keV.

2. Observation and spectra extraction

Abell 1835 was observed with Chandra on 25 August 2006 for a total of 119.48 ks (observation ID is 6880). The observation instrument was ACIS-I, and the observation model was VFAINT. We processed the Chandra data with CIAO 4.2 and CALDB 4.2.0.

Background images were extracted from the standard set of CTI-corrected ACIS blank sky images in the Chandra CALDB (Markevitch et al. 2003). To remove the particle background, we estimated the count rates in the hard energy band (10–12 keV) of Abell 1835 and the blank sky, and renormalized the blank sky. We used the tool LC_CLEAN in CIAO to scan the light curve of data for flares. The good time interval (GTI) was about 117 ks. Because Abell 1835 appears to be a relaxed cluster of galaxies, we assumed that the temperature structure of this cluster is spherically symmetric and applied a deprojection technique. The deprojected spectrum of each shell is calculated by subtracting the contributions from all the outer shells (e.g., Nulsen & Böringer 1995; Matsushita et al. 2002). The detailed calculation procedures were described in Chen et al. (2003) and Jia et al. (2004, 2006).

We divided the image of the cluster into seven annular regions centered on the emission peak for the extraction of spectra and used the outmost ring (8.33′−10.42′) to determine the local cosmic X-ray background (CXB). For each annular region, ancillary response files (ARFs) and response matrix files (RMFs) are generated using CIAO. The complete process is: a) select GTI using the light curve of data; b) subtract the point sources; c) subtract the background using blank sky data; d) extract the project spectra; e) extract the deprojected spectra.

For the purpose of comparing, we also reprocessed the XMM-Newton data of Abell 1835 (observation ID: 0551830201) in ΛCDM cosmology as done in Jia et al. (2004) using SAS 11.0.0.

3. Spectral analysis

For the spectral analysis, we used the plasma emission model MEKAL (Mewe et al. 1985, 1986; Kaastra 1992; Liedahl et al. 1995) and WABS model (Morrisson & McCammon 1983). To fit the spectra, XSPEC version 12.6.0 (Arnaud 1996) is used, and the model is 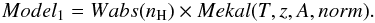(1)We fixed the redshift z to 0.2523 and nH to the Galactic absorption 2.24 × 1020 cm-2 (Dickey & Lockman 1990). The fitting results are listed in Table 1.

Table 1

Best-fit free parameters of Abell 1835: temperature T, abundance A, and normalized constant norm.

The abundance is higher in the cluster center, which is understandable because the excess metal in the cluster center is produced in the cD galaxy and ejected into the ICM (Makishima et al. 2001; Xiang et al. 2009). From the deprojected temperature profile (squares in Fig. 1), we see that the temperature decreases towards the center, which may be ascribed to the gas cooling. Here we find the temperature profile is fitted well with the formula 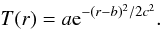(2)The best-fit parameters are a = 11.29 keV, b = 2.78 arcmin, and c = 2.14 arcmin. The best-fit profile is shown as a solid line in Fig. 1.

To establish a comparison, we also obtained the temperatures from the projected spectra of Chandra, plotted as diamonds in Fig. 1. The average temperature excluding core (r < 0.75′) is ~9.6 keV, which does not differ much from that of Markevitch (2002). After deprojection, the temperatures do not differ much from the projected temperatures. But they are still much higher than our new result of XMM-Newton, ~7.33 keV, which is consistent with that of Majerowicz et al. (2002) and Jia et al. (2004). Therefore, even when the same method of data analysis is used, the temperature differences derived from Chandra and XMM-Newton data still exist.

thumbnail Fig. 1

Temperature profiles of Abell 1835 with a confidence level of 90%. Squares: deprojected temperatures of Chandra; diamonds: projected temperatures of Chandra; triangles: deprojected temperatures of XMM-Newton. The solid line is the best-fit profile of Chandra deprojected temperatures.

4. Mass analysis

In our mass model, we measure the spatially resolved radial temperature distribution from the deprojected spectra. A double-β model is adopted to fit the ICM density distribution.

4.1. Electron density

For calculating the electron density profile, we divided the cluster into 19 annular regions. We calculated the deprojected photon counts in each shell. By using the deprojected abundance and the deprojected temperature profile, we could estimate the normalized constant of each region, norm. Then we derive the deprojected electron density ne of each region from Eq. (3), shown as squares in Fig. 2, (3)where DA is the angular size distance to the source (cm) and ne, nH (cm-3) are the electron and hydrogen densities, respectively. We fitted the electron density profile with the double-β model (Chen et al. 2003) (4)The best-fit parameters of Chandra are n01 = 0.041 ± 0.002 cm-3,β1 = 0.597 ± 0.006,rc1 = 0.325 ± 0.013 arcmin,n02 = 0.114 ± 0.003 cm-3,β2 = 12.81 ± 3.080,rc2 = 0.730 ± 0.094 arcmin,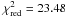, d.o.f. = 13.

The best-fit profiles of ne from Chandra and XMM-Newton data are depicted in Fig. 2, which shows that the electron density derived from Chandra is higher than that of XMM-Newton.

thumbnail Fig. 2

Top panel: electron density profiles of Abell 1835 from Chandra (squares) and XMM-Newton (triangles). The error bars are at a 68% confidence level. The solid line is the best-fit profile of Chandra results with a double-β model, and the dashed line for XMM-Newton results. Bottom panel: the ratio between the electron density profiles of Chandra and XMM-Newton.

4.2. Mass calculation

With the assumption of spherical symmetry and hydrostatic equilibrium, the total mass of cluster within radius r can be determined when the radial profiles of the gas density and temperature are known. We calculated the gravitational mass of Abell 1835 with the hydrostatic equation (Fabricant et al. 1980) (5)where kB is the Boltzmann constant, G is the gravitational constant, μ is the mean molecular weight of the gas in units of mp, and mp is the proton mass. For a fully ionized gas with a standard cosmic abundance, a suitable value is μ = 0.60.

Using the best-fit profiles of the electron density ne(r) and the deprojected temperature T(r), we could obtain the total mass profile, as shown in Fig. 3. The total masses within the radius of 6′ are Mtot − Chandra = 1.36 ± 0.42 × 1015 M⊙ and Mtot − XMM = 0.84 ± 0.10 × 1015 M⊙. This shows that the Chandra result is much higher than the XMM-Newton result. At the same time, the virial mass of Chandra is 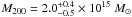with r200 = 1.99 Mpc, which is consistent with the result of Schmidt et al. (2001) when using the same cosmology model.

thumbnail Fig. 3

Total mass profiles of Abell 1835 from XMM-Newton (triangles), Chandra (squares) and a method in Sect. 5.2 (circles) fitting Chanda spectra with XMM-Newton temperatures.

4.3. Mass within the optical lensing arc

Allen et al. (1996) announced that there is a lensing arc inside the cluster center. Richard et al. (2010) accurately recalculated the mass inside the radius of 250 kpc, MSL = 2.83 ± 0.41 × 1014 M⊙, based on seven multiply imaged systems under ΛCDM cosmology. We estimated the X-ray projected mass inside the radius Marc − Chandra = 1.85 ± 0.20 × 1014 M⊙, Marc − XMM = 1.40 ± 0.15 × 1014 M⊙. The results, shown in Fig. 4, are lower than the strong lensing mass derived by Richard et al. (2010). The difference may be due to the assumption of spherical symmetry and hydrostatic equilibrium in the X-ray mass calculation (Gavazzi 2005).

The mass analysis of strong lensing cluster may be affected by orientation biases (Meneghetti et al. 2010b, 2011; Hennawi et al. 2007; Oguri & Blandford 2009; Zitrin et al. 2011). For Abell 1835, Corless et al. (2009) showed that the assumption of spherical symmetry is less problematic and that the orientation bias is weaker for this halo because of its smaller Einstein radius. Thus, the mass estimates of Abell 1835 mentioned above are reasonable. The radio plasma may provide some additional pressure to support the X-ray gas, so the assumption of hydrostatic equilibrium may be inaccurate.

thumbnail Fig. 4

Projected mass profiles within 250 kpc of Abell 1835 from Chandra (squares) and XMM-Newton (triangles). The dashed line presents the NFW profile of strong lensing mass of Richard et al. (2010).

4.4. Gas mass fraction

In galaxy clusters, gas, which has a temperature of a few keV, is an important component. From the electron density, we can calculate gas mass and then the gas mass fraction, defined as fgas(r) = Mgas(r)/Mtotal(r).

thumbnail Fig. 5

Gas mass fraction profiles of Abell 1835 from Chandra (squares) and XMM-Newton (triangles).

Figure 5 shows the gas mass fraction of Abell 1835, which drops clearly in the region r < 0.6′, while keeping approximately constant in the outer region. This indicates that the dark matter is more condensed than the gas in the central region of the cluster.

5. Discussion

Although we used the same method to analyse the data of Abell 1835 observed by XMM-Newton and Chandra, the temperature discrepancy still exists. The average temperatures of Abell 1835 (excluding cool core) derived by Chandra and XMM-Newton are 9.6 keV and 7.33 keV, respectively, in the following, we discuss the possible reasons for this.

5.1. PSF scatter

The effect of PSF of pn/XMM-Newton and MOS/XMM-Newton is larger than that of ACIS/Chandra. PSF may scatter a significant fraction of the adjacent regions’ emission into the regions that we analyze.

Applying a combined direct demodulation and deprojection technique to subtract the effects of PSF, Wang et al. (2010) found that the central electron density increases by 30%, while the temperature profile is similar to the result using only a deprojection method. They also estimated that the effects of PSF were not important for the temperature profile. Nevalainen et al. (2010) pointed out that PSF scattering may cause differences in temperature measurements with different instruments of a maximum of 2%, which is negligible compared to the statistical uncertainties with the minimum width of rings set to 1.5′. Therefore, PSF is not a primary reason for the temperature discrepancy.

5.2. Discrepancy between the temperatures

Since the effects of PSF and deprojection technology on temperature are not the primary reasons for the temperature discrepancy, the difference of the calibration of XMM-Newton and Chandra may lead to the temperature discrepancy. Nevalainen et al. (2010) found that the difference of the calibration of these two instruments is about 10–15% on average and the maximum difference is ~25%. Therefore, it may be the main factor of the temperature discrepancy of Abell 1835.

In order to contrast the temperatures of Abell 1835 determined by Chandra and XMM-Newton, we tried to fit Chandra and XMM-Newton spectra with temperatures fixed to the other one’s temperatures. Because the temperatures of XMM-Newton and Chandra are significantly different in annulus 0.75′−3.33′, we combined and rebinned the three spectra of 0.75′−3.33′. The fitting results are listed in Table 2. It seems that Chandra spectra can be fitted well with XMM-Newton temperature, while XMM-Newton spectra can not fit well with Chandra temperature. As a result, we think that XMM-Newton has a stronger restriction on temperature.

Table 2

Best-fit parameters of 0.75′−3.33′: temperature, abundance, and normalized constant norm.

Table 3

Projected masses of Abell 1835.

Table 4

Ratio between X-ray and weak lensing masses.

Furthermore, we calculated the total mass with XMM-Newton temperatures and Chandra electron density based on XMM-Newton temperatures (hereafter MChandra(T = TXMM)), which is 0.74 ± 0.05 × 1015 M⊙ within the radius of 6.0′ (circles in Fig. 3). It is similar to the total mass derived from XMM-Newton data.

To compare with the weak lensing mass, we also calculated the projected masses at r2500, r1000 and r500. The results are listed in Table 3, which shows that the weak lensing mass is lower than MChandra, and a little higher than MXMM and MChandra(T = TXMM) at r500.

Because of the non-hydrostatic state and non-equilibrium processes in clusters, the X-ray masses may be underestimated (e.g., Rasia et al. 2004; Piffaretti et al. 2004; Nagai et al. 2007). In Table 4, we list the comparison of the X-ray mass and the weak lensing mass from both the observational and simulated analyses. It shows that the X-ray mass is always consistent with, or a little smaller than, the weak lensing mass (Zhang et al. 2008; Mahdavi et al. 2008; Zhang et al. 2010; Meneghetti et al. 2010a; Rasia et al. 2012). Consequently, our MXMM and MChandra(T = TXMM) are more suitable.

With XMM-Newton temperatures, we can get more reliable masses from XMM-Newton and Chandra data. Because XMM-Newton has a stronger restriction on temperature, the temperatures derived from XMM-Newton data may be more reliable.

6. Conclusion

We have presented a detailed analysis of about 117 ks of Chandra observations on the galaxy cluster Abell 1835. Through the deprojected spectra analysis, we derived the deprojected temperatures, which do not differ much from the temperatures without deprojection and are still much higher than those of XMM-Newton.

The total mass within the radius of 6′, Mtot − Chandra = 1.36 ± 0.42 × 1015 M⊙, is much higher than the total mass of Mtot − XMM = 0.84 ± 0.10 × 1015 M⊙ derived from XMM-Newton data. The difference of total mass is due to the discrepancy of the temperatures derived from Chandra and XMM-Newton. We also calculated the projected mass within the optical lensing arc, which is lower than the strong lensing mass derived by Richard et al. (2010).

After deprojection and PSF correction (Wang et al. 2010), the temperature and total mass of Abell 1835 resulting from Chandra are still different from those of XMM-Newton. These differences may result from the calibration of the two instruments. We find that XMM-Newton has a stronger restriction on temperature. And with XMM-Newton temperatures, the projected mass from Chandra data is lower than the weak lensing

mass and consistent with other observational analyses. For these reasons, the temperatures obtained from XMM-Newton may be more reliable.

Acknowledgments

We would like to thank the referee for insightful and helpful comments, which improved the paper significantly. This research was supported by Project 1I2011030403 of IHEP, and Project 11003018 sponsored by National Nature Science Foundation of China.

References

  1. Andersson, K. E., & Madejski, G. M. 2004, ApJ, 607, 190 [NASA ADS] [CrossRef] [Google Scholar]
  2. Allen, S. W. 2000, MNRAS, 315, 269 [NASA ADS] [CrossRef] [Google Scholar]
  3. Allen, S. W., Fabian, A. C., Edge, A. C., et al. 1996, MNRAS, 283, 263 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bartelmann, M. 1995, A&A, 299, 11 [NASA ADS] [Google Scholar]
  5. Böhringer, H., Matsushita, K., Churazov, E., et al. 2002, A&A, 382, 804 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Chen, Y., Ikebe, Y., & Böhringer, H. 2003, A&A, 407, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Clowe, D., & Schneider, P. 2002, A&A, 395, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Corless, V. L., King, L. J., & Clowe, D. 2009, MNRAS, 393, 1235 [NASA ADS] [CrossRef] [Google Scholar]
  9. Fabian, A. C. 1988, Science, 242, 1586 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fabricant, D., Lecar, M., & Gorenstein, P. 1980, ApJ, 241, 552 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gavazzi, R. 2010, A&A, 443, 793 [Google Scholar]
  12. Hennawi, J. F., Dalal, N., Bode, P., & Ostriker, J. P. 2007, ApJ, 654, 714 [NASA ADS] [CrossRef] [Google Scholar]
  13. Jia, S. M., Chen, Y., Lu, F. J., et al. 2004, A&A, 423, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Jia, S. M., Chen, Y., & Chen, L. 2006, ChJAA, 6, 181 [NASA ADS] [CrossRef] [Google Scholar]
  15. Kaastra, J. S. 1992, An X-ray Spectral Code for Optically Thin Plasma (Internal Sron-Leiden Report, updated version 2.0) [Google Scholar]
  16. Lemze, D., Barkana, R., Broadhurst, T. J., et al. 2008, MNRAS, 386, 1092 [NASA ADS] [CrossRef] [Google Scholar]
  17. Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [NASA ADS] [CrossRef] [Google Scholar]
  18. Loeb, A., & Mao, S. 1994, ApJ, 435, 109 [Google Scholar]
  19. Majerowicz, S., Neumann, D. M., & Reiprich, T. H. 2002, A&A, 394, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Makishima, K., Ezawa, H., Fukuzawa, Y., et al. 2001, PASJ, 53, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Markevitch, M. 2002, unpublished [arXiv:astro-ph/0205333] [Google Scholar]
  22. Markevitch, M., Bautz, M. W., Biller, B., et al. 2003, ApJ, 583, 70 [NASA ADS] [CrossRef] [Google Scholar]
  23. Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
  24. Mewe, R., Lemen, J. R., & van den Oord, G. H. J. 1986, A&AS, 65, 511 [NASA ADS] [Google Scholar]
  25. Mahdavi, A., Hoekstra, H., Babul, A., et al. 2008, MNRAS, 384, 1567 [NASA ADS] [CrossRef] [Google Scholar]
  26. Meneghetti, M., Rasia, E., Merten, J., et al. 2010a, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Meneghetti, M., Fedeli, C., Pace, F., et al. 2010b, A&A, 519, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Meneghetti, M., Fedeli, C., Zitrin, A., et al. 2011, A&A, 530, A17 [CrossRef] [EDP Sciences] [Google Scholar]
  29. Morandi, A., Marceau, L., Jack, S., et al. 2012, MNRAS, 425, 2069 [NASA ADS] [CrossRef] [Google Scholar]
  30. Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
  31. Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]
  32. Nevalainen, J., David, L., & Guainazzi, M. 2010, A&A, 523, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Nulsen, P. E. J., & Böhringer, H. 1995, MNRAS, 274, 1093 [NASA ADS] [Google Scholar]
  34. Oguri, M., & Blandford, R. D. 2009, MNRAS, 392, 930 [NASA ADS] [CrossRef] [Google Scholar]
  35. Piffaretti, R., Kaastra, J., Tamura, T., et al. 2004, in Outskirts of Galaxy Clusters: Intense Life in the Suburbs, eds. A. Diaferio, IAU Colloq. 195, 131 [Google Scholar]
  36. Rasia, E., Tormen, G., & Moscardini, L. 2004, MNRAS, 351, 237 [NASA ADS] [CrossRef] [Google Scholar]
  37. Rasia, E., Meneghetti, M., Martino, R., et al. 2012, New J. Phys., 14, 055018 [NASA ADS] [CrossRef] [Google Scholar]
  38. Richard, J., Smith, G. P., Kneib, J. P., et al. 2010, MNRAS, 404, 325 [NASA ADS] [Google Scholar]
  39. Schmidt, R. W., Allen, S. W., & Fabian, A. C. 2001, MNRAS, 327, 1057 [NASA ADS] [CrossRef] [Google Scholar]
  40. Smith, G. P., Kneib, J.-P., Smail, I., et al. 2005, MNRAS, 359, 417 [NASA ADS] [CrossRef] [Google Scholar]
  41. Wang, Y. S., Jia, S. M., & Chen, Y. 2010, Science China Phys., Mech. Astron., 53, 183 [Google Scholar]
  42. Xiang, F., Rudometkin, E., Churazov, E., et al. 2009, MNRAS, 398, 575 [NASA ADS] [CrossRef] [Google Scholar]
  43. Zhang, Y. Y., Finoguenov, A., Böhringer, H., et al. 2008, A&A, 482, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Zhang, Y. Y., Okabe, N., Finoguenov, A., et al. 2010, ApJ, 711, 1033 [NASA ADS] [CrossRef] [Google Scholar]
  45. Zitrin, A., Broadhurst, T., Coe, D., et al. 2011, ApJ, 742, 117 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Best-fit free parameters of Abell 1835: temperature T, abundance A, and normalized constant norm.

In the text
Table 2

Best-fit parameters of 0.75′−3.33′: temperature, abundance, and normalized constant norm.

In the text
Table 3

Projected masses of Abell 1835.

In the text
Table 4

Ratio between X-ray and weak lensing masses.

In the text

All Figures

thumbnail Fig. 1

Temperature profiles of Abell 1835 with a confidence level of 90%. Squares: deprojected temperatures of Chandra; diamonds: projected temperatures of Chandra; triangles: deprojected temperatures of XMM-Newton. The solid line is the best-fit profile of Chandra deprojected temperatures.
In the text
thumbnail Fig. 2

Top panel: electron density profiles of Abell 1835 from Chandra (squares) and XMM-Newton (triangles). The error bars are at a 68% confidence level. The solid line is the best-fit profile of Chandra results with a double-β model, and the dashed line for XMM-Newton results. Bottom panel: the ratio between the electron density profiles of Chandra and XMM-Newton.
In the text
thumbnail Fig. 3

Total mass profiles of Abell 1835 from XMM-Newton (triangles), Chandra (squares) and a method in Sect. 5.2 (circles) fitting Chanda spectra with XMM-Newton temperatures.
In the text
thumbnail Fig. 4

Projected mass profiles within 250 kpc of Abell 1835 from Chandra (squares) and XMM-Newton (triangles). The dashed line presents the NFW profile of strong lensing mass of Richard et al. (2010).
In the text
thumbnail Fig. 5

Gas mass fraction profiles of Abell 1835 from Chandra (squares) and XMM-Newton (triangles).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.