| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219585 | |
| Published online | 30 July 2012 | |
WASP-42 b and WASP-49 b: two new transiting sub-Jupiters⋆,⋆⋆
1 Observatoire de Genève, Université de Genève, Chemin des maillettes 51, 1290 Sauverny, Switzerland
e-mail: monika.lendl@unige.ch
2 Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK
3 School of Physics and Astronomy, University of St. Andrews, North Haugh, Fife, KY16 9SS, UK
4 Université de Liège, Allée du 6 août 17, Sart Tilman, Liège 1, Belgium
5 Las Cumbres Observatory, 6740 Cortona Drive Suite 102, Goleta, CA 93117, USA
6 Astrophysics Research Centre, School of Mathematics & Physics, Queen’s University, University Road, Belfast BT7 1NN, UK
7 Department of Physics and Astronomy, University of Leicester, Leicester, LE1 7RH, UK
8 Department of Physics, University of Warwick, Coventry CV4 7AL, UK
Received: 11 May 2012
Accepted: 29 June 2012
We report the discovery of two new transiting planets from the WASP survey. WASP-42 b is a 0.500 ± 0.035 MJ planet orbiting a K1 star at a separation of 0.0548 ± 0.0017 AU with a period of 4.9816872 ± 7.3 × 10-6 days. The radius of WASP-42 b is 1.080 ± 0.057 RJ while its equilibrium temperature is Teq = 995 ± 34 K. We detect some evidence for a small but non-zero eccentricity of e = 0.060 ± 0.013. WASP-49 b is a 0.378 ± 0.027 MJ planet around an old G6 star. It has a period of 2.7817387 ± 5.6 × 10-6 days and a separation of 0.0379 ± 0.0011 AU. This planet is slightly bloated, having a radius of 1.115 ± 0.047 RJ and an equilibrium temperature of Teq = 1369 ± 39 K. Both planets have been followed up photometrically, and in total we have obtained 5 full and one partial transit light curves of WASP-42 and 4 full and one partial light curves of WASP-49 using the Euler-Swiss, TRAPPIST and Faulkes South telescopes.
Key words: planetary systems / methods: observational / techniques: photometric / techniques: spectroscopic / stars: individual: WASP-42 / stars: individual: WASP-49
Based on photometric observations made with WASP-South, EulerCam on the Euler-Swiss telescope, the Belgian TRAPPIST telescope, the Faulkes South Telescope and spectroscopic observations obtained with CORALIE on the Euler-Swiss telescope and HARPS on the ESO 3.6 m telescope (Prog. ID: 087.C-0649).
The photometric time series and radial velocity data in this work are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/544/A72
© ESO, 2012
1. Introduction
Since the discovery of the first extrasolar planet around a Solar-type star by Mayor & Queloz (1995) over 700 exoplanets have been found. In recent years an increasingly large number of planets have been discovered by transit surveys, i.e. surveys that search for planets that pass in front of their host stars producing characteristic photometric signals. At the time of writing, the two most prominent ground-based transit surveys are HATnet (Bakos et al. 2004) and WASP (Pollacco et al. 2006).
From ground-based transit surveys, a population of hot close-in giant planets has been explored. These Hot Jupiters are located at small separations, having periods of typically 2 to 5 days. While the formation of gas giants is accepted to take place in cooler regions of the protoplanetary disc at several AU from the star, the process by which the planets have migrated to the proximity of the star has been a matter of debate. Migration can occur from interactions with the disc itself (Goldreich & Tremaine 1980; Lin et al. 1996), or due to dynamical interactions between massive bodies in the system, namely scattering between planets (Rasio & Ford 1996) and Kozai migration (Kozai 1962; Eggleton & Kiseleva-Eggleton 2001; Wu & Murray 2003), which put the planet on a highly eccentric orbit that then becomes tidally circularized. Recent measurements of the sky-projected spin-orbit angles have revealed several misaligned systems (Hébrard et al. 2008; Triaud et al. 2010; Winn et al. 2010), a fact which could be caused by planets undergoing Kozai migration (Fabrycky & Tremaine 2007; Wu et al. 2007; Triaud et al. 2010).
Many of these planets have been shown to posses radii which are larger than expected from models of irradiated planets (e.g. Fortney et al. 2007). Low densities appear to be common for Saturn-mass planets (e.g. WASP-39 b, Faedi et al. 2011) and up to planets of the mass of Jupiter (e.g. HAT-P-32 b, Hartman et al. 2011). The most striking examples are WASP-17 b having a density of ρ = 0.06 ρJ (Anderson et al. 2010, 2011) and Kepler-12 b with a density of ρ = 0.09 ρJ (Fortney et al. 2011). It appears that there is a mechanism depositing energy into the planet and thus inflating it or slowing the contraction of the planet since its formation. A variety of mechanisms have been proposed to account for this effect: the deposition of kinetic energy stemming from strong winds driven by large day/night temperature contrasts (Showman & Guillot 2002); enhanced opacities due to higher planetary metallicity causing a slow-down in contraction (Burrows et al. 2007); heating by tidal forces from the circularization, synchronization and re-alignment of the planetary orbit (Bodenheimer et al. 2001); reduced heat transport efficiency by layered convection inside the planet (Chabrier & Baraffe 2007), and Ohmic heating from currents induced through winds in the planetary atmosphere (Batygin & Stevenson 2010). It has been found that the degree to which the planet is bloated is correlated with the incident stellar flux (Demory & Seager 2011; Enoch et al. 2011, 2012; Laughlin et al. 2011), favouring models which incorporate the absorption of stellar radiation as a cause of the planetary bloating.
In this paper, we announce the discovery of two additional transiting planets from the WASP-South survey. WASP-42 b is a 0.5 MJ planet in a 5 day orbit around a K1 star, and WASP-49 b, a bloated 0.4 MJ planet, is orbiting a metal poor G6 star every 2.8 days. In Sect. 2 we present the discovery and follow-up observations of WASP-42 and WASP-49, leading to their identification as harbouring transiting extrasolar planets. In Sect. 3 we describe the analysis of our data before putting the two planets into context in Sect. 4.
2. Observations
2.1. WASP-photometry
The objects WASP-42 (2MASS 12515557–4204249) and WASP-49 (2MASS 06042146–1657550) were observed using the WASP survey telescopes. The WASP survey is operated from two sites, one in each hemisphere: the Observatorio del Roque de los Muchachos in the Canary Islands in the North, and the Sutherland Station of the South African Astronomical Observatory (SAAO) in the South. Each site is equipped with eight commercial 11 cm, f = 200 mm Canon lenses on a single mount. Details of the WASP survey, its photometric reduction and candidate selection process can be found in Pollacco et al. (2006) and Collier Cameron et al. (2007). Both targets presented in this work were observed exclusively from the southern WASP site. In total 25 880 data points were obtained for WASP-42 between May 2006 and April 2008, while 18461 data points were obtained for WASP-49 between October 2006 and March 2010. The data obtained for both targets are shown in Fig. 1. In both cases a periodically occurring transit-like signal was detected in the data using the transit-search algorithms of Collier Cameron et al. (2006), triggering a closer inspection of the targets and their selection for further study.
2.2. Spectroscopic observations
 |
Fig. 1 Phase-folded WASP photometry of WASP-42 (top) and WASP-49 (bottom). The unbinned data are depicted in gray; the black points represent the same data set binned to 2 min. |
 |
Fig. 2 Upper panel: radial velocity observations of WASP-42 together with the circular (dashed line) and eccentric (solid line) models. Black dots denote CORALIE data, while blue triangles denote HARPS data. Middle panel: residuals of the circular model. Lower panel: residuals of the eccentric model. |
 |
Fig. 3 Radial velocity observations of WASP-49 together with the respective model and residuals. All data have been obtained with CORALIE. |
WASP-42 and WASP-49 were observed with the CORALIE spectrograph mounted on the 1.2 m Euler-Swiss telescope at the La Silla site (Chile). For WASP-42 and WASP-49, 27 and 25 data points were obtained from April 2010 to March 2011, and from August 2009 to October 2011, respectively. For all spectroscopic observations we obtained radial velocities using the weighted Cross-Correlation technique (Baranne et al. 1996) as implemented in the CORALIE and HARPS reduction pipelines. The radial velocities folded on the transit ephemeris are shown in Figs. 2 and 3. In order to ensure that the radial-velocity variations are not caused by star spots we checked the CCF bisector spans (shown in Fig. 4) according to the method described by Queloz et al. (2001). After the planetary nature of the signal had been confirmed, WASP-42 was also observed with the HARPS spectrograph (Mayor et al. 2003) which is located at the ESO 3.6 m telescope at La Silla observatory. 35 data points were obtained with HARPS, 25 of which were observed nearly consecutively on 4 April 2011 (UT) in order to measure the Rossiter-McLaughlin effect (Rossiter 1924; McLaughlin 1924) and thus determine the projected spin-orbit angle of the WASP-42 system. However, due to an inaccurate ephemeris at the time of planning of these observations, the continuous observations began only during the egress of the planet (see Fig. 6) and thus the Rossiter-McLaughlin effect was not measured.
2.3. Follow-up photometry
 |
Fig. 4 Bisector spans measured for WASP-42 (left) and WASP-49 (right). |
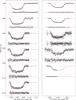 |
Fig. 5 Follow-up photometry of WASP-42 (left) and WASP-49 (right) together with the respective model and residuals. Each light curve has been divided by the respective photometric baseline model as described in Sect. 3.2. The light curves of WASP-42 are (from top to bottom) EulerCam on March 20 and 25, 2011, and TRAPPIST on March 5, 10, 30 and April 4, 2011 (UT). The light curves of WASP-49 are (from top to bottom) EulerCam on January 19 and March 24, 2011, TRAPPIST on January 19 and 24 October 2011, and FTS on 21 March 2011 (UT). |
Two transits each of both WASP-42 b and WASP-49 b were observed using EulerCam between January and March 2011. EulerCam is an e2v 4k × 4k back-illuminated deep-depletion silicon CCD detector which was installed at the Cassegrain focus of the 1.2 m Euler-Swiss telescope in September 2010. The field of view of EulerCam is 15.68 × 15.73 arcmin, producing a resolution of 0.23 arcsec per pixel. The instrument is operated at a temperature of − 115 °C, cool enough to make dark current negligible (measured at less than 2.6 e− in 30 min). EulerCam can be read out using either one or four ports, giving readout times of 6.5 s and 25 s. For single-port readout the readout noise is ~5 e−/pixel. For four-port readout the readout noise is the same except that the lower-left port shows a slightly elevated noise of ~8 e−/pixel. As flat-field uncertainties are often a limiting factor in high-precision photometry, EulerCam uses a feedback scheme for the telescope guiding to keep the stars on the same locations on the detector during the observations. This system, dubbed “Absolute Tracking” is based on a combination of the SCAMP (Bertin 2006) and Sextractor (Bertin & Arnouts 1996) software packages. After recording an image, the positions of the stars on the image are extracted and then matched with a catalogue. From this match, the offset of the telescope from the nominal position is calculated using a PID algorithm and the telescope pointing is adjusted between exposures in order to compensate for drifts. Due to technical problems the 4-port readout mode was not available during the first transit of WASP-49, leading to a slightly degraded time sampling. All EulerCam observations were done with a defocus of 0.1 mm in order to improve the duty cycle and spread the light over more pixels and thereby improve the sampling of the PSF.
Four transits of WASP-42 b and two transits of WASP-49 b were observed with the automated Belgian TRAPPIST telescope, also located at La Silla. For details of TRAPPIST see Gillon et al. (2011) and Jehin et al. (2011). Again, the telescope was defocused giving a FWHM of 3.2 arcsec on the images.
Finally, one partial transit of WASP-49 b was observed with the Faulkes Telescope South (FTS) which is based at Siding Spring, Australia. Details of all observations are summarized in Table 1 and the light curves are depicted in Fig. 5.
All follow-up light curves were obtained from bias- and flat-field-corrected images using relative Aperture Photometry where several apertures were tested and reference stars were chosen with great care. In the case of TRAPPIST, IRAF1 was used in the reduction process. For EulerCam, the standard reduction procedure is as follows. After overscan, bias and flat-field correction, the photometry is extracted from the images for several circular apertures with radii ranging from 12 to 50 pixels placed on the target and all other bright stars in the field. The optimal combination of reference stars is found by using the target itself to measure the quality of the references. We start the process with the reference star with which we obtain the lowest RMS transit light curve and iteratively add those other references which yield the best improvement at any given step. Typically, the final reference sources is made of between three and ten stable stars of similar brightness and color to the target and which are not affected by any short-term variations (caused, e.g., by proximity to bad pixels).
During the observations of WASP-49 with EulerCam we noticed a faint source, 9.2 arcsec North of the target. It is outside the smaller apertures for which we extracted photometry in the analysis of the EulerCam data. As the transit is present in light curves created using these apertures (while the data are noisier than for larger apertures), we are certain the transit is on the main target. However, in order to evaluate the contamination for larger apertures, we re-observed WASP-49 on 15 January 2012 with EulerCam without defocusing the telescope. The observations were performed outside of transit, a total of 8 images were obtained over 10 min using an r′ Gunn filter. We find the brightness ratio between the target and the contaminant to be 1:0.00343 ± (5 × 10-5), and, as its impact on the observed transit depth is much smaller (4 × 10-5) than the 1-σ-error quoted in Table 3, we neglect it in the analysis presented below.
Summary of follow-up photometry.
3. Determination of system parameters
3.1. Stellar parameters
3.1.1. Rotation period
We have analyzed the WASP lightcurves of WASP-42 and WASP-49 to determine whether they show periodic modulation due to the combination of magnetic activity and the rotation of the star. We used the sine-wave fitting method described in Maxted et al. (2011) to calculate periodograms for both stars over 4096 uniformly spaced frequencies from 0 to 2.5 cycles/day. The false alarm probability (FAP) for the strongest peak in these periodograms was calculated using the boot-strap Monte Carlo method also described in Maxted et al. (2011). Variability due to star spots is not expected to be coherent on long timescales as a consequence of the finite lifetime of star-spots and differential rotation in the photosphere, and so for both stars we analyzed the data from each observing season independently.
We did not find any significant periodic signals (FAP < 0.05) in our data apart from frequencies near 1 cycle/day and its harmonics. We examined the distribution of amplitudes for the most significant frequency in each Monte Carlo trial and used these results to estimate a 95% upper confidence limit of 1 milli-magnitude for the amplitude of any periodic signal in the lightcurves for both WASP-42 and WASP-49.
3.1.2. Spectroscopic analysis
For each star a total of 11 (WASP-42) and 23 (WASP-49) individual CORALIE spectra were co-added to produce single spectra with typical S/N values of 60:1 (WASP-42) and 100:1 (WASP-49). The standard pipeline reduction products were used in the analysis.
The analyses were performed using the methods given in Gillon et al. (2009). The Hα line was used to determine the effective temperature (Teff), while the Na i D and Mg i b lines were used as surface gravity (log g) diagnostics. The parameters obtained from the analysis are listed in Table 2. The elemental abundances were determined from equivalent width measurements of several clean and unblended lines. Values for microturbulence (ξt) were determined from Fe i using the method of Magain (1984). The quoted error estimates include those given by the uncertainties in Teff, log g and ξt, as well as the scatter due to measurement and atomic data uncertainties.
 |
Fig. 6 Photometric and radial velocity observations obtained on April 4, 2011 (UT). Upper panel: TRAPPIST transit light curve binned in 2 min intervals. Lower panel: the the HARPS time series observation aiming at measuring the Rossiter-McLaughlin effect. Depicted are the residual values from a purely Keplerian model. The dashed red line indicates the time of fourth contact. |
The projected stellar rotation velocities (vsini ∗ ) were determined by fitting the profiles of several unblended Fe i lines. Values for macroturbulence (vmac) of 1.4 ± 0.3 km s-1 (WASP-42) and 2.9 ± 0.3 km s-1 (WASP-49) were assumed, based on the tabulation by Gray (2008). For both cases, an instrumental FWHM of 0.11 ± 0.01 Å was determined from the telluric lines around 6300 Å. Best fitting values of vsini ∗ = 2.7 ± 0.4 km s-1 (WASP-42) and vsini ∗ = 0.9 ± 0.3 km s-1 (WASP-49) were obtained.
There is no significant detection of lithium in the spectra of either star, with equivalent width upper limits of 4 mÅ, corresponding to an abundance upper limit of log A(Li) < 0.5 ± 0.2 (WASP-42) and 8 mÅ, corresponding to an abundance upper limit of log A(Li) < 0.7 ± 0.1 (WASP-49).
Stellar parameters of WASP-42 and WASP-49 from spectroscopic analysis.
Planetary and stellar parameters for WASP-42 and WASP-49, as well as the radial-velocity rms.
 |
Fig. 7 The locations of WASP-42 and WASP-49 in the modified Hertzsprung-Russell diagram. |
3.2. Combined analysis
The combined analysis of discovery and follow-up photometry and spectroscopic data was performed in several steps with the Markov Chain Monte Carlo (MCMC) code described in Gillon et al. (2010, 2012). The code makes use of the transit light curve models by Mandel & Agol (2002) and uses a Keplerian model to fit the radial-velocity measurements. For radial-velocity measurements obtained during transit, the prescription of the Rossiter-McLaughlin effect provided by Giménez (2006) is used. Various models for the photometric baseline (e.g. 0th to 4th order polynomials with respect to time and external variables such as pixel shifts) can be included in the fit of the transit light curves via minimization of the model coefficients at each MCMC step. The basic jump parameters are transit depth dF, impact parameter b, transit duration d, epoch of mid-transit T0, period P and 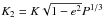 (where K and e denote the radial velocity semi-amplitude and eccentricity, respectively). For these parameters we assume a uniform prior distribution. In order to take into account the stellar limb-darkening, we adopt a quadratic law interpolating the coefficients tabulated by Claret & Bloemen (2011). However, we chose their combination c1 = 2u1 + u2 and c2 = u1 − 2u2 as jump parameters as introduced by Holman et al. (2006). The physical basis of these parameters leads us to assume a normal prior distribution with a width equal to the errors of these parameters. Where eccentricity is not set to e = 0, it is included in the analysis via including the jump parameters
(where K and e denote the radial velocity semi-amplitude and eccentricity, respectively). For these parameters we assume a uniform prior distribution. In order to take into account the stellar limb-darkening, we adopt a quadratic law interpolating the coefficients tabulated by Claret & Bloemen (2011). However, we chose their combination c1 = 2u1 + u2 and c2 = u1 − 2u2 as jump parameters as introduced by Holman et al. (2006). The physical basis of these parameters leads us to assume a normal prior distribution with a width equal to the errors of these parameters. Where eccentricity is not set to e = 0, it is included in the analysis via including the jump parameters 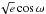 and
and 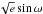 (where ω denotes the argument of periastron). We use the calibration technique devised by Enoch et al. (2010) which uses a fit to a set of well studied main-sequence eclipsing binaries in order to infer the stellar mass and radius from the mean stellar density (measured directly from the transit light curves, Seager & Mallén-Ornelas (2003), temperature and metallicity. This technique is based on a similar relation by Torres et al. (2010) where the stellar surface gravity is used in the place of the stellar density. A minimum of two chains is run in order to check their convergence using the Gelman & Rubin test (Gelman & Rubin 1992).
(where ω denotes the argument of periastron). We use the calibration technique devised by Enoch et al. (2010) which uses a fit to a set of well studied main-sequence eclipsing binaries in order to infer the stellar mass and radius from the mean stellar density (measured directly from the transit light curves, Seager & Mallén-Ornelas (2003), temperature and metallicity. This technique is based on a similar relation by Torres et al. (2010) where the stellar surface gravity is used in the place of the stellar density. A minimum of two chains is run in order to check their convergence using the Gelman & Rubin test (Gelman & Rubin 1992).
As a first step, the photometric data obtained by the WASP-South cameras were analyzed with the aim of finding a mean mid-transit time and period estimate from these long-term data. As the light curves from WASP contain many large outliers (i.e. points deviating by more than 10 times the transit depth), we discarded points deviating by more than 5σ before running two MCMC chains of 104 points each. Here the only parameters left to vary were the time of mid-transit and the period, while all other parameters were kept fixed at their approximate values. The period derived here was used as a starting point in the subsequent analysis of the high-precision follow-up data, while the mid-transit time was included as an extra constraint on the period.
Then, for each follow-up lightcurve we performed MCMC analyses including only the light curve itself and the CORALIE radial velocity measurements. We tested various models for the photometric baseline, using chains of 105 points. A second-order polynomial in time was assumed as a minimal baseline model to take care of stellar variability, airmass and other time-dependent effects. More complicated models (i.e. polynomials up to the fourth degree with respect to time, position shifts, sky background, and FWHM) were tested with the Bayesian Information Criterion (Schwarz 1978). Only for the EulerCam light curve obtained on 19 January 2011 (WASP-49) was a more complicated model (a linear fit to position plus the quadratic fit to time) found to be justified.
Finally, we performed a global analysis in order to find a single solution using all available follow-up data together with the mid-transit time obtained from the discovery photometry. The dependencies and orders in the photometric baseline models were set to those found before. For each planet we ran three sets of two chains of 105 points. From the first set, we determined correction factors for our photometric errors based on the calculation of the red noise (Pont et al. 2006) as described in Winn et al. (2008). In the further analysis, the photometric errors were multiplied by these factors. For the RV data, we determined “jitter” factors which serve to scale the measurement errors to the standard deviation of the best-fit model. These factors are added quadratically to the RV errors and compensate both instrumental and astrophysical effects (such as stellar activity) that are not included in the initial error calculation. The values for the RV jitter are 0 m s-1 (WASP-42, CORALIE), 2.4 m s-1 (WASP-42, HARPS) and 10 m s-1 (WASP-49, CORALIE).
The second and third sets of chains were run with the adapted errors, first setting the eccentricity to e = 0 and then leaving it free. For WASP-49, no significant deviation from a circular orbit is detected (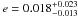 ), and all parameters agree well within one sigma for circular and eccentric case. The eccentric solution for WASP-42 yields
), and all parameters agree well within one sigma for circular and eccentric case. The eccentric solution for WASP-42 yields 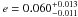 and will be further discussed in Sect. 4 while the planetary and stellar parameters of both objects are presented in Table 3.
and will be further discussed in Sect. 4 while the planetary and stellar parameters of both objects are presented in Table 3.
4. Discussion
We announce the discovery of two new transiting extrasolar planets in the southern hemisphere from the WASP-South survey.
4.1. WASP-42 b
WASP-42 b is a 0.5 MJ planet orbiting the K1 star 2MASS 12515557–4204249 every 5 days. The host-star metallicity is near the solar value.
Based on the vsini∗ and stellar radius of WASP-42, we deduce a maximal rotation period of P = 16.1 ± 3.2 d. Using the Barnes (2007) relation, this gives an upper age limit of ~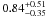 Gy from gyrochronology. We derived a second estimate based on the
Gy from gyrochronology. We derived a second estimate based on the  activity indices (Noyes et al. 1984) from the HARPS spectra following the procedures of Lovis et al. (2011). We find
activity indices (Noyes et al. 1984) from the HARPS spectra following the procedures of Lovis et al. (2011). We find 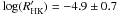 , indicative of a rather quiet star. Using the Mamajek & Hillenbrand (2008) relation we derive a rotation period of P = 40.1 ± 4.7 d and an age of 6.1 ± 1.2 Gy. We also interpolated the isochrones of Marigo et al. (2008) using z = 0.021 and compared them to the location of WASP-42 in the modified ((ρ ∗ /ρ⊙)1/3 vs. Teff) Hertzsprung-Russell diagram (Fig. 7(a)). Here we used the temperature determined from the spectroscopic analysis together with the stellar density determined from the global analysis described in Sect. 3.2. It should be noted that in the analysis of the spectra a degeneracy exists between macroturbulence vmac and stellar rotation vsini ∗ . As the value for vmac is not directly measured but taken from tables, it might not be accurate for WASP-42. For example, a higher vmac would produce a lower vsini ∗ , and thus a slower rotation and older gyrochronological age. Together with the absence of periodic brightness modulations (although we can not exclude non-periodic photometric variations of a few milli-magnitudes), the evidence points towards an older age of several Gyrs for WASP-42.
, indicative of a rather quiet star. Using the Mamajek & Hillenbrand (2008) relation we derive a rotation period of P = 40.1 ± 4.7 d and an age of 6.1 ± 1.2 Gy. We also interpolated the isochrones of Marigo et al. (2008) using z = 0.021 and compared them to the location of WASP-42 in the modified ((ρ ∗ /ρ⊙)1/3 vs. Teff) Hertzsprung-Russell diagram (Fig. 7(a)). Here we used the temperature determined from the spectroscopic analysis together with the stellar density determined from the global analysis described in Sect. 3.2. It should be noted that in the analysis of the spectra a degeneracy exists between macroturbulence vmac and stellar rotation vsini ∗ . As the value for vmac is not directly measured but taken from tables, it might not be accurate for WASP-42. For example, a higher vmac would produce a lower vsini ∗ , and thus a slower rotation and older gyrochronological age. Together with the absence of periodic brightness modulations (although we can not exclude non-periodic photometric variations of a few milli-magnitudes), the evidence points towards an older age of several Gyrs for WASP-42.
 |
Fig. 8 Mass-radius diagram of transiting exoplanets. WASP-42 b and WASP-49 b are depicted using upward and downward facing triangles, respectively. The dotted lines represent curves of equal density at (from top to bottom) ρ = 0.25 ρJ, ρ = 0.5 ρJ and ρ = ρJ. The planet parameters were taken from www.exoplanet.eu. |
Eccentricities, χ2 values and LS-test results of the eccentric and circular models for WASP-42 b found from all RV data and the datasets from the two instruments separately.
 |
Fig. 9 The distribution of eccentricity and argument of periastron for WASP-42 b obtained from the global analysis while adding a jitter of 5 m s-1 to the HARPS and 15 m s-1 to the CORALIE data. |
The planet’s position in the mass-radius diagram (see Fig. 8) is at the low-mass end of the Hot Jupiters. We used the tabulated radii of Fortney et al. (2007) in order to check whether the planetary radius is within predictions using the values for 0.1 AU = 875 K, and interpolating for a planetary mass of 0.5 MJ. Assuming the gyrochronologically determined age of 1 Gyr, we obtain a core mass of slightly above 10 M⊕, while using values for 4.5 Gyr would suggest a core mass close to 0 M⊕. Compared to other planets of similar mass, WASP-42 b is no outlier in terms of density, but with ρp = 0.40 ± 0.05 ρJ falls into the well-populated region between 0.25 ρJ and 0.5 ρJ. We also compared the planet’s radius to the radius predicted from the fits describing the Saturn-mass population presented in Enoch et al. (2012). Using Eq. (8) of Enoch et al. (2012) together with our uncertainties on stellar and planet parameters, we obtain a predicted radius of 1.31 ± 0.03 RJ, which is within the scatter around the model (Fig. 14 in Enoch et al. 2012).
Adopting an eccentric orbit for WASP-42 b allows for a small (0.060 ± 0.013) but non-zero eccentricity, while the argument of periastron is found to be ω = 167 ± 26 deg. We checked any dependence of the derived eccentricity on the jitter values assumed by re-running the analysis adding jitters of 3 m s-1 and 15 m s-1 quadratically to the CORALIE errors as well as a jitters of 5 m s-1 to the HARPS data. In all cases, the significance of the derived eccentricity remained above 3σ. To illustrate, the distribution of the argument of periastron and eccentricity found from the analysis including a jitter of 5 m s-1 for HARPS and 15 m s-1 for CORALIE is depicted in Fig. 9. In order to evaluate the robustness of this detection we computed the Bayes Factor (e.g. Carlin & Louis 2009) of the two models, resulting in a value of Bec = 2440. This is a very strong indication that the eccentric model is a better representation of the data. To provide a second evaluation we compared the reduced chi-squared values 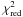 of the radial-velocity models, for datasets including all data (CORALIE and HARPS), as well as all data but leaving out the radial-velocity sequence obtained on April 4, 2011, and the HARPS or CORALIE data separately. For the latter cases we re-ran the MCMC analyses and found eccentricities compatible with the one derived from the complete dataset. We also used the prescription of Lucy & Sweeney (1971) (LS test) in order to test each of the above for the significance of the circular solution. The results are summarized in Table 4. In short, in all cases, the non-circular model gives a better fit to the data, and the values found for the eccentricity agree from all subsets. The LS test indicates a probability of 99.5% for the eccentric model to be required if the HARPS data are considered alone, and a 99% probability if the entire dataset is considered, both above the 5% limit suggested by Lucy & Sweeney (1971). The CORALIE data alone do not justify the eccentric model. Considering that there are only 10 HARPS points outside the consecutive time series, more data would be highly desirable in order to secure the detection. Based on these arguments, we conclude that there is considerable evidence for an eccentric orbit of WASP-42 b and we present the eccentric as well as the circular solution in Table 3.
of the radial-velocity models, for datasets including all data (CORALIE and HARPS), as well as all data but leaving out the radial-velocity sequence obtained on April 4, 2011, and the HARPS or CORALIE data separately. For the latter cases we re-ran the MCMC analyses and found eccentricities compatible with the one derived from the complete dataset. We also used the prescription of Lucy & Sweeney (1971) (LS test) in order to test each of the above for the significance of the circular solution. The results are summarized in Table 4. In short, in all cases, the non-circular model gives a better fit to the data, and the values found for the eccentricity agree from all subsets. The LS test indicates a probability of 99.5% for the eccentric model to be required if the HARPS data are considered alone, and a 99% probability if the entire dataset is considered, both above the 5% limit suggested by Lucy & Sweeney (1971). The CORALIE data alone do not justify the eccentric model. Considering that there are only 10 HARPS points outside the consecutive time series, more data would be highly desirable in order to secure the detection. Based on these arguments, we conclude that there is considerable evidence for an eccentric orbit of WASP-42 b and we present the eccentric as well as the circular solution in Table 3.
The planet is located on the outer edge of the known Hot-Jupiter pileup, at a separation of 4.05 times the Roche limit, well above the 2 RRL cutoff identified by Ford & Rasio (2006), below which planets are thought to be unable to attain that location by the circularization of previously eccentric orbits. This means WASP-42 b is compatible with the evolutionary scenario described by, for example, Matsumura et al. (2010): formation at farther orbital separations, scattering via planet-planet or Kozai interactions to an eccentric orbit, and subsequent tidal circularization.
4.2. WASP-49 b
WASP-49 b is a near Saturn-mass (M = 0.38 ± 0.03 MJ) planet in a 2.8-day orbit around the G6 star 2MASS 06042146–1657550. In WASP-49, lack of lithium would suggest an age of several Gy (Sestito & Randich 2005) and the low vsini∗ implies a long rotation period of around 50 d. The gyrochronological relation of Barnes (2007) gives an age of ~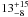 Gy. Hence, we conclude that WASP-49 is a relatively old main-sequence star. We performed an isochrone analysis the same way as for WASP-42 with z = 0.011 (Fig. 7(b)), finding an age above 10 Gyr, in good agreement with the age found from gyrochronology.
Gy. Hence, we conclude that WASP-49 is a relatively old main-sequence star. We performed an isochrone analysis the same way as for WASP-42 with z = 0.011 (Fig. 7(b)), finding an age above 10 Gyr, in good agreement with the age found from gyrochronology.
In the period-mass plane WASP-49 b lies clearly below the bulk of Hot Jupiters and is nearly a twin of the well known HD 149026 b (Sato et al. 2005), a planet known for its high density. While the two planets have almost identical mass and period, they show very different radii and orbit two very different stars – while WASP-49 is remarkable for having one of the lowest metallicities known for planet host stars ( − 0.23 ± 0.07), HD 149026 is one of the most metal-rich planet hosts. In contrast to HD 149026 b, WASP-49 b has a low density (0.27 ± 0.03 ρJ). WASP-49 b fills a gap between 0.32 and 0.42 MJ in the mass-radius plane (see Fig. 8), being the first low-density planet in this mass range. Using the tabulated values from Fortney et al. (2007) for system ages of 4.5 Gyr, an equilibrium temperature of 1300 K and interpolating for a planet mass of 0.38 MJ, we find a predicted maximal planet radius of 1.08 RJ (the case of a zero core mass). As with WASP-42 b, we employed Eq. (8) of Enoch et al. (2012) to obtain a predicted radius of 1.26 ± 0.02 RJ. Again, this value is within the scatter around the fit (Fig. 14 in Enoch et al. 2012). We conclude that WASP-49 b, while larger than predicted from models, is not an outlier in the set of known planets.
There is no evidence for a non-zero eccentricity of WASP-49 b, and we determine a 3-σ upper limit of e = 0.09. WASP-49 b is separated from its host star by 2.4 times the Roche Limit, a rather low value which, together with the planet’s old age, might indicate that orbital decay has occurred since the arrival of the planet at short orbital distances.
To summarize, WASP-42 b and WASP-49 b are two newly discovered close-in transiting planets with masses in the range 1–2 times that of Saturn. While WASP-49 b is old, inflated and orbiting close to a metal-poor G6 star, WASP-42 b is orbiting a cooler K1 star at the outer edge of the well-known planet pile-up, probably on a slightly eccentric orbit.
Acknowledgments
WASP-South is hosted by the South African Astronomical Observatory and we are grateful for their ongoing support and assistance. Funding for WASP comes from consortium universities and from the UK’s Science and Technology Facilities Council. TRAPPIST is funded by the Belgian Fund for Scientific Research (Fond National de la Recherche Scientifique, FNRS) under the grant FRFC 2.5.594.09.F, with the participation of the Swiss National Science Fundation (SNF). M. Gillon and E. Jehin are FNRS Research Associates. We would also like to thank the Geneva Stellar Variability group, particularly Richard I. Anderson, for continuing flexible and short-notice time exchanges on the Euler-Swiss telescope and carefully conducted observations.
References
- Anderson, D. R., Hellier, C., Gillon, M., et al. 2010, ApJ, 709, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, D. R., Smith, A. M. S., Lanotte, A. A., et al. 2011, MNRAS, 416, 2108 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G., Noyes, R. W., Kovács, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Stevenson, D. J. 2010, ApJ, 714, L238 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 112 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P., Lin, D. N. C., & Mardling, R. A. 2001, ApJ, 548, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Hubeny, I., Budaj, J., & Hubbard, W. B. 2007, ApJ, 661, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Carlin, B., & Louis, T. 2009, Bayesian methods for data analysis, Texts in statistical science (CRC Press) [Google Scholar]
- Chabrier, G., & Baraffe, I. 2007, ApJ, 661, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A., Pollacco, D., Street, R. A., et al. 2006, MNRAS, 373, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., & Seager, S. 2011, ApJS, 197, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P., & Kiseleva-Eggleton, L. 2001, ApJ, 562, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, B., Collier Cameron, A., Parley, N. R., & Hebb, L. 2010, A&A, 516, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enoch, B., Cameron, A. C., Anderson, D. R., et al. 2011, MNRAS, 410, 1631 [NASA ADS] [Google Scholar]
- Enoch, B., Collier Cameron, A., & Horne, K. 2012, A&A, 540, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Faedi, F., Barros, S. C. C., Anderson, D. R., et al. 2011, A&A, 531, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ford, E. B., & Rasio, F. A. 2006, ApJ, 638, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Demory, B.-O., Désert, J.-M., et al. 2011, ApJS, 197, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. 1992, Statist. Sci., 7, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Smalley, B., Hebb, L., et al. 2009, A&A, 496, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Lanotte, A. A., Barman, T., et al. 2010, A&A, 511, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Jehin, E., Magain, P., et al. 2011, Detection and Dynamics of Transiting Exoplanets, St. Michel l’Observatoire, France, eds. F. Bouchy, R. Díaz, & C. Moutou, EpJ Web Conf., 11, 6002 [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Fortney, J. J., et al. 2012, A&A, 542, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giménez, A. 2006, ApJ, 650, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2011, ApJ, 742, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Bouchy, F., Pont, F., et al. 2008, A&A, 488, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holman, M. J., Winn, J. N., Latham, D. W., et al. 2006, ApJ, 652, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Laughlin, G., Crismani, M., & Adams, F. C. 2011, ApJ, 729, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011 [arXiv:1107.5325] [Google Scholar]
- Lucy, L. B., & Sweeney, M. A. 1971, AJ, 76, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsumura, S., Peale, S. J., & Rasio, F. A. 2010, ApJ, 725, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Anderson, D. R., Collier Cameron, A., et al. 2011, PASP, 123, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Zucker, S., & Queloz, D. 2006, MNRAS, 373, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasio, F. A., & Ford, E. B. 1996, Science, 274, 954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, B., Fischer, D. A., Henry, G. W., et al. 2005, ApJ, 633, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz. 1978, Ann. Stat., 6, 461 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Triaud, A. H. M. J., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., Holman, M. J., Torres, G., et al. 2008, ApJ, 683, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Howard, A. W., et al. 2010, ApJ, 723, L223 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Murray, N. 2003, ApJ, 589, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, Y., Murray, N. W., & Ramsahai, J. M. 2007, ApJ, 670, 820 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Planetary and stellar parameters for WASP-42 and WASP-49, as well as the radial-velocity rms.
Eccentricities, χ2 values and LS-test results of the eccentric and circular models for WASP-42 b found from all RV data and the datasets from the two instruments separately.
All Figures
 |
Fig. 1 Phase-folded WASP photometry of WASP-42 (top) and WASP-49 (bottom). The unbinned data are depicted in gray; the black points represent the same data set binned to 2 min. |
| In the text | |
 |
Fig. 2 Upper panel: radial velocity observations of WASP-42 together with the circular (dashed line) and eccentric (solid line) models. Black dots denote CORALIE data, while blue triangles denote HARPS data. Middle panel: residuals of the circular model. Lower panel: residuals of the eccentric model. |
| In the text | |
 |
Fig. 3 Radial velocity observations of WASP-49 together with the respective model and residuals. All data have been obtained with CORALIE. |
| In the text | |
 |
Fig. 4 Bisector spans measured for WASP-42 (left) and WASP-49 (right). |
| In the text | |
 |
Fig. 5 Follow-up photometry of WASP-42 (left) and WASP-49 (right) together with the respective model and residuals. Each light curve has been divided by the respective photometric baseline model as described in Sect. 3.2. The light curves of WASP-42 are (from top to bottom) EulerCam on March 20 and 25, 2011, and TRAPPIST on March 5, 10, 30 and April 4, 2011 (UT). The light curves of WASP-49 are (from top to bottom) EulerCam on January 19 and March 24, 2011, TRAPPIST on January 19 and 24 October 2011, and FTS on 21 March 2011 (UT). |
| In the text | |
 |
Fig. 6 Photometric and radial velocity observations obtained on April 4, 2011 (UT). Upper panel: TRAPPIST transit light curve binned in 2 min intervals. Lower panel: the the HARPS time series observation aiming at measuring the Rossiter-McLaughlin effect. Depicted are the residual values from a purely Keplerian model. The dashed red line indicates the time of fourth contact. |
| In the text | |
 |
Fig. 7 The locations of WASP-42 and WASP-49 in the modified Hertzsprung-Russell diagram. |
| In the text | |
 |
Fig. 8 Mass-radius diagram of transiting exoplanets. WASP-42 b and WASP-49 b are depicted using upward and downward facing triangles, respectively. The dotted lines represent curves of equal density at (from top to bottom) ρ = 0.25 ρJ, ρ = 0.5 ρJ and ρ = ρJ. The planet parameters were taken from www.exoplanet.eu. |
| In the text | |
 |
Fig. 9 The distribution of eccentricity and argument of periastron for WASP-42 b obtained from the global analysis while adding a jitter of 5 m s-1 to the HARPS and 15 m s-1 to the CORALIE data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


