| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A154 | |
| Number of page(s) | 12 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201219417 | |
| Published online | 24 August 2012 | |
SPADES: a stellar parameters determination software
1 GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, Place Jules Janssen, 92190 Meudon, France
e-mail: helene.posbic@obspm.fr
2 Zentrum für Astronomie der Universität Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
Received: 14 April 2012
Accepted: 16 July 2012
Context. As increasingly more spectroscopic data are being delivered by medium- and high-resolving power multi-object spectrographs, more automatic stellar parameter determination softwares are being developed. The quality of the spectra collected also allows the determination of elemental abundances.
Aims. SPADES is an automated software for determining: the radial velocity (Vr), the effective temperature (Teff), the surface gravity (log g), the metallicity ( [Fe/H] ), and most importantly, the individual abundances. In this first version it is targeted on the analysis of mid-F-G dwarfs, but is meant to evolve to analyze any type of single stars.
Methods. SPADES relies on a line-by-line modeling to determine the stellar parameters.
Results. The internal systematic and random errors of SPADES were assessed by Monte Carlo method simulations with synthetic spectra and the external systematic errors by analysing real ground-based observed spectra. For example, by simulating the Giraffe setups HR13 and HR14B with synthetic spectra for a dwarf with K, , dex and with a signal-to-noise ratio (S/N) of 100, the stellar parameters are recovered with no significant bias and with 1-σ precisions of 8 K for Teff, 0.05 for log g, 0.009 for [Fe/H] , 0.003 for [Ti/Fe] and 0.01 for [Ni/Fe] .
Key words: methods: data analysis / techniques: spectroscopic / stars: fundamental parameters / stars: abundances
© ESO, 2012
1. Introduction
The present and future large spectroscopic surveys are going to significantly increase the number of spectroscopic data to be analyzed. A few examples are RAVE with some 250 000 stars observed so far (Boeche et al. 2011; Siebert et al. 2011), the Gaia-ESO Survey with about 105 stars to be observed, Gaia with about 200 million stars (Katz et al. 2004; Katz 2009). To analyze these quantities of data, automatic spectra analysis softwares are needed.
The development of automated spectra analysis software can be traced back to the early 1990s. Since then, many programs were developed based on a wide variety of methods: e.g.orthogonal vector projection (Cayrel et al. 1991; Perrin et al. 1995), minimum distance method, e.g. TGMET (Katz et al. 1998; Soubiran et al. 2003), and ETOILE (Katz 2001), artificial neural networks (Bailer-Jones 2000; Allende Prieto et al. 2000), feature fitting softwares such as Abbo (Bonifacio & Caffau 2003), projection vector softwares such as MATISSE (Recio-Blanco et al. 2006; Bijaoui et al. 2008), principal component analysis softwares such as MAχ (Jofré et al. 2010), and forward modeling algorithm ILIUM (Bailer-Jones 2010). One can also cite DAOSPEC (Stetson & Pancino 2008, 2010) and FITLINE (François et al. 2003), which automatically measure equivalent widths. DAOSPEC and FITLINE are not automated per-say parameter determination softwares, but coupled with programs that derive atmospheric parameters from equivalent widths, they are used by many astronomers to automatically parameterize stars.
The work presented here describes the development of a new automatic stellar spectra analysis software. This is based on line-by-line analysis. The reference lines are modeled. One of the motivations to develop SPADES (Stellar PArameters DEtermination Software) is the analysis of a set of 200 Giraffe HR13 and HR14 spectra, mainly F-G dwarfs, that were collected in the context of a study of the structure of the Galactic disk. Therefore, the first version of SPADES is illustrated and tested with simulated Giraffe-like spectra of mid-F-G dwarfs. SPADES is coded with Java.
SPADES is described in Sect. 2. It relies on auxiliary data: a line list and a grid of reference spectra. They are presented in Sect. 3. The performances of SPADES were evaluated by Monte Carlo method simulations against synthetic spectra and by comparison to observed spectra of the Sun, ν And, β Vir, μ Her, and σ Dra (see Sect. 4).
2. SPADES
2.1. General concept
SPADES automatically determine: the radial velocity (Vr), the effective temperature (Teff), the surface gravity (log g), the metallicity ( [Fe/H] ), and individual abundances ( [X/Fe] for the element X) for single stars. This first version of SPADES is focused on mid-F-G dwarfs and the micro-turbulence is set to 1 km s-1.
Many of existing automatic spectra analysis softwares uses global methods, meaning they process all pixels of the studied spectrum (Katz et al. 1998; Katz 2001; Soubiran et al. 2003; Recio-Blanco et al. 2006). With SPADES we aimed to explore another possibility, which is the line-by-line analysis. Each parameter is determined using a pre-defined set of lines. The merits of this technique are, first, the possibility to select lines that are particularly sensitive to the stellar parameter to be determined, and second, this allows one to exclude lines that are not correctly modeled. A drawback is that only a fraction of the total available information is used.
Often, whether automated or manual, methods using a line-by-line analysis rely on equivalent width measurement and use a curve-of-growth analysis. We chose to rely on synthetic spectra modeling and profile fitting. The motivation is twofold. First, this takes care of small blend problems. Assuming that the blend is correctly modeled, its contribution to the observation and to the modeled profile will (partly) cancel out. Second, some parameters can be derived by line profile fitting, e.g. Teff from the wings of the Balmer lines. A drawback of this method is the need for a very large library of synthetic spectra. Reading and processing many synthetic spectra is computationally demanding and therefore the analysis is slower.
In the line-by-line analysis the accuracy and precision of the results is very sensitive to the determination of the continuum or pseudo-continuum. Yet, this is often difficult particularly in cool and/or super metal-rich stars. SPADES determines “local” continuum from the comparison of the reference (synthetic) spectra and the studied spectrum (see Sect. 2.5.3).
As opposed to mean metallicities, SPADES determines iron and individual elements abundances. To derive of the individual abundances SPADES calculates on-the-fly atmospheric models and synthetic spectra for the values of Teff, log g, [Fe/H] it had determined (see Sect. 2.6).
SPADES can simultaneously analyze various spectral domains (possibly with different resolving powers) of the same target, e.g. different Giraffe setups, or different orders of an echelle spectrograph, or even spectral domains collected with different spectrographs.
2.2. Processing overview
A SPADES analysis proceeds in three steps: it first determines the radial velocity, then the atmospheric parameters, and finally it determines the individual abundances.
The radial velocity is determined by cross-correlation with a synthetic template (see Sect. 2.4).
The three atmospheric parameters (effective temperature, surface gravity, iron over hydrogen ratio) are determined independently (see Sect. 2.5). Currently, each parameter is associated to one diagnostics. SPADES was conceived to aggregate more diagnostics along its life span and more will be added in the future Current diagnostics are
-
effective temperature: Balmer line wings fitting (suited forTeff derivation in F-G dwarfs);
-
surface gravity: ionization equilibrium;
-
iron abundance: neutral iron line profile fitting.
The individual abundances are determined element per element by line profile fitting.
The reader will notice that some of these diagnostics are similar to those used in the so-called “detailed analysis”. Two differences should be emphasized: (i) SPADES relies on profile fitting and modeling rather than equivalent width measurement; and (ii) the SPADES precision is not limited by the step in the grid of atmospheric models and spectra (see Sect. 2.5.1).
2.3. Pre-processing
Each of the three processing steps includes pre-processing tasks. Pre-processing a spectrum includes shifting to rest frame, excluding cosmics, excluding telluric lines, convolving the synthetic spectrum to the resolving power of the ground-based observed spectrum, normalizing to continuum and excluding possible unexposed edges of the spectrum. Every functionality remains an option: it can be switched on and off in the configuration file by the user.
Shifting to rest frame is performed by using either a radial velocity provided by the user or that determined by SPADES (see Sect. 2.4).
The exclusion of cosmics is performed by detecting the fluxes that lie significantly above the continuum and replacing their value by interpolation with the neighboring pixels.
The wavelengths of the telluric lines were pre-tabulated. These lines are not cut. Their pixels are simply flagged as not valid and are excluded from all subsequent analysis.
The spectral resolution of the synthetic spectra should be matched to the resolution of the ground-based observed spectrum. To do so, the reference spectra are convolved using a Gaussian profile (valid for slow rotators).
 |
Fig. 1 Observed Giraffe/VLT (HR14B setup) Sun spectrum before normalization, with the polynomial fit shown as a thick blue line (top) and after normalization (bottom). |
The synthetic spectra are already normalized to continuum. The studied spectrum is iteratively fitted with a polynomial function, using a sigma-clipping technique to exclude the lines and cosmic rays from the fit. The degree of the polynomial is defined by the user, depending on the large-scale shape of the spectrum. The studied spectrum is normalized to 1 at the level of the continuum by division by the polynomial. Figure 1 presents an observed Giraffe/VLT (HR14 setup) Sun spectrum before normalization, with the polynomial shown as a thick blue line (top) and after normalization (bottom).
Edge exclusion is necessary if the ground-based observed spectrum suffers from underexposed or unexposed pixels. SPADES can automatically detect and flag as not valid the underexposed/unexposed pixels.
2.4. First step: radial velocity
The radial velocity determination is based on a cross-correlation of the studied spectrum and a synthetic template spectrum.
The atmospheric parameters of the template spectrum are chosen by the user. At this stage in the processing, SPADES has not yet provided estimates for the atmospheric parameters of the studied source. If no external information is available to guide the choice of the template, it is likely that there will be a mismatch between the ground-based observed spectrum and the selected template. Monte Carlo method simulations were performed to assess the impact of selecting a template 400 K and 1000 K warmer than the studied spectrum. The tests were conducted with 200 S/N = 50 synthetic studied spectra of solar parameters. In both cases (400 and 1000 K offsets), the mismatch leads to a bias of about 0.2 km s-1 and no significant change in the precision of the estimated radial velocities (see Table 1). A bias of 0.2 km s-1 represents about 1/60th of the full width at half maximum (FWHM) and has a negligible impact on the following steps of the analysis. If, a posteriori, the parameters estimated by SPADES and those of the selected template are significantly different, the radial velocity can be re-estimated with a better matching template.
The studied and the template spectrum are pre-processed. The reference spectrum is then shifted step by step in radial velocity over an interval defined by the user. In the tests, we used an interval of −500 to 500 km s-1. At each step, the synthetic spectrum is re-sampled to the same sampling as the studied spectrum. At each step, the correlation coefficient of the two spectra is calculated: 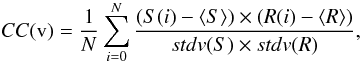 (1)where v is the velocity shift applied to the template spectrum, N is the number of valid pixels in the studied spectrum, S (resp. R) the studied (resp. reference) spectrum counts, ⟨ S ⟩ (resp. ⟨ R ⟩ ) the mean studied spectrum (resp. reference) counts, and stdv the standard deviation:
(1)where v is the velocity shift applied to the template spectrum, N is the number of valid pixels in the studied spectrum, S (resp. R) the studied (resp. reference) spectrum counts, ⟨ S ⟩ (resp. ⟨ R ⟩ ) the mean studied spectrum (resp. reference) counts, and stdv the standard deviation: 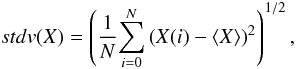 (2)the correlation coefficients as a function of the radial velocity shifts form the cross-correlation function. Figure 2 shows the cross-correlation function obtained for a synthetic studied spectrum of solar parameters (Teff = 5777 K, log g = 4.44 and [Fe/H] = 0.0 dex) and S/N = 100 (Poisson noise) and a noiseless synthetic template with the same atmospheric parameters.
(2)the correlation coefficients as a function of the radial velocity shifts form the cross-correlation function. Figure 2 shows the cross-correlation function obtained for a synthetic studied spectrum of solar parameters (Teff = 5777 K, log g = 4.44 and [Fe/H] = 0.0 dex) and S/N = 100 (Poisson noise) and a noiseless synthetic template with the same atmospheric parameters.
 |
Fig. 2 Correlation function for a synthetic studied spectrum of solar parameters (Teff = 5777 K, log g = 4.44 and [Fe/H] = 0.0 dex) and S/N = 100 (Poisson noise) and a noiseless synthetic template with the same atmospheric parameters. |
The radial velocity of the observed source corresponds to the maximum of the correlation function. The maximum is derived in two steps. First, the highest correlation coefficient is found and then a second-degree polynomial is adjusted to the correlation function in the vicinity of the highest coefficient. This allows one to estimate the radial velocity with a precision better than the step used to shift the template.
The error on the radial velocity determination, σVr is estimated with the Zucker (2003) formula: ![\begin{equation} \sigma_{V_r}^2 = - \left[ {N\times\frac{C''(m)}{C(m)}\frac{{C(m)}^2}{1-{C(m)}^2}} \right] ^{-1}, \end{equation}](/articles/aa/full_html/2012/08/aa19417-12/aa19417-12-eq24.png) (3)where C(m) is the value of the correlation function at its maximum, C′′(s) the value of the second derivative of the correlation function at the maximum of the correlation function and N the number of valid1 pixels in the ground-based observed spectrum.
(3)where C(m) is the value of the correlation function at its maximum, C′′(s) the value of the second derivative of the correlation function at the maximum of the correlation function and N the number of valid1 pixels in the ground-based observed spectrum.
The performances of the radial velocity estimation of the radial velocity were assessed with a Monte Carlo method. For three S/N: 30, 50 and 100, Giraffe HR13 and HR14B spectra were simulated (200 per S/N) by injecting a synthetic spectrum with Poisson noise. The synthetic spectrum was a solar-like spectrum in the rest frame. The same spectrum, but noiseless, was used as template. Table 1 presents the median and dispersion of the distributions of radial velocities derived by SPADES for each S/N. Because the true radial velocity of the studied spectra is 0 km s-1, the median of a distribution is an estimate of the systematic error and the dispersion an estimate of the random error.
Median and dispersion (in km s-1) of the radial velocity distribution derived by SPADES for 200 studied spectra for S/N 30, 50 and 100.
2.5. Second step: stellar parameter determination
2.5.1. Overview
SPADES determines the effective temperature (Teff), the surface gravity (log g), and the iron abundance ( [Fe/H] ). In this first version targeted on mid-F-G dwarfs, we assumed a micro-turbulence of 1 km s-1 for all our stars, including the tests with the observed spectra.
The determination of the atmospheric parameters is iterative. Initial values for the three parameters are provided either by the user or by SPADES (see Sect. 2.5.2). Each parameter is determined independently of the two others, leaving these two at their initial values. At the beginning of a new iteration, the values of the three parameters are updated, therefore providing new “initial” values. This is repeated until the convergence condition is met: i.e. absolute differences between the parameters obtained at iteration n and n − 1 all simultaneously lower than 10 K for Teff, 0.1 for log g, and 0.025 for [Fe/H] . The iterative approach was chosen over a direct approach (e.g. scanning the whole grid of 2000 reference spectra over all parameters at once), because it was computationally faster. Yet, the iterative approach could potentially be more complex in terms of convergence. The convergence performances of SPADES are assessed in Sect. 4.3.
At any iteration, the estimation of each parameter follows the same logic: SPADES first calculates a 1D grid of synthetic spectra, varying only along the parameter that is estimated. This 1D-subgrid is calculated from the large grid of synthetic spectra described in Sect. 3.1. The grid is linearly interpolated to the fixed values of the other parameters. As an example, at the start of iteration n, the starting values for the atmospheric parameters derived from iteration n − 1 are K, , and . The first parameter to be determined in iteration n is Teff. A 1D-subgrid is linearly interpolated for Teff ranging from 5200 to 6200 K by step of 200 K and and dex.
Each synthetic spectrum is then compared (not globally, but the selected lines) to the ground-based observed spectrum according to the diagnostic appropriate for the parameters to be determined. As an example for Teff, the Hα profile of the ground-based observed spectrum will be compared to that of each synthetic spectrum.
The result of the comparison is a similarity indicator for each node in the 1D-subgrid. This series of similarity indicators as a function of the parameter to be determined form a function that is analyzed (minimized or nulled, depending on the function) for the best similarity value, leading to the best estimate of the parameter to be determined. Interpolation or polynomial fit allows one to determine the parameter with a precision that is not limited by the step of the 1D-subgrid.
SPADES is iteratively searching for the best matching synthetic spectrum in a 3D space (Teff, log g and [Fe/H] ). In this first version of SPADES, the search is split in three 1D minimizations, rather than using a multi-dimensional search method. The motivation is that this facilitates visualizing and interpreting the residuals and similarity functions (see e.g. Fig. 5) that depend on a single parameter. In future versions, it would be interesting to experiment with multi-dimensional minimization algorithms such as Gauss-Newton, gradient, or Levenberg-Marquardt methods.
2.5.2. Starting parameters
SPADES proceeds iteratively to derive the atmospheric parameters. It therefore needs starting values for the effective temperature, surface gravity, and iron over hydrogen ratio prior to the first iteration. Those can be deduced from photometric or bibliographic information if available.
If no external information is available, SPADES offers the possibility to perform a first parameterization of the studied source, using the TGMET/ETOILE method (Katz et al. 1998; Katz 2001; Soubiran et al. 2003). The results of this first analysis are used as starting values for the iterative parameterization with SPADES.
The TGMET/ETOILE method is direct (not iterative). It compares a studied spectrum to a library of reference spectra, looking for those most similar in the least-squares-sense. The parameters deduced for the studied spectrum could either be the parameters of the most similar spectrum or a combination of the parameters of the most similar spectra. Because SPADES is only looking for starting values, it simply adopts the parameters of the most similar spectrum.
The performances of the SPADES implementation of the TGMET/ETOILE method (hereafter referred to as SPADES-TE) were assessed with a Monte Carlo method method. Starting from a synthetic spectrum with Teff = 5800 K, log g = 4.5, [Fe/H] = −1 dex (which is a node of the grid of synthetic spectra), three series of 200 studied spectra each were simulated for S/N = 100, 50 and 30, respectively, and the resolving power and wavelength range of the Giraffe HR13 and HR14B setups. At S/N = 50 and 100, the correct node in the grid is recovered in 100% of the cases. At S/N = 30, SPADES-TE returns most of the time a solution biased by one grid step in Teff (i.e. +200 K) and two grid steps in [Fe/H] (i.e. +0.4 dex).
SPADES-TE was also tested on a Sun spectrum observed with Giraffe HR13 and HR14B setups in twilight conditions. SPADES-TE found Teff = 5800 K, log g = 3.5 and [Fe/H] = −0.2 dex, to be compared to the canonical parameters for the Sun Teff = 5777 K, log g = 4.44, and [Fe/H] = 0 dex.
We recall that the version of SPADES presented here is limited by the GRID of synthetic spectra and by the list of reference lines to the mid-F-G dwarf stars. Future versions of the program will rely on larger grid(s) and on several fine-tuned line lists, which will extend the scope of SPADES.
 |
Fig. 3 Two examples: (i) pixel identification in the reference line (green crosses), (ii) pseudo-continuum selection (blue circles), and (iii) vertical adjustment of the synthetic reference spectrum (red line) to the studied spectrum (black line). In the top plot, the pseudo-continuum area (blue circles) were selected automatically by SPADES and were used for the vertical adjustment. In the bottom plot, no valid pseudo-continuum area was found. The pixels in the line (green crosses) were used for the vertical adjustment. |
2.5.3. Line and continuum identification and vertical adjustment
For each spectral line, the pixels constituting the line are dynamically identified using the synthetic spectra. Using the rest wavelength of the line, SPADES starts from its center and agregates pixels in each wing as long as the value of the signal increases. If less than five pixels are associated to the line, it is considered too weak and rejected from the subsequent analysis. This parameter is adjustable by the user. Figure 3 shows two examples of sets of pixels associated to a line, i.e. green crosses on the figures.
SPADES relies on profiles fitting. This requires adjusting the observed and synthetic spectra on the same vertical scale. It is possible, in the pre-processing, to normalize the overall continuum to 1. This is a global adjustment on the whole spectrum. This is not enough for the comparison of two lines. Therefore, SPADES systematically adjusts locally, line-by-line, the vertical level of the synthetic line to the one of the observed line.
SPADES first identifies flat areas (pseudo-continuum) in the synthetic spectrum in the vicinity of the studied line and selects one on each side of the line. It then checks that these two areas also correspond to pseudo-continuum in the studied spectrum. If the check is positive, it uses these areas to vertically scale the synthetic spectrum on the studied one, by linear regression, i.e. there are two degrees of freedom, vertical scaling, and slope.
If there are no flat areas in the synthetic spectrum or the studied spectrum contains (a) line(s) in the selected pseudo-continuum, another method is used for the vertical adjustement. The method depends on the diagnostic. For all diagnostics relying on the quadratic sum of the residuals (e.g. the iron abundance, Sect. 2.5.6), the pixels in the lines are directly used for the vertical adjustment (allowing here for a single degree of freedom, the vertical scale). For the diagnostic that relies on the the sum of residuals (i.e. the surface gravity, Sect. 2.5.5), SPADES uses pre-tabulated pseudo-continuum.
An exception to this scheme is the Hα line used to derive of the effective temperature, for which the pseudo-continuum and line area are pre-tabulated.
Figure 3 shows the local vertical adjustement of a synthetic spectrum (red) to a studied spectrum (black). In the top plot, the pseudo-continuum area (blue circles) were selected automatically by SPADES and were used for the vertical adjustment of the synthetic reference spectrum (red line) to the studied spectrum (black line). In the bottom plot, no valid pseudo-continuum area was found. The pixels in the line (green crosses) were used for the vertical adjustment.
2.5.4. Effective temperature
In this article, the stars considered are mid-F-G dwarfs, the wings of the Balmer lines are very sensitive to the effective temperature (van’t Veer-Menneret & Megessier 1996; Fuhrmann 1998, 2004, 2008; Barklem et al. 2002; Cayrel et al. 2011). In this study, SPADES used the wings of Hα present in Giraffe setup HR14B to derive the effective temperature. The core of Hα was excluded because it is less sensitive to Teff variation and poorly modeled, specially using 1D LTE models, which is the case here.
As presented in Sect. 2.5.1, a 1D grid of synthetic spectra was calculated, differing only by the effective temperature. After pre-processing and vertical adjustment, each synthetic spectrum was compared to the studied spectrum. For each synthetic spectrum, the degree of similarity of the synthetic Hα wings with the studied one, is calculated as the quadratic sum of the residuals between the pixels in the two lines: 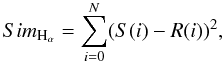 (4)where N is the number of valid pixels in the Hα line, S(i) (resp. R(i) the counts of the studied spectrum (resp. reference spectrum) for pixel i.
(4)where N is the number of valid pixels in the Hα line, S(i) (resp. R(i) the counts of the studied spectrum (resp. reference spectrum) for pixel i.
 |
Fig. 4 Comparison of the Hα wings in the studied spectrum (black line) with the 1D grid of synthetic spectra (red lines) ranging here from 5000 (narrowest wings) to 6600 K (broadest wing). The pseudo-continuum area is labeled with blue dots and the valid pixels in the Hα wings are identified with green crosses. The bottom plot is a zoom on the blue wing. |
 |
Fig. 5 Examples, for a synthetic studied spectrum, of similarity functions as a function of effective temperature (top left), surface gravity (top right), iron over hydrogen ratio (bottom left) and nickel over iron ratio (bottom right). The polynomial (or linear interpolation for the surface gravity) used to minimize the functions are represented as blue lines. |
 |
Fig. 6 ν And similarity functions as a function of effective temperature (top left), surface gravity (top right), iron over hydrogen ratio (bottom left), and nickel over iron ratio (bottom right). The polynomial (or linear interpolation for the surface gravity) used to minimize the functions are represented as blue lines. |
Figure 4 shows the comparison of the Hα wings in the studied spectrum (black line) with the 1D grid of synthetic spectra (red lines) ranging here from 5000 (narrowest wings) to 6600 K (broadest wing). The pseudo-continuum area is labeled with blue dots and the valid pixels in the Hα wings are identified with green crosses. The bottom plot is a zoom on the blue wing.
The degrees of similarity versus the effective temperature define a function that is minimum for the effective temperature of the studied source. The minimum is found by fitting a second-degree polynomial around the lowest similarity value. The top left plots in Figs. 5 and 6 give examples of similarity functions as a function of effective temperature, for a synthetic spectrum and for the ground-based observed spectrum of ν And respectively. Each synthetic spectrum in the 1D subgrid corresponds to a red dot. The second-degree polynomial fitted to the similarity function to minimize it is represented as a blue line.
The similarity functions for the synthetic spectra and ν And show similar degrees of regularity and smoothness. The first reason is that the spectrum of ν And has a good S/N. The second reason is that in each point (red dots) the similarity functions derives from the comparison of the same noisy studied spectrum with different noiseless synthetic spectra. The noises on the points of a similarity function are correlated. The noise in the studied spectrum and the systematic differences between the studied and synthetic spectra propagate to the similarity functions, not so much as fluctuation and irregularities in the functions, but as a vertical and horizontal shift and as a flattening of the curvature of the functions.
2.5.5. Surface gravity by ionization equilibrium
The ionization equilibrium method is based on the fact that the abundances determined from lines of the same element, but with different ionization stages, should be the same. Building on this idea, SPADES simultaneously models Fe lines in two ionization stages: FeI and FeII.
Similarly as for Teff, a 1D grid of synthetic spectra, differing only by the surface gravity (this time) was calculated. For each a “degree of ionization equilibrium” (hereafter refered to as “gravity similarity”) is calculated as 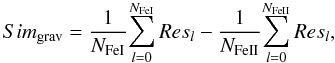 (5)where NFeI (resp. NFeII) are the numbers of FeI (resp. FeII) lines used and Ri the count residuals for the line l:
(5)where NFeI (resp. NFeII) are the numbers of FeI (resp. FeII) lines used and Ri the count residuals for the line l: 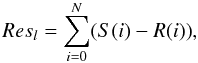 (6)where N is the number of valid pixels in the line, S(i) (resp. R(i) the count of the studied spectrum (resp. reference spectrum) for pixel i.
(6)where N is the number of valid pixels in the line, S(i) (resp. R(i) the count of the studied spectrum (resp. reference spectrum) for pixel i.
Figure 7 shows an FeI line (top, green crosses) and an FeII line (bottom, green crosses), used by SPADES to determine of log g. The studied spectrum (log g = 4.5) is denoted in black and the red lines are the synthetic reference spectra of the 1D subgrid ranging from log g = 2.0 to log g = 5.0 by steps of 0.5. The neutral iron line is alsmost insensitive to gravity, while the singly ionized iron line becomes stronger for decreasing gravities.
 |
Fig. 7 FeI line (top, green crosses) and an FeII line (bottom, green crosses), used by SPADES to determine log g. The studied spectrum (log g= 4.5) is given in black and the red lines are the synthetic reference spectra of the 1D subgrid ranging from log g= 2.0 to 5.0 by step of 0.5. |
The gravity similarity, as defined above, should be null for the surface gravity of the studied source. The zero of the gravity similarity function is found by interpolation. The top right plots in Figs. 5 and 6 give an example of similarity functions as a function of surface gravity. Each synthetic spectrum in the 1D subgrid corresponds to a red dot. The linear interpolation used to find the gravity corresponding to the zero gravity similarity is represented as a blue line.
2.5.6. iron over hydrogen ratio
The [Fe/H] determination is based on a global FeI line profile fitting. For the other parameters, a 1D grid of synthetic spectra, differing only by the iron abundance, was calculated. For each synthetic spectrum, the global similarity between all synthetic neutral iron lines and all observed neutral iron lines is derived as 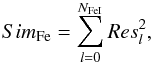 (7)where NFeI is the number of neutral iron lines in the list of reference lines,
(7)where NFeI is the number of neutral iron lines in the list of reference lines, 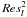 is the square of the count residuals for line l, given by formula (6).
is the square of the count residuals for line l, given by formula (6).
The iron content of the source corresponds to the minimum similarity degree. It is found by adjusting a third-degree polynomial through the “iron similarity function”. A third-degree polynomial is preferred over a second-degree polynomial, because the “iron similarity function” is usually asymmetric: steeper on the metal-rich side than on the metal-poor side. The bottom left plots in Figs. 5 and 6 give an example of similarity functions as a function of the iron over hydrogen ratio. Each synthetic spectrum in the 1D subgrid corresponds to a red dot. The third-degree polynomial fitted to the similarity function to minimize it is represented as a blue line.
2.6. Third step: individual abundances
Once the iterative determination of the three atmospheric parameters has converged, the individual abundances are determined. The general principle is very similar to the determination of the iron content, except that the determination is direct and not within an iterative loop with several other parameters.
Each element was determined individually, using a different pre-defined list of lines. The difference with the [Fe/H] determination method is that for each element, the 1D grid was calculated on-the-fly for the Teff, log g, and [Fe/H] determined by SPADES and varying only by the abundance of the element to be determined. SPADES interpolates on-the-fly the input files for the Kurucz programs (e.g. the opacity distribution functions – ODF, Castelli & Kurucz 2004) and calls Kurucz ATLAS9 (Kurucz 2005) to calculate the atmospheric models and Kurucz SYNTHE (Kurucz 2005) to compute the synthetic spectra. The GNU-Linux ported versions of ATLAS9 and SYNTHE were used (Sbordone et al. 2004; Sbordone 2005).
Element per element, for each synthetic spectrum the global similarity between all synthetic lines and all observed lines of the element X is derived as 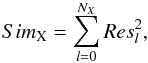 (8)where NX is the number of lines of the element X in the list of reference lines and
(8)where NX is the number of lines of the element X in the list of reference lines and  is the square of the count residuals for line l, given by formula (6).
is the square of the count residuals for line l, given by formula (6).
The abundance of the element X corresponds to the minimal similarity degree. It is found by adjusting a third-degree polynomial through the element X similarity function. The bottom right plots in Figs. 5 and 6 give an example of similarity functions as a function of nickel over iron ratio. Each synthetic spectrum in the 1D subgrid corresponds to a red dot. The third-degree polynomial fitted to the similarity function to minimize it is represented as a blue line.
3. Auxiliary data
3.1. Reference grid of models and synthetic spectra
The unidimensional reference grids used to derive the stellar parameters are calculated by SPADES by interpolation using a pre-calculated grid. Models and synthetic spectra were calculated using the Kurucz programs ATLAS9 and SYNTHE (Kurucz 2005) ported to GNU-Linux (Sbordone et al. 2004; Sbordone 2005). About 2000 models and spectra were generated over the following range of parameters:
-
Effective temperature: Teff from 4800 to 6800 Kwith a step of 200 K.
-
Surface gravity: log g from 2.0 to 5.5 with a step of 0.5.
-
iron abundance: [Fe/H] from − 3.0 to 1.0 dex with a step of 0.20 dex.
-
Microturbulence: ξ = 1 km s-1.
The models were calculated with the overshooting option switched off and l/Hp = 1.25. The convergence of each model was checked. The spectra were calculated for the spectral domain ranging from 600 to 680 nm, corresponding to the Giraffe/VLT HR13 and HR14 setups and a resolving power R = 300 000 (SPADES convolves and re-samples the synthetic spectra to the resolving power(s) of the studied spectrum).
3.2. List of reference lines
The reference lines used to derive the surface gravity, iron abundance, and individual abundances were extracted from the line list of Bensby et al. (2003). We note that the astrophysical oscillator strengths provided by Bensby et al. (2003) were not used in calculating of the synthetic spectra (see Sect. 3.1). For consistency, we used the Kurucz oscillator strengths for all lines (reference or not).
4. Performance assessment
To assess the performances of SPADES, three series of tests were performed.
The aim of the first series was to assess the internal systematic and random errors obtained as a function of the S/N, but independently of the question of the initialization parameters. We also investigated the correlations between the errors on the different parameters.
In the second tests, high S/N ground-based observed spectra were analyzed with SPADES to assess the external errors.
SPADES proceeds iteratively to derive the atmospheric parameters. The third series of tests aims to assess the convergence properties of SPADES when it is initialized with parameters that are significantly off the true values.
All tests were performed for the wavelength range and the resolving power of the HR13 (R = 22 500) and HR14B (R = 28 000) Giraffe setups. The three series of tests are presented below.
Medians and dispersions of the distributions of residuals, i.e. estimated minus true, on Teff, log g, [Fe/H] , [Ti/Fe] and [Ni/Fe] derived by SPADES for the S/N: 100, 50 and 30.
4.1. Internal errors
The internal systematic and random errors were assessed by Monte Carlo method. Starting from a synthetic spectrum from the reference grid with Teff = 5800 K, log g = 4.5, [Fe/H] = 0.0 dex, ξ = 1 km s-1 and solar abundance scale, three series of 200 noisy spectra were generated for S/N 30, 50 and 100. The noise was injected following a Poisson distribution. The 600 spectra were analyzed with SPADES to estimate their Teff, log g, [Fe/H] as well as [Ti/Fe] and [Ni/Fe] ratios as examples of abundance ratios estimates. In this first test, SPADES was initialized with the true parameters of the synthetic spectra. Table 2 presents the medians and dispersions of the distributions of residuals, i.e. estimated minus true, of the parameters derived by SPADES for each S/N. Figure 8 shows the distributions of Teff, log g, [Fe/H] , and [Ni/Fe] estimated by SPADES for the 200 S/N = 50 spectra.
The distributions of temperature and gravity residuals present no significant biases. The systematic errors on the iron over hydrogen and titanium and nickel over iron ratios are of about a few milli-dex and are most of the time one order of magnitude smaller than the random errors. The random errors are small, e.g. at S/N = 30: less than 30 K for Teff, 0.15 for log g and a few hundredths of dex for the abundance ratios. we emphasize that these are internal errors accounting only for photon noise. External errors are assessed in Sect. 4.2.
 |
Fig. 8 Distributions of the Teff (top left), log g (top right), [Fe/H] (bottom left) and [Ni/Fe] (bottom right), estimated by SPADES for 200 S/N = 50 simulated HR13 and HR14B Giraffe spectra. The true parameters are Teff = 5800 K, log g = 4.5, [Fe/H] = 0.0 dex, and [Ni/Fe] = 0.0 dex. |
Figure 9 presents the estimate by SPADES of Teff, log g, and [Fe/H] versus each other for the 200 stars with S/N = 100 (top), S/N = 50 (middle), and S/N = 30 (bottom). The clearer error correlation is between the effective temperature and the iron abundance: an error of − 50 K corresponds to an error of about − 0.075 dex. This correlation, as the others, is intrinsic to the physics of the stellar atmopsheres. While Hα is weakly sensitive to metallicity (van’t Veer-Menneret & Megessier 1996), the equivalent width of the iron lines is sensitive to the effective temperature.
 |
Fig. 9 SPADES estimate of Teff, log g, and [Fe/H] versus each others for the 200 stars with S/N = 100 (top), S/N = 50 (middle), and S/N = 30 (bottom). |
4.2. External errors: ground-based observed spectra
The first series of tests was devoted to internal errors. The source of noise was Poissonian photon noise. The aim of the second series was to assess the external systematic errors. There are several possible sources of external systematics. In particular, the physics of the stellar atmospheres do not reproduce the reality perfectly (e.g. discrepant oscillator strengths, local thermodynamical Equilibrium assumption, 1D modeling of the atmosphere), there are usually instrumental calibration residuals (e.g. from bias, flat-field, possibly fringing, etc.) and residuals from the observing conditions (e.g. from sky-subtraction).
4.2.1. The Giraffe solar spectrum
To investigate these problems, we retrieved from the Giraffe archive (Royer et al. 2005, 2008) the high S/N HR13 (R = 22 500) and HR14B (R = 28 000) observed solar spectrum. The Giraffe solar spectrum was acquired in twilight conditions, which could alter the equivalent widths (Molaro et al. 2008). Moreover, the library of reference spectra used by SPADES was calulated with the Kurucz oscillator strengths (log gf), not with astrophysical log gf, even for the reference lines used by the different diagnostics. We therefore proceeded in two steps to analyze the Giraffe solar spectrum. First the effective temperature and surface gravity were fixed to their bibliographic values, i.e. K and , and only the iron over hydrogen and titanium and nickel over iron ratios were determined by SPADES. Then, in a second step, the solar spectrum was re-analyzed, this time requesting SPADES to determine the five parameters Teff, log g, [Fe/H] , [Ti/Fe] , and [Ni/Fe] .
Table 3 lists the iron over hydrogen and titanium and nickel over iron ratios derived by SPADES when the effective temperature and surface gravity were fixed to their bibliographic values K and . The iron over hydrogen and titanium over iron ratios are underestimated by − 0.08 and − 0.09 dex respectively, while the nickel over iron ratio is close to the true value.
 |
Fig. 10 Zoom on the red wing of the Hα line from the Giraffe HR14B solar spectrum (black line). Two synthetic spectra are overplotted: in red a synthetic spectrum with Teff = 5689 K and in blue Teff = 5777 K (the values of the other parameters are those of the Sun: log g = 4.44 and [Fe/H] = 0.0 dex). |
iron over hydrogen and titanium and nickel over iron ratios derived by SPADES for a solar HR13 and HR14B solar spectrum, when the effective temperature and surface gravity were fixed to their bibliographic values K and .
The solar spectrum was then re-analyzed, requesting SPADES to also determine Teff and log g. SPADES was initialized with the bibliographic parameters Sun and converged in five iterations. Table 4 presents the parameters obtained by SPADES for the Giraffe solar spectrum.
Effective temperature, surface gravity, iron over hydrogen and titanium and nickel over iron ratios derived by SPADES for the Giraffe HR13 and HR14B solar spectra.
The effective temperature derived by SPADES, 5689 K, is 88 K lower than the bibliographic temperature Teff = 5777 K. Figure 10 shows a zoom on the red wing of the Hα line from the Giraffe HR14B solar spectrum (black line). Two synthetic spectra are overplotted: in red a synthetic spectrum with Teff = 5689 K and in blue Teff = 5777 K (the values of the other parameters are those of the Sun: log g = 4.44 and [Fe/H] = 0.0 dex). The red spectrum (Teff = 5689 K) agrees much better agreement with the Giraffe solar spectrum than the blue spectrum (Teff = 5777 K).
The surface gravity derived by SPADES, log g = 4.46 is consistent with the Sun’s gravity log g = 4.44.
The iron to hydrogen ratio derived by SPADES is underestimated by − 0.18 dex with respect to the Sun. There are two main origins for this offset. On the one hand, there is the offset of − 0.08 dex reported in Table 3 that is likely due to the modeling of the spectra, in particular slightly discrepant oscillator strengths, and also to possible equivalent width alterations due to twilight observing, as reported by Molaro et al. (2008). On the other hand, as discussed in Sect. 4.1, the error on the effective temperature propagates into an error on the iron abundance. The offset of − 88 K here propagates into an offset of − 0.1 dex.
The titanium and nickel over iron ratios derived when Teff and log g are determined by SPADES are similar to those obtained when Teff and log g were fixed to their bibliographic values. The reason is that the iron, titanium and nickel abundances are all similarly affected by the − 88 K offset and therefore the effect partly canceled out in the logarithmic ratios of titanium over iron and nickel over iron.
4.2.2. S4N reference spectra
The parameters of the Sun are very accurately known, which makes it a natural target to assess the performances of SPADES. On the other hand, Molaro et al. (2008) reported an alteration of the equivalent widths of the lines in the Giraffe solar spectrum, which was acquired in twilight conditions.
Bibliographic parameters and parameters derived by SPADES for the five test stars.
To further test the performances of SPADES with a ground-based observed spectrum, we selected 5 stars, the Sun, ν And (HD9826), β Vir (HD 102870), μ Her (HD 161797) and σ Dra (HD 185144) in Cayrel et al. (2011). The authors derived the effective temperatures of their stars from angular diameters measured with interferometry. All their stars have diameters known to 2% or better, leading to an accuracy on the effective temperatures of about 25 K. All stars are bright and were extensively studied. Cayrel et al. (2011) adopted for log g and [Fe/H] recent determinations from the PASTEL catalog (Soubiran et al. 2010). We proceeded similarly, adopting for log g and [Fe/H] the median over the five most recent determinations contained in PASTEL. The titanium and nickel over iron ratios were extracted from Valenti & Fischer (2005). The spectra for the five stars were retrieved from the S4N library (Allende Prieto et al. 2004). They were degraded in resolving power and in sampling and restricted in wavelength to the Giraffe HR13 and HR14B setups.
SPADES converged in two (ν And) to four (μ Her and σ Dra) iterations. Table 5 lists the bibliographic parameters and the parameters derived by SPADES for the five tests stars. Figure 11 displays the temperatures, gravities, iron over hydrogen and nickel over iron ratios estimated by SPADES versus their bibliographic values. Table 6 presents the mean and dispersion of the residuals (SPADES minus bibliographic) on the estimation of the atmospheric parameters as well as the titanium and nickel over iron ratios.
 |
Fig. 11 Temperatures (top left), gravities (top right), iron over hydrogen (bottom left), and nickel over iron ratios (bottom right) estimated by SPADES versus their bibliographic values. |
Means and dispersions of the residuals (SPADES minus bibliographic) on the estimation of the atmospheric parameters as well as the titanium and nickel over iron ratios.
On average, the effective temperature is recovered with a bias of +46 K. For the same stars, Cayrel et al. (2011) found a bias of similar amplitude, but with the opposite sign, of about −90 K. In addition to the small statistics and the details of the Hα profile fiting, we note that the physics used to compute the grids of models and synthetic spectra differ in several aspects. SPADES relies on Kurucz ATLAS9 models computed with the mixing length parameter l/Hp = 1.25 and SYNTHE spectra (see Sect. 3.1). Cayrel et al. (2011) used the Kurucz ATLAS9 models with l/Hp = 0.5 and a modified version of the Kurucz BALMER9 with the Stark broadening treatment of Stehlé & Hutcheon (1999) and impact broadening by neutral hydrogen collisions of Allard et al. (2008).
The iron over hydrogen and nickel over iron ratios are recovered without significant offsets. The titanium over iron ratio, determined from four Ti lines (without astrophysical log gf adjustement), presents an offset of − 0.05 dex. To the limit of the small statistics, the error on Teff shows no trend with Teff.
4.3. Convergence properties
4.3.1. First test
SPADES proceeds iteratively to derive the atmospheric parameters Teff, log g, and [Fe/H] . In the first series of tests, SPADES was initialized with the true parameters. Of course, in reality, the true parameters are unknown. The aim of this third series of tests is to assess the behavior of SPADES when it is initialized with parameters that are significantly different from the true values.
For this third test, 34 single stars were generated. Their parameters were randomly drawn following uniform distributions over the following intervals: Teff in [5200,6400] K, log g in [3.0,4.5], and [Fe/H] in [−2.0,0.6] dex. No star was simulated for [Fe/H] below −2.0, because the four Fe II lines present in the Giraffe HR13 and HR14B become too weak to allow derivating the surface gravity. This is illustrated in the top right plot of Fig. 12, which shows three synthetic spectra of metallicity [Fe/H] = 0.0 dex (blue), [Fe/H] = −1.0 dex (red), [Fe/H] = −2.0 dex (black). The line at 6456.39 Å is an Fe II line. At [Fe/H] = −2.0 dex, the line is barely visible.
 |
Fig. 12 Extract of three synthetic spectra of metallicity [Fe/H] = 0.0 dex (blue), [Fe/H] = −1.0 dex (red), [Fe/H] = −2.0 dex (black), showing the influence of the metallicity on an Fe I line (top left), an Fe II line at 6456.39 Å (top right), a Ni I line (bottom left) and a Ti I line at 6258.11 Å (bottom right). |
For each of the 34 single stars, three noisy HR13 and HR14B Giraffe spectra were simulated for S/N of 30, 50 and 100. The noise was Poissonian photon noise. The three series of 34 spectra were analyzed by SPADES. In all 102 cases SPADES was initialized with the same parameters: Teff = 5800 K, log g = 3.0 and [Fe/H] = −1.0 dex. The left side of Fig. 13 presents the differences between the true parameters of the 34 synthetic stars and the initialization parameters: Teff (top), log g (middle) and [Fe/H] (bottom).
 |
Fig. 13 Left: differences between the true parameters of the 34 synthetic stars and the initialization parameters: Teff (top), log g (middle) and [Fe/H] (bottom). Right: distributions of Teff (top), log g (middle) and [Fe/H] (bottom) residuals for S/N = 50. |
Medians and dispersions of the distributions of Teff, log g, and [Fe/H] residuals, i.e. estimated minus true, derived by SPADES for the S/N 100, 50 and 30.
SPADES converged for 33 out of the 34 stars in at most six iterations (for all S/N). It did not converge for one star with the parameters: Teff = 5386 K, log g = 4.3, and [Fe/H] = 0.4 dex. At the first iteration, the difference of 500 K between the true Teff and the initialization value and the high true metallicity [Fe/H] = 0.4 dex, led SPADES to look for a synthetic spectrum with a metallicity higher than 1 dex, i.e. beyond the upper boundary of the library of synthetic spectra. Unable to find the synthetic spectrum, SPADES stopped processing this spectrum (at all three S/N).
In all 33 converging stars, it was observed that the effective temperature converged faster than the other parameters. This is because in mid-F-G dwarfs the Hα wings are hardly sensitive to wrong log g and [Fe/H] (van’t Veer-Menneret & Megessier 1996), while on the contrary log g and [Fe/H] are sensitive to wrong Teff. This suggests a possible future evolution for SPADES, which could at the first iteration determine only Teff and then at the next iterations determine all three atmospheric parameters. This would probably have prevented SPADES from looking for spectra outside the boundaries of the library for the 34th spectrum.
Table 7 presents the medians and the dispersions of the distributions of Teff, log g, and [Fe/H] residuals, i.e. estimated minus true, derived by SPADES for each S/N. The right side of Fig. 13 shows the distributions of Teff (top), log g (middle), and [Fe/H] (bottom) residuals for S/N = 50. The performances derived from test 3 (for of a wider variety of input atmospheric parameters) are similar to those obtained in test 1. The convergence process has therefore a very moderate impact on SPADES final Teff, log g, and [Fe/H] .
Out of the 33 converged stars, [Ti/Fe] and [Ni/Fe] ratios were derived for 21. Below ametallicity of about −1.4 dex (the precise value is a function of Teff), the lines contained in the HR13 and HR14B become too weak to derive the abundances. This is illustrated by the bottom left and bottom right plots in Fig. 12. At [Fe/H] = −1 dex (red line), the Ni and Ti lines (at 6258.11 Å) are already weak and at [Fe/H] = −2 dex they are not visible anymore.
Table 8 presents the medians and the dispersions of the distributions of [Ti/Fe] and [Ni/Fe] residuals, i.e. estimated minus true, derived by SPADES for the S/N 100, 50 and 30. The systematic and random errors derived from test 3 are on average larger than those obtained from test 1. The main reason is very likely that in test 3, [Ti/Fe] and [Ni/Fe] ratios are obtained for a wide range of metallicities down to [Fe/H] ~ −1.4 dex, while in test 1 a solar abundance star was considered.
Medians and dispersions of the distributions of [Ti/Fe] and [Ni/Fe] residuals, i.e. estimated minus true, derived by SPADES for the S/N 100, 50 and 30.
Means and dispersions of the residuals (SPADES initialized randomly minus SPADES initialized with the true parameters) on the estimation of the atmospheric parameters as well as the titanium and nickel over iron ratios.
4.3.2. Second test
Iterative methods present the risk to converge toward a local minimum, rather than the global minimum. To investigate this risk in more detail, we selected one out of the 34 times 200 spectra analyzed in Sect. 4.3.1 above, with S/N = 50. The true parameters of the spectrum were Teff = 5992 K, log g = 4.4, [Fe/H] = −0.3 dex, [Ti/Fe] = 0 dex and [Ni/Fe] = 0 dex. SPADES analyzed the spectrum a first time, starting from its true parameters and found Teff = 6025 K, log g = 4.35, [Fe/H] = −0.26 dex, [Ti/Fe] = 0.04 dex and [Ni/Fe] = 0.05 dex. SPADES then reanalyzed the spectrum another 50 times, but with starting parameters randomly chosen following uniform distributions centered on the true parameters and widths of ± 500 K (Teff), ± 0.5 (log g) and ± 0.4 dex ( [Fe/H] ). The volume in the parameters space considered for the initialization is larger, i.e. conservative, with respect to the estimated performances of SPADES-TE (see Sect. 2.5.2). Table 9 presents the means and residuals of the parameters determined by SPADES when initialized randomly minus those determined by SPADES when initialized with the true parameters. Means and dispersions are all low, showing that at S/N = 50, SPADES is very weakly sensitive to the initialization conditions.
5. Summary
The automated stellar parameters determination software SPADES was presented. It relies on a line-by-line comparison between the studied spectrum and synthetic spectra. SPADES derives the radial velocity, the effective temperature, the surface gravity, and the iron and individual abundances.
SPADES internal systematic and random errors were assessed by Monte Carlo method. For example, simulating Giraffe HR13 and HR14B setups from synthetic spectra for a star with K, , dex and for a S/N of 100, the stellar parameters were recovered with no significant bias and with 1-σ precisions of 8 K for the temperature, 0.05 for the log g, 0.009 for [Fe/H] , 0.003 for [Ti/Fe] , and 0.01 for [Ni/Fe] . The external systematic errors were evaluated with ground-based observed spectra and the convergence properties were assessed by a Monte Carlo method.
Several evolutions of SPADES are planned. On the one hand, we aim to adapt and test SPADES for a greater variety of spectral
types and luminosity classes. This includes addingare the micro-turbulence to the parameters determined by SPADES. On the other hand, we plan to implement additional diagnostics to determine the atmospheric parameters, e.g. use the wings of the strong lines to derive the surface gravity (for example Mg Ib triplet in dwarfs or infra-red Ca II triplet in giants).
Some non-valid pixels affected by, e.g. telluric lines, could be excluded from the derivation of the correlation function (see Sect. 2.3).
Acknowledgments
This work is financed by the CNRS (Centre National de la Recherche Scientifique) and the CNES (Centre National d’Études Spatiales). We would like to thank R. Kurucz for making publicly available the ATLAS9 and SYNTHE programs and F. Castelli for providing the new ODF tables. We are grateful to the referee for his/her very fruitful comments and suggestions.
References
- Allard, N. F., Kielkopf, J. F., Cayrel, R., & van’t Veer-Menneret, C. 2008, A&A, 480, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allende Prieto, C., Rebolo, R., García López, R. J., et al. 2000, AJ, 120, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- Allen de Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L. 2000, A&A, 357, 197 [NASA ADS] [Google Scholar]
- Bailer-Jones, C. A. L. 2010, MNRAS, 403, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Stempels, H. C., Allen de Prieto, C., et al. 2002, A&A, 385, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundstrom, I. 2003, VizieR Online Data Catalog, 341, 527 [Google Scholar]
- Bijaoui, A., Recio-Blanco, A., & de Laverny, P. 2008, in AIP Conf. Ser. 1082, ed. C. A. L. Bailer-Jones, 54 [Google Scholar]
- Boeche, C., Siebert, A., Williams, M., et al. 2011, AJ, 142, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., & Caffau, E. 2003, A&A, 399, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, IAU Symp., 210, A20 [Google Scholar]
- Cayrel, R., Perrin, M.-N., Barbuy, B., & Buser, R. 1991, A&A, 247, 108 [NASA ADS] [Google Scholar]
- Cayrel, R., van’t Veer-Menneret, C., Allard, N. F., & Stehlé, C. 2011, A&A, 531, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- François, P., Depagne, E., Hill, V., et al. 2003, A&A, 403, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Fuhrmann, K. 2004, Astron. Nachr., 325, 3 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fuhrmann, K. 2008, MNRAS, 384, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Jofré, P., Panter, B., Hansen, C. J., & Weiss, A. 2010, A&A, 517, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, D. 2001, J. Astron. Data, 7, 8 [Google Scholar]
- Katz, D. 2009, in SF2A-2009: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. M. Heydari-Malayeri, C. Reyl’E, & R. Samadi, 57 [Google Scholar]
- Katz, D., Soubiran, C., Cayrel, R., Adda, M., & Cautain, R. 1998, A&A, 338, 151 [NASA ADS] [Google Scholar]
- Katz, D., Munari, U., Cropper, M., et al. 2004, MNRAS, 354, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 14 [Google Scholar]
- Molaro, P., Levshakov, S. A., Monai, S., et al. 2008, A&A, 481, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrin, M.-N., Friel, E. D., Bienayme, O., et al. 1995, A&A, 298, 107 [NASA ADS] [Google Scholar]
- Recio-Blanco, A., Bijaoui, A., & de Laverny, P. 2006, MNRAS, 370, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Royer, F., Prugniel, P., & Jégouzo, I. 2005, in SF2A-2005: Semaine de l’Astrophysique Francaise, eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 645 [Google Scholar]
- Royer, F., Jégouzo, I., Chiligarian, I., Prugniel, P., & Le Sidaner, P. 2008, in Astronomical Spectroscopy and Virtual Observatory, eds. M. Guainazzi, & P. Osuna, 53 [Google Scholar]
- Sbordone, L. 2005, Mem. Soc. Astron. It. Suppl., 8, 61 [Google Scholar]
- Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. It. Suppl., 5, 93 [Google Scholar]
- Siebert, A., Williams, M., Siviero, A., et al. 2011, VizieR Online Data Catalog, III/265 [Google Scholar]
- Soubiran, C., Bienaymé, O., & Siebert, A. 2003, A&A, 398, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soubiran, C., Le Campion, J.-F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stehlé, C., & Hutcheon, R. 1999, A&AS, 140, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Stetson, P. B., & Pancino, E. 2010, in Astrophysics Source Code Library, record ascl:1011.002, 11002 [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van’t Veer-Menneret, C., & Megessier, C. 1996, A&A, 309, 879 [NASA ADS] [Google Scholar]
- Zucker, S. 2003, MNRAS, 342, 1291 [Google Scholar]
All Tables
Median and dispersion (in km s-1) of the radial velocity distribution derived by SPADES for 200 studied spectra for S/N 30, 50 and 100.
Medians and dispersions of the distributions of residuals, i.e. estimated minus true, on Teff, log g, [Fe/H] , [Ti/Fe] and [Ni/Fe] derived by SPADES for the S/N: 100, 50 and 30.
iron over hydrogen and titanium and nickel over iron ratios derived by SPADES for a solar HR13 and HR14B solar spectrum, when the effective temperature and surface gravity were fixed to their bibliographic values K and .
Effective temperature, surface gravity, iron over hydrogen and titanium and nickel over iron ratios derived by SPADES for the Giraffe HR13 and HR14B solar spectra.
Bibliographic parameters and parameters derived by SPADES for the five test stars.
Means and dispersions of the residuals (SPADES minus bibliographic) on the estimation of the atmospheric parameters as well as the titanium and nickel over iron ratios.
Medians and dispersions of the distributions of Teff, log g, and [Fe/H] residuals, i.e. estimated minus true, derived by SPADES for the S/N 100, 50 and 30.
Medians and dispersions of the distributions of [Ti/Fe] and [Ni/Fe] residuals, i.e. estimated minus true, derived by SPADES for the S/N 100, 50 and 30.
Means and dispersions of the residuals (SPADES initialized randomly minus SPADES initialized with the true parameters) on the estimation of the atmospheric parameters as well as the titanium and nickel over iron ratios.
All Figures
 |
Fig. 1 Observed Giraffe/VLT (HR14B setup) Sun spectrum before normalization, with the polynomial fit shown as a thick blue line (top) and after normalization (bottom). |
| In the text | |
 |
Fig. 2 Correlation function for a synthetic studied spectrum of solar parameters (Teff = 5777 K, log g = 4.44 and [Fe/H] = 0.0 dex) and S/N = 100 (Poisson noise) and a noiseless synthetic template with the same atmospheric parameters. |
| In the text | |
 |
Fig. 3 Two examples: (i) pixel identification in the reference line (green crosses), (ii) pseudo-continuum selection (blue circles), and (iii) vertical adjustment of the synthetic reference spectrum (red line) to the studied spectrum (black line). In the top plot, the pseudo-continuum area (blue circles) were selected automatically by SPADES and were used for the vertical adjustment. In the bottom plot, no valid pseudo-continuum area was found. The pixels in the line (green crosses) were used for the vertical adjustment. |
| In the text | |
 |
Fig. 4 Comparison of the Hα wings in the studied spectrum (black line) with the 1D grid of synthetic spectra (red lines) ranging here from 5000 (narrowest wings) to 6600 K (broadest wing). The pseudo-continuum area is labeled with blue dots and the valid pixels in the Hα wings are identified with green crosses. The bottom plot is a zoom on the blue wing. |
| In the text | |
 |
Fig. 5 Examples, for a synthetic studied spectrum, of similarity functions as a function of effective temperature (top left), surface gravity (top right), iron over hydrogen ratio (bottom left) and nickel over iron ratio (bottom right). The polynomial (or linear interpolation for the surface gravity) used to minimize the functions are represented as blue lines. |
| In the text | |
 |
Fig. 6 ν And similarity functions as a function of effective temperature (top left), surface gravity (top right), iron over hydrogen ratio (bottom left), and nickel over iron ratio (bottom right). The polynomial (or linear interpolation for the surface gravity) used to minimize the functions are represented as blue lines. |
| In the text | |
 |
Fig. 7 FeI line (top, green crosses) and an FeII line (bottom, green crosses), used by SPADES to determine log g. The studied spectrum (log g= 4.5) is given in black and the red lines are the synthetic reference spectra of the 1D subgrid ranging from log g= 2.0 to 5.0 by step of 0.5. |
| In the text | |
 |
Fig. 8 Distributions of the Teff (top left), log g (top right), [Fe/H] (bottom left) and [Ni/Fe] (bottom right), estimated by SPADES for 200 S/N = 50 simulated HR13 and HR14B Giraffe spectra. The true parameters are Teff = 5800 K, log g = 4.5, [Fe/H] = 0.0 dex, and [Ni/Fe] = 0.0 dex. |
| In the text | |
 |
Fig. 9 SPADES estimate of Teff, log g, and [Fe/H] versus each others for the 200 stars with S/N = 100 (top), S/N = 50 (middle), and S/N = 30 (bottom). |
| In the text | |
 |
Fig. 10 Zoom on the red wing of the Hα line from the Giraffe HR14B solar spectrum (black line). Two synthetic spectra are overplotted: in red a synthetic spectrum with Teff = 5689 K and in blue Teff = 5777 K (the values of the other parameters are those of the Sun: log g = 4.44 and [Fe/H] = 0.0 dex). |
| In the text | |
 |
Fig. 11 Temperatures (top left), gravities (top right), iron over hydrogen (bottom left), and nickel over iron ratios (bottom right) estimated by SPADES versus their bibliographic values. |
| In the text | |
 |
Fig. 12 Extract of three synthetic spectra of metallicity [Fe/H] = 0.0 dex (blue), [Fe/H] = −1.0 dex (red), [Fe/H] = −2.0 dex (black), showing the influence of the metallicity on an Fe I line (top left), an Fe II line at 6456.39 Å (top right), a Ni I line (bottom left) and a Ti I line at 6258.11 Å (bottom right). |
| In the text | |
 |
Fig. 13 Left: differences between the true parameters of the 34 synthetic stars and the initialization parameters: Teff (top), log g (middle) and [Fe/H] (bottom). Right: distributions of Teff (top), log g (middle) and [Fe/H] (bottom) residuals for S/N = 50. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


