EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 544 (August 2012) A&A, 544 (2012) A63 Full HTML
Free Access
Issue
A&A
Volume 544, August 2012
Article Number A63
Number of page(s) 8
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201219067
Published online 26 July 2012

© ESO, 2012

1. Introduction

Over the past decade the Spitzer Space Telescope (Werner et al. 2004) has provided complementary information about known debris disks in multiple-star systems. Observations of pairs of main sequence stars made by Spitzer revealed stable circumbinary disks around pairs of stars with separations of 0.04–5.31 AU in 14 systems (Trilling et al. 2007, see Table 4 of that paper). In addition, two of these binary systems have an additional companion.

Another example of a debris disk in a multiple star system is the circumbinary disk of HD 98800. This system is a young (<10 Myr) member of the TW Hydra association (Fekel & Bopp 1993). HD 98800 has four stars in two binaries, A and B, travelling around each other in highly inclined and eccentric orbits. According to Furlan et al. (2007), the observations suggests the existence of an optically thick wall at 5.9 AU around the B components and an inner, empty region. However, some optically thin dust orbits the B binary in a ring between 1.5 and 2 AU. In particular, Furlan et al. (2007) have argued that the peculiar structure and apparent lack of gas in the HD 98800 disk suggest that this system is likely already at the debris disk stage.

In later studies of debris disks in triple star systems (Akeson et al. 2007; Verrier & Evans 2008), the quadruple stellar system HD 98800 was studied as a triple system consisting of the B inner binary orbited by a third star. Akeson et al. (2007) investigated the influence of a third star, with an orbital plane initially inclined at 10° with respect to the B inner binary orbital plane, on the HD 98800 disk. The authors found that the inclined stellar orbit could produce a warp in the disk around the B inner binary. Verrier & Evans (2008) considered the third star in three possible current orbital configurations of the HD 98800 system (Tokovinin 1999). The third star is considered to be in an orbital plane initially inclined at  ~143° with respect to the B inner binary orbital plane. The test particles are initially taken on placed in a cloud of orbits. Verrier & Evans (2008) showed gaps in the disk and three distinct stable populations of test particles: a prograde disk, a retrograde disk, and a high-inclination halo.

It is important to study what happens in debris disks to understand the role of stellar companions in planet formation. A stellar companion within 100 AU probably affects the formation of giant planets (e.g., Nelson 2000; Mayer et al. 2005; Thébault et al. 2006; and others).

In this work, we extend the investigations of debris disks performed by Akeson et al. (2007) and Verrier & Evans (2008). We have considered a range of inclinations for the third star and for the particle’s disk. We estimate the stable region in which particles can survive despite the third star’s inclination and eccentricity. Our goal is not to reproduce the current configuration of the debris disk of HD 98800, but to sample the range of possible outcomes for different initial inclinations of the disk and the third star. The astronomical motivation for our study is to investigate whether/where the orbital stability region of a debris disk is possible around the close binary, and to show how the disk structure can be shaped by its dynamical interaction with an eccentric and inclined third star. Investigating the details of these dynamical interactions is beyond the scope of the present work, therefore we will focus the possible impact of the mean motion resonances on the disk because recent studies have mentioned them as a powerful mechanism for instabilities and gaps in the disk, without investigating them in detail (Verrier & Evans 2008; Farago & Laskar 2010). An analytical study of mean motion resonances in this framework is intended to be carried out in the future.

This paper is structured as follows. In Sect. 2, an overview of the empirical expressions of the stability boundary applied here is presented. In Sect. 3, we present the initial conditions for the disk and the triple stellar system assumed here. In Sect. 4, we summarise the relevant results of our numerical simulations and discuss the effects of the inner binary and third star perturbations. In Sect. 5, we present a study on the identification of mean motion resonances in the particle disk. Finally, our conclusions are presented in Sect. 6.

2. Stability boundary

To study the stability boundary of a circumbinary disk in a triple stellar system, we have chosen the HD 98800 system. This system has been modelled as a triple stellar system in which the B binary is orbited by a particle disk and a more distant third star. The A pair is treated as a single star disturber.

The B binary orbit has a semi-major axis of aB = 0.983 AU and an eccentricity of eB = 0.7849. The solar masses of the B pair are M1 = 0.699 and M2 = 0.582, and the mass ratio μB = M2/(M1 + M2) is 0.45 (Boden et al. 2005). The A binary (hereafter, third star) has three possible orbital configurations (see Table 1), and its mass M3 was assumed to be the sum of the masses of the B pair (M3 = 1.281 solar masses). The mass ratio μA = M3/(M1 + M2 + M3) is then 0.5 (Tokovinin 1999).

Table 1

Orbital elements of the B-A orbit of the HD 98800 system (Tokovinin 1999).

To study the stability of planets in binary star systems, Holman & Wiegert (1999) have derived empirical expressions of stability boundaries for planetary orbits in binary star systems. According to their results, the stability region is delimited by what we called internal (aI) and outer (aO) critical semi-major axes. The internal critical semi-major axis is the closest stable orbit to the two stars (or one of the stars) due to the star pair’s circumbinary perturbations. The outer critical semi-major axis is the outermost stable orbit around the star pair (or one of the stars) due to the perturbations of a distant star.

Using the approximated expressions from Holman & Wiegert (1999), we give the values of aO for each orbital configuration of the third star in Table 2. We found an inner stability boundary of  ~4.04 AU.

Table 2

Outer critical semi-major axis, aO, for the three configurations investigated.

Verrier & Evans (2007) have performed numerical simulations on the stability zones for particles orbiting an inner binary in the presence of a more distant third star. They have presented empirical expressions of the stability boundary for coplanar circumbinary stability by modelling the stars as a low-inclination triple system. The empirical expressions for inner and outer borders are written as follows: 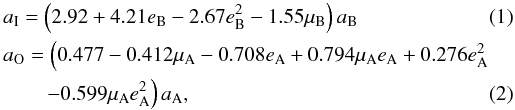aI=(2.92+4.21eB−2.67eB2−1.55μB)aBaO=(0.477−0.412μA−0.708eA+0.794μAeA+0.276eA2\begin{eqnarray} \label{equacao1} &&a_{\rm I} =\left(2.92 + 4.21e_{\rm B}-2.67e_{\rm B}^{2} - 1.55\mu_{\rm B}\right)a_{\rm B} \\ &&a_{\rm O} = \left(0.477 - 0.412\mu_{\rm A} - 0.708e_{\rm A} + 0.794\mu_{\rm A}e_{\rm A}+ 0.276e_{\rm A}^{2} \right.\nonumber \\ &&\qquad \left. -0.599\mu_{\rm A}e_{\rm A}^{2}\right)a_{\rm A}, \label{equacao2}\arraycolsep1.75pt \end{eqnarray}Table 2 gives the values of aO for each studied configuration. For the inner stability boundary, we found a value of  ~ 3.87 AU.

Another approximation of the stability boundary for planetary orbits in binary systems can be obtained using the results from Domingos et al. (2006), who numerically studied the orbital stability of a particle in the framework of the elliptic restricted three-body problem. Empirical expressions of the stability boundaries for prograde and retrograde orbits were also derived. The authors have found aO values that agree well with those from Holman & Wiegert (1999) and Verrier & Evans (2007). The results from Domingos et al. (2006) differ from previous works in that the empirical expression for the outer critical semi-major axis of the particle also depends on the eccentricity e of the particle. In the case of a prograde orbit, the outer semi-major axis is given by 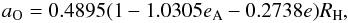aO=0.4895(1−1.0305eA−0.2738e)RH,\begin{equation} \label{equacao3} a_{\rm O} = 0.4895(1 - 1.0305e_{\rm A}- 0.2738e)R_{\rm H}, \end{equation}(3)where RH is the radius of the system’s B-A Hill’s sphere. The aO values for e = 0 for each configuration of the third star are shown in Table 2.

Analysing Eqs. (2) and (3), the aO value strongly depends on the eA, aA and μA values when the particle is on circular orbit. This relation may be a result of the fact that the third star’s gravitational perturbation on the particle can change significantly depending on those parameters. This changes the minimum distance between the third star and the inner binary. The third star’s gravitational perturbation on the components of the inner binary can also change, resulting in a perturbation on the particle. Thus, the combination of these two effects must be important to the particle’s dynamical stability. According to Eq. (3), the critical semi-major axis aO beyond which the particle would not be stable also depends on the e value.

For the inner stability boundary, the expression from Domingos et al. (2006) does not determine the aI value for the system considered here. In that study, the aI value represents the semi-major axis of the collision of the particle with the body that it was orbiting. Holman & Wiegert (1999) and Verrier & Evans (2007) have shown that aI depends on eB because it corresponds to the semi-major axis related to the centre of mass of the inner binary, from which the orbit of the particle can become unstable. However, the eccentricity of the particle was not considered in those studies.

Considering that particles can be in high-e orbits with a pericentre distance of Rp = a(1 − e) within the unstable region, particles might be removed by perturbations from the inner binary. To estimate the value of e as a function of the minimum semi-major axis a, in which the particle could move near the inner binary, we have assumed that Rp is given by Eq. (1). The eccentricity of the particle as a function of a is then given by 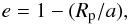e=1−(Rp/a),\begin{equation} \label{equacao4} e=1-(R_{\rm p}/a), \end{equation}(4)we notice that the difference between the aI values from Holman & Wiegert (1999) and those from Verrier & Evans (2007) were not significant. The advantage of our approach is that the aI value depends on not only μB, aB and eB, but also on a whole set of particle eccentricities.

Assuming a limit of eccentricity, elim, for an orbit with a semi-major axis limit, alim, to be within the stable region, it was possible to establish the eccentricity from expressions (3) and (4). The (alim, elim) maximum pair was estimated by setting Rp equal to the outer stability semi-major axis, aO. For the I, II and III configurations, these values are approximately (8.830 AU, 0.572), (6.670 AU, 0.433) and (5.963 AU, 0.366), respectively. For the a = alim case with e exceeding elim, the pericentre and/or apocentre distances can be located outside the stable region. When e = elim, the particle orbits have pericentre and apocentre distances on the inner and outer stability boundaries, respectively.

According to the goal of this work, we focused on particles within the stable region. In our analyses, we used the definition of the (alim, elim) pair as a reference value. These physical quantities represent the dynamical effects of the inner binary and third star companion on a circumbinary disk and consequently represent the particle stability. The limit radius is between aI and aO values. The combination of elim and alim represents a critical value of high eccentricity and semi-major axis values of orbits relative to the particle instabilities. A specific (a, e) pair can result in an orbit of collision with the inner binary or escape out of the system.

2.1. Critical inclination

It is particularly interesting to determine the conditions under which an inclined protoplanetary disk remains stable. The mean inclination i of a disk might also have implications for the stability region of a system in which large bodies disturb the disk, producing dust through collisional events. Depending on the system characteristics, something will disturb the disk’s increasing i value (Artymowicz 1997; Thébault & Augereau 2007; Quillen et al. 2007). An important question regarding this problem is the existence of a critical value for the inclination ( ~ 39.23°) between the orbital planes of the disturbed and disturbing bodies (restricted three-body problem). If the disturbing body is in a highly inclined orbit relative to the orbital plane of the disturbed body, the eccentricity increases and the near-circular orbit becomes highly elliptic. This effect is called the Kozai-Lidov mechanism (Kozai 1962) and (Lidov 1962).

The Kozai-Lidov mechanism causes strong periodic variations of the particle eccentricity and inclination while conserving their semi-major axes. The concurrent increase in the inclination and decrease in the eccentricity usually leads to instability in the system. Assuming that the particle’s initial eccentricity is close to zero, we can obtain the maximum eccentricity of a particle given an initial inclination (Innanen et al. 1997). Carruba et al. (2002) have shown that particles on higher inclination librating in the Kozai-Lidov resonance may not reach the maximum eccentricity and can be stable for millions of years.

In the system studied here, the Kozai-Lidov mechanism takes effect on the circumbinary disk when the relative inclination of the particle and third star orbital planes is greater than 40°. Verrier & Evans (2009) showed that the inner binary may cause a nodal libration instead of Kozai-Lidov cycles, which stabilises the test particles against any Kozai-Lidov instability driven by the outer star. These authors also reported that particles closer to the inner binary have nodal libration periods shorter than Kozai-Lidov cycles. Therefore, the nodal libration dominates, resulting in the stability of the particle. Otherwise, when particles more distant (closer to the outer border of the stability region) have Kozai-Lidov periods shorter than the nodal libration, they are destabilised and ejected from the system or collide with the inner binary.

3. Numerical simulations

Using the three possible fits for the third star given in Table 1, we numerically investigated the stability of the particles around the B pair. The B binary orbit was assumed to be in the plane. The orbit of the third star was placed around the centre of mass of the B pair. The initial inclinations for the third star (IA) are given with respect to the initial B binary plane and are taken to be from 0° to 50° with ΔIA = 10°.

The disk was formed by 30 000 massless particles (planetesimals) distributed on the same plane around the B binary with semi-major axis (a) from 2 to 30 AU. The initial inclination (i) of the disk was assumed to vary from 0° to 90° with Δi = 10° with respect to the initial B binary plane. The initial eccentricities (e) of the particles were randomly distributed within 10-3. Longitudes of pericentre and mean longitudes were distributed randomly between 0° and 360°. Our reference plane is the B orbital plane. In particular, our main interest is the final outcome of the evolution of the disk with respect to the initial B orbital plane at time t = 0.

The numerical simulations were stopped after 1 Myr and interrupted if any of the following situations occurred: (i) the planetesimal travelled closer than 0.01 AU from B binary components or (ii) the planetesimal travelled farther than 200 AU from B binary (ejection of the system). The particles surviving the full integration time were considered stable. We used the Swift package (Wisdom & Holman 1991; Levison & Duncan 1994) and the Hierarchical Jacobi Symplectic algorithm (Beust 2003).

4. Results and discussion

Our numerical results are summarised in Figs. 1 to 4, which refer to the final orbital evolution of the particles on the a − e and a − i planes. Similar results have been obtained for three orbital configurations. As an example, Figs. 2 to 4 show the final results for the orbital configuration I.

4.1. The coplanar case

Figure 1 shows the final results of the numerical simulations for orbital configurations I, II and III for the coplanar regime (IA = i = 0). In configuration I, the outer critical semi-major axis is much larger than that in configurations II and III. Figure 1 shows the final eccentricity as a function of the final semi-major axis of the particles. The stable region is delimited by the two borders, aI and aO. The left border (red curve) and the right border (green curve) are given by Eqs. (4) and (3). Table 2 gives the values of aO obtained for the simulations for each orbital configuration. The inner critical semi-major axis at and beyond which particles survive the integration is  ~3.3 AU.

thumbnail Fig. 1

Region of stability of the particles in the space of a versus e for the coplanar case (IA = i = 0). The plots represent the final results for the orbital configurations I, II and III. The red and green curves give the analytical estimates for the stability region (“protected region”). These curves represent the internal, aI and outer, aO, critical semi-major axes. The red and green curves are given by Eqs. (4) and (3), respectively. The dashed curve represent the (alim, elim) pair for a particle within the “protected region”.

In Fig. 1, it can be noted that particle orbits were not restricted to within a (a, e) triangular region. Orbits within this region are considered to be stable, and orbits located outside this region are considered to be unstable. It is important to note that the simulations were halted after 1 Myr, which corresponds to 10% of the age of a system such as HD 98800. If the simulations were continued, some of the remaining particles whose orbits were outside of the stability region would have also been ejected or collided.

The surviving particles within the stable region (hereafter the “protected region”) are expected not to be ejected or even collide with the central stars. All particles were initiated with near circular orbits; at some point, some particles achieved eccentric orbits. For orbital configuration I, some particles are excited to higher eccentricities around a =  4.0, 4.2, 10.0, 10.5 and 11.5 AU. For orbital configurations II and III, particles in high-e orbits appear around 5.0 AU and 5.5 AU, respectively, and appear close to the outer border. In general, when particles are not in high-e orbits, they remain in orbits with e ≤ 0.1 within the “protected region”.

Our results have indicated high sensitivity to the third star’s eccentricity. For configurations with a high eccentricity of the third star (0.5 and 0.6), particles in the outer region of the disk (a ≥ 8.0 AU) are ejected from the system on a short timescale. For large eccentricities of the third star, the value of elim decreases, and the timescale for particles reaching this limit must be shorter than that for systems with low eccentricities of the third star. The three estimates of the value of elim are in reasonable agreement with the results of our numerical simulations.

4.2. Stellar perturbations on inclined orbits

In this section, we present results for inclined orbits of the third star and the particle disk. First, we have considered the case of an inclination between the B pair orbit and the particle’s disk, followed by an inclination between the disk and the third star orbit.

4.2.1. Inclined particle disk

Figure 2 shows that for the initial inclinations of 10° and 20° the final results in a − e planes are identical to those shown in Fig. 1. The final distribution of the eccentricity of the particles within the “protected region” also does not significantly differ from those in Fig. 1. The particle concentrations in high-eccentricity orbits have not changed location with respect to the coplanar case. Figure 2 shows the final inclination of the particles. For the disk initially inclined by 20° the distribution of maximum final inclination of the particles was  ~ 60°. Despite a higher final inclination, the final distribution of the number of particles is similar to that for the coplanar case. In particular, for configuration I, we note that the particle concentration for the higher inclination occurs at a = 4.5 AU.

thumbnail Fig. 2

Regions of stability of an inclined particle disk for I orbital configuration. Each plot shows the final results of the particles in a − i planes. The initial inclination of the disk is indicated on the upper right corner of each panel.

Figure 3 shows the final orbital eccentricities and inclinations of the particles for a disk initially inclined by 30°, 50° and 90°. Evidently, a significant number of particles have their eccentricities and inclinations excited to very high values for the disk initially inclined by 30°. We have seen that many particles were quickly ejected in the vicinity of the outer boundary. In the inclination plot, we can note that between  ~4.0 and 7.5 AU particles are excited in inclination up to  ~160°.

For particle disks with initial inclinations 50° and 90°, results showed that some particles remained stable for high values of initial inclination. Note that these particles have significantly increased their eccentricities, but the eccentricities did not reach sufficiently high values to be removed from the system during the integration time. On the other hand, it can be noticed that many particles have not significantly increased eccentricities.

We can also note that for i = 90° particles are stable up to a ≲ 9.0 AU, with gaps appearing around  ~2.5 AU and 3.1 AU. In general, most of these particles have final eccentricities of e ≤ 0.1 when the disk orbit is inclined. Depending on the initial value of i, the aI value at and beyond which particles survive the integration is within 2.4 to 3.3 AU. The lower value for aI was obtained by considering high relative inclinations (i > 50°).

thumbnail Fig. 3

Plots of a − e and a − i for particle disks initially inclined by 30°, 50° and 90°.

thumbnail Fig. 4

Diagrams of a − e and a − i. The initial inclination of the particle disk was indicated in the upper right corner of the panel and is relative to the B binary orbital plane. The results shown are for the case IA = 30°.

4.2.2. Relative inclination between the particle disk and third star

Another perspective is to initially consider the particle disk and third star on non-coplanar orbits. Mazeh & Shaham (1979) have shown that when the inclination of the third star is nonzero, the eccentricity of the inner binary oscillates (with corresponding oscillations in its inclination), while IA and eA remain approximately constant. As expected, our numerical simulations have shown that for higher values of IA ( ≳ 40°), the effect of the inner binary perturbations on the inner edge of the particle disk becomes important in determining the inner stability boundary.

Figure 4 presents a representative sample of the final results when the particle disk and third star were placed in non-coplanar orbits. The initial IA value was 30°, and the initial inclinations of the particle disk were 20°, 50° and 90° (indicated in the upper right corner of the plot). Varying i and IA, the closest distance to the binary at which particles survived was 2.4 AU. As shown in the figure, some results revealed gaps (around 4.5 AU and 5.5 AU) and a diffusion of the particles, with subsequent particle ejection or collision with the inner binary.

In general, we found three distinct and clearly located structures: (i) a chaotic region closer to the inner binary, (ii) a stable region where particles on highly inclined orbits can survive, and (iii) an unstable region that depends on the distance of the third star and the relative inclination of the particles. Depending on initial conditions from the third star and the particle disk, eccentricity peaks and gaps can appear within the stable region.

5. Mean motion resonances

Our investigation was motivated by the eccentricity peaks shown by some particles with low inclination (i ≤ 30°), which might be due to resonant effects. Thus, instabilities and gaps appear around these resonances as a result of high eccentricities.

We are studying a system with four bodies, none of which can be considered a central body. Thus, there are four natural frequencies in the system given by the mean motions of each body. Given that the stars have highly eccentric orbits and that this section is restricted to the planar case, the resonant angle involves not only mean motions but also the pericentre longitude of the particle. The expression of the resonant angle associated with the resonance is then given by 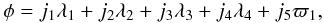φ=j1λ1+j2λ2+j3λ3+j4λ4+j5ϖ1,\begin{equation} \label{equacao5} \phi = j_1 \lambda_1 + j_2 \lambda _2 + j_3 \lambda _3 + j_4 \lambda _4 +j_5 \varpi_{1}, \end{equation}(5)where j’s are integers with j1 + j2 + j3 + j4 + j5 = 0 according to the first d’Alembert rule. The λ1, λ2, λ3 and λ4 are mean motion longitudes that correspond to the particle, the inner binary (Ba and Bb stars), and the third star, respectively, and ϖ1 is the pericentre longitude of the particle. 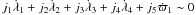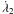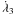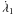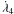A particle is involved in a mean motion resonance when the critical argument rate corresponds to \hbox{$j_1 \dot\lambda_1 + j_2 \dot\lambda _2 + j_3 \dot\lambda _3 + j_4 \dot\lambda _4 + j_5 \dot\varpi_1\sim 0$}, where \hbox{$\dot \lambda_2$} and \hbox{$\dot \lambda_3$} denote the mean motions of the inner binary, \hbox{$\dot \lambda_1$} and \hbox{$\dot \lambda_4$} are the mean motions of the particle and the third star, respectively, and 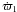\hbox{$\dot \varpi_1$} is the pericentre rate of the particle.

It is well known (see for instance Murray & Dermott 1999) that the orbital periods of each star of the B pair about its centre of mass are the same. The mean longitudes in their orbits differ by 180°. Therefore, there is only one frequency (the mean motion) associated with the B pair, rather than two.

Taking 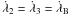\hbox{$\dot\lambda_2=\dot\lambda_3=\dot\lambda_{\rm B}$}, we rewrite 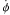\hbox{$\dot\phi$} in the following form: 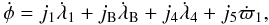φ̇=j1λ̇1+jBλ̇B+j4λ̇4+j5ϖ̇1,\begin{equation} \label{equacao6} \dot\phi = j_1 \dot\lambda_1 + j_{\rm B}\dot\lambda_{\rm B} + j_4 \dot\lambda _4+ j_5 \dot\varpi_{1}, \end{equation}(6)in Fig. 1, we can see peaks of eccentricity in regions close to the inner binary (3 AU  ≤ a ≤ 5 AU) and in regions farther away (9 AU  ≤ a ≤ 12 AU). Let us call the first region α and the second region β.

In region α, the gravitational effects of the third star do not destabilise the particle. The third star orbital frequency (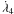\hbox{$\dot \lambda _4$}) is much lower than the inner binary orbital frequency (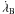\hbox{$\dot \lambda _{\rm B}$}), and thus contributes very little to the combination given by Eq. (6). In practice, we can consider j4 = 0 such that (6) becomes 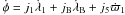\hbox{$\dot\phi = j_1 \dot\lambda_1 + j_{\rm B}\dot\lambda_{\rm B} + j_5 \dot\varpi_1$}. This equation involves two-body resonances because we only used two mean motion frequencies, but physically we have three bodies involved in the resonance with λBb = λBa + 180°.

In contrast, the third star plays an important role in region β. These interactions again involve two-body resonances, with the particle seeing the inner binary essentially as a single body. Now we can consider jB = 0 such that (6) becomes 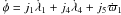\hbox{$\dot\phi = j_1 \dot\lambda_1 + \linebreak j_4\dot\lambda_4 + j_5 \dot\varpi_1$}.

Table 3 presents a list of the two-body mean motion resonances obtained here. In the first and second columns, we show the resonant argument and resonant semi-major axis of the particle, respectively. Figure 5 reproduces Fig. 1 with the locations of these two-body mean motion resonances. In Fig. 6, we show examples of temporal evolutions of a, e, and φ for two particles (P1 and P2) identified in the libration regime of the resonant angle.

Table 3

Mean motion resonances.

thumbnail Fig. 5

Region of stability of the particles in the space of a versus e for the coplanar case (IA = i = 0). The plot represents the final result for the orbital configuration I. The red vertical lines correspond to the locations of the resonances listed in Table 3.

The particle P1 is an example of a particle quite close to the inner binary. We note that the combination of the resonant angle φ = 8λ1 − λB − 7ϖ1 (second plot) shows that the particle is in the 8: − 1 two-body mean motion resonance with the inner binary. The time variations of the resonant angle show that it initially librates for approximately 3240 years, at which point the behaviour of φ, a and e clearly indicate the escape of the particle. An important point to note is the manner in which the resonance appears on the plot. There is no obvious pattern to the libration of the resonant angle, but this fact alone does not mean that the orbit is chaotic. The semi-major axis and eccentricity oscillations exhibit good correlation. Note that the variations in a and e are not different. After approximately 1900 years, the evolution of the eccentricity undergoes stronger irregular variations from 0.08 to 0.23 and the value of a remains close to the resonant value with increasingly erratic oscillations up to approximately 3240 years, when the particle escapes the system. Thus, we can say that the dynamical behaviour of this particle is governed by the 8: − 1 two-body mean motion resonance. 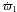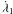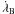To verify the importance of the frequency \hbox{$\dot\varpi_1$} in the resonant angle, we plotted the resonant angle using only \hbox{$\dot\lambda_1$} and \hbox{$\dot\lambda_{\rm B}$} (setting j5 = 0). We verified that the plots are almost identical. Therefore, the contribution of 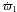\hbox{$\dot\varpi_1$} to the resonant angle is not significant.

The P2 particle is an example of a particle near the outer border of the stable region. In this resonance, the particle sees the inner binary essentially as a point mass. We show our results for 6000 years to provide a better graphic representation of the resonant angle, but the particle survives the full integration time. The resonant angle is φ =  −λ1 + 11λ4 − 10ϖ1, and the resonant semi-major axis is 9.9331 AU. According to the results, there is no obvious pattern to the libration of the resonant angle. The particles remain oscillating for all times among several values of the resonant angle, and there is no tendency for a circulating regime. The semi-major axis and eccentricity oscillations exhibit a good correlation with each other. 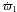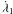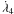To verify the importance of \hbox{$\dot\varpi_1$} on the resonant angle of P2, we plotted the resonant angle using only \hbox{$\dot\lambda_1$} and \hbox{$\dot\lambda_4$} (setting j5 = 0). We verified that the plots are quite different. Therefore, the contribution of 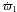\hbox{$\dot\varpi_1$} has a significant effect on the resonant angle and cannot be neglected.

In our study of mean motion resonances, we concentrated on the planar case. The resonant angle was defined using only the mean and pericentre longitudes. Certainly, when the disk and/or the third star is inclined, a study considering the node and pericentre longitudes would be required to gain a better understanding of the resonant effects.

thumbnail Fig. 6

Orbital evolutions of the semi-major axis, resonant angles, and eccentricity as functions of time. At the top of the first plot, we indicate the corresponding particle. The results in the first column are for a particle with initial conditions a = 3.8398 AU and e = 0.00070. The second column is for a particle with initial conditions a = 10.0980 AU and e = 0.00049. Note that the evolution of φ (second plot) shows that the P1 and P2 particles cross the two-body mean motion resonance and that the libration of the φ angle is evidence of an association between the orbits and the resonances.

6. Final remarks

In this work, we obtained the borders of the stable region for a particle disk around a close binary system disturbed by a gravitational field of a distant (minimum pericentre distance  ≲ 43 AU) companion star.

Our numerical results showed that the orbital evolution of the particle disk has been affected by the nodal libration due to the inner binary, the Kozai-Lidov effect and several mean motion resonances but is not dominated by any one of these factors in particular. In reality, the situation is much more complex. There are several mechanisms, overlaps of mean motion and/or secular resonances that increase the particle eccentricities, inducing instability. We have shown the following:

  • 1.

    There is an eccentricity limit for a particle to remain in thestability region. This limit depends on the a value of the particle. We recall that the value of the particle eccentricity can vary significantly due to the resonant effects (mean motion and secular resonances). For particles at high inclination, the orbits can be destabilised by the Kozai-Lidov mechanism. Depending on the initial conditions, eccentricity and inclination peaks appeared in regions where the effects of the nodal libration influence the stability of the particle orbit. We also showed that this eccentricity limit depends on the system parameters and should be considered when estimating the stability of orbits in triple systems.

  • 2.

    Among the mechanisms that can increase particle eccentricity, we have identified two-body mean motion resonances as a powerful mechanism to increase the particle eccentricity on short time-scales (10 kyr or less) and produce a longer-lived high-eccentricity population. These resonances are of high order and are considered a weak class of resonances in the outer asteroid belt; thus, they have not previously been considered in stellar systems. A study of the dynamic behaviour of particles in mean motion resonances is in progress and will be the subject of a future paper.

Although we have used the specific parameters for HD 98800, we hope that our results can contribute for understanding how stellar companions can affect the evolution of disks around close binaries for any system.

Acknowledgments

The authors thank Hervé Beust for providing his HJS algoritm and James Freddy L. Machuca for helpful discussions and comments on resonant dynamics. This work had financial support from UNESP, CNPq and FAPESP (grant number 2008/08679-4). These supports are gratefully acknowledged.

References

  1. Akeson, R. L., Rice, W. K. M., Boden, A. F., et al. 2007, ApJ, 670, 1240 [NASA ADS] [CrossRef] [Google Scholar]
  2. Artymowicz, P. 1997, Ann. Rev. Earth Planet Sci., 25, 175 [Google Scholar]
  3. Beust, H. 2003, A&A, 440, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Boden, A. F., Sargent, A. I., akeson, R. L., et al. 2005, AJ, 635, 442 [NASA ADS] [CrossRef] [Google Scholar]
  5. Carruba, V., Burns, J. A., Nicholson, P. D., & Gladman, B. J. 2002, Icarus, 158, 434 [NASA ADS] [CrossRef] [Google Scholar]
  6. Domingos, R. C., Winter, O. C., & Yokoyama, T. 2006, MNRAS, 373, 1227 [NASA ADS] [CrossRef] [Google Scholar]
  7. Farago, F., & Laskar, J. 2010, MNRAS, 401, 1189 [NASA ADS] [CrossRef] [Google Scholar]
  8. Fekel, F. C., & Bopp, B. W. 1993, ApJ, 419, L89 [NASA ADS] [CrossRef] [Google Scholar]
  9. Furlan, E., Sargent, B., Calvet, N., et al. 2007, AJ, 664, 1176 [NASA ADS] [CrossRef] [Google Scholar]
  10. Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [NASA ADS] [CrossRef] [Google Scholar]
  11. Innanen, K. A., Zheng, J. Q., Mikkola, S., & Valtonen, M. 1997, AJ, 113, 1915 [NASA ADS] [CrossRef] [Google Scholar]
  12. Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
  13. Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
  14. Lidov, M. L. 1962, P&SS, 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
  15. Mayer, L., Wadsley, J., Quinn, T., & Stadel, J. 2005, MNRAS, 363, 641 [NASA ADS] [CrossRef] [Google Scholar]
  16. Mazeh, T., & Shaham, J. 1979, A&A, 77, 145 [Google Scholar]
  17. Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge, England: Cambridge University Press) [Google Scholar]
  18. Nelson, A. F. 2000, ApJ, 537, L65 [NASA ADS] [CrossRef] [Google Scholar]
  19. Quillen, A. C., Morbidelli, A., & Moore, A. 2007, MNRAS, 380, 1642 [NASA ADS] [CrossRef] [Google Scholar]
  20. Thébault, P., & Augereau, J. C. 2007, A&A, 472, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Thébault, P., Marzari, F., & Scholl, H. 2006, Icarus, 183, 193 [NASA ADS] [CrossRef] [Google Scholar]
  22. Tokovinin, A. 1999, Astron. Lett., 25, 669 [NASA ADS] [Google Scholar]
  23. Trilling, D. E., Stansberry, J. A, Stapelfeldt, K. R., et al. 2007, ApJ, 658, 1289 [NASA ADS] [CrossRef] [Google Scholar]
  24. Verrier, P. E., & Evans, N. W. 2007, MNRAS, 382, 1432 [NASA ADS] [CrossRef] [Google Scholar]
  25. Verrier, P. E., & Evans, N. W. 2008, MNRAS, 390, 1377 [NASA ADS] [Google Scholar]
  26. Verrier, P. E., & Evans, N. W. 2009, MNRAS, 394, 1721 [NASA ADS] [CrossRef] [Google Scholar]
  27. Werner, M. W., Roelling, T. L., Low, F. J., et al. 2004, Ap&SS, 154, 1 [Google Scholar]
  28. Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Orbital elements of the B-A orbit of the HD 98800 system (Tokovinin 1999).

In the text
Table 2

Outer critical semi-major axis, aO, for the three configurations investigated.

In the text
Table 3

Mean motion resonances.

In the text

All Figures

thumbnail Fig. 1

Region of stability of the particles in the space of a versus e for the coplanar case (IA = i = 0). The plots represent the final results for the orbital configurations I, II and III. The red and green curves give the analytical estimates for the stability region (“protected region”). These curves represent the internal, aI and outer, aO, critical semi-major axes. The red and green curves are given by Eqs. (4) and (3), respectively. The dashed curve represent the (alim, elim) pair for a particle within the “protected region”.
In the text
thumbnail Fig. 2

Regions of stability of an inclined particle disk for I orbital configuration. Each plot shows the final results of the particles in a − i planes. The initial inclination of the disk is indicated on the upper right corner of each panel.
In the text
thumbnail Fig. 3

Plots of a − e and a − i for particle disks initially inclined by 30°, 50° and 90°.
In the text
thumbnail Fig. 4

Diagrams of a − e and a − i. The initial inclination of the particle disk was indicated in the upper right corner of the panel and is relative to the B binary orbital plane. The results shown are for the case IA = 30°.
In the text
thumbnail Fig. 5

Region of stability of the particles in the space of a versus e for the coplanar case (IA = i = 0). The plot represents the final result for the orbital configuration I. The red vertical lines correspond to the locations of the resonances listed in Table 3.
In the text
thumbnail Fig. 6

Orbital evolutions of the semi-major axis, resonant angles, and eccentricity as functions of time. At the top of the first plot, we indicate the corresponding particle. The results in the first column are for a particle with initial conditions a = 3.8398 AU and e = 0.00070. The second column is for a particle with initial conditions a = 10.0980 AU and e = 0.00049. Note that the evolution of φ (second plot) shows that the P1 and P2 particles cross the two-body mean motion resonance and that the libration of the φ angle is evidence of an association between the orbits and the resonances.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.