| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 7 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201118509 | |
| Published online | 20 July 2012 | |
Astrometric results of observations of mutual occultations and eclipses of the Saturnian satellites in 2009⋆
1 Institut de mécanique céleste et de calcul des éphémérides – Observatoire de Paris, UMR 8028 du CNRS, 77 Av. Denfert-Rochereau, 75014 Paris, France
e-mail: arlot@imcce.fr
2 Sternberg astronomical institute, 13 Universitetskij prospect, 119992 Moscow, Russia
e-mail: emelia@sai.msu.ru
3 Terskol Observatory, Kabardino-Balkaria Republic, 361605, Russian Federation
4 Institut de Ciéncies de l’Espai (IEEC-CSIC), Campus UAB, Facultat de Ciéncies, Torre C5 parell, 08193 Bellaterra, Spain
5 Armagh Observatory, College Hill, Armagh BT61 9DG, UK
6 20 rue Jean Monnet, 78180 Montigny-le-Bretonneux, France
7 Université de Bordeaux, Observatoire Aquitain des Sciences de l’Univers, CNRS, UMR 5804, Laboratoire d’Astrophysique de Bordeaux, 2 rue de l’observatoire, BP 89, 33271 Floirac Cedex, France
8 Sparta Astronomical Society, Sparta, Greece
9 22 Booker Road, 2777 Hawkesbury Heights, Australia
10 136 Rio Senda, Umatilla, Oregon, 97882, USA
11 Paris Observatory, place J. Janssen, 92190 Meudon, France
12 14 Craigieburn Street, 7510 Darfield, New Zealand
13 c/ Anselm Clav, 14, 08635 Sant Esteve Sesrovires, Catalonia, Spain
14 Universidad de Monterrey, Departamento de Física y Matemáticas Av. I. Morones Prieto 4500 Pte, San Pedro Garza García, N.L., CP 66238, México
15 Yunnan Observatory, PR China
16 St. Patrick’s Grammar School, Cathedral Road, Armagh BT61 7QZ, UK
17 St. Louis Grammar School, 151 Newry Road, Kilkeel BT34 4EU, UK
18 Pulkovo Observatory, Saint Petersburg, Russia
19 3 Lupin Pl, Murrumbateman, NSW 2582, Australia
20 Ellinogermaniki Agogi School Observatory, Pallini Attikis, Athens, Greece
21 Observatório Nacional/MCTI, rua Gal. J. Cristino 77, Rio de Janeiro, Brazil
22 Department of Physics, Universidad de La Serena, Cisternas 1200 La Serena, Chile
23 Observatorio do Valongo/UFRJ, Ladeira Pedro Antonio 43, Rio de Janeiro, Brazil
24 Agrupació Astronómica de Sabadell, PO Box 50, 08200 Sabadell, Spain
Received: 23 November 2011
Accepted: 10 April 2012
Context. The photometry of mutual occultations and eclipses of natural planetary satellites can be used to infer very accurate astrometric data. This can be achieved by processing the light curves of the satellites observed during international campaigns of photometric observations of these mutual events.
Aims. This work focuses on processing the complete database of photometric observations of the mutual occultations and eclipses of the Saturnian satellites made during the international campaign in 2009. The final goal is to derive new accurate astrometric data.
Methods. We develop an accurate photometric model of mutual event observations of sufficiently high accuracy. Our original method is applied to derive astrometric data from photometric observations of the mutual occultations and eclipses of the Saturnian satellites.
Results. We process the 26 light curves obtained during the international campaign of photometric observations of the Saturnian satellites in 2009. Compared with the theory TASS 1.7 by Vienne and Duriez, we find that the root mean square of the “O–C” residuals for the 23 highest quality observations are equal to 48.5 and 21.7 mas in right ascension and declination, respectively, we obtain 16.4 and 20.7 mas with the new theory by Lainey and collaborators and 17.3 and 21.6 mas with JPL SAT351 ephemerides. Topocentric or heliocentric angular differences for satellites pairs are obtained for 16 time instants during the time period from December 19, 2008 to July 16, 2009.
Key words: planets and satellites: dynamical evolution and stability / occultations / catalogs / astrometry
Light curves are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/544/A29
© ESO, 2012
1. Introduction
Photometric observations of the mutual occultations and eclipses of natural satellites of planets are an invaluable source of astrometric data. Mutual events involving the Saturnian satellites are rare and difficult to obtain but their astrometric accuracy ensure that they provide useful data to complement direct ground-based CCD imaging and data acquired by space probes.
2. The mutual events
The Earth and the Sun traverse the equatorial plane of Saturn every 15 years. The Saturnicentric declinations of the Earth and the Sun then become zero and, since the orbital plane of the satellites is close to the equatorial plane of Saturn, the satellites occult and eclipse each other.
The 2009 period was not particularly favorable because the equatorial plane crossing occurred during the conjunction of Saturn and the Sun.
Arlot & Thuillot (2008) compiled predictions of all 2009 events using the TASS and D93 ephemerides based upon the studies of Vienne (1995) and Dourneau (1993) for the motion of the Saturnian satellites. We computed 441 mutual events, although only 123 were easily observable. Before 2009, several observational campaigns were completed during previous occurrences (Thuillot et al. 2001; Aksnes et al. 1984). Table 1 presents the results derived for each campaign until the present one. Our goal was to observe as many events as possible. Two separate events were at least desirable to eliminate any biases in the present observations.
Since no thick atmosphere surrounds any of the Saturnian satellites, the photometric observations of these phenomena are extremely accurate for astrometric purposes. The results previously obtained after similar observations of the Saturnian satellites, demonstrated that high astrometric accuracy could be achieved: an accuracy of higher than 30 mas was expected.
This allows us to provide the data necessary to improve the theoretical models of the orbital motions and determine the accelerations in the dynamics of the Saturnian satellites.
Observations made during the observational campaigns.
3. The PHESAT09 campaign
We coordinated an international PHESAT09 campaign to monotor a significant number of events. These events occur in a short period of time, so numerous observers located at several sites were necessary to both help avoid meteorological problems and observe different events from different longitudes. However, observations were more difficult than with the Galilean satellites, which represent similar events: the bright ring of Saturn prevents us from observing the events close to the planet.
3.1. Receptors
When observing mutual events, only relative photometry can generally be performed. This is because the elevation of Saturn above the horizon may be small, the air mass is often too high, and absolute photometry then becomes impossible. Telescopes were equipped with the receptors listed in Table 2.
Receptors used for the observations.
3.2. Sites of observation
Coordinated by the IMCCE, this campaign involved the different locations given in Table 3. This table gives the names, longitudes, latitudes, and elevations of the observational sites and the telescopes used (L means refractor and T means reflector, followed by the aperture in cm).
Sites of observation for the PHESAT09 campaign.
List of the photometric observations.
4. The observed lightcurves
4.1. The reduction procedure
Light curves were deduced from photometric measurements performed with CCD cameras.
For observations completed with television (TV) cameras with CCD detectors, the signal was digitized with digitizing boards. The light curves were also obtained for most of them by aperture photometry and for others by fitting a Gaussian profile to the images. Two-dimensional observations generally allow us to calibrate the signal from a particular satellite to that from a nearby satellite as photometric reference and eventually to acquire data under difficult conditions such as twilight and light clouds (see for example Arlot & Stavinschi 2007).
4.2. The photometric data
Table 4 provides the list of the observed events, including some that are not analyzed in the next sections. Filters and receptors are given. We note that filter L means Large i.e. R+V+B, whereas C means clear i.e. no filter. In the latter case, the wavelengths recorded are centered on the sensitivity of the receptor. In most cases, the CCD used for the observations has a sensitivity centered on R.
Our light curves are available from NSDC server1 as ASCII files, including for each observed photometric point, the date in UTC, and the corresponding recorded light flux. Plots are also provided. The satellites, the flux of which is recorded, are listed in the last column of the table. In the next section, we extract the astrometric data from the light curves.
5. Extracting astrometric data from the photometry of mutual events. General assumptions
We use our original method to derive positional and astrometric data from the measurements of satellite fluxes during their mutual occultations and eclipses. The principal idea behind the method is to model the deviation of the observed relative satellite motion from the theoretical motion provided by the relevant ephemeris rather than analyze the apparent relative motion of one satellite with respect to the other.
The measured flux E during an event at a given time t can be expressed by 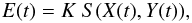 where X(t) and Y(t) are the projections of the differences of planetocentric cartesian coordinates of the two satellites onto the tangent plane of the event. The function S(x,y) describes a model of the phenomenon. It is assumed that S(x,y) = 1 outside each event. The parameter K is a scale factor for the light drop during the event, equivalent to the total flux outside the event.
where X(t) and Y(t) are the projections of the differences of planetocentric cartesian coordinates of the two satellites onto the tangent plane of the event. The function S(x,y) describes a model of the phenomenon. It is assumed that S(x,y) = 1 outside each event. The parameter K is a scale factor for the light drop during the event, equivalent to the total flux outside the event.
Given appropriate theories of the motion of planets and satellites, one can compute the theoretical values of functions X(t),Y(t), i.e., Xth(t),Yth(t) for the time ti(i = 1,2,....m) of each photometric measurement, where m is the number of photometric counts during a single event. The real values of X(ti) and Y(ti) differ from Xth(t) and Yth(t) by corrections Dx,Dy. Our method consists of solving conditional equations 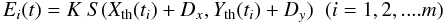 (1)for parameters Dx, Dy, and K where Ei is the photometry recorded at time ti. We linearize conditional equations with respect to parameters Dx,Dy and then solve them using the least squares method.
(1)for parameters Dx, Dy, and K where Ei is the photometry recorded at time ti. We linearize conditional equations with respect to parameters Dx,Dy and then solve them using the least squares method.
The function S(x,y) is calculated as an integral of the flux detected by each point of the satellite detector over the hemisphere facing the Earth. For each point, we consider wavelength-dependent reflective properties of the satellites, various laws of light scattering by a rough surface, a variation in the reflective properties over the satellite surface, wavelength-dependent solar limb-darkening. We also consider the wavelength-dependent sensitivity of the detector.
We refer to Emelyanov (2000, 2003) and Emelyanov & Gilbert (2006) for a more detailed description of the method, which we previously used in our work (Emelyanov 2009).
6. Adopted photometric model of the satellites
Information about the photometric properties of satellites is necessary to obtain more accurate astrometric results from the available observations. We need mainly the disk-resolved albedo as a function of the solar phase angle α in the range of one to six degrees and imaging in the V and R band, as well as information about the scattering properties of the satellite surface.
An extensive analysis of the properties of the Saturnian icy satellites Rhea, Dione, Tethys, Mimas, and Enceladus is performed in Pitman et al. (2010), using the observations of these bodies provided by Cassini space probe. The disk-integrated photometric parameters are provided in the IR bands (0.90−3.60 μm) and for the solar phase angles in the entire range up to 180 degrees. Only for Rhea and Dione do we find that some polynomials provide the closest possible fit to the phase curve for all α and wavelengths given. Owing to the wide range of α allowed, we cannot expect a good presentation of the satellite albedo for the range of one to six degrees.
Voyager disk-resolved photometry of the Saturnian satellites is presented in the papers (Buratti 1984; Buratti & Veverka 1984). The scattering properties of the satellites surfaces are obtained by extracting photometric scans across their disks. Scans along the photometric equators at the phase angles of 17, 13, 10, 7 and 5 degrees for Mimas, Enceladus, Tethys, Dione, and Rhea are accordingly provided in Buratti (1984). Mimas, Enceladus, and Tethys show a non-lunarlike photometric function with significant limb darkening. Therefore, a combined photometric function of 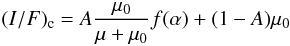 (2)is proposed in this paper. In this function, μ0 and μ are the cosines of the incident and emission angles, and f(α) is the surface phase function, which expresses changes in intensity due to factors such as the single particle phase function and mutual shadowing among regolith particles. Two terms in Eq. (2) represent photometric functions corresponding to two different properties of satellite surface and parameter A gives the relation between them.
(2)is proposed in this paper. In this function, μ0 and μ are the cosines of the incident and emission angles, and f(α) is the surface phase function, which expresses changes in intensity due to factors such as the single particle phase function and mutual shadowing among regolith particles. Two terms in Eq. (2) represent photometric functions corresponding to two different properties of satellite surface and parameter A gives the relation between them.
The best-fit photometric function for different areas of the satellites is shown in the papers (Buratti 1984; Buratti & Veverka 1984), where the values of A are determined. Unfortunately, no analytic representation for f(α) is given. The only values of f(0) with corresponding values of A are shown in Fig. 13 of (Buratti 1984). These values are also given in Table 5 below.
We note that in (Buratti 1984) the surface phase function f(α) can be found from the disk-integrated phase effect Φ(α) using the equations ![\begin{eqnarray} \label{falpha} &&f(\alpha)=\frac{\Phi(\alpha) \; p - q }{D} , \\ \label{palbedo} && p= \frac{2}{3}(1-A)+\frac{Af(0)}{2} , \\ && q= \frac{2}{3} \frac{1}{\pi}(1-A)[\sin\alpha+(\pi-\alpha)\cos\alpha] ,\nonumber \\ \nonumber &&D=\frac{Af(0)}{2}\left(1-\sin\frac{\alpha}{2}\tan\frac{\alpha}{2}\ln\cot\frac{\alpha}{4}\right) \end{eqnarray}](/articles/aa/full_html/2012/08/aa18509-11/aa18509-11-eq40.png) which follows from the integration of the photometric function in Eq. (2) over the satellite hemisphere facing the Earth.
which follows from the integration of the photometric function in Eq. (2) over the satellite hemisphere facing the Earth.
The disk-integrated phase function Φ(α) is defined by 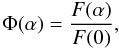 where F(α) is the light flux from the satellite.
where F(α) is the light flux from the satellite.
Disk-integrated phase curves were constructed for each of the satellites using Voyager clear-filter data (Buratti & Veverka 1984). These phase curves can be fitted adequately by a quadratic polynomial of the form 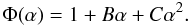 (5)The values of B and C are given in (Buratti & Veverka 1984) but cannot be used in our application, which are determined over the observed range of phase angles of 2–68 degrees for Rhea and 7 − 133 degrees for other satellites.
(5)The values of B and C are given in (Buratti & Veverka 1984) but cannot be used in our application, which are determined over the observed range of phase angles of 2–68 degrees for Rhea and 7 − 133 degrees for other satellites.
We note that the geometric albedo p at α = 0 of an object whose surface scatters light according to Eq. (2) is given by Eq. (4).
The phase effect in ground-based photometric observations is usually described by the equation 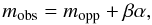 where mobs is the observed magnitude of satellite, mopp is the opposition magnitude, and β is the phase coefficient measured in magnitudes/degree. With the phase coefficient β, the disk-integrated phase function Φ(α) can be expressed by
where mobs is the observed magnitude of satellite, mopp is the opposition magnitude, and β is the phase coefficient measured in magnitudes/degree. With the phase coefficient β, the disk-integrated phase function Φ(α) can be expressed by 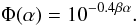 (6)Buratti & Veverka (1984) published the geometric albedo of five Saturnian satellites obtained from Voyager observations in the clear filter and reduced to α = 0. These values designated by pV are given in Table 5.
(6)Buratti & Veverka (1984) published the geometric albedo of five Saturnian satellites obtained from Voyager observations in the clear filter and reduced to α = 0. These values designated by pV are given in Table 5.
Results of the ground-based photometry of the Saturnian satellites are published in (Buratti et al. 1998). We derive the geometric albedo pI reduced to α = 0 and the phase coefficient β from near-infrared (0.9 μm) photometric observations. These values are also given in Tables 5 and 6.
Using the photometric function (2) and the values of A and f(0) from (Buratti 1984), we calculate the appropriate geometric albedo of satellites p reduced to α = 0, whose values are given in Table 5. As can be seen in Table 5, the geometric albedo p differs from pV and pI for all five satellites.
The rotational lightcurve in astronomical magnitudes is derived for each satellite from ground-based photometry of the Saturnian satellites in (Buratti et al. 1998). The data were fit to the two-parameter equation 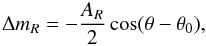 where θ is the planetographic longitude of the target center as seen by the observer (with the synchronous rotation of the satellite θ = 0 and θ = 90° correspond to the upper conjunction and Eastern elongation, respectively), and AR and θ0 are parameters. Similar studies are presented in (Kulyk 2008). We take the parameters AR and θ0 from (Buratti et al. 1998) for Mimas and from (Kulyk 2008) for other satellites. For these parameters, we refer to Table 6.
where θ is the planetographic longitude of the target center as seen by the observer (with the synchronous rotation of the satellite θ = 0 and θ = 90° correspond to the upper conjunction and Eastern elongation, respectively), and AR and θ0 are parameters. Similar studies are presented in (Kulyk 2008). We take the parameters AR and θ0 from (Buratti et al. 1998) for Mimas and from (Kulyk 2008) for other satellites. For these parameters, we refer to Table 6.
In our method for deriving astrometric results, we take the values of A and f(0) from (Buratti 1984) to determine an appropriate relation between the two terms in Eq. (2). We take the phase coefficient β from (Buratti et al. 1984) and define the disk-integrated phase function Φ(α) with Eq. (6). We then use the Eq. (3) to define the disk-resolved phase function f(α). Finally, we adopt the photometric function 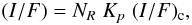 where
where 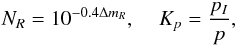 and (I/F)c is defined by Eq. (2). Thus, the rotational variations in the light flux from the satellite is taken into consideration with the coefficient NR, and the coefficient Kp reduces the photometric function to the albedo pI. We choose the albedo pI as the most appropriate values determined from the ground-based photometry at the wavelength 0.9 μm. Most of the photometric observations of the mutual events of satellites are performed with R or I filters. We disregard the wavelength dependence of the reflective properties of the satellites as it is insignificant for the Saturnian satellites from Mimas to Rhea and determined with low precision.
and (I/F)c is defined by Eq. (2). Thus, the rotational variations in the light flux from the satellite is taken into consideration with the coefficient NR, and the coefficient Kp reduces the photometric function to the albedo pI. We choose the albedo pI as the most appropriate values determined from the ground-based photometry at the wavelength 0.9 μm. Most of the photometric observations of the mutual events of satellites are performed with R or I filters. We disregard the wavelength dependence of the reflective properties of the satellites as it is insignificant for the Saturnian satellites from Mimas to Rhea and determined with low precision.
Adopted values of the phase coefficient β and the parameters AR, θ0 (in degrees) of the rotational lightcurves of satellites.
The astrometric reduction of lightcurves observed during the PHESAT95 campaign of Saturnian satellites was performed by Noyelles et al. (2003). The method developed and applied in this paper is based on the Aksnes calculation (Aksnes & Franklin 1976). Modeling mutual events was made using the photometric model of the Saturnian satellites based on the results of Buratti (1984) and Buratti et al. (1984). Noyelles et al. (2003) adopt an interpretation of these results given by Devyatkin and Miroshnichenko (2001). In both papers, the photometric function given in Eq. (2) is taken into account. Unfortunately, Devyatkin and Miroshnichenko (2001) adopt the expression f(α) = A + Bα + Cα2 for the disk-resolved phase function f(α) with the cofficients B and C given in (Buratti & Veverka 1984) not for the disk-resolved phase function but the disk-integrated one given in Eq. (5). This expression contradicts the formula in Eq. (3) of Buratti (1984). Noyelles et al. (2003) erroneously replace this expression by f(α) = f(0) + Bα + Cα2, which also contradicts the results of Buratti (1984).
7. Astrometric parameters
In addition to cartesian coordinates X,Y, one can also consider angular coordinates X′′ and Y′′ defined by the equations 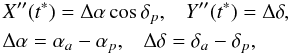 where αa, δa are the right ascension and declination of occulting or eclipsing satellite, αp, δp are the corresponding coordinates of the occulted or eclipsed satellite. In the cases of mutual eclipses, these coordinates are heliocentric.
where αa, δa are the right ascension and declination of occulting or eclipsing satellite, αp, δp are the corresponding coordinates of the occulted or eclipsed satellite. In the cases of mutual eclipses, these coordinates are heliocentric.
Precise relationships between X′′,Y′′ and X,Y can be found in Emelyanov (1999). Given the topocentric or heliocentric distances R of the satellites, one can compute X′′,Y′′ from X,Y using approximate relations 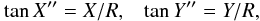 which are accurate for the considered observations to 0.00001 arcsecond.
which are accurate for the considered observations to 0.00001 arcsecond.
In a similar way, we designate by 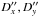 the angular values corresponding to the corrections Dx,Dy.
the angular values corresponding to the corrections Dx,Dy.
After the solution of the Eqs. (1), the astrometric result of the observation is derived as the corrected relative position of satellites 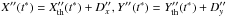 , together with the associated time instant t ∗ inside the time interval of the event. Although this is not mandatory, we assume that t ∗ is the time instant when
, together with the associated time instant t ∗ inside the time interval of the event. Although this is not mandatory, we assume that t ∗ is the time instant when 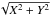 takes its minimum value, i.e., t ∗ is the time of the closest apparent approach of the satellites.
takes its minimum value, i.e., t ∗ is the time of the closest apparent approach of the satellites.
The errors σx and σy in the parameters 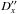 ,
, 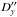 estimated via the least squares method can then be interpreted as internal errors in the astrometric results following from the random errors in the photometry.
estimated via the least squares method can then be interpreted as internal errors in the astrometric results following from the random errors in the photometry.
We apply the theory TASS 1.7 of the main Saturnian satellites (Vienne & Duriez 1995; Duriez & Vienne 1997) to compute the theoretical values of Xth(t) and Yth(t). The derived values of 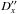 and
and 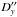 are the residuals (O–C) with respect to the applied theory of satellite motion.
are the residuals (O–C) with respect to the applied theory of satellite motion.
8. Fitting the dynamical model: the NOE solution
The IMCCE ephemeris NOE-6-2011-MAIN was produced from the numerical integration of the orbital motion of the eight main Saturnian moons (Lainey et al. 2012). This model includes essentially the mutual perturbations of each moon, the gravity field of the primary up to order six, the Solar and Jovian perturbations, as well as tidal effects between each moon and their primary (see Lainey et al. 2012 for a full description of the numerical modeling). Astrometric observations covering the years [1886, 2009] including the present data are considered when fitting the numerical model. The internal accuracy of the integration is expected to be on the order of a few hundreds of meters. The expected accuracy of this ephemeris is highly dependent on the satellite and epoch of concern. Over the whole covered period, it is estimated to be about 600 km for the six innermost moons, and 1,800 km for Hyperion and Iapetus. This ephemeris is available under SPICE format and can be downloaded from the IMCCE FTP server2.
Residuals 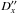 ,
, 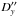 (O–C) with respect to the applied theory TASS 1.7, with respect to the theory by Lainey (2011), and with respect to the ephemerides SAT351 of JPL find by HORIZONS web-interface.
(O–C) with respect to the applied theory TASS 1.7, with respect to the theory by Lainey (2011), and with respect to the ephemerides SAT351 of JPL find by HORIZONS web-interface.
9. Derived astrometric results
This section presents the astrometric results obtained from the observations of the satellites during their mutual eclipses and occultations in 2009. From all available data, two coordinates X′′(t∗), Y′′(t∗) for each event are successfully determined. Every final astrometric result of the observation of a single mutual phenomenon at a given observatory consists of the following fields: date, the type of the phenomenon (eclipse or occultation) including the satellite numbers, observatory code, the time instant t∗ in the UTC scale, X′′(t∗), Y′′(t∗), σx, σy, 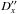 and
and 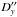 . The type of phenomenon is coded as naonp or naenp for a mutual occultation or eclipse, respectively, where na is the number of the occulting or eclipsing satellite and np is the number of either the occulted or eclipsed satellite. We give the results in the form of the angular separation s (in arcseconds) and position angle A (in degrees) corresponding to X′′(t∗) and Y′′(t∗). The minimum level Smin of normalized flux is also given. We assign flag Q to each observation in order to indicate the quality and the reliability of the result. Flag Q may have one of the following two values: “0” for normally determined coordinates and “1” for the results obtained from poor photometric data.
. The type of phenomenon is coded as naonp or naenp for a mutual occultation or eclipse, respectively, where na is the number of the occulting or eclipsing satellite and np is the number of either the occulted or eclipsed satellite. We give the results in the form of the angular separation s (in arcseconds) and position angle A (in degrees) corresponding to X′′(t∗) and Y′′(t∗). The minimum level Smin of normalized flux is also given. We assign flag Q to each observation in order to indicate the quality and the reliability of the result. Flag Q may have one of the following two values: “0” for normally determined coordinates and “1” for the results obtained from poor photometric data.
Right ascensions and declinations are measured in the ICRF. All angular quantities are in arcseconds but the positon angle is given in degrees. In the case of a mutual occultation t∗, is the time of topocentric observation of satellites, and for a mutual eclipse t∗ is the time of topocentric observation of the eclipsed satellite. Table 7 gives the astrometric results. This table is available in electronic form from the Natural Satellites Data Center service3.
The residuals (O–C) with respect to the applied theories of satellite motion are given in Table 7. We compare the extracted astrometric data with the following models: TASS 1.7 (Duriez & Vienne 1997), Lainey et al. (2011) made with the numerical integration and based on a large series of observations and to the ephemerides SAT351 of JPL find by HORIZONS web-interface.
Estimates of the accuracy of the results of astrometric reduction performed to determine two coordinates X′′(t∗), Y′′(t∗).
10. Estimation of the accuracy of the derived astrometric results
We estimate the accuracy of the derived astrometric results using the least-squares method, which derives the standard errors σx, σy in the parameters 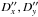 from the observed light curves. These errors are due to random errors in the photometry and characterize the internal accuracy of the astrometric results. We calculate the root mean square (r.m.s.) values of these estimates for all the light curves reduced. Only 23 good results with Q = 0 are taken into consideration. These estimates are listed in Table 8 as total random errors. A 4 mas geocentric uncertainty corresponds to 24 km in situ which we compare with space-based astrometric observations assumed to have an internal accuracy of 10 km. We also calculate the total rms of all
from the observed light curves. These errors are due to random errors in the photometry and characterize the internal accuracy of the astrometric results. We calculate the root mean square (r.m.s.) values of these estimates for all the light curves reduced. Only 23 good results with Q = 0 are taken into consideration. These estimates are listed in Table 8 as total random errors. A 4 mas geocentric uncertainty corresponds to 24 km in situ which we compare with space-based astrometric observations assumed to have an internal accuracy of 10 km. We also calculate the total rms of all 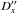 and
and 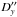 computed over all events and all observatories for the 23 cases with Q = 0. These values are given with respect to the applied theory (Vienne & Duriez 1995; Duriez & Vienne 1997), as well as with respect to the theory of Lainey et al. (2011). These estimates are given in Table 8 as the rms of O–C. We note that the (O–C)s are larger than the random error. This is indicative of a systematic error that is either observational or theoretical. We know that observational errors may occur but differently depending on the kind of observations, hence different kinds of observations must be used to fit the theoretical models. However, the difference in the mean (O–C)s between the three ephemerides shows that the theoretical models still contains some errors. It is interesting to see that both the ephemerides of Lainey (2012) and that of JPL (SAT351) have similar (O–C)s demonstrating that ground-based observations, including the present ones, have similar usefulnesses for ephemerides as Cassini’s ones.
computed over all events and all observatories for the 23 cases with Q = 0. These values are given with respect to the applied theory (Vienne & Duriez 1995; Duriez & Vienne 1997), as well as with respect to the theory of Lainey et al. (2011). These estimates are given in Table 8 as the rms of O–C. We note that the (O–C)s are larger than the random error. This is indicative of a systematic error that is either observational or theoretical. We know that observational errors may occur but differently depending on the kind of observations, hence different kinds of observations must be used to fit the theoretical models. However, the difference in the mean (O–C)s between the three ephemerides shows that the theoretical models still contains some errors. It is interesting to see that both the ephemerides of Lainey (2012) and that of JPL (SAT351) have similar (O–C)s demonstrating that ground-based observations, including the present ones, have similar usefulnesses for ephemerides as Cassini’s ones.
11. Conclusions
We have compiled the entire database of photometric observations of the mutual occultations and eclipses of the Saturnian satellites made during the international campaign in 2009 to determine the topocentric or heliocentric angular differences for satellite pairs at 16 time instants in the time interval from December 19, 2008 to July 16, 2009. The standard errors in the relative satellite coordinates caused by the random errors of the photometry are equal to 3.7 and 4.3 mas in right ascension and declination, respectively. The rms of “O–C” residuals with respect to the theory TASS 1.7 developed by (Vienne & Duriez 1995; Duriez & Vienne 1997) are equal to 48.5 and 21.7 mas in right ascension and declination, respectively, for successful observations. The comparison of the astrometric results with the theory of Lainey et al. (2012) fitted to ground-based observations including the present ones shows rms of “O–C” residuals of 16.4 and 20.7 mas in right ascension and declination, respectively and the comparison with JPL SAT351 ephemerides fitted to Cassini’s observations shows rms in the (O–C)s of 17.3 and 21.6 mas. This demonstrates that ground-based observations are still a useful complement to space-based observations.
Acknowledgments
This work was made possible thanks to the Russian Foundation for Basic Research, project no. 07-02-92169-a, to the PNP (Programme National de Planetologie, CNES-INSU), to the PICS CNRS- Russian Academy of Sciences, to UPMC-EMERGENCE (contract number EME0911) and to the Scientific Council of Paris Observatory.
References
- Aksnes, K., & Franklin, F. 1976, AJ, 81, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Aksnes, K., Franklin, F., Millis, R., et al. 1984, AJ, 89, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Arlot, J. E., & Thuillot, W. 2008, A&A, 485, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlot, J. E., & Stavinschi, M. 2007, Solar and Stellar Physics Through Eclipses, eds. O. Demircan, S. O. Selam, & B. Albayrak (San Francisco: ASP), ASP Conf. Ser., 370, 58 [Google Scholar]
- Buratti, B. J. 1984, Icarus, 59, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Buratti, B. J., & Veverka, J. 1984, Icarus, 58, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Buratti, B. J., Mosher, J. A., Nicholson, P. D., McGhee, C. A., & French, R. G. 1998, Icarus, 136, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Devyatkin, A. V., & Miroshnichenko, A. S. 2001, Astron. Lett., 27, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Dourneau, G. 1993, A&A, 267, 292 [NASA ADS] [Google Scholar]
- Duriez, L., & Vienne, A. 1997, A&A, 324, 366 [NASA ADS] [Google Scholar]
- Emelianov, N. V. 1999, Sol. Syst. Res., 33, 133 [Google Scholar]
- Emel’yanov, N. V. 2000, Sol. Syst. Res., 34, 226 [Google Scholar]
- Emelianov, N. V. 2003, Sol. Syst. Res., 37, 314 [Google Scholar]
- Emelyanov, N. V. 2009, MNRAS, 394, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Emelyanov, N. V., & Gilbert, R. 2006, A&A, 453, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulyk, I. 2008, Planet. Space Sci., 56, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Karatekin, O., Desmars, J., et al. 2012, ApJ, 752, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Noyelles, B., Vienne, A., & Descamps, P. 2003, A&A, 401, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pitman, K. M., Buratti, B. J., & Mosher, J. A. 2010, Icarus, 206, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillot, W., Arlot, J.-E., Ruatti, C., et al. 2001, A&A, 371, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vienne, A., & Duriez, L. 1995, A&A, 297, 588 [NASA ADS] [Google Scholar]
All Tables
Adopted values of the phase coefficient β and the parameters AR, θ0 (in degrees) of the rotational lightcurves of satellites.
Residuals 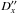 ,
, 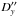 (O–C) with respect to the applied theory TASS 1.7, with respect to the theory by Lainey (2011), and with respect to the ephemerides SAT351 of JPL find by HORIZONS web-interface.
(O–C) with respect to the applied theory TASS 1.7, with respect to the theory by Lainey (2011), and with respect to the ephemerides SAT351 of JPL find by HORIZONS web-interface.
Estimates of the accuracy of the results of astrometric reduction performed to determine two coordinates X′′(t∗), Y′′(t∗).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


