| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118160 | |
| Published online | 17 August 2012 | |
The equilibrium tide in stars and giant planets
I. The coplanar case
1 LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
e-mail: jean-paul.zahn@obspm.fr; jean-paul.zahn@obspm.fr
2 IMCCE, Observatoire de Paris, UMR 8028 CNRS, UPMC, USTL, 77 avenue Denfert-Rochereau, 75014 Paris, France
3 Laboratoire AIM, CEA/DSM, CNRS, Université Paris Diderot, IRFU/SAp Centre de Saclay, 91191 Gif-sur-Yvette, France
e-mail: stephane.mathis@cea.fr
4 LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
Received: 27 September 2011
Accepted: 9 May 2012
Context. Since 1995, more than 500 extrasolar planets have been discovered orbiting very close to their parent star, where they experience strong tidal interactions. Their orbital evolution depends on the physical mechanisms that cause tidal dissipation, which remain poorly understood.
Aims. We refine the theory of the equilibrium tide in fluid bodies that are partly or entirely convective, to predict the dynamical evolution of the systems. In particular, we examine the validity of modeling the tidal dissipation using the quality factor Q, which is commonly done. We consider here the simplest case where the considered star or planet rotates uniformly, all spins are aligned, and the companion is reduced to a point mass.
Methods. We expand the tidal potential as a Fourier series, and express the hydrodynamical equations in the reference frame, which rotates with the corresponding Fourier component. The results are cast in the form of a complex disturbing function, which may be implemented directly in the equations governing the dynamical evolution of the system.
Results. The first manifestation of the tide is to distort the shape of the star or planet adiabatically along the line of centers. This generates the divergence-free velocity field of the adiabatic equilibrium tide, which is stationary in the frame rotating with the considered Fourier component of the tidal potential; this large-scale velocity field is decoupled from the dynamical tide. The tidal kinetic energy is dissipated into heat by means of turbulent friction, which is modeled here as an eddy-viscosity acting on the adiabatic tidal flow. This dissipation induces a second velocity field, the dissipative equilibrium tide, which is in quadrature with the exciting potential; this field is responsible for the imaginary part of the disturbing function, which is implemented in the dynamical evolution equations, from which one derives the characteristic evolutionary times.
Conclusions. The rate at which the system evolves depends on the physical properties of the tidal dissipation, and specifically on both how the eddy viscosity varies with tidal frequency and the thickness of the convective envelope for the fluid equilibrium tide. At low frequency, this tide is retarded by a constant time delay, whereas it lags behind by a constant angle when the tidal frequency exceeds the convective turnover rate.
Key words: binaries: close / planetary systems
© ESO, 2012
1. Introduction and general context
Stellar binaries provide invaluable information about the structure of stars and the dynamical processes operating within them. The analysis of the motion of a binary’s components allows us to determine their masses and radii, and through the apsidal precession it places constraints on their internal mass distribution. Furthermore, their orbital evolution due to tidal dissipation sheds some light on their formation and past history. Quite naturally, similar benefits may be expected from the study of extrasolar planets. Since 1995, more than five hundred of those have been discovered orbiting very close to their host star, and their number continues to increase thanks to dedicated space missions (CoRoT and Kepler) and extensive ground-based programs, with powerful instruments such as HARPS (for a review, see Udry & Santos 2007, and references therein). Furthermore, recent studies of the orbital evolution of natural satellites in our solar system have allowed an improved quantification of the tidal dissipation in both Jupiter (Lainey et al. 2009) and Saturn (Lainey et al. 2012). This renewed interest in the gravitational interaction between various celestial bodies motivates us to refine our knowledge of the physical processes that intervene in tides.
The dynamical evolution of a binary system is driven by the conversion of its mechanical energy into heat. Provided that the system loses no angular momentum, it resorts to the state of minimum energy in which the orbits are circular, the rotation of the components is synchronized with the orbital motion, and the spins are aligned. However, in very close systems with high mass ratios, these final states cannot be achieved: the planet instead spirals toward the star and may eventually be engulfed by it (Hut 1981; Levrard et al. 2009). To predict the fate of a binary system, one has to identify the dissipative processes that achieve the conversion of kinetic energy into thermal energy, from which one may then draw the characteristic times of circularization, synchronization, and spin alignment. Before reviewing these processes, we recall the two types of tides that operate in stars and the fluid parts of giant planets. The equilibrium tide designates the large-scale flow induced by the hydrostatic adjustment of the star in response to the gravitational force exerted by the companion (Zahn 1966a,b, we refer to that paper as Z66). On the other hand, the dynamical tide corresponds to the eigenmodes (gravity, inertial, or gravito-inertial waves) that are excited by the tidal potential (Zahn 1975; Goldreich & Nicholson 1989; Ogilvie & Lin 2004; Goodman & Lackner 2009; Rieutord & Valdetarro 2010; Barker & Ogilvie 2010). These tides experience two main dissipative mechanisms: turbulent friction in convective regions and thermal dissipation acting on the gravito-inertial modes excited in radiative zones.
We focus here on the equilibrium tide acting in the convective envelopes of solar-like stars or giant planets. The physical description of this tide, with turbulent dissipation, was formulated by Z66. Several authors have applied this theory to binary stars (see Koch & Hrivnak 1981; Bouchet & Zahn 1989; Verbunt & Phinney 1995), finding that it agrees well with the observations (pre-main-sequence binaries, red giants, etc.), except for main-sequence stars older than about one Gyr (Mathieu et al. 2004). Here, we revisit the theoretical formalism of Z66 by expressing the velocity field of the equilibrium tide in the appropriate reference frame, i.e. that rotating with each Fourier component of the tidal potential. This treatment filters out properly the dynamical tide, suppressing the spurious “pseudo-resonances” encountered in Z66. Our second goal, in the present work, is to improve the description of the equilibrium tide by tying the quality factor Q, which is commonly used in planetology and celestial mechanics, with the physical process of convective turbulent dissipation (Goldreich & Soter 1966; Goldreich & Nicholson 1977). We assume here, for simplicity, that all spins are aligned, i.e. that the rotation axes of the primary and secondary are perpendicular to the orbital plane; the case of non-aligned spins will be treated in an upcoming paper. Furthermore, differential rotation, which is present in stellar and planetary interiors, is not accounted for in this first work and the rotation is assumed to be uniform.
2. Reference frame and tidal potential
2.1. The reference frame
We consider a system consisting of two bodies A and B, of mass mA and mB, and we describe the tide exerted by B on A, which we assume to be in a fluid state, i.e. to be either a star or a giant planet. Owning to their mutual attraction, they move in elliptic orbits around their common center of mass, but it is often convenient to choose a reference frame ℛA, whose origin is placed at the center of A (designated by the same letter) and whose axes {X,Y,Z} have fixed directions in space. We assume that all spins are aligned along the 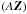 axis; hence the position of B is entirely determined by the three Keplerian elements: the semi-major axis a of the relative orbit of B around A, its eccentricity e, and its mean anomaly M = nt, where n is the mean motion.
axis; hence the position of B is entirely determined by the three Keplerian elements: the semi-major axis a of the relative orbit of B around A, its eccentricity e, and its mean anomaly M = nt, where n is the mean motion.
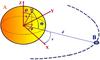 |
Fig. 1 Spherical coordinates system attached to the reference frame ℛA centered on A. The spin of A is perpendicular to the orbital plane of B. The dashed line illustrates the orbit of B. |
2.2. The tidal potential
The tidal force exerted by B on A derives from a potential, which may be expanded in Legendre polynomials as 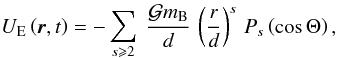 (1)where
(1)where 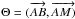 , M is the current position r, and d is the distance AB. Kepler’s third law
, M is the current position r, and d is the distance AB. Kepler’s third law 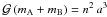 allows us to rewrite Eq. (1)in the slightly different form
allows us to rewrite Eq. (1)in the slightly different form 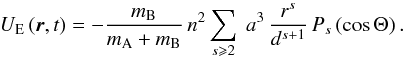 (2)Finally, introducing the angular variables (θ,ϕ) related to the reference frame ℛA and the associated Legendre functions
(2)Finally, introducing the angular variables (θ,ϕ) related to the reference frame ℛA and the associated Legendre functions 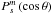 , we get
, we get ![\begin{eqnarray} &&{U_{\rm E}}\left(r,\theta,\varphi,t\right) = -\frac{m_{\rm B}}{m_{\rm A}+m_{\rm B}} \, n^2 \sum_{s \se 2} \, \Re \left[ \frac{r^s}{a^{s-2}} \, \sum_{m=0}^{s} \, \frac{(s-m)!}{(s+m)!} \right. \nonumber\\ &&\quad\left. \times\, \left(2-\delta_{0,m}\right) P_s^m \left(0\right) \, P_s^m \left(\cos\theta\right) \, \exp \left[ {\rm i} m \varphi \right] \left( \frac{a}{d} \right)^{s+1}\, \exp \left[-{\rm i} m v\right] \right], \label{UE_Legendre} \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq21.png) (3)where v designates the true anomaly of B. The next step is to expand the time-dependent terms as a Fourier series
(3)where v designates the true anomaly of B. The next step is to expand the time-dependent terms as a Fourier series ![\begin{equation} \left( \frac{a}{d} \right)^{s+1}\, \exp \left [-{\rm i} m v \right] = \sum_{l} G_{s,\frac{s-m}{2},l-m} \left(e\right) \, \exp \left[-{\rm i} l n t \right], \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq23.png) (4)where we have used Kaula’s functions Gj,p,q(e) (Kaula 1962). Furthermore, we have
(4)where we have used Kaula’s functions Gj,p,q(e) (Kaula 1962). Furthermore, we have 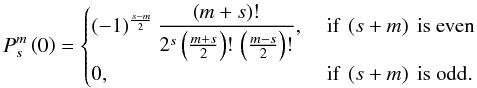 (5)We chose the Kaula’s functions in the Fourier expansion, instead of the Hansen coefficients, to prepare the ground for a subsequent paper, where we shall treat the case of non-aligned spins. These functions
(5)We chose the Kaula’s functions in the Fourier expansion, instead of the Hansen coefficients, to prepare the ground for a subsequent paper, where we shall treat the case of non-aligned spins. These functions 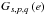 are polynomials in e, whose lowest power is | q | . We give their expressions in Table 1 for the most frequently used triplets {s,p,q}, since for a low eccentricity it suffices to retain only a few q values (q ∈ [[−2,2]]).
are polynomials in e, whose lowest power is | q | . We give their expressions in Table 1 for the most frequently used triplets {s,p,q}, since for a low eccentricity it suffices to retain only a few q values (q ∈ [[−2,2]]).
From now on, we retain only the time-dependent part of the potential UE, which we call U, the tidal potential 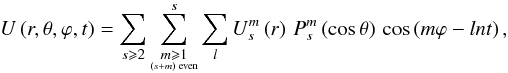 (6)where the radial parts
(6)where the radial parts 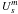 of the potential are given by:
of the potential are given by: 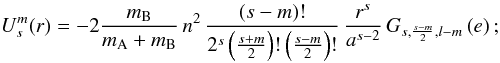 (7)the tidal potential is thus the interaction potential, from which we have subtracted the acceleration responsible for the movement of the center of mass of A:
(7)the tidal potential is thus the interaction potential, from which we have subtracted the acceleration responsible for the movement of the center of mass of A: ![\hbox{$\mathcal G\,m_{\rm B}/d\,\left[1+\left(\vec r_{\rm B}\cdot\vec r\right)/d^2\right]$}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq36.png) .
.
Values of the eccentricity function 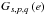 in the quadrupolar case where s = 2.
in the quadrupolar case where s = 2.
We may further simplify this expression of the tidal potential if we consider binary systems that are separated enough to allow the companion to be treated as a point mass; this approximation was discussed by Mathis & Le Poncin-Lafitte (2009). In this quadrupolar approximation, we retain only the lowest term of the potential (s = 2). Furthermore, since we consider the coplanar case, the sole value of m that remains is m = 2 in Eq. (6), and U thus becomes 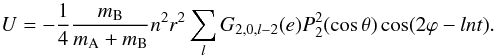 (8)
(8)
3. The tidal velocity field
3.1. Governing equations
The tidal potential in Eq. (8)induces in the star (or the giant planet) pressure and density perturbations and a modified velocity field W, which obeys the equations of motion 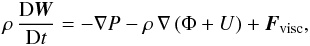 (9)continuity
(9)continuity 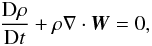 (10)Poisson
(10)Poisson 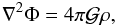 (11)and entropy
(11)and entropy  where we use the total derivative
where we use the total derivative 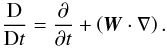 (13)These are completed by the expressions for the radiation flux
(13)These are completed by the expressions for the radiation flux 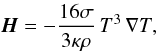 (14)and the specific entropy
(14)and the specific entropy 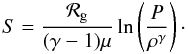 (15)The physical quantities intervening in these equations, are the pressure P, the temperature T, the density ρ, the gravitational potential created by the star Φ, the viscous force Fvisc, the nuclear energy-production rate per unit mass ε, the absorption coefficient κ, the ratio γ = CP/CV of specific heats at both constant pressure (CP) and constant density (Cρ), the molecular mass μ, σ the Stefan-Boltzmann constant, and ℛg the perfect gas constant.
(15)The physical quantities intervening in these equations, are the pressure P, the temperature T, the density ρ, the gravitational potential created by the star Φ, the viscous force Fvisc, the nuclear energy-production rate per unit mass ε, the absorption coefficient κ, the ratio γ = CP/CV of specific heats at both constant pressure (CP) and constant density (Cρ), the molecular mass μ, σ the Stefan-Boltzmann constant, and ℛg the perfect gas constant.
Treating the tides as a small amplitude perturbation of the hydrostatic structure of the object, we separate all scalar quantities into 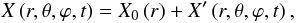 (16)where X0 designates the spherically symmetrical profile of X, and X′ represents the perturbation due to the tidal potential. The reference state is drawn from an up-to-date stellar or planetary structure model.
(16)where X0 designates the spherically symmetrical profile of X, and X′ represents the perturbation due to the tidal potential. The reference state is drawn from an up-to-date stellar or planetary structure model.
We now turn to the global velocity field W, from which we substract the star’s rotation (assumed here to be uniform) to isolate the time-dependent tidal velocity field V′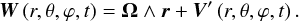 This tidal velocity field may be expanded in the same way as the tidal potential in Eq. (6), and each component
This tidal velocity field may be expanded in the same way as the tidal potential in Eq. (6), and each component  may be analyzed in the reference frame ℛC that rotates with the corresponding tidal frequency, i.e. the angular velocity
may be analyzed in the reference frame ℛC that rotates with the corresponding tidal frequency, i.e. the angular velocity 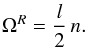 (17)In this reference frame, all quantities X′ induced by the equilibrium tide are stationary, particularly the density and the velocity field
(17)In this reference frame, all quantities X′ induced by the equilibrium tide are stationary, particularly the density and the velocity field 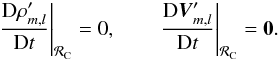 (18)From the continuity equation (Eq. (10)), we then deduce that
(18)From the continuity equation (Eq. (10)), we then deduce that 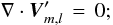 (19)this property will hold in any reference frame, thus also for the total tidal velocity field V′. This confirms the solenoidal character of that flow, in contrast to the claim made by Scharlemann (1981).
(19)this property will hold in any reference frame, thus also for the total tidal velocity field V′. This confirms the solenoidal character of that flow, in contrast to the claim made by Scharlemann (1981).
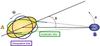 |
Fig. 2 Typical system of tidal interaction. Body B exerts a tidal force on body A, which adjusts itself with a phase lag δ, because of internal friction. This adjustment may be divided into an adiabatic component, which is in phase with the tide, and a dissipative one, which is in quadrature. |
3.2. Adiabatic system – dissipative system
In our treatment of the equilibrium tide, we separate all quantities and equations into two parts:
-
first, an adiabatic system (I) in phase with the perturbing potential U (Eq. (8)), which corresponds to the adiabatic tide, i.e. the star’s response to the tidal excitation, ignoring all dissipative processes;
-
second, a dissipative system (II) in quadrature with the perturbing potential, which corresponds to the star’s response due to the dissipative processes (here, the turbulent friction due to the convective motions).
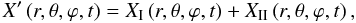 (20)where XI designates the contribution of the adiabatic tide, in phase with the potential U
(20)where XI designates the contribution of the adiabatic tide, in phase with the potential U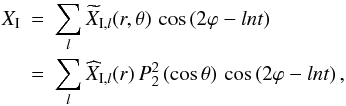 (21)and XII that of the dissipative tide, in quadrature with U
(21)and XII that of the dissipative tide, in quadrature with U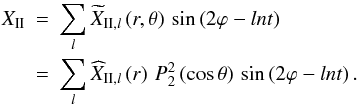 (22)We apply the same distinction to the adiabatic tidal flow
(22)We apply the same distinction to the adiabatic tidal flow 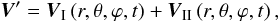 (23)where the tidal field VI induces a radial displacement that is in phase with the potential U
(23)where the tidal field VI induces a radial displacement that is in phase with the potential U![\begin{equation} \vec{V}_\I = \sum_{l} \left[ \begin{array}{l} u_\I(r,\theta) \, \sin(2\varphi-ln t)\\ v_\I(r,\theta) \, \sin(2\varphi-ln t)\\ w_\I(r,\theta) \, \cos(2\varphi-ln t) \end{array} \right], \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq92.png) (24)and the velocity field VII associated with the dissipative tide that is in quadrature
(24)and the velocity field VII associated with the dissipative tide that is in quadrature ![\begin{equation} \vec{V}_\II = \sum_{l} \left[ \begin{array}{l} \quad\, u_\II(r,\theta) \, \cos(2\varphi-ln t) \\ \quad\, v_\II(r,\theta) \, \cos(2\varphi-ln t) \\ -\, w_\II(r,\theta) \, \sin(2\varphi-ln t) \end{array} \right]. \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq94.png) (25)We now linearize the original system of equations (Eqs. (9) − (11)), and divide it likewise into the systems (I) and (II), both with their equations of motion, continuity, Poisson, and entropy, in this order.
(25)We now linearize the original system of equations (Eqs. (9) − (11)), and divide it likewise into the systems (I) and (II), both with their equations of motion, continuity, Poisson, and entropy, in this order.
Adiabatic system (I)
Dissipative system (II)
![\begin{eqnarray} \label{eqNS_II} &&\hspace{-3mm}\rho_0 \left[ \frac{\mrm D \vec{V}_\II}{\mrm Dt} + 2\mbf\Omega\wedge\vec{V}_\II \right] = -\nabla P_\II - \rho_0 \, \nabla\Phi_\II - \rho_\II \, \nabla\Phi_0 +\vec{F}_\II, \\ \label{eqCONT_II} &&\hspace{-3mm} \frac{\mrm D \rho_\II}{\mrm D t} + \rho \nabla \cdot \vec{V}_\II = 0, \\ \label{eqPOIS_II} &&\hspace{-3mm}\nabla^2\Phi_\II =4\pi \mcal{G} \rho_\II, \\ &&\hspace{-3mm} \rho_0 \frac{\mrm D S_\II}{\mrm D t} =0. \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq97.png) As shown in Z66, the dissipative tide is much weaker than the adiabatic tide. That means that for a given scalar field X′ = XI + XII, we have XII ≪ XI. Moreover, this allows us to neglect the viscous force FI(VII) in system (I), but we retain FII(VI) in system (II), where it induces the dissipative tide.
As shown in Z66, the dissipative tide is much weaker than the adiabatic tide. That means that for a given scalar field X′ = XI + XII, we have XII ≪ XI. Moreover, this allows us to neglect the viscous force FI(VII) in system (I), but we retain FII(VI) in system (II), where it induces the dissipative tide.
3.3. The adiabatic equilibrium tide
3.3.1. Adiabatic response to the tidal potential – Love number
We begin with the study of the adiabatic equilibrium tide, which is the hydrostatic response to the perturbing potential U exerted by the companion body, in the absence of dissipation. We expand the perturbations of pressure as in Eq. (21) 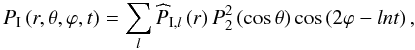 (34)and likewise for ρI(r,θ,ϕ,t) and ΦI(r,θ,ϕ,t). These perturbations obey the equation of motion in Eq. (26) of system (I), from which we remove the acceleration term on the left-hand side (l.h.s.):
(34)and likewise for ρI(r,θ,ϕ,t) and ΦI(r,θ,ϕ,t). These perturbations obey the equation of motion in Eq. (26) of system (I), from which we remove the acceleration term on the left-hand side (l.h.s.): 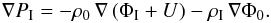 (35)From the vertical balance, we draw
(35)From the vertical balance, we draw 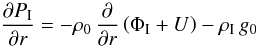 (36)and likewise from the horizontal balance
(36)and likewise from the horizontal balance 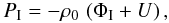 (37)where
(37)where 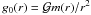 designates the unperturbed gravity. Eliminating PI, we get the expression for the density perturbation
designates the unperturbed gravity. Eliminating PI, we get the expression for the density perturbation 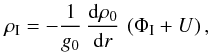 (38)which we implement in the perturbed Poisson equation (Eq. (28)), taking into account that U is an harmonic potential (i.e. ∇2U = 0), to finally obtain (cf. Sweet 1950)
(38)which we implement in the perturbed Poisson equation (Eq. (28)), taking into account that U is an harmonic potential (i.e. ∇2U = 0), to finally obtain (cf. Sweet 1950) 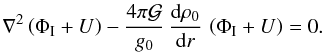 (39)The potential perturbation ΦI has the same dependence on (θ,ϕ,t) as U; we may therefore introduce a function h(r) that depends only on the radial coordinate, such that (ΦI + U) = hU. This function obeys the differential equation
(39)The potential perturbation ΦI has the same dependence on (θ,ϕ,t) as U; we may therefore introduce a function h(r) that depends only on the radial coordinate, such that (ΦI + U) = hU. This function obeys the differential equation 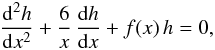 (40)where x = r/R, R being the total radius. The function f(x) depends on the internal mass distribution at equilibrium
(40)where x = r/R, R being the total radius. The function f(x) depends on the internal mass distribution at equilibrium 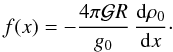 (41)The solution of Eq. (40)is constrained by two boundary conditions: regularity at center x = 0 and h → 1 as x → ∞, which may be written as
(41)The solution of Eq. (40)is constrained by two boundary conditions: regularity at center x = 0 and h → 1 as x → ∞, which may be written as ![\begin{eqnarray} \Phi_\I(x,\theta,\varphi,t) &=& \sum_{l} {\widehat \Phi}_{\I,l} (x)\,{P}_{2}^{2}\left(\cos\theta\right)\,\cos\left(2\varphi-ln t\right) \nonumber \\ & =& \left[ h(x) - 1 \right] \, U (x,\theta,\varphi,t) \nonumber \\ & =& \left[ h(x) - 1 \right] \, \sum_{l} U_l \, x^2 \, P_2^2(\cos \theta) \cos (2\varphi -ln t), \label{PhiI_hs} \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq125.png) (42)where from Eq. (8)
(42)where from Eq. (8)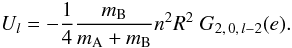 (43)The surface value of the ratio ΦI/U is the second-order Love number in the adiabatic case
(43)The surface value of the ratio ΦI/U is the second-order Love number in the adiabatic case 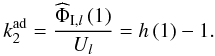 (44)This constant is twice the classical apsidal motion constant, and it is approximatively the fifth moment of the mass distribution (see Eq. (2.15) of Zahn 1966a).
(44)This constant is twice the classical apsidal motion constant, and it is approximatively the fifth moment of the mass distribution (see Eq. (2.15) of Zahn 1966a).
3.3.2. The poloidal component of the adiabatic velocity field
We have established earlier that each Fourier component of the tidal perturbation is stationary in the reference frame ℛC rotating with the angular velocity ΩR = (l/2) n. This is true in particular for the potential (ΦI + U), and therefore 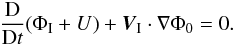 (45)From this, we can derive the vertical component of the velocity field
(45)From this, we can derive the vertical component of the velocity field 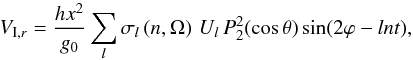 (46)whose amplitude varies linearly with the tidal frequency
(46)whose amplitude varies linearly with the tidal frequency 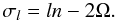 (47)We have now to complement this vertical field with its horizontal counterpart. Since VI is divergence-free, with a radial component, it is natural to seek VI in form of a poloidal field. Following Z66 and Rieutord (1987), we write
(47)We have now to complement this vertical field with its horizontal counterpart. Since VI is divergence-free, with a radial component, it is natural to seek VI in form of a poloidal field. Following Z66 and Rieutord (1987), we write ![\begin{equation} \vec{V}_\I^{\rm P} \, {\equiv} \, \nabla \wedge \nabla \wedge \left[ \left(r\chi^{\rm P}\right) \vec{r} \right], \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq134.png) (48)and expand the poloidal current function χP(x,θ,ϕ,t) in its Fourier components
(48)and expand the poloidal current function χP(x,θ,ϕ,t) in its Fourier components 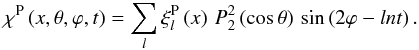 (49)In the inertial frame, the poloidal velocity field is thus given by
(49)In the inertial frame, the poloidal velocity field is thus given by
![\begin{eqnarray} \vec{V}_\I^{\rm P} = \sum_l \left[ \begin{array}{c} \\ 6 \, \xi_l^{\rm P} \, P_2^2\left(\cos\theta\right) \, \sin\left(2\varphi - ln t\right)\\ \\ \dfrac{1}{x} \dfrac{\rm d}{{\rm d}x} \left(x^2 \xi_l^{\rm P} \right)\, \dfrac{\mrm d P_2^2\left(\cos\theta\right)}{\mrm d \theta} \, \sin\left(2\varphi - ln t\right)\\ \end{array} \right]. \label{VIP_hs} \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq137.png) (50)Comparing the radial component with Eq. (46), we obtain the expression for
(50)Comparing the radial component with Eq. (46), we obtain the expression for 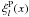
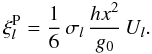 (51)
(51)
3.3.3. The toroidal component of the adiabatic velocity field
The description of the adiabatic velocity field is not yet complete. In the presence of rotation, the equation of motion in Eq. (26) cannot be satisfied by the sole poloidal velocity field, but one must add a toroidal field 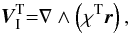 (52)where χT is the toroidal stream function. As for χP before, this function may be expanded as a Fourier series
(52)where χT is the toroidal stream function. As for χP before, this function may be expanded as a Fourier series 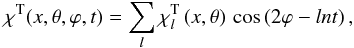 (53)with the projections in spherical coordinates
(53)with the projections in spherical coordinates ![\begin{eqnarray} \vec{V}_\I^{\rm T} &=& \sum_l \left[ \begin{array}{c} \\ 0 \\ \\ - \dfrac{2}{\sin\theta} \, \chi^{\rm T}_l \, \sin \left(2\varphi - ln t\right) \\ \end{array} \right]. \label{VIT_hs} \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq144.png) (54)Here, our treatment departs from that followed in Z66. Instead of working in the inertial frame, we adopt the reference frame ℛC rotating with the Fourier component of the tidal potential U, i.e. with the angular velocity
(54)Here, our treatment departs from that followed in Z66. Instead of working in the inertial frame, we adopt the reference frame ℛC rotating with the Fourier component of the tidal potential U, i.e. with the angular velocity 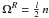 . In this frame, all quantities are stationary, hence the momentum equation reduces to
. In this frame, all quantities are stationary, hence the momentum equation reduces to 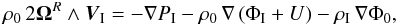 (55)for each Fourier component. Their θ and ϕ projections may be written
(55)for each Fourier component. Their θ and ϕ projections may be written ![% subequation 2173 0 \begin{equation} 2 \Omega^R \, \cos\theta \left[ \, \frac{\partial \chi_l^{\rm T}}{\partial\theta} - \frac{P_2^2\left(\cos\theta\right)}{\sin\theta} \, {2\over x} {{\rm d} \over {\rm d}x}(x^2 \xi^{\rm P}_l )\,\right] = \frac{\partial \mcal F\left(r,\theta\right)}{\partial\theta}, \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq149.png) (56a)and
(56a)and ![% subequation 2173 1 \begin{eqnarray} && 2 \Omega^R \left[ \, \frac{\cos\theta}{\sin \theta} \, 2 \,\chi_l^{\rm T} + \, \sin\theta \, P_2^2\left(\cos\theta\right)\, 6 \, \xi^{\rm P}_l\,\phantom{\frac{\mrm d P_2^2\left(\cos\theta\right)}{\mrm d\theta}}\right. \nonumber\\ &&\qquad + \left. \, \cos\theta \frac{\mrm d P_2^2\left(\cos\theta\right)}{\mrm d\theta} {1 \over x} {{\rm d} \over {\rm d}x}\left(x^2 \xi^{\rm P}_l \right) \, \right] = \frac{2 \mcal F\left(r,\theta\right)}{\sin\theta}, \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq150.png) (56b)where the function ℱ includes all functions on the right-hand side (r.h.s.) of the momentum equation. Its elimination, by applying the curl to Eq. (55), leads to
(56b)where the function ℱ includes all functions on the right-hand side (r.h.s.) of the momentum equation. Its elimination, by applying the curl to Eq. (55), leads to ![\begin{eqnarray} 2 \chi_l^{\rm T} &=& 6 \, \xi_l^{\rm P} \, \frac{1}{\sin\theta} \, \frac{\mrm d}{\mrm d\theta} \left[ \sin^2\theta \, P_2^2\left(\cos\theta\right) \right] \nonumber\\ &&- {1 \over x} {{\rm d} \over {\rm d}x}\left(x^2 \xi^{\rm P}_l\right) \left[ 6 \, \cos\theta \,P_2^2(\cos\theta) + \sin\theta \, \frac{\mrm d P_2^2}{\mrm d\theta} \right] \cdot \label{eqchil} \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq152.png) (57)After some straightforward manipulations (see Z66), we get
(57)After some straightforward manipulations (see Z66), we get 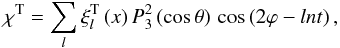 (58)with
(58)with 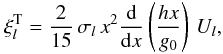 (59)and finally reach the expression for the toroidal field, in the inertial frame
(59)and finally reach the expression for the toroidal field, in the inertial frame ![\begin{eqnarray} && \vec{V}_\I^{\rm T} = - \sum_{l} \frac{2}{15} \, \sigma_l \, x^2 \, \frac{\mrm d}{\mrm dx} \left( \frac{hx}{g_0} \right) \, U_l \nonumber\\ &&\qquad \times \, \left[ \begin{array}{c} \\ 0 \\ \\ 2 \dfrac{P_3^2(\cos\theta)}{\sin\theta} \, \sin\left(2\varphi-ln t\right) \\ \end{array} \right]. \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq155.png) (60)Using the reference frame rotating with each component of the tidal potential, we are thus able to rigorously decouple the equilibrium tide, which is stationary in this frame, and the dynamical tide. Therefore, the “pseudo-resonances” found in Z66 disappear.
(60)Using the reference frame rotating with each component of the tidal potential, we are thus able to rigorously decouple the equilibrium tide, which is stationary in this frame, and the dynamical tide. Therefore, the “pseudo-resonances” found in Z66 disappear.
 |
Fig. 3 Top-left: three-dimensional view of the total (poloidal and toroidal) adiabatic equilibrium tide velocity field (white arrows). The red and orange arrows indicate the direction of the primary’s rotation axis and the line of centers, respectively. Top-right: representation of this velocity field at the surface of the primary (black arrows); the color-scaled background represents the normalized tidal potential intensity (blue and red for the minimum and maximum values, respectively). Bottom-left: view of the velocity field (white arrows) in its equatorial plane of symmetry; the color-scaled background represents the velocity value (black and orange for the minimum and maximum values, respectively). Bottom-right: view of the velocity field (white arrows) in its meridional plane of symmetry; the color-scaled background represents the velocity value (black and purple for the minimum and maximum values, respectively). |
3.4. The dissipative equilibrium tide
We now proceed with the treatment of the dissipation of the equilibrium tide. We assume that the scale separation (in time and size) between the large-scale tidal flow and the turbulent convective motions is sufficient to allow their interaction to be represented by an eddy viscosity η(r) acting on the tidal velocity field VI. For simplicity, we assume this viscosity to be a scalar function of r, although we are aware that it is actually a diagonal tensor, as shown by Penev et al. (2007)1. This viscous force causes a lag in the tide and contributes to the forcing term in system (II), giving rise to a flow VII, which is in quadrature with the adiabatic tidal flow. For brevity, we refer to this flow as the dissipative velocity field.
3.4.1. The viscous force
The treatment of the dissipation of the equilibrium tide first requires us to express the viscous force induced by the adiabatic velocity field FII = Fvisc(VI). Since VI is solenoidal, this force takes the form 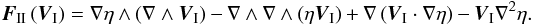 (61)Once again, we divide the adiabatic velocity field into poloidal and toroidal components
(61)Once again, we divide the adiabatic velocity field into poloidal and toroidal components 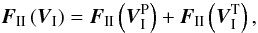 (62)for which we find the expressions in terms of the functions
(62)for which we find the expressions in terms of the functions 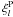 and
and 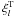 that we have introduced in Eqs. (49)and (53)
that we have introduced in Eqs. (49)and (53)![% subequation 2394 0 \begin{equation} \vec{F}_{\II}\left(\vec{V}_\I^{\rm P}\right) = \sum_{l} \left[ \begin{array}{l} f_{l}^{V}\left(x\right) \, P_2^2 \left(\cos\theta\right) \, \sin\left(2\varphi - ln t\right) \\ \\ f_{l}^{H}\left(x\right) \dfrac{\mrm d P_2^2\left(\cos\theta\right)}{\mrm d\theta} \, \sin\left(2\varphi - ln t\right) \\ \\ 2 f_{l}^{H}\left(x\right) \, \dfrac{P_2^2\left(\cos\theta\right)}{\sin\theta} \, \cos\left(2\varphi - ln t\right) \end{array} \right] \text{ ,} \label{FVIP} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq163.png) (63a)where
(63a)where ![% subequation 2394 1 \begin{equation} \left\{\begin{array}{l} f_{l}^{V} = \dfrac{6}{R^2} \, \left\{ \dfrac{\eta}{x^2} \left[ \dfrac{\mrm d^2}{\mrm dx^2} \left( x^2 \xi_l^{\rm P} \right) - 6 \xi_l^{\rm P} \right] + 2 \, \dfrac{\mrm d\eta}{\mrm dx} \dfrac{\mrm d \xi_l^{\rm P}}{\mrm dx} \right\} \\{}\\ R^2 x f_{l}^{H} = \eta \left[ \dfrac{\mrm d^3}{\mrm dx^3} \left( x^2\xi_l^{\rm P} \right) - 6 \dfrac{\mrm d}{\mrm dx} \xi_l^{\rm P} \right]\\ \end{array} \right. \label{ftfthetaAB} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq164.png) (63b)and
(63b)and ![% subequation 2423 0 \begin{equation} \vec{F}_{\II}\left(\vec{V}_\I^{\rm T}\right) = \sum_{l} \left[ \begin{array}{l} 0 \\ \\ 2 f_{l}^{\rm T}\left(x\right) \, \dfrac{P_3^2\left(\cos\theta\right)}{\sin\theta} \, \sin\left(2\varphi - ln t\right) \\ \\ f_{l}^{\rm T}\left(x\right)\, \dfrac{\mrm d P_3^2\left(\cos\theta\right)}{\mrm d\theta} \, \cos\left(2\varphi - ln t\right) \end{array} \right] \text{ ,} \label{FVIT} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq165.png) (64a)with
(64a)with ![% subequation 2423 1 \begin{equation} f_{l}^{\rm T} = - \frac{1}{R^2}\left\{ \eta \left[ \frac{1}{x} \frac{\mrm d^2}{\mrm dx^2} \left( x\, \xi_l^{\rm T} \right) - 12\frac{\xi_l^{\rm T}}{x^2} \right] + \frac{\mrm d \eta}{\mrm dx} x \frac{\mrm d}{\mrm dx} \left(\frac{\xi_l^{\rm T}}{x} \right) \right\} \cdot \label{ft} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq166.png) (64b)
(64b)
3.4.2. Toroidal velocities of the dissipative tide
We here rewrite the momentum equation that governs the dissipative tide (cf. Eq. (30)) in the reference frame rotating with the l-component of the tidal potential ![\begin{equation} \rho_0 \left[ 2\mbf\Omega^R\wedge\vec{V}_\II \right] = -\nabla P_\II - \rho_0 \, \nabla\Phi_\II - \rho_\II \, \nabla\Phi_0 +\vec{F}_\II. \label{eqbisNS_II} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq168.png) (65)The viscous force FII has a toroidal component (see Eq. (64a)) and therefore generates a toroidal velocity field
(65)The viscous force FII has a toroidal component (see Eq. (64a)) and therefore generates a toroidal velocity field 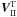 that obeys
that obeys ![\begin{equation} \rho_0 \left[ 2\mbf\Omega^R\wedge\vec{V}^{\rm T}_\II \right] = \vec{F}_\II \left(\vec{V}^{\rm T}_\I\right). \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq171.png) (66)To determine this velocity field, we introduce the stream function Dl(x,θ) and project
(66)To determine this velocity field, we introduce the stream function Dl(x,θ) and project 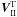 onto θ and ϕ
onto θ and ϕ![\begin{equation} \label{VIIT} \vec{V}_\II^{\rm T} = \sum_{l} \left[ \begin{array}{c} 0 \\ \\ 2 D_{l}\left(x,\theta\right) \, \cos\left(2\varphi-ln t\right) \\ \\ - \dfrac{\partial}{\partial\theta} \left[ \sin\theta \, D_{l}\left(x,\theta\right) \right] \, \sin\left(2\varphi-ln t\right) \\{} \end{array} \right]. \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq174.png) (67)We next implement the Coriolis acceleration associated with this velocity field in Eq. (65), which we project onto the horizontal coordinates
(67)We next implement the Coriolis acceleration associated with this velocity field in Eq. (65), which we project onto the horizontal coordinates ![% subequation 2533 0 \begin{eqnarray} &&\hspace{-3mm} 2\, \rho_0\, \Omega^R\, \cos\theta \, \frac{\partial}{\partial \theta} \left[ \sin\theta \, D_{l}\right] = \frac{\partial \mcal F}{\partial\theta} + 2\,f_{l}^{\rm T} \, \frac{P_3^2\left(\cos\theta\right)}{\sin\theta}, \\ &&\hspace{-3mm} 4\, \rho_0\, \Omega^R\, \cos\theta \, D_{l} = \frac{2 \, \mcal F}{\sin\theta} + \,f_{l}^{\rm T} \, \frac{\mrm d P_3^2\left(\cos\theta\right)}{\mrm d\theta}, \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq175.png) where ℱ contains the scalar functions of the r.h.s. of the momentum equation other than the toroidal part of the viscous force. As before, we proceed with the elimination of ℱ and obtain the expression for Dl
where ℱ contains the scalar functions of the r.h.s. of the momentum equation other than the toroidal part of the viscous force. As before, we proceed with the elimination of ℱ and obtain the expression for Dl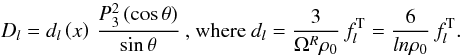 (69)We rewrite the toroidal velocity field induced by the dissipation tide as
(69)We rewrite the toroidal velocity field induced by the dissipation tide as ![\begin{equation} \label{VIITl} \vec{V}_\II^{\rm T} = \sum_{l} \left[ \begin{array}{c} \\ 0 \\ \\ \dfrac{6}{\Omega^R \rho_0} \, f_{l}^{\rm T} \, \dfrac{P_3^2\left(\cos\theta\right)}{\sin\theta} \, \cos\left(2\varphi-ln t\right) \\ \end{array} \right]. \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq178.png) (70)The viscous force, as well as its associated toroidal velocity field, produces a mass redistribution inside the star or planet, thus a perturbation of density ρII and gravific potential ΦII. This causes a tidal torque to be applied to the object, which will be responsible for the dynamical evolution of the system.
(70)The viscous force, as well as its associated toroidal velocity field, produces a mass redistribution inside the star or planet, thus a perturbation of density ρII and gravific potential ΦII. This causes a tidal torque to be applied to the object, which will be responsible for the dynamical evolution of the system.
3.4.3. Perturbation of the gravific potential ΦII
We saw in the previous section that viscous dissipation generates a toroidal velocity field 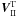 , which is in quadrature with the toroidal part
, which is in quadrature with the toroidal part 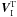 of the adiabatic flow. We still need to determine the associated gravitational potential ΦII which is in quadrature with the tidal potential U. Perturbed Poisson equation We now return to the Navier-Stokes equation (Eq. (30)) satisfied by the toroidal velocity field
of the adiabatic flow. We still need to determine the associated gravitational potential ΦII which is in quadrature with the tidal potential U. Perturbed Poisson equation We now return to the Navier-Stokes equation (Eq. (30)) satisfied by the toroidal velocity field 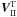 , whose expression is given in Eq. (67), after taking into acount Eqs. (63a)and (64a)of the viscous forces due respectively to the poloidal and toroidal adiabatic velocity fields. Projection onto r and θ leads us to the equations
, whose expression is given in Eq. (67), after taking into acount Eqs. (63a)and (64a)of the viscous forces due respectively to the poloidal and toroidal adiabatic velocity fields. Projection onto r and θ leads us to the equations 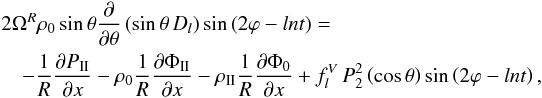 (71a)and
(71a)and ![% subequation 2660 1 \begin{eqnarray} && 2\Omega^R \rho_0 \sin\theta \frac{\partial}{\partial\theta}\left(\sin\theta \, D_l\right) \sin\left(2\varphi-ln t\right) = -\frac{1}{R}\frac{1}{x}\frac{\partial P_\II}{\partial\theta} - \frac{1}{R} \frac{\rho_0}{x} \frac{\partial \Phi_\II}{\partial\theta} \nonumber\\ && \quad + \left[ f_{l}^{H} \frac{\mrm d P_2^2\left(\cos\theta\right)}{\mrm d\theta} +2 f_{l}^{\rm T} \frac{P_3^2\left(\cos\theta\right)}{\sin\theta} \right] \sin\left(2\varphi-ln t\right). \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq185.png) (71b)The Coriolis acceleration on the l.h.s. of these equations projects onto the associated Legendre polynomials of second and fourth order
(71b)The Coriolis acceleration on the l.h.s. of these equations projects onto the associated Legendre polynomials of second and fourth order 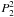 and
and 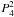 , since
, since ![\begin{eqnarray} 2\Omega^R \rho_0 \sin\theta \frac{\partial}{\partial\theta}\left(\sin\theta \, D_l\right) &=& 6 \sin\theta \frac{\partial}{\partial\theta} P_3^2\left(\cos\theta\right) f_{l}^{\rm T} \nonumber \\ &=& \frac{6}{7}\left[ - 20 P_2^2 + 6 P_4^2 \right] f_{l}^{\rm T}. \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq188.png) (72)Thus, the viscous force causes perturbations in the density, pressure, and internal potential that contain only these spherical functions, which we may expand as
(72)Thus, the viscous force causes perturbations in the density, pressure, and internal potential that contain only these spherical functions, which we may expand as ![\begin{equation} \label{devscal} X_\II = \sum_{l} \left[ X_{2,l}\left(x\right) \, P_2^2\left(\cos\theta\right) + X_{4,l}\left(x\right) \, P_4^2\left(\cos\theta\right) \right] \, \sin\left(2\varphi-ln t\right). \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq189.png) (73)However, we agreed earlier that the tidal potential could be represented by a quadrupole only. In this approximation, the perturbations in
(73)However, we agreed earlier that the tidal potential could be represented by a quadrupole only. In this approximation, the perturbations in 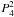 do not contribute to the tidal torque, and we no longer consider them. Keeping only the
do not contribute to the tidal torque, and we no longer consider them. Keeping only the 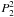 harmonics, dropping the index II, and setting s = 2, we rewrite (65) as
harmonics, dropping the index II, and setting s = 2, we rewrite (65) as 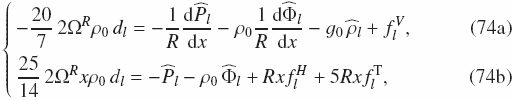 where we have used the identity
where we have used the identity 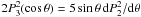 .
.
By eliminating the pressure and gravity perturbations, we isolate the term, which is next implemented in the Poisson equation (Eq. (32)) ![\begin{eqnarray} \label{PhiRho} &&\hspace{-3mm} g_0 \, {\widehat\rho}_{l} = - \frac{\mrm d\rho_0}{\mrm dx}{\widehat\Phi}_{l} + Z_{l}\left(x\right),\nonumber \\ &&\hspace{-3mm} \text{where} \quad Z_{l} = f_l^V - \frac{\mrm d}{\mrm dx} \left(x f_l^H \right) + \frac{40}{7} \left[ 3 f_l^{\rm T} + \frac{\mrm d}{\mrm dx} \left(x f_l^{\rm T} \right)\right], \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq192.png) (75)which finally yields
(75)which finally yields ![\begin{equation} \frac{1}{x} \, \frac{\mrm d^2}{\mrm dx^2} \left( x\,{\widehat\Phi}_{l} \right) - \left[ \frac{6}{x^2} - f(x) \right] \, {\widehat\Phi}_{l} = -\frac{4\pi \mathcal G R^2}{g_0} \, Z_{l}, \label{eqPhiII} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq193.png) (76)where as above
(76)where as above  . We still need to solve the differential equation with the appropriate boundary conditions
. We still need to solve the differential equation with the appropriate boundary conditions 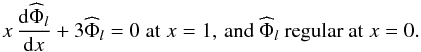 (77)
(77)
Application to a thin convective envelope
Equation (76) allows for an approximate solution in the case where the primary possesses a convective envelope. If that envelope is not too thick, we may assume that its mass is negligible, so that g0(x) ≈ gs/x2, and that the function h (cf. Eq. (40)), may be assumed to be constant h(x) ≈ 1. The poloidal and toroidal stream functions then take the simple monomial form
 where gs = g0(1) designates the surface gravity. From Eq. (63b), we then deduce that
where gs = g0(1) designates the surface gravity. From Eq. (63b), we then deduce that 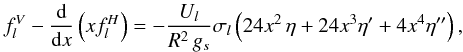 (80a)and from Eq. (64b)
(80a)and from Eq. (64b) ![% subequation 2815 1 \begin{eqnarray} \label{f2} 3 f_l^{\rm T}\! + \!\frac{\mrm d}{\mrm dx} \left( x f_l^{\rm T} \right) \!= \! -\!\frac{U_{l}}{R^2 \, g_s} \sigma_l \frac{2}{5} \, \left[ 48 x^2 \, \eta\! +\! 29x^3\,\eta' \!+\! 3x^4\,\eta''\right]. \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq202.png) (80b)Then, introducing these expressions into Eq. (76), we get:
(80b)Then, introducing these expressions into Eq. (76), we get: ![\begin{eqnarray} Z_{l} &=& -\frac{U_l}{R^2 g_s} \, \sigma_l\, \frac{1}{7}\left[ 936\,x^2\,{\eta} + 632\,x^3\,{\eta}' +76 \,x^4\,{\eta}'' \right]. \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq203.png) (81)The last step consists in solving Poisson’s equation (Eq. (76)), which we rewrite
(81)The last step consists in solving Poisson’s equation (Eq. (76)), which we rewrite 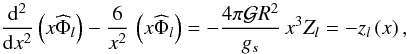 (82)assuming again g0(x) ≈ gs/x2 and neglecting the function f(x) compared to 6/x2 (for a justification of this approximation we refer to Z66). This can be done semi-analytically by using the method of Green’s integral kernels (Morse & Feshbach 1953; see also Z66); the formal solution is
(82)assuming again g0(x) ≈ gs/x2 and neglecting the function f(x) compared to 6/x2 (for a justification of this approximation we refer to Z66). This can be done semi-analytically by using the method of Green’s integral kernels (Morse & Feshbach 1953; see also Z66); the formal solution is 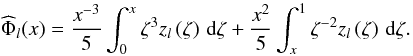 (83)At the surface,
(83)At the surface, 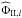 , as we name it again to recall the dissipative origin of this tide, then takes the value
, as we name it again to recall the dissipative origin of this tide, then takes the value ![\begin{eqnarray} {\widehat\Phi}_{\II,l}(1) = - \frac{4 \pi}{35} \frac{{\mathcal G} R^2}{g_s} \, \frac{U_l}{R^2 g_s} \, \sigma_l \nonumber\\ \times \int_{x_{\rm BCZ}}^1 \left[ 936\,x^8\,{\eta} + 632\,x^9\,{\eta}' +76 \,x^{10}\,{\eta}'' \right] \mrm dx, \label{PhiII} \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq208.png) (84)where the summation is made over the convective envelope, whose lower boundary is at x = xBCZ and upper boundary at x = 1. Thus, the gravific potential due to viscous dissipation
(84)where the summation is made over the convective envelope, whose lower boundary is at x = xBCZ and upper boundary at x = 1. Thus, the gravific potential due to viscous dissipation 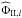 , which is in quadrature with the tidal potential Ul, is proportional to the tidal frequency σl, provided that the turbulent viscosity is not a function of σl.
, which is in quadrature with the tidal potential Ul, is proportional to the tidal frequency σl, provided that the turbulent viscosity is not a function of σl.
Equation (84)can be recast as 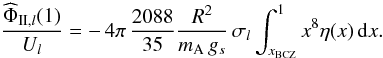 (85)We see that this ratio, which quantifies the tidal dissipation, is a function of the tidal frequency, unless the turbulent viscosity is inversely proportional to that frequency. Finally, we stress that the equilibrium tide dissipation depends strongly on the internal structure of the considered body, particularly the thickness (or the mass) of the convective envelope.
(85)We see that this ratio, which quantifies the tidal dissipation, is a function of the tidal frequency, unless the turbulent viscosity is inversely proportional to that frequency. Finally, we stress that the equilibrium tide dissipation depends strongly on the internal structure of the considered body, particularly the thickness (or the mass) of the convective envelope.
3.4.4. Turbulent viscosity
As stated above, we assumed that the convective motions and the tidal flow are separated enough on temporal and spatial scales that their interaction can be described by an eddy viscosity η acting on the tidal velocity field. As long as this scale separation is fulfilled, we may assume that 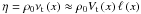 , where νt is the kinematic turbulent viscosity, Vt the vertical rms velocity of the turbulent eddies, and ℓ their mean-free path, also called mixing length. The radial profile of η is readily drawn from a classical mixing-length model, since
, where νt is the kinematic turbulent viscosity, Vt the vertical rms velocity of the turbulent eddies, and ℓ their mean-free path, also called mixing length. The radial profile of η is readily drawn from a classical mixing-length model, since 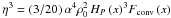 , where Hp = | dlnP0/dlnr | -1 is the pressure scale-height, α = ℓ/HP the mixing-length parameter, and Fconv the convective enthalpy flux (cf. Z66; Zahn 1989).
, where Hp = | dlnP0/dlnr | -1 is the pressure scale-height, α = ℓ/HP the mixing-length parameter, and Fconv the convective enthalpy flux (cf. Z66; Zahn 1989).
However, this simple prescription no longer holds when the tidal period Ptide = 2π/σl becomes shorter than the life span tconv = ℓ/Vt of the convective elements. One then expects the tidal dissipation to be reduced, although by how much is still a matter of debate. For phenomenological reasons, it then seems natural to replace the mean-free path by the distance traveled by the convective eddies during, say, half a tidal period; the eddy-viscosity then varies proportionally to the tidal period (Z66) 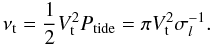 (86)This scaling was confirmed by means of numerical simulations performed by Penev et al. (2007) with a code designed to model stellar convection. They also found that νt is a diagonal tensor, with stronger transport in the vertical than in the horizontal direction, but we do not take these refinements into account and simply treat η as a scalar.
(86)This scaling was confirmed by means of numerical simulations performed by Penev et al. (2007) with a code designed to model stellar convection. They also found that νt is a diagonal tensor, with stronger transport in the vertical than in the horizontal direction, but we do not take these refinements into account and simply treat η as a scalar.
Another prescription was proposed by Goldreich & Keeley (1977), where the turbulent viscosity varies as the square of the tidal period. It implies a too strong reduction in the viscosity that is incompatible with most observations, for example the circularization of binaries with a red giant component (Verbunt & Phinney 1995); but it could be adequate for the dynamical tide involving inertial modes, which develop boundary layers that are of much shorter timescale than that of the equilibrium tide (cf. Ogilvie & Lin 2004).
It thus appears that turbulent dissipation operates in two regimes, depending on how the tidal period compares with the local convective turn-over time, which in a convection zone can vary with depth by several orders of magnitude. To ensure a smooth transition between these two regimes, one may take ![\begin{equation} \label{nut2} \nu_{\rm t} = V_{\rm t}\,\ell \, \left[ 1 + \left({2 \, t_{\rm conv} \over P_{\rm tide}} \right)^2 \right]^{-1/2} = V_{\rm t}\,\ell \, \left[ 1 + \left(\frac{t_{\rm conv}\,\sigma_l}{\pi} \right)^2 \right]^{-1/2},\vspace{-1mm} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq226.png) (87)as illustrated in Fig. 4.
(87)as illustrated in Fig. 4.
In the upper part of a convective envelope, where the convective turnover time is shorter than the tidal period, νt does not depend on the tidal period; the tidal dissipation then varies proportionally to the tidal frequency (cf. Eq. (85)). However, in the opposite case, when the life span of the convective eddies exceeds the tidal period, which is likely to occur at the base of convection zones, tidal dissipation is independent of the tidal frequency. We note that these two regimes still persist once the summation over η has been performed in Eq. (85).
4. The dynamical evolution of binary systems
After deriving the tidal velocity field and the associated mass redistribution, we are ready to determine the tidal torque, which causes the exchange of angular momentum between each component and the orbital motion. Let us recall the role played respectively by the adiabatic and the dissipative tide. First, the companion exerts a tidal force on the considered component, which is elongated in the direction of the line of centers: this mass redistribution described by the perturbed density ρI corresponds to the adiabatic tide. In the absence of dissipative processes, the induced torque 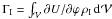 undergoes periodic variations of zero average and no secular exchanges of angular momentum are allowed. However, turbulent friction generates a mass redistribution described by ρII. This dissipative tide produces the torque
undergoes periodic variations of zero average and no secular exchanges of angular momentum are allowed. However, turbulent friction generates a mass redistribution described by ρII. This dissipative tide produces the torque 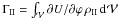 of non-zero average, which causes the net exchange of angular momentum between the components of the system, as illustrated in Fig. 2.
of non-zero average, which causes the net exchange of angular momentum between the components of the system, as illustrated in Fig. 2.
4.1. The dissipation quality factor
The expression of the torque ΓII involves the ratio 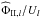 , which we have established above in Eq. (85), or equivalently the quality factor Q, which we now introduce. For this, it is convenient to work in complex notations with the real part representing the adiabatic tide and the imaginary part characterizing the dissipative contribution. For the perturbed gravific potential, we then have
, which we have established above in Eq. (85), or equivalently the quality factor Q, which we now introduce. For this, it is convenient to work in complex notations with the real part representing the adiabatic tide and the imaginary part characterizing the dissipative contribution. For the perturbed gravific potential, we then have ![\begin{equation} \label{PhiComplex} \Phi'\left({\vec r},t\right) = \sum_{l} \Re \left\{ \widehat{\Phi}_{l}(x) P_{2}^{2}(\cos\theta) \exp\left[ {{\rm i}} \left( 2\varphi - lnt \right) \right] \right\}, \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq232.png) (88)where we define, following the notations of Eqs. (21), (22),
(88)where we define, following the notations of Eqs. (21), (22), 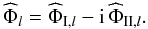 (89)For each Fourier component l, the complex second-order Love number
(89)For each Fourier component l, the complex second-order Love number 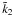 , which characterizes the deformation response of A to the stress exerted by B, is defined by
, which characterizes the deformation response of A to the stress exerted by B, is defined by 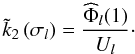 (90)Since the turbulent friction introduces a phase delay
(90)Since the turbulent friction introduces a phase delay  of the reaction relative to the load,
of the reaction relative to the load, 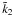 is also of the form
is also of the form 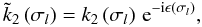 (91)where k2 is the norm of
(91)where k2 is the norm of 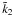 . From Eq. (90), we identify the real part of
. From Eq. (90), we identify the real part of 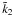 as the adiabatic second-order Love number given by Eq. (44), thus
as the adiabatic second-order Love number given by Eq. (44), thus 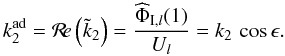 (92)The ratio
(92)The ratio 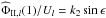 is similar to
is similar to 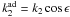 , but applied here to the dissipative tide. By analogy with an electric circuit, we then define the quality factor Q > 0 (see Ferraz-Mello et al. 2008; Efroimsky 2012) by
, but applied here to the dissipative tide. By analogy with an electric circuit, we then define the quality factor Q > 0 (see Ferraz-Mello et al. 2008; Efroimsky 2012) by 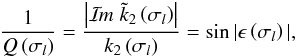 (93)such that the tidal dissipation is given by
(93)such that the tidal dissipation is given by 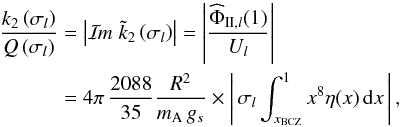 (94)where we have recalled the expression of Eq. (85). We note that the ratio
(94)where we have recalled the expression of Eq. (85). We note that the ratio 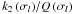 can be frequency-dependent, whereas
can be frequency-dependent, whereas 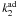 cannot. This tidal quality factor is also linked to the geometrical lag angle δ, which is half the phase lag ϵ (see Efroimsky & Lainey 2007)
cannot. This tidal quality factor is also linked to the geometrical lag angle δ, which is half the phase lag ϵ (see Efroimsky & Lainey 2007) 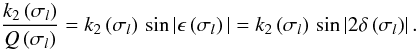 (95)Recalling Eq. (85)of
(95)Recalling Eq. (85)of 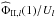 , we notice that when the turbulent viscosity does not depend on tidal frequency, the tidal lag angle
, we notice that when the turbulent viscosity does not depend on tidal frequency, the tidal lag angle 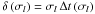 is proportional to the tidal frequency, which means that the time lag
is proportional to the tidal frequency, which means that the time lag 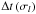 of the tide is then constant, and takes the same value for each Fourier component of the tide: this has been referred to as the weak friction approximation (Hut 1981). It corresponds to the slow tide (tconv < Ptide), as illustrated in Fig. 4. In the opposite case where tconv > Ptide, the tidal angle δ is independent of the tidal frequency, as are both the phase lag ϵ and the quality factor Q, such that the time lag Δt = δ/σl is inversely proportional to the tidal frequency.
of the tide is then constant, and takes the same value for each Fourier component of the tide: this has been referred to as the weak friction approximation (Hut 1981). It corresponds to the slow tide (tconv < Ptide), as illustrated in Fig. 4. In the opposite case where tconv > Ptide, the tidal angle δ is independent of the tidal frequency, as are both the phase lag ϵ and the quality factor Q, such that the time lag Δt = δ/σl is inversely proportional to the tidal frequency.
 |
Fig. 4 The two regimes of turbulent dissipation (Eq. (87)). As long as the local convective turn-over time remains shorter than the tidal period (tconv < Ptide), the turbulent viscosity νt (in black dashed line) is independent of the tidal frequency, and the inverse quality factor k2/Q = |ΦII/U| (in red continuous line), given by Eq. (94), varies proportionally to the tidal frequency σl (so does also the tidal lag angle). When tconv > Ptide, νt varies proportionally to the tidal period, whereas k2/Q = |ΦII/U| no longer depends on the tidal frequency. We note that νt and k2/Q have been scaled by the value they take respectively for tconv/Ptide → 0 and + ∞. |
4.2. The disturbing function
We now use the disturbing function method described in Brouwer & Clemence (1961), Kaula (1962), Yoder (1995–97), Correia & Laskar (2003a,b), and Mathis & Le Poncin-Lafitte (2009) (hereafter MLP09) to determine ΓII and the associated variations in both the bodies’ angular momentum and the orbital Keplerian elements of B (namely, a and e).
The first step in achieving this goal is to introduce a supplementary body C with a mass mC, which we call the orbiter, to the primary A and the perturber B (see Fig. 5 and Kaula 1962). The Keplerian elements of its orbit are a∗, e∗, and M∗ = n∗t where n∗ is the associated mean motion.
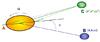 |
Fig. 5 Here, we illustrate the set-up of the perturbing function method. The primary A is deformed because of the tides exerted by the perturber B. Because of A’s internal friction processes, the tidal bulge is shifted from the line of centers with the tidal angle δl given in Eq. (94) for a given l Fourier component of the tidal potential. The Keplerian elements of B’s orbit are a, e, and M. Next, a third body C, which orbits around A with a mean motion n∗, is introduced, and the variations in the Keplerian elements of its orbit (a∗,e∗,M∗) are derived. After using Lagrange’s equation (Eqs. (108), (109)), we finally assume that the orbiter and the perturber are the same (i.e. C = B). |
We next identify the disturbing function on C with the perturbed external gravific potential of A ![\begin{equation} \mcal R =\Phi'\left({\vec r}_{\rm C},t\right) =\sum_{l^{*}}\Re\left\{\widehat{\Phi}_{l^{*}}\left(x_{\rm C}\right)P_{2}^{2}\left(0\right)\exp\left[{{\rm i}}\left(2\varphi_{\rm C}-l^{*}n^{*}t\right)\right]\right\}, \label{Cdef} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq270.png) (96)where rC ≡ (rC = xCR,θC = π/2,ϕC), for xC > 1, is the position of C in the equatorial plane of A, which is also the plane of the orbit, and where the index l∗ is associated with the Fourier expansion of the orbital motion of C.
(96)where rC ≡ (rC = xCR,θC = π/2,ϕC), for xC > 1, is the position of C in the equatorial plane of A, which is also the plane of the orbit, and where the index l∗ is associated with the Fourier expansion of the orbital motion of C.
From now on, we choose to follow the systematic method developed in MLP09 to derive the expression of ℛ as a function of the Keplerian elements of B and C. In this work devoted to the study of the tidal dynamics of extended bodies, the perturbing function is derived for components X having an external gravific potential 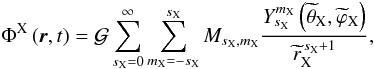 (97)where
(97)where 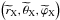 are the spherical coordinates attached to their equatorial planes. We introduce the gravitational moments of X
are the spherical coordinates attached to their equatorial planes. We introduce the gravitational moments of X 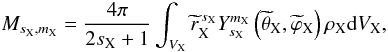 (98)where
(98)where 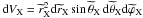 ; the non-spherical components of ΦX are due to tides and to the particular structural shape of the body. We use the spherical harmonics
; the non-spherical components of ΦX are due to tides and to the particular structural shape of the body. We use the spherical harmonics ![\begin{equation} Y_{s}^{m}\left(\theta,\varphi\right)=\left(-1\right)^{\frac{\vert m\vert+m}{2}}\!\!\!\sqrt{\frac{2 s\!+\!1}{4\pi}\frac{\left(s\!-\!\vert m\vert\right)!}{\left(s\!+\!\vert m\vert\right)!}}P_{s}^{m}\left(\cos \theta\right)\exp\left[{\rm i}\, m\varphi\right]. \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq280.png) (99)Here, we apply this general formalism to the interaction between A, which has a tidal gravitational moment
(99)Here, we apply this general formalism to the interaction between A, which has a tidal gravitational moment 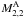 (the quadrupolar approximation is assumed for the perturbed external gravific potential of A as for the tidal potential U), and C, which is assumed to be a point mass, as well as B. The Kaula expansion (Kaula 1962) then allows us to convert the multipolar expansion to a Fourier one in Keplerian elements (see Eq. (79) in MLP09). Applied to our coplanar case, this gives for X ≡ {B,C}
(the quadrupolar approximation is assumed for the perturbed external gravific potential of A as for the tidal potential U), and C, which is assumed to be a point mass, as well as B. The Kaula expansion (Kaula 1962) then allows us to convert the multipolar expansion to a Fourier one in Keplerian elements (see Eq. (79) in MLP09). Applied to our coplanar case, this gives for X ≡ {B,C} ![\begin{equation} \frac{Y_{2}^{2}\left(\pi/2,\varphi_{\rm X}\right)}{r_{\rm X}^{3}}=\frac{1}{4}\sqrt{\frac{15}{2\pi}}\frac{1}{a_{\rm X}^{3}}\sum_{l_{\rm X}}G_{2,0,l_{\rm X}-2}\left(e_{\rm X}\right)\exp\left[{\rm i}\,\Psi_{l_{\rm X}}\right], \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq283.png) (100)where
(100)where 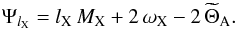 (101)The spherical coordinates of the X position in the A reference frame are (rX,π/2,ϕX), while lX ≡ {l,l∗}, aX ≡ {a,a∗}, eX ≡ {e,e∗}, and MX = nXt ≡ {M = nt,M∗ = n∗t}. The argument of the periapsis ωX ≡ {0,ω∗} is also introduced since it can be different for B and C. Finally,
(101)The spherical coordinates of the X position in the A reference frame are (rX,π/2,ϕX), while lX ≡ {l,l∗}, aX ≡ {a,a∗}, eX ≡ {e,e∗}, and MX = nXt ≡ {M = nt,M∗ = n∗t}. The argument of the periapsis ωX ≡ {0,ω∗} is also introduced since it can be different for B and C. Finally, 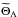 is the mean sideral angle between the minimal axis of inertia and the (AX) axis, thus
is the mean sideral angle between the minimal axis of inertia and the (AX) axis, thus 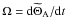 .
.
This transformation leads in the general case to the expansion of ℛ given in Eq. (144) in MLP09, which, once applied to our case, reduces to the expression 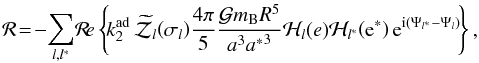 (102)where
(102)where 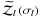 is the so-called dissipative impedance, defined as
is the so-called dissipative impedance, defined as 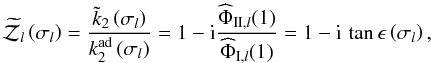 (103)while
(103)while 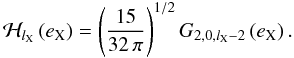 (104)Thus, we can recast Eq. (102)as
(104)Thus, we can recast Eq. (102)as 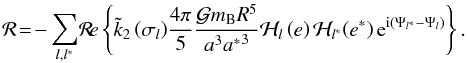 (105)The adiabatic component ℛI (which only involves
(105)The adiabatic component ℛI (which only involves 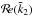 ) of the perturbing function ℛ contributes only as zero-average perturbations to the angular momentum and the orbital elements, whereas its dissipative component ℛII (i.e. the one proportional to
) of the perturbing function ℛ contributes only as zero-average perturbations to the angular momentum and the orbital elements, whereas its dissipative component ℛII (i.e. the one proportional to 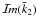 ) given by
) given by 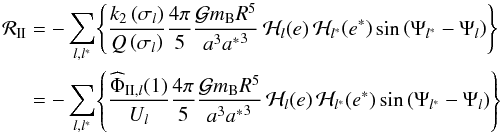 (106)acts on secular timescales.
(106)acts on secular timescales.
We thus obtain for the mean disturbing function the same form as Correia & Laskar (2003b). The main difference is that in our case we link the viscous dissipation with the physical processes operating in the considered bodies,i.e. here turbulent convection. Since the turbulent viscosity depends on the tidal frequency, we have to treat the dissipation separately for each mode l of the tidal potential, as already shown in Zahn (1977) and Ogilvie & Lin (2007). The general method presented here, based on Zahn (1977) and MLP09, thus allows us to go beyond the usual constant Q or tidal lag approximations that can only constitute a first approach as shown in Sect. 3.4.4 and in Ogilvie & Lin (2004). In the near future, we will be able to apply this method to the fluid dynamical tide and to the anelastic tide for planets that have a rocky region (Efroimsky & Lainey 2007; Henning et al. 2009).
4.3. Equations of dynamic evolution of the system
We are now ready to derive the evolution equations for both the angular momentum of A and the orbital elements of C. First, following Yoder (1995–1997) and Correia & Laskar (2003a,b), we obtain the equation for the angular momentum of the primary 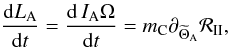 (107)where IA designates its inertial momentum. Next, applying Lagrange’s equations (see for example Brouwer & Clemence 1961), we find for the evolution of the semi-major axis of the C’s orbit and its eccentricity that
(107)where IA designates its inertial momentum. Next, applying Lagrange’s equations (see for example Brouwer & Clemence 1961), we find for the evolution of the semi-major axis of the C’s orbit and its eccentricity that 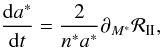 (108)
(108)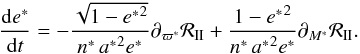 (109)Finally, variations in its mean anomaly M ∗ given by
(109)Finally, variations in its mean anomaly M ∗ given by 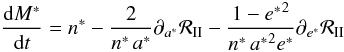 (110)are filtered.
(110)are filtered.
Applying the previous Eqs. (108), (109) to ℛII (Eq. (106)) using results derived in MLP09 (Eqs. (134, 136, 137)), we get, assuming that the orbiter is the perturber (i.e. B = C), ![\begin{equation} \frac{\mrm d L_{\rm A}}{\mrm dt} = - \frac{8\pi}{5} \frac{\mcal G m_{\rm B}^{2} R^5}{a^6} \sum_l \left\{ \frac{{\widehat\Phi}_{\II,l}(1)}{U_l} \left[\mcal H_{l}\left(e\right)\right]^2 \right\} = \Gamma_{\II}, \label{D1} \end{equation}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq311.png) (111)where we identify ΓII with the secular torque applied to A, and
(111)where we identify ΓII with the secular torque applied to A, and ![\begin{eqnarray} \frac{1}{a} \, \frac{\mrm da}{\mrm dt} &=& - \frac{2}{n} \frac{4\pi}{5} \frac{\mcal G m_{\rm B} R^5}{a^8} \sum_l \left\{ l\frac{ {\widehat\Phi}_{\II,l}(1) }{U_l} \left[ \mcal{H}_{l}(e) \right]^2 \right\}, \label{D2} \\ \frac{1}{e} \, \frac{\mrm de}{\mrm dt} &=& - \frac{1}{n} \frac{1-e^2}{e^2} \frac{4\pi}{5} \frac{\mcal G m_{\rm B} R^5}{a^8} \nonumber\\ & & \times \sum_l \! \left\{ \left[ 2 \left( 1 \!-\! \frac{1}{\sqrt{1\!-\!e^2}} \right) \!+\! (l\!-\!2) \right]\! \frac{ {\widehat\Phi}_{\II,l}(1) }{U_l}\! \left[ \mcal{H}_{l}(e) \right]^2 \right\}, \label{D3} \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq312.png) where we recall (from Eqs. (85), (94)) that
where we recall (from Eqs. (85), (94)) that 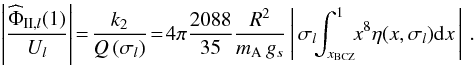 (114)From these equations, one readily draws the characteristic synchronisation and circularisation times
(114)From these equations, one readily draws the characteristic synchronisation and circularisation times 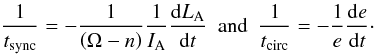 (115)W now comment on this system of equations. First, as discussed in the previous section, the equilibrium tide dissipation is consistently described, taking into account its dependence on the tidal frequency. Moreover, we never made any assumption about the value of the eccentricity. More precisely, we chose to keep the most general expansion in e of the tidal potential U and the resulting disturbing function ℛII. This means that, provided we take a large enough number of modes in the tidal potential expansion, as illustrated in Savonije (2008), we are able to consider the general case of eccentric orbits. Therefore, the present formalism allows us to take into account the complexity of both a general eccentric orbital motion and the physical processes that act on the tidal velocity field that it generates.
(115)W now comment on this system of equations. First, as discussed in the previous section, the equilibrium tide dissipation is consistently described, taking into account its dependence on the tidal frequency. Moreover, we never made any assumption about the value of the eccentricity. More precisely, we chose to keep the most general expansion in e of the tidal potential U and the resulting disturbing function ℛII. This means that, provided we take a large enough number of modes in the tidal potential expansion, as illustrated in Savonije (2008), we are able to consider the general case of eccentric orbits. Therefore, the present formalism allows us to take into account the complexity of both a general eccentric orbital motion and the physical processes that act on the tidal velocity field that it generates.
Finally, we note that the equilibrium states resulting from Eqs. (111) − (113) will differ from those predicted when assuming a constant Q factor or tidal lag because of the different dissipation of each Fourier component of the velocity field; this will be explored in paper II where inclination and obliquity will be taken into account.
5. Conclusion
The originality of this work is the formulation of the equilibrium tide problem in the rotating frame associated with each Fourier component of the tidal potential. This has allowed us to filter correctly the dynamical tide (due to the free oscillations of the considered body), and avoid the so-called “pseudo-resonances”, which appeared in Z66 when the equations were written in an inertial frame. Morever, the solenoidal behavior of the velocity field of the equilibrium tide, which was questioned by Scharlemann (1981), is confirmed. We have revisited the derivation of the adiabatic and the dissipative components of the equilibrium tide (the velocity fields and the associated perturbations of the gravific potential), taking into account the most general expansion of the tidal potential, in the case where the orbital spin and those of each body are aligned. This allows us to treat the general eccentric case by taking a sufficient number of Fourier components into account. We have obtained the associated rate of dissipation of the tidal kinetic energy into heat, given by the k2/Q ratio, which depends on both the thickness of the convective envelope and the tidal frequency 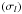 . Owing to the dependence of the turbulent friction on σl, two dissipation regimes are identified. First, as long as the local convective turn-over time remains shorter than the tidal period (tconv < Ptide), the turbulent viscosity νt is independent of σl, and the inverse quality factor k2/Q varies proportionally to the tidal frequency (as does the tidal lag angle). When tconv > Ptide, νt varies proportionally to the tidal period
. Owing to the dependence of the turbulent friction on σl, two dissipation regimes are identified. First, as long as the local convective turn-over time remains shorter than the tidal period (tconv < Ptide), the turbulent viscosity νt is independent of σl, and the inverse quality factor k2/Q varies proportionally to the tidal frequency (as does the tidal lag angle). When tconv > Ptide, νt varies proportionally to the tidal period 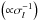 , whereas k2/Q no longer depends on the tidal frequency. This emphasizes the need to go beyond the classical constant tidal lag approximation, not only
, whereas k2/Q no longer depends on the tidal frequency. This emphasizes the need to go beyond the classical constant tidal lag approximation, not only
for the dynamical tide, as shown in Ogilvie & Lin (2004), but also for the equilibrium tide.
In an upcoming paper, we shall take into account the orbital inclination and the obliquities of the bodies. Moreover, we will examine the impact of differential rotation on the equilibrium tide, and that of an anelastic core, which may well be present in giant planets. We also plan to confront the theoretical predictions with observations in our solar system as well as in exoplanetary systems and binary stars.
Acknowledgments
The authors express their gratitude to the referee M. Efroimsky for his constructive remarks and suggestions. They thank V. Lainey, C. Le Poncin-Lafitte, A.-S. Brun, S. Udry, R. Mardling, and A. Triaud for fruitful discussions throughout this work, which was supported in part by the Programme National de Planétologie (CNRS/INSU), the EMERGENCE-UPMC project EME0911, and the CNRS Physique théorique et ses interfaces program.
References
- Barker, A. J., & Ogilvie, G. I. 2010, MNRAS, 404, 1849 [NASA ADS] [Google Scholar]
- Bouchet, L., & Zahn, J.-P. 1989, A&A, 223, 112 [NASA ADS] [Google Scholar]
- Brouwer, D., & Clemence, G. M. 1961, Planets and Satellites, eds. G. P. Kuiper, & B. M. Middlehurst (Chicago: The University of Chicago Press), 31 [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2003a, Icarus, 163, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Laskar, J., & de Surgy, O. N. 2003b, Icarus, 163, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Efroimsky, M. 2012, Cel. Mech. Dyn. Astron., 112, 283 [Google Scholar]
- Efroimsky, M., & Lainey, V. 2007, J. Geophys. Res., 112, 12003 [Google Scholar]
- Ferraz-Mello, S., Rodriguez, A., & Hussmann, H. 2008, Cel. Mech. Dyn. Astron., 101, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2005, Ann. Rev. Earth Planet. Sci., 33, 493 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Goldreich, P., & Nicholson, P. D. 1977, Icarus, 30, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Nicholson, P. D. 1989, ApJ, 342, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Soter, S. 1966, Icarus, 5, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Lackner, C. 2009, ApJ, 696, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, W. G., O’Connel, R. J., & Sasselov, D. D. 2009, ApJ, 707, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Kaula, W. M. 1962, AJ, 67, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, R. H., & Hrivnak, B. J. 1981, A&A, 248, 249 [Google Scholar]
- Lainey, V., Arlot, J.-E., Karatekin, O., & Van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lainey, V., Karatekin, Ö., Desmars, J., et al. 2012, ApJ, 752, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bars, M., Lacaze, L., Le Dizès, S., Le Gal, P., & Rieutord, M. 2010, Phys. Earth Planet. Inter., 178, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Levrard, B., Winisdoerffer, C., & Chabrier, G. 2009, ApJ, 692, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D., Meibom, S., & Dolan, C. J. 2004, ApJ, 602, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S., & Le Poncin-Lafitte, C. 2009, A&A, 497, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morse, P. M., & Feshbach, H. 1953, International Series in Pure and Applied Physics (New York: McGraw-Hill) [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2007, ApJ, 661, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Penev, K., Sasselov, D., Robinson, F., & Demarque, P. 2007, ApJ, 655, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M. 1987, Geophys. Astrophys. Fluid Dyn., 39, 163 [Google Scholar]
- Rieutord, M., & Valdettaro, L. 2010, J. Fluid Mech., 643, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Scharlemann, E. T. 1981, ApJ, 246, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Savonije, G.-J. 2008, Tidal Effects in Stars, Planets and Disks, eds. M.-J. Goupil, & J.-P. Zahn, EAS Publ. Ser., 29, 91 [Google Scholar]
- Udry, S., & Santos, N. C. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Verbunt, F., & Phinney, E. S. 1995, A&A, 296, 709 [NASA ADS] [Google Scholar]
- Yoder, C. F. 1995, Icarus, 117, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Yoder, C. F. 1997, Venus II: Geology, Geophysics, Atmosphere, and Solar Wind Environment, 1087 [Google Scholar]
- Zahn, J.-P. 1966a, Ann. Astrophys., 29, 313 [NASA ADS] [Google Scholar]
- Zahn, J. P. 1966b, Ann. Astrophys., 29, 489 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1989, A&A, 220, 112 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spherical coordinates system attached to the reference frame ℛA centered on A. The spin of A is perpendicular to the orbital plane of B. The dashed line illustrates the orbit of B. |
| In the text | |
 |
Fig. 2 Typical system of tidal interaction. Body B exerts a tidal force on body A, which adjusts itself with a phase lag δ, because of internal friction. This adjustment may be divided into an adiabatic component, which is in phase with the tide, and a dissipative one, which is in quadrature. |
| In the text | |
 |
Fig. 3 Top-left: three-dimensional view of the total (poloidal and toroidal) adiabatic equilibrium tide velocity field (white arrows). The red and orange arrows indicate the direction of the primary’s rotation axis and the line of centers, respectively. Top-right: representation of this velocity field at the surface of the primary (black arrows); the color-scaled background represents the normalized tidal potential intensity (blue and red for the minimum and maximum values, respectively). Bottom-left: view of the velocity field (white arrows) in its equatorial plane of symmetry; the color-scaled background represents the velocity value (black and orange for the minimum and maximum values, respectively). Bottom-right: view of the velocity field (white arrows) in its meridional plane of symmetry; the color-scaled background represents the velocity value (black and purple for the minimum and maximum values, respectively). |
| In the text | |
 |
Fig. 4 The two regimes of turbulent dissipation (Eq. (87)). As long as the local convective turn-over time remains shorter than the tidal period (tconv < Ptide), the turbulent viscosity νt (in black dashed line) is independent of the tidal frequency, and the inverse quality factor k2/Q = |ΦII/U| (in red continuous line), given by Eq. (94), varies proportionally to the tidal frequency σl (so does also the tidal lag angle). When tconv > Ptide, νt varies proportionally to the tidal period, whereas k2/Q = |ΦII/U| no longer depends on the tidal frequency. We note that νt and k2/Q have been scaled by the value they take respectively for tconv/Ptide → 0 and + ∞. |
| In the text | |
 |
Fig. 5 Here, we illustrate the set-up of the perturbing function method. The primary A is deformed because of the tides exerted by the perturber B. Because of A’s internal friction processes, the tidal bulge is shifted from the line of centers with the tidal angle δl given in Eq. (94) for a given l Fourier component of the tidal potential. The Keplerian elements of B’s orbit are a, e, and M. Next, a third body C, which orbits around A with a mean motion n∗, is introduced, and the variations in the Keplerian elements of its orbit (a∗,e∗,M∗) are derived. After using Lagrange’s equation (Eqs. (108), (109)), we finally assume that the orbiter and the perturber are the same (i.e. C = B). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} \label{eqNS_I} &&\hspace{-3mm} \rho_0 \left[ \frac{\mrm D \vec{V}_\I}{\mrm Dt} + 2\mbf\Omega\wedge\vec{V}_\I \right] = -\nabla P_\I - \rho_0 \, \nabla \left( \Phi_\I + U \right) - \rho_\I \, \nabla \Phi_0, \\ \label{eqCONT_I} &&\hspace{-3mm}\frac{\mrm D \rho_\I}{\mrm D t} + \rho \nabla \cdot \vec{V}_\I = 0, \\ \label{eqPOIS_I} &&\hspace{-3mm}\nabla^2\Phi_\I = 4\pi \mcal{G} \rho_\I, \\ &&\hspace{-3mm} \rho_0 \frac{\mrm D S_\I}{\mrm D t} = 0. \end{eqnarray}](/articles/aa/full_html/2012/08/aa18160-11/aa18160-11-eq96.png)