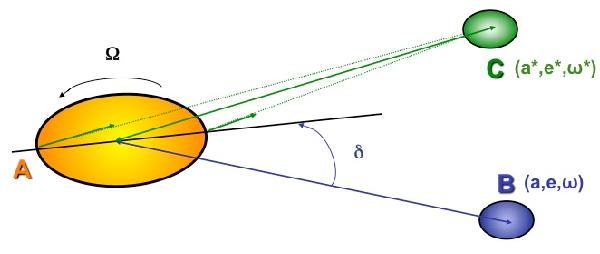
Here, we illustrate the set-up of the perturbing function method. The primary A is deformed because of the tides exerted by the perturber B. Because of A’s internal friction processes, the tidal bulge is shifted from the line of centers with the tidal angle δ_l given in Eq. (94) for a given l Fourier component of the tidal potential. The Keplerian elements of B’s orbit are a, e, and M. Next, a third body C, which orbits around A with a mean motion n^∗, is introduced, and the variations in the Keplerian elements of its orbit (a^∗,e^∗,M^∗) are derived. After using Lagrange’s equation (Eqs. (108), (109)), we finally assume that the orbiter and the perturber are the same (i.e. C = B).