| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219359 | |
| Published online | 09 July 2012 | |
Polarization of synchrotron emission from relativistic reconfinement shocks with ordered magnetic fields
1 University of Colorado, 440 UCB, Boulder, CO 80309, USA
e-mail: knalew@colorado.edu
2 Nicolaus Copernicus Astronomical Centre, Bartycka 18, 00-716 Warsaw, Poland
Received: 5 April 2012
Accepted: 8 June 2012
We calculate the polarization of synchrotron radiation produced at the relativistic reconfinement shocks, taking into account globally ordered magnetic field components, in particular toroidal and helical fields. In these shocks, toroidal fields produce high parallel polarization (electric vectors parallel to the projected jet axis), while chaotic fields generate moderate perpendicular polarization. Helical fields result in a non-axisymmetric distribution of the total and polarized brightness. For a diverging downstream velocity field, the Stokes parameter U does not vanish and the average polarization is neither strictly parallel nor perpendicular. A distance at which the downstream flow is changing from diverging to converging can be easily identified on polarization maps as the turning point at which polarization vectors switch, e.g., from clockwise to counterclockwise.
Key words: galaxies: jets / magnetic fields / polarization / radiation mechanisms: non-thermal / relativistic processes / shock waves
© ESO, 2012
1. Introduction
Relativistic jets are present in all radio-loud active galaxies and are responsible for the bulk of their non-thermal emission. The spectral energy distributions of these sources usually show two broad components. The low-energy one, extending from radio wavelengths to the optical/UV band, and in some cases even to hard X-rays, is commonly interpreted as the synchrotron radiation. This interpretation is supported by significant linear polarization measured routinely in the optical (e.g., Stockman & Angel 1978; Impey et al. 1991; Wills et al. 1992; Ikejiri et al. 2011), radio (e.g., Lister 2001; Marscher et al. 2002; Homan et al. 2002; Pollack et al. 2003; Massardi et al. 2011) and other bands.
Polarization measurements in sources dominated by relativistic jets provide important constraints on the structure of the dominant emitting regions. In particular, a significant polarization degree indicates an anisotropic distribution of magnetic fields. This anisotropy may reflect a large-scale order in the magnetic field lines (Begelman et al. 1984) or may arise from chaotic magnetic fields compressed at shocks (Laing 1980; Hughes et al. 1985; Jones 1988) or sheared at the jet boundary layer (Laing 1981; Matthews & Scheuer 1990). For purely chaotic magnetic fields compressed by perpendicular or conical shocks, high polarization degrees are found only when the polarization (electric) vectors are parallel to the projected jet axis (“parallel polarization”), while for polarization vectors perpendicular to the jet axis (“perpendicular polarization”), the polarization degrees are below 10% (Cawthorne & Cobb 1990). To produce higher perpendicular polarization degrees, Cawthorne (2006) introduced a large-scale poloidal magnetic field component. Diverging conical shocks can be caused by collision of the jet with a dense cloud (Lind & Blandford 1985) or appear when the jet rapidly becomes overpressured with respect to its environment (Agudo et al. 2012).
A different shock structure can result if a jet becomes underpressured. Then, the interaction between the relativistic jet and its gaseous environment leads to the formation of so-called reconfinement or recollimation shocks (Sanders 1983; Komissarov & Falle 1997). These shocks deflect the jet flow and focus it on a cross section much smaller compared to that of a freely propagating jet. Nalewajko (2009, hereafter Paper I calculated the linear polarization of synchrotron emission associated with reconfinement shocks for purely chaotic magnetic fields. He found that perpendicular polarization degrees can exceed 20%. Because a reconfinement shock is an ensemble of conical shocks, this result appears to be in conflict with the work of Cawthorne & Cobb (1990). The crucial difference is that while Cawthorne & Cobb (1990) assumed a parallel upstream flow, in Paper I a spherically diverging upstream flow was considered. Because parallel upstream flows are often adopted in studies of relativistic jet polarization (Lyutikov et al. 2005; Cawthorne 2006), we would like to point out that jet divergence makes a substantial difference in the resulting polarization.
Reconfinement shocks with purely chaotic magnetic fields cannot account for the high parallel polarization often observed in blazars. Therefore, we extend the study presented in Paper I to include large-scale ordered magnetic field components. High parallel polarization can be achieved by introducing a toroidal magnetic field component, but in general ordered magnetic fields may consist of both toroidal and poloidal components, forming a helical structure. In Sect. 2, we describe our model of synchrotron emission and polarization from relativistic reconfinement shocks, introducing a simply parametrized family of global helical magnetic fields. In Sect. 3, we present the results demonstrating the effect of mixing chaotic and ordered (toroidal) magnetic fields (Sect. 3.1), and the effect of changing the pitch angle of the purely helical magnetic field (Sect. 3.2). Our results are discussed in Sect. 4 and summarized in Sect. 5. Preliminary results were already presented in Nalewajko & Sikora (2010).
2. Synchrotron emission and polarization
We used the model of the structure of reconfinement shocks from Nalewajko & Sikora (2009) to investigate its polarimetric properties. Our attention is focused on the optical wavelengths, which in blazars are dominated by the synchrotron emission of highly relativistic electrons. The cooling time scale for these particles is very short, so that the emitting region is closely aligned with the sites of particle acceleration1. Relativistic shock fronts provide natural conditions for efficient particle acceleration (e.g. Achterberg et al. 2001). We are not concerned with details of these processes, it is only assumed that the relativistic electrons tap a constant fraction ηrad of the post-shock internal energy. Since radiative cooling of these electrons is very efficient, practically their entire energy is transferred to the non-thermal radiation, which includes the synchrotron and inverse-Compton components. Although the inverse-Compton luminosity exceeds the synchrotron luminosity in radio-loud quasars, here we assume that their ratio is roughly constant along the jet. This is justified because both the magnetic energy density and the total synchrotron and external radiation energy densities scale roughly like r-2 (Sikora et al. 2009). Hence, a constant fraction ηsyn of the energy contained in relativistic electrons goes to the synchrotron radiation. In this case, the power emitted in the form of synchrotron radiation can be determined from the rate of energy transfer into relativistic electrons, which in turn is proportional to the rate of energy dissipation.
Let I′(Ω′) be the synchrotron radiation intensity, as measured in the co-moving frame of the post-shock fluid (denoted with a prime). It is directly related to the emitted flux density, which is Lorentz-invariant, and can therefore be written in the external frame: 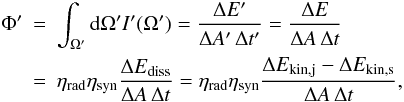 (1)where ΔA is the shock front area. Consider a shock front element covering distance Δz and azimuthal angle Δφ. The surface area of this element is
(1)where ΔA is the shock front area. Consider a shock front element covering distance Δz and azimuthal angle Δφ. The surface area of this element is 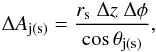 (2)where rs is the local jet radius and θj(s) is the angle between the fluid velocity vector and the jet axis. The volume of jet (shocked jet) matter crossing this shock front element over time Δt is
(2)where rs is the local jet radius and θj(s) is the angle between the fluid velocity vector and the jet axis. The volume of jet (shocked jet) matter crossing this shock front element over time Δt is 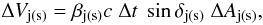 (3)where βj(s) is the fluid velocity and δj(s) is the angle made by the velocity vector to the shock tangent. Its kinetic energy is then
(3)where βj(s) is the fluid velocity and δj(s) is the angle made by the velocity vector to the shock tangent. Its kinetic energy is then 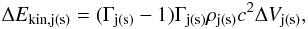 (4)where Γj(s) = (1 − βj(s)) − 1/2 is the corresponding Lorentz factor and ρj(s) is the co-moving mass density. Substituting this into Eq. (1), we can calculate Φ′ for every shock front element.
(4)where Γj(s) = (1 − βj(s)) − 1/2 is the corresponding Lorentz factor and ρj(s) is the co-moving mass density. Substituting this into Eq. (1), we can calculate Φ′ for every shock front element.
Radiation produced in the post-shock co-moving frame is subject to relativistic Doppler boosting into the external frame. Since this emitting region is fixed in the external frame, the transformation law for the stationary pattern should be used instead of a moving blob (see Appendix A in Sikora et al. 1997). Let k be the unit vector toward the observer and e the unit vector along the fluid velocity. Then, we have 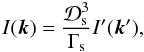 (5)where
(5)where 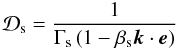 (6)is the Doppler factor. From the law of relativistic aberration, we find
(6)is the Doppler factor. From the law of relativistic aberration, we find ![\begin{equation} \vec{k}'=\mathcal{D}_{\rm s}\left\{\vec{k}+\left[\left(\Gamma_{\rm s}-1\right)\left(\vec{k}\cdot\vec{e}\right)-\Gamma_{\rm s}\beta_{\rm s}\right]\vec{e}\right\}. \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq28.png) (7)Polarization of the synchrotron emission can be described by the polarization degree Π and the positional angle of the electric vector χE (EVPA; “polarization angle”). The maximum polarization degree of the synchrotron radiation, corresponding to a uniform magnetic field, is Πmax = (3p + 3)/(3p + 7), where p is the index of the electron energy distribution N(γ) ∝ γ − p (e.g., Laing 1980). When combining polarized emission from many sources, it is convenient to use the Stokes parameters
(7)Polarization of the synchrotron emission can be described by the polarization degree Π and the positional angle of the electric vector χE (EVPA; “polarization angle”). The maximum polarization degree of the synchrotron radiation, corresponding to a uniform magnetic field, is Πmax = (3p + 3)/(3p + 7), where p is the index of the electron energy distribution N(γ) ∝ γ − p (e.g., Laing 1980). When combining polarized emission from many sources, it is convenient to use the Stokes parameters  When EVPA is measured from the same reference positional angle for all sources, the Stokes parameters are linearly additive. In this work, χE is always measured from the projected direction of the jet axis z. To calculate the polarization angle, one needs to know the direction of the magnetic field, represented by a unit vector b.
When EVPA is measured from the same reference positional angle for all sources, the Stokes parameters are linearly additive. In this work, χE is always measured from the projected direction of the jet axis z. To calculate the polarization angle, one needs to know the direction of the magnetic field, represented by a unit vector b.
Following Paper I, we introduce a cartesian coordinate system (x,y,z), in which the jet axis is aligned with the z-axis and the observer is in the xz-plane, inclined to the jet axis at angle θobs, hence ![\begin{equation} \vec{k}=[\sin\theta_{\rm obs},0,\cos\theta_{\rm obs}]. \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq40.png) (10)The post-shock fluid velocity βs = βse is inclined to the jet axis at angle θs, hence
(10)The post-shock fluid velocity βs = βse is inclined to the jet axis at angle θs, hence ![\begin{equation} \vec{e}=[\sin\theta_{\rm s}\cos\phi,\sin\theta_{\rm s}\sin\phi,\cos\theta_{\rm s}]. \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq43.png) (11)Next, we introduce an orthogonal coordinate system in the plane of the sky:
(11)Next, we introduce an orthogonal coordinate system in the plane of the sky: ![\begin{eqnarray} \vec{v}' &=& \left[\frac{k_{z}'}{\sqrt{1-k_{y}'^2}}, 0, \frac{-k_{x}'}{\sqrt{1-k_{y}'^2}}\right], \\ \vec{w}' &=& \left[\frac{-k_{x}'k_{y}'}{\sqrt{1-k_{y}'^2}}, \sqrt{1-k_{y}'^2}, \frac{-k_{y}'k_{z}'}{\sqrt{1-k_{y}'^2}}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq44.png) The positional angle of the magnetic field vector is
The positional angle of the magnetic field vector is 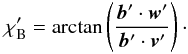 (14)From this, we subtract the positional angle of the fluid velocity vector:
(14)From this, we subtract the positional angle of the fluid velocity vector: 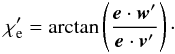 (15)The relative electric vector polarization angle is
(15)The relative electric vector polarization angle is 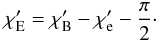 (16)When transformed back to the external frame, the total flux is boosted according to Eq. (5). The polarization degree and the polarization angle, measured with respect to the projection of transformation velocity vector onto the plane of the sky, are Lorentz-invariant. To find the absolute polarization angle in the external frame, one needs to add the positional angle of the fluid velocity with respect to the jet axis, which is given by
(16)When transformed back to the external frame, the total flux is boosted according to Eq. (5). The polarization degree and the polarization angle, measured with respect to the projection of transformation velocity vector onto the plane of the sky, are Lorentz-invariant. To find the absolute polarization angle in the external frame, one needs to add the positional angle of the fluid velocity with respect to the jet axis, which is given by 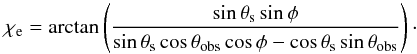 (17)The final formula for the electric vector polarization angle is
(17)The final formula for the electric vector polarization angle is 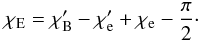 (18)Using a particular model of the reconfinement shock structure, one can calculate Stokes parameters for every shock front element and then integrate them to produce simulated two-dimensional maps, longitudinal one-dimensional profiles, or the average signal. In the following sections, we consider different distributions of the magnetic fields and calculate the polarization of light observed at different viewing angles.
(18)Using a particular model of the reconfinement shock structure, one can calculate Stokes parameters for every shock front element and then integrate them to produce simulated two-dimensional maps, longitudinal one-dimensional profiles, or the average signal. In the following sections, we consider different distributions of the magnetic fields and calculate the polarization of light observed at different viewing angles.
2.1. Chaotic magnetic field
For a chaotic magnetic field of initially isotropic distribution, considered in detail in Paper I, the symmetry is broken by compression at the shock front. The resulting magnetic field distribution can be characterized by the shock compression factor κ = (ρj/ρs) and the unit vector normal to the shock front n. For a shock front element located at an azimuthal angle φ and inclined to the jet axis by angle αs, ![\begin{equation} \vec{n}=[\cos\alpha_{\rm s}\cos\phi,\cos\alpha_{\rm s}\sin\phi,-\sin\alpha_{\rm s}]. \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq54.png) (19)This unit vector transforms into the co-moving frame as
(19)This unit vector transforms into the co-moving frame as ![\begin{equation} \vec{n}'=[\cos\alpha_{\rm s}'\cos\phi,\cos\alpha_{\rm s}'\sin\phi,-\sin\alpha_{\rm s}'], \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq55.png) (20)where
(20)where 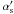 is the co-moving inclination angle:
is the co-moving inclination angle: ![\begin{equation} \alpha_{\rm s}'=\theta_{\rm s}-\arctan\left[\Gamma_{\rm s}\tan\left(\theta_{\rm s}-\alpha_{\rm s}\right)\right]\cdot \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq57.png) (21)Polarization degree of the resulting synchrotron radiation is given by (Hughes et al. 1985; see also Appendix A)
(21)Polarization degree of the resulting synchrotron radiation is given by (Hughes et al. 1985; see also Appendix A) ![\begin{equation} \Pi(\vec{k}') = \Pi_{\rm max}\frac{\left(1-\kappa^2\right)\left[1-\left(\vec{k}'\cdot\vec{n}'\right)^2\right]}{2-\left(1-\kappa^2\right)\left[1-\left(\vec{k}'\cdot\vec{n}'\right)^2\right]}\cdot \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq58.png) (22)The total intensity is related to the total radiation flux by2
(22)The total intensity is related to the total radiation flux by2![\begin{equation} I'(\vec{k}') = \left(\frac{3}{8\pi}\right)\left\{\frac{2-\left(1-\kappa^2\right)\left[1-\left(\vec{k}'\cdot\vec{n}'\right)^2\right]}{2+\kappa^2}\right\}\Phi'. \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq59.png) (23)The magnetic polarization vector is tangent to both the shock front and the plane of the sky, therefore b′ ∝ (k′ × n′).
(23)The magnetic polarization vector is tangent to both the shock front and the plane of the sky, therefore b′ ∝ (k′ × n′).
2.2. Ordered magnetic field
Models of the formation of relativistic jets involve magnetic fields that are ordered on a global scale (Blandford & Znajek 1977; Blandford & Payne 1982; for a recent review see Spruit 2010; Beskin 2010). Initially of poloidal orientation, at large distances the magnetic fields are shaped by the rotation of the central engine and the jet lateral expansion. Their most general form is that of a tightly wound helical structure, which at large distances is increasingly dominated by the toroidal component. Here, we introduce a one-parameter family of globally ordered magnetic field structures that can be easily implemented into the reconfinement shock models.
At every point (z,r,φ) of the jet region, the magnetic field, measured in the fluid co-moving frame, has a toroidal component Bt along the azimuthal angle φ and a poloidal component along the fluid velocity vector, i.e. the 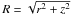 coordinate. The third component, which would be directed along the polar angle θ = arctan(r/z), is neglected. The combination of these components forms a helix of pitch angle αB = arctan(Bp/Bt).
coordinate. The third component, which would be directed along the polar angle θ = arctan(r/z), is neglected. The combination of these components forms a helix of pitch angle αB = arctan(Bp/Bt).
For each magnetic field component, a relation between its values across the different locations needs to be established. First of all, the magnetic field structure is assumed to be axisymmetric, i.e. Bp and Bt are independent of φ. For a particular fluid element, conservation of the magnetic flux implies the following scaling laws: Bp ∝ R-2 and Bt ∝ R-1. However, the dependence of the magnetic field components on the polar angle θ is arbitrary. Here, a choice is made that for the same values of R, Bp is independent of θ and Bt ∝ sinθ. This scaling satisfies a condition that Bt has to vanish at θ = 0. The explicit formulas for the magnetic field components at any point within the jet region are 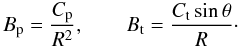 (24)We relate the constants Cp and Ct to the value of the pitch angle αB,m at the jet maximum radius rm at
(24)We relate the constants Cp and Ct to the value of the pitch angle αB,m at the jet maximum radius rm at 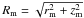 ,
, 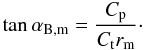 (25)Thus, the pitch angle at any point in the jet region is
(25)Thus, the pitch angle at any point in the jet region is 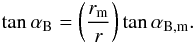 (26)Since r < rm, αB,m is the minimum value of the pitch angle that can be achieved anywhere at the shock front. Eliminating Cp, we calculate the magnetic field components before crossing the shock front
(26)Since r < rm, αB,m is the minimum value of the pitch angle that can be achieved anywhere at the shock front. Eliminating Cp, we calculate the magnetic field components before crossing the shock front 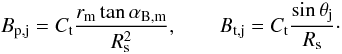 (27)The value of Ct is not important for the resulting polarization, hence the only free parameter of the magnetic field structure is αB,m. Across the shock front, the poloidal component is conserved, Bp,s = Bp,j, while the toroidal component is compressed by a factor κ = (ρj/ρs), i.e. Bt,s = Bt,j/κ. Thus, the post-shock pitch angle is
(27)The value of Ct is not important for the resulting polarization, hence the only free parameter of the magnetic field structure is αB,m. Across the shock front, the poloidal component is conserved, Bp,s = Bp,j, while the toroidal component is compressed by a factor κ = (ρj/ρs), i.e. Bt,s = Bt,j/κ. Thus, the post-shock pitch angle is 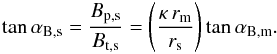 (28)In the coordinate system introduced in Sect. 2 to calculate the Stokes parameters, the magnetic field direction is
(28)In the coordinate system introduced in Sect. 2 to calculate the Stokes parameters, the magnetic field direction is 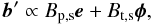 (29)where e is the unit vector along the fluid velocity and φ = [−sinφ,cosφ,0] . Since the magnetic field is locally uniform, the polarization degree is equal to Πmax and the total intensity is
(29)where e is the unit vector along the fluid velocity and φ = [−sinφ,cosφ,0] . Since the magnetic field is locally uniform, the polarization degree is equal to Πmax and the total intensity is ![\begin{equation} I'(\vec{k}')=\left(\frac{3}{8\pi}\right)\left[1-\left(\vec{b}'\cdot\vec{k}'\right)^2\right]\Phi' \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq89.png) (30)(see Appendix A).
(30)(see Appendix A).
3. Results
In this section, we extend the calculations presented in Paper I to cases involving ordered magnetic field components. We used the same model of the reconfinement shock structure as in Paper I. It is assumed that the jet plasma is cold and lowly magnetized, so that the jet does not accelerate and expands conically, and the shock equations can be solved in hydrodynamical approximation. In all models presented here, a jet with the Lorentz factor of Γj = 10 and the half-opening angle of Θj = 5° interacts with the external medium of pressure distribution pe ∝ r−η with η = 0. We do not explore the dependence of the results on the values of these parameters, but rather on the viewing angle θobs, and on the parameters describing the magnetic field structure.
3.1. Toroidal magnetic field
For αB,m = 0, in our model of the global magnetic field structure, the poloidal component vanishes everywhere, leaving the purely toroidal field. In this section, we investigate the polarimetric properties of reconfinement shocks filled with a toroidal field component or a combination of chaotic and toroidal components. This combination is calculated by introducing a parameter f that describes what fractions of the total intensity are emitted from each component: 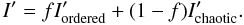 (31)It can also be understood as the fraction of the total magnetic energy density uB = B2/(8π) contained in the ordered magnetic field component. Polarized intensities Q′ and U′ are combined in the same way.
(31)It can also be understood as the fraction of the total magnetic energy density uB = B2/(8π) contained in the ordered magnetic field component. Polarized intensities Q′ and U′ are combined in the same way.
In Fig. 1, we present emission maps of reconfinement shocks filled with toroidal magnetic fields. They can be directly compared to the maps calculated for a chaotic magnetic field, presented in Paper I, since the shock structure is the same. The total flux distribution is more concentrated toward the jet axis. Shock outlines at the largest jet radius are less pronounced for θobs = Θj/2 and barely visible for θobs = Θj. The longitudinal profiles of the total flux calculated for toroidal magnetic fields (not shown) are similar to those for the chaotic magnetic field. A major difference is that for θobs ≤ Θj, the central areas between the two emission peaks are up to ~ 30% dimmer. These differences arise because emission from a uniform magnetic field is more anisotropic than emission from a two-dimensional chaotic distribution. In the areas close to the shock outline at the maximum radius, the magnetic field lines are pointing more closely toward the observer, and consequently less emission can be seen.
 |
Fig. 1 Synthetic emission maps of the reconfinement shock with jet Lorentz factor Γj = 10, opening angle Θj = 5° and external pressure index η = 0, filled with a toroidal magnetic field and seen from different viewing angles θobs. The jet origin is marked with an empty circle, the reconfinement point with a filled circle. The outline of the shock fronts is shown with orange lines. Gray shading indicates the intensity of synchrotron radiation, while the blue bars mark the electric polarization vector of length proportional to the polarization degree. |
The polarization maps are very different from those for chaotic magnetic fields. For θobs = Θj, we find a very simple structure of parallel polarization vectors and polarization degrees very close to the maximum, as is generally expected for toroidal magnetic fields. However, the picture is more complicated for a smaller viewing angle. For θobs = Θj/2, in the vicinity of the shock outline the polarization vectors are perpendicular to the projected shock fronts, which is very similar to the case of chaotic fields. But the central regions of the image show strong parallel polarization. Because the total flux is dominated by the areas close to the projected jet axis, their parallel polarization is expected to dominate the perpendicularly polarized areas.
 |
Fig. 2 Profiles of the polarization degree along the projected jet axis calculated for different viewing angles θobs in two cases: a pure toroidal magnetic field (upper panel; same as models shown in Fig. 1) and an even mix of toroidal and compressed magnetic fields (lower panel). Projected coordinate (z/zr)proj equals 0 for the jet origin and 1 for the reconfinement point. |
In Fig. 2, we show the longitudinal profiles of polarization degree for several viewing angles for a toroidal magnetic field. Polarization is generally parallel to the jet axis, with the exception of the middle region for θobs = Θj/2, where the maximum polarization degree is ~12%. Parallel polarization degrees reach very high values, almost ~60%, for θ ≤ 2Θj. For θobs = 30°, the polarization degree reaches only ~9%. The polarization degree profile is very uniform along the jet axis for θobs ≥ Θj, while for θobs = Θj/2 it is qualitatively similar to the profile calculated for the chaotic magnetic field.
In the lower panel of Fig. 2, we show the polarization degree profiles for an even mix of toroidal and compressed magnetic fields (f = 0.5). Since the total flux (I) profiles for both magnetic field distributions are similar, the combined polarization degree closely reflects the linear combination used to calculate the combined polarized flux Q. Indeed, the polarization profiles for f = 0.5 have properties on average between cases f = 0 (Paper I) and f = 1 (upper panel of Fig. 2). For θobs = Θj/2, the profile is similar to that for f = 1, with slightly lower parallel polarization maxima and higher perpendicular polarization maximum. For higher viewing angles, polarization is still parallel everywhere along the jet axis. For θobs = Θj, the polarization degree profile is less uniform, with polarization degree maxima at the level of ~42% around the jet origin and reconfinement point, and much lower polarization degrees in the middle region. For θobs = 2Θj and θobs = 30°, polarization profiles are uniform with maximum degrees of ~21% and ~3%, respectively. Note that the highest sensitivity of the polarization degree on f is evident for θobs = Θj and θobs = 2Θj.
In Fig. 3, we show the average polarization degree as a function of the viewing angle for several values of f, spanning between purely toroidal magnetic fields (f = 1) and purely chaotic magnetic fields (f = 0). The polarization degree changes monotonically with f for every viewing angle. For the purely toroidal magnetic field, the average polarization degree is always parallel. The highest polarization degree, found at θobs ~ 7° ~1.4Θj, is very close to the maximum value Πmax ~ 69% (for electron distribution index p = 2). Around this viewing angle, the average polarization from a reconfinement shock depends very strongly on the value of f. One can obtain a wide range of polarization degrees, from ~16% perpendicular to ~70% parallel by adjusting the balance between ordered and chaotic magnetic field components. On the other hand, observation of very high polarization degrees from reconfinement shocks puts rather strong constraints on the actual viewing angle.
For small viewing angles, θobs < 3°, the perpendicular polarization signal produced by the chaotic magnetic field will be canceled by the parallel polarization from the toroidal field for f ~ 0.1, while for large viewing angles, θobs > 20°, this depolarization will occur at f ~ 0.3.
 |
Fig. 3 Average polarization degree as a function of the viewing angle θobs calculated for different combinations of toroidal and chaotic magnetic field components. The thick line on the top corresponds to a purely toroidal magnetic field (f = 1), the consecutive lines are calculated with steps Δf = 0.1 down to f = 0 corresponding to a purely chaotic magnetic field. The shock structure is the same as in the models shown in Figs. 1 and 2. The vertical line indicates the jet opening angle of Θj = 5°. |
3.2. Helical magnetic field
Here, we investigate the case of non-vanishing pitch angle of the magnetic field lines, αB,m ≠ 0. Equation (28) indicates that the local post-shock pitch angles at different points of the shock front will vary from arctan(κtanαB,m) at the jet maximum radius rm to 90° when rs → 0, i.e. close to the jet origin and the reconfinement point. Using analytical approximation for the shock structure (Nalewajko & Sikora 2009) for the flat external pressure distribution (η = 0), the pitch angle can be explicitly estimated as 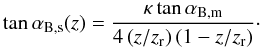 (32)In our numerical model for η = 0, the shock compression parameter κ changes from 0.25 for z ≪ zr to ~0.2 for z → zr. Hence, the dependence of the downstream pitch angle on z is not very different from that of the upstream pitch angle.
(32)In our numerical model for η = 0, the shock compression parameter κ changes from 0.25 for z ≪ zr to ~0.2 for z → zr. Hence, the dependence of the downstream pitch angle on z is not very different from that of the upstream pitch angle.
In Fig. 4, we show emission maps for three values of αB,m = 3°,7°,15°. They are calculated for the same shock structure as the maps calculated for the toroidal magnetic field (αB,m = 0) shown in Fig. 1. The viewing angle is fixed at θobs = Θj. Our first observation is that both the total and polarized flux maps are not symmetric with respect to the projected jet axis. This is because the observed brightness depends on the orientation of the magnetic field lines, while the projection of the helical magnetic field distribution is not axisymmetric, even if it has an axial symmetry in the three-dimensional space. As a consequence of this asymmetry, the integrated Stokes parameter U will not vanish. The average polarization angle will not be strictly parallel nor perpendicular to the jet axis.
 |
Fig. 4 Synthetic emission maps of the reconfinement shock with jet Lorentz factor Γj = 10, opening angle Θj = 5° and external pressure index η = 0, filled with a helical magnetic field of different minimum pitch angle αB,m and seen from the viewing angle θobs = Θj. Dashed orange lines mark the turning point for polarization angle profiles in Fig. 5. See Fig. 1 for more explanation. |
Maps of the total flux have a brighter lower rim and a dimmer upper rim with increasing αB,m. The bright spots are shifted toward the lower rim and become less prominent. Longitudinal profiles of the total flux (not shown) show a systematic increase of the flux from the middle region relative to the peak around the reconfinement point. For αB,m = 15°, the bright spots become very distorted and the upper rim becomes visible. For all values of αB,m, the central region of the image contributes little to the integrated flux.
Polarization vectors show a dramatic structural change with a moderate increase of the minimum pitch angle. For the toroidal magnetic field (αB,m = 0), the polarization is strong and parallel across the entire image. For αB,m = 3°, the emission from the lower rim shows significantly lower polarization degrees, at one point it is almost completely depolarized. Polarization vectors corresponding to the main bright spot around the reconfinement point appear to rotate clockwise (CW) by ~20° with respect to the jet axis, while those around the secondary bright point around the jet origin appear to rotate counterclockwise (CCW) by ~15°. Polarization vectors on the upper rim show little change compared to those for αB,m = 0.
For αB,m = 7°, the polarization degrees decrease in the central region and along the upper rim, but remain very high around the bright spots. The polarization vectors are aligned with the upper rim and perpendicular to the lower rim. Around the main bright spot the polarization vectors are rotated CW by ~40°, and around the secondary spot they are rotated CCW by ~30°.
For αB,m = 15°, polarization degrees are significantly higher along the lower rim than the upper rim. Their orientation is roughly perpendicular to the lower rim and perpendicular to the projected jet axis along the upper rim. Polarization vectors at the projected reconfinement point are rotated CW by ~60° and those at the projected jet origin are rotated CCW by ~45°.
Not surprisingly, increasing the pitch angle in the helical magnetic field distribution has the effect of turning the polarization vectors from parallel to perpendicular with respect to the projected jet axis. At the same time, the total emission pattern changes from that dominated by bright spots at both ends of the reconfinement structure to that dominated by one of the rims. The average polarization degree can be expected to be very sensitive to the value of αB,m.
 |
Fig. 5 Profiles of the average polarization degree (upper panel) and the polarization angle (lower panel) along the projected jet axis, calculated for a helical magnetic field with different values of the minimum pitch angle αB,m, indicated in the legend. Both panels show exactly the same models, three of them are shown in Fig. 4. See Fig. 2 for more explanation. |
In Fig. 5, we show the longitudinal profiles of the polarization degree for αB,m ranging from 0 to 15°. Since the Stokes parameter U integrated over slices of the same zproj is non-zero, the polarization degree and angle are plotted separately. The case of αB,m = 0 is shown with the dashed line in the upper panel of Fig. 2. With increasing values of the pitch angle, the polarization degree decreases in the middle part of the projected jet. At the same time, it remains very high (~55−60%) around the positions of the jet origin and the reconfinement point. For αB,m ~ 7°, the average emission becomes depolarized at (z/zr)proj ~ 0.62. We call this point the turning point and mark it with the vertical dashed lines in Figs. 4 and 5. For higher values of αB,m, the polarization degree increases in the middle section and slightly decreases at the extremes. For αB,m = 15°, the polarization degree at the turning point is at the level of ~40%.
 |
Fig. 6 Average polarization degree (upper panel) and polarization angle (lower panel) as a function of the viewing angle, calculated for a helical magnetic field with different values of the minimum pitch angle αB,m, indicated in the legend. The shock structure is the same as in the models shown in Figs. 4 and 5. Solid vertical line indicates the jet opening angle Θj = 5°. |
For small pitch angles, the polarization angle increases (rotates CCW) before the turning point and decreases otherwise. For αB,m < 7° the modulus of the polarization angle does not exceed 45%, i.e. Q > 0 and the polarization can be described as closer to parallel than perpendicular. Also, the polarization at the turning point is parallel. This changes for αB,m > 7°, when the polarization vectors rotate mostly CCW with increasing zproj and the polarization at the turning point becomes perpendicular. For αB,m = 15°, the modulus of the polarization angle is generally higher than 45%, hence Q < 0.
The nature of the turning point is that the average value of Stokes parameter U is always close to 0. The case of αB,m ~ 7° is transitional, because the average Stokes parameter Q changes sign there. It is also evident in the emission maps in Fig. 4. Polarization vectors in the vicinity of the turning point are either parallel or perpendicular to the projected jet axis. In the map for αB,m = 3°, the polarization is mostly parallel or very low. For αB,m = 15°, the polarization is perpendicular. And for αB,m = 7°, roughly half of the vectors are parallel and the other half perpendicular, with relatively uniform total flux.
In Fig. 6, we show the average polarization degree and angle as functions of the viewing angle for the same values of αB,m as in Fig. 5. The average polarization degree initially decreases with the increasing pitch angle. The average polarization angle is very close to 0 for θobs < Θj and rotated in the CW direction, by a value roughly proportional to αB,m, for θobs > Θj. It does not depend on the viewing angle for θobs > 20°.
The case of αB,m ~ 7° is once again of special interest. The polarization degree for all viewing angles is lower than ~11%. The polarization angle changes sharply between ~0 for θobs = Θj to ~ −70° for θobs = 2Θj and remains at this level for larger viewing angles. For higher values of the minimum pitch angle, the polarization degree increases and the polarization angle is generally close to 90°, i.e. polarization is perpendicular to the jet axis. For αB,m = 10°, polarization angle deviates from 90° for very small viewing angles, but the corresponding polarization degrees are very low. For αB,m = 15°, the maximum polarization degree is ~40% for θobs ~ 9°.
4. Discussion
Polarization surveys, combined with knowledge of the inner jet structure inferred from VLBI imaging, can provide information on the orientation of magnetic fields with respect to the projected jet axis. Optical polarization electric vectors in compact radio sources are preferentially parallel to the inner jet (e.g. Rusk & Seaquist 1985). This polarization alignment can be explained with transverse internal shocks. In the reconfinement shock scenario discussed in this work, strong parallel polarization can only be produced in the presence of ordered magnetic fields that contribute at least half the total magnetic energy density (see Fig. 3) and have a minimum pitch angle of less than ~5° (see Fig. 6).
Polarization measured in large-scale jets between prominent knots is usually perpendicular, both in radio (e.g. Bridle et al. 1994) and optical bands (e.g. Perlman et al. 2006). It indicates the presence of a strong poloidal component of the magnetic field. However, in expanding jet the poloidal magnetic field component decays faster than the toroidal component. In large-scale jets, the poloidal component of the magnetic field can arise through the velocity shear at the jet boundary (Laing 1981). Cawthorne (2006) studied polarization of synchrotron radiation from conical shocks filled with a combination of chaotic and poloidal magnetic fields. He calculated polarized emission maps and compared them with resolved polarimetric VLBI map of blazar 3C 380. He was able to reproduce a fan-like structure of the polarization vectors for an equal contribution of chaotic and poloidal magnetic field components (f = 0.5). His motivation for introducing the poloidal component was to obtain higher degrees of the perpendicular polarization. Reconfinement shocks or conical shocks with diverging upstream flow can produce higher perpendicular polarization degrees without an ordered magnetic field component.
Lyutikov et al. (2005) studied polarization from helical magnetic fields in relativistic cylindrical jets. In this case, the pitch angle is constant along the jet and therefore their results are difficult to compare directly with the results of Sect. 3.2, where the pitch angle is strongly position-dependent. However, the dependence of the average polarization degree on the viewing angle and the minimum pitch angle (Fig. 6) is in qualitative agreement with their Fig. 7a. One important difference is that in their model the average Stokes parameter ⟨U⟩ vanishes. In our model, ⟨U⟩ ≠ 0, since we have defined the poloidal component of the magnetic field along the fluid velocity unit vector e (see Eq. (29)). Only when e is parallel to the jet axis, as is the case for a cylindrical jet model, ⟨U⟩ = 0. This provides a physical interpretation for the turning point found in Fig. 5. It corresponds to a distance z along the jet, for which the post-shock velocity inclination angle θs = 0. Since θs is a monotonically decreasing function of z, there can be only one such turning point, located closely to the point of maximum jet radius.
Lyutikov et al. (2005) also studied the transverse profiles of polarization degree. In their Figs. 9a,b they show that those profiles should be symmetric with respect to the jet axis for θobs = 1/Γ and strongly asymmetric for θobs = 1/(2Γ) or θobs = 2/Γ. Polarization vectors close to the jet boundary should always be perpendicular. Using the emission maps shown in Fig. 4, one can evaluate the transverse polarization degree profiles along the lines indicating the turning point. These models correspond to θobsΓj = 0.9 and θobsΓs slightly lower. The Q/I profiles are strongly asymmetric, with the Q/I value increasing from the lower rim to the upper rim. Polarization vectors are not always perpendicular at the jet boundary, but this may be due to the low resolution of the maps. Our polarization profiles appear to be roughly consistent with their case of θobs = 1/(2Γ). This may indicate that the transverse polarization profile for cylindrical jets filled with helical magnetic fields is very sensitive to θobs for values close to 1/Γ.
On the other hand, some observed radio structures in jets can be understood without invoking any ordered magnetic field component. An interesting recent example is the C80 knot in the jet of radio galaxy 3C 120, reported by Agudo et al. (2012). It has a bow-like shape with polarization vectors aligned perpendicularly to its outline. It was well reproduced by a conical shock model with compressed chaotic magnetic field distribution. However, this model can hardly explain the polarization vectors perpendicular to the jet axis observed immediately downstream of the C80 knot, even when a poloidal field component is introduced. Additional perpendicular shock waves can explain a parallel polarization measured even farther downstream (knot C99), but are inconsistent with a perpendicular polarization. We propose a simple explanation of the perpendicular polarization vectors downstream of the C80 knot by a gradual collimation of the conical shock into a roughly cylindrical structure. In the absence of large-scale magnetic fields, the polarization vectors will be perpendicular to the local shock outline (Paper I).
Our model predicts a relatively uniform distribution of the total brightness, especially at large viewing angles. Hence, it cannot reproduce very bright and compact features like HST-1 in radio galaxy M 87. Clearly, an additional dissipation mechanism is required to explain its behavior, in particular the high optical/UV polarization reported by Perlman et al. (2011).
5. Summary
We calculated emission maps and longitudinal profiles of total flux and polarization degree, and average polarization degree for relativistic reconfinement shocks with different combinations of chaotic and ordered magnetic field distributions.
For toroidal magnetic fields (Sect. 3.1), the average polarization is always parallel to the jet axis, and the average polarization degree can reach the maximum value allowed for a particular electron distribution. The total flux emission maps for θobs > Θj are similar to those for the case of chaotic magnetic fields, for small viewing angles they lack emission from the rims.
For helical magnetic fields (Sect. 3.2), which are characterized by the value of the minimum pitch angle αB,m measured at the point of maximum jet radius, emission maps are asymmetric with respect to the projected jet axis and hence the Stokes parameter U ≠ 0. For αB,m ≳ 7°, the total flux is concentrated on one side of the jet axis, where polarization vectors align with the shock outline and the polarization degrees are higher than on the other side. Longitudinal profiles show a characteristic turning point at (z/zr)proj ~ 0.6, where average U ~ 0, regardless of the pitch angle. It corresponds to the point at which the post-shock velocity vectors are parallel to the jet axis, as for the cylindrical jet models studied by Lyutikov et al. (2005). It separates the initial jet section in which polarization vectors are rotated counterclockwise to the jet axis from the section in which the polarization vectors are rotated clockwise. The average polarization angle is | χE | < 45° (Q > 0) for αB,m < 7°, and the opposite is generally true (see Fig. 6). For αB,m ~ 7°, the reconfinement shock appears to be effectively depolarized for all observers.
Observed frequency of the peak of synchrotron emission produced by electrons of Lorentz factor γ is 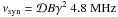 . Assuming that cooling is dominated by radiative losses due to the synchrotron emission, the cooling length scale, a typical distance covered by a particle before losing a significant fraction of its energy, is
. Assuming that cooling is dominated by radiative losses due to the synchrotron emission, the cooling length scale, a typical distance covered by a particle before losing a significant fraction of its energy, is 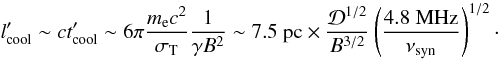 For magnetic fields strength B = 1G and Doppler factor
For magnetic fields strength B = 1G and Doppler factor 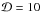 , optical-emitting electrons (νsyn = 6 × 1014Hz) have
, optical-emitting electrons (νsyn = 6 × 1014Hz) have 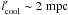 . For comparison, high-frequency radio-emitting electrons (νsyn = 43GHz) have
. For comparison, high-frequency radio-emitting electrons (νsyn = 43GHz) have 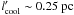 .
.
The co-moving anisotropy of the total intensity has been neglected in Nalewajko (2009), but the consequences of this effect are not significant.
Acknowledgments
This work has been partly supported by the Polish MNiSW grants N N203 301635 and N N203 386337, the Polish ASTRONET grant 621/E-78/SN-0068/2007, the Polish NCN grant DEC-2011/01/B/ST9/04845, and the NSF grant AST-0907872 and the NASA Astrophysics Theory Program grant NNX09AG02G.
References
- Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Gómez, J. L., Casadio, C., Cawthorne, T. V., & Roca-Sogorb, M. 2012, ApJ, 752, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, RvMP, 56, 255 [Google Scholar]
- Beskin, V. S. 2010, Phys. Uspekhi, 53, 1199 [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Bridle, A. H., Hough, D. H., Lonsdale, C. J., Burns, J. O., & Laing, R. A. 1994, AJ, 108, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Cawthorne, T. V. 2006, MNRAS, 367, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Cawthorne, T. V., & Cobb, W. K. 1990, ApJ, 350, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Ojha, R., Wardle, J. F. C., et al. 2002, ApJ, 568, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, P. A., Aller, H. D., & Aller, M. F. 1985, ApJ, 298, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Ikejiri, Y., Uemura, M., Sasada, M., et al. 2011, PASJ, 63, 639 [NASA ADS] [Google Scholar]
- Impey, C. D., Lawrence, C. R., & Tapia, S. 1991, ApJ, 375, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. W. 1988, ApJ, 332, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., & Falle, S. A. E. G. 1997, MNRAS, 288, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A. 1980, MNRAS, 193, 439 [NASA ADS] [Google Scholar]
- Laing, R. A. 1981, ApJ, 248, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K. R., & Blandford, R. D. 1985, ApJ, 295, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L. 2001, ApJ, 562, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M., Pariev, V. I., & Gabuzda, D. C. 2005, MNRAS, 360, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., Mattox, J. R., & Wehrle, A. E. 2002, ApJ, 577, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Massardi, M., Ekers, R. D., Murphy, T., et al. 2011, MNRAS, 412, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, A. P., & Scheuer, P. A. G. 1990, MNRAS, 242, 616 [NASA ADS] [Google Scholar]
- Nalewajko, K. 2009, MNRAS, 395, 524 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K., & Sikora, M. 2009, MNRAS, 392, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K., & Sikora, M. 2010, ASPC, 427, 205 [NASA ADS] [Google Scholar]
- Perlman, E. S., Padgett, C. A., Georganopoulos, M., et al. 2006, ApJ, 651, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Adams, S. C., Cara, M., et al. 2011, ApJ, 743, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, L. K., Taylor, G. B., & Zavala, R. T. 2003, ApJ, 589, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Rusk, R., & Seaquist, E. R. 1985, AJ, 90, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 1983, ApJ, 266, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Madejski, G., Moderski, R., & Poutanen, J. 1997, ApJ, 484, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Stawarz, Ł., Moderski, R., Nalewajko, K., & Madejski, G. M. 2009, ApJ, 704, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 2010, LNP, 794, 233 [Google Scholar]
- Stockman, H. S., & Angel, J. R. P. 1978, ApJ, 220, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Wills, B. J., Wills, D., Breger, M., Antonucci, R. R. J., & Barvainis, R. 1992, ApJ, 398, 454 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Polarization and anisotropy of the synchrotron radiation
In Sect. 2, we calculated the polarization properties of synchrotron radiation arising from different distributions of the magnetic field. The total emitted power is constrained, but the intrinsic anisotropy of the synchrotron emission has to be accounted for. The exact results depend on the index p of the electron energy distribution N(γ) ∝ γ − p. However, Laing (1980) and Hughes et al. (1985) showed that the formulas are greatly simplified for p = 3.
A.1. Uniform magnetic field
For a uniform magnetic field B, we have 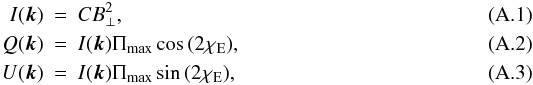 where k is the unit vector toward the observer, B ⊥ is the magnetic field component normal to the line of sight, χE is the electric vector polarization angle, Πmax = (3p + 3)/(3p + 7) is the maximum polarization degree of the synchrotron radiation, and C is a constant. We note that
where k is the unit vector toward the observer, B ⊥ is the magnetic field component normal to the line of sight, χE is the electric vector polarization angle, Πmax = (3p + 3)/(3p + 7) is the maximum polarization degree of the synchrotron radiation, and C is a constant. We note that 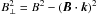 and χE = χB − π/2, where χB is the magnetic field polarization angle. We introduce orthogonal coordinates in the plane of the sky (v,w), in which the polarization angle is measured. The magnetic vector polarization angle is
and χE = χB − π/2, where χB is the magnetic field polarization angle. We introduce orthogonal coordinates in the plane of the sky (v,w), in which the polarization angle is measured. The magnetic vector polarization angle is 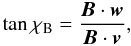 (A.4)hence
(A.4)hence 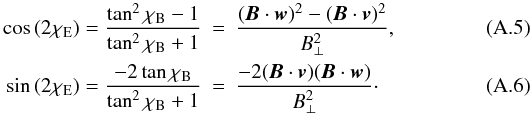 General formulas for the Stokes parameters are
General formulas for the Stokes parameters are ![\appendix \setcounter{section}{1} \begin{eqnarray} I(\vec{k}) &=& C\left[B^2-(\vec{B}\cdot\vec{k})^2\right], \\ Q(\vec{k}) &=& C\Pi_{\rm max}\left[(\vec{B}\cdot\vec{w})^2-(\vec{B}\cdot\vec{v})^2\right], \\ U(\vec{k}) &=& C\Pi_{\rm max}\left[-2(\vec{B}\cdot\vec{v})(\vec{B}\cdot\vec{w})\right]\cdot \end{eqnarray}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq200.png) The C constant can be found from the total radiation flux:
The C constant can be found from the total radiation flux: 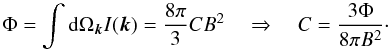 (A.10)
(A.10)
A.2. Compressed chaotic magnetic field
Following the calculations of Hughes et al. (1985), we consider an isotropic magnetic field distribution ![\appendix \setcounter{section}{1} \begin{equation} \vec{B}=B\vec{b}=B[\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta]. \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq202.png) (A.11)It is then compressed along unit vector n = [0,0,1] by factor κ ≤ 1
(A.11)It is then compressed along unit vector n = [0,0,1] by factor κ ≤ 1 ![\appendix \setcounter{section}{1} \begin{equation} \tilde{\vec{B}}=B\left[\frac{1}{\kappa}\sin\theta\cos\phi,\frac{1}{\kappa}\sin\theta\sin\phi,\cos\theta\right]. \end{equation}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq205.png) (A.12)The average Stokes parameters are found by integration over all possible unit vectors b. For an observer located at k = [sinα,0,cosα] (and plane-of-the-sky coordinate vectors v = [cosα,0, − sinα] and w = [0,1,0] ), the results are
(A.12)The average Stokes parameters are found by integration over all possible unit vectors b. For an observer located at k = [sinα,0,cosα] (and plane-of-the-sky coordinate vectors v = [cosα,0, − sinα] and w = [0,1,0] ), the results are ![\appendix \setcounter{section}{1} \begin{eqnarray} I(\vec{k}) &=& \frac{C}{4\pi}\int {\rm d}\Omega_{\vec{b}}\left[\tilde{B}^2-(\tilde{\vec{B}}\cdot\vec{k})^2\right] \nonumber\\ &=&\frac{CB^2}{3\kappa^2}\left[2-\left(1-\kappa^2\right)\sin^2\alpha\right], \\ Q(\vec{k}) &=& \frac{C\Pi_{\rm max}}{4\pi}\int {\rm d}\Omega_{\vec{b}}\left[(\tilde{\vec{B}}\cdot\vec{w})^2-(\tilde{\vec{B}}\cdot\vec{v})^2\right] \nonumber\\ &=& \frac{C\Pi_{\rm max}B^2}{3\kappa^2}\left(1-\kappa^2\right)\sin^2\alpha, \\ U(\vec{k}) &=& \frac{C\Pi_{\rm max}}{4\pi}\int {\rm d}\Omega_{\vec{b}}\left[-2(\tilde{\vec{B}}\cdot\vec{v})(\tilde{\vec{B}}\cdot\vec{w})\right] = 0. \end{eqnarray}](/articles/aa/full_html/2012/07/aa19359-12/aa19359-12-eq209.png) Hence, the polarization degree is
Hence, the polarization degree is 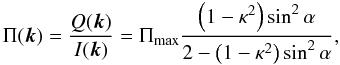 (A.16)in agreement with Hughes et al. (1985). The polarization angle is χE = 0, since Q(k) > 0 and U(k) = 0. The C constant is found from
(A.16)in agreement with Hughes et al. (1985). The polarization angle is χE = 0, since Q(k) > 0 and U(k) = 0. The C constant is found from 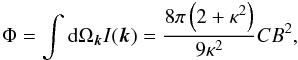 (A.17)hence
(A.17)hence 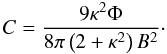 (A.18)
(A.18)
All Figures
 |
Fig. 1 Synthetic emission maps of the reconfinement shock with jet Lorentz factor Γj = 10, opening angle Θj = 5° and external pressure index η = 0, filled with a toroidal magnetic field and seen from different viewing angles θobs. The jet origin is marked with an empty circle, the reconfinement point with a filled circle. The outline of the shock fronts is shown with orange lines. Gray shading indicates the intensity of synchrotron radiation, while the blue bars mark the electric polarization vector of length proportional to the polarization degree. |
| In the text | |
 |
Fig. 2 Profiles of the polarization degree along the projected jet axis calculated for different viewing angles θobs in two cases: a pure toroidal magnetic field (upper panel; same as models shown in Fig. 1) and an even mix of toroidal and compressed magnetic fields (lower panel). Projected coordinate (z/zr)proj equals 0 for the jet origin and 1 for the reconfinement point. |
| In the text | |
 |
Fig. 3 Average polarization degree as a function of the viewing angle θobs calculated for different combinations of toroidal and chaotic magnetic field components. The thick line on the top corresponds to a purely toroidal magnetic field (f = 1), the consecutive lines are calculated with steps Δf = 0.1 down to f = 0 corresponding to a purely chaotic magnetic field. The shock structure is the same as in the models shown in Figs. 1 and 2. The vertical line indicates the jet opening angle of Θj = 5°. |
| In the text | |
 |
Fig. 4 Synthetic emission maps of the reconfinement shock with jet Lorentz factor Γj = 10, opening angle Θj = 5° and external pressure index η = 0, filled with a helical magnetic field of different minimum pitch angle αB,m and seen from the viewing angle θobs = Θj. Dashed orange lines mark the turning point for polarization angle profiles in Fig. 5. See Fig. 1 for more explanation. |
| In the text | |
 |
Fig. 5 Profiles of the average polarization degree (upper panel) and the polarization angle (lower panel) along the projected jet axis, calculated for a helical magnetic field with different values of the minimum pitch angle αB,m, indicated in the legend. Both panels show exactly the same models, three of them are shown in Fig. 4. See Fig. 2 for more explanation. |
| In the text | |
 |
Fig. 6 Average polarization degree (upper panel) and polarization angle (lower panel) as a function of the viewing angle, calculated for a helical magnetic field with different values of the minimum pitch angle αB,m, indicated in the legend. The shock structure is the same as in the models shown in Figs. 4 and 5. Solid vertical line indicates the jet opening angle Θj = 5°. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


