| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 7 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201219160 | |
| Published online | 22 June 2012 | |
A novel technique to control differential birefringence in optical interferometers
Demonstration on the PIONIER-VLTI instrument
1 Institut de Planétologie et d’Astrophysique de Grenoble, BP 53, 38041 Grenoble Cedex 9, France
e-mail: bernard.lazareff@obs.ujf-grenoble.fr
2 European Southern Observatory Alonso de Córdova 3107, Vitacura Casilla 19001, Santiago de Chile 19, Chile
Received: 2 March 2012
Accepted: 16 April 2012
Context. Optical interferometers are subject to many atmospheric and instrumental artifacts that contribute to the degradation of their instrumental contrast, hence their performances. The differential birefringence is, among these effects, one of the trickiest to control, in particular for instrument using fibers, where it can be far larger than the one arising in the optical mirror trains. Several solutions have been tested in the past, ranging from polarization splitting to fiber tweaking. We adopt a new solution for the PIONIER instrument, a four-telescope (4T) combiner at the Very Large Telescope Interferometer (VLTI).
Aims. We present a method to cancel the instrumental birefringence in an optical interferometer, allowing the joint detection of the fringe patterns of both polarizations, and substantial gains to be made in both signal-to-noise ratio and readout speed.
Methods. A thin (2 mm) plate of birefringent material (LiNbO3) is inserted in each of the four beams. The incidence angle of each plate is adjustable. This allows us to introduce a controlled amount of birefringence in each beam and to cancel the instrumental differential birefringence. We present our derivation of the induced birefringence versus incidence angle and discuss the design choices.
Results. Our proposed solution is implemented in the Pionier instrument. Before correction, the instrumental birefringence was of order 5 μm (path length). The adjustment takes about one hour, results in a birefringence of less than 0.1 μm, and is stable for at least the duration of an observing run (several days).
Conclusions. We demonstrate on an operational near-infrared interferometer a novel, simple, low-cost, and effective technique to control the differential birefringence. The predictability and stability of the correction make this technique ideal for an automated correction in the VLTI second generation instruments.
Key words: instrumentation: interferometers / instrumentation: polarimeters / instrumentation: high angular resolution
© ESO, 2012
1. Introduction
In an astronomical optical interferometer, light gathered by several telescopes is brought to a common recombination point. The design of the optical trains must be such that the polarization orientation is preserved, since orthogonal polarizations of natural light are mutually incoherent. This is generally achieved by enforcing identical (angles, not lengths) geometry of the optical trains in the various arms of the interferometer in a way known as the golden rule (Traub 1988; Elias 2001; García et al. 2003; Schöller 2003). However, as demonstrated early on (Rousselet-Perraut et al. 1996) that condition is not sufficient. The light path is generally birefringent, regardless of whether this is due to either mirror reflections or optical fiber propagation. If the birefringence in two light paths is not perfectly balanced, the interference fringe patterns in the two orthogonal polarizations suffer a relative shift, and a polarization-insensitive detection of the fringe pattern suffers a loss of contrast with respect to the separate detection of pure polarization states. To avoid that loss, two main approaches have been proposed in the context of single-mode instrumentation. In the first one, the two polarizations must be detected separately. In particular, Delage & Reynaud (2000) recommended the use of highly birefringent fibers together with polarization splitting. This carries a signal-to-noise penalty in the presence of a noisy detector and slows down the fringe acquisition process. However, polarization separation is crucial for scientific applications where polarized coherence is an astrophysical observable (Rousselet-Perraut et al. 1997, 2006; Elias 2001; Ireland et al. 2005; Le Bouquin et al. 2008). In the second approach, an optical device is used to introduce a differential birefringence compensation. Following this idea, Lagorceix & Reynaud (1995) proposed a fibered Babinet compensator while the FLUOR instrument succesfully used mechanically stressed fiber loops (Coudé du Foresto et al. 1998).
This paper addresses one definite issue of polarization in optical interferometry: the loss of fringe contrast due to birefringence in the instrument. We define the instrument to be the equipment that resides in a central location and complements the light gathering and beam transport functions of the telescopes. We do not consider the case of scientific polarimetric interferometry (Rousselet-Perraut et al. 1997; Murakami et al. 2009). Neither do we address the impact of the birefringence of the optical trains of the telescopes; one can note that in practical terms such birefringence may be significant for precision polarimetry but has a negligible impact on fringe contrast. We propose a solution to the problem of instrument-induced birefringence, that allows us to restore a full fringe contrast. It is characterized by its ease of implementation and precise quantitative control. We demonstrate its feasibility in the practical context of the Pionier visitor instrument at VLTI.
This paper is organized as follows. In Sect. 2, we state the problem as it arises in the context of the Pionier instrument. In Sect. 3, we derive the differential path length between two plane waves across a birefringent plate. In Sect. 4, we examine the relative merits of various candidate birefringent materials. In Sect. 5, we describe how the proposed solution has been implemented in the Pionier instrument, and, more importantly, we demonstrate its effectiveness.
2. Context of the Pionier instrument
Pionier (Le Bouquin et al. 2011) is a four-telescope instrument developed for the European Southern Observatory (ESO) Very Large Telescope Interferometer (VLTI). The light beams from four telescopes are brought to the input of Pionier, in the underground interferometry laboratory. Following per-beam processing (tip-tilt correction, path length modulation), each beam is focused by an off-axis parabola to the input of an optical fiber, which transports the light to the input of an integrated optics beam combiner (IOBC). As already mentioned, it is important to preserve the orientation of the light beams, hence, polarization maintaining fibers were chosen. Such fibers are, by nature, strongly anisotropic, and induce a birefringence between the two orthogonal linear polarizations (say, h and v) δφvh = δφv − δφh, at a rate of typically one turn every few centimeters of fiber travel. The lengths of the fibers can be equalized only to finite accuracy, and, furthermore, group delay equalization (or, better, dispersion equalization) has priority and will generally not coincide with birefringence equalization, even when consecutive lengths of fiber are taken from the same fabrication lot.
Early in the design of Pionier, this issue was identified. The differential birefringence δφvh21 = δφvh2 − δφvh1 between two group delay equalized fibers was measured to be (expressed in path length) about 5 μm, much more than can be tolerated in an H band (λ ≃ 1.65 μm) interferometer. The baseline design included, between the IOBC and the camera, a Wollaston prism to allow the separate detection of the fringes in the two linear polarizations. This affects the performance of the instrument in two ways: i) since the instrument does not operate in a photon-noise-limited regime, the signal-to-noise is degraded; ii) twice as many pixels must be read, limiting the scanning speed of the fringes, a key performance limitation when observing through the atmosphere with a coherence time of a few milliseconds.
Figure 1 shows a typical offset between the fringe packets in the Pionier instrument for the orthogonal polarizations, showing the impact of the uncorrected birefringence. The measurement was made during technical time using the internal calibration source. In reality, since we did not have the forethought to measure the offsets between polarizations before implementing the proposed corrective device, we threw out of adjustment the corrections of beams 2 and 3 to achieve an optical path difference (opd) mismatch typical of what was observed before the implementation.
 |
Fig. 1 Measured fringe packets in the Pionier instrument, between inputs 2 and 3, for the two linear polarizations, and with birefringence uncorrected. |
An alternate design was developed and implemented, where a birefringent plate with adjustable inclination is used to modify and cancel the differential path length between the two orthogonal polarizations. Such a simple approach is possible because the birefringence introduced by the polarization maintaining fibers has a known orientation. The principle of the correction is shown schematically in Fig. 2.
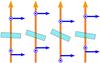 |
Fig. 2 Principle of the correction. Before traversing the birefringent plates, each beam is plagued by a differential delay between the horizontal and vertical polarizations. This differential delay can be canceled by suitably adjusting the inclination of each birefringent plate. The beam-to-beam delay is generally affected, but is easy to equalize once birefringence is taken care of. This figure is drawn as if the correction is performed after the unwanted birefringence has occurred; in the case of Pionier, the correction is in fact made upstream of the point where birefringence occurs. |
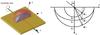 |
Fig. 3 In case 1, the optical axis is along the x direction. Left: a schematic of the birefringent plate, the rotation axis used to adjust the angle of incidence, and the two sheets of the index surface. Right: the geometry of wave vectors. The two circles and the ellipse are the intersections with the plane of incidence of the two sheets of the index surface and the unity sphere, all scaled by 2π/λ0, such that they are the locus of the tips of wave vectors k′. |
 |
Fig. 4 In case 2, the optical axis is perpendicular to the plane of incidence. The two schematics are drawn as in case 1. |
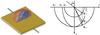 |
Fig. 5 In case 3, the optical axis is perpendicular to the vacuum-crystal interface, i.e. along the z axis. The two schematics are drawn as in case 1. |
3. Derivation of differential path lengths
We compute the differential path length introduced by a tilted birefringent uniaxial plate, between the two principal polarizations, propagating as plane waves. We could find only a few derivations of this result, and the method is often more complex than it needs to be. To make our presentation self-contained, we provide our derivation below. Three cases are considered, according to the orientation of the crystal optical axis with respect to the plane of incidence and the plane of the compensating plate.
The relevant property for the propagation phase is the wave vector, which is distinct from the ray direction (for the extraordinary ray). For an arbitrary direction of propagation, the wave vectors for the two waves lie on the index surface, which is composed of two sheets, a sphere and an ellipsoid of revolution.
Figures 3–5 are drawn in the case of negative birefringence, with indices chosen for clarity, not realism. The expressions derived below are equally valid for (uniaxial) positive or negative materials.
Notations
-
i
Angle of incidence
-
λ
0
wavelength in vacuum (no distinction from air at the relevant level of accuracy)
-
1, no, ne
vacuum, ordinary, and extraordinary main indices
-
kv, ko, ke
corresponding wave numbers (physics definition, 2π/λ)
-
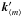
wave vectors along arbitrary directions for the three involved waves, with m denoting: v: vacuum (incident), o: ordinary wave, e extraordinary wave.
-
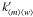
scalar components of the above, with w = x,y,z
3.1. Case 1
In case 1, the optical axis is parallel to both the plane of the plate (X-cut) and the plane of incidence.
We deal with three plane waves at the vacuum-crystal interface: incident, ordinary and extraordinary transmitted; we need not consider the reflected waves. Irrespective of the details of the boundary conditions at the vacuum-crystal interface, all relevant waves must have the same spatial dependence in the plane of the interface. Therefore, the x component of the three wave vectors share a common value
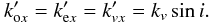 And, since
And, since 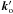 and
and 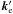 lie on their respective sheets of the index surface, i.e.
lie on their respective sheets of the index surface, i.e. 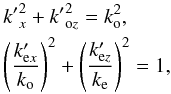 we can derive
we can derive ![\begin{eqnarray} k'_{{\rm o}z} &=& \left[ k_{\rm o}^2 - {k'}_x^2 \right] ^{1/2}, \nonumber \\ &=& \frac{2 \pi}{\lambda} \left[ n_{\rm o}^2 - \sin ^2 i \right] ^{1/2}, \nonumber \\ k'_{{\rm e}z} &=& k_{\rm e} \left[1 - \left(\frac{k'_x}{k_{\rm o}}\right)^2 \right] ^{1/2}, \nonumber \\ k'_{{\rm e}z} &=& \frac{2 \pi}{\lambda} \frac{n_{\rm e}}{n_{\rm o}} \left[ n_{\rm o}^2 - \sin^2 i \right] ^{1/2}. \end{eqnarray}](/articles/aa/full_html/2012/07/aa19160-12/aa19160-12-eq33.png) (1)
(1)
3.2. Case 2
As in case 1, the plate is X-cut, but the optical axis is perpendicular to the plane of incidence. This is illustrated in Fig. 4. The expression for the ordinary wave vector is unchanged, and we derive for the extraordinary wave vector ![\begin{equation} k'_{{\rm e}z} = \frac{2 \pi}{\lambda} \left[ n_{\rm e}^2 - \sin ^2 i \right] ^{1/2}. \end{equation}](/articles/aa/full_html/2012/07/aa19160-12/aa19160-12-eq34.png) (2)
(2)
3.3. Case 3
In this case, the plate is Z-cut, i.e. the optical axis is perpendicular to the plate, as shown in Fig. 5. As previously, we derive for the extraordinary wave vector ![\begin{equation} k'_{{\rm e}z} = \frac{2 \pi}{\lambda} \frac{n_{\rm o}}{n_{\rm e}}\left[ n_{\rm e}^2 - \sin ^2 i \right] ^{1/2}. \end{equation}](/articles/aa/full_html/2012/07/aa19160-12/aa19160-12-eq35.png) (3)
(3)
3.4. Optical path difference
The differential phase between the extraordinary and the ordinary wave, when traveling between arbitrary points M1 and M2 respectively on the entrance and exit faces of the plate, is given by 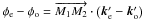 , where we use the sign convention in which phase increases along the propagation direction. Since the two wave vectors have zero components in the y direction and equal components in the z direction, this reduces to:
, where we use the sign convention in which phase increases along the propagation direction. Since the two wave vectors have zero components in the y direction and equal components in the z direction, this reduces to: 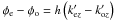 , where h is the plate thickness. Expressed in terms of the vacuum path length normalized to the plate thickness, which can be considered as the effective (incidence-dependent) birefringence index for each of the three configurations
, where h is the plate thickness. Expressed in terms of the vacuum path length normalized to the plate thickness, which can be considered as the effective (incidence-dependent) birefringence index for each of the three configurations 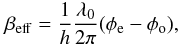 (4)this becomes
(4)this becomes ![\begin{eqnarray} \beta_{\rm eff1} &=& \frac{n_{\rm e}}{n_{\rm o}} \left[ n_{\rm o}^2 - \sin^2 i \right] ^{1/2} - \left[ n_{\rm o}^2 - \sin ^2 i \right] ^{1/2},\\ \beta_{\rm eff2} &=& \left[ n_{\rm e}^2 - \sin ^2 i \right] ^{1/2} - \left[ n_{\rm o}^2 - \sin ^2 i \right] ^{1/2},\\ \beta_{\rm eff3} &=& \frac{n_{\rm o}}{n_{\rm e}}\left[ n_{\rm e}^2 - \sin ^2 i \right] ^{1/2} - \left[ n_{\rm o}^2 - \sin ^2 i \right] ^{1/2}. \end{eqnarray}](/articles/aa/full_html/2012/07/aa19160-12/aa19160-12-eq42.png) To illustrate these equations, and as we consider in the next section, we have plotted these dependencies in the case of lithium niobate, at λ = 1.65 μm in Figs. 6–8.
To illustrate these equations, and as we consider in the next section, we have plotted these dependencies in the case of lithium niobate, at λ = 1.65 μm in Figs. 6–8.
 |
Fig. 6 Effective birefringence (βeff, see text) versus incidence, for Lithium Niobate at λ = 1.65 μm, for configuration case 1. |
4. Material properties
Here we focus more on applications in the near-infrared bands (atmospheric windows), i.e. J(1.15–1.35 μm), H(1.5–1.8 μm), and K(2.0–2.4 μm). To first order, the quantity of interest is the difference B = ne − no. One would like the birefringence correction to have a dispersion (versus wavelength) that is as small as possible. To quantify this, we introduce a dimensionless number that is analogous to the Abbe number, but applied to birefringence, and without reference to specific wavelengths. This number A is defined as a figure of merit 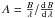 such that the larger (in absolute value), the better.
such that the larger (in absolute value), the better.
 |
Fig. 9 Birefringence of quartz versus wavelength. Left-hand scale: the difference B = ne − no. Right-hand scale, dashed curve: the figure of merit A (see text). |
 |
Fig. 10 Birefringence of lithium niobate versus wavelength. |
We examine three candidate materials, all uniaxial: crystalline quartz, lithium niobate, and beta barium borate (BBO). We use the Sellmeyer equations from, respectively, Ghosh (1999), Zelmon et al. (1997), and Kato et al. (2010). In Figs. 9–11, we have plotted for each material the birefringence B = ne − no and the figure of merit A. Quartz has a good transmission up to 2.5 μm (the long wavelength limit in our plot is set by the validity of the published Sellmeyer equations). The figure of merit A is relatively good, degrading at long wavelengths. The birefringence, however, is relatively small. Lithium niobate has a birefringence larger than quartz. The A figure of merit is not as good as quartz in the J band, but is better in the K band. In addition, Lithium niobate has good transmission up to 2.5 μm. Beta barium borate has a birefringence that is even larger than lithium niobate, and its A is significantly larger. However, it is usable only up to ≈ 2.1 μm, excluding applications in K band. Furthermore, BBO is reported to be relatively soft and mildly hygroscopic.
 |
Fig. 11 Birefringence of BBO versus wavelength. |
5. Implementation in the Pionier instrument
5.1. Design choices
We chose lithium niobate as the material for the compensation plates. The relatively small birefringence of quartz would have required a plate thickness in excess of 5 mm, while a choice of BBO would have precluded a planned extension from H band to K band.
Among the three possible configurations examined in Sect. 3, we chose case 1. The non-zero effective birefringence at zero incidence (see Fig. 6) is not an issue in this interferometric application, where identical compensation devices are inserted in each of the four incoming beams. The excursion of effective birefringence (for identical incidence) is less than in case 3, but one can note that a simple rotation of a one quarter turn about the plate normal changes case 1 to case 2, while reversing the excursion of the effective birefringence. This allows us to use in our design a relatively small plate thickness, based on the nominal goal of the correction amplitude, while having a contingency plan in case a larger differential correction is ultimately needed.
Our measurements show that the required birefringence correction was of order 5 μm, expressed in path length. Adopting an incidence excursion 0° → 40°, one can infer from Fig. 6 an effective birefringence excursion of ≈ 3 × 10-3; a plate thickness of 2 mm has been specified, providing a peak-to-peak correction of 6 μm path length. The plates were procured from a commercial source. A broad-band anti-reflection coating covering the H and K bands was specified, accepting the degraded efficiency at non-zero incidence. Each plate is fixed in a simple goniometric mount and inserted in the vicinity of a pupil (beam diameter 19 mm).
At a typical incidence of 25°, the beam lateral shift is of order 0.35 mm; this induces no loss of throughput since the aperture of the following pupil (parabolic mirror) is 25 mm, compared with the 19 mm beam diameter.
We must also consider the dispersive nature of the correction. Given the figure of merit of lithium niobate inthe H band: 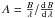 with | A | ≈ 10, and the fractional bandwidth b = δλ/λ ≈ 0.185, we expect that when correcting (at the center of the H band) a typical birefringence of nf = 5 fringes we introduce a differential birefringence at the band edges of
with | A | ≈ 10, and the fractional bandwidth b = δλ/λ ≈ 0.185, we expect that when correcting (at the center of the H band) a typical birefringence of nf = 5 fringes we introduce a differential birefringence at the band edges of 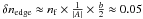 fringes, causing a 1% loss of contrast at the band edges.
fringes, causing a 1% loss of contrast at the band edges.
 |
Fig. 12 A compensation plate and its goniometric mount installed (center of picture) in the Pionier instrument. On the right, one of the piezo-driven mirrors for path length modulation. On the left, an off-axis parabola and the input of one of the polarization-maintaining optical fibers that carries the science signal to the integrated beam combiner. |
5.2. Verification of performance
For the adjustment of the birefringence compensation, a Wollaston prism is inserted between the beam recombiner and the camera, allowing us to detect and visualize separately the fringes in the two linear polarizations in each of the six baselines. Initially, all four plates are set near the middle of the compensation excursion, at an angle of approximately 25° incidence. The fringe packets are displayed at low magnification, with emphasis on the envelopes, as, e.g., in Figs. 1 and 13. One reference beam is identified such that the other three beams will require, with respect to that reference, differential birefringence corrections of both positive and negative signs. A coarse adjustment is performed on each of these three beams against the reference, the goal being to superpose, on each baseline, the fringe packet envelopes for the two polarizations. The display is then changed to a higher path length resolution, and the procedure is refined, to superpose the actual fringes. One extra iteration may be required to balance the residual errors, some of which may be inevitable if part of the differential birefringence seen on the six baselines cannot be factored into four telescope terms, as may be the case in the beam combiner.
The above procedure is for the initial alignment. In operation, the adjustment has been verified to be stable at least over the duration of an observing run (several days). The adjustment (fine part only) is tweaked at the beginning of each observing run, which takes typically 15–30 min. The adjustment is not critical and can generally be made by manually rotating the plate mounts, without recourse to the micrometer.
 |
Fig. 14 Cross-correlation of the two polarizations, for each of the six baselines, versus delay in μm. Blue, dashed line: before adjustment for the birefringence correction; red line: after adjustment. |
Offset between the fringes for the two linear polarizations, expressed in terms of optical path difference (microns), before and after re-adjusting the birefringence compensators.
To illustrate the procedure, we de-tuned the birefringence compensators, and re-adjusted them. Figure 1 shows the fringe packets produced between inputs 2 and 3, with the compensators de-tuned, and the Wollaston prism in place. Figure 13 shows the same fringe packets after adjustment. The differential delay between the two polarizations on each baseline is evaluated by numerically cross-correlating (in Fourier space, with extra resolution provided by zero padding) the two fringe packets. The results are shown in Fig. 14, and in Table 1. The worst-case path difference after adjustment corresponds to a phase difference of ≲ 20°, leading to a superposition efficiency of 98.5%.
6. Conclusion
We have demonstrated on an operational instrument, Pionier at the VLTI, a novel, simple, low-cost, and effective technique to control differential birefringence in an optical interferometer. The method is based on the use of birefringent crystal plates inclined with respect to the incoming beam in order to introduce a controlled differential phase between two orthogonal polarisations that compensates for the instrumental one. The precision is sufficient to reach instrumental contrasts of the order of 98.5% with a loss in throughput limited to 10%. This represents a significant increase in sensitivity compared with instruments that split the light of different polarizations or those that (even worse) simply ignore the drop in contrast. The intrinsic experimental stability and environmental conditions at VLTI require this correction to be checked at worst on a weekly basis. The simplicity and predictability of the correction make this technique ideally suited for the automation of the birefrigence correction in the VLTI second generation instruments. We believe that this technique, associated with our current methodology to control the differential dispersion by controlling the fiber length, demonstrates that the polarization differential properties
of a single-mode instrument can be controlled to a level that meets the requirements of all astrophysical programs.
References
- Coudé du Foresto, V., Perrin, G., Ruilier, C., et al. 1998, in SPIE Conf. Ser. 3350, ed. R. D. Reasenberg, 856 [Google Scholar]
- Delage, L., & Reynaud, F. 2000, J. Opt. A: Pure Appl. Opt., 2, 147 [Google Scholar]
- Elias, II, N. M. 2001, ApJ, 549, 647 [NASA ADS] [CrossRef] [Google Scholar]
- García, P., Glindemann, A., & Henning, T. 2003, The Very Large Telescope Interferometer: Challenges for the Future, Astrophysics and space science (Kluwer Academic Publishers), 18 [Google Scholar]
- Ghosh, G. 1999, Opt. Comm., 163, 95 [Google Scholar]
- Ireland, M. J., Tuthill, P. G., Davis, J., & Tango, W. 2005, MNRAS, 361, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, K., Umemura, N., & Mikami, T. 2010, in SPIE Conf. Ser. 7582, ed. P. E. Powers, 75821 [Google Scholar]
- Lagorceix, H., & Reynaud, F. 1995, Opt. Comm., 118, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bouquin, J.-B., Berger, J.-P., Lazareff, B., et al. 2011, A&A, 535, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bouquin, J.-B., Rousselet-Perraut, K., Berger, J.-P., et al. 2008, in SPIE Conf. Ser. 7013, eds. M. Schöller, W. C. Danchi, & F. Delplancke, 70130 [Google Scholar]
- Murakami, N., Ohishi, N., Nishikawa, J., & Yoshizawa, M. 2009, Appl. Opt., 48, 5774 [NASA ADS] [CrossRef] [Google Scholar]
- Rousselet-Perraut, K., Vakili, F., & Mourard, D. 1996, Opt. Eng., 35, 2943 [Google Scholar]
- Rousselet-Perraut, K., Vakili, F., Mourard, D., et al. 1997, A&AS, 123, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rousselet-Perraut, K., Le Bouquin, J. B., Mourard, D., et al. 2006, A&A, 451, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöller, M. 2003, Mem. Soc. Astron. Ital. Suppl., 2 [Google Scholar]
- Traub, W. 1988, in European Southern Observatory Astrophysics Symposia, 29 [Google Scholar]
- Zelmon, D. E., Small, D. L., & Jundt, D. 1997, J. Opt. Soc. Am. B Opt. Phys., 14, 3319 [Google Scholar]
All Tables
Offset between the fringes for the two linear polarizations, expressed in terms of optical path difference (microns), before and after re-adjusting the birefringence compensators.
All Figures
 |
Fig. 1 Measured fringe packets in the Pionier instrument, between inputs 2 and 3, for the two linear polarizations, and with birefringence uncorrected. |
| In the text | |
 |
Fig. 2 Principle of the correction. Before traversing the birefringent plates, each beam is plagued by a differential delay between the horizontal and vertical polarizations. This differential delay can be canceled by suitably adjusting the inclination of each birefringent plate. The beam-to-beam delay is generally affected, but is easy to equalize once birefringence is taken care of. This figure is drawn as if the correction is performed after the unwanted birefringence has occurred; in the case of Pionier, the correction is in fact made upstream of the point where birefringence occurs. |
| In the text | |
 |
Fig. 3 In case 1, the optical axis is along the x direction. Left: a schematic of the birefringent plate, the rotation axis used to adjust the angle of incidence, and the two sheets of the index surface. Right: the geometry of wave vectors. The two circles and the ellipse are the intersections with the plane of incidence of the two sheets of the index surface and the unity sphere, all scaled by 2π/λ0, such that they are the locus of the tips of wave vectors k′. |
| In the text | |
 |
Fig. 4 In case 2, the optical axis is perpendicular to the plane of incidence. The two schematics are drawn as in case 1. |
| In the text | |
 |
Fig. 5 In case 3, the optical axis is perpendicular to the vacuum-crystal interface, i.e. along the z axis. The two schematics are drawn as in case 1. |
| In the text | |
 |
Fig. 6 Effective birefringence (βeff, see text) versus incidence, for Lithium Niobate at λ = 1.65 μm, for configuration case 1. |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but for case 2. |
| In the text | |
 |
Fig. 8 Same as Fig. 6, but for case 3. |
| In the text | |
 |
Fig. 9 Birefringence of quartz versus wavelength. Left-hand scale: the difference B = ne − no. Right-hand scale, dashed curve: the figure of merit A (see text). |
| In the text | |
 |
Fig. 10 Birefringence of lithium niobate versus wavelength. |
| In the text | |
 |
Fig. 11 Birefringence of BBO versus wavelength. |
| In the text | |
 |
Fig. 12 A compensation plate and its goniometric mount installed (center of picture) in the Pionier instrument. On the right, one of the piezo-driven mirrors for path length modulation. On the left, an off-axis parabola and the input of one of the polarization-maintaining optical fibers that carries the science signal to the integrated beam combiner. |
| In the text | |
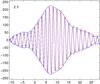 |
Fig. 13 Same as Fig. 1, after adjusting the birefringence compensators. |
| In the text | |
 |
Fig. 14 Cross-correlation of the two polarizations, for each of the six baselines, versus delay in μm. Blue, dashed line: before adjustment for the birefringence correction; red line: after adjustment. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


