| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219094 | |
| Published online | 06 July 2012 | |
Recognizing magnetic structures by present and future radio telescopes with Faraday rotation measure synthesis
1 MPI für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: rbeck@mpifr-bonn.mpg.de
2 Institute of Continuous Media Mechanics, Korolyov str. 1, 614013 Perm, Russia
3 State National Research Polytechnical University of Perm, Komsomolskii av. 29, 614990 Perm, Russia
4 Department of Physics, Moscow State University, 119991 Moscow, Russia
Received: 22 February 2012
Accepted: 29 April 2012
Context. Modern radio telescopes allow us to record a large number of spectral channels. The application of a Fourier transform to spectropolarimetric data in radio continuum, Faraday rotation measure (RM) synthesis, yields the “Faraday spectrum”, which hosts valuable information about the magneto-ionic medium along the line of sight.
Aims. We investigate whether the method of wavelet-based RM synthesis can help us to identify structures of regular and turbulent magnetic fields in extended magnetized objects, such as galaxies and galaxy clusters.
Methods. The analysis of spectropolarimetric radio observations of multi-scale targets calls for a corresponding mathematical technique. Wavelets allow us to reformulate the RM synthesis method in a scale-dependent way and to visualize the data as a function of Faraday depth and scale.
Results. We present observational tests to recognize magnetic field structures. A region with a regular magnetic field generates a broad “disk” in Faraday space, with two “horns” when the distribution of cosmic-ray electrons is broader than that of the thermal electrons. Each field reversal generates one asymmetric “horn” on top of the “disk”. A region with a turbulent field can be recognized as a “Faraday forest” of many components. These tests are applied to the spectral ranges of various synthesis radio telescopes. We argue that the ratio of maximum to minimum wavelengths determines the range of scales that can be identified in Faraday space.
Conclusions. A reliable recognition of magnetic field structures in spiral galaxies or galaxy clusters requires the analysis of data cubes in position-position-Faraday depth space (“PPF cubes”), observed over a wide and continuous frequency range, allowing the recognition of a wide range of scales as well as high resolution in Faraday space. The planned Square Kilometre Array (SKA) will fulfill this condition and will be close to representing a perfect “Faraday telescope”. The combination of data from the Low Frequency Array (LOFAR, at low frequencies) and the Expanded Very Large Array (EVLA, at high frequencies) appears to be a promising approach for the recognition of magnetic structures on all scales. The addition of data at intermediate frequencies from the Westerbork Synthesis Radio Telescope (WSRT) or the Giant Meterwave Radio Telescope (GMRT) would fill the gap between the LOFAR and EVLA frequency ranges. The Global Magneto-Ionic Medium Survey (GMIMS), planned with several single-dish telescopes at low angular resolution, will also provide good scale recognition and high resolution in Faraday space.
Key words: methods: observational / techniques: polarimetric / galaxies: magnetic fields / galaxies: clusters: intracluster medium / radio continuum: galaxies / galaxies: spiral
© ESO, 2012
1. Introduction
Modern radio telescopes are equipped with digital correlators that allow us to record a large number of spectral channels. While radio spectroscopy in total intensity is well-developed, the possibilities of spectropolarimetry in radio continuum have been explored for only a few years. The fundamentals were presented by Burn (1966), while the first application to multi-channel polarization data (data cubes) was presented by Brentjens & de Bruyn (2005).
Faraday rotation measure (RM) synthesis generates the “Faraday dispersion function” or, in short, the “Faraday spectrum” F(φ), which is the (complex-valued) polarized intensity spectrum as a function of “Faraday depth” φ (1)where B ∥ is the line-of-sight magnetic field component measured in μG, ne is the thermal electron density measured in cm-3, and the integral is taken along the line of sight through the region containing both magnetic fields and thermal electrons, where x′ is measured in parsecs. Our adopted convention is that φ is positive when B is pointing towards the observer.
(1)where B ∥ is the line-of-sight magnetic field component measured in μG, ne is the thermal electron density measured in cm-3, and the integral is taken along the line of sight through the region containing both magnetic fields and thermal electrons, where x′ is measured in parsecs. Our adopted convention is that φ is positive when B is pointing towards the observer.
Burn (1966) showed that the complex polarized intensity P at different wavelengths λ can be calculated from F(φ) via a Fourier transform 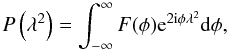 (2)which means that the Faraday spectrum F is the Fourier transform of the complex polarized intensity:
(2)which means that the Faraday spectrum F is the Fourier transform of the complex polarized intensity:  (3)Equation (3) is the basis of RM synthesis. A major limitation emerges from the fact that P can be measured only for λ2 > 0 and practically only in a finite spectral band λmin < λ < λmax.
(3)Equation (3) is the basis of RM synthesis. A major limitation emerges from the fact that P can be measured only for λ2 > 0 and practically only in a finite spectral band λmin < λ < λmax.
The quantity F can be used to determine the Faraday depth and the intrinsic polarization angle of each component in the Faraday spectrum. As in classical spectroscopy, the interpretation of this spectrum is not straightforward. In particular, there is no simple relation between Faraday depth and geometrical depth. Furthermore, the Faraday spectrum suffers from sidelobes of the main components caused by limited coverage of the wavelength space, and in the case of point-like “sources” these sidelobes can be removed by “RM clean” (Heald 2009).
Spectral ranges of various radio telescopes and parameters crucial for RM synthesis (see text for details).
Models of the density distributions of cosmic-ray electrons (nc) and thermal electrons (nth) considered in this paper.
 |
Fig. 1 Several typical examples of a region with and without reversals of the regular magnetic field: the solid black line shows the Gaussian magnetic field distribution, the dot-dashed blue line stands for one reversal and the dashed red line shows the distribution with two reversals. Top: magnetic field profile B(x) along the line of sight. Bottom: Faraday depth distribution φ(x) along the line of sight. |
 |
Fig. 2 Several typical examples of the Faraday spectrum in Faraday depth space F(φ). Top: Gaussian magnetic field distribution for four different models (see Table 2): solid green line (model 1); dashed black line (model 2); dashed red line (model 3); dot-dashed blue line (model 4). Bottom: the case of magnetic field reversals and model 1): one reversal (dot-dashed blue line); two reversals (dashed red line). |
RM synthesis is characterized by three basic parameters (Brentjens & de Bruyn 2005):
-
the resolution δφ in Faraday space, which is inversely proportionalto the coverage Δλ2 in wavelength (λ2) space;
-
the maximum observable |φmax| of point-like sources in Faraday space, which is inversely proportional to the width of a single frequency channel;
-
the maximum width |Δφmax| of extended structures in Faraday space (Faraday-rotating and synchrotron-emitting regions), which is inversely proportional to the square of the minimum wavelength of the observations. Wide-band observations at long wavelengths yield high resolution in Faraday space but cannot detect extended structures.
We argue below (Sect. 3) that the ratio of maximum to minimum wavelengths is another important parameter in helping us to recognize a range of scales in Faraday space.
A region of any extent in physical space that is synchrotron-emitting but not Faraday-rotating (i.e. no thermal electrons) generates a “point source” in Faraday space at φ = 0. A non-emitting region with thermal electrons and magnetic fields in front of the emitting region is called “Faraday screen”; it shifts the point source in Faraday space to a non-zero value of φ.
RM synthesis has been applied to spectropolarimetric data from the Westerbork telescope (de Bruyn & Brentjens 2005; Schnitzeler et al. 2009; Heald et al. 2009; Mao et al. 2010; Brentjens 2011; Pizzo et al. 2011), from the Parkes telescope and the Australia Telescope Compact Array (ATCA) (Feain et al. 2009; Harvey-Smith et al. 2010; O’Sullivan et al. 2012), from the VLA (Van Eck et al. 2011) and from the EVLA (Heesen et al. 2011). The Δλ2 coverages of these observations were small, so that the resolution in Faraday space was limited. Nevertheless, many Faraday spectra have revealed complex structures (Brentjens 2011). By means of the application of RM synthesis, the fine-scale structure of the magnetic field in the Milky Way around a local HI bubble (Wolleben et al. 2010a) and around a supernova remnant (Harvey-Smith et al. 2010) could be measured.
 |
Fig. 3 Model example of a turbulent magnetic field in the intergalactic medium of a galaxy cluster. Panels from above: magnetic field profile along the line of sight B(x), Faraday depth distribution along the line of sight φ(x), and Faraday spectrum in Faraday depth space F(φ). |
On the other hand, as RM synthesis is regularly applied in radio astronomy, the number of questions discussed about its technical problems (algorithms, software) and practical limitations for existing instruments similarly increases (Heald 2009; Farnsworth et al. 2011; Frick et al. 2011; Li et al. 2011; Andrecut et al. 2011; Bell et al. 2011). A combination of RM synthesis and two-dimensional image synthesis into three-dimensional (3D) “Faraday synthesis” of data from synthesis telescopes has been proposed as a possible way of improving the technique (Bell & Enßlin 2012).
In this paper, we reconsider the problem of observations of large magnetized objects, such as galaxies or the intergalactic medium in galaxy clusters. Two factors are crucial in this context: the objects are very extended and composed of numerous structures of very different spatial scales, namely galaxies containing a disk, halo, spiral arms, turbulent star-forming regions, and supernova remnants, and galaxy clusters containing radio galaxies, jets, outflows, turbulent gas, and “relic” shock fronts. The multi-scale structure calls for the use of a mathematical technique developed in the framework of wavelet analysis. Wavelets do not only provide a more robust algorithm on which to base the RM synthesis method (Frick et al. 2010), but can also be used as an illustrative tool for the presentation of results. We will determine here the information that can be recovered from RM synthesis based on wide-band observations with existing and future radio telescopes.
For simplicity, we neglect in this paper the effects of different angular resolutions and, in the case of synthesis telescopes, of different distributions of baselines (uv coverage) when combining data from different telescopes. We also neglect the spectral variations in the polarized emission and the instrumental noise.
 |
Fig. 4 Wavelet planes wF(a,φ) for the magnetic field with a Gaussian profile and in energy equipartition with cosmic rays (model 1). The calculations are done for the frequency bands available for several telescopes. Left column, panels from above: LOFAR, EVLA (or ATCA), and ASKAP (POSSUM + FLASH); right column, panels from above: WSRT (or GMRT), ASKAP (POSSUM), and SKA phase 1. |
 |
Fig. 5 Wavelet planes wF(a,φ) for the magnetic field with Gaussian profile and the same scale-heights of thermal and CRE electrons (model 2). Panels are the same as in Fig. 4. |
 |
Fig. 6 Wavelet plane for the regular field with one reversal. Panels are as in Fig. 4. Note that the disk at large scales is much weaker than the horn on small scales and, in the case of the SKA in the last panel, could not be plotted within the range of the color bar. |
 |
Fig. 9 Wavelet plane for the turbulent field superimposed on the regular field. Panels are as in Fig. 4. |
 |
Fig. 10 Wavelet plane for the turbulent field superimposed on the regular field with one reversal. Panels are as in Fig. 4. |
 |
Fig. 11 RM synthesis applied to data from a combination of data from LOFAR and EVLA. Panels in the left column from above: box-like magnetic field, one reversal, and box-like field + turbulent field; right column from above: Gaussian-like distribution, two reversals, and regular field with one reversal + turbulent field. |
 |
Fig. 12 RM synthesis for a signal from a combination of data from LOFAR, WSRT (or GMRT), and EVLA. Panels are as in Fig. 11. |
2. Present and future radio telescopes
Spectropolarimetric data can be obtained with the following present and future radio telescopes:
-
Low Frequency Array (LOFAR, Europe), which is the firstonline-connected synthesis telescope at low frequencies andoperates since 2011 (Stapperset al. 2011). Polarization frompulsars has been detected in the “lowband” (10−80 MHz) and in the lower “highband” (110 − 190 MHz). Observations in the lowband, lower highband, and higher highband (about 170−240 MHz) need different setups and cannot be performed simultaneously. The lower highband has maximum sensitivity and is used to search for diffuse polarized emission, which is one task of the “magnetism key science project” (Beck 2010). The lowband has lower sensitivity and signals suffer from strong Faraday depolarization. In this paper, the full frequency range of the “highband” (HBA) of 110−240 MHz (or about 1.25−2.7 m) is considered.
-
Westerbork Synthesis Radio Telescope (WSRT, the Netherlands), which has successfully supplied spectropolarimetric data in the frequency range 1300 − 1763 MHz of a sample of nearby galaxies, the SINGS survey (Heald et al. 2009), clusters (Pizzo et al. 2011), and to measure RMs of background sources (Mao et al. 2010). The low resolution in Faraday space only allowed measurement of one φ component at most locations, except for the central regions of several galaxies where three components were detected. The lower frequency range 310−390 MHz (or 0.77−0.97 m) allows higher resolution in Faraday space and hence is of great interest to RM synthesis, e.g. as applied to data of the diffuse Galactic foreground (Schnitzeler et al. 2009) and of galaxy clusters (de Bruyn & Brentjens 2005; Brentjens 2011; Pizzo et al. 2011). A survey of nearby galaxies is underway in this frequency band. After installation of the APERTIF system, the WSRT will only observe around 1 GHz.
-
Giant Meterwave Radio Telescope (GMRT, India), a synthesis telescope that operates in the frequency ranges 150−156, 236−244, 305−345, 580−640, and 1000−1450 MHz. The polarization calibration of the GMRT is more difficult than that of the WSRT, and only a few successful detections of polarized signals from bright radio sources in the two highest frequency bands have been reported so far (Joshi & Chengalur 2010). In the following we assume that the frequency range 305−1450 MHz can be used for future polarization observations, which is similar to that of the WSRT.
-
DRAO 26 m single dish (Penticton, Canada), for which a northern sky polarization survey (GMIMS) is ongoing in the frequency range 1277−1762 MHz (Wolleben et al. 2010b).
-
Parkes 64 m single dish (Australia), where a southern sky survey (S-PASS) has been performed in the frequency range 2180−2420 MHz (Carretti 2010). The southern part of the GMIMS survey at 300 − 900 MHz is planned.
-
Effelsberg 100 m single dish (Germany), at which a northern sky polarization survey (GMIMS) is planned in the frequency range 300−900 MHz.
-
Arecibo 305 m single dish (USA), where a deep spectropolarimetric survey (GALFACTS) of the sky visible from Arecibo is ongoing in the frequency range 1225−1525 MHz (George et al. 2011).
-
Expanded VLA (Jansky VLA) synthesis telescope (EVLA, USA), whose new correlator (WIDAR) allows measurements in the frequency range 1−12 GHz (0.025−0.30 m) with continuous coverage at four frequency settings (L, S, C, and X-band). Polarization data from the frequency bands at even higher frequencies are needed only for sources with | Δφ | > 5000 rad/m2. The first polarization observations of the dwarf irregular galaxy IC 10 in C band (4.5−7.8 GHz) were still limited in resolution in Faraday space (Heesen et al. 2011). The full wavelength coverage available with the EVLA still needs to be investigated.
-
Australia Telescope Compact Array (ATCA), whose new correlator (CABB) allows measurements in the frequency range 1.1−10 GHz (0.03−0.27 m) with an almost continuous coverage at two frequency settings (L+S and C+X band). Complex Faraday spectra were observed in active galactic nuclei in the L+S bands (O’Sullivan et al. 2012).
-
Australian Square Kilometre Array Pathfinder (ASKAP), which is a synthesis telescope under construction in Western Australia (Johnston et al. 2008). The all-sky polarization survey POSSUM in the frequency range 1130−1430 MHz (or 0.21−0.265 m) is planned in 2013, together with surveys in HI and continuum. A combination of these data with other data from the all-sky transient survey FLASH in the frequency range 700−1000 MHz is under discussion; this would extend the frequency coverage to 700−1430 MHz (or 0.21−0.428 m) and improve the resolution in Faraday space by a factor of about five compared to data from the POSSUM survey alone.
-
Square Kilometre Array (SKA): Construction should start in 2016 in South Africa, with extensions into central Africa, and in Australia. The frequency coverage of the receiving systems under investigation for “phase 1” (which will be available from about 2018) is about 70 MHz−3 GHz (or 0.1−4.3 m) with continuous coverage, to be extended in “phase 2” to 10 GHz, opening excellent possibilities for RM synthesis. Measuring a dense grid of RM measurements is one of the key science projects for the SKA (Gaensler et al. 2004; Beck 2010, 2011).
Table 1 summarizes the properties of the present-day and future radio telescopes. The highest resolution in Faraday space (largest Δλ2) is achieved by LOFAR and the SKA, while the ATCA, ELVA, and the SKA provide the largest range of scales in Faraday space (largest (λmax/λmin)2, see Sect. 3).
The following combinations of data from synthesis telescopes yield an excellent frequency coverage and high angular resolution, and are considered in this paper:
-
LOFAR + EVLA data of high angular resolution over a hugefrequency range (110 − 240 MHz + 1−12 GHz or 0.025 − 0.30 m + 1.25−2.7 m), but the frequency gap hampers detection of certain structures in Faraday space.
-
LOFAR + WSRT/GMRT + EVLA data help to partly fill the gap in the data from LOFAR + EVLA. Faraday structures can be detected on a large range of scales, similar to the planned capability of the SKA.
Data from ATCA/ASKAP and EVLA could also be combined, but this makes little sense because the frequency coverages are similar. Data from ATCA/ASKAP and LOFAR are hard to combine because they cover different parts of the sky.
The Global Magneto-Ionic Medium Survey (GMIMS) planned with several single-dish telescopes (Wolleben et al. 2010b) will provide a similarly wide frequency coverage as WSRT or GMRT, but with lower angular resolution.
3. Wavelet-based RM synthesis
The wavelet transform of the Faraday spectrum F(φ) is given by  (4)where ψ(φ) is the analyzing wavelet, a defines the scale, and φ is the Faraday depth of the wavelet center. We use as the analyzing wavelet the real-value “Mexican hat” ψ(φ′) = (1 − φ′2)exp( − φ′2/2). The coefficient wF gives the contribution of the corresponding structure of scale a located at position φ to the function F. Wavelet-based RM synthesis was introduced by Frick et al. (2010) and directly calculates the coefficients wF from the complex-valued polarized intensities P(λ2). The algorithm is described in detail by Frick et al. (2011) and allows us to combine the RM synthesis procedure and the wavelet filtering. With the additional assumption of symmetry of the radio sources, one can recover more accurately the Faraday spectrum F(φ), particularly its complex part yielding the intrinsic polarization angles.
(4)where ψ(φ) is the analyzing wavelet, a defines the scale, and φ is the Faraday depth of the wavelet center. We use as the analyzing wavelet the real-value “Mexican hat” ψ(φ′) = (1 − φ′2)exp( − φ′2/2). The coefficient wF gives the contribution of the corresponding structure of scale a located at position φ to the function F. Wavelet-based RM synthesis was introduced by Frick et al. (2010) and directly calculates the coefficients wF from the complex-valued polarized intensities P(λ2). The algorithm is described in detail by Frick et al. (2011) and allows us to combine the RM synthesis procedure and the wavelet filtering. With the additional assumption of symmetry of the radio sources, one can recover more accurately the Faraday spectrum F(φ), particularly its complex part yielding the intrinsic polarization angles.
We take advantage of the wavelet coefficient distribution as a multi-scale representation of the signal. The scale analysis is worth performing when the range of recognizable scales in Faraday space is sufficiently wide, in other words, the ratio of maximum to minimum wavelengths of the observations is considerably larger than unity  Table 1 shows that the EVLA, the ATCA, the SKA, and a combination of LOFAR, WSRT/GMRT, and EVLA fulfil this condition. The SKA will provide the largest value of (λmax/λmin)2 in its phase 1, which will be further increased in phase 2.
Table 1 shows that the EVLA, the ATCA, the SKA, and a combination of LOFAR, WSRT/GMRT, and EVLA fulfil this condition. The SKA will provide the largest value of (λmax/λmin)2 in its phase 1, which will be further increased in phase 2.
We note that a large value of (λmax/λmin)2 is also needed to obtain a small error Δψ0 of the intrinsic polarization angle ψ0 (5)where S/N is the signal-to-noise ratio of a “source” at Faraday depth φ.
(5)where S/N is the signal-to-noise ratio of a “source” at Faraday depth φ.
4. Models
We first consider a model region hosting a regular magnetic field with different profiles along the line of sight, as shown in Fig. 1. The maximum regular field strength of ≈2 μG is typical of the Milky Way and nearby galaxies. The modeled region also contains thermal electrons (responsible for Faraday rotation) and cosmic-ray electrons (CRE, responsible for synchrotron emission). Thus, the investigated region emits polarized synchrotron emission and rotates its polarization angles according to the Faraday effect.
The distributions of relativistic electrons nc and thermal electrons nth are assumed to have Gaussian profiles in the radial direction within the plane, or with height perpendicular to the plane ![\begin{eqnarray} \label{dise} n_{\rm c}(x) & = & C \, {\rm exp}\left[-\left(x-x_0\right)^2/ h_{\rm c}^2\right], \nonumber\\ n_{\rm th}(x) & = & 0.03~{\rm cm}^{-3}\, {\rm exp}\left[-\left(x-x_0\right)^2/ h_{\rm th}^2\right] . \end{eqnarray}](/articles/aa/full_html/2012/07/aa19094-12/aa19094-12-eq66.png) (6)Here C is the maximum CRE number density, which is normalized to 1 in our models. Our models are applicable to galaxies observed at any inclination angle. If the scale-radius is, for example, ten times as large as the scale-height, the scale-height dominates the distribution for inclinations smaller than 84°, which is otherwise dominated by the scale-radius.
(6)Here C is the maximum CRE number density, which is normalized to 1 in our models. Our models are applicable to galaxies observed at any inclination angle. If the scale-radius is, for example, ten times as large as the scale-height, the scale-height dominates the distribution for inclinations smaller than 84°, which is otherwise dominated by the scale-radius.
We assume that the Gaussian scale-height (respectively the scale-radius) of the thermal electrons hth is half that of the scale-height (respectively scale-radius) of the regular magnetic field hB. The synchrotron scale-height hsyn is derived according to 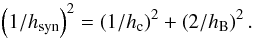 For the CRE scale-height (resp. scale-radius) hc, four models are considered (Table 2):
For the CRE scale-height (resp. scale-radius) hc, four models are considered (Table 2):
-
(1)
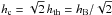 . This is the standard case expected for equipartition between the energy densities of cosmic rays and the regular magnetic field. The region of CRE is more extended than that of thermal electrons. The resulting hsyn is the same as that of the thermal electrons.
. This is the standard case expected for equipartition between the energy densities of cosmic rays and the regular magnetic field. The region of CRE is more extended than that of thermal electrons. The resulting hsyn is the same as that of the thermal electrons. -
(2)
hc = hth = hB/2. The regions of CRE and thermal electrons have identical extents and
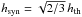 .
. -
(3)
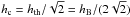 . The region of CRE is less extended than that of thermal electrons and
. The region of CRE is less extended than that of thermal electrons and  . This case is expected to occur at high frequencies and/or in regions with strong total magnetic fields where the energy losses of CRE are high and hence their propagation lengths are small.
. This case is expected to occur at high frequencies and/or in regions with strong total magnetic fields where the energy losses of CRE are high and hence their propagation lengths are small. -
(4)
hc = 2 hth = hB. The region of CRE is much more extended than that of thermal electrons and
 . This case is expected at low frequencies and/or in regions with weak total magnetic fields where CRE lifetimes and hence their propagation lengths are large.
. This case is expected at low frequencies and/or in regions with weak total magnetic fields where CRE lifetimes and hence their propagation lengths are large.
Changing the CRE scale-height leads to strong differences in the shape of the Faraday spectrum. The first model results in a broad Faraday spectrum F with two strong “horns” at each end (Fig. 2). These horns are the result of the two regions with very low density of thermal electrons on the far and the near side of the pathlength. One horn is correspondingly located at Faraday depth φ = 0 (Fig. 1). These horns disappear for the second model, in which both distributions have the same scale-height. However, the Faraday spectrum F still has sharp edges. The third model with a narrow CRE distribution has neither horns nor sharp edges. On the other hand, the extended CRE distribution in model 4 leads to very strong horns.
We conclude that the contrast between the amplitudes of the horns and of the broad part of the Faraday spectrum is controlled by the relative distributions of cosmic-ray electrons and thermal electrons. The larger the ratio hc/hth, the stronger the horns. No horns are visible for hc ≤ hth.
In addition, we consider two cases with magnetic field reversals. The distributions of relativistic and thermal electrons are the same as in model 1, but the magnetic field includes one or two reversals (see Fig. 1, upper panel). Reversals along the line of sight can be the result of an axi- or bisymmetric spiral magnetic field structure in the disk when a galaxy is observed almost edge-on, or of an antisymmetric field structure with a reversal of the toroidal field component above and below the galactic plane when a galaxy is observed almost face-on. In the Milky Way, one field reversal is observed, which is located inside the solar radius and extends over several kpc in azimuth (Van Eck et al. 2011).
The typical signature of the model with one reversal is the strong asymmetry of the Faraday spectrum F, called a “Faraday caustic” by Bell et al. (2011), which becomes symmetric for two reversals, with two narrow features at the edges that are much stronger than in the basic case without reversals.
Finally, having in mind objects such as the intergalactic medium in a galaxy cluster, we consider the case of a Kolmogorov-type turbulent field, without a regular field (Fig. 3). The standard deviation  G is typical of the intracluster medium near the center of a radio-bright galaxy cluster. The field strength and both thermal and cosmic-ray electron densities are assumed to have Gaussian distributions along the line of sight with scale-radii
G is typical of the intracluster medium near the center of a radio-bright galaxy cluster. The field strength and both thermal and cosmic-ray electron densities are assumed to have Gaussian distributions along the line of sight with scale-radii  .
.
5. Results
5.1. Recognizing regular fields and reversals in magnetized regions
As noted above, the wavelet decomposition gives a graphical representation of a structure in the scale versus Faraday depth plane. We present in Figs. 4 − 12 the modulus of the wavelet decomposition of the Faraday spectrum (Eq. (4)), reconstructed from the range of λ2 provided by various radio telescopes, for the model examples described in the previous section. The horizontal axis in all panels gives the Faraday depth φ and the vertical axis shows the scale of the reconstructed structure (also in Faraday space). The color in the wavelet plane corresponds to the amplitude | WF(a,φ) | .
For simplicity, we assume for all wavelet transforms a constant polarized intensity of the emitting source and a constant wavelength response of the telescopes, to demonstrate the effects of wavelength coverage. If the emitting source has a power-law frequency spectrum with a negative spectral index, the lower frequencies get a higher weight, so that the smaller scales in the wavelet plane are enhanced with respect to the larger scales. On the other hand, Faraday depolarization increases towards low frequencies, so that the frequency spectrum of polarized intensity can reveal a positive spectral index (Arshakian & Beck 2011).
The wavelet plane for the first model (Gaussian profile of the regular magnetic field, 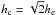 ) is shown in Fig. 4. One horn is located at φ = 0, while the location of the second horn gives the total Faraday depth of the region. The amplitude of the two horns on small scales is larger than that of the broad structure, which we call “disk” in the following. We note that LOFAR can only recognize the two horns that cannot be distinguished from two point sources in Faraday space. Observing with the WSRT range picks up some of the medium-scale structures, but the small wavelength coverage and the large gap between the two frequency bands leads to high sidelobes that need to be removed with “RM clean”. With the range of short wavelengths of ATCA, EVLA, and ASKAP (POSSUM) only the large scales are observable. Inclusion of FLASH indicates the presence of the two horns. However, only two broad structures are detected with ASKAP, which cannot be distinguished from two emitting and rotating regions with similar properties located along the line of sight. Only the SKA phase 1 can recognize all scales and is close to a perfect “Faraday telescope”. Extending the frequency coverage of the SKA to 10 GHz (0.03 m) in phase 2 would help us to observe galaxies with large | Δφ | .
) is shown in Fig. 4. One horn is located at φ = 0, while the location of the second horn gives the total Faraday depth of the region. The amplitude of the two horns on small scales is larger than that of the broad structure, which we call “disk” in the following. We note that LOFAR can only recognize the two horns that cannot be distinguished from two point sources in Faraday space. Observing with the WSRT range picks up some of the medium-scale structures, but the small wavelength coverage and the large gap between the two frequency bands leads to high sidelobes that need to be removed with “RM clean”. With the range of short wavelengths of ATCA, EVLA, and ASKAP (POSSUM) only the large scales are observable. Inclusion of FLASH indicates the presence of the two horns. However, only two broad structures are detected with ASKAP, which cannot be distinguished from two emitting and rotating regions with similar properties located along the line of sight. Only the SKA phase 1 can recognize all scales and is close to a perfect “Faraday telescope”. Extending the frequency coverage of the SKA to 10 GHz (0.03 m) in phase 2 would help us to observe galaxies with large | Δφ | .
The wavelet plane for the Gaussian profile of the regular magnetic field and hc = he (model 2) is shown in Fig. 5. The sharp edges of F (see Fig. 2) generate horns in the wavelet plane as in the case of model 1, but the amplitude of the horns is lower than that of the “disk”. This is clearly seen with the wide wavelength coverage of the SKA phase 1. Observations with ASKAP are already helpful in this case because the scale of the transition between disk and horns lies in the range of scales covered by POSSUM + FLASH (but not with POSSUM data alone). The other telescopes are unable to distinguish between models 1 and 2.
The wavelet plane for a distribution of a regular field with one reversal is shown in Fig. 6. The dominating horn is easily detectable with LOFAR, WSRT/GMRT, and the SKA phase 1. However, observations at long wavelengths alone cannot distinguish this structure from a single point source in Faraday space. Other than for a point source, the structure of the horn is asymmetric, which can be recognized by the inclusion of data at higher frequencies, such as with the SKA or by combining POSSUM + FLASH. On the other hand, the response from high frequencies alone (ATCA, EVLA, and POSSUM) is a somewhat asymmetric disk that cannot be distinguished from e.g. asymmetric Gaussian profiles. The second horn is weaker by a factor of ten and is hardly detectable. Observations at several telescope pointings or complete mapping of the source is needed to determine the structure of sources and the extent of field reversals in the resulting data cube.
The wavelet plane for a distribution of a regular field with two reversals, which may exist in spiral galaxies, is shown in Fig. 7. The horn to the left is shifted to negative φ because of the negative components of the magnetic field along the line of sight (Fig. 1). The “disk” at large scales is very weak compared to the horns, even weaker than in Fig. 6, and is hard to detect at short wavelengths. At long wavelengths (LOFAR and WSRT/GMRT), the two horns cannot be distinguished from two point sources (Faraday screens). The asymmetric nature of the two horns is visible at intermediate scales and can be recognized from the shift of the maximum at different scales.
Double features in the Faraday spectrum were found in the central regions of several spiral galaxies from the WSRT SINGS survey at 1300 − 1763 MHz (Heald et al. 2009). As the WSRT is sensitive only to large-scale structures in Faraday space, these features cannot be interpreted as field reversals and are probably distinct emitting and rotating regions along the line of sight, e.g. a regular field component associated with the nuclear region as proposed by Heald et al. (2009). Observations at lower frequencies are needed to achieve higher resolution in Faraday space.
5.2. Turbulent fields
The signatures of turbulent fields are many components on small scales, which we call the “Faraday forest”, can only be observed at long wavelengths (Fig. 8). In addition, owing to the tail of the continuous turbulence spectrum on large scales, a weaker structure is visible on yet larger scales of a ≈ 5 rad m-2. This structure is less extended in φ than the “disk” in the model with turbulent + regular fields (Fig. 9). However, observations at only high frequencies cannot distinguish the extended structures generated by either the tail of the turbulence spectrum or a regular field.
In real observations, the emission is smoothed over the telescope beam and distorted by instrumental noise. The “Faraday forest” is most clearly visible when the spatial scale corresponding to the beam is similar to the turbulence scale or smaller. For a larger beam, the “Faraday forest” is less visible and causes depolarization.
Instrumental noise is spread over the whole Faraday spectrum and hence is easy to distinguish from the “Faraday forest”, even if the amplitude of the “forest” is similar to that of noise (Frick et al. 2011).
The case of a Gaussian regular field superimposed on a Kolmogorov-type turbulent field is shown in Fig. 9. The standard deviation 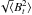 is assumed to be three times larger than the regular field strength, which is approximately valid for spiral galaxies. In contrast to Fig. 8, the Faraday forest extends only over a limited range in φ. On intermediate scales (WSRT/GMRT), the disk becomes asymmetric, but no clear signatures of the turbulent field are visible.
is assumed to be three times larger than the regular field strength, which is approximately valid for spiral galaxies. In contrast to Fig. 8, the Faraday forest extends only over a limited range in φ. On intermediate scales (WSRT/GMRT), the disk becomes asymmetric, but no clear signatures of the turbulent field are visible.
The corresponding result for a regular field with one reversal + turbulent field is shown in Fig. 10. The components of the “Faraday forest” are stronger at one edge of their distribution, as can easily be recognized at long wavelengths.
5.3. Recognizing magnetic structures by combining data from several telescopes
Finally, we combine the wavelength ranges of LOFAR and EVLA and apply RM synthesis for our different field models (Fig. 11). The lack of intermediate wavelengths leads to a separation between small and large scales in Faraday space. Box-like, Gaussian, and double-reversal models can be distinguished from the relative amplitudes of the horns and the disk.
By combining data from LOFAR, WSRT (or GMRT), and EVLA (Fig. 12), structures at intermediate scales can also be recognized and yield an almost complete picture of the magnetic field distribution, comparable to the SKA.
6. Conclusion and discussion
Our conclusions are as follows:
-
1.
We have found that a reliable recognition of magnetic fieldstructures in either the interstellar medium of spiral galaxies orthe intracluster medium of galaxy clusters requires us toapply RM synthesis tospectropolarimetric data cubes observed with high angularresolution and over a wide frequency range, fromabout 100 MHz toseveral GHz. Such a wide frequency coverageprovides high resolution in Faraday space (as determinedby Δλ2), as well as recognition of a wide range of scales in Faraday space (as determined by (λmax/λmin)2).
-
2.
The combination of data from the POSSUM and FLASH surveys (both planned with the ASKAP telescope) would improve the recognition of structures on intermediate scales.
-
3.
The combination of data from the present telescopes LOFAR and EVLA appears to provide a promising means of recognizing magnetic structures on all scales.
-
4.
The combination of WSRT (or GMRT) data with those from LOFAR and EVLA would fill the gap between the LOFAR and EVLA frequency ranges and hence can also recognize intermediate scales in Faraday space, which is helpful for measuring magnetic structures.
-
5.
The detection of two “horns” on small and intermediate scales plus an extended “disk” on large scales in the wavelet plane of galaxies indicates that the scale-height (or scale-radius) of cosmic-ray electrons (CRE) is larger than that of thermal electrons, as expected especially at low frequencies. The amplitude of these “horns” relative to that of the “disk” allows the determination of the ratio of the scale-heights (or the scale-radii) of both electron populations. To distinguish these horns from point sources in Faraday space, detection of intermediate scales would be required.
-
6.
The detection of an extended “disk” without “horns” in the wavelet plane of galaxies indicates that the scale-height (or scale-radius) of CRE is smaller than that of thermal electrons, owing to e.g. the strong energy losses of CRE, which are expected at high frequencies.
-
7.
Recognition of field reversals in spiral galaxies needs detection of structures on small and large scales, e.g. by combining data from LOFAR + WSRT/GMRT + EVLA, or with the SKA, which is close to a perfect “Faraday telescope”.
-
8.
Turbulent fields in galaxies or the intracluster medium can be recognized on small scales as a “Faraday forest” of many components, observable with high angular resolution and at long wavelengths, e.g. with LOFAR or the SKA.
-
9.
The single-dish, all-sky polarization survey GMIMS will provide excellent resolution and scale recognition in Faraday space. The low angular resolution allows us to investigate the structure of the magnetized medium in the Milky Way.
-
10.
For simplicity, the effects of instrumental noise and variations in both angular resolution and polarized intensity with frequency have been neglected in this paper. In practice, the combination of data from different telescopes suffers from varying angular resolutions and, in the case of synthesis telescopes, from different distributions of baselines (uv coverage). Furthermore, both a non-zero spectral index of polarized intensity and the signal averaging within the telescope beam modify the visibility of scales in Faraday space. Understanding these effects will require more detailed modeling.
-
11.
Mapping of the source is required to help us recognize the magnetic structures in the 3D data cubes (spatial coordinates + Faraday depth coordinate). As the next step, the wavelet analysis will be extended to analyzing Faraday data cubes.
-
12.
We propose to call the data cubes generated by RM synthesis “PPF (position-position-Faraday depth) cubes”, to be analogous to the PPV (position-position-velocity) cubes in spectroscopy.
Acknowledgments
We thank Dominic Schnitzeler for careful reading of the manuscript, as well as Mike Bell and Shea Brown for valuable comments. This work was supported by the DFG–RFBR grant 08-02-92881. R.B. acknowledges support from the DFG Research Unit FOR 1254.
References
- Andrecut, M., Stil, J. M., & Taylor, A. R. 2011, AJ, 143, 33 [Google Scholar]
- Arshakian, T. G., & Beck, R. 2011, MNRAS, 418, 2336 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2010, in ISKAF2010 Science Meeting [Google Scholar]
- Beck, R. 2011 [arXiv:1111.5802] [Google Scholar]
- Bell, M. R., & Enßlin, T. A. 2012, A&A, 540, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, M. R., Junklewitz, H., & Enßlin, T. A. 2011, A&A, 535, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brentjens, M. A. 2011, A&A, 526, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Carretti, E. 2010, in ASP Conf. Ser. 438, ed. R. Kothes, T. L. Landecker, & A. G. Willis, 276 [Google Scholar]
- de Bruyn, A. G., & Brentjens, M. A. 2005, A&A, 441, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farnsworth, D., Rudnick, L., & Brown, S. 2011, AJ, 141, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Feain, I. J., Ekers, R. D., Murphy, T., et al. 2009, ApJ, 707, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Frick, P., Sokoloff, D., Stepanov, R., & Beck, R. 2010, MNRAS, 401, L24 [NASA ADS] [Google Scholar]
- Frick, P., Sokoloff, D., Stepanov, R., & Beck, R. 2011, MNRAS, 414, 2540 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Beck, R., & Feretti, L. 2004, NewAR, 48, 1003 [Google Scholar]
- George, S. J., Stil, J. M., Andrecut, M., & Taylor, A. R. 2011 [arXiv:1111.4890] [Google Scholar]
- Harvey-Smith, L., Gaensler, B. M., Kothes, R., et al. 2010, ApJ, 712, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G. 2009, IAU Symp., 259, 591 [Google Scholar]
- Heald, G., Braun, R., & Edmonds, R. 2009, A&A, 503, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heesen, V., Rau, U., Rupen, M. P., Brinks, E., & Hunter, D. A. 2011, ApJ, 739, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, S., Taylor, R., Bailes, M., et al. 2008, Exp. Astron., 22, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, S., & Chengalur, J. N. 2010, in ISKAF2010 Science Meeting [Google Scholar]
- Li, F., Brown, S., Cornwell, T. J., & de Hoog, F. 2011, A&A, 531, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mao, S. A., Gaensler, B. M., Haverkorn, M., et al. 2010, ApJ, 714, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., Brown, S., Robishaw, T., et al. 2012, MNRAS, 421, 3300 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzo, R. F., de Bruyn, A. G., Bernardi, G., & Brentjens, M. A. 2011, A&A, 525, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schnitzeler, D. H. F. M., Katgert, P., & de Bruyn, A. G. 2009, A&A, 494, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stappers, B. W., Hessels, J. W. T., Alexov, A., et al. 2011, A&A, 530, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Eck, C. L., Brown, J. C., Stil, J. M., et al. 2011, ApJ, 728, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Wolleben, M., Fletcher, A., Landecker, T. L., et al. 2010a, ApJ, 724, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Wolleben, M., Landecker, T. L., Hovey, G. J., et al. 2010b, AJ, 139, 1681 [NASA ADS] [CrossRef] [Google Scholar]
Appendix
Figure A.1 shows the wavelet decompositions of the various models for complete frequency sampling, as will nearly be reached by the SKA phase 2. The result is almost the same as SKA phase 1, except for very large scales a > 100 rad m-2.
 |
Fig. A.1 Wavelet plane of the models considered in Sect. 5 but for complete coverage in frequency. Top: regular field of model 1 (compare with Fig. 4) and of model 2 (compare with Fig. 5). Middle: regular field with one reversal (compare with Fig. 6) and with two reversals (compare with Fig. 7). Bottom: turbulent field superimposed on the regular field of model 1 (compare with Fig. 9) and turbulent field superimposed on the regular field with one reversal (compare with Fig. 10). |
All Tables
Spectral ranges of various radio telescopes and parameters crucial for RM synthesis (see text for details).
Models of the density distributions of cosmic-ray electrons (nc) and thermal electrons (nth) considered in this paper.
All Figures
 |
Fig. 1 Several typical examples of a region with and without reversals of the regular magnetic field: the solid black line shows the Gaussian magnetic field distribution, the dot-dashed blue line stands for one reversal and the dashed red line shows the distribution with two reversals. Top: magnetic field profile B(x) along the line of sight. Bottom: Faraday depth distribution φ(x) along the line of sight. |
| In the text | |
 |
Fig. 2 Several typical examples of the Faraday spectrum in Faraday depth space F(φ). Top: Gaussian magnetic field distribution for four different models (see Table 2): solid green line (model 1); dashed black line (model 2); dashed red line (model 3); dot-dashed blue line (model 4). Bottom: the case of magnetic field reversals and model 1): one reversal (dot-dashed blue line); two reversals (dashed red line). |
| In the text | |
 |
Fig. 3 Model example of a turbulent magnetic field in the intergalactic medium of a galaxy cluster. Panels from above: magnetic field profile along the line of sight B(x), Faraday depth distribution along the line of sight φ(x), and Faraday spectrum in Faraday depth space F(φ). |
| In the text | |
 |
Fig. 4 Wavelet planes wF(a,φ) for the magnetic field with a Gaussian profile and in energy equipartition with cosmic rays (model 1). The calculations are done for the frequency bands available for several telescopes. Left column, panels from above: LOFAR, EVLA (or ATCA), and ASKAP (POSSUM + FLASH); right column, panels from above: WSRT (or GMRT), ASKAP (POSSUM), and SKA phase 1. |
| In the text | |
 |
Fig. 5 Wavelet planes wF(a,φ) for the magnetic field with Gaussian profile and the same scale-heights of thermal and CRE electrons (model 2). Panels are the same as in Fig. 4. |
| In the text | |
 |
Fig. 6 Wavelet plane for the regular field with one reversal. Panels are as in Fig. 4. Note that the disk at large scales is much weaker than the horn on small scales and, in the case of the SKA in the last panel, could not be plotted within the range of the color bar. |
| In the text | |
 |
Fig. 7 Wavelet plane for the regular field with two reversals. Panels are as in Fig. 4. |
| In the text | |
 |
Fig. 8 Wavelet plane for the turbulent field. Panels are as in Fig. 4. |
| In the text | |
 |
Fig. 9 Wavelet plane for the turbulent field superimposed on the regular field. Panels are as in Fig. 4. |
| In the text | |
 |
Fig. 10 Wavelet plane for the turbulent field superimposed on the regular field with one reversal. Panels are as in Fig. 4. |
| In the text | |
 |
Fig. 11 RM synthesis applied to data from a combination of data from LOFAR and EVLA. Panels in the left column from above: box-like magnetic field, one reversal, and box-like field + turbulent field; right column from above: Gaussian-like distribution, two reversals, and regular field with one reversal + turbulent field. |
| In the text | |
 |
Fig. 12 RM synthesis for a signal from a combination of data from LOFAR, WSRT (or GMRT), and EVLA. Panels are as in Fig. 11. |
| In the text | |
 |
Fig. A.1 Wavelet plane of the models considered in Sect. 5 but for complete coverage in frequency. Top: regular field of model 1 (compare with Fig. 4) and of model 2 (compare with Fig. 5). Middle: regular field with one reversal (compare with Fig. 6) and with two reversals (compare with Fig. 7). Bottom: turbulent field superimposed on the regular field of model 1 (compare with Fig. 9) and turbulent field superimposed on the regular field with one reversal (compare with Fig. 10). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


