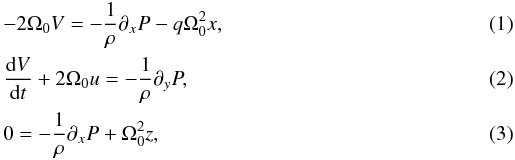| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201218803 | |
| Published online | 10 July 2012 | |
Potential vorticity dynamics in the framework of disk shallow-water theory
II. Mixed barotropic-baroclinic instability
School of Mathematical Sciences, Queen Mary University of London, London E1 4NS, UK School of Natural Sciences, University of California Merced, Merced, CA 95343, USA
Astronomy Deplartment, City College of San Francisco, San Francisco, CA 94112, USA
e-mail: oumurhan@ucmerced.edu
Received: 10 January 2012
Accepted: 11 April 2012
Context. We consider potential vorticity dynamics for astrophysical disks.
Aims. The aim of this work is to extend exploration of shear instabilities in cold astrophysical disks that are three-dimensional and whose mean states are baroclinic. In particular, we seek to demonstrate the potential existence of traditional baroclinic instabilities in meteorological studies. We show this in a simplified two-layer Philips disk model of a midplane symmetric disk.
Methods. We analyze the dynamical normal-mode response of thin annular disks with two strongly localized potential vorticity gradients, one in each of two disk layers. Each disk layer is of constant but differing densities. The resulting mean azimuthal velocity profile shows a variation in the vertical direction, implying that the system is baroclinic in the mean state. The stability of the system is treated in the context of disk shallow-water theory, wherein azimuthal disturbances are much longer than the corresponding radial or vertical scales. The normal-mode problem is solved numerically using two different methods.
Results. The results of a symmetric single-layer barotropic model is considered and it is found that instability persists for models in which the potential vorticity profiles are not symmetric, consistent with previous results. The instaiblity is interpreted in terms of interacting Rossby waves. For a two-layer system, in which the flow is fundamentally baroclinic, we report here that instability takes on the form of mixed barotropic-baroclinic type: instability occurs, but it qualitatively follows the pattern of instability found in the barotropic models. Instability arises because of the phase locking and interaction of the Rossby waves between the two layers. The strength of the instability weakens as the density contrast between layers increases.
Conclusions. Baroclinic instability is feasible for astrophysical disks but has the character of mixed barotropic-baroclinic type. The instability as explored in this study could be present in protoplanetary disks with weak vertical density stratification.
Key words: accretion, accretion disks / hydrodynamics / instabilities / waves / protoplanetary disks
© ESO, 2012
1. Introduction
The phenomenon of baroclinic instability has been studied with intensity for more than 70 years. Sometimes referred to as sloping convection (Vallis 2006), it is an instability that relies on the presence of a vertical shear in a zonal flow in a rotating atmosphere. This archetypical sheared flow exists as a result of a thermal-wind relationship that balances Coriolis effects with meridional (equator-to-pole) temperature gradients. It is ultimately a reflection of the mismatch in the isobars and isopycnals in an atmosphere. It is alternatively interpreted as an instability resulting from the interaction of inter-layer Rossby waves (Hoskins et al. 1985; Baines & Mitsudera 1994; Heifetz et al. 2004). Baroclinic instability is important for a variety of geophysical and astrophysical phenonomena. Among others, it plays a well-known role in the generation of terrestrial weather as well as in the dynamics of the Ocean Mixed Layer (Haine & Marshall 1998). It has been conjectured to play an important role in the mixing processes in stars (Knobloch & Spruit 1982; Fujimoto 1988).
The original studies of the instability (e.g. Charney 1947; Eady 1949; Philips 1954) considered the process in the small Rossby number limit in which the Rossby number, Ro, is given by 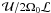 , where the terms are (respectively) the typical speed of a vortex, planetary rotation rate (at latitude), and the typical horizontal length scale of the flow. Baroclinic instability is a process that figures prominently in the geostrophic limit (Ro ≪ 1) but theoretical considerations have shown that it persists relatively unabated even when Ro is ~1 (Stone 1970, 1971; Molemaker et al. 2005). These studies also argue that the instability also persists for significant deviations from hydrostasy.
, where the terms are (respectively) the typical speed of a vortex, planetary rotation rate (at latitude), and the typical horizontal length scale of the flow. Baroclinic instability is a process that figures prominently in the geostrophic limit (Ro ≪ 1) but theoretical considerations have shown that it persists relatively unabated even when Ro is ~1 (Stone 1970, 1971; Molemaker et al. 2005). These studies also argue that the instability also persists for significant deviations from hydrostasy.
The possibility that baroclinic instability is present in accretion disk flows, which are characterized by Ro = 0.75, was examined in the studies of Cabot (1984) and Knobloch & Spruit (1985, 1986). Owing to the fundamental inseparability of the resulting linearized problem (even in the relatively simplified Boussinesq limit), Knobloch & Spruit (1986) were only able to conclude that the instability is feasible for radial and vertical disturbances comparable to the local scale height of the disk. Due to the dominance of the Keplerian shear, an analysis of the resulting linearized problem is intractably inseparable in the radial and vertical coordinate variables. Consequently, traditionally employed small-Ro analyses of meteorological studies are unusable here.
Adding to the challenge is that because the Keplerian shear is barotropic, the resulting problem for a disk is fundamentally of mixed baroclinic-barotropic type. This type of mixed problem has been examined in the context of quasigeostrophic flows by McIntyre (1970), Ioannou & Lindzen (1986) and James (1987). These studies generally agree that the structure of baroclinic waves become increasingly confined in the shearwise direction with increasing strength of the barotropic shear. The confinement, due to the barotropic governor mechanism (James 1987), appears to have the effect of weakening growth rates.
Keplerian disks are notoriously difficult to finesse into a geostrophic-hydrostatic framework familiar in traditional meteorology. Knobloch & Spruit (1985, 1986) note that it is only in the long streamwise wavelength limit (azimuthal in disk geometry) of a Keplerian flow that some of the formalism of quasigeostrophy will carry over. Umurhan (2008) developed a scaling analysis in which a local annular disk section can be viewed in a semi-geostrophic, quasi-hydrostatic framework (see also Balmforth & Spiegel 1996). This, in turn, permits a dynamical analysis purely in terms of the potential vorticity, which is typical of meteorological studies. This construction was used to re-examine the Rossby wave instability (Li et al. 2000; Meheut et al. 2010) by illustrating it in a setting stripped down to its essential components (Umurhan 2010).
We use the limit developed in Umurhan (2008) to examine baroclinic instability in an annular section of a cold accretion disk. We circumvent the difficulties encountered in Knobloch and Spruit’s calculation by constructing a two-layer Philips model (Philips 1954). The Philips model is an effective simplification of the governing equations which allows for analytical tractability without losing the underlying physics at play in the baroclinic instability (see the extensive discussion of this in the text of Vallis 2006).
This work is organized as follows. In Sect. 2 we develop a two-layer Philips disk model from the disk shallow-water equations found in Umurhan (2008) using several simplifications and assumptions. In Sect. 3 we set up the general normal mode problem for this two-layer, mid-plane symmetric model system, including the boundary conditions and numerical methods employed. We describe the model whose stability we test including a description of the features that we included and that are designed to strip away the complications arising from critical layers. In Sect. 4 we consider the stability properties of a purely barotropic (single-layer) configuration and interpret the results from the perspective of interacting Rossby waves developed in previous studies. In Sect. 5 we build upon the picture developed for the barotropic calculation, describe a baroclinic model configuration, and examine its stability properties. In Sect. 6 we offer a summary of our principle results and some brief reflections and remarks.
2. Derivation of the two-layer Philips disk model
The analysis of this study assumes that dynamics occur on azimuthal length scales that are much longer than the system’s vertical and radial scales. The equations appropriate for such a thin annular setting were developed from the scaling analysis detailed in Umurhan (2008). But these same arguments can be found in various other forms in older studies as well, e.g. Knobloch & Spruit (1985, 1986) and Balmforth & Spiegel (1996).
These equations describe dynamics in a thin annular section of a disk centered at some radius R rotating with the local Keplerian rate 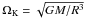 . If the local soundspeed of the disk is given by cs, then the ratio ε = cs/(RΩK) forms a natural small parameter of the disk equations. Formally this means we will take ε ≪ 1. The equations are therefore derived by assuming a number of scalings, namely that the azimuthal velocity scales as cs and that the vertical and radial velocities scale as εcs. Together with the assumption that the radial and vertical scales are a factor of ε smaller than the azimuthal scale R, the velocity assumptions here imply a long timescale
. If the local soundspeed of the disk is given by cs, then the ratio ε = cs/(RΩK) forms a natural small parameter of the disk equations. Formally this means we will take ε ≪ 1. The equations are therefore derived by assuming a number of scalings, namely that the azimuthal velocity scales as cs and that the vertical and radial velocities scale as εcs. Together with the assumption that the radial and vertical scales are a factor of ε smaller than the azimuthal scale R, the velocity assumptions here imply a long timescale 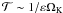 . It is important to note that this long timescale necessarily filters out gravity/acoustic-wave-type motions from these dynamics. Combining these scalings with the fundamental equations of motion results in the following set of reduced non-dimensionalized equations
. It is important to note that this long timescale necessarily filters out gravity/acoustic-wave-type motions from these dynamics. Combining these scalings with the fundamental equations of motion results in the following set of reduced non-dimensionalized equations
 in which
in which 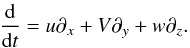 P = ρT is the pressure, where ρ and T denote density and temperature respectively. The velocity vector u = (u,V,w) is comprised of components in the radial (x), azimuthal (y) and disk vertical (z) directions. The lengths x and z represent the radial and vertical scales scaled by εR while the azimuthal scales y are scaled by R. The entropy is S ≡ lnP/ργ, where γ is the ratio of specific heats. Ω0 represents the non-dimensionalization of the usual Coriolis terms that emerge when one moves into a rotating frame. In this formulation it is formally “1”, but we keep it in this form for clarity. For Keplerian disk systems q = 3/2.
P = ρT is the pressure, where ρ and T denote density and temperature respectively. The velocity vector u = (u,V,w) is comprised of components in the radial (x), azimuthal (y) and disk vertical (z) directions. The lengths x and z represent the radial and vertical scales scaled by εR while the azimuthal scales y are scaled by R. The entropy is S ≡ lnP/ργ, where γ is the ratio of specific heats. Ω0 represents the non-dimensionalization of the usual Coriolis terms that emerge when one moves into a rotating frame. In this formulation it is formally “1”, but we keep it in this form for clarity. For Keplerian disk systems q = 3/2.
The lack of the usual inertial terms in the resulting radial and vertical momentum equations expresses the extremeness of the scalings describing the thin annular disk region. The resulting equations describe dynamics that are vertically hydrostatic but, moreover, geostrophic in the radial direction. In meteorological studies this is sometimes referred to as semi-geostrophic because the azimuthal flow dynamics are not in fundamental geostrophic balance.
 |
Fig. 1 Configuration of the two-layer Philips model. |
To derive a Philips model that is tractable and transparent, the following assumptions are made:
-
1.
dynamics are symmetric about the midplane z = 0;
-
2.
two layers are examined with differing uniform densities (and the configuration is stable to buoyant instabilities);
-
3.
the flow in each layer is incompressible.
The assumption of incompressibility means that the continuity equation is replaced, instead, by 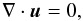 (6)in each layer. A pictoral representation of the system envisioned for this analysis is shown in Fig. 1. Throughout, the quantities in the upper layer are designated with a subscript “0”, while in the lower layer they are represented by the subscript “1”. Thus, for example, the uniform density of the upper layer is ρ0, while in the lower layer it is ρ1. Because incompressibility has been assumed for each layer, there is no longer any need for the energy Eq. (5). Instead, the evolution of each layer’s thickness will be followed (see below).
(6)in each layer. A pictoral representation of the system envisioned for this analysis is shown in Fig. 1. Throughout, the quantities in the upper layer are designated with a subscript “0”, while in the lower layer they are represented by the subscript “1”. Thus, for example, the uniform density of the upper layer is ρ0, while in the lower layer it is ρ1. Because incompressibility has been assumed for each layer, there is no longer any need for the energy Eq. (5). Instead, the evolution of each layer’s thickness will be followed (see below).
A qualitative inspection of the state of affairs depicted in Fig. 1 shows that, indeed, the isopycnals and isobars of the atmosphere are misaligned, which means that the basic state will be baroclinic with the in-layer azimuthal velocities being different from one another. The misalignment has been placed here by hand and is controlled by the functional form of the heights h0 and h1. The origins of their respective distributions ultimately rest upon radially dependent thermal processes that involv radiation and disk chemistry, which requires detailed calculations (e.g. Turner et al. 2012) without making the simplifying assumptions we have made. For the purpose of this model, we are not concerned with the way the atmosphere became arranged into this configuration: it is enough that the profile is in steady state.
The azimuthal velocity in both layers is written as a sum of the local Keplerian part − qΩ0x plus a deviation vi, where i is either “0” or “1” as in, Vi = −qΩ0x + vi. Assuming that the pressure of the disk is zero at its top, the vertical momentum equation may be immediately integrated to yield 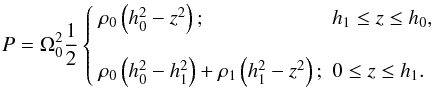 (7)Returning this solution for the pressure into the horizontal momentum equations shows that for each layer
(7)Returning this solution for the pressure into the horizontal momentum equations shows that for each layer
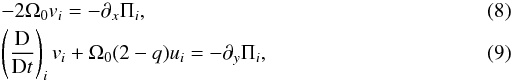 where
where ![\begin{equation} \Pi_0 = \frac{1}{2}\Omega_0^2 h_0^2, \qquad \Pi_1 = \frac{1}{2}\Omega_0^2 \left[\delta h_0^2 + (1-\delta)h_1^2 \right]. \label{Pi_eqns} \end{equation}](/articles/aa/full_html/2012/07/aa18803-12/aa18803-12-eq44.png) (10)The quantity Πi may be viewed as the analog of the streamfunction in meteorological studies. Each layer height, which is in effect an integration constant, is designated by hi(x,y,t). The parameter δ ≡ ρ0/ρ1 measures the ratio of the two densities. Henceforth, since our interest is in configurations that are buoyantly stable, we only consider values of δ < 1.
(10)The quantity Πi may be viewed as the analog of the streamfunction in meteorological studies. Each layer height, which is in effect an integration constant, is designated by hi(x,y,t). The parameter δ ≡ ρ0/ρ1 measures the ratio of the two densities. Henceforth, since our interest is in configurations that are buoyantly stable, we only consider values of δ < 1.
Inspection reveals that the resulting horizontal momentum equations are independent of the vertical coordinate. Therefore the time derivative operator in each layer has been written as 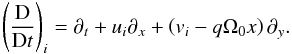 The incompressiblity equations may be integrated in each layer, revealing
The incompressiblity equations may be integrated in each layer, revealing 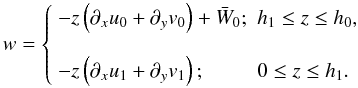 (11)The symmetry condition has been imposed on the vertical velocity profile by enforcing that its value is zero at z = 0. The velocity term
(11)The symmetry condition has been imposed on the vertical velocity profile by enforcing that its value is zero at z = 0. The velocity term 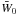 is determined by enforcing certain matching conditions when following the motion of the individual interfaces. Since
is determined by enforcing certain matching conditions when following the motion of the individual interfaces. Since 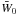 plays no essential role in the subsequent linear theory, we do not detail its form here. The motion of each layer edge is viewed from both layers and is accordingly set equal to the vertical velocities found in (11). Combining this with the criterion that there is no layer separation reveals that the dynamics of each layer’s thickness is governed by
plays no essential role in the subsequent linear theory, we do not detail its form here. The motion of each layer edge is viewed from both layers and is accordingly set equal to the vertical velocities found in (11). Combining this with the criterion that there is no layer separation reveals that the dynamics of each layer’s thickness is governed by 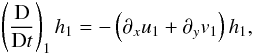 (12)and
(12)and 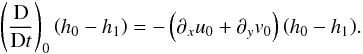 (13)The above equations may be combined and simplified following standard procedures resulting in
(13)The above equations may be combined and simplified following standard procedures resulting in 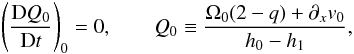 (14)in the upper layer while, for the lower layer,
(14)in the upper layer while, for the lower layer, 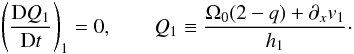 (15)The above is related to the fact that the potential vorticities in each layer, represented by Q0 and Q1, are materially conserved by the flow. It should be noted here that the layers are linked to one another even though each layer’s potential vorticity is materially conserved. The inter-connectivity between layers arises because each layer’s Qi is composed of quantities that evolve in layers outside of its own.
(15)The above is related to the fact that the potential vorticities in each layer, represented by Q0 and Q1, are materially conserved by the flow. It should be noted here that the layers are linked to one another even though each layer’s potential vorticity is materially conserved. The inter-connectivity between layers arises because each layer’s Qi is composed of quantities that evolve in layers outside of its own.
Equations (14), (15) together with (8) − (10) completely describe the model system. It is referred to hereafter as the two-layer Philips disk model.
3. Steady states, their perturbations, and the numerical method implemented
Because the purpose of this work is to demonstrate the possible normal-mode responses for various configurations of this two-layer Philips model, we develop the formalism for the perturbative study of generalized steady state configurations in this section. These steady states are assumed to be radially dependent, but perturbations of these states are non-axisymmetric. In the subsequent two sections we will detail the normal-mode response for a variety of specific steady-state profiles.
For the sake of transparency, Ω0 shall be set to its nominal value of 1. We study perturbations of already existing potential vorticity profiles. These steady profiles describe mean azimuthal velocities that are deviations around the Keplerian base flow. There are no mean radial velocities. This means in effect, that the mean PV profiles will depend only upon the radial coordinate x. Therefore, assuming 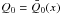 and
and 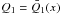 it follows from the relationship between Qi and Πi(h0,h1) found in (14), (15) that
it follows from the relationship between Qi and Πi(h0,h1) found in (14), (15) that 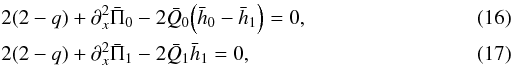 in which the relationship between Π and hi, found in (10), have been inverted:
in which the relationship between Π and hi, found in (10), have been inverted: 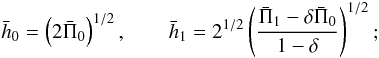 (18)expressing the mean steady height’s
(18)expressing the mean steady height’s 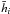 in terms of the steady in-layer pressures
in terms of the steady in-layer pressures 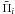 . In deriving the above expressions the following relationships have also been explicitly used,
. In deriving the above expressions the following relationships have also been explicitly used,  (19)Linear perturbations of the Philips model system are developed by writing for all dependent quantities “f”
(19)Linear perturbations of the Philips model system are developed by writing for all dependent quantities “f” 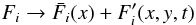 (20)where the primes denote perturbations. Equations (14), (15) and (8) − (10) are explicitly written out
(20)where the primes denote perturbations. Equations (14), (15) and (8) − (10) are explicitly written out 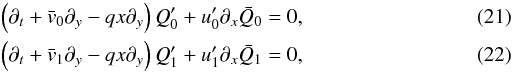 in which
in which 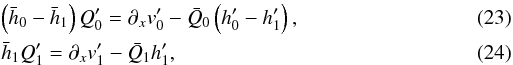 together with
together with 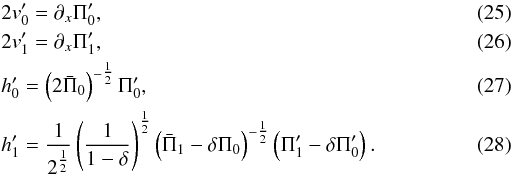 The linear equations resulting from perturbations of (9) are rewritten to express the perturbation radial velocity,
The linear equations resulting from perturbations of (9) are rewritten to express the perturbation radial velocity, 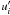 , in terms of the other perturbation quantities,
, in terms of the other perturbation quantities, 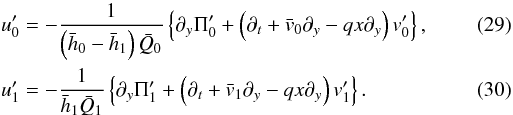 Inserting (23) − (26) and (29), (30) into (21), (22) reduces the system to two coupled PDE for the variables
Inserting (23) − (26) and (29), (30) into (21), (22) reduces the system to two coupled PDE for the variables 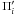 . This is to say,
. This is to say, ![\begin{eqnarray} & & \left(\partial_t + \bar v_0 \partial_y - qx \partial_y\right) \bigg[\partial_x^2 \Pi_0' - \partial_x\Pi_0' \cdot D\ln \bar Q_0 \nonumber \\ \label{single_Pi_0_eqn}& & \hskip 1.75cm - 2\bar Q_0 \left(h_0'-h_1'\right)\bigg] -2\partial_y \Pi_0'\cdot D\ln Q_0 = 0, \end{eqnarray}](/articles/aa/full_html/2012/07/aa18803-12/aa18803-12-eq78.png) (31)and
(31)and ![\begin{eqnarray} & & \left(\partial_t + \bar v_1 \partial_y - qx \partial_y\right) \left[\partial_x^2 \Pi_1' - \partial_x\Pi_1' \cdot D\ln\bar Q_1 - 2\bar Q_1 h_1'\right] \nonumber \\ \label{single_Pi_1_eqn}& & \hskip 3.0cm -2\partial_y \Pi_1'\cdot D\ln\bar Q_1 = 0, \end{eqnarray}](/articles/aa/full_html/2012/07/aa18803-12/aa18803-12-eq79.png) (32)where the equations relating the perturbation heights to the perturbation pressures are given in (27), (28). The symbol “D” denotes differentiation with respect to x.
(32)where the equations relating the perturbation heights to the perturbation pressures are given in (27), (28). The symbol “D” denotes differentiation with respect to x.
All perturbation quantities are assumed to be periodic in the azimuthal direction and, furthermore, we assume a normal-mode temporal structure. That is to say, the solution ansatz we adopt is 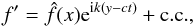 (33)where k > 0 is the azimuthal direction wavenumber and c is the wavespeed. The goal will be to find the admitted values of c for the variety of configurations examined in the following sections. Values in which Im(c) > 0 correspond to instability.
(33)where k > 0 is the azimuthal direction wavenumber and c is the wavespeed. The goal will be to find the admitted values of c for the variety of configurations examined in the following sections. Values in which Im(c) > 0 correspond to instability.
For the radial boundary conditions it will be assumed that the fluctuation perturbation pressures go to zero at symmetrically placed radial boundaries, i.e. that 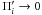 as x → ± L. These boundaries L will be placed significantly far from the region where there are nontrivial variations in the mean flow. Typical values taken are L ~ 10 (unless otherwise specified). We aim to uncover effects that are insensitive to the effects introduced by an artificial boundary condition such as ours. Therefore we verified throughout that indeed the growth rates we determine are insensitive to the position of the boundaries themselves by recalculating the growth rates for several values of L that are significantly greater than 10. Because all eigenfunctions we generate show exponential decay as one approaches these artificial boundaries, we are confident that there does exist a minimum value of L beyond which the effects of the boundaries are unimportant in determining the dynamics we study. (An exception is the special case discussed at the end of Sect. 5.)
as x → ± L. These boundaries L will be placed significantly far from the region where there are nontrivial variations in the mean flow. Typical values taken are L ~ 10 (unless otherwise specified). We aim to uncover effects that are insensitive to the effects introduced by an artificial boundary condition such as ours. Therefore we verified throughout that indeed the growth rates we determine are insensitive to the position of the boundaries themselves by recalculating the growth rates for several values of L that are significantly greater than 10. Because all eigenfunctions we generate show exponential decay as one approaches these artificial boundaries, we are confident that there does exist a minimum value of L beyond which the effects of the boundaries are unimportant in determining the dynamics we study. (An exception is the special case discussed at the end of Sect. 5.)
The coupled linearized ordinary differential equations are solved using a two-step procedure. The x-domain is discretized on a Chebyshev grid x(n). The number of grid points is N. The solutions are assumed to be represented by the corresponding Chebyshev decomposition on this grid:
-
1.
Step 1. This step involves expressing the governingEqs. (31), (32) and their operators inphysical space. For a solution to
 represented in physical space by
represented in physical space by 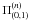 the two coupled equations form a single matrix-equation
the two coupled equations form a single matrix-equation 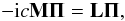 (34)where
(34)where ![\begin{equation*} {\mathbf \Pi} = \left[\Pi^{(1)}_0, \Pi^{(2)}_0,\ldots,\Pi^{(N-1)}_0,\Pi^{(N)}_0,\Pi^{(1)}_1,\ldots,\Pi^{(N)}_1 \right]^{\mathtt{T}}, \end{equation*}](/articles/aa/full_html/2012/07/aa18803-12/aa18803-12-eq93.png) in which the superscript “T” denotes the vector transpose operation. Π is a vector of length 2N, while M and L are 2N × 2N matrices. M and L are matrices containing the Chebyshev representation of the linear operators of the problem. The boundary condition that
in which the superscript “T” denotes the vector transpose operation. Π is a vector of length 2N, while M and L are 2N × 2N matrices. M and L are matrices containing the Chebyshev representation of the linear operators of the problem. The boundary condition that 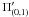 is zero at the endpoints is implemented the following way. The rows corresponding to the boundaries are replaced by the equation
is zero at the endpoints is implemented the following way. The rows corresponding to the boundaries are replaced by the equation 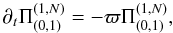 where we choose ϖ to be a very large number (typically ~ 109). We then determine the full eigenvalue set, c(n) using standard packages for determining numerical eigenvalues as found in Matlab. We note that the four eigenvalues of
where we choose ϖ to be a very large number (typically ~ 109). We then determine the full eigenvalue set, c(n) using standard packages for determining numerical eigenvalues as found in Matlab. We note that the four eigenvalues of 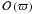 are discarded since they are unphysical1. The remaining eigenvalues and corresponding eigenvectors represent the responses of the system. The boundary conditions are satisfied with an error of
are discarded since they are unphysical1. The remaining eigenvalues and corresponding eigenvectors represent the responses of the system. The boundary conditions are satisfied with an error of 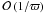 . We assume a value of N = 300, which typically yields converged solutions.
. We assume a value of N = 300, which typically yields converged solutions. -
Step 2 We verify and further refine the solutions we determine in Step 1 by solving (34) using the standard Newton-Raphson-Kantorovich (NRK) method. We insert into the procedure a solution vector Π together with its corresponding eigenvalue ω. The error tolerance required of the NRK solution was that it is correct to one part in 109.
All quoted converged solutions in this study passed both of the outlined steps above. Furthermore, we checked the resolution convergence with the NRK method by taking a given solution that was determined on a grid of size N, interpolating it onto a grid of size 2N, and then using this resulting interpolated solution as an initial guess for the NRK method. In rare instances we found solutions determined via Step 1 to have false unstable eigenvalues, i.e. Im(c) ≠ 0. These were identified using the grid refinement procedure: for those spurious eigenvalues, Im(c) → 0 asymptotically as N → ∞.
 |
Fig. 2 Single layer configuration and model. Particular values in reference to the “double-tanh” model (35): h1(∞) = 2.4, h1( − ∞) = 3.77 with Δ = 0.75 and φ = ξ = 0.1, q = 1.5. The top panel shows the corresponding mean height h1. The middle panel depicts the fundamental PV profile together with descriptive annotations relating various features of the profile to the parameters describing it in the text. The bottom panel shows the deviation from the Keplerian flow |
4. Barotropic configurations
In order to anchor our intuition we begin this analysis by recalling the dynamics in a single-layer configuration. Under those conditions the shear is barotropic. The linearized equations we will need to solve are those given in the previous section with δ set to zero. With δ = 0 the upper layer has no dynamical effect upon the lower layer and, as such, the resulting dynamics describe the flow of the lower layer entirely isolated from the upper layer. Therefore, the equations for the steady state are (17) with 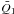 given and
given and 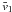 , as given in (19). For the linearized dynamics we solve only (32) with (28) to generate solutions for the lower layer perturbation enthalpy
, as given in (19). For the linearized dynamics we solve only (32) with (28) to generate solutions for the lower layer perturbation enthalpy 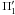 . We also assume the normal mode ansatz (33) and enforce that
. We also assume the normal mode ansatz (33) and enforce that 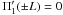 .
.
Figure 2 depicts the PV profile we examine here. We refer to it as the “double-tanh” profile and it is given by the form ![\begin{equation} \bar Q_1 = A_1\left[1+ \tanh\left(\frac{\Delta-x}{\xi}\right)\right] + B_1\left[1+ \tanh\left(\frac{x-\Delta}{\xi}\right)\right] + C_1, \label{double_tanh_profile} \end{equation}](/articles/aa/full_html/2012/07/aa18803-12/aa18803-12-eq124.png) (35)where the constants are specified below. This functional form roughly represents a two-step PV-profile with the steps located at x = ± Δ, where Δ > 0 is some parameter. We will refer to twice this parameter as quantifying the width of this type of PV profile. The parameter ξ represents the width of the transition in moving from one region of PV to the other. In the limit ξ → 0 the transition from one region of PV to the other (e.g. near x = ± Δ in Fig. 2) is proportional to a Heaviside step function. On one hand we numerically try to avoid the ξ → 0 limit, yet on the other hand we aim to have ξ small to relate the results of the model to our simplified understanding of the system. Therefore we typically choose ξ = 0.1. Thus, as depicted in Fig. 2, the limit ξ → 0 makes the PV-profile look like two successive step functions or “defects” in the PV. We interpret the length 2Δ as quantifying the separation of these nominal defects of the PV.
(35)where the constants are specified below. This functional form roughly represents a two-step PV-profile with the steps located at x = ± Δ, where Δ > 0 is some parameter. We will refer to twice this parameter as quantifying the width of this type of PV profile. The parameter ξ represents the width of the transition in moving from one region of PV to the other. In the limit ξ → 0 the transition from one region of PV to the other (e.g. near x = ± Δ in Fig. 2) is proportional to a Heaviside step function. On one hand we numerically try to avoid the ξ → 0 limit, yet on the other hand we aim to have ξ small to relate the results of the model to our simplified understanding of the system. Therefore we typically choose ξ = 0.1. Thus, as depicted in Fig. 2, the limit ξ → 0 makes the PV-profile look like two successive step functions or “defects” in the PV. We interpret the length 2Δ as quantifying the separation of these nominal defects of the PV.
We must now relate the constants A1, B1, C1 to physically intuitive features of the model. Because we envisage a PV profile that has an induced velocity profile (as a deviation from the background Keplerian flow, i.e. 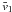 ) that is zero as x → ± ∞, inspection of (15) or (17) requires of us that
) that is zero as x → ± ∞, inspection of (15) or (17) requires of us that 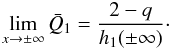 (36)In other words, we design this profile to yield constant mean heights, h1( ± ∞), in the limit of x → ± ∞. Of course, these heights may be different from one another but their constant asymptotic form ensures that the mean induced flow
(36)In other words, we design this profile to yield constant mean heights, h1( ± ∞), in the limit of x → ± ∞. Of course, these heights may be different from one another but their constant asymptotic form ensures that the mean induced flow 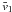 correspondingly asymptotes to zero as x → ± ∞. This implies that
correspondingly asymptotes to zero as x → ± ∞. This implies that 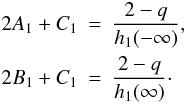 To complete this description we suppose that the depth of the depression in
To complete this description we suppose that the depth of the depression in 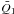 , located in the region − Δ < x < Δ, is some factor φ > 0 of the asymptotic value of the PV as x → − ∞, i.e.
, located in the region − Δ < x < Δ, is some factor φ > 0 of the asymptotic value of the PV as x → − ∞, i.e. 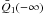 . This amounts to
. This amounts to 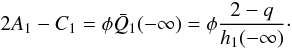 In summary, then, the barotropic model (35) is characterized by five parameters: the asymptotic heights h1( ± ∞), the symmetric positioning of the steps from x = 0, Δ > 0, the relative depth of the PV-dip in the middle-zone of this model, φ, and the width of the transition zones ξ. Note that the middle-zone has a width equal to 2Δ. The normal-mode system is additionally described by the shear parameter q.
In summary, then, the barotropic model (35) is characterized by five parameters: the asymptotic heights h1( ± ∞), the symmetric positioning of the steps from x = 0, Δ > 0, the relative depth of the PV-dip in the middle-zone of this model, φ, and the width of the transition zones ξ. Note that the middle-zone has a width equal to 2Δ. The normal-mode system is additionally described by the shear parameter q.
A model similar to this one was considered in Umurhan (2010). Unlike here, however, the assumed PV-profile adopted in that previous study were (symmetric) step functions chosen to facilitate analytical tractability. In comparison to the model considered here, the step function used in Umurhan (2010) would correspond to the limit of this model in which ξ → 0. Note also that the symmetry of the profiles studied in Umurhan (2010) is recovered here by choosing h1(∞) = h1( − ∞). We therefore introduced the parameter ξ to control the thickness of the transition from one zone to the next.
The rationale of introducing this feature into the model is to clearly represent the propagation and interaction of Rossby waves without having to consider the complexities of critical layers. Because Rossby waves represent disturbances that propagate in regions where the PV changes, setting ξ to be small ensures that the waves are localized in those places where the PV changes most markedly. In this model, for example, there will be two Rossby waves, each of which are localized in x at x = ± Δ with a radial width of scale ξ. We typically used values of ξ = 0.1 and this usually represented the Rossby wave dynamics without the appearance of critical layers. The robustness of some solutions was evaluated by also generating solutions with values of ξ = 0.025 (which necessitated using a higher resolution grid to resolve the transition zone with at least 5 − 7 grid points). Critical layers tended to appear for values of Δ ~ ξ. However, we did not examine these situations in this study.
 |
Fig. 3 Single-layer barotropic results for three different values of the background shear. Parameters of the “double-tanh” model (35): depth φ = 0.1, h1( − ∞) = 3.77, ξ = 0.1. Growth rates shown as a function of varying the relative position of the PV jump, Δ, and variations of the asymptotic height as x → ∞, i.e. h1(∞). Instability growth rates in units of 1/(εΩ0) (with α = 1). Instability boundaries shown as shaded region. Top figure: q = 1.5 (Keplerian). Middle and bottom figures: q = 0.5, 0.25, respectively. Vertical line designates symmetric step profiles. As the shear decreases, the corresponding growth rates decreases, but the range of possible unstable values of Δ increases. |
The barotropic incarnation of the Rossby wave instability was interpreted in Umurhan (2010) to arise as a result of the interaction of the two Rossby waves that propagate along the azimuthal directions at the two locations, consistent with the more generic picture of interacting edgewave disturbances (Baines & Mitsudera 1994). An analogous form of this dynamic is present in this model and is especially pronounced for ξ ≪ 1. For example, in reference to the PV profile shown in Fig. 2, we observe that the jump in the PV is positive at the step located at x = 1. Therefore, in the local frame of reference of the flow at x = 1 and when taken in isolation, the supported Rossby wave propagates in the negative y direction. Similarly, since the average change in the PV profile at x = −1 is negative, it can support a Rossby wave propagating in the positive y direction when viewed from the local reference frame of the flow at x = −1. When the laboratory measured wavespeeds of both waves are nearly equal, instability may manifest itself, i.e. when the Hayashi-Young criterion is satisfied (Hayashi & Young 1987). Instability exists when the Rossby waves are essentially counterpropagating along the flow (Heifetz et al. 1999) because it is only when the local propagating tendency of the Rossby wave is against the mean flow that the Hayashi-Young criteria of instability can be met.
In the next section we will also refer to an effective surface density. We define this here as 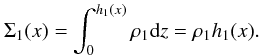 (37)Evidently, Σ1 is equivalent to h1 in the single-layer model, but will not be so in the two-layer model. Henceforth we take ρ1 = 1.
(37)Evidently, Σ1 is equivalent to h1 in the single-layer model, but will not be so in the two-layer model. Henceforth we take ρ1 = 1.
A representative summary of the results of this section is displayed in Fig. 3. Even though we solved for the wavespeed c, we depict the growth rates Im( − ω) = Im(kc), together with having here (and henceforth) set k = 12. The growth rates are quoted in time units used to derive the disk shallow-water equations (see Sect. 2), namely, time is scaled in the longtime units 1/ϵΩ0.
The results we plot here are an extension of the symmetric models considered in Umurhan (2010). Here we see that that the models do not have to display symmetric PV profiles for instability to surface and that, consistent with the results of Li et al. (2000), asymmetric PV profiles can just as easily lead to instability. We find that for a given set of layer parameters h1( ± ∞) and φ (the depth of the PV depression) – as the background shear q is lessened, the range of separation values Δ that admits instability is shifted toward higher values. In other words, weakening the shear means that profiles with steps farther separated from one another will result in instability.
In terms of the picture of interacting Rossby waves, this is easily rationalized in the way outlined above: (i) for instability to occur, the laboratory measured phase speed of the Rossby waves along each step must be nearly the same; (ii) since the phase speeds of the Rossby waves are a sum of both the background flow speed at the location of the step and the intrinsic Rossby wave speed (as measured in the moving frame at the step) induced by the local change in PV at the transition region it follows that; (iii) with all else held equal, a reduction in the background shear requires the location of the defects at x = ± Δ to be set farther apart so that the laboratory measured phase speeds may be, once again, nearly equal.
When the step profiles are symmetric, i.e. when h1( − ∞) = h1(∞), instability may occur for separation Δ = 0 consistent with previous results in Umurhan (2010). However, as h1(∞) begins to deviate away from the value h1( − ∞), there exists a minimum value for the defect separation above which instability may occur. It is also interesting to note that there is a maximum disparity of heights beyond which no instability is possible. E.g. for values of h1(∞) > 4.15 with q = 1.5, φ = 0.1 no instability is possible in the model in Fig. 3. The interpretation of this stability quality is once again similar to the above: varying h1(∞) beyond some critical value results in individual waves whose speeds cannot possibly match each other. In particular, an increase of the speed of the wave at the step x = Δ occurs because increasing h1(∞) means that the average PV-gradient increases at x = Δ step which, in turn, boosts the (in frame) counterpropagating Rossby wavespeed at the step.
We have verified that the results quoted are insensitive to L sufficiently large. It is important to keep in mind that the growth rate values convergence to the values quoted once L is greater than about 5. For values of L < 5 the growth rates weaken. The presence of channel walls in problems like these creates the effect of “image” waves (like image charges in electrostatics problems, Drazin & Reid 1981), which act to inhibit phase locking. This behavior has been detailed in a study of the Rayleigh problem with variable wall positions by Heifetz et al. (2009) and the trend for instability suppression with more narrowly set walls is consistent with their findings.
The same character follows in the baroclinic cases studied except for one instance discussed later. Finally, consistent with the Howard semicircle theorem, we observe that as the shear is weakened the maximum value of the growth rate is reduced.
 |
Fig. 4 Baroclinic-jet profile model considered in this work. |
5. Baroclinic profiles
In this section we solve the two-layer problem. We assume that each layer has a single jump in PV but that their positions in x are, in general, different from one another. We employ the basic type of model encountered in the previous section. In particular we assume that the mean PV profiles ![\begin{eqnarray} \bar Q_0 &=& C_0 + A_0\left[1-\tanh\left(\frac{x-x_0}{\xi}\right)\right], \nonumber \\ \bar Q_1 &=& C_1 + A_1\left[1-\tanh\left(\frac{x-x_1}{\xi}\right)\right]\cdot \end{eqnarray}](/articles/aa/full_html/2012/07/aa18803-12/aa18803-12-eq177.png) (38)The steps for each layer are located at x = x0 and x1. Without loss of generality we place these positions symmetrically about the point x = 0 and assign the position values x0 = −Δ and x1 = Δ. Δ is a parameter as before, but Δ can take on all values (and is not restricted to being strictly positive). As before, the thickness of the step in each layer is governed by the parameter ξ.
(38)The steps for each layer are located at x = x0 and x1. Without loss of generality we place these positions symmetrically about the point x = 0 and assign the position values x0 = −Δ and x1 = Δ. Δ is a parameter as before, but Δ can take on all values (and is not restricted to being strictly positive). As before, the thickness of the step in each layer is governed by the parameter ξ.
Following the arguments laid out in the previous section, we require of the steady PV states to correspond to zero-induced azimuthal flow 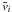 as x → ± ∞. Inspection of (14), (15) indicates that the constants Ai, Ci must simultaneously satisfy
as x → ± ∞. Inspection of (14), (15) indicates that the constants Ai, Ci must simultaneously satisfy 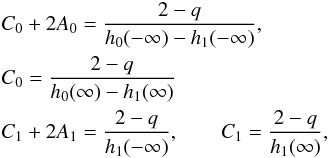 where the parameters hi( ± ∞) are the asymptotic values of the layer heights in the appropriate limit of x. The only requirement we place upon the these are that h0(∞) > h1(∞) and h0( − ∞) > h1( − ∞).
where the parameters hi( ± ∞) are the asymptotic values of the layer heights in the appropriate limit of x. The only requirement we place upon the these are that h0(∞) > h1(∞) and h0( − ∞) > h1( − ∞).
We solve for the steady configuration (16) − (19) using the above model for the PV profiles, which are governed by the six parameters hi( ± ∞),Δ,ξ. The parameters of the steady configuration are also determined by the three remaining other parameters: the shear q, the density ratio δ, and the domain size L. A qualitative example of the resulting states is shown in Fig. 4. It is evident from the resulting flow that the mean deviation velocity fields are different from one another between layers, indicating that the resulting flow state is baroclinic.
Figure 5 depicts the character that typifyies instability in these models. The parameters chosen here were meant to best match the results shown in the top graph of Fig. 3. The top layer has a density ratio δ = 0.85 of the bottom layer. The results are qualitatively similar to the behavior of the barotropic model with a certain modification to the region and degree of instability. Since, by design, there are only two waves that can interact – one emanating from the step in the upper layer and the other from the step in the lower layer – the interpretation of the instability is the same as for the barotropic case. Thus, baroclinic instability in this kind of baroclinic problem closely shadows the character of the instability in the barotropic case. The fundamental difference is, of course, the fact that the sources of the Rossby waves are from different vertical layers.
 |
Fig. 5 Mixed barotropic-baroclinic results. The basic baroclinic model is examined for variations in Δ and h0(∞). The pattern of regions of growth is similar to similar barotropic configurations. Note the particular absence of instability when Δ = 0. |
 |
Fig. 6 Baroclinic results depicting growth rates for varying values of the density ratio δ against the separation parameter Δ. Shown are the growth rates for fixed values of h0( ± ∞), h1( ± ∞) for Keplerian shear (q = 1.5) and ξ = 0.05. The range in separation values Δ in which instability occurs is reduced as δ is reduced. The growth rates are reduced as well. The implications are that interlayer interaction is weakened with a reduction of δ. |
 |
Fig. 7 Baroclinic results depicting growth rates for varying values of the shear parameter q against the separation parameter Δ with similar parameters found in the previous figure. As the shear tends to zero, the values of Δ for instability increases. The growth rates also tend to zero. Growth rates become less reliable in the Rayleigh limit, q → 2 (see text). |
The coupling between layers is governed by the density contrast δ. In Fig. 6 we display how the growth rates are modified for a model in which we vary the separation Δ and the density contrast δ. Indeed, as one might expect, both the occurrence of instability and its corresponding growth rate diminish as δ → 0. When viewed from the perspective of a normal-mode problem, the lower layer essentially experiences no dynamical influence of the upper layer when the mass of the upper layer is vanishingly small (the lower layer “knows” of the upper layer through the pressure fluctuations that the upper layer induces upon the lower layer). From the mathematical viewpoint of a normal-mode problem, both layers decouple from one another when δ = 0 (see the previous section). Nonetheless, even for δ ≈ 0 the Rossby waves in each layer are finite (and non-zero) and propagate in isolation. Thus when δ is increased the bottom layer feels the upper layer in proportion to δ, while the upper layer feels the bottom layer by the latter’s influence upon the upper layer’s thickness3. We also note here that the figures show that growth rates persist as δ → 1, but we are less inclined to infer very much about this limit because as δ → 1 the fundamental scaling relations leading to the Philips disk model begin to cause a break in the scaling assumptions behind the disk shallow-water equations. Nevertheless, the propensity for instability in these baroclinic models for δ not very close to zero suggests that baroclinic instability may be manifest in disks that are weakly stratified. We discuss this more in Sect. 6.
For a given set of model parameter values, varying the shear q → 0 reduces the growth rate of the instability and pushes the unstable range of step separations Δ toward higher values. In Fig. 7 we depict the growth rate trends for variable values of q and Δ. Although the pattern of instability in this parameter diagram is more complex than the previous graphs, we clearly see that as the shear weakens (holding the separation fixed) the instability generally vanishes. At the other end of the spectrum, as the Rayleigh limit is approached, i.e. q → 2, the instability also appears to become suppressed. However, we note here that the scaling ordering that is used to develop the disk shallow-water equations begins to break down as q approaches 2 (see Umurhan 2008). We therefore consider these observed trends (in this particular limit) with more caution. A proper investigation of what happens in the Rayleigh limit should involve re-examining the equations of motion in that particular limit.
For given values of the shear q we found no parameter configuration that shows instability with the jets lying exactly on top of each other (Δ = 0) and an instability that does not vanish as L → ∞. Such a configuration might correspond to a flow profile in which the jets model a baroclinically unstable setup relevant for more “traditional” baroclinic flow problems (like for the Earth and other solar system planets). As we noted earlier, all results we report in this study retain unaltered growth rates as the artificial domain walls in x are made very large L ≫ 1. In Fig. 8 we show an example set of parameters in which there is instability, but where the separation in x of the two PV jumps is zero. The values of the top of the atmosphere h0( ± ∞) are represented in a way such that the ratio of h0(∞)/h0( − ∞) remains fixed, but the overall height of the atmosphere can vary with the parameter α. For the example depicted, h0(∞) = 3.55α and h0( − ∞) = 5.44α. Thus α acts like a parameter that varies the lid of the atmosphere. The values of the lower layer parameters h1( ± ∞) are fixed. Consequently Fig. 8 displays the growth rates as a function of α and q with L = 10. Instability appears to exist, but for values of α so high that the atmosphere is effectively thin and tall. When we then increase the value of L (holding fixed the remaining atmosphere parameters), the instability eventually vanishes.
We therefore conclude that the possibility of instability in a model in which the jets lie on top of each other, e.g. as implied by the results shown in Fig. 8, is an artifact of the narrowness of the radial boundaries and is not likely to be possible for a real protoplanetary disk.
 |
Fig. 8 Model admitting baroclinic instability in which the jets in each layer lie exactly on top of each other (Δ = 0). The plot depicts the variation of the growth rates as a function of the shear q and the so-called “lid” of the atmosphere α (see text). For this atmosphere model the radial boundaries are set to L = 10. Keeping all parameters fixed but rerunning this atmosphere model with L = 15 reveals that all instabilities depicted in this figure vanish. |
6. Summary and discussion
Baroclinic instability in the guise familiar in meteorology (in which isopycnals and isobars are misaligned) is feasible for cold protoplanetary disks, albeit in a mixed baroclinic-barotropic form owing to the strength of the underlying Keplerian shear. By using a two-layer Philips model we have further substantiated the conjecture made by Cabot (1984) and Knobloch & Spruit (1984, 1985) that baroclinic instability is relevant for accretion disks. In addition to determining growth rates and interpreting the mechanics of the instability in terms of Rossby waves interacting across layers, we also showed that the instability weakens in strength as the vertical density stratification of the layer is increased. The results of the two-layer model suggests that meteorological-type of baroclinic processes, which wholly depend on the mismatch of isobars and isopycnals in the mean state, is likely for disks that have weak vertical density stratification. Of course, this does not limit the full scope of possibilities and must therefore be analyzed more fully in the setting of more realistic disk models.
The use of the simple Philips two-layer model has been shown to be very good at capturing the essence of baroclinic flow dynamics present in continuously layered models of atmospheres (Vallis 2006). Comparison of growth rates determined for both the Eady model (continuous vertical shear) and the Philips model show that, although they are not precisely the same, the qualitative behaviours are consistent with one another, and it is for this reason why the Philips model is so widely regarded as a useful theoretical platform to examine the physics of these and related processes. In fact, studies have been performed in which multiple-layer Philips models are examined for the same problem, yielding no significantly different results in classical meteorological investigations. This has partly to do with the geometry of the system that is analyzed: in a planetary atmosphere there is usually a bottom boundary and the direction of gravity is the same.
In contrast, we investigated a disk model in which symmetry with respect to the disk midplane was imposed a priori. Thus the dynamics possible here, which allows only for a subset of possible phase relationships and Rossby wave interactions between the midplane layer and the layer above it, is a subset of a wider class of possible dynamical responses. For instance, if the restriction of midplane symmetry were relaxed, the possibility of new types of Rossby wave interactions arises independently involving three layers (the midplane and the two layers sandwiching the midplane) that will contain the dynamics of the two-layer system studied here. This will yield qualitatively new dynamical possibilities.
We note here the similarities between traditional “meteorological” baroclinic instabilities to other types of baroclinic processes investigated for both disks (e.g. Klahr & Bodenheimer 2003; Petersen et al. 2007a,b; Lesur & Papaloizou 2010; Lyra & Klahr 2011) and the Sun (Gilman & Fox 1997; Zaqarashvili et al. 2010; to name only a few studies). In these analyses potential vorticity disturbances are effectively baroclinically torqued by some process that is either thermal or magnetic or, in some investigations, a combination of both. In those studies of magnetic Rossby waves in the Sun (e.g. Gilman & Fox 1997; Zaqarashvili et al. 2010), Rossby waves will propagate along those places where there are strong gradients in the solar differential rotation. Treated as a hydrodynamic problem, these Rossby waves are not necessarily unstable on their own, especially for the differential rotation profiles inferred to be characteristic of the Sun’s tachochline (Spiegel & Zahn 1992). However, when a strong toroidal field is added to the mix, an effective baroclinic source term (owing to the Lorentz force) arises that render the wave unstable. In all of these studies the instabilities are global in character, as is the instability investigated in this study because we have examined the fate of disturbances with azimuthal wavelengths on the scale of the disk.
Upcoming papers in this series examines an alternative derivation of the shallow-water equations for disks, which lifts the restrictions placed upon the azimuthal scales as compared to the vertical and radial scales as well as examining the response of the Rossby wave instability when thermal relaxation is included. Recently published studies (Lin 2012; Meheut et al. 2012) indicate and confirm that the Rossby wave instability both endures in three-dimensional settings and appears to be dominated by the (largely) two-dimensional dynamical process originally characterizing the effect. A reduced shallow-water system that is non-asymptotic will aid in better understanding the development of this instability as well as others that may be concurrently present in these flow configurations.
Disk shallow-water theory has that the streamwise wavenumber drops out of all calculations owing to it being, essentially, a long-wavelength theory. See also Knobloch & Spruit (1985, 1986).
We note in passing that when treated as an initial value problem the situation is different for δ nearly zero. The lower layer still dynamically evolves free of the influence of the upper layer, but the upper layer’s dynamics are influenced by the motion of the lower layer because it shows up in the upper layer’s dynamical evolution as an external forcing term. We do not take up this problem in this study.
References
- Baines, P. G., & Mitsudera, H. 1994, J. Fluid Mech., 276, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Balmforth, N. J., & Spiegel, E. A. 1996, Phys. D, 97, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cabot, W. 1984, ApJ, 277, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Charney, J. G. 1947, J. Meteor., 4, 135 [CrossRef] [Google Scholar]
- Drazin, P. G., & Reid, W. H. 1981, Hydrodynamic Stability (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Eady, E. T. 1949, Tellus, 1, 33 [CrossRef] [MathSciNet] [Google Scholar]
- Fujimoto, M. Y. 1988, A&A, 198, 163 [NASA ADS] [Google Scholar]
- Gilman, P. A., & Fox, P. A. 1997, ApJ, 484, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Haine, T. W. N., & Marshall, J. 1998, J. Phys. Ocean., 28, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, Y.-Y., & Young, W. R. 1987, J. Fluid Mech., 184, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Heifetz, E., Bishop, C. H., & Alpert, P. 1999, Q. J. R. Meteorol. Soc., 125, 2835 [NASA ADS] [CrossRef] [Google Scholar]
- Heifetz, E., Bishop, C. H., Hoskins, B. J., & Methven, J. 2004, Q. J. R. Meteorol. Soc., 130, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Heifetz, E., Harnik, N., & Tamarin, T. 2009, Q. J. R. Meteorol. Soc., 135, 2161 [CrossRef] [Google Scholar]
- Hoskins, B. J., McIntyre, M. E., & Robertson, A. W. 1985, Q. J. R. Meteorol. Soc., 111, 877 [Google Scholar]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Knobloch, E., & Spruit, H. C. 1982, A&A, 113, 261 [NASA ADS] [Google Scholar]
- Knobloch, E., & Spruit, H. C. 1986a, Geophys. Astrophys. Fluid Dyn., 32, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Knobloch, E., & Spruit, H. C. 1986b, A&A, 166, 359 [NASA ADS] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2010, A&A, 513, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Finn, J. M., Lovelace, R. V. E., & Colgate, S. A. 2000, ApJ, 533, 1023 (LFLC-2000) [NASA ADS] [CrossRef] [Google Scholar]
- Lin, M.-K. 2012, ApJ, 754, 21 [Google Scholar]
- Lyra, W., & Klahr, H. 2011, A&A, 527, 138 [Google Scholar]
- Meheut, H., Casse, F., Varniere, P., & Tagger, M. 2010, A&A, 516, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meheut, H., Yu, C., & Lai, D. 2012, MNRAS, 422, 2399 [NASA ADS] [CrossRef] [Google Scholar]
- Molemaker, M. J., McWilliams, J. C., & Yavneh, I. 2005, J. Phys. Ocean., 35, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Pedlosky, J. 1987, Geophysical Fluid Dynamics, 2nd edn. (New York: Springer-Verlag) [Google Scholar]
- Petersen, M. R., Keith, J., & Stewart, G. R. 2007a, ApJ, 658, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, M. R., Keith, J., & Stewart, G. R. 2007b, ApJ, 658, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, N. A. 1954, Tellus, 6, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, E. A., & Zahn, J.-P. 1992, A&A, 265, 106 [NASA ADS] [Google Scholar]
- Stone, P. H. 1970, J. Atm. Sci., 27, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, P. H. 1971, J. Fluid Mech., 48, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., Choukroun, M., Castillo-Rogez, J., & Bryden, G. 2012, ApJ, 748, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Vallis, G. K. 2006, Atmospheric and Oceanic Fluid Dynamics (New York: Cambridge University Press) [Google Scholar]
- Umurhan, O. M. 2008, A&A, 489, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umurhan, O. M. 2010, A&A, 521, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Carbonell, M., Oliver, R., & Ballester, J. L. 2010, ApJ, 709, 749 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Configuration of the two-layer Philips model. |
| In the text | |
 |
Fig. 2 Single layer configuration and model. Particular values in reference to the “double-tanh” model (35): h1(∞) = 2.4, h1( − ∞) = 3.77 with Δ = 0.75 and φ = ξ = 0.1, q = 1.5. The top panel shows the corresponding mean height h1. The middle panel depicts the fundamental PV profile together with descriptive annotations relating various features of the profile to the parameters describing it in the text. The bottom panel shows the deviation from the Keplerian flow |
| In the text | |
 |
Fig. 3 Single-layer barotropic results for three different values of the background shear. Parameters of the “double-tanh” model (35): depth φ = 0.1, h1( − ∞) = 3.77, ξ = 0.1. Growth rates shown as a function of varying the relative position of the PV jump, Δ, and variations of the asymptotic height as x → ∞, i.e. h1(∞). Instability growth rates in units of 1/(εΩ0) (with α = 1). Instability boundaries shown as shaded region. Top figure: q = 1.5 (Keplerian). Middle and bottom figures: q = 0.5, 0.25, respectively. Vertical line designates symmetric step profiles. As the shear decreases, the corresponding growth rates decreases, but the range of possible unstable values of Δ increases. |
| In the text | |
 |
Fig. 4 Baroclinic-jet profile model considered in this work. |
| In the text | |
 |
Fig. 5 Mixed barotropic-baroclinic results. The basic baroclinic model is examined for variations in Δ and h0(∞). The pattern of regions of growth is similar to similar barotropic configurations. Note the particular absence of instability when Δ = 0. |
| In the text | |
 |
Fig. 6 Baroclinic results depicting growth rates for varying values of the density ratio δ against the separation parameter Δ. Shown are the growth rates for fixed values of h0( ± ∞), h1( ± ∞) for Keplerian shear (q = 1.5) and ξ = 0.05. The range in separation values Δ in which instability occurs is reduced as δ is reduced. The growth rates are reduced as well. The implications are that interlayer interaction is weakened with a reduction of δ. |
| In the text | |
 |
Fig. 7 Baroclinic results depicting growth rates for varying values of the shear parameter q against the separation parameter Δ with similar parameters found in the previous figure. As the shear tends to zero, the values of Δ for instability increases. The growth rates also tend to zero. Growth rates become less reliable in the Rayleigh limit, q → 2 (see text). |
| In the text | |
 |
Fig. 8 Model admitting baroclinic instability in which the jets in each layer lie exactly on top of each other (Δ = 0). The plot depicts the variation of the growth rates as a function of the shear q and the so-called “lid” of the atmosphere α (see text). For this atmosphere model the radial boundaries are set to L = 10. Keeping all parameters fixed but rerunning this atmosphere model with L = 15 reveals that all instabilities depicted in this figure vanish. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.