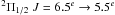| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 34 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118686 | |
| Published online | 12 July 2012 | |
Nitrogen hydrides in interstellar gas
II. Analysis of Herschel/HIFI observations towards W49N and G10.6 − 0.4 (W31C) ⋆,⋆⋆
1 Chalmers University of TechnologyDepartment of Earth and Space Sciences, Onsala Space Observatory, 43992 Onsala, Sweden
e-mail: carina.persson@chalmers.se
2 LERMA-LRA, UMR 8112 du CNRS, Observatoire de Paris, École Normale Supérieure, UPMC & UCP, 24 rue Lhomond, 75231 Paris Cedex 05, France
3 Tata Institute of Fundamental Research, Homi Bhabha Road, 400005 Mumbai, India
4 Department of Chemistry, University of Virginia, McCormick Road, Charlottesville, VA 22904, USA
5 Centro de Astrobiologìa, CSIC-INTA, 28850 Madrid, Spain
6 Université de Toulouse, UPS-OMP, 31028 Toulouse, France
7 CNRS, IRAP, 9 Av. Colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
8 Department of Physics & Astronomy, Siena College, Loudonville, NY 12211, USA
9 Laboratoire d’Astrophysique de Grenoble, UMR 5571-CNRS, Université Joseph Fourier, 38042 Grenoble Cedex 9, France
10 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
11 I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
12 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Dr., Pasadena CA 91109, USA
Received: 20 December 2011
Accepted: 30 May 2012
As a part of the Herschel key programme PRISMAS, we have used the Herschel/HIFI instrument to observe interstellar nitrogen hydrides along the sight-lines towards eight high-mass star-forming regions in order to elucidate the production pathways leading to nitrogen-bearing species in diffuse gas. Here, we report observations towards W49N of the NH N = 1–0, J = 2–1, and J = 1–0, ortho-NH2NKa,KcJ = 11,13/2–00,01/2, ortho-NH3JK = 10–00 and 20–10, para-NH3JK = 21–11 transitions, and unsuccessful searches for NH+. All detections show absorption by foreground material over a wide range of velocities, as well as absorption associated directly with the hot-core source itself. As in the previously published observations towards G10.6−0.4, the NH, NH2 and NH3 spectra towards W49N show strikingly similar and non-saturated absorption features. We decompose the absorption of the foreground material towards W49N into different velocity components in order to investigate whether the relative abundances vary among the velocity components, and, in addition, we re-analyse the absorption lines towards G10.6−0.4 in the same manner. Abundances, with respect to molecular hydrogen, in each velocity component are estimated using CH, which is found to correlate with H2 in the solar neighbourhood diffuse gas. The analysis points to a co-existence of the nitrogen hydrides in diffuse or translucent interstellar gas with a high molecular fraction. Towards both sources, we find that NH is always at least as abundant as both o-NH2 and o-NH3, in sharp contrast to previous results for dark clouds. We find relatively constant N(NH)/N(o-NH3) and N(o-NH2)/N(o-NH3) ratios with mean values of 3.2 and 1.9 towards W49N, and 5.4 and 2.2 towards G10.6−0.4, respectively. The mean abundance of o-NH3 is ~2 × 10-9 towards both sources. The nitrogen hydrides also show linear correlations with CN and HNC towards both sources, and looser correlations with CH. The upper limits on the NH+ abundance indicate column densities ≲2–14% ofN(NH), which is in contrast to the behaviour of the abundances of CH+ and OH+ relative to the values determined for the corresponding neutrals CH and OH. Surprisingly low values of the ammonia ortho-to-para ratio are found in both sources, ≈ 0.5–0.7 ± 0.1, in the strongest absorption components. This result cannot be explained by current models as we had expected to find a value of unity or higher.
Key words: astrochemistry / line: formation / ISM: abundances / ISM: molecules / submillimeter: ISM / molecular processes
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendices are only available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Nitrogen is among the six most abundant elements in the universe and, despite its fundamental role in the chemistry of molecules connected with life, the chemical network of nitrogen in the interstellar medium is still poorly understood due to severe difficulties to observe key molecules from the ground. Today about 55 molecules containing nitrogen have been discovered in interstellar space and a few more in circumstellar envelopes1. The major reservoir of nitrogen is believed to be in the form of atomic N and molecular N2. The latter is extremely difficult to observe since it has no permanent dipole moment (Sandford et al. 2001). In dense molecular clouds N2H+ is instead often used as a tracer of N2, which remained undetected until Knauth et al. (2004) reported far-ultraviolet observations towards HD 124314. The total abundance of nitrogen therefore still relies, to a high degree, on chemical modelling and observations of nitrogen-bearing species other than N2.
In order to constrain the nitrogen formation pathways, observations of nitrogen hydrides are crucial since they are at the root of the nitrogen chemical network, appearing in its first steps in chains of reactions that lead to other more complex species. The abundances of these species are thus key diagnostics for the nitrogen chemistry. The nitrogen hydrides are, however, also problematic to observe since their ground state rotational transitions lie at sub-mm wavelengths and are thus very difficult, or impossible, to reach from the ground. Key species, such as imidogen (NH) and amidogen (NH2), have therefore previously not been widely observed, and there is still no detection of the NH+ radical.
Although very few observations exist of NH and NH2 in interstellar space, they are well known in comets (e.g. Swings et al. 1941; Meier et al. 1998; Feldman et al. 1993), and have been observed in stellar photospheres (e.g. Schmitt 1969; Farmer & Norton 1989) via their electronic, vibration-rotation, and high rotational transitions. The first detection of interstellar NH was made by Meyer & Roth (1991) by optical absorption spectroscopy. Subsequent observations by Crawford & Williams (1997) and Weselak et al. (2009) have yielded several lines of sight in diffuse and translucent gas where column densities of NH, CH, CN, and H2 have been directly measured. The average value of the column density ratio in these diffuse and translucent sight-lines is N(NH)/N(H2) = 3 × 10-9.
Interstellar NH2 was first detected by van Dishoeck et al. (1993) in absorption towards Sgr B2 in three fine-structure components of the para-symmetry form of NH2, the NKa,Kc = 11,0 − 10,1 transition, with partially resolved hyperfine structure at frequencies 461 to 469 GHz. The Infrared Space Observatory (ISO) was later used to observe unresolved absorption lines of both ortho and para symmetry forms of NH2, as well as NH, towards this source through the use of the long-wavelength spectrometer (Cernicharo et al. 2000; Goicoechea et al. 2004; Polehampton et al. 2007).
In contrast to NH and NH2, ammonia (NH3) has been extensively observed for more than 40 years and was in fact the first polyatomic molecule to be identified in interstellar space (Cheung et al. 1968) by means of its J = K inversion transitions at cm wavelengths (K is the quantum number of the projection of total angular momentum J on the molecule’s symmetry axis). The ammonia molecule has, however, two symmetries, like NH2, which arise due to the possible orientations of the hydrogen spins and behave like two distinct species: ortho-NH3 (all H spins parallel, K = 3n where n is an integer ≥ 0) and para-NH3 (not all H spins parallel, K ≠ 3n). Important information about the ammonia formation pathways could be inferred from observations of both symmetries. Unfortunately, only the para form has relatively low-excitation transitions accessible from ground since the K = 0 ladder of energy levels has no inversion splitting and the JK = 33 inversion transitions’ lower energy level is 122 K above ground. Ortho inversion lines (K = 3n, n ≥ 1) can thus only be observed in relatively warm molecular gas. Only a few ammonia observations of the cold diffuse interstellar gas exist, using para inversion lines (Nash 1990; Tieftrunk et al. 1994; Liszt et al. 2006) which leaves the ammonia formation mechanism poorly constrained in diffuse gas. The (0, 0) ammonia ground state, with ortho symmetry, can only be studied by sub-mm rotational transitions. Observations of the fundamental rotational transition of ortho-NH3JK = 10–00 at 572 GHz, which has similar upper state energy as the inversion lines, but several orders of magnitudes higher critical densities, thus requires space telescopes. The Kuiper Airborne Observatory (Keene et al. 1983) performed the first observations of the JK = 10–00 transition using heterodyne receivers, and later on the Odin satellite continued such observations in a number of environments, for instance in photo-dissociation and star-forming regions (e.g. Larsson et al. 2003; Persson et al. 2009), circumstellar envelopes (Hasegawa et al. 2006), diffuse clouds in absorption towards Sgr B2 (Wirström et al. 2010), and in comets (Biver et al. 2007).
Observed transitions towards W49N and G10.6−0.4.
With the launch of the Herschel Space Observatory (Pilbratt et al. 2010) in May 2009, unique opportunities to perform observations of transitions between 157 and 625 μm (0.48−1.9 THz) became feasible with the Heterodyne Instrument for the Far-Infrared (HIFI; de Graauw et al. 2010) owing to its very high sensitivity and spectral resolution. This allowed, for the first time, searches for spectrally resolved, rotational transitions involving the ground states of NH+, NH, NH2, and NH3 with the same instrument. Several observations have already been reported. For instance, using Herschel/HIFI, Bacmann et al. (2010) found very high column densities of NH and ND in the cold envelope of the class 0 protostar IRAS 16293-2422 (2 × 1014 cm-2 and ~1.3 × 1014 cm-2, respectively). Hily-Blant et al. (2010) found NH:NH2:NH3 abundance ratios of ~5:1:300 towards the same source.
The PRISMAS2 key programme (PRobing InterStellar Molecules with Absorption line Studies) is targeting absorption lines in the line-of-sight towards eight bright sub-millimetre-wave continuum sources using Herschel/HIFI: G10.6−0.4 (W31C), W49N, W51, G34.3+0.1, DR21(OH), SgrA (+50 km s-1 cloud), G005.9-0.4 (W28A) and W33A. High-resolution absorption line spectroscopy is generally a very sensitive and model-independent method for measuring column densities of interstellar molecules, and a powerful tool to probe the diffuse interstellar gas clouds with no or little excitation.
The first results and analysis of absorption lines of nitrogen hydrides along the sight-line towards the massive star-forming region G10.6−0.4 (W31C) have already been presented in Persson et al. (2010, hereafter Paper I). Similar abundances with respect to the total amount of hydrogen NH = 2 N(H2) + N(H), were found for all three species: approximately 6 × 10-9, 3 × 10-9, and 3 × 10-9 for NH, NH2, and NH3, respectively. They were estimated across the whole line-of-sight and using the high temperature ortho-to-para limits of three and one for NH2 and NH3, respectively. NH+ was not detected at a 1σ rms level of 74 mK with a resolution of 1.1 MHz. The abundance patterns that we see in diffuse molecular gas are thus clearly very different from those in IRAS 16293-2422 and Sgr B2, where NH:NH2:NH3 ~ 1:10:100 and the fractional abundance of NH is a few times 10-9. The Sgr B2 results may, however, not be representative of cold dark clouds since this source is very complex and atypical.
The unexpectedly high NH abundance has been difficult to explain with chemical models and both the NH and NH2 production by purely gas-phase processes is inhibited by a lack of a sufficient source of N+. The models fail to simultaneously predict the absolute and relative abundances of the nitrogen hydrides. Typical steady state dark cloud models (n = 1 × 103–5 × 104 cm-3, T = 10–40 K, AV ≳ 10), predict an NH2 abundance of (1–10) × 10-8, an NH abundance 10 times lower, and an NH2/NH3 ratio of 0.3–1.5 for a wide range of assumptions (e.g. Langer & Graedel 1989; Millar et al. 1991), but these are not directly applicable to diffuse molecular gas. Examples of chemical models for diffuse cloud conditions are found in Figs. A.1 and A.2 in Paper I. These models were also unable to explain the observed abundances and ratios. Processes on dust grains have previously been proposed as a way to increase the NH production (Meyer & Roth 1991; Wagenblast et al. 1993). Such models, however, often predict up to 1000 times more NH3 than NH2 (Hasegawa & Herbst 1993, Paper I). The importance of grain surface chemistry in diffuse clouds is also not clear since water ice mantles have not been detected in diffuse gas, and strong (UV) radiation fields counteract molecular formation on grains. Grain surface production of NH is therefore still debated, and would, if true, change our understanding of surface chemistry in diffuse gas. On the other hand, if grains indeed were unimportant in diffuse gas nitrogen chemistry it would imply that either key gas-phase reactions must have been overlooked, or that the uncertainty of some reaction rates could make a difference. Both additional high-quality observations and chemical modelling are needed to solve this problem.
In this paper, we present new observations and analyses of absorption lines in the line-of-sight towards the high-mass star-forming region W49N, and, we also re-analyse the absorption towards G10.6−0.4 in more detail. W49N is one of the most luminous high-mass star-forming regions in the Galaxy (~107 L⊙) with a core that contains more than a dozen ultra-compact H II regions (Dreher et al. 1984; Dickel & Goss 1990; De Pree et al. 2000). It is located on the far side of the Galaxy at a distance of 11.4 kpc with Galactic coordinates l = 43.17° and b = 0.012°, in one of the most massive giant molecular clouds (~106 M⊙) in the Milky Way. The source velocity is about +8 km s-1 and the foreground gas along the line-of-sight is detected at vLSR ≈ 30−75 km s-1, revealing gas at two locations in the near and far side of the Sagittarius spiral arm around 40 and 60 km s-1 (Dame & Thaddeus 1985). The ultra-compact H II region G10.6−0.4 in the star-forming W31 complex is an extremely luminous sub-millimetre and infrared continuum source. The source is located within the so-called 30 km s-1 arm at a kinematic distance of 4.8 kpc (Fish et al. 2003). The gas associated directly with G10.6−0.4 is detected at a systemic source velocity of vLSR ≈ −1 km s-1, determined from OH maser emission observations, while the foreground gas is detected at vLSR ≈ 10−55 km s-1.
Section 2 summarises the observations and data reduction, and the results from our Herschel observations are found in Sect. 3. The hyperfine structure (hfs) components of the nitrogen hydrides are discussed in Sect. 4. In Sect. 5 we use three different methods to decompose the absorption lines along the sight-lines towards both sources in different velocity components, and estimate column densities, N, and relative abundances, X, in each component. We also compare the column densities of the nitrogen hydrides, both with each other to investigate possible correlations, and with other species tracing regions with both low and high molecular fractions. Section 6 presents our estimates of the ortho-to-para ratio (OPR) of NH3. We end this paper with a summary and outlook in Sect. 7. Note that the analysis of the background source emissions and absorptions is left for a future paper.
2. Observations and data reduction
All the reported observations are a part of the more extended PRISMAS programme towards G10.6−0.4 and W49N. The nitrogen observations, which took place between March 2 and April 18, 2010, are summarised in Table 1. All Herschel identification numbers (OBSID’s) are found in Table A.1. Note that NH NJ = 10–01 was observed together with CH2 at 946 GHz, and ortho-NH3JK = 20–10 was observed together with para-NH3JK = 21–11 (the absorptions from the source are 97 km s-1 apart). Before the launch of Herschel, no observations of these NH3 transitions, nor the NH+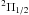 J = 3/2 ← 1/2 transition, had been performed. We do not, however, analyse the ortho-NH3JK = 20–10 transition in this paper since this line shows absorption only at the background source velocities.
J = 3/2 ← 1/2 transition, had been performed. We do not, however, analyse the ortho-NH3JK = 20–10 transition in this paper since this line shows absorption only at the background source velocities.
We used the dual beam switch mode and the wide band spectrometer (WBS) with a bandwidth of 4 × 1 GHz and an effective spectral resolution of 1.1 MHz. The corresponding velocity resolution is about 0.3 km s-1 at the highest frequencies and 0.6 km s-1 at 572 GHz. In addition, simultaneous observations were performed using the high resolution spectrometer (HRS) with an effective spectral resolution of 0.25 MHz (Δv ~ 0.1 km s-1) and a bandwidth of 240–340 MHz except for the 1214 and 1215 GHz lines which had an effective resolution of 0.5 MHz (Δv ~ 0.1 km s-1) and a bandwidth of 780 MHz in order to cover both lines in the same band. Note that the channel separation of the observations is 0.5 MHz in the WBS and 0.12 MHz in the HRS (0.24 MHz for the 1215 GHz line). Each line was observed with three different frequency settings of the local oscillator (LO) corresponding to a change of approximately 15 km s-1 to determine the sideband origin of the lines. During all observations two orthogonal polarisations were used.
The pointings were centred at α = 19h10m13  2, δ = 09° 06′ 12″ (J2000) for W49N, and α18h10m28
2, δ = 09° 06′ 12″ (J2000) for W49N, and α18h10m28  7, δ − 19° 55′ 5″ (J2000) for G10.6 − 0.4. The recommended values for half-power beam width of the telescope are
7, δ − 19° 55′ 5″ (J2000) for G10.6 − 0.4. The recommended values for half-power beam width of the telescope are 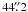 ,
, 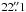 , and
, and 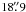 at 480, 960 and 1120 GHz, respectively. The reference beams were located within 3′ on either side of the source. The total calibration uncertainties are ≲ 9% for band 1 and ≲ 13% for band 5, including the sideband gain ratio uncertainty which is 3–4% for band 1b (ortho-NH3), and 4–6% for band 5a (para-NH3). All errors are added in quadrature. Detailed information about the HIFI calibration including beam efficiency, mixer sideband ratio, pointing, etc., can be found on the Herschel internet site3. The in-flight performance is described by Roelfsema et al. (2012). Since we are interested in absorption lines and their relative strength compared to the continuum in this paper, the forward efficiency of 96% and the main beam-efficiency of 64–76% (between 1120 and 480 GHz) do not affect our results and we have therefore used a
at 480, 960 and 1120 GHz, respectively. The reference beams were located within 3′ on either side of the source. The total calibration uncertainties are ≲ 9% for band 1 and ≲ 13% for band 5, including the sideband gain ratio uncertainty which is 3–4% for band 1b (ortho-NH3), and 4–6% for band 5a (para-NH3). All errors are added in quadrature. Detailed information about the HIFI calibration including beam efficiency, mixer sideband ratio, pointing, etc., can be found on the Herschel internet site3. The in-flight performance is described by Roelfsema et al. (2012). Since we are interested in absorption lines and their relative strength compared to the continuum in this paper, the forward efficiency of 96% and the main beam-efficiency of 64–76% (between 1120 and 480 GHz) do not affect our results and we have therefore used a 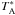 intensity scale throughout this paper.
intensity scale throughout this paper.
The data were processed using the standard Herschel Interactive Processing Environment (HIPE4, Ott 2010), version 5.1, up to level 2 which provides fully calibrated spectra. The data quality is excellent with very low intensity ripples in most cases, typically below a few percent of the double sideband continuum. For NH+ in both sources and both polarisations, and o-NH3 at 572 GHz in the vertical polarisation towards G10.6 − 0.4, we corrected the data from ripples using the fitHifiFringe tool in HIPE (in Paper I we only used one polarisation for these two transitions). The FITS files were then exported to the spectral line software package xs5 which was used in the subsequent data reduction.
The two polarisations are generally in agreement to better than 10%. The three LO-tunings are also in very good agreements without contamination from the image sideband with one exception in W49N around the o-NH3 at 572 GHz line (see Sect. 3.1.1). In all other spectra we averaged the three LO-tunings and both polarisations.
For the above line identification work we used the Cologne Database for Molecular Spectroscopy6 (CDMS, Müller et al. 2005), the Jet Propulsion Laboratory catalogue 7 (JPL, Pickett et al. 1998), and Frank Lovas’ Spectral Line Atlas of Interstellar Molecules8 (SLAIM). Laboratory measurements of NH transitions have been performed by e.g. Klaus et al. (1997) and Flores-Mijangos et al. (2004), and measurements of o-NH2 by e.g. Müller et al. (1999). A review on ammonia is found in Ho & Townes (1983), and an investigation of the hyperfine structure components of ortho-NH3 at 572 GHz was recently performed by Cazzoli et al. (2009). NH+ measurements have been made by Verhoeve et al. (1986) and Hübers et al. (2009).
3. Observational results
Figures 1 and G.1 show the averaged double sideband WBS spectra of the transitions listed in Table 1 towards W49N and G10.6 − 0.4, respectively (special treatment of o-NH3 10–00 in W49N is found in Sect. 3.1.1). All detected species show very similar absorption patterns over a wide range of velocities, although W49N has fewer absorbing velocity components in the line-of-sight. No detections of NH+ have been found in any of the two sources.
The resulting noise and single sideband (SSB) continuum levels, for each transition, are found in Table 1. Note that since HIFI uses double side band (DSB) receivers, the observed continuum has to be divided by two to obtain the SSB continuum. The sideband gain ratio is assumed to be unity throughout this paper. This has proven to be a good assumption based on PRISMAS observations of saturated absorption lines like HF that establish the true zero levels (Neufeld et al. 2010b).
3.1. Background source emission
Even though we only analyse the absorption lines in the foreground clouds in this paper we still have to take the source emission into account in the analysis. Several spectra show broad emission features from the background sources which extend far into the velocity range pertaining to the line-of-sight clouds.
 |
Fig. 1 Nitrogen hydrides towards W49N: double sideband WBS spectra of NH, ortho-NH2, ortho- and para-NH3, and NH+ over the LSR velocity range –50 to 85 km s-1. Quantum numbers are found in Table 1. Note that we only analyse the absorption in the velocity range 30 − 75 km s-1 in this paper and leave the source absorption and emission for a future paper. |
Ammonia in particular shows strong emission at the background source velocities with self-absorption around +13 and 0 km s-1 for W49N and G10.6 − 0.4, respectively. A large part of the NH 974 GHz emission at the source velocities in both sources is most likely not from NH, but from HCN J = 11–10 at 974.487 GHz, only 9 MHz above the NH line corresponding to 2.5 km s-1. The PRISMAS observations of these sources have detected three additional HCN emission lines: J = 6–5 at 532 GHz, J = 7–6 at 620 GHz, and J = 10–9 at 886 GHz which strengthens our identification. In addition, we detect no NH emission in the 946 GHz transition which is a further confirmation that the emission is due to another species. HCN in foreground gas is unlikely to produce measurable absorption in the J = 11–10 transition because the excitation energy of the lower state, E10/k = 234 K, is much too high to be populated at the density and temperature of diffuse or translucent gas.
In the analysis performed in Sect. 5 using three different methods, we have removed the broad emission lines that overlap with the absorption in the line-of-sight by means of Gaussian fits.
3.1.1. Emission line contamination
In W49N, close to the o-NH3 line at 572 GHz, an emission line from the lower sideband, identified as the JKa,Kc = 166,10–165,11 SO2 line, moves across the ammonia absorption lines in the different LO-tunings. Thus for the o-NH3 572 GHz transition in W49N we were only able to use the A and C LO-settings in Table A.1, which also had to be cut to remove the parts contaminated by the SO2 line.
The o-NH2 absorption towards W49N is contaminated by a an emission line in the same sideband from the source. We identify the emission line as a blend of three unresolved hfs components of NO 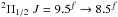 , F = 10.5−9.5, 9.5–8.5, and 8.5–9.5, at 952.464201 GHz. The NO emission line is removed from the o-NH2 absorption (described in Sect. B), and in all following figures in this paper we show o-NH2 in W49N with removed NO emission. The NO identification is strengthened by the PRISMAS observations of three additional NO lines towards W49N shown in Fig. B.2. No emission of NO is found towards G10.6 − 0.4.
, F = 10.5−9.5, 9.5–8.5, and 8.5–9.5, at 952.464201 GHz. The NO emission line is removed from the o-NH2 absorption (described in Sect. B), and in all following figures in this paper we show o-NH2 in W49N with removed NO emission. The NO identification is strengthened by the PRISMAS observations of three additional NO lines towards W49N shown in Fig. B.2. No emission of NO is found towards G10.6 − 0.4.
 |
Fig. 2 W31C: o-14NH3 and o-15NH3. Both isotopologues show emission from the source. Absorption in the line-of-sight is only seen in the o-14NH3 spectra. The emission line at vLSR ≈ 41 km s-1 in the o-15NH3 spectra, is an SO2 line from the upper sideband. |
3.1.2. The 15NH3 isotopologue: only in G10.6−0.4
Since our observations also covered the frequency of o-15NH3JK = 10–00 at 572.113 GHz, we have checked the averaged spectra for emission and/or absorption features of this isotopologue. In Figs. 2 and G.2 we show a 5σ emission feature in G10.6 − 0.4 with an amplitude of 40 mK and a line-width of about 4 km s-1, which we identify as o-15NH3 10–00, giving a source velocity of ~–4 km s-1. Checking the possibility of absorption lines of o-15NH3 in the line-of-sight towards G10.6 − 0.4, we note that there seems to be an absorption feature corresponding to the strongest velocity components of o-14NH3 at ~ 27 − 32 km s-1. This feature is, however, probably not a real detection since it would otherwise imply that 14N/15N ~ 20. This is about 20 times lower than the 14N/15N ratio in the local ISM which is about ~450 (Wilson & Rood 1994), or 441 ± 5 in the Solar nebula (Marty et al. 2011). Odin observations of absorption towards Sgr B2 show 14NH3/15NH3 > 600 (Wirström et al. 2010). Lower ratios have been found, for instance, in low mass cores, 334 ± 50 (Lis et al. 2010), and on Earth, ~270. Adande & Ziurys (2011) find values of ~100–350 using CN and HNC in ten dense molecular clouds located at various galactic distances from the Galactic Centre, but this is still several times higher than inferred from a possible o-15NH3 absorption. The 14N/15N ratio is also difficult to determine and the results using cyanides may differ from the ratio inferred from other species such as N2H+, and may not reflect the true 14N/15N abundance ratio. More observations are needed to lower the noise in order to obtain a real detection of 15NH3 and to determine the true 14N/15N ratio towards G10.6 − 0.4.
In W49N, no o-15NH3 detection is made due to blending SO2 lines from the upper sideband which are both stronger and broader than in G10.6−0.4. In addition, the o-14NH3 emission is more than two times weaker than in G10.6 − 0.4, and the spectrum has a three times higher noise level which does not allow a detection of o-15NH3 emission from the source.
 |
Fig. 3 NH hfs components: normalised WBS spectrum towards W49N. Also shown are Gaussian fits with a line width of 1 km s-1 of the NH 974 GHz hfs components in the +39 km s-1 velocity component. |
 |
Fig. 4 Ortho-NH2 hfs components: normalised WBS spectrum towards W49N. Also shown are Gaussian fits with a line width of 1 km s-1 of the o-NH2 953 GHz hfs components in the +39 km s-1 velocity component. |
4. Hyperfine structure components
Both NH and NH2 have numerous hyperfine structure (hfs) components which require a high resolution spectrometer, such as HIFI, to be spectrally resolved. Tables C.1–C.3 list the hfs components of the NH 974 and 946 GHz, and the o-NH2 953 GHz transitions which have 21, 9, and 30 hfs components, respectively. The observed NH 974 GHz and o-NH2 transitions in the +39 km s-1 velocity component towards W49N are shown in Figs. 3 and 4 together with models of respective transition, including hfs components, using Gaussian opacity profiles and a line width of 1 km s-1. Here, the intensities have been normalised to the continuum in single sideband as TA/TC-1 assuming a sideband gain ratio of unity where TA is the observed intensity and TC is the SSB continuum as measured in line-free regions in the spectra. The large number of hfs components, in addition to many different, overlapping, velocity components in the line-of-sight, complicates the analysis substantially. In particular, the o-NH2 hfs components in the line-of-sight absorption overlap with the source emission/absorption, thus requiring a source model in the analysis.
The much simpler hyperfine structure of the ortho- and para-NH3 ground state rotational transitions has never been resolved in space before Herschel. The Odin satellite was able to observe the 572 GHz ammonia transition, but the velocity resolution of about 0.5 km s-1 was not enough to spectrally resolve the hfs components even though the asymmetric line shapes hinted the hfs components (e.g. Liseau et al. 2003). Figure 5 shows an example of our observations of the 572 GHz o-NH3 transition in the +39 km s-1 absorption velocity component towards W49N with the HRS and a velocity resolution of 0.13 km s-1. Three hfs components are seen at 38.4, 39.4 and 40.0 km s-1 although the line width of 1.0 km s-1 prevents a detailed check of the relative intensities. In the Gaussian fit we therefore use 0.2, 1 and 0.6 as relative intensities, with corresponding relative offsets at –1.05, 0.0, and 0.52 km s-1 found by Cazzoli et al. (2009) (Table C.4). The positions and relative intensities of the hfs components and the fitted opacity profiles are also shown in Fig. 5. The six hfs components in the para-NH3 line at 1215 GHz are even more closely spaced and not resolved (Table C.5).
 |
Fig. 5 Ortho-NH3 hfs components: normalised high resolution spectra (Δv = 0.13 km s-1) towards W49N in the +39 km s-1 velocity component. Three hfs components are seen at 38.4, 39.4 and 40.0 km s-1. Also shown are the positions and relative intensities of the hfs components and their fitted opacity profiles with a line width of 1.0 km s-1. |
The WBS ammonia observations do not spectrally resolve the NH3 hfs components (Δv = 0.6 km s-1 at 572 GHz and Δv = 0.3 km s-1 at 1215 GHz), but we still take the hfs components into account in the following NH3 modelling since they produce a slightly asymmetric line shape and a systematic line broadening.
5. Analysis: velocity decomposition, column densities, and abundances
In Paper I we estimated the abundances towards G10.6 − 0.4 simply by evaluating the integrated opacity of each line over the velocity range 11–54 km s-1. This approach gave a first estimate of the average abundance in the full line-of-sight, but did not take into account possible abundance variations in the different velocity components. In addition, no source model was included, and thus the blend of the NH and o-NH2 hfs components from the foreground absorptions with the source absorption was neglected.
In this paper we use three different approaches to decompose the absorption into separate velocity components, and to obtain column densities and abundances in each component. Each method has its own strengths and weaknesses, and differences in the results can be considered an estimate of the errors of the methods. If all three methods point to the same result, it will be considered as robust. We note, however, that the uncertainties of the data are higher towards W49N than for G10.6 − 0.4, since we have removed a SO2 line from the upper sideband in the ortho-NH3 absorption, and an NO line in the o-NH2 absorption.
In this work we also only estimate N and X for the ortho-symmetries of NH2 and NH3 since our own measurements of the ammonia OPR in Sect. 6 do not point to the high temperature limit, but instead suggest an OPR lower than unity, which cannot be straightforwardly explained. If this unexpected low ammonia OPR is true, then the processes that affect the ammonia OPR perhaps also could affect the OPR of NH2 in diffuse clouds about which we have no information. And since we want to compare relative abundances, we choose to focus on the ortho-symmetries since both are observed in NH2 and NH3, and also since the o-NH3 observations have higher S/N than the p-NH3.
To obtain integrated opacities of each transition, in each velocity component, the first method uses Gaussian fitting (Sect. 5.2), while the second one uses the observed spectra of ortho-NH3 and CH as templates for other species (Sect. 5.3). Both methods calculate the opacity as . The derived integrated opacities are then used to estimate column densities by means of the non-LTE (Local Thermodynamic Equilibrium) RADEX code (Sect. 5.1). As a third method, we have used XCLASS (Sect. 5.4) which, in contrast to RADEX, assumes fixed excitation temperatures, to obtain column densities in each velocity component directly.
In order to be able to use our results as comparisons with chemical models, we need to derive the abundance of the species with respect to the total amount of gas. The difficulty is to obtain reliable estimates of N(H) and/or N(H2). In Paper I, we compared the nitrogen hydrides column densities to the total amount of hydrogen in the line-of-sight, NH = N(H)+2N(H2). This can not be done in the present work since the neutral hydrogen absorption shows too broad and overlapping absorption components over much larger velocity ranges as compared to the nitrogen hydrides. In order to estimate the amount of molecular hydrogen in each (narrow) velocity component, we therefore consider the comparison with CH (Gerin et al. 2010b) as an abundance determination. This can be made using the CH/H2 correlation (CH/H2 = 3.5 × 10-8) observed by Sheffer et al. (2008) in the solar neighbourhood diffuse medium. This correlation is assumed to be valid in regions which are dominated by ultraviolet radiation where N(CH) ≲ 2 × 1014 cm-2. In this way we can use our own PRISMAS observations of CH and measure abundance ratios obtained with the same instrument.
The physical properties of the bulk of the absorbing gas in our sight-lines are (Gerin et al. 2010b), according to the definitions of Snow & McCall (2006), a mixture of diffuse (NH ≲ 500 cm-3 and Av ≲ 1) and translucent gas (500 ≲ NH ≲ 5000 cm-3 and a shielding 1 ≲ Av ≲ 5). And since the comparison later in this section of the nitrogen hydrides with other species tracing both high and low density gas, points to an existence in the denser parts of the gas, molecular hydrogen is most likely the dominant form of hydrogen in these components.
Assuming that the nitrogen hydrides co-exist with HF and H2O in the line-of-sight material we use the fact that the saturated absorptions of the latter two species reach the zero level, for a sideband ratio of unity, to support our assumption that the foreground absorbing material completely covers the continuum within the beam. Comparison spectra of o-NH3 and o-H2O are shown in Figs. 8, 9, and with HF, ortho- and para-H2O in Figs. G.9, G.10.
5.1. RADEX
Observations of absorption lines can provide accurate determinations of molecular column densities if the observed transitions trace all of the populated states. In the case of NH3 we observe two transitions of the ortho (A-symmetry) form, arising in the JK = 00 and 10 states, and one transition of the para (E-symmetry) form arising in the lower 11 rotation-inversion level. Although the upper 11 inversion level is less metastable than the lower one, it may still be significantly populated. The metastable 22 para levels and 33 ortho levels may also have significant populations in diffuse molecular clouds at low density, nH ≲ 104 cm-3, owing to infrared pumping and formation. Because we are directly sensitive to three lower states and lack direct information about the excitation temperatures of the observed transitions, we use the non-equilibrium RADEX code (van der Tak et al. 2007) to relate the total column density of ammonia to the observed integrated optical depths. The models provide integrated opacities of both observed and unobserved excited levels and quantify possible effects of stimulated emission, chemistry, and electron collisions. Results for one reference model are summarised in Table 2, where conversion factors for all nitrogen hydrides and comparison species are listed in terms of the total column density N(x) of molecule x that is needed to achieve an integrated optical depth ∫τdv = 1.0 km s-1 in the specified transition. In this model we treat ortho- and para-symmetries separately. The integrated optical depth is a sum over all hyperfine structure in the transition.
We have assumed diffuse molecular cloud conditions with a kinetic temperature of 30 K and a density of molecular hydrogen n(H2) = 500 cm-3, which corresponds to nH ≳ 103 cm-3. The resulting conversion factors for the rotational ground state transitions are not very sensitive to density, temperature or electron collisions. The critical densities of the fundamental rotational transitions of NH, NH2, and NH3 are high, ncrit ~ 108 cm-3. This means the upper energy levels of these transitions must be excited almost entirely radiatively at the low densities in diffuse gas. We find, however, that electron collisions can be responsible for excitation temperatures of ~4 K in the cm-wave inversion transitions rather than ≲ 3 K that would be found in conventional excitation analyses at low densities, n(H2) ≲ 103 cm-3. Where collision rates are unknown, we have made guesses scaled in proportion to radiative line strengths. The background radiation field includes both the 2.725 K cosmic microwave background and a model of the Galactic infrared radiation in the solar neighborhood. The resulting excitation temperatures of the observed sub-millimetre transitions are typically 3–4 K, which are small enough compared to hν/k that no correction for emission is required. Note that the lower state of the 572 GHz transition contains 95% of the ortho molecules while the lower state of the 1215.2 GHz transition occupies only 43% of the para molecule.
5.2. Method I: Multi-Gaussian fit of the nitrogen hydrides simultaneously
We have modelled the observed spectra of NH, o-NH2, and o-NH3 using Gaussian optical depth profiles. These were generated for each hfs component of each species in separate velocity intervals, and were made to fit the observations under the condition that the LSR velocity and width in each velocity component must be the same for all molecules. This can be made assuming that all species co-exist in the same velocity ranges and therefore show absorption at the same velocities. This assumption is supported by the striking similarities of the strongest NH, o-NH2 and o-NH3 absorptions, despite the complicated hyperfine structure patterns of NH and o-NH2, shown in normalised comparison spectra in Fig. G.9. We note that a good fit therefore is a good indicator if this assumption is valid.
The observed line profiles are thus modelled by Gaussian components of both the hfs components and all velocity components according to ![\begin{eqnarray} \frac{T_\mathrm{A}}{T_\mathrm{C}} &=& \exp\,\Biggl[-\sum_{i=1}^{N_{v}} \sum_{j=1}^{N_\mathrm{hfs}} \tau_\mathrm{hfs}(j) \, \tau_0(i) \nonumber\\ &&\quad\times \exp[-4 \ln(2)\,\biggl[\frac{v-v_\mathrm{0}(i)-v_\mathrm{hfs}(j)} {\Delta v} \biggr]^2 \Biggl], \end{eqnarray}](/articles/aa/full_html/2012/07/aa18686-11/aa18686-11-eq148.png) (1)where Nv is the number of the modelled velocity components (same for all species), Nhfs is the number of hfs components (which differs between species), τhfs is the theoretical relative line strength of each hfs component, τ0 is the opacity of the strongest hfs component in each velocity component, v0 is the LSR velocity of each velocity component, vhfs is the relative velocity offset of the hfs components with respect to the strongest, and Δv is the FWHM (full width of half maximum). We assume that τhfs = Aul × gu/(Aul(main) × gu(main)) for the hfs components of NH and o-NH2, since the many overlapping velocity components prevent a check of the relative intensities of these components.
(1)where Nv is the number of the modelled velocity components (same for all species), Nhfs is the number of hfs components (which differs between species), τhfs is the theoretical relative line strength of each hfs component, τ0 is the opacity of the strongest hfs component in each velocity component, v0 is the LSR velocity of each velocity component, vhfs is the relative velocity offset of the hfs components with respect to the strongest, and Δv is the FWHM (full width of half maximum). We assume that τhfs = Aul × gu/(Aul(main) × gu(main)) for the hfs components of NH and o-NH2, since the many overlapping velocity components prevent a check of the relative intensities of these components.
We have used both ortho- and para-NH3, which are not significantly complicated by hfs splitting, to determine the minimum number of velocity components needed, and also to set-up reasonable initial guesses for the line properties necessary for the fitting procedure to converge at all. The fitting was done for each velocity component at a time in a loop until all fits had converged. The fits are most likely not unique. Provided that the fits are good and that we use the same velocity parameters for all species, this is, however, not considered important as we do not ascribe any physical meaning to the Gaussian components.
The results from Method I are peak opacities, line widths and centre velocities for each velocity component and species. The integrated opacity in each velocity component was assumed to be well represented by ∫τ dv = 1.06 Δv τpeak. The non-detections of NH+ are used to put upper limits on its integrated opacities (3σ). We then used the conversion factors in Table 2 to calculate the column densities tabulated in Table 3. Typical errors in the G10.6 − 0.4 resulting column densities for NH, o-NH2 and o-NH3 are between 7 and 15%. In the vLSR = 45 km s-1 component, the errors are 22% for all three species, and 23% in the vLSR = 39 km s-1 component for NH. The errors in W49N varies between 8 to 11% for all three species, except in the 33 km s-1 component where the uncertainties are 37, 26 and 31% for NH, o-NH2 and o-NH3, respectively. The errors include calibration uncertainties (see Sect. 6) as well as uncertainties from the fitting procedure.
In addition to the nitrogen hydrides, we also modelled the PRISMAS CH 532 GHz transition, and the CN 113 GHz and HNC 91 GHz transitions observed with the IRAM 30 m antenna (Godard et al. 2010). These species were not included in the fitting procedure described above. Instead we have used the resulting velocity parameters from the fits of the nitrogen hydrides (vLSR and line widths) since we want to investigate possible correlations and make abundance determinations only in the same parts of velocity space as the nitrogen hydrides. The resulting CH column densities are found in Table 3, and the CN and HNC column densities in Table F.1.
Figures 6 and 7 show the fits and residuals of the nitrogen hydrides together with CH. The resulting fits are well reproducing the observations for all species except for CH suggesting that CH exist in a more widely spread gas than the nitrogen hydrides.
The CH column densities are then used together with the relation [CH]/[H2] = 3.5 × 10-8 (Sheffer et al. 2008) to estimate the abundances listed in Table 3.
5.3. Method II: ortho-NH3 and CH as templates for other species
This method directly compares the opacity line profile of the non-saturated o-NH3 line at 572 GHz with the line profiles of NH and o-NH2, convolved with respective hyperfine structure. This assumes that all species co-exist in the same velocity ranges, and that the opacity ratios depend only on their column density ratios, which may vary from one velocity component to another. No opacity profile is assumed for a given absorbing cloud so, unlike what is done by methods I and III, we do not attempt to decompose the velocity structure of the template line into a number of Gaussian curves. We perform, instead, simple cuts of the template profile into large velocity bins.
The hfs of the o-NH3 line is not resolved in the WBS data and introduces only a small broadening of the lines that is dealt with by smoothing the NH and o-NH2 spectra. Before comparing the opacity profiles, we mask out those portions of the spectra where a simple scaling between template and target is not expected, such as the velocity range associated to the background sources, and remove the emission line wing by Gaussian fitting. We note that the removal of the line wing introduces very large uncertainties towards W49N around 33 km s-1 where a weak absorption component is visible. This method therefore disregards the results in this velocity component.
The velocity bins into which the o-NH3 opacity profile is split are chosen to be significantly larger than the original resolution, but narrow enough to separate the most prominent velocity features (typically a few km s-1, see Table D.1). Each velocity bin of the o-NH3 template is then convolved, channel by channel, with the NH and o-NH2 hfs components. We thus obtain an intermediate opacity model of how the NH and o-NH2 spectra would appear if absorption were limited to the selected velocity bin. The observed o-NH3 opacity is then fitted by the IDL Least Squares Fitting routine MPFIT (Markwardt 2009) with a linear combination of the intermediate models. The output of the fits consists of the opacity ratios, between the o-NH3 and the modelled NH and o-NH2 spectra, in the various velocity bins.
To obtain column densities in each velocity bin, we sum the opacities of all channels of the template transition, and then apply the RADEX conversion factors from Table 2. The resulting abundance ratios are finally used to obtain column densities of the other species. Typical errors (including both calibration and fitting uncertainties) are 5–15% except for the 43.5–50 km s-1 velocity bin in G10.6 − 0.4 and the 50–57 km s-1 velocity bin in W49N which both have an uncertainty of approximately 25%.
The main advantage of this method is that a small number of free parameters is needed to obtain a reasonable fit since it uses, as much as possible, the information carried by the template spectrum. The model also avoids the problem of non-uniqueness of Gaussian decompositions of the absorption profiles and allows a straightforward comparison of column densities evaluated for exactly the same velocity intervals. On the other hand, such rigidity in the definition of the velocity bins does not allow us to reliably retrieve the column density ratios if the absorption comes from very different gas volumes resulting in significant velocity shifts of the absorption features between the two species. We note that the fit quality, estimated with ∫ | residuals | × dv /∫τ × dv, is a good indicator of such cases. Note also that residual baseline structures, like those produced by standing waves or by an imperfect removal of ammonia emission line wings, may introduce artificial discrepancies between the template spectra and the modelled species.
 |
Fig. 6 W49N: fits of Method I and the SSB normalised spectra of the nitrogen hydrides and CH. The black lines are the observations, and the coloured lines are the model fits. In the bottom the residuals are plotted on top of each other with respective colour. The three transitions used in Method I to determine the vLSR and line widths of the velocity components are marked in bold. |
 |
Fig. 7 G10.6 − 0.4: fits of Method I and the SSB normalised spectra of the nitrogen hydrides and CH. Same notation as in Fig. 6. |
In addition to the above modelling, we use the o-NH3 as a template for CN and HNC (Godard et al. 2010), and also use the deconvolved CH spectrum at 532.724 GHz (Gerin et al. 2010b) as a template to model all three nitrogen hydrides, in order to obtain an estimate of the abundance with respect to molecular hydrogen.
The resulting column densities and relative abundances in different velocity bins are given in Table D.1, except for the CN and HNC results which are found in Table F.2.
The model fits compared to the normalised spectra in both sources are shown in Figs. G.3–G.6. The fit qualities of the comparisons between the o-NH3, NH and o-NH2 are excellent, except in the narrow and deep +39 km s-1 component towards W49N which was very difficult to model. The modelling of the nitrogen hydrides using CH as a template show on the other hand rather low fit qualities, suggesting that the assumption that the nitrogen hydrides and CH only come from the same gas is less justified, also supported by Method I.
5.4. Method III: XCLASS
Finally, we have generated synthetic spectra separately for NH, o-NH2, o-NH3, CH, CN, and HNC using the software XCLASS9 (created by Schilke, and described by Comito et al. 2005, and references therein) by considering for each species all hfs components and velocity components and the assumption of a fixed excitation temperature. The synthetic spectra generated with XCLASS were fitted to the observed spectra using MAGIX, an iterating engine that allows automatic minimization to constrain model parameters. XCLASS accesses the CDMS and JPL molecular databases, and models each molecule with the following free parameters: source size, temperature, column density, line width and velocity offset relative to the systemic velocity of the source, and derives the column density corresponding to the different velocity components detected in absorption and emission in the observed spectra. The source size refers to the relative size of the absorbing cloud vs. the continuum source, which is assumed to be fully covered within the beam. We have assumed a Gaussian profile for each hfs component, and an excitation temperature of 4 K. Since Method III explicitly assumes a fixed excitation temperature for the estimate of column densities, it is significantly different from Methods I and II.
Figures G.7 and G.8 show the model fits together with the observed SSB normalised spectra. Resulting column densities and abundance ratios of the nitrogen hydrides and CH are found in Table E.1, and the CN and HNC column densities in Table F.1.
5.5. Comparison of results
The results from all three methods agree very well, especially considering that the velocity bins used are not the same.
The total N(CH) from all methods are lower than found by Gerin et al. (2010b), which is expected since we only use parts of the CH absorptions. Comparisons of CH in different velocity bins give much more similar results in both sources. Since we use CH as a tracer of H2, we also compare our estimate of N(H2) with Nyman & Millar (1989) towards W49N: for the +39 km s-1 component they suggest N(H2) = 3 × 1021 cm-2 and they also quote N(13CO) = 7–30 × 1015 cm-2 which gives N(H2) = 7–30 × 1021 cm-2 using a standard conversion factor of 10-6. They also suggest column densities towards W49N between 50–70 km s-1: N(H2) = 5 × 1021 cm-2 and N(H2) = 5.5–23 × 1021 cm-2 from 13CO observations. All these suggestions for N(H2) are several times higher than inferred from our CH observations. This is, however, not surprising because the 13CO conversion factor is rather uncertain at such low column densities. Plume et al. (2004) also obtain higher N(H2) than we do towards W49N. The total amount of N(H2) in the sight-lines towards our sources, can also be compared with estimates from the K-band extinction (Marshall et al. 2006): N(H2) = 1.3 × 1022 and 7.5 × 1021 cm-2 towards W49N and G10.6−0.4, respectively.
The resulting NH mean abundances of all three methods in all velocity components are 5.5 × 10-9 and 1.1 × 10-8 in W49N and G10.6−0.4, respectively. This can be compared to the average N(NH)/N(H2) value of 3 × 10-9 in diffuse and translucent sight-lines found by Weselak et al. (2009). The mean values of o-NH2 are 3.1 × 10-9 and 4.5 × 10-9 in W49N and G10.6 − 0.4, respectively, and 1.5 × 10-9 and 1.9 × 10-9 for o-NH3.
Our upper limits on the NH+ abundances, relative to molecular hydrogen, are similar in both sources with mean value N(NH+)/N(H2) ≲ 4 × 10-10. This is orders of magnitudes lower than previous findings from ultraviolet observations towards ρ Oph (Snow 1979; de Almeida & Singh 1982), but still much higher than the predictions from the chemical models presented in Paper I: approximately 10-13–10-14. The upper limits of the NH+ abundance compared to NH are ≲ 2–14% in the different velocity components (except in the uncertain velocity feature around +33 km s-1 in W49N), with a mean ratio of ≲ 6%. This is in contrast to the behaviour of CH+ and marginally with that of OH+(Wyrowski et al. 2010; Gerin et al. 2010a) with respect to the corresponding neutrals. The CH+ radical reaches comparable column densities to those of CH (e.g. Crane et al. 1995), and N(OH+) is a factor 30 below N(OH) in the visible data (Krełowski et al. 2010).
Since our different approaches to deconvolve the velocity components for the observed species agree well, we estimate that the uncertainties in our derived absolute column densities are ≲ 20–50%. The column densities for CH have larger uncertainties, but we estimate that the absolute N(CH) results are correct within a factor of approximately two. Furthermore, the scatter in the CH to H2 relationship is estimated by Sheffer et al. (2008) to a factor of 1.6. In summary, we believe that the abundance determinations from CH are correct within a factor of a few. The abundance ratios of the nitrogen hydrides, relative to each other, are on the other hand more accurately determined.
The results of all three methods confirm our conclusion of the analysis of G10.6 − 0.4 in Paper I that NH is more abundant than NH2 and NH3 by a factor of approximately 1.5–3.5, assuming the high temperature ortho-to-para limits of three and one, respectively. Note that the mean abundances of o-NH3 are similar towards both sources, ~2 × 10-9, in contrast to o-NH2, and, in particular NH, which have higher mean abundances towards G10.6 − 0.4 than towards W49N.
5.6. Comparison and correlations of species
Figures 8 and 9 show o-NH3 and five SSB normalised comparison spectra, and in Figs. G.9, G.10 we show additional comparisons of the nitrogen hydrides with the deconvolved CH absorption, the HI 21 cm line, H2O+, OH+, HNC, CN, ortho- and para-H2O, HF, and HCO+.
The CH spectra show absorption over a much wider range of velocities in both sources than the nitrogen hydrides. Ammonia largely follows the CH absorptions, but there are also large differences in some parts of the spectra where there is no or very little absorption of NH3, while CH shows a much broader and stronger absorption, for instance at 35–38, 41–55 and 65–70 km s-1 towards W49N. Ammonia seems to trace CH slightly better towards G10.6 − 0.4 than W49N. This comparison suggests that CH exists in both relatively low and high density gas, while the nitrogen hydrides only exist in the parts of the interstellar gas with a relatively high density.
These differences are even more pronounced when comparing with neutral hydrogen as observed by the VLA λ21 cm absorption by Fish et al. (2003), which shows absorption over a very wide range of velocities with a resolution of 2.5 km s-1. The much more extended velocity space coverage of the HI absorption is expected since not all foreground clouds have molecular gas.
 |
Fig. 8 Line-of-sight absorptions towards W49N: normalised (SSB) spectra of ortho-ammonia and species tracing both high and low molecular fractions. Strong similarities are seen between ammonia, CN, HNC and water, but not with H2O+ and HI tracing the atomic diffuse gas. |
The ammonia absorption also follow similar trends as HCO+J = 1 ← 0 (Godard et al. 2010), and H2O, which is known to trace clouds of high molecular fraction (Neufeld et al. 2010b; Sonnentrucker et al. 2010). HCO+ and H2O seem to have a rather constant abundance ratio in these sight-lines, in contrast to their abundances with respect to ammonia. The comparison of ammonia to H2O+ and OH+, which mostly reside in lower density gas containing considerable amounts of atomic hydrogen (Gerin et al. 2010a; Neufeld et al. 2010a), shows no similarities.
When we compare ammonia with CN and HNC we find very similar absorption patterns. The CN J = 1 ← 0 F = 1/2–3/2, 1/2–1/2 single hyperfine component and the HNC J = 1 ← 0 line were observed with the IRAM 30 m antenna (Godard et al. 2010). Note, that HNC has three hfs components that, however, lie very close in velocities (0.2 and 0.5 km s-1), which mostly leads to a broadening of the absorption features. These species mainly reside in denser gas than CH, and both are closely connected to the NH and NH2 chemistry (e.g. Nejad et al. 1990; Liszt & Lucas 2001).
5.6.1. Column density correlations
In order to quantitatively examine abundance correlations of the nitrogen hydrides, CH, HNC and CN, we show column density plots in Figs. 10–11. We have here plotted the results from Method I. The parameters of the linear least square fits to the data are found in the figures in addition to the correlation coefficient R. In the appendix we also show column density plots with all three methods (Fig. H.1).
Column density plots of the nitrogen hydrides are shown on the left hand side in Fig. 10. We note that the scatter is larger for N(NH) vs. N(o-NH3) than compared to N(o-NH2) vs. N(o-NH3) which show a rather tight correlation. This may indicate that NH does not entirely exist in the same gas as o-NH2 and o-NH3. There is also a possibility that the NH and o-NH3 correlation may only be valid for N(o-NH3) ≲ 5 × 1012 cm-2. The N(NH) towards G10.6 − 0.4 appear to increase up to a maximum of ~3 × 1013 cm-2. Also N(o-NH2) show a slight tendency of this behaviour towards G10.6 − 0.4 with a maximum of ~1.2 × 1013 cm-2. This possible “chemical saturation” corresponds to a few AV (estimated from our CH measurements and NH ~ 1.7 × 1021 cm-2 mag-1 × AV). This may be explained by a more efficient ammonia production at higher column densities, or that NH, and o-NH2, are somehow consumed in the ammonia formation.
 |
Fig. 10 Column density comparison plots. On the left hand side: NH, o-NH2 and o-NH3. On the right hand side: nitrogen hydrides vs. CH. The blue lines show linear least square fits to all data points towards both sources. The correlation coefficients and the linear fit equations are given in respective figure. |
 |
Fig. 11 Column density comparison plots. On the left hand side we show comparisons of the nitrogen hydrides with CN, and on the right hand side comparisons with HNC. Notation as in Fig. 10. |
On the right hand side in Fig. 10 we show column density plots of the nitrogen hydrides vs. CH. The spread of the data points reflects the difficulty of finding a velocity structure common to hydrides and CH.
In Fig. 11 we show column density plots of the nitrogen hydrides vs. CN on the left and vs. HNC on the right. All three nitrogen hydrides show linear correlations with both CN and HNC. In dark cloud chemistry, CN and HNC are closely related to NH and NH2 through the reactions of C + NH2 → HNC + H, N + CH → CN + H, and C + NH → CN + H (Nejad et al. 1990). Also Weselak et al. (2009) found a slightly better correlation between NH and CN than compared to CH, and no correlations with species such as CH+.
6. Ortho-to-para ratio of NH3
There are two ways to produce molecules in interstellar space: in the gas-phase or on grain surfaces. If ammonia is formed in the gas-phase, by highly exoergic processes, the ammonia ortho-to-para ratio has been expected to be very close to the statistical equilibrium value of 1.0 (the spin statistical value is 4–2 for ortho-para, but the number of para states is on the other hand almost a factor of two larger). If ammonia is formed at temperatures lower than 40 K on cold dust grains, and then desorbed when the grains are heated above 100 K, the OPR may differ from unity since the lowest ortho level is 22 K below the lowest para level. If no conversion processes between the two symmetries exist, the OPR of ammonia is expected to increase above unity at low formation temperatures.
Prior to Herschel, ortho-to-para ratios have been derived from measurements of inversion transitions, the (1,1) and (2,2) transitions involving para states, and the (3,3) and (6,6) transitions probing highly excited, metastable ortho states. For example, Umemoto et al. (1999) have found OPR = 1.3–1.7 in the L 1157 outflow from the observation of six inversion lines (J,K) = (1,1) to (6,6). Similarly, Nagayama et al. (2009) have inferred an even higher value of OPR = 1.5–3.5 in the central molecular zone of the Galaxy.
Using Herschel/HIFI observations of the fundamental rotational transitions of both ortho- and para-ammonia, it is for the first time possible to estimate the ammonia OPR in cold and diffuse interstellar gas of low excitation. Our results do, however, point to the surprising result of an OPR lower than unity.
This is shown in Figs. 12 and 13 where the upper panels show the normalised 10–00 ortho-NH3 and 21–11 para-NH3 spectra, and the lower panels show the corresponding optical depth ratios for absorptions larger than 3σ as a function of LSR velocity towards both sources (channel widths are 0.26 km s-1). An ortho-to-para optical depth ratio of 4.2 corresponds to a column density ratio of unity using the RADEX conversion factors in Table 2. The resulting column density ratios are given by the right hand y-axis in both figures. The para line has lower S/N than the ortho line in both sources and several velocity components are weak. Still, most column density ratios are found to be below unity within the uncertainties.
 |
Fig. 12 W49N. (Upper) WBS spectra of 10–00 ortho-NH3 and 21–11 para-NH3 normalised to SSB continuum. (Lower) The optical depth ratios are shown for absorptions larger than 3σ as a function of LSR velocity. The column density ratios (OPR), estimated with RADEX, are given by the right hand y-axis. The horisontal dashed line marks an ortho-to-para optical depth ratio of 4.2 corresponding to a column density ratio of unity. |
We have also used Method I and II to estimate the OPR. Method I gives OPR(NH3) = 0.7 ± 0.1 and 0.6–0.7 ± 0.1 in the strongest velocity components towards W49N (+39 km s-1 component) and G10.6 − 0.4 (+16, 28, 30 and 41 km s-1 components), respectively. The results from Method II gives similar results towards G10.6 − 0.4: 0.5–0.7 ± 0.1 in the velocity bins vLSR = 12.5–20, 25–29, 29–31 and 39.5–43.5 km s-1; but lower results towards W49N in vLSR = 36–42 km s-1, 0.4 ± 0.2.
The errors are dominated by the noise and the uncertainty in the sideband gain ratio. We have used the errors in sideband gain ratios stated on the Herschel internet site (4% for ortho and 6% for para). There is also an additional error arising from the rather large sideband separation of 12 GHz which means that the assumption of equal continuum temperature is not fully valid. This effect mimics a sideband gain ratio different from unity and is also taken into account (4 and 2% for ortho and para, respectively, estimated by TC,L/TC,U = (νL/νU)β with β = 2). The errors from the noise is estimated by δτ = exp(τ) × δI/I0, and the errors from the sideband gain ratio and differences in the continuum in the sidebands are estimated by δτ = ϵ − ln(1 + ϵexp(τ)) where ϵ is both errors added in quadrature. The derivation of this formula assumes that the depth of the absorption line is correct, which means that TC(SSB)–TA is conserved but the continuum level is not. The noise and calibration errors are finally added in quadrature. The error estimates for Method I and II add respective uncertainties from the methods to the calibration errors.
Some previous measurements of ammonia have resulted in an OPR lower than unity, although not in diffuse gas. In Orion KL Hermsen et al. (1988) obtained OPR(NH3) = 0.5 from inversion emission lines, and Hermsen et al. (1985) found OPR(15NH3) = 0.7. The latter low value was suggested to be caused by an excitation effect: a possible over-abundance of the unobserved K = 0 state. This explanation cannot be applied in our case, since we actually observe the K = 0 ortho state. Flower et al. (1995) modelled several NH3 inversion transitions in the frame of C-shock models towards the warm and dense Sgr B2 envelope and their best OPR of ammonia was ~0.5, also lower than the statistical value of unity. Ceccarelli et al. (2002), however, observed 21 high excitation ortho- and para-ammonia lines, both metastable and non-metastable levels, towards Sgr B2 using ISO, and derived an ammonia OPR of unity.
There are to our knowledge no previous estimate of the OPR(NH3) in diffuse gas, and it may very well be very different from the OPR in dense gas. We can, however, compare our strong absorption of the para-NH3 line to the observations by Tieftrunk et al. (1994) who observed the two lowest inversion lines of para-NH3 towards W49N. Their estimate of N(p-NH3) is 2.5 × 1012 cm-2 which is less than half our value, ~6 × 1012 cm-2. If this column density is correct, it would imply an OPR higher than unity in this velocity component in W49N. In our excitation model, however, the integrated optical depth observed by Tieftrunk et al. (1994) in the 11 inversion line at + 39 km s-1 implies a N(p-NH3) in good agreement with our value, since we obtain a higher excitation temperature than the 2.7 K used by Tieftrunk et al. (1994) for the 11 inversion transition.
We have no clear explanation yet of our surprising result and we can only speculate about its origin. Either there are to us unknown instrumental effects, or that our assumption that the line-of-sight gas completely covers the background continuum within the beam is not correct, or there must exist some physical or chemical processes that affect the OPR in diffuse gas. In general, the fact that interstellar clouds are weak plasmas allows for conversion processes at low temperatures that would not be present in a purely neutral gas. What OPR these processes lead to must be determined by careful modelling. In diffuse molecular clouds of relatively low density, n(H2) ≲ 103, but relatively high ionisation fraction, n(e)/n(H2) ≳ 10-4, the rate of destruction of NH3 by reactions with C+, H+, and H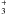 , can be as high as 10-9 s-1 at kinetic temperatures T ~ 30 K. The latter two ions can also interchange ortho and para states directly by proton substitution, perhaps at a comparable rate. These rates of destruction and interchange can approach the rates of radiative and collisional excitation out of the metastable levels, which means that the excitation and chemistry of NH3 should be treated together in a self-consistent fashion. Under these conditions, NH3 is a non-equilibrium system and a “spin temperature” derived from an ortho-to-para ratio is not expected to be meaningful.
, can be as high as 10-9 s-1 at kinetic temperatures T ~ 30 K. The latter two ions can also interchange ortho and para states directly by proton substitution, perhaps at a comparable rate. These rates of destruction and interchange can approach the rates of radiative and collisional excitation out of the metastable levels, which means that the excitation and chemistry of NH3 should be treated together in a self-consistent fashion. Under these conditions, NH3 is a non-equilibrium system and a “spin temperature” derived from an ortho-to-para ratio is not expected to be meaningful.
The NH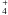 molecule could also affect the ammonia OPR in a similar manner. The fastest gas-phase reaction sequence of ammonia is
molecule could also affect the ammonia OPR in a similar manner. The fastest gas-phase reaction sequence of ammonia is 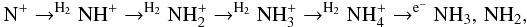 where N+ is formed by cosmic ray ionisation, or by reactions of He+ with N2 or CN which are formed by neutral-neutral reactions. Whether or not ammonia is produced on grains or in the gas, its destruction in the gas by protonating ions such as H
where N+ is formed by cosmic ray ionisation, or by reactions of He+ with N2 or CN which are formed by neutral-neutral reactions. Whether or not ammonia is produced on grains or in the gas, its destruction in the gas by protonating ions such as H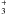 also leads to NH
also leads to NH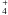 , which can have a variety of nuclear spin states depending on the overall nuclear spin of H
, which can have a variety of nuclear spin states depending on the overall nuclear spin of H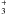 . The ammonia OPR could then simply reflect the spin states of NH
. The ammonia OPR could then simply reflect the spin states of NH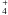 .
.
In addition, some laboratory evidence exists that dissociative recombination reactions have different rate coefficients depending upon the nuclear spin configuration of the molecular ion.
Observations of the ortho-to-para ratio of NH3 could thus provide a valuable insight into the competing processes of formation and destruction, radiative and collisional excitation, and reactive interchange processes.
7. Summary
Our spectrally resolved rotational transitions of NH, o-NH2, ortho- and para-NH3 along the sight-lines towards the high-mass star-forming regions W49N and G10.6−0.4 show remarkable similarities of line profiles and abundances. We find similar abundances of all three species and a co-existence in diffuse or translucent interstellar gas with a high molecular fraction. The mean abundance of ortho-NH3 abundance is ~2 × 10-9 towards both sources. The mean ratios of all three methods of the nitrogen hydrides in all velocity components, are N(NH)/N(o-NH3) = 5.9 and 3.5, and N(o-NH2)/N(o-NH3) = 2.4 and 2.0, towards G10.6 − 0.4 and W49N, respectively. This is in sharp contrast to previous observations of the nitrogen hydrides in dark clouds where the ammonia abundances are found to be ~100 times higher than X(NH), and ~10–300 times higher than X(NH2). NH and o-NH2 are found to be linearly correlated with o-NH3 at least for N(o-NH3) ≲ 5 × 1012 cm-2 which corresponds to a few AV. Upper limits of N(NH+) in both sources indicate a N(NH+)/N(NH) ratio of ≲ 2–14%, with a mean of ≲ 6%.
Linear correlations are also found for all three nitrogen hydrides with respect to CH, CN and HNC, although CH displays a more loose correlation than the latter two species. The nitrogen hydrides also largely follow the absorption pattern in Doppler velocity space of HCO+ and water, a species also known to trace regions of a high molecular fraction.
We have obtained a surprisingly low ortho-to-para ratio of ammonia, ≈ 0.5–0.7 ± 0.1, in the strongest velocity components, which is below the high-temperature limit of unity. No clear explanation has been found. More observations are needed of both the rotational transitions and the inversion lines with ground-based facilities, to be able to make firm conclusions about the ammonia OPR in diffuse gas.
We will continue to investigate the absorption lines in the sight-lines towards the other six PRISMAS sources. This will allow an analysis of the nitrogen chemistry at various galactic distances from the Galactic Centre. We will also use new Open Time 1 (OT1) Herschel/HIFI data of higher excitation lines to analyse the hot core sources which will be compared and contrasted with the diffuse interstellar gas. The ortho-to-para ratio of NH3 will also be further investigated both in the sources and in the diffuse gas, in addition to the OPR of NH2, for which new OT1 data in four of the PRISMAS sources will be analysed and compared to the ammonia OPR.
Online material
Appendix A: Herschel observations
Herschel OBSID’s of the observed transitions analysed in this paper.
Appendix B: Emission line contamination of o-NH2 towards W49N
The o-NH2 absorption towards W49N is contaminated by an emission line in the same sideband from the source, a more complicated situation than an emission line from the other sideband. In Fig. B.3 an emission line is clearly visible around 47 km s-1 in the o-NH2 spectrum. Here, the intensities have been normalised to the continuum in single sideband as TA/TC-1 assuming a sideband gain ratio of unity where TA is the observed intensity and TC is the SSB continuum as measured in line-free regions in the spectra. We identify the emission line as a blend of three unresolved hfs components of NO 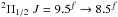 , F = 10.5 − 9.5, 9.5–8.5, and 8.5–9.5, at 952.464201 GHz (weighted mean frequency, cf. Varberg et al. 1999). The emission line appearing near 142 km s-1 in this figure is consequently identified as the hfs blend in the lower half of the same spin-rotation doublet of NO
, F = 10.5 − 9.5, 9.5–8.5, and 8.5–9.5, at 952.464201 GHz (weighted mean frequency, cf. Varberg et al. 1999). The emission line appearing near 142 km s-1 in this figure is consequently identified as the hfs blend in the lower half of the same spin-rotation doublet of NO 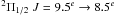 at an average rest frequency of 952.145441 GHz. The PRISMAS observations have also found three additional NO lines in W49N shown in Fig. B.2, each one consisting of unresolved hfs components, while no emission of NO is found in G10.6 − 0.4.
at an average rest frequency of 952.145441 GHz. The PRISMAS observations have also found three additional NO lines in W49N shown in Fig. B.2, each one consisting of unresolved hfs components, while no emission of NO is found in G10.6 − 0.4.
Since the two NO lines seen in Fig. B.3 have almost equal line strength, and are also observed with the same instrument in the same band, we have used the observed 952.145 GHz transition as a template to remove the interfering NO line at 952.464 GHz from the o-NH2 absorption. In order to do this we use 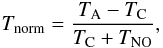 (B.1)to calculate the normalised SSB intensity Tnorm in K, where TC is the SSB continuum, and TNO is the intensity of the NO line (TA − TC,DSB). The model NO line, shown in Fig. B.1, is then moved to the velocity of the emission line. The resulting absorption line spectrum of o-NH2 towards W49N with removed NO emission is shown in green in Fig. B.3.
(B.1)to calculate the normalised SSB intensity Tnorm in K, where TC is the SSB continuum, and TNO is the intensity of the NO line (TA − TC,DSB). The model NO line, shown in Fig. B.1, is then moved to the velocity of the emission line. The resulting absorption line spectrum of o-NH2 towards W49N with removed NO emission is shown in green in Fig. B.3.
 |
Fig. B.1 W49N: model of the 952.464 GHz NO line to be removed from the o-NH2 absorption lines. The model is using the NO 952.145 GHz emission line observed at vLSR = +7.7 km s-1 and only shifted in velocity to a vLSR of +43.5 km s-1 corresponding to a vLSR of +7.7 km s-1 for that line. |
 |
Fig. B.2 W49N: double sideband WBS spectra of four NO emission lines from the source itself. Each NO line consists of 3 hfs components, with quatum numbers |
 |
Fig. B.3 NO emission from W49N in the line-of-sight o-NH2 absorption: normalised SSB spectrum of o-NH2. The emission line at 142 km s-1 is from NO at ν0 = 952.145 GHz. The NO ν0 = 952.464 GHz emission feature is seen at 47 km s-1 in the o-NH2 absorption. The two NO lines have similar line strengths. The red line shows the SSB normalised o-NH2 line without removal of the NO-line, and the green shows the spectra with removed NO-line. |
Appendix C: Hyperfine structure components
Hyperfine structure components of NH  N = 1 ← 0, J = 2 ← 1.
N = 1 ← 0, J = 2 ← 1.
Hyperfine structure components of NH  N = 1 ← 0, J = 0 ← 1.
N = 1 ← 0, J = 0 ← 1.
Hyperfine structure components of ortho-NH2 11,1–00,0.
Hyperfine structure components of ortho-NH3 10–00.
Hyperfine structure components of para-NH3 21–11.
Appendix D: Method II results
Appendix E: Method III results
Appendix F: Results for CN and HNC
Method I and III results for CN and HNCa.
Appendix G: Figures
 |
Fig. G.1 G10.6−0.4 (W31C): double sideband spectra of NH, ortho-NH2, ortho- and para-14NH3, ortho-15NH3, and NH+ over the LSR velocity range –50 to 85 km s-1. |
 |
Fig. G.2 G10.6−0.4 (W31C): normalised ammonia and the ammonia isotopologue 15NH3. (The emission line at vLSR ≈ 41 and 72 km s-1 is an SO2 line from the upper sideband.) |
 |
Fig. G.3 W49N: fits of method II to NH and o-NH2, and their observed spectra. Residuals are found at the bottom. Template spectrum is o-NH3 at 572 GHz. |
 |
Fig. G.4 W49N: fits of method II to NH, o-NH2 and o-NH3, and their observed spectra. Residuals are found at the bottom. Template spectrum is CH at 532 GHz. |
 |
Fig. G.5 G10.6−0.4 (W31C): fits of method II to NH and o-NH2, and their observed spectra. Residuals are found at the bottom. Template spectrum is o-NH3 at 572 GHz. |
 |
Fig. G.6 G10.6−0.4 (W31C): fits of method II to NH, o-NH2 and o-NH3, and their observed spectra. Residuals are found at the bottom. Template spectrum is CH at 532 GHz. |
 |
Fig. G.7 W49N: method III (XCLASS) fits to the nitrogen hydrides and CH. |
 |
Fig. G.8 G10.6−0.4 (W31C): method III (XCLASS) fits to the nitrogen hydrides and CH. |
 |
Fig. G.9 Comparison of absorption lines towards W49N and G10.6−0.4. The intensities have been normalised to single sideband continuum. An NO emission line from the source (952.464 GHz) has been removed from the o-NH2 spectrum (see Sect. B.) |
 |
Fig. G.10 Comparison of absorption lines towards W49N and G10.6−0.4. The intensities have been normalised to single sideband continuum. |
Appendix H: Comparison plots of different methods
In Fig. H.1 we plot the resulting column densities from our three different methods.
Note that since Method I and Method III use Gaussians with smaller line widths than the velocity bins of Method II towards G10.6−0.4, the number of velocity components is not the same in this source. The +33 km s-1 component towards W49N is not used in Method II, which on the other hand models a velocity bin that is difficult to fit using Gaussians in Method I and III (50–57 km s-1). The comparison of the nitrogen hydrides vs. CH in W49N, in two of the four velocity bins, shows the only cases in which the results do not agree reasonably well between the methods. The resulting CH column densities also show a larger
spread between the methods than the other species. The reason is not fully understood, but is probably caused by the different approaches to the CH modelling. Method II uses the deconvolved CH spectra as a template for the nitrogen hydrides and is thereby trying to fit the broader CH absorption to the more narrow features of the nitrogen hydrides with moderate success. The other two methods use an opposite approach: they use the output of the fitting of the nitrogen hydrides as an input to CH to fit Gaussians only in the same parts in velocity space, and are thereby trying to fit narrow features to the broader CH absorption. The fit is good in some parts of the velocity space, and very bad in the velocity space in which CH has absorption but the nitrogen hydrides do not, which is expected.
 |
Fig. H.1 Column density comparison plots. The results from all three methods are plotted. The scatter in the results can be considered as an estimate of the errors. |
 |
Fig. H.1 continued. |
 |
Fig. H.1 continued. |
 |
Fig. H.1 continued. |
Developed by Per Bergman at Onsala Space Observatory, Sweden; http://www.chalmers.se/rss/oso-en/observations/data-reduction-software
Acknowledgments
The Herschel spacecraft was designed, built, tested, and launched under a contract to ESA managed by the Herschel/Planck Project team by an industrial consortium under the overall responsibility of the prime contractor Thales Alenia Space (Cannes), and including Astrium (Friedrichshafen) responsible for the payload module and for system testing at spacecraft level, Thales Alenia Space (Turin) responsible for the service module, and Astrium (Toulouse) responsible for the telescope, with in excess of a hundred subcontractors. HIFI has been designed and built by a consortium of institutes and university departments from across Europe, Canada and the United States under the leadership of SRON Netherlands Institute for Space Research, Groningen, The Netherlands and with major contributions from Germany, France and the US. Consortium members are: Canada: CSA, U.Waterloo; France: CESR, LAB, LERMA, IRAM; Germany: KOSMA, MPIfR, MPS; Ireland, NUI Maynooth; Italy: ASI, IFSI-INAF, Osservatorio Astrofisico di Arcetri- INAF; The Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronmico Nacional (IGN), Centro de Astrobiologa (CSIC-INTA). Sweden: Chalmers University of Technology – MC2, RSS & GARD; Onsala Space Observatory; Swedish National Space Board, Stockholm University – Stockholm Observatory; Switzerland: ETH Zurich, FHNW; USA: Caltech, JPL, NHSC. C.P. and J.H.B. acknowledge generous support from the Swedish National Space Board. M.d.L. and M.G. acknowledge funding by CNES and by the ANR SCHISM project (ANR-09-BLAN-0231-01). T.A.B., B.G. and J.R.G. thank the Spanish MICINN for funding support through grants AYA2009-07304 and CSD2009-00038. H.S.P.M. is very grateful to the Bundesministerium für Bildung und Forschung (BMBF) for financial support aimed at maintaining the Cologne Database for Molecular Spectroscopy, CDMS. This support has been administered by the Deutsches Zentrum für Luft- und Raumfahrt (DLR). We also thank the referee Harvey Liszt whose constructive comments led to a significant improvement of the paper.
References
- Adande, G., & Ziurys, L. 2011, in IAU Symp., 280, 76 [Google Scholar]
- Bacmann, A., Caux, E., Hily-Blant, P., et al. 2010, A&A, 521, L42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biver, N., Bockelée-Morvan, D., Crovisier, J., et al. 2007, Planet. Space Sci., 55, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., Dore, L., & Puzzarini, C. 2009, A&A, 507, 1707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Baluteau, J.-P., Walmsley, M., et al. 2002, A&A, 383, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Goicoechea, J. R., & Caux, E. 2000, ApJ, 534, L199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cheung, A. C., Rank, D. M., Townes, C. H., Thornton, D. D., & Welch, W. J. 1968, Phys. Rev. Lett., 21, 1701 [Google Scholar]
- Comito, C., Schilke, P., Phillips, T. G., et al. 2005, ApJS, 156, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Coudert, L. H., & Roueff, E. 2006, A&A, 449, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coudert, L. H., & Roueff, E. 2009, A&A, 499, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crane, P., Lambert, D. L., & Sheffer, Y. 1995, ApJS, 99, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, I. A., & Williams, D. A. 1997, MNRAS, 291, L53 [NASA ADS] [Google Scholar]
- Dame, T. M., & Thaddeus, P. 1985, ApJ, 297, 751 [NASA ADS] [CrossRef] [Google Scholar]
- de Almeida, A. A., & Singh, P. D. 1982, A&A, 113, 199 [NASA ADS] [Google Scholar]
- de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L4 [EDP Sciences] [Google Scholar]
- De Pree, C. G., Wilner, D. J., Goss, W. M., Welch, W. J., & McGrath, E. 2000, ApJ, 540, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Dickel, H. R., & Goss, W. M. 1990, ApJ, 351, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Dreher, J. W., Johnston, K. J., Welch, W. J., & Walker, R. C. 1984, ApJ, 283, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Farmer, C. B., & Norton, R. H. 1989, A high-resolution atlas of the infrared spectrum of the sun and the earth atmosphere from space, A compilation of ATMOS spectra of the region from 650 to 4800 cm-1 (2.3 to 16 μm), Vol. I, The sun [Google Scholar]
- Feldman, P. D., Fournier, K. B., Grinin, V. P., & Zvereva, A. M. 1993, ApJ, 404, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Fish, V. L., Reid, M. J., Wilner, D. J., & Churchwell, E. 2003, ApJ, 587, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Flores-Mijangos, J., Brown, J. M., Matsushima, F., et al. 2004, J. Mol. Spectr., 225, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forets, G., & Walmsley, C. M. 1995, A&A, 294, 815 [NASA ADS] [Google Scholar]
- Gerin, M., de Luca, M., Black, J., et al. 2010a, A&A, 518, L110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., de Luca, M., Goicoechea, J. R., et al. 2010b, A&A, 521, L16 [Google Scholar]
- Godard, B., Falgarone, E., Gerin, M., Hily-Blant, P., & de Luca, M. 2010, A&A, 520, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Rodríguez-Fernández, N. J., & Cernicharo, J. 2004, ApJ, 600, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 263, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., Kwok, S., Koning, N., et al. 2006, ApJ, 637, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Hermsen, W., Wilson, T. L., Walmsley, C. M., & Batrla, W. 1985, A&A, 146, 134 [NASA ADS] [Google Scholar]
- Hermsen, W., Wilson, T. L., Walmsley, C. M., & Henkel, C. 1988, A&A, 201, 285 [NASA ADS] [Google Scholar]
- Hily-Blant, P., Maret, S., Bacmann, A., et al. 2010, A&A, 521, L52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Hübers, H., Evenson, K. M., Hill, C., & Brown, J. M. 2009, J. Chem. Phys., 131, 034311 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Keene, J., Blake, G. A., & Phillips, T. G. 1983, ApJ, 271, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Klaus, T., Takano, S., & Winnewisser, G. 1997, A&A, 322, L1 [NASA ADS] [Google Scholar]
- Knauth, D. C., Andersson, B., McCandliss, S. R., & Warren Moos, H. 2004, Nature, 429, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Krełowski, J., Beletsky, Y., & Galazutdinov, G. A. 2010, ApJ, 719, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., & Graedel, T. E. 1989, ApJS, 69, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Larsson, B., Liseau, R., Bergman, P., et al. 2003, A&A, 402, L69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., Wootten, A., Gerin, M., & Roueff, E. 2010, ApJ, 710, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Liseau, R., Larsson, B., Brandeker, A., et al. 2003, A&A, 402, L73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H., & Lucas, R. 2001, A&A, 370, 576 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., Lucas, R., & Pety, J. 2006, A&A, 448, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marty, B., Chaussidon, M., Wiens, R. C., Jurewicz, A. J. G., & Burnett, D. S. 2011, Science, 332, 1533 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, R., Wellnitz, D., Kim, S. J., & A’Hearn, M. F. 1998, Icarus, 136, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M., & Roth, K. C. 1991, ApJ, 376, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., Bennett, A., Rawlings, J. M. C., Brown, P. D., & Charnley, S. B. 1991, A&AS, 87, 585 [NASA ADS] [Google Scholar]
- Müller, H. S. P., Klein, H., Belov, S. P., et al. 1999, J. Mol. Spectr., 195, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nagayama, T., Omodaka, T., Handa, T., et al. 2009, PASJ, 61, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Nash, A. G. 1990, ApJS, 72, 303 [Google Scholar]
- Nejad, L. A. M., Williams, D. A., & Charnley, S. B. 1990, MNRAS, 246, 183 [NASA ADS] [Google Scholar]
- Neufeld, D. A., Goicoechea, J. R., Sonnentrucker, P., et al. 2010a, A&A, 521, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A., Sonnentrucker, P., Phillips, T. G., et al. 2010b, A&A, 518, L108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nyman, L.-A., & Millar, T. J. 1989, A&A, 222, 231 [NASA ADS] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Persson, C. M., Olberg, M., Hjalmarson, Å., et al. 2009, A&A, 494, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., Black, J. H., Cernicharo, J., et al. 2010, A&A, 521, L45 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, I. R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Trans., 60, 883 [Google Scholar]
- Pilbratt, G., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Plume, R., Kaufman, M. J., Neufeld, D. A., et al. 2004, ApJ, 605, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Polehampton, E. T., Baluteau, J., Swinyard, B. M., et al. 2007, MNRAS, 377, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Rist, C., Alexander, M. H., & Valiron, P. 1993, J. Chem. Phys., 98, 4662 [NASA ADS] [CrossRef] [Google Scholar]
- Roelfsema, P. R., Helmich, F. P., Teyssier, D., et al. 2012, A&A, 537, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandford, S. A., Bernstein, M. P., Allamandola, L. J., Goorvitch, D., & Teixeira, T. C. V. S. 2001, ApJ, 548, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. L. 1969, PASP, 81, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, Jr., T. P. 1979, Ap&SS, 66, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Neufeld, D. A., Phillips, T. G., et al. 2010, A&A, 521, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swings, P., Elvey, C. T., & Babcock, H. W. 1941, ApJ, 94, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Tieftrunk, A., Pineau des Forets, G., Schilke, P., & Walmsley, C. M. 1994, A&A, 289, 579 [NASA ADS] [Google Scholar]
- Umemoto, T., Mikami, H., Yamamoto, S., & Hirano, N. 1999, ApJ, 525, L105 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Jansen, D. J., Schilke, P., & Phillips, T. G. 1993, ApJ, 416, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Varberg, T. D., Stroh, F., & Evenson, K. M. 1999, J. Mol. Spectr., 196, 5 [Google Scholar]
- Verhoeve, P., Ter Meulen, J. J., Meerts, W. L., & Dyamanus, A. 1986, Chem. Phys. Lett., 132, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Wagenblast, R., Williams, D. A., Millar, T. J., & Nejad, L. A. M. 1993, MNRAS, 260, 420 [NASA ADS] [Google Scholar]
- Weselak, T., Galazutdinov, G. A., Beletsky, Y., & Krełowski, J. 2009, MNRAS, 400, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wirström, E. S., Bergman, P., Black, J. H., et al. 2010, A&A, 522, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyrowski, F., Menten, K. M., Güsten, R., & Belloche, A. 2010, A&A, 518, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Nitrogen hydrides towards W49N: double sideband WBS spectra of NH, ortho-NH2, ortho- and para-NH3, and NH+ over the LSR velocity range –50 to 85 km s-1. Quantum numbers are found in Table 1. Note that we only analyse the absorption in the velocity range 30 − 75 km s-1 in this paper and leave the source absorption and emission for a future paper. |
| In the text | |
 |
Fig. 2 W31C: o-14NH3 and o-15NH3. Both isotopologues show emission from the source. Absorption in the line-of-sight is only seen in the o-14NH3 spectra. The emission line at vLSR ≈ 41 km s-1 in the o-15NH3 spectra, is an SO2 line from the upper sideband. |
| In the text | |
 |
Fig. 3 NH hfs components: normalised WBS spectrum towards W49N. Also shown are Gaussian fits with a line width of 1 km s-1 of the NH 974 GHz hfs components in the +39 km s-1 velocity component. |
| In the text | |
 |
Fig. 4 Ortho-NH2 hfs components: normalised WBS spectrum towards W49N. Also shown are Gaussian fits with a line width of 1 km s-1 of the o-NH2 953 GHz hfs components in the +39 km s-1 velocity component. |
| In the text | |
 |
Fig. 5 Ortho-NH3 hfs components: normalised high resolution spectra (Δv = 0.13 km s-1) towards W49N in the +39 km s-1 velocity component. Three hfs components are seen at 38.4, 39.4 and 40.0 km s-1. Also shown are the positions and relative intensities of the hfs components and their fitted opacity profiles with a line width of 1.0 km s-1. |
| In the text | |
 |
Fig. 6 W49N: fits of Method I and the SSB normalised spectra of the nitrogen hydrides and CH. The black lines are the observations, and the coloured lines are the model fits. In the bottom the residuals are plotted on top of each other with respective colour. The three transitions used in Method I to determine the vLSR and line widths of the velocity components are marked in bold. |
| In the text | |
 |
Fig. 7 G10.6 − 0.4: fits of Method I and the SSB normalised spectra of the nitrogen hydrides and CH. Same notation as in Fig. 6. |
| In the text | |
 |
Fig. 8 Line-of-sight absorptions towards W49N: normalised (SSB) spectra of ortho-ammonia and species tracing both high and low molecular fractions. Strong similarities are seen between ammonia, CN, HNC and water, but not with H2O+ and HI tracing the atomic diffuse gas. |
| In the text | |
 |
Fig. 9 Line-of-sight absorptions towards G10.6 − 0.4: notation as in Fig. 8. |
| In the text | |
 |
Fig. 10 Column density comparison plots. On the left hand side: NH, o-NH2 and o-NH3. On the right hand side: nitrogen hydrides vs. CH. The blue lines show linear least square fits to all data points towards both sources. The correlation coefficients and the linear fit equations are given in respective figure. |
| In the text | |
 |
Fig. 11 Column density comparison plots. On the left hand side we show comparisons of the nitrogen hydrides with CN, and on the right hand side comparisons with HNC. Notation as in Fig. 10. |
| In the text | |
 |
Fig. 12 W49N. (Upper) WBS spectra of 10–00 ortho-NH3 and 21–11 para-NH3 normalised to SSB continuum. (Lower) The optical depth ratios are shown for absorptions larger than 3σ as a function of LSR velocity. The column density ratios (OPR), estimated with RADEX, are given by the right hand y-axis. The horisontal dashed line marks an ortho-to-para optical depth ratio of 4.2 corresponding to a column density ratio of unity. |
| In the text | |
 |
Fig. 13 G10.6 − 0.4 (W31C). Notation as in Fig. 12. |
| In the text | |
 |
Fig. B.1 W49N: model of the 952.464 GHz NO line to be removed from the o-NH2 absorption lines. The model is using the NO 952.145 GHz emission line observed at vLSR = +7.7 km s-1 and only shifted in velocity to a vLSR of +43.5 km s-1 corresponding to a vLSR of +7.7 km s-1 for that line. |
| In the text | |
 |
Fig. B.2 W49N: double sideband WBS spectra of four NO emission lines from the source itself. Each NO line consists of 3 hfs components, with quatum numbers |
| In the text | |
 |
Fig. B.3 NO emission from W49N in the line-of-sight o-NH2 absorption: normalised SSB spectrum of o-NH2. The emission line at 142 km s-1 is from NO at ν0 = 952.145 GHz. The NO ν0 = 952.464 GHz emission feature is seen at 47 km s-1 in the o-NH2 absorption. The two NO lines have similar line strengths. The red line shows the SSB normalised o-NH2 line without removal of the NO-line, and the green shows the spectra with removed NO-line. |
| In the text | |
 |
Fig. G.1 G10.6−0.4 (W31C): double sideband spectra of NH, ortho-NH2, ortho- and para-14NH3, ortho-15NH3, and NH+ over the LSR velocity range –50 to 85 km s-1. |
| In the text | |
 |
Fig. G.2 G10.6−0.4 (W31C): normalised ammonia and the ammonia isotopologue 15NH3. (The emission line at vLSR ≈ 41 and 72 km s-1 is an SO2 line from the upper sideband.) |
| In the text | |
 |
Fig. G.3 W49N: fits of method II to NH and o-NH2, and their observed spectra. Residuals are found at the bottom. Template spectrum is o-NH3 at 572 GHz. |
| In the text | |
 |
Fig. G.4 W49N: fits of method II to NH, o-NH2 and o-NH3, and their observed spectra. Residuals are found at the bottom. Template spectrum is CH at 532 GHz. |
| In the text | |
 |
Fig. G.5 G10.6−0.4 (W31C): fits of method II to NH and o-NH2, and their observed spectra. Residuals are found at the bottom. Template spectrum is o-NH3 at 572 GHz. |
| In the text | |
 |
Fig. G.6 G10.6−0.4 (W31C): fits of method II to NH, o-NH2 and o-NH3, and their observed spectra. Residuals are found at the bottom. Template spectrum is CH at 532 GHz. |
| In the text | |
 |
Fig. G.7 W49N: method III (XCLASS) fits to the nitrogen hydrides and CH. |
| In the text | |
 |
Fig. G.8 G10.6−0.4 (W31C): method III (XCLASS) fits to the nitrogen hydrides and CH. |
| In the text | |
 |
Fig. G.9 Comparison of absorption lines towards W49N and G10.6−0.4. The intensities have been normalised to single sideband continuum. An NO emission line from the source (952.464 GHz) has been removed from the o-NH2 spectrum (see Sect. B.) |
| In the text | |
 |
Fig. G.10 Comparison of absorption lines towards W49N and G10.6−0.4. The intensities have been normalised to single sideband continuum. |
| In the text | |
 |
Fig. H.1 Column density comparison plots. The results from all three methods are plotted. The scatter in the results can be considered as an estimate of the errors. |
| In the text | |
 |
Fig. H.1 continued. |
| In the text | |
 |
Fig. H.1 continued. |
| In the text | |
 |
Fig. H.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.