| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118408 | |
| Published online | 27 June 2012 | |
Determination of binary asteroid orbits with a genetic-based algorithm
1 Institut de mécanique céleste et de calcul des éphémérides, Observatoire de Paris, Avenue Denfert-Rochereau, 75014 Paris, France
e-mail: frederic.vachier@imcce.fr
2 Carl Sagan Center, SETI Institute, 189 Bernardo Avenue, Mountain View CA 94043, USA
Received: 5 November 2011
Accepted: 28 April 2012
Aims. Over the past decade, discoveries of multiple and binary asteroid systems have played a significant role in our general understanding of small solar system bodies. Direct observations of satellites of asteroids are rare and difficult since they require the use of already over-subscribed facilities such as adaptive optics (AO) on large 8−10 m class telescopes and the Hubble Space Telescope (HST). The scarcity of data and the long temporal baseline of observations (up to 10 years) significantly complicate the determination of the mutual orbits of these systems.
Methods. We implemented a new approach for determining the mutual orbits of directly-imaged multiple asteroids using a genetic-based algorithm. This approach was applied to several known binary asteroid systems (22 Kalliope, 3749 Balam, and 50 000 Quaoar) observed with AO systems and HST. This statistical method is fast enough to permit the search for an orbital solution across a large parameter space and without a priori information about the mutual orbit.
Results. From 10 years of observation, we derived an orbital solution for Linus, companion of (22) Kalliope, with an accuracy close to the astrometric limit provided by the AO observations, assuming a purely Keplerian orbit. A search for non-Keplerian orbit confirmed that a J2 ~ 0 is the best-fitting solution. We show that the precession of the nodes could be detected without ambiguity, implying that Kalliope’s primary may have an inhomogeneous internal structure. HST astrometric observations of Weywot, companion of the trans-Neptunian object (50 000) Quaoar, were used to derive its mass and its bulk density, which appears to be higher than the density of other TNOs. Finally, we derived a bundle of orbital solutions for (3749) Balam, with equally good fits, from the limited set of astrometric positions. They provide a realistic density between 1.3 and 3.7 g/cm3 for this S-type asteroid.
Key words: celestial mechanics / instrumentation: adaptive optics / minor planets, asteroids: general / methods: data analysis / ephemerides
© ESO, 2012
1. Introduction
More than 200 multiple asteroid systems are known in all populations of minor bodies in the solar system. Approximatively forty of them can be directly imaged using the high angular resolution provided by adaptive optics on ground-based telescopes and the Hubble Space Telescope for binary main-belt or Trojan asteroids, or using classical imaging for trans-Neptunian objects (TNOs) with wide separations. Direct imaging allows us to derive the masses of such system, providing a unique opportunity to extract constraints on the formation processes and evolution of these small solar system bodies.
The determination of the mutual orbit of a binary asteroid is complicated by parallax due to the relative motion between the observer and the target, and by the non-sphericity of the primary (the larger component of the system). To address these problems and derive the orbital parameters of the mutual orbits of these systems, several strategies have been developed since the discovery of the first binary asteroid system, Ida and its companion Dactyl (Chapman et al. 1995).
If the asteroid’s companion is detected on a short arc of its orbit, as Ida was detected during a flyby of the Galileo spacecraft, its orbit can be determined by finding a range of stable orbits which properly fit the arc of the orbit. Additional assumptions, such as a range of possible densities for the system and the absence of non-gravitational perturbations, are also necessary to derive a range of orbital solutions (Belton et al. 1996).
If a binary system is better constrained through a few astrometric positions spanning several revolutions, and sampling the apparent orbit well, then geometrically fitting orbits can be used to derive the orbital parameters. In this case, several orbits with identical likelihoods can be found, and the search ranges for the orbital parameters are manually set (Noll et al. 2004). We added non-gravitational effects, such as the precessions of the lines of nodes due to an irregularly shaped primary, to the geometrical model developed by Descamps (2005), giving us the possibility of deriving an estimate of the dynamical J2 of the triple asteroid system (87) Sylvia (Marchis et al. 2005).
More recently, the number of astrometric positions and periods of observations of several main-belt binary asteroids have significantly increased because of the development and availability of ground-based adaptive optics observations. It is currently possible to derive the elements of mutual orbits using a model which includes complex dynamical effects, such as mutual interactions between moons, and non-Keplerian effects, such as perturbations by the sun (Marchis et al. 2010). However, these models are limited to a narrow range of orbital parameters, since the convergence toward an orbital solution is highly dependent on the initial set of parameters.
In this work, we develop an innovative algorithm to fit the orbit of binary asteroid systems. It includes an exploration of a wide range of orbital parameters without any a priori knowledge of the satellite orbit, and it implements non-Keplerian effects due to the irregular shape of the primary. In Sect. 2 we present the N-body problem and the two dynamical models that we used. Section 3 describes the metaheuristic which was developed to optimize the search for a good solution. Observations of three binary systems, and their orbital solutions obtained using our algorithm, are described in Sect. 4. Finally we conclude our analysis in Sect. 5, and we provide a way to access these solutions through the IMCCE ephemerides web server.
2. The N-body problem
The orbit inversion code used for this work, named Genoid (GENetic Orbit IDentification), relies on a metaheuristic method (cf. Sect. 3) and a dynamical model of the solar system. We made use of two dynamical models: a simple Keplerian model (named Genoid-Kepler) and a full N-body problem which includes the gravitational field of the primary asteroid up to 4th order (named Genoid-ANIS). To minimize the search-time for an orbital solution, we first used the Keplerian model to explore a wide space of solutions, even based on a limited number of astrometric positions. We then ran the full N-body model on a set of parameters around the Keplerian solution to search for the most accurate solution when taking into account the full physical behavior of dynamical systems.
2.1. Kepler
Genoid-Kepler is a purely Keplerian algorithm which provides a 2-Body solution for computing the position of the satellite w.r.t. the primary. It is very computationally efficient and allows us to quickly perform statistical analyses. The primary is assumed to be a point-like mass, and the satellite is assumed to be a massless test-particle. The center of mass of the system is orbiting around the sun, taking into account the major perturbations from the planets in the framework of the post-Newtonian approximation.
The parameters which are determined are the orbital period, the semi-major axis, the eccentricity, the timing of perihelion, the inclination, the longitude of the ascending node, and the argument of periapsis. All the parameters are expressed in an equatorial J2000 reference frame (EQJ2000).
2.2. Taylor series of high orders
Genoid-ANIS is based on a numerical integration of the N-body problem (Le Guyader 1993), considering the differential equations of motion expanded in a Taylor series to high orders (up to 21). This method was previously used to derive an orbital solution for Neptune’s satellite Nereid (Veiga et al. 1999), which was found to be similar to Jacobson et al. (1991).
We also implemented the possibility of taking into account perturbations due to the shape of the primary through their zonal coefficients. In addition to the Keplerian orbital parameters (cf. Sect. 2.1), we therefore fit the zonal harmonic coefficients J2 and J4, the mean radius, and the coordinates of the pole in an ecliptic J2000 reference frame. In comparison with the more classical Bulirsh-Stoer and Radau algorithms, this method combines high precision, when the degrees of the Taylor series derivatives are large, with fast calculation speeds. Our algorithm uses a 21st order Taylor expansion, which leads to a numerical error of 10-3 milli-arcsec (mas) over 20 years of integration time.
3. Metaheuristic
A large number of numerical methods have been developed to solve the numerical problem by finding the best candidate solutions. Most of the time, a problem can be solved by dealing with it as an optimization problem. Metaheuristics, which appeared in the 1980s, are computational methods which optimize a problem by iteratively improving a candidate solution. They are capable of solving problems considered to be hard optimization problems (Dréo et al. 2006). Moreover, metaheuristics make few or no assumptions about the problem to be optimized, and are able to scan a very large volume of the phase-space of candidate solutions. Of the many existing metaheuristics, we chose to use the evolutionary algorithm, also called the genetic algorithm since it is inspired by mechanisms from organic evolution. The two main mechanisms that govern the evolution of living beings are:
-
Selection the encouragement of reproduction and the survival of individuals of best performance; and
-
Reproduction the opportunity for mixing, recombination, and changes in the hereditary characteristics passed from parents, forming new individuals with better potentials.
In the case of our study, orbital parameters are the equivalent of chromosomes, the complete set of which compose an individual: the orbit. For each individual, we can compute a function of performance which will be used to compare it to others.
3.1. fitness function
To transform a differential equation resolution problem into an optimization problem, we first defined a fitness function, fp, as the quadratic mean of observed minus computed positions, such that: 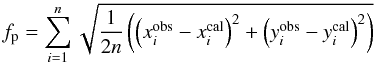 (1)where n is the number of observations, and xi and yi are the observed and computed differential positions between the satellite and its primary. With this definition, our problem becomes one of minimizing fp. The main advantage of this fitness function is that it provides a link between the quality of the fitted orbit and the uncertainties of the astrometric positions provided by the observations. fp is expressed in milli-arc seconds.
(1)where n is the number of observations, and xi and yi are the observed and computed differential positions between the satellite and its primary. With this definition, our problem becomes one of minimizing fp. The main advantage of this fitness function is that it provides a link between the quality of the fitted orbit and the uncertainties of the astrometric positions provided by the observations. fp is expressed in milli-arc seconds.
3.2. Algorithm
The following enumeration provides a step-by-step description of the Genoid algorithm (Fig. 1).
-
1.
Initialization: first, we consider a population composed of Npop individuals in the space of parameters to be explored. These parameters are randomly chosen and follow the uniform distribution.
-
2.
Fitness function (population): for each newly created individual, we compute the fitness function, fp, to be able to compare orbit candidates.
-
3.
Selection: we select the Npar individuals which have the best fp. They will be the parents for the reproduction process.

Fig. 1 Schematic workflow of the Genoid algorithm.
-
4.
Reproduction and Mutation: the reproduction is a crossover process which consists to combine two individuals, the parents, to form two new individuals, the childrens, by combining the orbital parameters of the two parents. For this step, it is necessary to include random changes in the orbital parameters to provoke mutation. The process generates also Nmut childrens with orbital parameters radically different from those of the parents. One common drawback of many fitting algorithms is that they often converge towards local minima of the fitting parameters, rather than global ones. The mutation process is used to avoid this issue, and to prevent the reproduction process to create a degenerated population. It allows the algorithm to escape local minima and to find other paths of convergence towards a better solution, with respect to the fitness function.
-
5.
Fitness function (childrens): for each children orbit, we compute the fitness function.
-
6.
End of the loop: we use three criteria to exit the program:
-
(a)
the best individual has a fitness function lower than the chosen limit, which corresponds to the level of mean uncertainty of the observations (user defined parameter, e.g. 10 mas);
-
(b)
the population degenerated. It happens when the fitness function of the best and worst candidate is lower than 10-2. In that case, based on the genetic principles, the population and their descendants will be almost identical, consequently the function of performance will not improve anymore;
-
(c)
the maximum number of generations has reached its maximum value (user defined parameter, between 500 and 1000 generations).
-
(a)
-
7.
Resizing search space: to speed up the convergence, we coined a new biological mechanism that we call cataclysmic extermination. After x generations (x ~ 30), all individuals of all generations are exterminated and a new space of solutions is calculated by removing parts of the space with no previous individuals. Then we restart the process by generating a new population of individuals with a simple uniform law in this new restrained space. This mechanism improves the convergence of the algorithm by minimizing the volume of the phase-space, and it avoids the degeneration of the population which may carry the solution towards a local minimum.
 |
Fig. 2 Convergence of orbital parameters for Linus, moon of (22) Kalliope, derived from our genetic algorithm using a Keplerian model Genoid-Kepler. One solution with an orbital period of 3.595712 days is evident. The other orbital elements and their 3-sigma errors are listed in Table 1. The 3-sigma error bar corresponds to the mean precision of astrometry provided by the adaptive optic observations. |
4. Observations and solutions
To validate our algorithm, we derived the orbital elements of three well-known binary asteroid systems. To show the ability of our genetic algorithm to be used on a wide variety of data, we collected astrometric positions of binary systems (i.e. relative positions of the moon w.r.t. the primary) from different sources of observations (HST, AOs), time spans covered by observations, and types of populations of small solar system bodies.
All the collected astrometric positions were obtained with very similar telescopes/instruments (with the same plate scale) and under similar observing conditions (providing a similar angular resolution). The average uncertainty on the measured astrometric positions is estimated to ~ 10 mas. The uncertainties of the astrometric positions are not used to compute the fitness function. Taking into account a standard deviation up to 3-sigma for each parameter of the problem, the solution is composed by all the individuals for which the fitness function is lower than 30 mas. The error of each parameter is estimated by determining the minimum and maximum values of the parameter for this region of individuals. The error is most likely over-estimated using this method since it is assumed that each individual are equal in quality with respect to the astrometric position error.
In the figures for which we show the convergence of the orbital parameters, we adopted a color pattern such as the red individuals are characterized by fp larger than 100 mas (poor solution), the blue color shows individuals for which fp ≤ 100 mas (mediocre solution), and the green color enlightens the individuals which are close to a satisfactory solution (fp ≤ 20 mas).
4.1. A well-constrained dynamical model of (22) Kalliope and its satellite Linus
The minor planet (22) Kalliope and its satellite Linus is one of the binary asteroids which has been most observed by adaptive optic and comparative photometry technics. Since its discovery in 2001, it has been the topic of a large number of studies to determine its mutual orbit, and the size and shape of the primary and the satellite (Descamps et al. 2008; Laver et al. 2009). These studies were possible because of the relatively small difference in brightness between the large primary and its satellite, allowing observations of the satellite even with a 3 m-class telescope equipped with AO. (22) Kalliope is a main-belt asteroid with an equivalent diameter of 166.2 ± 2.8 km, estimated by combining mutual eclipses, adaptive optics and stellar occultation observations (Descamps et al. 2008), and confirmed in 2011 by the NEOWISE thermal observations (167 ± 15.3 km, Masiero et al. 2011). The satellite diameter is estimated to be 28 ± 2 km, derived from analyses of the mutual events and the 2006 stellar occultation (Descamps et al. 2008).
We focused our study on 52 observations collected with the VLT, Keck, and Gemini North 8 − 10 m class telescopes, with the Shane-3m Lick telescope (Marchis et al. 2003) and Palomar 5m-telescope (Margot & Brown 2003, both equipped with AO systems. Recent observations collected with W.M. Keck II and Gemini-North telescopes in 2010 were added to this set of astrometric positions. During the time span of observations (2001 − 2010), the projected angular separation between the satellite and its primary varied from 239 mas to 887 mas.
The Genoid-Kepler model (Sect. 2.1) was used to derive an optimized mutual orbit, of which the satellite circulates with a period of 3.595712 ± 7 × 10-5 days, at 1081.5 ± 33.5 km from the primary. The astrometric positions used to fit the model are well spread over the 10-year period of observations (~900 orbital periods), so we are confident that the dynamical problem of (22) Kalliope system is extremely well-constrained. Figure 2 shows the range of each orbital parameter which was explored by Genoid-Kepler. The best Keplerian solution is obvious with a very low fp = 15.06 mas, so the final solution is unambiguous in that case. Consequently, the high accuracy of the orbital elements makes it possible to compute the position of Linus over the next 10 years with an accuracy better than 15 mas.
Among all the observations used to fit the orbit of Linus, we included the astrometric position of Linus obtained from the 2006 stellar occultation (Descamps et al. 2008). Our orbit of Linus adjusts this position with observed minus computed (O − C) values of the differential position of 7 ± 1 mas and 3 ± 1 mas in RA and Dec, respectively. This corresponds to an offset between the predicted and observed positions of Linus of dx = 9 ± 1 km and dy = 4 ± 1 km in the plane of occultation (Fig. 4). In comparison, Descamps et al. (2008), found dx = 10 ± 10 km (8 ± 8 mas) and dy = 57 ± 10 km (44 ± 8 mas), demonstrating the great improvement of our new orbital solution.
Physical and dynamical parameters derived with Genoid with the keplerian model (EQJ2000).
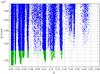 |
Fig. 3 Search for the best J2 for the binary asteroid system (22) Kalliope with Genoid-ANIS. The best candidate solution is obtained for J2 ~ 0. |
We also applied the Genoid-ANIS model (Sect. 2.2) to study the influence of the irregular shape of the primary with a theoretical J2 of 0.19, assuming a uniform mass distribution (Descamps et al. 2008). No precession effects of the apsidal and nodal nodes have been detected, and the final orbit is not better than the purely Keplerian solution. To validate this result, we also ran a series of best-candidate searches freeing the J2 parameter in the interval from 0.0 to 0.26 (Fig. 3). We found a best solution for J2 ~ 0.0022, so a solution very close to the Keplerian orbit. There are, however, several solutions with fp < 18 mas and J2 < 0.15 which are least-likely candidate solutions, but which could be close to the real orbit considering the uncertainty of the astrometric positions. As visually shown in Fig. 5, these solutions are very similar in shape and clustered inside a torus of solutions which also contains the Keplerian orbit.
 |
Fig. 4 Predicted position of Linus (upper right blue cross) compared with the adjusted chords of Linus stellar occultation, see Descamps et al. (2008): Δx = 9 km = −7 mas, Δy = 3.6 km = 3 mas. |
Selecting three orbits with different values of J2, Fig. 6 shows that precession effects will modify the projected appearance of the orbits, with angular separations differing by ~30 mas at most, 3 to 4 times more than the 1-sigma accuracy of the astrometric positions. Over the next ten years, additional high resolution observations of the (22) Kalliope system could help to constrain the oblateness of the primary, and thus its interior structure.
If Kalliope’s primary is differentiated as suggested by this low J2, it should have a dense core surrounded by a less dense material. Partial differentiation is suggested for (21) Lutetia (Weiss et al. 2012), a 100-km main-belt asteroid with the same density than (22) Kalliope, which could have been affected by large-scale melting, leading to a metallic core formation.
 |
Fig. 5 Nine orbital solutions of the binary asteroid system (22) Kalliope are displayed in the equatorial J2000 reference plane. They represent the solutions for which fp < 18 mas (see Fig. 3) and the Keplerian solution. This 3D-representation of the orbits spanned over 10 years shows that they are very close in shape due to the low eccentricity and inclination of the orbits. |
 |
Fig. 6 Display of the projected orbits in the tangential plane derived from three orbital solutions as seen from Earth after 10 years of evolution, starting from the initial conditions with J2 = 0.0022, 0.1522, and 0.1891 (with fp = 13.9, 15.5, 19.2 mas, respectively). The red orbit corresponds to the best candidate from Genoid-ANIS with J2 ~ 0.0022, so very close to the Keplerian solution. The blue orbit corresponds to the best solution with J2 ~ 0.19 assuming a homogenous distribution of material in Kalliope’s primary and using the 3D-shape model by Descamps et al. (2008). The green orbit is an intermediate case with J2 = 0.15. |
4.2. The TNO binary system (50 000) Quaoar and its satellite Weywot
Weywot, the satellite of (50 000) Quaoar, was discovered in 2007 from observations with the Hubble Space Telescope (HST). Reanalyzing 2006 HST observations and adding data taken in 2008, Fraser & Brown (2010) we derived one best-fitting elliptical orbit.
 |
Fig. 7 Illustration of the convergence of the period obtained with a purely Keplerian model for Weywot, the moon of (50 000) Quaoar. All orbital elements necessary to reconstruct this orbit are listed in Table 1. |
The five astrometric positions published in Fraser & Brown (2010) were used as inputs into the Genoid-Kepler algorithm to estimate the mutual orbit of Weywot. The best-fitted orbital solution, with an excellent fp of 15.4 mas (see Table 1), is slightly different than the one published by our colleagues, with a period shorter by half of a day (P = 12.057 ± 0.005) and a semi-major axis of 14 470 ± 445 km, considering a 3-sigma error. This orbit leads to a mass of 1.65 ± 0.16 × 1021 kg. Fraser & Brown (2010) reported the absence of any detection of the satellite on 2 dates (Julian dates: 2 454 550.31485 and 2 454 556.44075). Based on our orbital model, we calculated the apparent positions of Weywot at the time of these observations, and found that the satellite was at 0.1914 arcsec (X = −0.1231 arcsec and Y = −0.1466 arcsec) and 0.2078 arcsec (X = −0.1531 arcsec and 0.1405 arcsec) from the primary, inside the core-region for which the satellite would not have been detected based on Fraser & Brown (2010).
Quaoar’s primary size has been estimated to be D = 1260 ± 190 km (Brown & Trujillo 2004), and by mid-infrared observation of its thermal emission to be D = 890 ± 70 km by combining Stansberry et al. (2008) and corrected HST estimates (Fraser & Brown 2010). Based on these measurements and our orbital solution, we derive average densities of 1.6 ± 1.3 g/cm3 and 4.5 ± 1.8 g/cm3 respectively.
More recently, a stellar occultation involving (50 000) Quaoar was successfully observed by Braga-Ribas et al. (2011) on May 04, 2011. The observation gives 5 positive chords, the longest of which suggests that Quaoar’s primary is elongated with a diameter at least of 1170 km, corresponding to an average density of 2 g/cm3 using our orbital model.
The density of (50 000) Quaoar is higher than for other multiple TNOs, implying that it has a significant rocky portion (larger than 70%) in its interior, most likely indicating a different origin and evolution.
4.3. Orbital solutions for (3749) Balam outermost companion
(3749) Balam is a complex multiple asteroid system with a complex history. Its first satellite was discovered in 2002 using an AO system mounted on the Gemini North telescope. Marchis et al. (2008a) attempted to derive the orbital parameters of this 2-km satellite diameter and found a solution with the satellite describing a highly eccentric orbit (e ~ 0.9 and a ~ 290 km) around the primary in 60 − 70 days. More recently, a careful photometric analysis of the lightcurves of Balam suggested that the primary of the system is in fact composed of two components with 6 and 2 km diameters orbiting at 20 km (Marchis et al. 2008b). We know that Marchis et al. (2008a) solution is flawed since they attempted to fit the position of the satellite when it was closer to its primary, confusing the outer and the inner moon position (the inner moon was unknown at the time of this analysis). Additionally, recently published observations of the triple system in the mid-infrared with Spitzer/IRS by Enriquez et al. (2010) were used to derive the equivalent size Deq = 4.68 ± 0.54 km, leading to an unrealistic average density of 8 g/cm3 based on the orbital solution of Marchis et al. (2008a). Vokrouhlický (2009) showed that Balam is a very young system with an age estimated to less than a million years old. This makes this asteroid an interesting body for understanding the evolution of small solar bodies, and for extending the study of the history of our solar system.
Our collected data for (3749) Balam are different from the previously studied systems shown in Sects. 4.1 and 4.2, since in this case we have significantly fewer observations, distributed over 17 months and corresponding to 4 − 13 periods of revolution. We used the astrometric positions from Marchis et al. (2008a), after having removed the astrometric positions which may be related to a marginal detection of the inner satellite. Using Genoid-Kepler we derived a bundle of 10 solutions with fp < 14 mas (Fig. 8), implying that we don’t have enough astrometric positions to derive a unique and accurate orbital solution. The complete set of orbital parameters for the best-fitted solution (fp = 12.36 mas) derived from Genoid is listed in Table 1.
Some of the orbital parameters of the 10 solutions for the outer satellite of Balam are listed in Table 2. From the periods and semi-major axes of the mutual orbits, we derived the corresponding masses and used the radiometric diameter derived by Enriquez et al. (2010) to calculate average densities which vary from 1.3 to 3.7 g/cm3. In contrast with Marchis et al. (2008a), these orbits give a realistic density for the (3749) Balam system, since this asteroid is classified as an S-type asteroid (Marchis et al. 2011).
Based on the derived orbital solutions, we show in Fig. 8 the projected shape of the satellite of (3749) Balam at the time of its next opposition at the end of February 2012. All orbits are significantly different from the others, so additional observations, if properly scheduled, should allow us to refine this analysis and derive a unique orbital solution for the outermost moon of (3749) Balam.
 |
Fig. 8 Period convergence obtained with our genetic-based algorithm with a purely Keplerian model for the outer-moon of (3749) Balam. Ten solutions with fp < 14 mas were identified, corresponding to various orbits drawn on January 2012 at the next Balam opposition. Additional data will help refining the orbit of this interesting triple asteroid system. |
Orbital parameters of 10 solutions derived by Genoid with the keplerian model for the outer moon of (3749) Balam with a similar fp.
5. Conclusion
Over the last ten years, our team has observed multiple asteroid systems and derived their physical properties from the analysis of their mutual orbits. We have used several different algorithms to estimate the orbital elements of the asteroid satellites, including geometrical (Descamps 2005), statistical (Hestroffer et al. 2005), and dynamical (Marchis et al. 2010) methods. Other groups have used similar types of algorithms to derive the orbits of a moon around the dwarf planet Pluto (Stern et al. 2006), Binary TNOs (Grundy et al. 2011), and Triple NEAs (Fang et al. 2011). For these works, assumptions have been made in the searched range of solutions linked to the physical properties (such as the mass, period, and eccentricity of the orbits). Our Genoid method has provided accurate orbit estimates capable of confirming the uniqueness of such solutions by exploring a large space of orbital parameters. In the last decade, metaheuristics, and more specifically the genetic algorithms, have become popular in many domains of astronomy and astrophysics. To our knowledge, this work is the first use of such an algorithm to derive the mutual orbits of asteroid satellites. This algorithm will allow us to regularly derive the orbital parameters of multiple asteroid systems as new data become available.
Our genetic algorithm, utilizing both a purely Keplerian and a more complex dynamical model, permitted the quick exploration of a broad space of orbital solutions for the satellites of (22) Kalliope, (3749) Balam and (50 000) Quaoar. Our tool can be used with high angular resolution data, as collected with adaptive optics for (22) Kalliope and (3749) Balam and HST for (50 000) Quaoar. We validated the Keplerian algorithm by comparison with already published works in the case of (22) Kalliope and (50 000) Quaoar. Despite the limited amount of data for (3749) Balam, our algorithm provided a bundle of possible orbital solutions which could be used to schedule future observations with high angular resolution telescopes to pinpoint a unique solution. We should be able to derive the best candidate orbit for (3749) Balam from a few additional observations during the upcoming oppositions.
The case of (22) Kalliope is particularly interesting. As shown using both Genoid algorithms, a purely Keplerian model can fit 10 years of observations collected with AO systems very well. However, there are still marginal solutions, assuming an elongated primary, that can be delivered by a more complex dynamical model. In the near future, additional observations will help to constrain the J2 and J4, and therefore the oblateness of the primary and the distribution of material in its interior. Our current analysis implies that the J2 of Kalliope primary is smaller than the expected value, assuming a homogenous distribution of mass, implying that the 166-km asteroid could be differentiated.
The binary asteroid systems for which Genoid was used to determine orbital parameters are now available on the Ephemeris IMCCE Web server (http://www.imcce.fr). The predicted positions of their moons and a display of the systems at any time can be generated using this server. This tool could be useful to predict or verify the position of the satellites at the time of stellar occultations (Berthier et al. 2004) or if a mutual occultation event is detectable in lightcurves. These observations are particularly encouraged since they could yield more accurate information about the system, such as the size and shape of the satellite.
Acknowledgments
The authors would like to thank an anonymous referee for his/her valuable comments and Keaton Burns for improving the quality of this manuscript. Part of this work was supported by the IMCCE computation service. Special thanks to S. Vaillant for maintaining the grid cluster and M. Allain for his contribution to this work. F.M. was supported by the National Science Foundation Under award number AAG-08077468 and the NASA grant NNX11AD62G. Most of the figures have been plotted using STILTS plotting tool (Taylor 2009).
References
- Belton, M. J. S., Mueller, B. E. A., D’Amario, L. A., et al. 1996, Icarus, 120, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Berthier, J., Marchis, F., Descamps, P., & Hestroffer, D. 2004, BAAS, 36, 1142 [NASA ADS] [Google Scholar]
- Braga-Ribas F., Sicardy B., Ortiz, J. L., et al. 2011, EPSC-DPS2011, 1060 [Google Scholar]
- Brown, M. E., & Trujillo, C. A. 2004, AJ, 127, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Brucker, M. J., Grundy, W. M., Stansberry, J. A., et al. 2009, Icarus, 201, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, C. R., Veverka, J., Thomas, P. C., et al. 1995, Nature, 374, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Descamps, P. 2005, Celest. Mech. Dyn. Astron., 92, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Descamps, P., Marchis, F., Pollock, J., et al. 2008, Icarus, 196, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Dréo, J., Siarry, P., Pétrowski, A., & Taillard, E. 2006, Metaheuristics for hard optimization (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Enriquez, J. E., Marchis, F., Emery, J. P., & Im, S. 2010, BAAS, 42, 1037 [NASA ADS] [Google Scholar]
- Fang, J., Margot, J.-L., Brozovic, M., et al. 2011, AJ, 141, 154 [CrossRef] [Google Scholar]
- Fraser, W. C., & Brown, M. E. 2010, ApJ, 714, 1547 [Google Scholar]
- Grundy, W. M., Noll, K. S., Nimmo, F., et al. 2011, Icarus, 213, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Hestroffer, D., Vachier, F., & Balat, B. 2005, Earth Moon and Planets, 97, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, R. A., Riedel, J. E., & Taylor, A. H. 1991, A&A, 247, 565 [NASA ADS] [Google Scholar]
- Laver, C., de Pater, I., Marchis, F., Ádámkovics, M., & Wong, M. H. 2009, Icarus, 204, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Le Guyader, C. 1993, A&A, 272, 687 [NASA ADS] [Google Scholar]
- Marchis, F., Descamps, P., Hestroffer, D., et al. 2003, Icarus, 165, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Marchis, F., Descamps, P., Hestroffer, D., & Berthier, J. 2005, Nature, 436, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Marchis, F., Descamps, P., Berthier, J., et al. 2008a, Icarus, 195, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Marchis, F., Pollock, J., Pravec, P., et al. 2008b, IAU Circ., 8928, 4 [NASA ADS] [Google Scholar]
- Marchis, F., Lainey, V., Descamps, P., et al. 2010, Icarus, 210, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Marchis, F., Enriquez, J. E., & Emery, J. P. 2011, Lunar and Planetary Institute Science Conference Abstracts, 42, 2035 [NASA ADS] [Google Scholar]
- Margot, J. L., & Brown, M. E. 2003, Science, 300, 1939 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2011, ApJ, 741, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, K. S., Stephens, D. C., Grundy, W. M., & Griffin, I. 2004, Icarus, 172, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Scaltriti, F., Zappala, V., & Stanzel, R. 1978, Icarus, 34, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Stansberry, J., Grundy, W., Brown, M., et al. 2008, The Solar System Beyond Neptune, 161 [Google Scholar]
- Stern, S. A., Weaver, H. A., Steffl, A. J., et al. 2006, Nature, 439, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2009, STILTS Plotting Tools, Astronomical Data Analysis Software and Systems XVIII, ASP Conf. Ser., 411 [Google Scholar]
- Veiga, C. H., Martins, R. V., & Le Guyader, C. 1999, A&AS, 136, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D. 2009, ApJ, 706, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, B. P., Elkins-Tanton, L. T., Barucci, M. A., et al. 2012, Planet. Space Sci., 66, 137 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Physical and dynamical parameters derived with Genoid with the keplerian model (EQJ2000).
Orbital parameters of 10 solutions derived by Genoid with the keplerian model for the outer moon of (3749) Balam with a similar fp.
All Figures
 |
Fig. 1 Schematic workflow of the Genoid algorithm. |
| In the text | |
 |
Fig. 2 Convergence of orbital parameters for Linus, moon of (22) Kalliope, derived from our genetic algorithm using a Keplerian model Genoid-Kepler. One solution with an orbital period of 3.595712 days is evident. The other orbital elements and their 3-sigma errors are listed in Table 1. The 3-sigma error bar corresponds to the mean precision of astrometry provided by the adaptive optic observations. |
| In the text | |
 |
Fig. 3 Search for the best J2 for the binary asteroid system (22) Kalliope with Genoid-ANIS. The best candidate solution is obtained for J2 ~ 0. |
| In the text | |
 |
Fig. 4 Predicted position of Linus (upper right blue cross) compared with the adjusted chords of Linus stellar occultation, see Descamps et al. (2008): Δx = 9 km = −7 mas, Δy = 3.6 km = 3 mas. |
| In the text | |
 |
Fig. 5 Nine orbital solutions of the binary asteroid system (22) Kalliope are displayed in the equatorial J2000 reference plane. They represent the solutions for which fp < 18 mas (see Fig. 3) and the Keplerian solution. This 3D-representation of the orbits spanned over 10 years shows that they are very close in shape due to the low eccentricity and inclination of the orbits. |
| In the text | |
 |
Fig. 6 Display of the projected orbits in the tangential plane derived from three orbital solutions as seen from Earth after 10 years of evolution, starting from the initial conditions with J2 = 0.0022, 0.1522, and 0.1891 (with fp = 13.9, 15.5, 19.2 mas, respectively). The red orbit corresponds to the best candidate from Genoid-ANIS with J2 ~ 0.0022, so very close to the Keplerian solution. The blue orbit corresponds to the best solution with J2 ~ 0.19 assuming a homogenous distribution of material in Kalliope’s primary and using the 3D-shape model by Descamps et al. (2008). The green orbit is an intermediate case with J2 = 0.15. |
| In the text | |
 |
Fig. 7 Illustration of the convergence of the period obtained with a purely Keplerian model for Weywot, the moon of (50 000) Quaoar. All orbital elements necessary to reconstruct this orbit are listed in Table 1. |
| In the text | |
 |
Fig. 8 Period convergence obtained with our genetic-based algorithm with a purely Keplerian model for the outer-moon of (3749) Balam. Ten solutions with fp < 14 mas were identified, corresponding to various orbits drawn on January 2012 at the next Balam opposition. Additional data will help refining the orbit of this interesting triple asteroid system. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


