| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 4 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219231 | |
| Published online | 18 June 2012 | |
Research Note
Fermi I particle acceleration in converging flows mediated by magnetic reconnection
Dublin Institute for Advanced Studies, 31 Fitzwilliam Place, Dublin 2, Ireland
e-mail: valenti@cp.dias.es
Received: 16 March 2012
Accepted: 14 May 2012
Context. Converging flows with strong magnetic fields of different polarity can accelerate particles through magnetic reconnection. If the particle mean free path is longer than the reconnection layer is thick, but much shorter than the entire reconnection structure, the particle will mostly interact with the incoming flows potentially with a very low escape probability.
Aims. We explore, in general and also in some specific scenarios, the possibility of particles to be accelerated in a magnetic reconnection layer by interacting only with the incoming flows.
Methods. We characterize converging flows that undergo magnetic reconnection, and derive analytical estimates for the particle energy distribution, acceleration rate, and maximum energies achievable in these flows. We also discuss a scenario, based on jets dominated by magnetic fields of changing polarity, in which this mechanism may operate.
Results. The proposed acceleration mechanism operates if the reconnection layer is much thinner than its transversal characteristic size, and the magnetic field has a disordered component. Synchrotron losses may prevent electrons from entering in this acceleration regime. The acceleration rate should be faster, and the energy distribution of particles harder than in standard diffusive shock acceleration. The interaction of obstacles with the innermost region of jets in active galactic nuclei and microquasars may be suitable sites for particle acceleration in converging flows.
Key words: magnetic reconnection / acceleration of particles / radiation mechanisms: non-thermal
© ESO, 2012
1. Introduction
The interaction of outflows with themselves or their environment usually leads to particle acceleration (e.g. Rieger et al. 2007), and the most common acceleration mechanism in these circumstances is thought to be diffusive shock (Fermi I) acceleration (e.g. Krymskii 1977; Bell 1978a,b; Blandford & Ostriker 1978; Drury 1983). This process works well when a plasma with a weak disordered magnetic field (B) suffers a strong shock. The Fermi I acceleration efficiency depends on the energy gain when particles cross the shock, and on the escape probability downstream the shock, which is related to the shock compression ratio R = v/v′, v′(v) being the post(pre)-shock velocity.
In strong non-relativistic adiabatic shocks in the test-particle approximation R equals 4, and the resulting energy distribution is Q(E) ∝ 1/E2 (e.g. Drury 1983). In radiative shocks, R ≫ 4, but densities become very high and energy losses and damping of magnetic irregularities may limit the efficiency of the acceleration process (e.g. Drury et al. 1996; Reville et al. 2007; see nevertheless Sect. 2.2). For plasmas that carry a strong perpendicular B-component, R is ~1, and Fermi I acceleration is suppressed. However, if the B-field has reversals, energy can be dissipated via magnetic reconnection in regions where the charge density is not sufficiently high to sustain different polarity B-lines (e.g. Parker 1957; Petschek 1964; Speiser 1965; Sonnerup 1971; Zenitani & Hoshino 2001), allowing for R ≫ 1 (e.g. Drury 2012).
Studies show that magnetic reconnection can accelerate the bulk of particles up to the pre-reconnection Alfvénic speed, with some particles reaching even higher energies (e.g. Zenitani & Hoshino 2001; Lyubarsky & Liverts 2008; Kowal et al. 2011). Magnetic reconnection may also lead to the formation of strong shocks, accelerating particles through the standard Fermi I mechanism in an otherwise weakly compressive flow (e.g. Forbes 1988; Blackman & Field 1994; Sironi & Spitkovsky 2011). Fermi I particle acceleration may operate in the reconnection region itself (e.g. de Gouveia dal Pino & Lazarian 2005; Giannios 2010; Drury 2012), since particles can bounce back and forth between the layer and the converging flows. The mean free path λ of these particles can eventually overcome the layer thickness, ΔY, and then particles will not interact significantly with the reconnection layer, but with the perpendicular B-lines of the converging flows (Giannios 2010). In this case, the advection escape probability becomes formally zero because the flows do not move away from the reconnection layer. This is true as long as the mean free path of the particle parallel to B, λ∥, is much shorter than the characteristic size of the entire reconnection region, ΔX (to order the magnetic field reversal scale). Escape in the opposite direction to the incoming flow can be neglected unless the region extension in this direction is ≪ΔX. A schematic picture of this scenario is presented in Fig. 1, which shows two cases: the interaction of a flow carrying different polarity B-lines with an obstacle (described in Sect. 3); and the interaction of two flows with different polarity B-lines. As shown in the figure, particles can spiral back and forth between the two sides of the reconnection layer until they diffuse away from the region.
In this note, we analytically explore the Fermi I mechanism when particles interact with converging flows in the null-escape probability regime. We assume that particles can effectively diffuse through the incoming flows. We focus on the case when magnetic reconnection is the mechanism that leads to R ≫ 1. We derive in Sect. 2 analytical estimates for the acceleration rate, the maximum energy and energy distribution of the accelerated particles, and present in Sect. 3 an illustrative case in the context of galactic and extragalactic jets. For simplicity, the discussions are restricted to Newtonian flows, although our conclusions qualitatively apply to the relativistic case as well. For some magnitudes, we will adopt the convention Qx = (Q/10x cgs).
 |
Fig. 1 Sketch of the considered scenario: a) the interaction of one flow carrying different polarity B-lines with an obstacle (see Sect. 3); b) the interaction of two flows with different polarity B-lines. |
2. Particle acceleration in converging flows
In converging flows, particles slowly diffuse perpendicularly to the B-lines, with λ⊥ ~ rg/χ, where χ, with value ≥ 1, is the total to the disordered magnetic energy density ratio. Remarkably, a disordered B-component can enhance the reconnection rate and the reconnecting flow velocity v, as shown for instance in Lazarian & Vishniac (1999). The following limit for Fermi I to operate between the converging flows can be imposed: in the current sheet, λ ⊥ > ΔY, i.e. Emin ~ χ q Br ΔY, where Br is the B-field in there. Although one can expect that Br ≪ B close to the center of the current sheet, we conservatively assume that over the whole reconnection layer Br ~ B. On the other hand, the B-lines become more and more entangled close to the reconnection layer, so one can set there χ = 1. The previous condition becomes 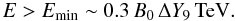 (1)In addition, to be efficiently accelerated, particles in the incoming flows should not drift too early along the B-lines, parallel to the layer, out of the reconnection region (cross-field diffusive escape will be slower by 1/χ2). This is a sort of Hillas limit: λ∥ ~ χ rg < ΔX, or
(1)In addition, to be efficiently accelerated, particles in the incoming flows should not drift too early along the B-lines, parallel to the layer, out of the reconnection region (cross-field diffusive escape will be slower by 1/χ2). This is a sort of Hillas limit: λ∥ ~ χ rg < ΔX, or 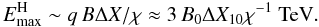 (2)This gives the maximum dynamical range
(2)This gives the maximum dynamical range 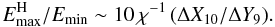 (3)Giannios (2010) accounted for the electric field between the sides of the reconnection layer: ϵ ~ v B. The ϵ-field accelerates the particles perpendicularly to B and v, with Emax ~ (v/c)qBΔX. The fraction of time spent by particles within the reconnection layer during an acceleration cycle is ΔY/c tcycle, and thus this effect will be important at E ~ Emin or for very ordered fields.
(3)Giannios (2010) accounted for the electric field between the sides of the reconnection layer: ϵ ~ v B. The ϵ-field accelerates the particles perpendicularly to B and v, with Emax ~ (v/c)qBΔX. The fraction of time spent by particles within the reconnection layer during an acceleration cycle is ΔY/c tcycle, and thus this effect will be important at E ~ Emin or for very ordered fields.
From Eqs. (2), (3) one can see that the quantities χ and ΔX/ΔY are crucial for the efficiency of the discussed acceleration mechanism. The derivation of χ requires a detailed treatment of the plasma, but as mentioned, given the dramatic change of the B-geometry, close to the reconnection layer χ ~ 1. On scales of ΔX, and given the high plasma characteristic speeds, the disordered B-field generated in the reconnection layer may propagate to the converging flows, although such a B-component may also have an external origin. To estimate ΔX/ΔY, we briefly discuss the flow dynamics below.
 |
Fig. 2 Sketch of the converging and the outgoing flows in the reconnection region. |
2.1. Flow dynamics
The plasma that enters, flows along, and eventually leaves the reconnection layer, as shown in Fig. 2, can be described by the particle and energy flux conservation equations:  where unprimed/primed quantities correspond to the incoming/outgoing flows, ρ is the density, v the velocity, and A ~ ΔX2 and A′ ~ 4ΔXΔY are the in- and out-flow areas, respectively. The flow pressure is assumed to be negligible in the converging flows because of strong B-dominance. When leaving the region, under negligible external pressure and reasonable geometries, the flow kinetic energy becomes dominant and pressure can be neglected as well.
where unprimed/primed quantities correspond to the incoming/outgoing flows, ρ is the density, v the velocity, and A ~ ΔX2 and A′ ~ 4ΔXΔY are the in- and out-flow areas, respectively. The flow pressure is assumed to be negligible in the converging flows because of strong B-dominance. When leaving the region, under negligible external pressure and reasonable geometries, the flow kinetic energy becomes dominant and pressure can be neglected as well.
Given the symmetry of the problem, there is no momentum conservation equation, and the conditions deep within the reconnection layer are hard to determine. Equations (4) and (5) yield 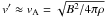 and thus ρ′ ≈ ρ (A/A′)(v/vA), but one has to make additional assumptions to obtain ΔX/ΔY. An estimate may be derived assuming one-dimensional adiabatic compression of Br, the remaining field after reconnection in the layer, until it balances the incoming field pressure. This gives ρ′/ρ ~ (B/Br) and therefore an area ratio A′/A = (Br/B)(v/vA), or ΔX/ΔY ~ 4(B/Br)(vA/v). An upper limit for ΔX/ΔY would come from ΔY ~ ⟨ rg ⟩ , where ⟨ rg ⟩ is the gyroradius of the average particle in the reconnection layer. A lower limit may be derived assuming equilibrium between the upstream magnetic pressure and the thermal pressure inside the layer of thickness ΔY, implying (ΔX/ΔY) ~ 4(vA/v). One can therefore conclude that the dynamical range may span several orders of magnitude in energy, but it needs an efficient magnetic-to-kinetic energy transfer (which may be reasonable, as suggested in Drury 2012).
and thus ρ′ ≈ ρ (A/A′)(v/vA), but one has to make additional assumptions to obtain ΔX/ΔY. An estimate may be derived assuming one-dimensional adiabatic compression of Br, the remaining field after reconnection in the layer, until it balances the incoming field pressure. This gives ρ′/ρ ~ (B/Br) and therefore an area ratio A′/A = (Br/B)(v/vA), or ΔX/ΔY ~ 4(B/Br)(vA/v). An upper limit for ΔX/ΔY would come from ΔY ~ ⟨ rg ⟩ , where ⟨ rg ⟩ is the gyroradius of the average particle in the reconnection layer. A lower limit may be derived assuming equilibrium between the upstream magnetic pressure and the thermal pressure inside the layer of thickness ΔY, implying (ΔX/ΔY) ~ 4(vA/v). One can therefore conclude that the dynamical range may span several orders of magnitude in energy, but it needs an efficient magnetic-to-kinetic energy transfer (which may be reasonable, as suggested in Drury 2012).
2.2. Acceleration and radiation processes
Like in standard diffusive shock acceleration, particles gain energy by moving back and forth between the incoming flows as ΔE/E ~ v/c per cycle. In addition, since there is no advection directed outwards, the probability to cross back to the other side of the reconnection layer becomes 1 after covering few λ ⊥ in each incoming flow, i.e. tcycle ~ (k/χ) rg/c, with k ~ 10. This tcycle gives an acceleration rate 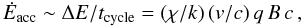 (6)and the zero advection escape probability renders a particle energy distribution Q(E) ∝ 1/E up to energies a few times lower than
(6)and the zero advection escape probability renders a particle energy distribution Q(E) ∝ 1/E up to energies a few times lower than 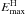 , at which the distribution drops very quickly. Note that this mechanism is faster in Ėacc ((v/c) vs. (v/c)2) and yields a harder Q(E) (1/E vs. 1/E2) than standard Fermi I. Such a hard distribution of accelerated particles can become dominant in pressure. This should smooth the v profile and affect Q(E) (as in non-linear Fermi I acceleration; e.g. Drury 1983).
, at which the distribution drops very quickly. Note that this mechanism is faster in Ėacc ((v/c) vs. (v/c)2) and yields a harder Q(E) (1/E vs. 1/E2) than standard Fermi I. Such a hard distribution of accelerated particles can become dominant in pressure. This should smooth the v profile and affect Q(E) (as in non-linear Fermi I acceleration; e.g. Drury 1983).
Radiation losses can stop the acceleration at 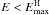 . Typically, for protons these losses are fairly inefficient, whereas for electrons synchrotron cooling (e.g. Blumenthal & Gould 1970) tends to be important, which renders a maximum energy
. Typically, for protons these losses are fairly inefficient, whereas for electrons synchrotron cooling (e.g. Blumenthal & Gould 1970) tends to be important, which renders a maximum energy 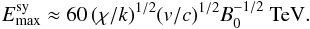 (7)In environments with very dense matter or photon fields, other cooling processes might be relevant, such as relativistic Bremsstrahlung and inverse Compton (IC) for electrons (e.g. Blumenthal & Gould 1970), and proton-proton collisions (pp), synchrotron and photomeson production for protons (e.g. Kelner et al. 2006; Aharonian 2000; Kelner & Aharonian 2008). Diffusive escape parallel to B can also be more restrictive than the Hillas limit:
(7)In environments with very dense matter or photon fields, other cooling processes might be relevant, such as relativistic Bremsstrahlung and inverse Compton (IC) for electrons (e.g. Blumenthal & Gould 1970), and proton-proton collisions (pp), synchrotron and photomeson production for protons (e.g. Kelner et al. 2006; Aharonian 2000; Kelner & Aharonian 2008). Diffusive escape parallel to B can also be more restrictive than the Hillas limit:  (8)The corresponding dynamical ranges are
(8)The corresponding dynamical ranges are 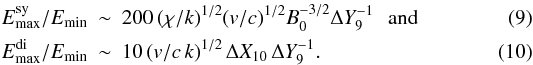 In general, to accelerate particles to TeV energies, at least mildly relativistic vA-values will be required. In addition, for electrons, if converging flow acceleration is to be efficient,
In general, to accelerate particles to TeV energies, at least mildly relativistic vA-values will be required. In addition, for electrons, if converging flow acceleration is to be efficient, 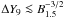 . This will typically require in astrophysical sources either very high compression ratios, or very low magnetic fields, the latter implying a very large structure (e.g. magnetized turbulent ISM) if the process is to have observable radiative effects. For protons, the Hillas and diffusive limits lead to the more reasonable conditions ΔX > χΔY and > (v/c k) − 1/2ΔY, respectively. Note nevertheless that electrons remaining within the reconnection layer may still be accelerated by electric fields generated in the reconnection process, resulting in energies ≲ Emin. In this case, the accelerated energy distribution could also be Q(E) ∝ 1/E (e.g. Zenitani & Hoshino 2001).
. This will typically require in astrophysical sources either very high compression ratios, or very low magnetic fields, the latter implying a very large structure (e.g. magnetized turbulent ISM) if the process is to have observable radiative effects. For protons, the Hillas and diffusive limits lead to the more reasonable conditions ΔX > χΔY and > (v/c k) − 1/2ΔY, respectively. Note nevertheless that electrons remaining within the reconnection layer may still be accelerated by electric fields generated in the reconnection process, resulting in energies ≲ Emin. In this case, the accelerated energy distribution could also be Q(E) ∝ 1/E (e.g. Zenitani & Hoshino 2001).
Synchrotron emission from electrons injected with Q(E) ∝ 1/E and cooled through this process would have a spectral energy distribution ν Lν ∝ ν1/2. On the other hand, proton radiation would show ν Lν ∝ ν for synchrotron (or ∝ ν1/2 in saturation) and for π0-decay from pp and photomeson production (above threshold). The last two processes also generate secondary e± pairs from π ± -decay with spectra and luminosities similar to those of the photons from π0-decay. These pairs will predominantly cool through synchrotron, like primary electrons, also with ν Lν ∝ ν1/2 but peaking at much higher energies.
Before exploring the case of magnetized jets, we note that our results may also be applied to weakly magnetized flows with radiative shocks. Particle acceleration between the upstream and the cooled downstream would require sufficiently energetic particles to cross the adiabatic region of the post-shock flow and reach the cooled downstream medium. Another condition would be that the particle cooling/escape timescales were longer everywhere than the acceleration one. In this context, young stellar object jet shocks, or the dense winds of two massive stars colliding, may be sources worthy of being investigated.
3. The case of magnetized jets
Powerful astrophysical outflows, such as pulsar winds, and microquasar and AGN jets, are expected to be magnetically dominated at their formation and acceleration zones (e.g. Coroniti 1990; Bogovalov & Tsinganos 1999; Beskin & Nokhrina 2006; Komissarov et al. 2007). In pulsar winds, magnetic reconnection may take place naturally in a current sheet that originated at the wind equatorial region (Coroniti 1990; Lyubarsky & Kirk 2001). In relativistic jets, a B-field with reversals could come from the accretion disc (e.g. Barkov & Baushev 2011), but magnetic dissipation may need to be triggered through jet acceleration, which could drive magnetic reconnection through the Kruskal-Schwarzschild instability (see Lyubarsky 2010). A similar though more extreme effect can be expected if an obstacle is entrained by the jet (e.g. Hubbard & Blackman 2006; Araudo et al. 2009, 2010; Barkov et al. 2010, 2012; Perucho & Bosch-Ramon 2012; Bosch-Ramon et al. 2012) with a dominant B-field with polarity reversals of size ΔX. Under the ongoing magnetic reconnection, the incoming jet material and the obstacle itself can play the role of converging flows with a high ΔX/ΔY ratio. To avoid the suppression of the acceleration process, the shocked obstacle must fulfil the following conditions: high inertia, to avoid quick dragging by the jet; not too high density, to avoid fast radiation cooling; and a mean free path much shorter than the obstacle size (Do), to avoid fast particle escape.
For a jet/obstacle interaction at zj ~ 100 RSch from the central object, where RSch ≈ 3 × 1013 (M/108 M⊙) cm, a jet width Dj ~ 0.1 zj ~ 3 × 1014 (M/108 M⊙) cm and magnetic field 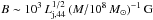 , and Do ≳ ΔX, the luminosity budget available for dissipation will be Ld ~ (Do/Dj)2 Lj ≤ Lj, where Lj is the jet power. Assuming ΔX ~ RSch, the electron and proton maximum energies will be
, and Do ≳ ΔX, the luminosity budget available for dissipation will be Ld ~ (Do/Dj)2 Lj ≤ Lj, where Lj is the jet power. Assuming ΔX ~ RSch, the electron and proton maximum energies will be  , and
, and 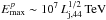 .
.
Given the strong magnetic fields, the condition 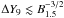 may not hold; if so, electrons could only be accelerated within the reconnection layer. Thus, in AGN jet/obstacle interactions, magnetic reconnection itself could potentially accelerate electrons up to TeV energies. Protons, on the other hand, could be accelerated in the converging flows1 to ultra high energies or even beyond depending on ΔX, Lj, and Do (see Giannios 2010, for similar results). Electrons would yield hard synchrotron radiation peaking around 10 MeV. Proton synchrotron emission, of hard spectrum and peaking around 100 GeV, may be efficient as well under these conditions (see, e.g., Barkov et al. 2012). Emission through pp inside the obstacle could be also significant (Barkov et al. 2010), as well as photomeson production in very bright AGN. Secondary very energetic e± pairs from π ± -decay would radiate ultra high-energy photons through synchrotron emission that could pair-create in the jet radio fields on pc-scales, being reprocessed as synchrotron and IC photons of lower energies.
may not hold; if so, electrons could only be accelerated within the reconnection layer. Thus, in AGN jet/obstacle interactions, magnetic reconnection itself could potentially accelerate electrons up to TeV energies. Protons, on the other hand, could be accelerated in the converging flows1 to ultra high energies or even beyond depending on ΔX, Lj, and Do (see Giannios 2010, for similar results). Electrons would yield hard synchrotron radiation peaking around 10 MeV. Proton synchrotron emission, of hard spectrum and peaking around 100 GeV, may be efficient as well under these conditions (see, e.g., Barkov et al. 2012). Emission through pp inside the obstacle could be also significant (Barkov et al. 2010), as well as photomeson production in very bright AGN. Secondary very energetic e± pairs from π ± -decay would radiate ultra high-energy photons through synchrotron emission that could pair-create in the jet radio fields on pc-scales, being reprocessed as synchrotron and IC photons of lower energies.
In microquasar jets, where, say, M ~ 10 M⊙ and Lj ~ 1036 erg s-1, magnetic reconnection in the jet/obstacle boundary at zj ~ 100 RSch could lead to synchrotron MeV flares produced by GeV electrons. A minor synchrotron self-Compton component in GeV may be also expected. PeV protons may be accelerated in the converging flows, and if they met a nearby thick target, for instance the obstacle itself or a dense field of energetic photons, they could produce hard emission peaking at ~100 TeV through pp or photomeson production, plus hard TeV synchrotron radiation from the subsequent e± pairs. In compact and powerful objects photon-photon absorption would be severe, radiation being re-emitted as soft gamma rays via synchrotron emission. It is not clear which kind of obstacle may be present in the innermost regions of a microquasar jet, although in the (unlikely) event that the jet remained strongly magnetized up to the binary scales ( ≫ 100 RSch), a clumpy stellar wind could provide those obstacles (Araudo et al. 2009).
In both microquasars and AGN, the reconnection process can be efficient as long as the obstacle has a velocity different from that of the flow. In this process, for Do ~ Dj, a significant fraction of Lj may be released, with potential fluxes at high energies F ~ 10-10 erg cm-2 s-1 × Ld,44 (d/100 Mpc)-2 for AGN, and × Ld,36 (d/10 kpc)-2 for microquasars. This radiation would be roughly isotropic, but for obstacles small and light enough to be accelerated by the jet, the emission would become progressively Doppler-boosted and enhanced for specific viewing angles. The obstacle may expand, enhancing the radiation, and possibly fragment while accelerated. All this should lead to complex spectral and variability patterns (e.g. Barkov et al. 2010, 2012). The typical timescale of the whole interaction process will be the time the
obstacle remains as such (see, e.g., Bosch-Ramon et al. 2012), whereas the reconnection events will have a variability timescale ~min [Do,ΔX] /v, where v ≲ c.
Acknowledgments
We thank an anonymous referee for constructive and useful comments and suggestions. We are grateful to Maxim Barkov, Luke Drury and Dmitry Khangulyan for fruitful discussions. The research leading to these results has received funding from the European Union Seventh Framework Program (FP7/2007-2013) under grant agreement PIEF-GA-2009-252463. V.B.-R. acknowledges support by the Spanish Ministerio de Ciencia e Innovación (MICINN) under grants AYA2010-21782-C03-01 and FPA2010-22056-C06-02.
References
- Aharonian, F. A. 2000, New Astron., 5, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2009, A&A, 503, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2010, A&A, 522, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barkov, M. V., & Baushev, A. N. 2011, New Astron., 16, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Barkov, M. V., Aharonian, F. A., & Bosch-Ramon, V. 2010, ApJ, 724, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Barkov, M. V., Aharonian, F. A., Bogovalov, S. V., Kelner, S. R., & Khangulyan, D. 2012, ApJ, 749, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978a, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978b, MNRAS, 182, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Beskin, V. S., & Nokhrina, E. E. 2006, MNRAS, 367, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Blackman, E. G., & Field, G. B. 1994, Phys. Rev. Lett., 73, 3097 [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Bogovalov, S., & Tsinganos, K. 1999, MNRAS, 305, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., Perucho, M., & Barkov, M. V. 2012, A&A, 539, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coroniti, F. V. 1990, ApJ, 349, 538 [NASA ADS] [CrossRef] [Google Scholar]
- de Gouveia dal Pino, E. M., & Lazarian, A. 2005, A&A, 441, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drury, L. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. 2012, MNRAS, 422, 2474 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L., Duffy, P., & Kirk, J. G. 1996, A&A, 309, 1002 [NASA ADS] [Google Scholar]
- Forbes, T. G. 1988, Sol. Phys., 117, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D. 2010, MNRAS, 408, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, A., & Blackman, E. G. 2006, MNRAS, 371, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., & Aharonian, F. A. 2008, Phys. Rev. D, 78, 034013 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Kowal, G., de Gouveia Dal Pino, E. M., & Lazarian, A. 2011, ApJ, 735, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Krymskii, G. F. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- Lazarian, A., & Vishniac, E. T. 1999, ApJ, 517, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y. 2010, ApJ, 725, L234 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y., & Kirk, J. G. 2001, ApJ, 547, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y., & Liverts, M. 2008, ApJ, 682, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1957, J. Geophys. Res., 62, 509 [Google Scholar]
- Perucho, M., & Bosch-Ramon, V. 2012, A&A, 539, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petschek, H. E. 1964, NASA Special Publ., 50, 425 [Google Scholar]
- Reville, B., Kirk, J. G., Duffy, P., & O’Sullivan, S. 2007, A&A, 475, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieger, F. M., Bosch-Ramon, V., & Duffy, P. 2007, Ap&SS, 309, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2011, ApJ, 741, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnerup, B. U. Ö. 1971, J. Geophys. Res., 76, 8211 [NASA ADS] [CrossRef] [Google Scholar]
- Speiser, T. W. 1965, J. Geophys. Res., 70, 4219 [NASA ADS] [CrossRef] [Google Scholar]
- Zenitani, S., & Hoshino, M. 2001, ApJ, 562, L63 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of the considered scenario: a) the interaction of one flow carrying different polarity B-lines with an obstacle (see Sect. 3); b) the interaction of two flows with different polarity B-lines. |
| In the text | |
 |
Fig. 2 Sketch of the converging and the outgoing flows in the reconnection region. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


