| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219134 | |
| Published online | 12 June 2012 | |
Unique sextuple system: 65 Ursae Majoris⋆
1 Astronomical Institute, Faculty of Mathematics and Physics, Charles University Prague, 180 00 Praha 8, V Holešovičkách 2, Czech Republic
e-mail: zasche@sirrah.troja.mff.cuni.cz
2 Private Observatory, Pohoří 71, 25401 Jílové u Prahy, Czech Republic
3 Astronomical Institute, Academy of Sciences, Fričova 298, 251 65 Ondřejov, Czech Republic
Received: 29 February 2012
Accepted: 28 March 2012
Context. The study of stellar multiple systems provides us with important information about the stellar formation processes and can help us to estimate the multiplicity fraction in the Galaxy. 65 UMa belongs to a rather small group of stellar systems of higher multiplicity, whose inner and outer orbits are well-known. This allows us to study the long-term stability and evolution of the orbits in these systems.
Aims. We obtained new photometric and spectroscopic data that when combined with interferometric data enables us to analyze the system 65 UMa and determine its basic physical properties.
Methods. We perform a combined analysis of the light and radial velocity curves, as well as the period variation by studying the times of the minima and the interferometric orbit. A disentangling technique is used to perform the spectra decomposition. This combined approach allows us to study the long-term period changes in the system for the first time, identifying the period variation due to the motion on the visual orbit, in addition to some short-term modulation.
Results. We find that the system contains one more component, hence we tread it as a sextuple hierarchical system. The most inner pair of components consists of an eclipsing binary orbiting around a barycenter on a circular orbit, both components being almost identical of spectral type about A7. This pair orbits on an eccentric orbit around a barycenter, and the third component orbits with a period of about 640 days. This motion is reflected in the period variation in the minima times of the eclipsing pair, as well as in the radial velocities of the primary, secondary, and tertiary components. Moreover, this system orbits around a barycenter with the distant component resolved interferometrically, whose period is of about 118 years. Two more distant components (4′′ and 63′′) are also probably gravitationally bound to the system. The nodal period of the eclipsing-pair orbit is on the order of only a few centuries, which makes this system even more interesting for a future prospective detection of changing the depths of minima.
Conclusions. We identify a unique solution of the system 65 UMa, decomposing the individual components and even shifting the system to higher multiplicity. The study of this kind of multiple can help us to understand the origin of stellar systems. Besides 65 UMa, only another 11 sextuple systems have been studied.
Key words: binaries: eclipsing / stars: fundamental parameters / stars: individual: 65 UMa / stars: early-type
Reduced photometric and spectroscopic data, and Tables A.1–A.4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/542/A78
© ESO, 2012
1. Introduction
As members of more complex multiple systems, the eclipsing binaries can provide us important information about their physical properties, as derived from different methods. This is the case for 65 UMa, a system whose the close components form an eclipsing binary, and additional components found to be gravitationally bounded to this pair (Pourbaix et al. 2004). Thanks to the combined analysis, we have been able to derive the radii, masses, and evolutionary statuses of the close components, in addition to some properties of the distant ones. These systems are still very rare and mostly lie relatively close to the solar system. Only 39 such systems are known where a close eclipsing binary is a member of a wide visual binary and we know both orbits, their mutual inclinations, ratio of periods, etc. For instance, the ratio of periods can tell us something about the long-term stability of the system. These unique systems are the most suitable for studies of dynamical effects, the short and long-term evolution of the orbits, etc. (see e.g. Söderhjelm 1975).
The study of systems of higher multiplicity is still relatively undeveloped yet, and can provide insight into their formation. Moreover, Goodwin & Kroupa (2005) found that the majority of the early-type stars are found in multiple systems. Star-forming theories are still based on many ad hoc assumptions and the physical characteristics of the multiple systems can provide strong constraints on some of them. These can be e.g. the mass ratios of the inner and outer pairs, the ratio of periods, and inclinations, see for instance (Goodwin et al. 2007; Tokovinin 2008). In addition, the multiplicity fraction is one of the most crucial parameters in theoretical models and nowadays we know of only 20 quintuples, 11 sextuples, and 2 septuple systems (Eggleton & Tokovinin 2008).
2. The system 65 UMa
The multiple system 65 UMa (=WDS J11551+4629) consists of four visible components. The angular distance between the primary and component D (=HR 4561) is about 63′′, while the C component is at a distance of about 4′′. The primary 65 UMa AB = DN UMa, the brightest member of the system, was also resolved to be a binary via classical micrometric measurements by Aitken (1908). Since then, many precise interferometric observations of this close pair were carried out. Moreover, the primary component was discovered to be a variable (Gimenez & Quesada 1979). Later, Gimenez & Quesada (1982) found the star to be an eclipsing binary with the orbital period of about 1.7304 d. Its variability was not discovered earlier owing to its rather shallow eclipses of only about 0.09 mag. This is caused by the presence of other components in the aperture and therefore a large fraction of the third light, which reduces the photometric amplitude of the eclipses. The light curve (hereafter LC) analysis presented by Garcia & Gimenez (1986) was slightly indicative of an eccentric orbit. The radial velocity curve (hereafter RV) was analyzed by Popper (1986). All of these studies found that the close binary consists of two very similar stars.
The position angle between the A and B components slowly changes, therefore an orbit of this pair was derived most recently by Aristidi et al. (1999), who found a period of about 137 yr and a semi-major axis about 225 mas. The position angle of the pair has changed since this last paper by about 40°, hence a new analysis is required. Moreover, the combined analysis of the visual orbit together with the times-of-minima variation due to the movement on this orbit and the radial-velocity variations can reveal some of the other parameters of the orbit and also of both AB and C components. The more distant C and D components also belong to this multiple system, but these show no detectable mutual motion and can be assumed to be motionless. The MSC catalog by Tokovinin (1997) gives their periods 11 kyr and 591 kyr, respectively.
A distance to 65 UMa was derived from the Hipparcos data. Perryman et al. (1997) gives the value of distance d = 246 ± 108 pc, while the new reduction of van Leeuwen (2007) presented the value d = 212 ± 30 pc. The combined spectral type of the AB pair was classified as A3Vn by Cowley et al. (1969), while the spectrum of the D component is A2p (Slettebak 1963), and Joshi et al. (2010) carried out an analysis of this star. On the other hand, the spectral classification of the C component has never been performed. Therefore, the mass of the C component is also poorly constrained and the only information about this star that we have is a rough estimate of the magnitude difference (see below).
3. Observations and data reduction
In total, the target was observed on 82 nights: 29 nights for photometry, and 53 nights for spectroscopy. The complete BVRI light curves of the eclipsing pair were obtained in 2010 at the private observatory of one of the authors (RU). However, owing to the relatively high brightness of the target, only a small 254-mm reflector of moderate focal length was used. This telescope was unable to separate the two 4′′ distant components, therefore the resultant LC was a composite AB+C light curve. The CCD photometric observations were obtained in standard B, V, and R filters according to the specification of Bessell (1990). All of the observations used for the LC were obtained with the same telescope and instrument setup, and the reduction was also identical. Furthermore, the complete set of minima times used for the analysis is given in Tables A.1–A.4 (available at the CDS), two new minima were measured by Petr Svoboda, Czech Republic.
The CCD spectra were obtained at Ondřejov observatory, Czech Republic, using the 2.0-m telescope equipped with a SITe-005 800 × 2000 CCD detector. These spectra cover a wavelength region 626–676 nm. All of them were secured between March 2010 and July 2011 and have a resolving power R ~ 12 700. Their S/N values range typically between 100 and 300.
For all of the spectra, the wavelength calibration was done using a ThAr comparison spectra obtained before and after the stellar spectra itself. The data reduction was performed following the standard procedures of the data reduction package IRAF1. The flatfields were taken in the beginning and end of each night and their means were used in the data reduction. After then, the radial velocities were obtained with the program SPEFO (Horn et al. 1996; Škoda 1996), using the zero point correction by measuring the telluric lines. In total, 55 spectra were obtained in this way.
All available data used for the analysis, the photometry, times of minima, spectroscopy, and the interferometric measurements are also listed (see the CDS tables).
Parameters of the visual (A-B) orbit.
4. Visual orbit and the period analysis
To begin with, we analyzed the visual orbit. The orbital motion influences the apparent period of the inner eclipsing pair, hence the periodic variation in the times of minima are analyzed according to the visual orbit parameters.
 |
Fig. 1 Visual orbit of 65 UMa pair (A-B) as displayed on the sky. The eclipsing binary is placed in [0, 0]. The dotted line represents the line of the apsides, while the dashed one is the line of the nodes. See Sect. 4. |
Since its discovery as a double, 35 observations of the A-B pair have been obtained. These have been collected in the Washington Double Star Catalog (hereafter WDS2, Mason et al. 2001). We analyzed the data, obtaining the parameters of the visual orbit presented in Table 1, and the final fit together with the data is given in Fig. 1. As one can see from Table 1, the parameters differ significantly in some aspects. Besides the higher precision, the most significant difference is found for the orientation of the orbit in space. It is obvious that the same fit to the data can be obtained with different sets of parameters when we only interchange the values of two parameters: (Ω,ω) → (Ω + 180°,ω + 180°). However, when dealing with astrometric data set only, one cannot distinguish between these two identical solutions. The only way to do so is to use also the RV data, or the times-of-minima variation.
For the minimum-times observations, we have only a limited set of data points. If we consider the period of the A-B pair to be about 118 yr, we have data for only about one-quarter of the orbital period covered with minima times at the present day. Yet, we can try to carry out an analysis of these data, by fixing the orbital parameters from astrometry (these in Table 1). We have regularly observed the minima of this interesting target for the past four years to detect the period variation.
 |
Fig. 2 Period variations of the eclipsing pair. Primary minima have been plotted as dots, and secondary as circles. The dashed line represents the 118 yr orbit, while the solid one is the 640 day orbit. |
This led to an interesting finding that there is also an additional variation. We therefore analyzed our data set (43 data points in total) assuming two periodic terms. We used the LIght-Time-Effect hypothesis (hereafter LITE, described e.g. by Irwin 1959). The results of our analysis can clearly be seen in Figs. 2 and 3. The long-term periodic modulation (blue) is caused by the 118 yr visual orbit, while the short-period one is the newly discovered orbit, whose final parameters derived from our analysis are given in Table 2. This variation is clearly visible especially in the more precise recent data points after subtraction of the long-period term, see Fig. 3. Here we use the following labeling of the components: Aa1 and Aa2 for the eclipsing binary components, Ab for the 640 day orbit, and B for the 118 yr orbit (i.e. following the WDS notation). Thanks to the high precision of our new observations, the hypothesis of a non-circular orbit for 65 UMa eclipsing pair was ruled out. The complete list of times of minima together with the original BVRI photometry are given in Tables A.1–A.4 (available at the CDS). There is a problem with some of the minima times, whose accuracy is not always given, hence we cannot perform a reliable chi-square test of the 640 day hypothesis. However, using the weightening scheme for the data points, the LITE fit based on the 640 day hypothesis gives the sum of square residuals 0.00318, while disregarding the possibility of a 640 day period the sum is 0.01222.
Using the approach of combining the two LITE terms, one can also derive the parallax of the system independently of the Hipparcos value and the total mass of the system. The method is as follows: (AA − B,aA − B) ⇒ π ⇒ Mtot. To briefly describe the method, the amplitude of LITE and the angular semi-major axis of the visual orbit are directly connected via the parallax (Mayer 1990). Using our new computed parallax and the Kepler’s third law, we calculated the total mass of the system (e.g. Hilditch 2001). The values presented in Table 2 and the LITE semi-amplitude AA − B were calculated using this approach. This means that the values of pA − B,TA − B,ΩA − B,ωA − B,iA − B, and eA − B were fixed, but the parameters AA − B,pAa − Ab,AAa − Ab,TAa − Ab,ωAa − Ab, and eAa − Ab were fitted as free parameters. From this analysis, a new value of the parallax π = 4.28 ± 0.49 mas was obtained, which yields the distance d = 234 ± 29 pc. Such a value of parallax is slightly lower than the Hipparcos value (πHip = 4.72 ± 0.58 mas). Using this new value of the parallax, we than computed the total mass of the system Mtot = 8.25 ± 1.85 M⊙.Aristidi et al. (1999) found that Mtot = 9.1 ± 11.6 M⊙.
 |
Fig. 3 Period variation in the times of minima after subtraction of the 118 yr term. Only the variation caused by the component Ab and the most recent minima have been displayed. |
Final parameters of the short (Aa-Ab) orbit.
The relative motion of the component C around AB is very slow, but detectable. During more than 200 years of observations, over 60 measurements were obtained (see the WDS) that revealed a change in position angle of about 5°. We analyzed these data, determining a period of longer than 14 000 yr. However, this result is very preliminary owing to the poor coverage of only 1/64 of the orbital period.
5. Light and radial velocity curves
To analyze the LC and RV curves, we had to consider a precise ephemeris of the eclipsing pair. These followed from the minimum times analysis and resulted in the elements for the primary minima 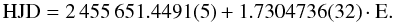 (1)However, the analysis was not straightforward because of the additional components in the system. We assumed that the C component does not affect the spectra significantly, since its distance is about 4′′. The observing conditions and seeing were usually better than 2′′ during most nights. Hence, four other components were found to be present in each of the spectra. We used the program korel (Hadrava 2004) to disentangle the spectra.
(1)However, the analysis was not straightforward because of the additional components in the system. We assumed that the C component does not affect the spectra significantly, since its distance is about 4′′. The observing conditions and seeing were usually better than 2′′ during most nights. Hence, four other components were found to be present in each of the spectra. We used the program korel (Hadrava 2004) to disentangle the spectra.
To perform the spectral disentangling, the orbital elements of both orbits were fixed. Hence, the most crucial for the analysis were the values of the mass ratios and amplitudes of the radial velocity curves. The ephemerides of the close eclipsing pair were also kept fixed because these are much more reliably known from the minima-times analysis.
Parameters from the korel analysis.
The parameters pAa−Ab, TAa−Ab, ωAa−Ab, eAa−Ab, pA−B, TA−B, ωA−B, and eA−B were fixed. The results of the other relevant parameters using korel are listed in Table 3. Despite the results of the mass ratios not being very conclusive, we were able to make some preliminary estimations of the masses of the individual components, as described below in Sect. 6. Since korel does not provide an error estimation, the errors in the individual parameters given in Table 3 resulted from the following analysis. Several solutions in korel were calculated, from which only those with χ2 value closer than 5% from our best solution were considered. The errors in the parameters were assumed to be the maximum difference between these different solutions.
 |
Fig. 4 Radial velocity curves of the 65 UMa eclipsing pair. The upper plot shows the original RVs before correction for the 640 day variation. The bottom plot shows the RVs of the eclipsing pair after the correction. |
The program korel enables us to obtain the RVs of the individual components, which can be used for some further analysis. We used our knowledge of the ephemerides of the inner pair and the orbital parameters of the third body (i.e. 640 day orbit), to subtract the 640 day term from the RVs of the eclipsing pair. This can be clearly seen in Fig. 4, where the upper plot represents the original radial velocities, while the bottom plot represents the velocities after the subtraction of this term. We achieved significant improvement in the quality of the RVs, which could be used to perform a combined LC and RV analysis.
The LC and RV curves of the eclipsing pair were analyzed using the program phoebe (Prša & Zwitter 2005), which is based on the Wilson-Devinney program (WD, Wilson & Devinney 1971). The derived quantities are given in Table 4, while the LC has been plotted in Fig. 5. The values of synchronicity Fi for both eclipsing components were not derived from the combined LC and RV analysis. These were calculated from the spectra, and used to compute the values vsini yielding the Fi values. The errors in Fi are the standard deviations in Fi measured for different spectra and different lines. The limb darkening was approximated using a linear cosine law, and the values of xi were interpolated from the tables given in van Hamme (1993). In Table 4, we used the labeling of the two eclipsing components 1 and 2 in the indices instead of Aa1 and Aa2 for a better clarity.
 |
Fig. 5 BVRI light curves of 65 UMa together with the final phoebe fit. The light curve parameters are given in Table 4. |
The primary temperature was fixed at value T1 = 8000 K, which agrees with both the A7 spectral type (Cox 2000) and the masses of the components (see Table 4). Therefore, it is legitimate to ask why a spectral classification of an A3 star was made for the eclipsing binary (Cowley et al. 1969). This is due to presence of the component Ab on a 640 day orbit, whose spectral type is probably of A3 and its light dominates the spectra. Moreover, Garcia & Gimenez (1986) speculated that the eclipsing binary components might be of A8-9 spectral type. The large value of the third light is also well-established owing to the three components that are present in the photometric aperture (in our notation, components Ab+B+C).
Light curve parameters of 65 UMa eclipsing pair.
The component Ab dominates the spectrum. This body has a well-defined orbit, hence its lines can also be plotted with the 640 day period. On the other hand, Ab orbits around a barycenter with the eclipsing pair. We can also plot the residuals from the LC fit from the eclipsing pair (from the original RVs), which should vary in anti-phase with respect to the Ab lines. This is shown in Fig. 6, where we have plotted the 640 day fit to our spectra, which were acquired over two consecutive seasons 2010 and 2011.
Moreover, during the photometric monitoring of 65 UMa, two new variables were identified in the field. One of them was HD 103795 (spectrum K2III, according to Upgren 1962), while the other one was SAO 43913 (spectrum F0, according to Slettebak & Stock 1959). Neither was ever reported to be a variable, despite both having been observed by the Hipparcos satellite. However, our CCD photometry indicates that both are probably variable with amplitudes a few hundreds of magnitude. SAO 43913 is probably a pulsating star (maybe δ Sct) with a period of about three hours, but the type of variability of HD 103795 remains unclear.
 |
Fig. 6 Radial velocity curves on the 640 day orbit. The black squares stand for the Ab lines in the spectrum, while the red circles represent the radial velocity residuals after subtraction of the eclipsing pair RV curve (filled for primary, open for secondary). |
6. Discussion and conclusions
We have performed our first attempt to perform a detailed combined solution of all available data for 65 UMa, namely photometry, spectroscopy, and interferometry, obtaining quite a reliable picture of this unusual sextuple hierarchical system (see Fig. 7).
 |
Fig. 7 Schematic structure of the whole system 65 UMa. |
The inner close eclipsing pair consists of two almost-identical stars of A7 spectral type. This finding is consistent with the photometric indices B − V, V − R, and R − I being constant for the whole phase of the eclipsing binary at a level of 0.005 mag. The stars move on circular orbits with periods of about 1.73043 d, both being located on the main sequence. Thanks to the combined analysis, we were also able to compute its distance as d = 234 ± 29 pc, independently of the Hipparcos satellite data. The 640 day orbit was confirmed by both the minima times and the RV variations. Applying the spectral disentangling and rough estimation of the mass ratios from this analysis, one can estimate the masses of the outer components. The Ab component is probably of A1 spectral type and has a mass of about 2.4 ± 0.4 M⊙, from the total mass of the 118 yr visual orbit, we can estimate the mass of the fourth component (in WDS named B), to be about 2.4 ± 2.0 M⊙. If we assume both these masses of Ab and B components, we can estimate the magnitude difference. Aristidi et al. (1999) found this value to be 1.9 ± 0.1 mag, while here we derive 0.7 ± 4.5 mag. The very large error is due to the large uncertainty in the mass of the fourth body. Another approach is to use the standard mass-luminosity relation and derive the individual luminosities of the components. Using this approach, we have plotted Fig. 8, where all components of the system 65 UMa are placed in the color–magnitude diagram. As one can see, the two eclipsing binaries are slightly under-luminous, while the D component seems to be over-luminous. The same finding about its higher luminosity was found elsewhere, e.g. Joshi et al. (2010) or Aurière et al. (2007).
However, some properties of the Aa-Ab orbit remain unclear, such as the inclination angle between the orbits. We can do some rough estimation of this quantity. The korel KAa value and the predicted amplitude of radial-velocity variations from the LITEAa−Ab are connected via siniAa−Ab. Hence, we obtain iAa−Ab ≈ 47°, which lies well between the inclinations i of the eclipsing pair and the iA−B of the visual orbit. Nevertheless, its error is large but this is still only an estimation. We can also compute the predicted minimal angular separation of the Aa-Ab pair for a prospective interferometric detection. This resulted in about 11 mas, which is very favorable for modern stellar interferometers, because the magnitude difference between the Aa and Ab components should also be rather low. On the other hand, the angular separation of the eclipsing pair components is still rather low, at about only 0.18 mas.
 |
Fig. 8 Color–magnitude diagram for all components of the system. Their position is compared with the Hipparcos stars (small black dots). |
Dealing with a multiple system, we should also consider the nodal period of the close pair and the 640 day orbit, hence the change in the inclination of the eclipsing binary (Söderhjelm 1975). The most crucial here is the ratio of periods pAa−Ab2/P, which implies that the nodal period was about 650 years, a duration that should be practical to observe. Unfortunately, we do not have a complete set of orbital parameters of the Aa-Ab pair, so this is only first rough estimation. However, this nodal period is not too long and potentially detectable. Further observations would help us to detect the change in the eclipse depths. Despite these being rather shallow, this effect was detected in only nine other cases, hence it would be interesting to reattempt detections, especially with the modern ultra-precise satellite photometry.
Nevertheless, 65 UMa is a rather unusual system, we presently know of only 11 other sextuple systems (see Eggleton & Tokovinin 2008). The mass ratio of close to unity for the inner pair seems to agree with some theoretical models of star formation, e.g. Delgado-Donate et al. (2003). Moreover, some studies (e.g. Tokovinin & Smekhov 2002) indicate that about one-third of all multiples are higher-order systems. Goodwin et al. (2007) discussed a finding that there is a difference between the number of observed and expected higher-order multiples (quadruples and higher). Perhaps the discovery of other systems similar to 65 UMa would diminish this discrepancy.
Acknowledgments
Dr. Pavel Mayer is acknowledged for a useful discussion and valuable advices. We would like to thank Mr. P. Chadima for obtaining the two spectra of 65 UMa at Ondřejov observatory and P. Svoboda for sending us his photometric data for 65 UMa. This work was supported by the Czech Science Foundation grant No. P209/10/0715, by the research programme MSM0021620860 of the Czech Ministry of Education, and by the grant UNCE 12 of the Charles University in Prague. This research has made use of the Washington Double Star Catalog maintained at the US Naval Observatory, the SIMBAD database, operated at CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Bibliographic Services.
References
- Aitken, R. G. 1908, LicOB, 5, 28 [NASA ADS] [Google Scholar]
- Aitken, R. G., & Doolittle, E. 1932, in New general catalogue of double stars within 120 of the North pole (Washington, D.C.: Carnegie institution of Washington Publications) [Google Scholar]
- Aitken, R. G., & Moore, C. E. 1937, LicOB, 18, 53 [NASA ADS] [Google Scholar]
- Aristidi, É., Prieur, J.-L., Scardia, M., et al. 1999, A&AS, 134, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Brát, L., Trnka, J., Smelcer, L., et al. 2011, OEJV, 137, 1 [Google Scholar]
- Bulut, I., & Demircan, O. 2003, IBVS, 5476, 1 [NASA ADS] [Google Scholar]
- Cowley, A., Cowley, C., Jaschek, M., & Jaschek, C. 1969, AJ, 74, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N. 2000, in Allen’s Astrophysical Quantities, 4th edn., ed. A. N. Cox (New York: Springer Verlag) [Google Scholar]
- Delgado-Donate, E. J., Clarke, C. J., & Bate, M. R. 2003, MNRAS, 342, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Drózdz, M. 1997, International Amateur-Professional Photoelectric Photometry Communications, 67, 30 [NASA ADS] [Google Scholar]
- Eggleton, P. P., & Tokovinin, A. A. 2008, MNRAS, 389, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, J. M., & Gimenez, A. 1986, Ap&SS, 125, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Gimenez, A., & Quesada, J. A. 1979, IBVS, 1648, 1 [NASA ADS] [Google Scholar]
- Gimenez, A., & Quesada, J. A. 1982, IBVS, 2068, 1 [NASA ADS] [Google Scholar]
- Goodwin, S. P., & Kroupa, P. 2005, A&A, 439, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodwin, S. P., Kroupa, P., Goodman, A., & Burkert, A. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 951, 133 [Google Scholar]
- Hadrava, P. 2004, PAICz, 92, 15 [Google Scholar]
- Hartkopf, W. I., & Mason, B. D. 2009, AJ, 138, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Hartkopf, W. I., McAlister, H. A., & Franz, O. G. 1992, AJ, 104, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Hartkopf, W. I., McAlister, H. A., Mason, B. D., et al. 1994, AJ, 108, 2299 [NASA ADS] [CrossRef] [Google Scholar]
- Hilditch, R. W. 2001, in An Introduction to Close Binary Stars, ed. R. W. Hilditch (Cambridge, UK: Cambridge University Press), 392 [Google Scholar]
- Horn, J., Kubát, J., Harmanec, et al. 1996, A&A, 309, 521 [NASA ADS] [Google Scholar]
- Irwin, J. B. 1959, AJ, 64, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, S., Ryabchikova, T., Kochukhov, O., et al. 2010, MNRAS, 401, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Krajci, T. 2006, IBVS, 5690, 1 [Google Scholar]
- Krajci, T. 2007, IBVS, 5806, 1 [NASA ADS] [Google Scholar]
- Kuiper, G. P. 1961, ApJS, 6, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lampens, P., Kleidis, S., van Cauteren, P., et al. 2010, IBVS, 5933, 1 [NASA ADS] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Mayer, P. 1990, BAICz, 41, 231 [Google Scholar]
- McAlister, H. A., Hartkopf, W. I., Gaston, B. J., Hendry, E. M., & Fekel, F. C. 1984, ApJS, 54, 251 [NASA ADS] [CrossRef] [Google Scholar]
- McAlister, H. A., Hartkopf, W. I., Hutter, D. J., & Franz, O. G. 1987, AJ, 93, 688 [NASA ADS] [CrossRef] [Google Scholar]
- McAlister, H. A., Hartkopf, W. I., Sowell, J. R., Dombrowski, E. G., & Franz, O. G. 1989, AJ, 97, 510 [NASA ADS] [CrossRef] [Google Scholar]
- McAlister, H., Hartkopf, W. I., & Franz, O. G. 1990, AJ, 99, 965 [NASA ADS] [CrossRef] [Google Scholar]
- McAlister, H. A., Mason, B. D., Hartkopf, W. I., & Shara, M. M. 1993, AJ, 106, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, H.-H., Hartkopf, W. I., Mason, B. D., et al. 1997, AJ, 114, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, K. 2006, Var. Star Bull., 44, 1 [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Popper, D. M. 1986, PASP, 98, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prieur, J.-L., Oblak, E., Lampens, P., et al. 2001, A&A, 367, 865 [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Slettebak, A. 1963, ApJ, 138, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Slettebak, A., & Stock, J. 1959, AAHam, 5, 105 [NASA ADS] [Google Scholar]
- Söderhjelm, S. 1975, A&A, 42, 229 [NASA ADS] [Google Scholar]
- Škoda, P. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes (San Fransicso: ASP), ASP Conf. Ser., 101, 187 [Google Scholar]
- Tokovinin, A. A. 1997, A&AS, 124, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokovinin, A. 2008, MNRAS, 389, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. A., & Smekhov, M. G. 2002, A&A, 382, 118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Upgren, A. R. 1962, AJ, 67, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Van Biesbroeck, G. 1954, PYerO, 8, 6 [Google Scholar]
- van den Bos, W. H. 1960, PYerO, 9, 1 [Google Scholar]
- van den Bos, W. H. 1962, AJ, 67, 555 [NASA ADS] [CrossRef] [Google Scholar]
- van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Worley, C. E. 1971, PUSNO, 22, 1 [NASA ADS] [Google Scholar]
- Zasche, P., Wolf, M., Hartkopf, W. I., et al. 2009, AJ, 138, 664 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Visual orbit of 65 UMa pair (A-B) as displayed on the sky. The eclipsing binary is placed in [0, 0]. The dotted line represents the line of the apsides, while the dashed one is the line of the nodes. See Sect. 4. |
| In the text | |
 |
Fig. 2 Period variations of the eclipsing pair. Primary minima have been plotted as dots, and secondary as circles. The dashed line represents the 118 yr orbit, while the solid one is the 640 day orbit. |
| In the text | |
 |
Fig. 3 Period variation in the times of minima after subtraction of the 118 yr term. Only the variation caused by the component Ab and the most recent minima have been displayed. |
| In the text | |
 |
Fig. 4 Radial velocity curves of the 65 UMa eclipsing pair. The upper plot shows the original RVs before correction for the 640 day variation. The bottom plot shows the RVs of the eclipsing pair after the correction. |
| In the text | |
 |
Fig. 5 BVRI light curves of 65 UMa together with the final phoebe fit. The light curve parameters are given in Table 4. |
| In the text | |
 |
Fig. 6 Radial velocity curves on the 640 day orbit. The black squares stand for the Ab lines in the spectrum, while the red circles represent the radial velocity residuals after subtraction of the eclipsing pair RV curve (filled for primary, open for secondary). |
| In the text | |
 |
Fig. 7 Schematic structure of the whole system 65 UMa. |
| In the text | |
 |
Fig. 8 Color–magnitude diagram for all components of the system. Their position is compared with the Hipparcos stars (small black dots). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


