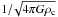| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201218961 | |
| Published online | 12 June 2012 | |
Physical properties of interstellar filaments
1 Canadian Institute for Theoretical Astrophysics, University
of Toronto, 60 St. George Street, ON M5S3H8, Canada
e-mail: fischera@cita.utoronto.ca
2
Research School of Astronomy Astrophysics, Institute of Advanced
Studies, The Australian National University, Cotter Road, Weston Creek, ACT
2611,
Australia
Received:
4
February
2012
Accepted:
13
April
2012
We analyze the physical parameters of interstellar filaments that we describe by an idealized model of isothermal self-gravitating infinite cylinder in pressure equilibrium with the ambient medium. Their gravitational state is characterized by the ratio fcyl of their mass line density to the maximum possible value for a cylinder in a vacuum. Equilibrium solutions exist only for fcyl < 1. This ratio is used in providing analytical expressions for the central density, the radius, the profile of the column density, the column density through the cloud centre, and the FWHM. The dependence of the physical properties on external pressure and temperature is discussed and directly compared to the case of pressure-confined isothermal self-gravitating spheres. Comparison with recent observations of the FWHM and the central column density NH(0) show good agreement and suggest a filament temperature of ~10 K and an external pressure in the range 1.5 × 104 K cm-3 to 5 × 104 K cm-3. Stability considerations indicate that interstellar filaments become increasingly gravitationally unstable with mass line ratio fcyl approaching unity. For intermediate fcyl > 0.5 the instabilities should promote core formation through compression, with a separation of about five times the FWHM. We discuss the nature of filaments with high mass line densities and their relevance to gravitational fragmentation and star formation.
Key words: stars: formation / ISM: clouds / ISM: structure / submillimeter: ISM / infrared: ISM
© ESO, 2012
1. Introduction
Filamentary structures are an ubiquitous phenomenon in the interstellar medium. Thanks to the high angular resolution and signal to noise of dust imaging with the Herschel Space Observatory, it is now possible to quantify the basic empirical properties of filaments. Filaments have been imaged in the submillimetre in exquisite detail in non star-forming such as Polaris (Men’shchikov et al. 2010; Miville-Deschênes et al. 2010), in molecular regions with low-mass star formation such as Aquila and IC 5146 (André et al. 2010; Arzoumanian et al. 2011; Men’shchikov et al. 2010), and in higher-mass regions including Vela C and the Rosette molecular cloud (Hill et al. 2011; Schneider et al. 2012). At least in the low-mass star forming regions and in Polaris, the characteristic filament sizes are about 0.1 pc (Arzoumanian et al. 2011)1.
Clear evidence for star formation seems to be related to cloud structures with a typical extinction larger then AV ≈ 7 mag (Onishi et al. 1998; Johnstone et al. 2004; André et al. 2010), which corresponds to a column density NH about 0.6 × 1022 cm-2 (see comments in Appendix A)2. Furthermore, the Herschel studies show that high column densities are typically associated with filaments and, finally, that cold dense clouds called “prestellar cores” possibly related to the very early stages of the star formation (Könyves et al. 2010), are observed mainly along filaments (André et al. 2010; Men’shchikov et al. 2010; Arzoumanian et al. 2011). Empirically, it is found that filaments that are star forming are characterized by not only a higher central column density but also a higher mass per unit length (André et al. 2010; Arzoumanian et al. 2011). It is argued that the cores are possibly created out of the elongated structures through gravitational instabilities (Schneider & Elmegreen 1979; Gaida et al. 1984; Hanawa et al. 1993; Curry 2000; André et al. 2010; Men’shchikov et al. 2010).
It is important to develop a physical model for the filaments so that the new measurements can be exploited. That is the goal of this paper. The basic model that we explore is an isothermal cylinder confined at a finite boundary rcyl by an external pressure pext provided by an ambient or embedding medium. This is certainly more realistic than an isothermal cylinder in vacuum, whose properties (such as the radial profile) are not surprisingly in disagreement with observations (e.g., Men’shchikov et al. 2010; Arzoumanian et al. 2011). Even these pressure-confined models are unlikely to describe what is a very complex interstellar medium where the origin of the filamentary structures is still a mystery, but the models can serve the same role in developing our understanding that has been played by the spherically-symmetric analog, the Bonnor-Ebert sphere (Ebert 1955; Bonnor 1956; Nagasawa 1987; Inutsuka & Miyama 1992, 1997; Curry & McKee 2000; Fiege & Pudritz 2000; Kandori et al. 2005; Fischera & Dopita 2008). Furthermore, we find that the models do actually provide a consistent description of the sizes and column densities recently reported for filaments and some insight into the instabilities relating to filaments.
We analyze systematically the physical properties of pressure-confined filaments, comparing and contrasting these results with the corresponding properties for spheres. We develop analytical solutions for several observables. Parts of the results, on which we build, can be found in earlier work on the spectral energy distribution of interstellar clouds (Fischera & Dopita 2008 – Paper I) and on the spectral energy distribution of condensed cores embedded in pressurized elongated or spherical clouds (Fischera 2011 – Paper II).
Our paper is organized as follows. The physical model is presented in Sect. 2, from which properties are derived in Sect. 3. Observed properties corresponding to size and column density are compared with the model in Sect. 4 with remarkable agreement. Structure formation due to instability of the filaments is discussed in Sect. 5. It seems plausible that dominant protostellar cores arranged along filaments could arise from a “compressive instability” (Nagasawa 1987) in high column density filaments. Some other instabilities seem less relevant. A summary and discussion is provided in Sect. 6. Several appendices deal with the astronomical context and details of some calculations.
2. Physical model
We assume that the filaments can be described by a model of isothermal self-gravitating
infinitely long cylinders. For the isothermal gas, the relationship between gas pressure
p and gas density ρ is 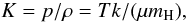 (1)where
k is the Boltzmann constant, μ the mean molecular weight
(2.36 for a molecular cloud with cosmic abundances), and mH the
mass of the hydrogen atom; the isothermal temperature T is considered to be
an effective value related to both the thermal and the turbulent motion of the gas (see
Appendix A.4). If the effective temperature is equal
to the thermal or kinetic temperature then
(1)where
k is the Boltzmann constant, μ the mean molecular weight
(2.36 for a molecular cloud with cosmic abundances), and mH the
mass of the hydrogen atom; the isothermal temperature T is considered to be
an effective value related to both the thermal and the turbulent motion of the gas (see
Appendix A.4). If the effective temperature is equal
to the thermal or kinetic temperature then 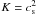 , the square of
the sound speed. Furthermore, as discussed in the introduction, the clouds are assumed to be
in pressure equilibrium with the surrounding medium of
pressure pext. This does not imply that the external medium is
isothermal or at the same temperature; it is simply a boundary condition.
, the square of
the sound speed. Furthermore, as discussed in the introduction, the clouds are assumed to be
in pressure equilibrium with the surrounding medium of
pressure pext. This does not imply that the external medium is
isothermal or at the same temperature; it is simply a boundary condition.
2.1. Cloud profile
Isothermal self-gravitating infinitely long cylinders have a well-known density or
pressure profile given by (see e.g. Stodólkiewicz
1963; Ostriker 1964) 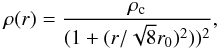 (2)where
(2)where 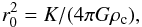 (3)ρc
is the central density, and G the gravitational constant. For
pressure-confined clouds the profile terminates where the cloud pressure is equal to the
external pressure pext; this defines the cylinder radius
rcyl. As in Papers I and II, in the following we refer to
the ratio
pc/pext as
the “overpressure”.
(3)ρc
is the central density, and G the gravitational constant. For
pressure-confined clouds the profile terminates where the cloud pressure is equal to the
external pressure pext; this defines the cylinder radius
rcyl. As in Papers I and II, in the following we refer to
the ratio
pc/pext as
the “overpressure”.
2.2. Mass line density
Analogous to the cloud mass in the case of spherical clouds we have in the case of
cylinders the mass per cloud length (mass line density), given by 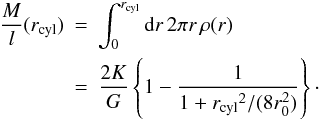 (4)In
the limit
(4)In
the limit 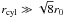 the mass per
cloud lengths approaches asymptotically a maximum value given by
the mass per
cloud lengths approaches asymptotically a maximum value given by
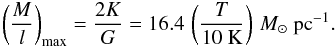 (5)For pressurized
clouds this gravitational state corresponds to an infinite overpressure, but there is no
dependence on pext.
(5)For pressurized
clouds this gravitational state corresponds to an infinite overpressure, but there is no
dependence on pext.
For comparison, in the case of an isothermal self-gravitating pressurized sphere, the
maximum mass is identical to its critical mass, given by (see
Appendix B) 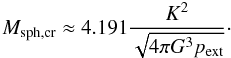 (6)This gravitational state
is characterized by an overpressure
pc/pext ≈ 14.04.
As shown in Paper II, a critical stable state is related to the maximum possible pressure
that a sphere of given mass and K (temperature) can produce at the cloud
outskirts under compression. If the external pressure is increased slightly, the resulting
equilibrium configuration is unstable to gravitational collapse, and so this is aptly
called a “critical stable sphere”. The spherical clouds can be characterized as
“subcritical” or “supercritical” depending on whether the overpressure is lower or higher
than the value for a critical stable sphere. Note that for overpressures higher than
14.04, the mass of an equilibrium configuration is smaller than the
critical mass. Thus we can also say that for given pext and
K the critical mass is the maximum mass for which an equilibrium
solution exists.
(6)This gravitational state
is characterized by an overpressure
pc/pext ≈ 14.04.
As shown in Paper II, a critical stable state is related to the maximum possible pressure
that a sphere of given mass and K (temperature) can produce at the cloud
outskirts under compression. If the external pressure is increased slightly, the resulting
equilibrium configuration is unstable to gravitational collapse, and so this is aptly
called a “critical stable sphere”. The spherical clouds can be characterized as
“subcritical” or “supercritical” depending on whether the overpressure is lower or higher
than the value for a critical stable sphere. Note that for overpressures higher than
14.04, the mass of an equilibrium configuration is smaller than the
critical mass. Thus we can also say that for given pext and
K the critical mass is the maximum mass for which an equilibrium
solution exists.
Unlike Msph,cr, the maximum mass line density depends only linearly (compared to quadratically) on K or cloud temperature and does not depend at all on the size of the external pressure confining the cloud. We discuss the basic consequences in Sects. 3.6 and 3.6.3.
There are no equilibrium solutions for cylinders or spheres with masses above the corresponding maximum values (McCrea 1957). They would collapse radially towards a line (spindle) or to a singular point, respectively. This has led to the terminology “supercritical mass” when M > Msph,cr, or “supercritical filament” when M/l > (M/l)max. The gravitational states considered in this paper are all equilibrium solutions. We prefer to reserve the term “supercritical” to describe the equilibrium states for spheres, as above, and note the fundamental difference that there are no such supercritical equilibrium states for cylinders (Sect. 3.6 ).
2.2.1. Mass fraction fcyl
A very useful quantity is the mass fraction 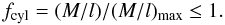 (7)For cylinders we
find directly from Eqs. (1) to (7) that the overpressure is given by
(7)For cylinders we
find directly from Eqs. (1) to (7) that the overpressure is given by
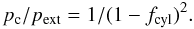 (8)We can therefore use
fcyl to characterize the gravitational state of the
cylinders. This mass ratio therefore appears in the formulae below for the derived
properties of cylinders in different gravitational states. Two instructive limits to
consider are the case of high overpressure or fcyl → 1,
which we shall see corresponds to a narrow high column density filament with strong
self-gravity, and the case of vanishing overpessure or
fcyl → 0, corresponding to a filament much more difficult to
recognize or characterize. There is, however, no distinction between “pressure-confined”
and “self-gravitating” cylinders, since both features are intrinsic to all equilibrium
models.
(8)We can therefore use
fcyl to characterize the gravitational state of the
cylinders. This mass ratio therefore appears in the formulae below for the derived
properties of cylinders in different gravitational states. Two instructive limits to
consider are the case of high overpressure or fcyl → 1,
which we shall see corresponds to a narrow high column density filament with strong
self-gravity, and the case of vanishing overpessure or
fcyl → 0, corresponding to a filament much more difficult to
recognize or characterize. There is, however, no distinction between “pressure-confined”
and “self-gravitating” cylinders, since both features are intrinsic to all equilibrium
models.
This parallels the approach used in Paper I where the gravitational state of pressurized spheres was described by the mass ratio fsph = M/Msph,cr of the cloud mass relative to the mass of a critical stable sphere. While in Paper I the physical parameters for spheres were discussed only for the physically stable regime with overpressures below the critical value 14.04, we consider here the whole physical range. This leads to the curious situation that for large overpressures above the critical value the gravitational state is described by fsph < 1.
3. Derived properties
In the following we describe the physical properties of molecular cylinders and compare spheres for a given cloud temperature and external pressure. We adopt illustrative reference values for temperature and pressure. See Appendix A for further discussion. For the cold molecular clouds we adopt K corresponding to 10 K (cs = 0.19 km s-1). For the external pressure we adopt pext/k = 2 × 104 K cm-3, consistent with Papers I and II.
3.1. Central density
 |
Fig. 1 Central density of an isothermal self-gravitating molecular cylinder (black) and sphere (grey), for fixed values of the ambient pressure. pext/k = 2 × 104 K cm-3 and cloud temperature T = 10 K. The dotted line is the value achieved by a critical stable sphere. This same central density (or overpressure) is reached in a cylinder with fcyl = 0.733 (filled black circle). |
For the central density we have from Eqs. (1) and (8) 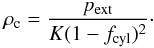 (9)The central number
density
nH(r = 0) ≡ nH(0)
is obtained by evaluating
(9)The central number
density
nH(r = 0) ≡ nH(0)
is obtained by evaluating 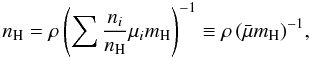 (10)where
ni/nH
is the relative abundance of element i compared to H, and
μi is its relative mass units of
mH; on the right, the effective mass per H,
(10)where
ni/nH
is the relative abundance of element i compared to H, and
μi is its relative mass units of
mH; on the right, the effective mass per H,
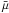 ,
is 1.4 for cosmic abundances. Figure 1 shows these
central values as a function of the mass fraction.
,
is 1.4 for cosmic abundances. Figure 1 shows these
central values as a function of the mass fraction.
For a given temperature and external pressure the central density increases as 1/(1 − fcyl)2 and so in the limit fcyl → 1 the density becomes infinite.
For a given mass fraction, the density in the cloud centre is proportional to pextμ/T. Cylinders have a higher overpressure or overdensity in the cloud centre compared to spheres (Fig. 1) for the same mass fraction, except in the case of small mass fractions (fcyl < ≈0.15). In cylinders the overpressure of 14.04 corresponding to critical stable spheres is achieved for a mass fraction of fcyl ≈ 0.733.
3.2. Cloud radius
Solving Eq. (4) for
rcl, using Eq. (9) and recasting Eq. (3) as
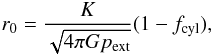 (11)provides
(11)provides
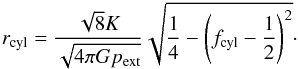 (12)This along with the
boundary radius of the pressure-confined sphere is plotted as
rcl in Fig. 2 as a
function of mass fraction.
(12)This along with the
boundary radius of the pressure-confined sphere is plotted as
rcl in Fig. 2 as a
function of mass fraction.
 |
Fig. 2 Like Fig. 1, but for the radius of an isothermal self-gravitating cylinder (black) and sphere (grey). |
The size of the cloud for given mass fraction f is proportional to
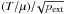 .
The radius for cylinders is symmetrical around f = 0.5 where the cloud
shows its maximum size. The filament grows in size through accretion of new material as
long as the mass ratio fcyl < 0.5.
Further accretion will cause a shrinking of the filament. In the limit
fcyl → 1 (the mass-line density approaches the maximum value
2K/G) the cylinder will become
infinitely thin.
.
The radius for cylinders is symmetrical around f = 0.5 where the cloud
shows its maximum size. The filament grows in size through accretion of new material as
long as the mass ratio fcyl < 0.5.
Further accretion will cause a shrinking of the filament. In the limit
fcyl → 1 (the mass-line density approaches the maximum value
2K/G) the cylinder will become
infinitely thin.
Spheres by contrast have a finite size at large mass ratios. As pointed out in Paper I the spherical cloud has a maximum size at fsph ≈ 0.870. Pushed above this value by accretion an isothermal cloud size shrinks to the size of a critical stable cloud. Supercritical stable spheres have smaller sizes still.
3.3. Radial profile of the pressure or density
 |
Fig. 3 Pressure profiles of isothermal self-gravitating cylinders (black) and spheres (grey), for various overpressures pc/pext from 2 to 20. The dashed curves show density profiles for simple power laws normalized at the cloud boundary. |
The radial dependence of pressure given by Eq. (2) is shown in Fig. 3 for various overpressures, which according to Eq. (9) are equivalent to 1/(1 − fcyl)2. For comparison, profiles are also shown for spheres for the same set of overpressures; in the central region of the cloud their density falls off more strongly towards larger radii.
In the limit of 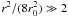 the clouds show a steep density
profile at the cloud edges with
ρ(r) ∝ r-4. However, this
property requires clouds with very high overpressures (large
fcyl, close to the maximum possible mass-line density).
n the outer half of the cylinders the density profiles for
overpressures less than 20 are shallower than a r-4 profile.
For overpressures in the regime 6 to 12 the density profile at the outer half is more
consistent with a r-2-profile.
the clouds show a steep density
profile at the cloud edges with
ρ(r) ∝ r-4. However, this
property requires clouds with very high overpressures (large
fcyl, close to the maximum possible mass-line density).
n the outer half of the cylinders the density profiles for
overpressures less than 20 are shallower than a r-4 profile.
For overpressures in the regime 6 to 12 the density profile at the outer half is more
consistent with a r-2-profile.
A useful characteristic size for describing properties of the cylinder is
rcyl for small fcyl and
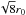 for large
fcyl.
for large
fcyl.
3.4. Projection of the density profile
3.4.1. Column density profile
The column density at an impact parameter x (in units of cloud radius
rcl) is given by the integral
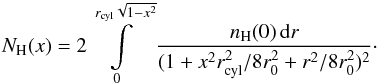 (13)The integral evaluates
to:
(13)The integral evaluates
to: 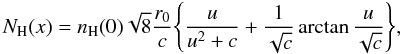 (14)with
(14)with
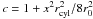 and
and
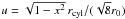 . Using the replacement
. Using the replacement
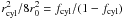 it is straightforward to show
that the column density profile for given fcyl is given by:
it is straightforward to show
that the column density profile for given fcyl is given by:
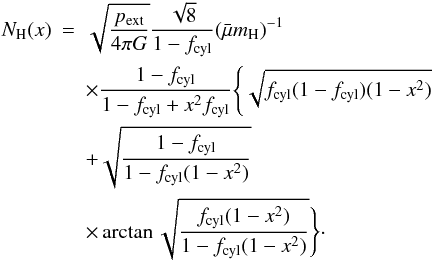 (15)The
profile shape is solely determined by the mass fraction
fcyl. The amplitude of the profile with fixed
fcyl is proportional to
(15)The
profile shape is solely determined by the mass fraction
fcyl. The amplitude of the profile with fixed
fcyl is proportional to
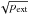 and is independent of the cloud temperature.
and is independent of the cloud temperature.
In the limit fcyl → 1 the profile for
x ≪ 1 can be approximated by: 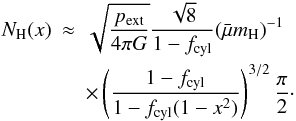 (16)In
the limit of low fcyl
(16)In
the limit of low fcyl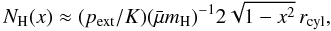 (17)as for a
uniform-density cylinder.
(17)as for a
uniform-density cylinder.
 |
Fig. 4 Like Fig. 1, but for the central column density (left panel) and mean column density (right panel) through an isothermal self-gravitating cylinder (black) and sphere (grey), as a function of mass fraction f. The dashed line in the left-hand plot is the approximation given in Eq. (19). The dashed lines in the right-hand plot echo the central column densities from the left-hand plot for comparison. The horizontal dotted lines give the values achieved by a critical stable sphere. The values for a cylinder with that overpressure, mass fraction 0.733, are shown as filled black circles. |
3.4.2. Central column density
An important characteristic of self-gravitating clouds is the column density through
the cloud centre, NH(0), which for cylinders is a trivial
solution of Eq. (15) for
x = 0: 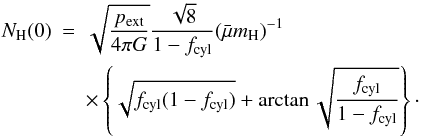 (18)Figure 4 shows that the column density increases more strongly
with mass fraction in the case of cylinders.
(18)Figure 4 shows that the column density increases more strongly
with mass fraction in the case of cylinders.
In the limit of high mass fraction
(fcyl > ≈0.6) the column density
can be approximated by 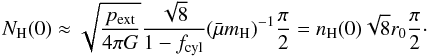 (19)For given
external pressure the central column density increases as
1/(1 − fcyl). In the limit of maximum
mass fraction the column density would be infinite. If we replace the mass fraction
through the overpressure we find that the column density for high overpressure
increases, as found in Paper II, proportional to
(19)For given
external pressure the central column density increases as
1/(1 − fcyl). In the limit of maximum
mass fraction the column density would be infinite. If we replace the mass fraction
through the overpressure we find that the column density for high overpressure
increases, as found in Paper II, proportional to  .
The limit for low fcyl follows from Eq. (17).
.
The limit for low fcyl follows from Eq. (17).
Column densities in the molecular environments in question are measured via near-infrared colour excess or, in the case of the filaments being discussed, the submillimetre optical depth (Appendix A). Nevertheless, AV is widely used as “shorthand” for column density, which we do here as well, even though it is not a direct observable in dense molecular clouds. A column density of H nucleons of 1022 cm-2 is taken to correspond to AV = 5.3 mag (Appendix A)3. In other units, this is equivalent to 2.3 × 10-2 g cm-2 or 1.1 × 102 M⊙ pc-2. This conversion relates the left and right vertical scales in Fig. 4.
For the adopted external pressure, the column density lies between 2 × 1021 and 2 × 1022 cm-2 (AV in the range 1 to 10 mag) for mass fractions fcyl in the range roughly 0.2 to 0.8.
Cylinders with the same overpressure pc/pext as spheres are characterized by a lower central extinction (Paper II). For example, for the adopted external pressure, the central extinction through a cylinder with the same overpressure as a critical stable sphere is approximately AV ≈ 6.4 mag compared to 8 mag for that sphere (Fig. 4).
3.4.3. Average column density
For unresolved filaments we also give the mean column density (see also Paper II). The
mean value for cylinders is given by
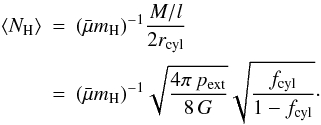 (20)We
see that the mean column density of cylinders also approaches infinity asymptotically in
the limit of large mass ratio.
(20)We
see that the mean column density of cylinders also approaches infinity asymptotically in
the limit of large mass ratio.
By contrast, the mean column density even for a supercritical sphere is finite. In the
limit of large mass fraction the mean value is given by 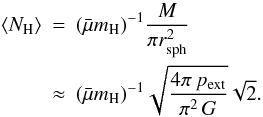 (21)As
shown in Appendix B, the value is exact where a
cloud of given mass produces a pressure maximum at the clouds outskirts. The value is
for example exact for the special case of a critical stable sphere or in the limit of
infinite overpressure. For
pext/k = 2 × 104 K cm-3
we have ⟨NH⟩ ≈ 4.36 × 1021 cm-2
(AV ≈ 2.33 mag). As shown in Fig. 4 stable spherical clouds above
fsph > 0.1 have mean column
densities not smaller than 1021 cm-2 and all spherical clouds,
even if we include the supercritical cases, mean column densities not larger than
6 × 1021 cm-2.
(21)As
shown in Appendix B, the value is exact where a
cloud of given mass produces a pressure maximum at the clouds outskirts. The value is
for example exact for the special case of a critical stable sphere or in the limit of
infinite overpressure. For
pext/k = 2 × 104 K cm-3
we have ⟨NH⟩ ≈ 4.36 × 1021 cm-2
(AV ≈ 2.33 mag). As shown in Fig. 4 stable spherical clouds above
fsph > 0.1 have mean column
densities not smaller than 1021 cm-2 and all spherical clouds,
even if we include the supercritical cases, mean column densities not larger than
6 × 1021 cm-2.
3.4.4. Column density profiles for different central AV
According to the previous sections, for a given external pressure the column density or
extinction in these interstellar clouds can be specified by their overpressure or
f, without explicit specification of either the cloud temperature or
their mass line density (filaments) or mass (spheres). For filaments the extinction is
related monotonically to the mass ratio fcyl. The same
applies to spherical clouds up to overpressures
pc/pext ≈ 14.04.
The extinction varies as 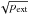 .
.
 |
Fig. 5 Column density profiles of isothermal self-gravitating cylinders (black lines) and spheres (grey lines) for several central extinction values from AV = 1 mag to AV = 8 mag. The clouds are pressurized by pext/k = 2 × 104 K cm-3. |
 |
Fig. 6 Pressure profiles (density profiles) for the column density profiles shown in Fig. 5. Recall that profiles for the same overpressure are compared in Fig. 3. |
In Fig. 5, for the adopted pext/k = 2 × 104 K cm-3, we give the profiles of the column densities of cylinders and spheres for a number of different values of the central extinction. The column density profile steepens as a function of the central extinction or f. For the same central extinction, the column density of a cylinder falls off more quickly with impact parameter x compared to a sphere. This relative behaviour is opposite that for the pressure profile (Fig. 3).
For the same central extinction, cylinders have a higher overpressure pc/pext compared to spheres, as discussed in Sect. 3.4.2 and shown in Fig. 6.
3.5. The FWHM
Observationally the full width at half maximum (FWHM) has more relevance than the
physical radius which is either not directly observable or difficult to determine because
of the fluctuating background. The impact parameter xFWHM of
the FWHM is given by 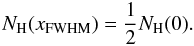 (22)The FWHM of
cylinders and spheres is examined in Appendix C.
For the adopted external pressure, values are shown in Fig. 7.
(22)The FWHM of
cylinders and spheres is examined in Appendix C.
For the adopted external pressure, values are shown in Fig. 7.
 |
Fig. 7 Like Fig. 2, but for the FWHM of an isothermal self-gravitating cylinder (black line) and sphere (grey line). The dashed line gives the asymptotic behaviour of the FWHM of an isothermal self-gravitating cylinder for high f (Eq. (23)). The vertical dashed-dotted lines mark the mass fraction of the maxima of FWHM (Eq. (25)). The horizontal dotted line shows the FWHM of a critical stable sphere. The FWHM of a cylinder with this overpressure 14.04 (fcyl = 0.733) is shown as the filled black circle (FWHMcyl = 0.0812 pc). |
For the limit fcyl → 1 an asymptotic behaviour of the FWHM of
the cylinder can be found. Using the approximation of the column density profile
(Eq. (16)) leads to 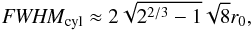 (23)which decreases
linearly as (1 − fcyl). As seen in Fig. 7 this behaviour is valid for
fcyl > ~ 0.7. If we replace the
mass ratio by Eq. (9) we see that the FWHM
decreases inversely as the square root of its overpressure
pc/pext. The
same behaviour is valid for spheres (see Appendix C).
(23)which decreases
linearly as (1 − fcyl). As seen in Fig. 7 this behaviour is valid for
fcyl > ~ 0.7. If we replace the
mass ratio by Eq. (9) we see that the FWHM
decreases inversely as the square root of its overpressure
pc/pext. The
same behaviour is valid for spheres (see Appendix C).
For the limit fcyl → 0 the asymptotic behaviour is
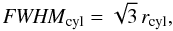 (24)which varies as
(24)which varies as
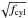 .
.
In between these limits, the FWHM shows a maximum size for both spheres and cylinders,
just as seen for rcl. Because of the steepening shape of the
column density profile towards higher f the maxima appear at lower
f then that for the maximum rcl. The maxima
are given by 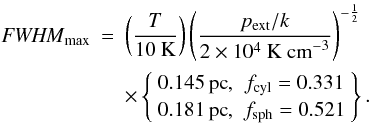 (25)We
also note that for spheres the decrease of the FWHM from the maximum to that of the
critical value is also stronger than in case of the cloud radius. The value of a critical
stable sphere is given by:
(25)We
also note that for spheres the decrease of the FWHM from the maximum to that of the
critical value is also stronger than in case of the cloud radius. The value of a critical
stable sphere is given by: 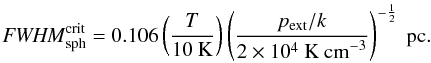 (26)
(26)
3.5.1. The FWHM-NH(0) relation
There is a relationship between the two observables FWHM and
NH(0), as shown in Fig. 8 for both spheres and cylinders. 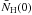 ,
the column density corresponding to the above FWHMmax, is
given by
,
the column density corresponding to the above FWHMmax, is
given by ![\begin{eqnarray} \bar N_{\rm H}(0) &=& 10^{21}\left(\frac{p_{\rm ext}/k}{2\times 10^4~{\rm K~cm}^{-3}}\right)^{\frac{1}{2}} \nonumber \\ &&\times \left\{ \begin{array}{cc} 3.524\, {\rm cm^{-2}}, & f_{\rm cyl} = 0.331 \\[0.05cm] 4.552\, {\rm cm^{-2}}, & f_{\rm sph} = 0.521 \end{array} \right\}, \end{eqnarray}](/articles/aa/full_html/2012/06/aa18961-12/aa18961-12-eq129.png) (27)which
is independent of K, and using Eq. (25) for cylinders
(27)which
is independent of K, and using Eq. (25) for cylinders 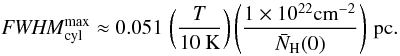 (28)
(28)
 |
Fig. 8 Relation of the FWHM and the central column density NH(0) through an isothermal self-gravitating cylinder (black) and sphere (grey). The cloud temperature is 10 K and the external pressure is 2 × 104 K cm-3, except for the long-dashed curve where half the pressure is assumed. The column densities corresponding to the maxima in the FWHM are marked with vertical dashed-dotted lines. The asymptotic behaviour for low and high overpressure is shown by short-dashed curves. The dotted curves (almost hidden by the solid curves) are approximations using Eq. (32). The values for a cloud with the overpressure of a critical stable sphere are shown as filled circles. |
For high mass ratios
(fcyl > ~0.7) if we eliminate the
dependence on (1 − fcyl) in approximation Eq. (23) for the FWHM using the inverse
dependence in approximation Eq. (19) for
the central column density we obtain the simple relationship (see also Eq. (C.9) in Appendix C) 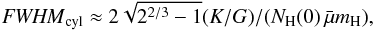 (29)which is independent
of both pext and fcyl but does
respond to K. For molecular gas, we have in the case of high
overpressure
(29)which is independent
of both pext and fcyl but does
respond to K. For molecular gas, we have in the case of high
overpressure 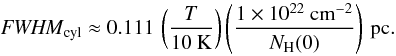 (30)Note that this is
identical to Eq. (28), except for a
larger prefactor.
(30)Note that this is
identical to Eq. (28), except for a
larger prefactor.
At small overpressure (flat density profile) the FWHM and
NH(0) increase for given temperature and external pressure
proportionally with the cloud size. We obtain the asymptotic behaviour for low mass
ratio or low overpressure (see also Eqs. (17), (24), and (C.3)) 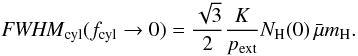 (31)For
intermediate values of the mass fraction, the
FWHM-NH(0) relation for both of cylinders
and spheres can be interpolated to high accuracy between the above limiting behaviours,
as discussed in Appendix D. The relation is
(31)For
intermediate values of the mass fraction, the
FWHM-NH(0) relation for both of cylinders
and spheres can be interpolated to high accuracy between the above limiting behaviours,
as discussed in Appendix D. The relation is
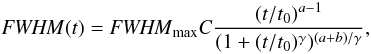 (32)where
(32)where
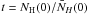 is the normalized central column density, a, b,
t0, γ, and C are
appropriate constants described in Appendix D. The corresponding values for molecular
cylinders and spheres are given in Table 1, for
T = 10 K and the adopted external pressure (denoted with
superscript 0). For cylinders and spheres the analytical function is an excellent
approximation of the numerical solution overplotted in Fig. 8. For cylinders the approximation also provides the correct power law
behaviour for small and high overpressure, by construction. For the spheres we allowed
for a variation of index of the power law behaviour for large overpressure; however, the
change is small.
is the normalized central column density, a, b,
t0, γ, and C are
appropriate constants described in Appendix D. The corresponding values for molecular
cylinders and spheres are given in Table 1, for
T = 10 K and the adopted external pressure (denoted with
superscript 0). For cylinders and spheres the analytical function is an excellent
approximation of the numerical solution overplotted in Fig. 8. For cylinders the approximation also provides the correct power law
behaviour for small and high overpressure, by construction. For the spheres we allowed
for a variation of index of the power law behaviour for large overpressure; however, the
change is small.
From Appendix D follows the scaling relation of
the column density at the maximum
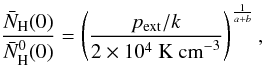 (33)and the scaling
relation for the maximum FWHM
(33)and the scaling
relation for the maximum FWHM 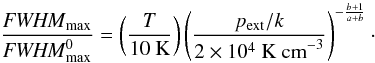 (34)Combining these with
the values in Table 1 we recover Eq. (28).
(34)Combining these with
the values in Table 1 we recover Eq. (28).
For constant pext, 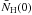 is also fixed. The dependence of both asymptotes and FWHMmax
on K or T is the same and so the locus of
FWHM vs. NH(0) is simply scaled by
K.
is also fixed. The dependence of both asymptotes and FWHMmax
on K or T is the same and so the locus of
FWHM vs. NH(0) is simply scaled by
K.
3.6. Dependence on basic parameters
 |
Fig. 9 Physical parameters of an isothermal self-gravitating cylinder (left panel) and sphere (right panel) with fixed pext/k = 2 × 104 K cm-3 as a function of cloud temperature. Plotted are the cloud diameter (2rcl, dotted line, scale on left axis), the central density (dashed line, right axis), and the column density through the cloud centre (solid line, right axis). The values given for the size and the density depend on the minimum temperature Tmin assumed to be 10 K. For spherical clouds the parameters are shown for all physical solutions including the supercritical ones characterized through an overpressure larger than pc/pext ≈ 14.04. The grey dashed-dotted line in the left hand figure gives the temperature ratio for fcyl = 0.75. |
In the previous sections we have examined how the physical properties of isothermal self-gravitating cylinders and spheres, subject to a fixed external pressure and with a fixed K or temperature, change with the mass, parameterized through the mass ratio f. We can therefore directly understand how the properties would be affected by a change of mass, say through accretion of additional material.
In this subsection we discuss how the physical parameters are affected by altering the external pressure and the temperature (through cooling), respectively.
3.6.1. Changing external pressure
As we have seen in Sect. 2.2, the maximum mass
line density of a cylinder does not depend on the external pressure. Therefore, in the
case of constant mass line density fcyl and fixed
temperature, a change of the external pressure has no effect on the gravitational state.
In a quasi-equilibrium situation a cylinder can always compensate for a higher external
pressure through compression; the central pressure rises so that the overpressure
(Eq. (8)) remains the same. While a
change of the external pressure has no effect on the density profile it does affect the
appearance because a cylinder becomes more opaque in higher pressure regions in
accordance with 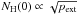 (Eq. (18)).
(Eq. (18)).
The case of a sphere with constant temperature and constant mass M is
quite different; a change of the external pressure affects the gravitational state. The
ratio of M to the critical mass changes as
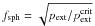 ,
where
,
where 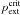 is the
maximum possible pressure that the cloud of fixed M can sustain at its
edge (see Eq. (6)). As the external
pressure is increased the central pressure reaches a finite maximum
14.04pcrit when fsph = 1,
after which there is no stable configuration.
is the
maximum possible pressure that the cloud of fixed M can sustain at its
edge (see Eq. (6)). As the external
pressure is increased the central pressure reaches a finite maximum
14.04pcrit when fsph = 1,
after which there is no stable configuration.
Furthering the discussion in Sect. 2.2, a cloud is considered to be stable if the compression leads to a pressure increase at the cloud edge, i.e., the response −(dp(rcl)/drcl) > 0 where rcl is the cloud radius. Subcritical spheres, those with overpressure below 14.04, are stable against compression with a pressure response −(dp(rsph)/drshp) > 0. Just above the critical state, a sphere is unstable4. However, we also note that supercritical spheres significantly above the critical overpressure are not all unstable according to the above definition.
In the case of a cylinder the response is simply given by
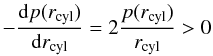 (35)for all mass ratios
0 < fcyl < 1.
Because of this, all gravitational states are stable. In the context of the equilibrium
solutions being discussed, there is no critical state (or supercritical states) for
cylinders as there is for spheres (see also Ebert
1955; McCrea 1957).
(35)for all mass ratios
0 < fcyl < 1.
Because of this, all gravitational states are stable. In the context of the equilibrium
solutions being discussed, there is no critical state (or supercritical states) for
cylinders as there is for spheres (see also Ebert
1955; McCrea 1957).
3.6.2. Embedded filaments
Filaments are often characterized by comparing their mass line density to the maximum value 2K/G. A basic problem of interpretation which arises concerns the effective temperature of the filament, in particular if the filament itself is not entirely isothermal. For example, larger filaments with a relatively high effective temperature of 50 K or more might form/contain small dense interior filaments which are a factor five or more colder. The profile of the column density would show a narrow distribution on top of a broader one. The small size of the narrow feature is related to the colder gas temperature and to its higher external pressure, which in this case is the pressure in the interior in the broad filament. Depending on the distribution of mass assigned, both broad and narrow filaments might be below their relevant maximum mass line density (the fact that they were observed would suggest this conclusion). See further discussion in Sects. 4.2 and 5.3.
3.6.3. Dependence on temperature
To understand how the isothermal self-gravitating clouds are affected through cloud
cooling we consider a spherical cloud of fixed mass and a cylindrical filament with
fixed mass line density. For a given external pressure, equilibrium solutions of
isothermal self-gravitating clouds exist only above a temperature
Tmin. For a sphere, Tmin is
the temperature corresponding to the critical stable cloud, from Eq. (6) for the fixed mass. For a cylinder,
Tmin derives from Eq. (5) for the fixed mass line density. Mathematically we can express
ratio of the temperature to Tmin in terms of
f and so the gravitational state of the cloud is given by
T/Tmin ≥ 1. For
spheres 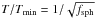 and for cylinders
T/Tmin = 1/fcyl.
and for cylinders
T/Tmin = 1/fcyl.
The cloud parameters (diameter, central density, and column density) for both cylinders and spheres are shown in Fig. 9 where as a minimum temperature we have chosen Tmin = 10 K. As the cloud cools at fixed mass line density and pext, its size shrinks while both central density and the column density through the centre rise. The variation of the radius and central density with temperature is stronger in the case of a cylinder compared to a sphere. For a given temperature ratio, the central column density through a cylinder is larger than that through a sphere if we neglect the complication of supercritical stable cases.
As it cooled to Tmin, a cylinder would approach asymptotically a singular state of an infinitely thin cylinder with infinite overpressure, assuming it was not in the meantime fragmented through instabilities. At a lower temperature still, there would not be an equilibrium solution at all: it would collapse to a spindle.
Through cooling a sphere reaches the critical point beyond which further cooling would cause a pressure drop at the cloud edge so that the cloud would collapse in a free fall time. The physical solutions presented in Fig. 9 for pressurized supercritical spheres correspond to cloud temperatures above the critical temperature; these supercritical spheres are not accessible simply by cooling at fixed mass and external pressure.
For fixed low mass or low mass line density Tmin might lie
at a value that cannot be reached by any efficient cooling mechanism. For example Bok
globules show temperatures not much lower than typical 10 K (Myers et al. 1983; Benson &
Myers 1989). See also Appendix A.4.
Clouds with Tmin below this empirical physical limit would
therefore remain as gravitational stable equilibrium configurations. A filament might
possibly enhance its mass line density through accretion, raising
Tmin and obviating this cooling barrier. Such spheres
would also need to accrete more material to become physically unstable and/or they might
become unstable through increased compression which raises
Tmin as 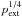 .
.
4. Observed physical parameters of filaments
In the following we validate the model by comparing the theoretical prediction with recent observations. This is important to confirm because then application of this model to interstellar filaments would allow an independent estimate of astrophysical quantities. For example, it could be used to estimate the interstellar pressure and the distance to cloud complexes and star formation regions, and it could be used in combination of measurements of the dust emission to estimate the dust emissivity.
 |
Fig. 10 FWHM-NH(0) relation of filaments.
Observed values in Polaris (dark grey
symbols), IC 5146 (black symbols), and
Aquila (light grey symbols), from Fig. 7 of
Arzoumanian et al. (2011). Note that we are
plotting the column density of H nucleons rather than H2. We also lowered
their values by 2.33/2.8 to correct for the value of
|
Imaging submillimetre observations with Herschel provide estimates of the
FWHM of the filaments, their density profiles, and of the central column densities. Some
uncertainties relating to such measurements are discussed in Appendix A. Here, we discuss the results for individual filaments in Polaris, IC 5146,
and Aquila presented by Arzoumanian et al. (2011). To describe the filament profiles, they adopted
a generalization of Eq. (2) for the density
profile, parameterized by index α:
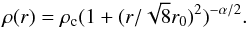 (36)At large cloud radii
(
(36)At large cloud radii
(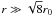 ) the profiles of the
filaments in IC 5146 indicated
α ~ 1.6 ± 0.3, less steep than the value four they expected for clouds in a
vacuum, in agreement with previous measurements discussed by Fiege & Pudritz (2000). Our interpretation is simply that an equilibrium
cylinder that is pressure confined is the relevant model. Relatively flat profiles are a
natural outcome for cylinders with a mass ratio fcyl
considerably smaller than unity (Sect. 3.3).
) the profiles of the
filaments in IC 5146 indicated
α ~ 1.6 ± 0.3, less steep than the value four they expected for clouds in a
vacuum, in agreement with previous measurements discussed by Fiege & Pudritz (2000). Our interpretation is simply that an equilibrium
cylinder that is pressure confined is the relevant model. Relatively flat profiles are a
natural outcome for cylinders with a mass ratio fcyl
considerably smaller than unity (Sect. 3.3).
In Fig. 10 the deconvolved FWHM and NH(0) results of Arzoumanian et al. (2011) are compared with the self-consistent prediction of our model of pressure-confined cylinders, including the asymptotic behaviours. The parameters for the filaments of the three observed regions occupy different areas in the FWHM-NH(0) plane. The filaments in Polaris show the lowest central column densities with most values below NH(0) < 1021 cm-2. The sizes are also apparently smaller compared to the two other samples. The filaments in IC 5146 have intermediate central column densities with a mean NH ~ 6 × 1021 cm2. The highest column densities were observed for filamentary structures in Aquila with values up to ~1023 cm-2. Overall, the data indicate a trend that filaments with low column densities are on average smaller than those with high column densities.
As we see in Fig. 10 the model of pressurized cylinders shows a good agreement with the observations, although obvious deviations do exist. The observations are broadly consistent with a cloud temperature T = 10 K and an ambient pressure of pext/k = 2 × 104 K cm-3. Such a pressure is in the range expected, as discussed in Appendix A.3. The data show a dispersion around the theoretical curve which can be attributed to a variation of the external pressure alone. Most data points lie in a pressure regime pext/k from 1.5 × 104 K cm-3 to 5 × 104 K cm-3. Note how the position of the maximum lies on a line parallel to the high fcyl asymptote. An additional horizontal deviation of data from the model is expected because of the distribution of inclination angles; as shown in Fig. 10, higher inclination could in principle explain some of the high values of the column densities. Note that at constant pressure, the FWHM-NH(0) curve translates vertically with T.
Kandori et al. (2005) studied the physical parameters of Bok Globules using an idealized model of a pressurized isothermal self-gravitating sphere to fit the column density profile obtained from extinction measurements. The derived external pressures ranged from 2.1 × 104 K cm-3 to 1.8 × 105 K cm-3 with a mean of 5.7 × 104 K cm-3. There is overlap with the pressures derived here but on average they are higher.
4.1. Behaviour at small column density
Comparison of the data to the asymptotic behaviour at low fcyl (Eq. (C.3)) constrains the ratio T/pext. In combination with this, the position of the maximum (Eq. (28)) constrains T. At low column density, a higher pressure could be accommodated by raising T, but for higher column densities near the predicted maximum the FWHM might become too large. Likewise, if no efficient cooling mechanisms exist to cool the cloud temperature below 10 K, then we have a lower limit on the required external pressure close to the cited values.
The parameters of most of the filaments in Polaris seem to follow the relation expected for rather low mass ratio, fcyl < 0.1. Those structures are therefore not strongly self-gravitating and so possibly transient density enhancements. If they exist, filaments with even lower fcyl would be small compared to the instrumental resolution and of low contrast in the images. Stronger background fluctuations (cirrus noise; e.g., Martin et al. 2010) in the other two cloud complexes would produce a more challenging limitation to identifying faint low column density structures, and so the fact that filaments with low mass ratio are less frequent or entirely absent in the two other samples might result from this selection effect.
4.2. Behaviour at large column density
We think that inclination effects are unlikely responsible for the extremely high column densities reported. High column densities without the expected small sizes might instead be related to cold filaments which are embedded and pressure-confined within larger filamentary structures, as mentioned in Sect. 3.6.2. Our simple idealized model is therefore not easily applicable.
For example, in the IC 5146 sample, the filament with the highest column density (numbered 6 by Arzoumanian et al. 2011) also has the highest reported mass line density (152 M⊙ pc-1), much higher than the expected maximum value for a filament with K corresponding to 10 K. This is a very interesting but complex filament with large variations in central column density and FWHM along the sinuous ridge. The images and average line profile show one or more cold irregular inner filaments inside a broader structure. The narrow filaments are often paired in parallel segments. How high the mass line density is judged to be depends on how far out radially the column density is integrated and this depends on where the adopted model profile meets the “background”. Measurement of the embedded filament(s) above the complex background of the broad filament would produce physical parameters closer to the simple model. A slightly higher K would help too, moving the predicted curve vertically in Fig. 10.
Our sense is that this whole filament is not in free fall radial collapse, in which case the self-gravity of the larger embedding structure needs to be balanced too; an isothermal model is probably not appropriate, but a higher K (or perhaps even extra magnetic pressure) would be needed. This is open to experimental investigation by molecular velocity and line-width measurements such as reported by Pineda et al. (2010). Kramer et al. (1999) have in fact mapped a 0.4 pc square region on the ridge of this filament in some lines of the rare isotopologues of CO. Even within this small region they find many clumps and two ridges with differing velocites and line widths. Overall this dense central region, while clumpy, is fairly cold in terms of K though perhaps warmer than 10 K. On the other hand, for 13CO on a larger scale (2.5 pc) the velocity dispersion σ ≈ 1 km s-1 (position C3 in Dobashi et al. 1992). While perhaps exaggerated by optical depth effects, this is suggestive of K being an order of magnitude larger in the broad embedding filament. The situation seems to be similar for the widest filament (numbered 12) where the profile suggests an interior cold (sometimes paired) filamentary structure surrounded by a more turbulent gas.
Interestingly, no filaments with high central extinction (NH(0) > ~2 × 1022 cm-2) and the corresponding low size (FWHM < 0.08 pc) were found. There is no obvious selection effect against finding these high fcyl filaments though, as suggested above, measurement of their parameters might be an issue depending on their environment.
If strongly self-gravitating filaments, those above a certain mass ratio, do not exist, then why? This might be inherent to the process responsible for the formation and evolution of filaments generally, or might be because of their disruption and/or short lifetimes. While interesting, the former possibility is beyond the scope of this paper. One clue to the latter possibility is that according Fig. 10 the empirical cut-off in fcyl is near 0.75, where the cylinders have about the same overpressure as a critical stable sphere and so if appropriately fragmented might form structures that would collapse. This is explored further in the following section.
5. Structure formation along filaments
In most cases observed filaments show substructure, contributing to the difficulty of measuring their parameters. Most interesting for understanding the potential role of filaments, as opposed to just high column and volume density, in the star formation process are the condensed structures extracted, “prestellar cores” having strong self-gravity. By definition they are cool, not having detectable emission at 70 μm or 24 μm (Könyves et al. 2010), and so while they have the potential for forming protostars or young stellar objects (YSOs) (André et al. 2010) they are not yet vigorously doing so. They are being externally heated (stage E, Roy et al. 2011) with little internal energy being generated. These “prestellar cores” appear in the higher column density filaments at typically AV > 8 mag, as in Aquila and IC 5146 (André et al. 2010; Arzoumanian et al. 2011). Cold protostars are rarer and also often associated with filaments (André et al. 2010; Bontemps et al. 2010).
Even filaments with much lower column density, those with low fcyl such as in Polaris, have substructure. These are dubbed “starless cores” as well, potentially confusing nomenclature: although they have sizes typical of what defines cores (radii less than a few tenths of a parsec) they comprise much less than a solar mass and are not significantly gravitationally bound and so do not seem destined to form stars (André et al. 2010).
5.1. Equilibrium filaments
If the basic structure is described by an equilibrium filament, as we have argued, then
the question arises as to the origin of the substructure. Equilibrium filaments are
subject to gravitational instabilities that are axisymmetric, producing structure along
the axial directions. Two types may be distinguished (Nagasawa 1987). For high fcyl
(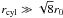 ) the instability
forms out of compression. A local density increase raises the self-gravity and lowers the
gravitational energy, leading to a growth in the amplitude of the structure. For low
fcyl, those with a fairly flat profile
(
) the instability
forms out of compression. A local density increase raises the self-gravity and lowers the
gravitational energy, leading to a growth in the amplitude of the structure. For low
fcyl, those with a fairly flat profile
(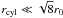 ), the
instability relates to deformation of the surface; in such a “sausage instability” it is
the volume energy of the surface integral of the external pressure that is lowered.
Transitional behaviour mixing these cases occurs near
fcyl = 1/2
(
), the
instability relates to deformation of the surface; in such a “sausage instability” it is
the volume energy of the surface integral of the external pressure that is lowered.
Transitional behaviour mixing these cases occurs near
fcyl = 1/2
(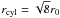 ).
).
 |
Fig. 11 Length and time scales relevant to fragmentation as a function of
fcyl, in units of the FWHM (left axis) and
|
Linear analysis of the dispersion relation (Nagasawa
1987) shows that the critical wavelength above which perturbations grow is, for
fcyl → 1, 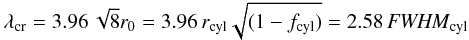 (37)and,
for fcyl → 0,
(37)and,
for fcyl → 0, 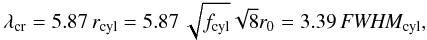 (38)with a smooth
variation for values of fcyl in between. The wavelength
corresponding to the maximum growth rate, λm, is about twice
λcr (a factor 1.96 and 1.84 for the above limiting cases,
respectively). Figure 11 shows the
fcyl dependence of λcr and
λm, relative to the FWHM. At least initially, the fastest
growing mode is quite elongated, with
λm/FWHMcyl ≈ 5.
This would also be the separation of the cores, in units of FWHM. But in absolute terms,
both λm and FWHM become arbitrarily small in the two limits.
This is shown in Fig. 12.
(38)with a smooth
variation for values of fcyl in between. The wavelength
corresponding to the maximum growth rate, λm, is about twice
λcr (a factor 1.96 and 1.84 for the above limiting cases,
respectively). Figure 11 shows the
fcyl dependence of λcr and
λm, relative to the FWHM. At least initially, the fastest
growing mode is quite elongated, with
λm/FWHMcyl ≈ 5.
This would also be the separation of the cores, in units of FWHM. But in absolute terms,
both λm and FWHM become arbitrarily small in the two limits.
This is shown in Fig. 12.
 |
Fig. 12 Like Fig. 11, but with lengths and time scales expressed in physical units. The molecular cylinders are assumed to have temperatures of Tcl = 10 K and to be pressurized by a medium with pext/k = 2 × 104 K/cm3. Also shown is the corresponding FWHM (see Fig. 7). |
An important issue is the growth time scale, which is proportional to
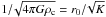 ,
the sound crossing time across r0. As shown in Fig. 11, for the fastest growing mode the constant of
proportionality falls from 4.08 to 2.95 as fcyl increases from
0 to 1 (Nagasawa 1987). It is also convenient to
define a time scale
,
the sound crossing time across r0. As shown in Fig. 11, for the fastest growing mode the constant of
proportionality falls from 4.08 to 2.95 as fcyl increases from
0 to 1 (Nagasawa 1987). It is also convenient to
define a time scale 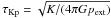 ,
that evaluates to 0.4 My for the adopted values of K and
pext. Thus for fcyl → 1,
,
that evaluates to 0.4 My for the adopted values of K and
pext. Thus for fcyl → 1,
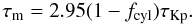 (39)This clearly arbitrarily
short. For fcyl near 0 the time scale is
(39)This clearly arbitrarily
short. For fcyl near 0 the time scale is 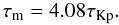 (40)While this is much
faster than the crossing time
(40)While this is much
faster than the crossing time 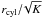 ,
because rcyl ≪ r0, it is still
finite, of order 1.6 My for the canonical values, even longer for a warmer or more
turbulent gas. This would set up “sausage instabilities.” The time scale
τm in My is shown in Fig. 12.
,
because rcyl ≪ r0, it is still
finite, of order 1.6 My for the canonical values, even longer for a warmer or more
turbulent gas. This would set up “sausage instabilities.” The time scale
τm in My is shown in Fig. 12.
The effect of a uniform magnetic field along the filament has also been studied by Nagasawa (1987). The “compressive instability” (finite fcyl) is not much affected because the field is axial, but the “sausage instability” (low fcyl) is strongly suppressed because the field limits the surface distortion. In that case, both λm (see Fig. 11) and the time scale τm are increased significantly, even for a field much smaller than equipartition strength (where p2 = B2/(4πρcK) = 1). Thus, in the ISM this instability seems unlikely to be relevant to determining the substructure seen in filaments with low mass fraction as in Polaris.
The question of the final outcome of the non-linear growth of the “compressive instability” is of course critical. Curry (2000) found a sequence of equilibrium structures within filaments. Their shape is prolate along the cylinder axis, within a tidal lobe within which the equidensity contours are closed. These equilibria are gravitationally dominated and so are rounder as the pressure (density) contrast between centre and lobe increases (limiting axial ratio about 1.7). The behaviour of the lobe radius and the mass contained within the lobe with increasing pressure contrast is reminiscent of the Bonnor-Ebert sequence, though it is not known whether these cores become unstable to collapse at similar overpressures.
The non-linear growth of the instability has been followed numerically by Inutsuka & Miyama (1997) for two cases of equilibrium cylinders with fcyl = 0.9 and 0.2. For the former they find a complete disintegration of the filament into well separated spherical clouds suggestive of gravitational collapse. For the latter a distinctive spherical core forms as well, with the central density increased by a factor nine, but it does not collapse.
5.1.1. Mass of the fragment
The maximum mass available to be concentrated by a perturbation of wavelength
λ is 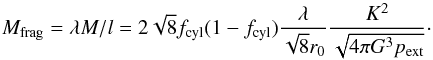 (41)This is deliberately
cast in the same form as Eq. (6) for the
mass of a critical stable sphere, where the prefactor is simply 4.191.
(41)This is deliberately
cast in the same form as Eq. (6) for the
mass of a critical stable sphere, where the prefactor is simply 4.191.
Even if the growth of the perturbation is effective in concentrating material into a
fairly spherical core, it seems intuitive to us that the outcome is unlikely to be
gravitational collapse unless the mass of the core is comparable to the critical
Bonnor-Ebert mass for the external pressure confining the original cylinder. To
accumulate the critical mass, the required wavelength
λsph,cr is, when
fcyl is close to 1, 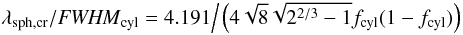 (42)and,
when fcyl is close to 0,
(42)and,
when fcyl is close to 0, 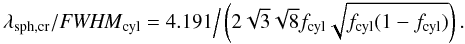 (43)Thus for both of these
limiting cases the perturbations would initially have to be extremely elongated compared
to the FWHM. The locus of
λsph,cr/FWHMcyl
in Fig. 11 contrasts these extreme values with the
finite value of
λm/FWHMcyl
(in the range 5−6). Thus in both limits of fcyl, any
condensations resulting from perturbations would be of low mass compared to the critical
Bonnor-Ebert mass; this is not a promising scenario for forming prestellar or
protostellar cores.
(43)Thus for both of these
limiting cases the perturbations would initially have to be extremely elongated compared
to the FWHM. The locus of
λsph,cr/FWHMcyl
in Fig. 11 contrasts these extreme values with the
finite value of
λm/FWHMcyl
(in the range 5−6). Thus in both limits of fcyl, any
condensations resulting from perturbations would be of low mass compared to the critical
Bonnor-Ebert mass; this is not a promising scenario for forming prestellar or
protostellar cores.
Indeed none are observed for filaments with low fcyl. Also, because of suppression by the magnetic field, we are less interested in the case fcyl close to 0. It is hard to imagine a perfectly uniform filament being created in a turbulent medium; whether the structure that does exist is just a natural by-product of formation of the filament needs to be investigated.
For filaments with very high overpressure, or fcyl close to unity, the implication is that a series of small dense condensations would develop, each of insufficient mass to collapse. On a longer time scale these might merge to form more massive cores (Inutsuka & Miyama 1997), perhaps arriving at the high density equilibrium configuration found by Curry (2000). According to the findings presented in Fig. 10 this fcyl → 1 limiting case has little relevance to the interstellar medium as the precursor narrow high column density filaments have not been observed. How far the results are biased through the method applied to characterize highly opaque filaments need to investigate as well.
However, for intermediate fcyl we see in Fig. 11 that λsph,cr can actually be less than λm (and even λcr) and comparable to the FWHM. This is a more propitious situation, starting from a much less elongated perturbation, to accumulate a mass comparable to the critical Bonnor-Ebert mass.
For such intermediate fcyl, τm ≈ 3.5(1 − fcyl)τKp. This is sufficiently rapid (Fig. 12) that initially uniform filaments could develop structure on astronomically relevant timescales. As discussed above, it seems plausible that some of these could accumulate a critical Bonnor-Ebert mass and become the observed cold protostars. If this were the explanation, then the protostars ought to be separated by about λm, about five times the FWHM of the embedding/undisturbed filament (Fig. 11). This appears to be on the order of what is observed (see below) but needs to be carefully quantified.
5.2. Pearls on a string
According to Men’shchikov et al. (2010), the above-mentioned prestellar cores, observed along high column density filaments, are about the same size as the width of the filament. Inspection of the images of source positions presented (Men’shchikov et al. 2010; Arzoumanian et al. 2011) shows that they are also separated by about the FWHM of the filament. Therefore, remarkably, they are arranged “almost like pearls on threads in a necklace” (Men’shchikov et al. 2010). Because of the small separation it appears unlikely that those structures are caused directly by the gravitational instabilities discussed above. We have seen that condensations resulting from that origin would have a separation of at least 2.5 times the FWHM (for intermediate mass ratios fcyl > ≈ 0.5). We have examined the above-mentioned filament 6 in IC 5146 in both SCUBA (Di Francesco et al. 2008) and Herschel archival submillimetre images. There are many clumps that would be extracted as prestellar cores, but not all are equal, and our impression is that these are somewhat clustered with major concentrations typically separated by 2′ to 5′, corresponding to 2.2 to 5.5 times the given FWHM. The YSOs associated with this filament found in the Spitzer study by Harvey et al. (2008) are also well separated. This is perhaps more in line with what would be expected from gravitational instabilities, but then a hierarchy and perhaps time sequence of fragmentation is suggested.
At this point, we feel that the origin of the substructure is an open question. Other than gravitational instability, perhaps it is a natural consequence of the formation of such filaments; in the presence of strong self-gravity, it might be difficult to form a perfectly straight and uniform cylinder. In our experience it is also a challenge to extract and characterize “sources” found as closely spaced inhomogeneities along a filament.
Because a separation of one FWHM is less than λcr,sph (Fig. 11), these prestellar cores, while strongly self-gravitating, would probably be stable against collapse, consistent with their being starless. Whether these presently starless clouds will form any stars in the future and therefore be relevant to the initial mass function of the stars is also an interesting open question.
5.3. Filaments with high mass line density
For a filamentary structure with more than the maximum mass line density (Eq. (4)), there is no equilibrium solution. If they could be created, somehow, because of their high density they would collapse on a rapid timescale.
There are certainly filamentary configurations observed that have a large mass line density, considerably greater than the maximum line density if evaluated for K corresponding to a low value like 10 K which we find appropriate to simple narrow filaments. André et al. (2010) conclude that the gravitational fragmentation of such “supercritical”5 filaments is responsible for the formation of the observed self-gravitating prestellar cores and protostars. There are two problems with this scenario.
First, our interpretation of the numerical calculations of Inutsuka & Miyama (1997) is that there is fragmentation only if the mass line density is finely tuned to being just above the maximum value and/or if the initial conditions already contain large perturbations, which begs the question. Perhaps a relevant configuration could be set up beginning with an equilibrium filament with fcyl close to 1 and then making it “supercritical” by lowering the temperature. Otherwise, the predominant outcome is radial collapse of the cylinder to a spindle. Eventually the collapsing spindle would become optically thick and could develop substructure; but this would be on a small scale because of the large density and small size of the collapsed filament (Inutsuka & Miyama 1997).
Second, in the process of forming the fragments, a “supercritical” filament itself would collapse, be consumed, and disappear on the same rapid time scale. However, the observations indicate that prestellar cores, and even YSOs, occur along identifiable filaments of finite size, even if it appears that the mass line density is “supercritical”. This coexistence is a challenge to be satisfied by any model of the structure formation, even for initially equilibrium filaments.
While high column and volume density are arguably fundamental to any process of fragmentation, our conclusion is that protostar and cluster formation must be a more complex process than simply the gravitational fragmentation of “supercritical” filaments. Based on the complex radial profiles of these high mass line density filaments, we think that some progress might be made by considering cold embedded filaments within a broader structure supported by a gas with higher effective K, in which case the overall configuration is not actually “supercritical” and in free fall.
6. Summary and discussion
We have analyzed the physical properties of interstellar filaments on the basis of an idealized model of isothermal self-gravitating infinitely long cylinders which are pressurized by the ambient medium. The pressure-confined cylinders have a mass-line density smaller than cylinders extending into a vacuum. The mass fraction fcyl, the ratio of the mass-line density to the maximum possible for equilibrium configurations, describes the gravitational state of the cylinder. For given temperature and external pressure, it is used in deriving analytical expressions for the central density, the radius, the column density profile, the central and average column densities and the FWHM. The dependence of the physical properties on external pressure and temperature is clear in these expressions. The results are compared to the case of pressure-confined isothermal self-gravitating (Bonnor-Ebert) spheres, characterized by the mass fraction fsph, the ratio of the mass to the mass of the critical stable sphere.
We compared the model prediction for the relation between the size and the central column density with recent observations of filaments. Given the complexity seen it is gratifying to find good agreement, even surprising considering the idealization of the model. In practice the model seems best applicable to those filaments that are cold and show a simple smooth elongated structure. On the basis of the model the filaments appear to experience an ambient pressure pext/k in the range 1.5 × 104 K cm-3 to 5 × 104 K cm-3 and to have a gas temperature T ≈ 10 K. For these parameters, the observations indicate an apparent physical upper limit to the mass ratio fcyl ≈ 0.75; higher column density narrower filaments are not seen. The corresponding maximum central extinction for the observed filaments fitting the model is AV ≈ 7 mag. This is interestingly close to the empirical threshold for star formation, but we think this is coincidental, especially given the variable threshold from region to region (Enoch et al. 2007).
We have summarized and discussed previous stability studies that have shown that all unmagnetized infinitely long cylinders fcyl < 1 are subject to gravitational instabilities. While a magnetic field can have a stabilizing effect for fcyl < 0.5, in particular suppressing “sausage instabilities” for fcyl ≈ 0, there is a negligible effect on compressive instabilities for fcyl > 0.5. Interstellar magnetized filaments would seem to become increasingly unstable towards large fcyl because of a strongly increasing growth rate of the instabilities. The disintegration of filaments close to the maximum mass line density (fcyl > 0.9) would produce fragments whose masses are well below the critical value to form stars. We found no indication in the theory for a strong threshold for the formation of fragments that would collapse. However, intermediate values of fcyl seem most favorable. The fastest growing disturbance for fcyl > 0.5 occurs at a length approximately five times the FWHM, so that protostars or clusters would be well separated.
It is difficult to understand in this model why in high column density filaments there would be substructure akin to the extracted prestellar cores separated along the filament by only one FWHM, which is well below the minimum length at which a disturbance would grow (λcrit > ≈ 2.5 × FWHMcyl). This might point to external influences accompanying the process that formed the filament in the first place, resulting in the non-uniform mass line density along these filaments, not the idealized model considered here. On the other hand, if one concentrates on the major mass concentrations along the filament, their separation might be more compatible with an origin in gravitational instability along the cylinder.
High mass line density filaments are observed that would appear to have more than the maximum mass line density that could exist in equilibrium, at least if evaluated for the low adopted K. The coexistence of embedded narrow high column density filaments, even in pairs, and considerable substructure (prestellar cores) and protostars suggests to us a scenario more complex than simply the free-fall collapse and fragmentation of cylinders with more than the maximum line density. Although the simple model cannot explain such complex structure, it points to a situation in which the embedding structure is supported by gas with a K larger than the low value that might reasonably be adopted for the narrow embedded structure. This is obviously open to observational scrutiny via mapping of velocities and line widths of appropriate molecules.
As McCrea (1957) has emphasized, “genuine” gravitational collapse to form stars and clusters is best realized in configurations with roughly the same dimensions in all directions so that gravitational effects are three-dimensional. He argued that the breakup of less favorable one-dimensional configurations like filaments must be due to irregularities in the density distribution and the external pressure to which they are subjected, or to differential motions. Empirically, there is suggestive evidence that such breaking of the symmetry of an idealized long cylinder is important, as occurs for example where filaments appear to cross. These are matters that could be explored now in the results of numerical simulations.
Appendix A discusses uncertainties in this and other important physical parameters like column density.
According to Enoch et al. (2007), however, such a threshold might vary from region to region.
Despite our comments in Sect. 2.2, their terminology is adopted here in this subsection.
Using a dimensional analysis of a cloud in virial equilibrium, McKee & Tan (2003) derive a similar relationship between the average internal pressure and the column density. There is a similar coefficient of proportionality, not surprisingly because both configurations are strongly self-gravitating and because the average pressure in a critical sphere is only 2.5 times larger than the external pressure (Spitzer 1968).
Acknowledgments
J.F. is thankful for financial support from CITA and the MSO. Personally he likes to thank Prof. B. Schmidt and Prof. M. Dopita. This work was supported by grants from the Natural Sciences and Engineering Research Council of Canada and the Canadian Space Agency.
References
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Benson, P. J., & Myers, P. C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnor, W. B. 1956, MNRAS, 116, 351 [CrossRef] [Google Scholar]
- Bontemps, S., André, P., Könyves, V., et al. 2010, A&A, 518, L85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulares, A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Curry, C. L. 2000, ApJ, 541, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Curry, C. L., & McKee, C. F. 2000, ApJ, 528, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Di Francesco, J., Johnstone, D., Kirk, H., MacKenzie, T., & Ledwosinska, E. 2008, ApJS, 175, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Dobashi, K., Yonekura, Y., Mizuno, A., & Fukui, Y. 1992, AJ, 104, 1525 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., & Sutherland, R. 2003, Astrophysics of the Diffuse Universe (Springer) [Google Scholar]
- Ebert, R. 1955, Z. Astrophys., 37, 217 [Google Scholar]
- Enoch, M. L., Glenn, J., Evans, II, N. J., et al. 2007, ApJ, 666, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Fiege, J. D., & Pudritz, R. E. 2000, MNRAS, 311, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Fischera, J. 2011, A&A, 526, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischera, J., & Dopita, M. 2008, ApJS, 176, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, J. B., Rosolowsky, E. W., Kauffmann, J., et al. 2009, ApJ, 696, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Gaida, M., Ungerechts, H., & Winnewisser, G. 1984, A&A, 137, 17 [NASA ADS] [Google Scholar]
- Glover, S. C. O., & Mac Low, M.-M. 2011, MNRAS, 412, 337 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Goldsmith, P. F. 2001, ApJ, 557, 736 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hanawa, T., Nakamura, F., Matsumoto, T., et al. 1993, ApJ, 404, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Huard, T. L., Jørgensen, J. K., et al. 2008, ApJ, 680, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1997, ApJ, 480, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Di Francesco, J., & Kirk, H. 2004, ApJ, 611, L45 [Google Scholar]
- Kalberla, P. M. W., & Kerp, J. 2009, ARA&A, 47, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Kandori, R., Nakajima, Y., Tamura, M., et al. 2005, AJ, 130, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, C., Alves, J., Lada, C. J., et al. 1999, A&A, 342, 257 [NASA ADS] [Google Scholar]
- Martin, P. G., Miville-Deschênes, M.-A., Roy, A., et al. 2010, A&A, 518, L105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, P. G., Roy, A., Bontemps, S., et al. 2012, ApJ, 751, 28 [NASA ADS] [CrossRef] [Google Scholar]
- McCrea, W. H. 1957, MNRAS, 117, 562 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2010, A&A, 518, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., Martin, P. G., Abergel, A., et al. 2010, A&A, 518, L104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myers, P. C., Linke, R. A., & Benson, P. J. 1983, ApJ, 264, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Nagasawa, M. 1987, Prog. Theor. Phys., 77, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, T., Mizuno, A., Kawamura, A., Ogawa, H., & Fukui, Y. 1998, ApJ, 502, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pineda, J. E., Goodman, A. A., Arce, H. G., et al. 2010, ApJ, 712, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A., Ade, P. A. R., Bock, J. J., et al. 2011, ApJ, 727, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1968, in Stars and Stellar Systems, Nebulae and Interstellar Matter, ed. B. Middlehurst, & L. Aller (University of Chicago Press), 1 [Google Scholar]
- Stodólkiewicz, J. S. 1963, Acta Astronomica, 13, 30 [Google Scholar]
Appendix A: Questions of scale
In comparing the models with the data we need to be aware of the context, what can be measured and the related uncertainties. In this appendix we discuss column density, size, external pressure, and effective temperature.
A.1. Column density
Column densities of filaments from Herschel data are fundamentally in units of the dust optical depth in the submillimetre. This is converted to NH using a submillimetre dust opacity. This opacity appears to show a dependence on environment and might be uncertain by a factor two (Martin et al. 2012). For the overview comparison in Fig. 10, where NH(0) is on a logarithmic scale, this might not be a major concern.
In the diffuse and largely atomic interstellar medium, where both NH and optical interstellar extinction curves can be observed directly, we have the ratio NH/E(B − V) = 5.8 × 1021 cm-2/mag (Bohlin et al. 1978) and an absolute to relative extinction RV = AV/E(B − V) = 3.1 (Fitzpatrick 1999). A column density of 1022 cm-2 therefore corresponds to AV = 5.3 mag. We use this same conversion when AV is being used a “shorthand” for column density in dense molecular environments, recognizing that the actual visual extinction, if it could be measured, would probably not be this value.
Another measure more applicable at higher column densities is near infrared color excess. This is also often converted to AV, which again should be regarded as a “shorthand” because the shape of the interstellar extinction curve through the optical probably varies. It might be more reliable to convert the near infrared colour excess directly to NH, but that calibration is not actually known for the high column densities encountered in star-forming regions (Martin et al. 2012).
Another uncertainty might be related to radiative transfer which produces a radial variation of the dust temperature within externally-heated filaments. While the dust opacity seems to be larger for dust in denser environments, the averaging of the dust emission over a distribution of temperatures leads to a reduced effective emission coefficient and a spectral dependence of the emissivity that is less steep than is intrinsic for dust in a diffuse environment as theoretically demonstrated for condensed cores (Fischera 2011). The radiative transfer effects increase with central column density and could therefore play a larger role at high mass ratios. The column density profile indicated by the surface brightness would be flatter than the intrinsic profile.
A.2. Size
Sizes of filaments are measured from the profile of the column density in the direction orthogonal to the axis of the filament. The FWHM could be measured directly but is more usually found as a parameter of a model fit to the profile. The model fit also needs to account for the background on which the filament appears superimposed. In practice both the background and the profile can vary along the filament, adding to the challenges (Arzoumanian et al. 2011, resorted to using a Gaussian model to find the FWHM) and the reported standard deviation in the parameters. Even in nearby molecular clouds, the filaments, while resolved, are often not a lot larger than the imaging resolution. Therefore, the reported sizes have been “deconvolved”. In the future, this might be avoided by forward modeling, adopting analytical models like we have presented, convolving the predictions to the resolution of the data, and then iteratively fitting the parameters.
The background is still something to be fit too. Depending on the circumstances, this background could be from foreground or background material unrelated to the filament, and/or a contribution from the medium providing the pressure confinement. A well-defined edge of a filament might suggest, for example, that the filament can be regarded as cold material which is surrounded by a warmer or more turbulent but less dense environment. This relates to the following discussion of external pressure.
A.3. External pressure
Boulares & Cox (1990) presented a model of the vertical support of the Galactic disk. The mid-plane pressure near the sun is at least pext/k = 2.5 × 104 K cm-3. About a third of this is the effective vertical support by cosmic rays; however, on the size scale of the structures of interest here, cosmic ray pressure can be ignored (Curry & McKee 2000; Fischera & Dopita 2008; Fischera 2011). The remainder is a combination of kinetic pressure (thermal and turbulent motions) and magnetic pressure. For a magnetic field of less than equipartition strength, the kinetic pressure would be at least 0.8 × 104 K cm-3. The thermal pressure is only about a third of this (Kalberla & Kerp 2009), the rest being turbulent pressure.
The filaments being discussed are within clouds with sufficient column density to have
become molecular (⟨AV⟩ > 1 mag;
e.g., Glover & Mac Low 2011). If it is
assumed that these clouds can themselves be described as pressure-confined isothermal
spheres, with enough self-gravity to be near the critical mass, then following
Eqs. (21) and (B.10) the external pressure required to
produce a mass surface density ⟨Σ⟩ averaged over the projected radius is given by6 (A.1)A
subcritical sphere would require a greater external pressure to produce the same average
column density (Fig. 4). The average column density
in the GMC sample discussed by Heyer et al.
(2009) corresponds to ⟨AV⟩ ≈ 2.8 mag, which would
require a pressure of 2.9 × 104 K cm-3. This seems consistent
with the fact that this cloud sample is in the inner Galaxy where the midplane pressure
is probably higher.
(A.1)A
subcritical sphere would require a greater external pressure to produce the same average
column density (Fig. 4). The average column density
in the GMC sample discussed by Heyer et al.
(2009) corresponds to ⟨AV⟩ ≈ 2.8 mag, which would
require a pressure of 2.9 × 104 K cm-3. This seems consistent
with the fact that this cloud sample is in the inner Galaxy where the midplane pressure
is probably higher.
The central extinction through a critical stable isothermal sphere is
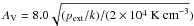 mag
(Fischera & Dopita 2008, Fig. 4). This predicted amount of extinction seems to be in
agreement with that observed for molecular clouds (Dopita & Sutherland 2003).
mag
(Fischera & Dopita 2008, Fig. 4). This predicted amount of extinction seems to be in
agreement with that observed for molecular clouds (Dopita & Sutherland 2003).
Two conclusions are that the midplane pressure is indeed quite high, and that the pressure within the molecular cloud due to its self gravity – the ambient external pressure experienced by the filaments – will be higher still, depending on where the filaments lie within the pressure profile of the molecular cloud.
Another contribution could be due to ram pressure, for example related to the sweeping up of the North Celestial Loop of which the Polaris field is a part.
A.4. Effective temperature
For the model we need the effective temperature embodied in K, related to both the thermal and the turbulent (non-thermal) motion of the gas. The most direct way to measure this would be through the line width of an appropriate molecular tracer. For example, the ammonia mapping of B5 in Perseus by Pineda et al. (2010) revealed a sharp decrease in line width in the central 0.1 pc. This is thought to be the result of the decay of supersonic turbulence present on larger scales; the observed line widths are subsonic for a thermal/kinetic temperature of 10 K. Foster et al. (2009) present results from an ammonia survey of many other cores in Perseus and find them mostly quiescent (σnonthermal ≈ 0.12 km s-1, but see their histograms for details of the full survey). The modeling of two lines gives kinetic temperatures about 12 K; derived excitation temperatures are lower (Foster et al. 2009). The dust temperature from the submillimetre spectral energy distribution observable by Herschel is typically low (down to 10 K) in the high column density regions in low mass star forming regions (see the temperature maps in, e.g., Bontemps et al. 2010; Arzoumanian et al. 2011). Coupling of the kinetic temperature in the gas to the dust temperature comes into play for nH2 > 104 cm-3 (Goldsmith 2001). According to Fig. 1, this becomes relevant for strongly self-gravitating cylinders (fcyl > 0.7). Taken together, while perhaps a platonic ideal, a small dense isothermal core with K corresponding to 10 K is reasonable as a reference value. However, K might be higher than this in some environments or stages of evolution. And of course the structure might not be exactly isothermal.
Appendix B: Mean column density of spheres
In Paper II the approximation for the mean column densities of cylinders and spheres as a function of the overpressure were presented. Here, we want to comment on the values for spheres and give an exact expression for the asymptotic behaviour at large overpressures.
The mass of a spherical isothermal self-gravitating cloud which is in pressure
equilibrium with the surrounding medium
(p(zcl) = pext)
is given by (Paper I) 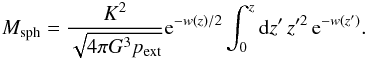 (B.1)Here,
w = φ/K = lnpc/pext
is the unit free potential and z = rA the unit free
radius of the Lane-Emden equation
(B.1)Here,
w = φ/K = lnpc/pext
is the unit free potential and z = rA the unit free
radius of the Lane-Emden equation
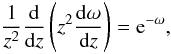 (B.2)where
(B.2)where
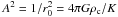 . Using the expression for the
mass (Eq. (B.1)) and
. Using the expression for the
mass (Eq. (B.1)) and
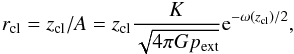 (B.3)for the cloud
radius we obtain for the mean mass surface density of an isothermal self-gravitating
sphere
(B.3)for the cloud
radius we obtain for the mean mass surface density of an isothermal self-gravitating
sphere 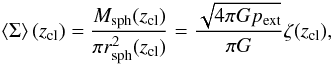 (B.4)where
(B.4)where 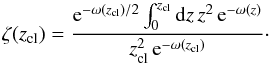 (B.5)We want to analyze the
function ζ(z) for the values
zi with
i = 1, 2, ... at which
a spherical cloud of a fixed mass produces pressure maxima at the cloud outskirts for
changing cloud size zcl (Fischera & Dopita 2008). The global pressure maximum at
z1 = zmax with
zmax ≈ 6.451 characterizes the critical stable cloud which
has an overpressure
eω(zmax) ≈ 14.04. The last two
terms in Eq. (B.1) for a critical stable
cloud produce a value of approximately 4.191. We obtain the condition for the pressure
maxima from Eq. (B.1) which we transform
to an expression for the pressure at the cloud outskirts
p(zcl). At the pressure maxima we find that
the derivative of the potential needs to fulfill the condition
(B.5)We want to analyze the
function ζ(z) for the values
zi with
i = 1, 2, ... at which
a spherical cloud of a fixed mass produces pressure maxima at the cloud outskirts for
changing cloud size zcl (Fischera & Dopita 2008). The global pressure maximum at
z1 = zmax with
zmax ≈ 6.451 characterizes the critical stable cloud which
has an overpressure
eω(zmax) ≈ 14.04. The last two
terms in Eq. (B.1) for a critical stable
cloud produce a value of approximately 4.191. We obtain the condition for the pressure
maxima from Eq. (B.1) which we transform
to an expression for the pressure at the cloud outskirts
p(zcl). At the pressure maxima we find that
the derivative of the potential needs to fulfill the condition 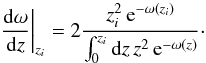 (B.6)On the other hand, from
the Lane-Emden equation it follows that
(B.6)On the other hand, from
the Lane-Emden equation it follows that
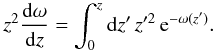 (B.7)Using this expression to
replace the derivative in Eq. (B.6) we
obtain for the condition for the pressure maxima
(B.7)Using this expression to
replace the derivative in Eq. (B.6) we
obtain for the condition for the pressure maxima 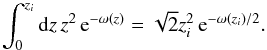 (B.8)For clouds
producing maxima at the cloud outskirts the two last terms in Eq. (B.1) of the cloud mass are therefore equal to
(B.8)For clouds
producing maxima at the cloud outskirts the two last terms in Eq. (B.1) of the cloud mass are therefore equal to
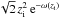 .
For those clouds we get the alternative mass equation
.
For those clouds we get the alternative mass equation
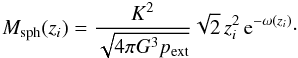 (B.9)For the critical stable
cloud we have the condition
(B.9)For the critical stable
cloud we have the condition 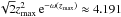 with
zmax ≈ 6.451.
with
zmax ≈ 6.451.
If we insert the condition B.8 in
Eq. (B.5) we see that the pressure
maxima are at z-values where 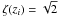 and we obtain as the asymptote for large overpressure:
and we obtain as the asymptote for large overpressure: 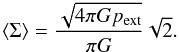 (B.10)The asymptotic value of
the mean column density given in Eq. (21)
is obtained using the relation
(B.10)The asymptotic value of
the mean column density given in Eq. (21)
is obtained using the relation 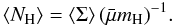 (B.11)
(B.11)
Appendix C: The FWHM of isothermal self-gravitating clouds
To derive the FWHM we replaced the density through
ρ(r) = ρce−ω
and the radius by
r = z/A. In case
of cylinders the potential is given by
ω(z) = 2ln {1 + z2/8}
(Eq. (2)). The mass surface density at
impact parameter 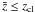 is then given by
is then given by 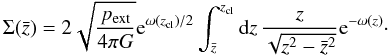 (C.1)The impact
parameter zFWHM for the FWHM for an
isothermal pressurized cloud is determined by
(C.1)The impact
parameter zFWHM for the FWHM for an
isothermal pressurized cloud is determined by
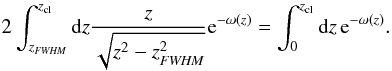 (C.2)For
zcl ≪ 1 the density profile is essentially flat and we
obtain the simple asymptotic behaviour
(C.2)For
zcl ≪ 1 the density profile is essentially flat and we
obtain the simple asymptotic behaviour 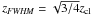 which gives
which gives
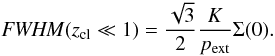 (C.3)At sizes
zcl ≫ 1 the right hand side approaches asymptotically a
constant value. For spheres we get
(C.3)At sizes
zcl ≫ 1 the right hand side approaches asymptotically a
constant value. For spheres we get
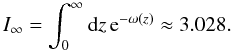 (C.4)For cylinders we
obtain
(C.4)For cylinders we
obtain 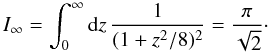 (C.5)This constant determines
the impact parameter for high overpressure or large zcl. For
spheres we find
(C.5)This constant determines
the impact parameter for high overpressure or large zcl. For
spheres we find 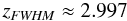 (C.6)and for cylinders
(C.6)and for cylinders
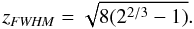 (C.7)The relation
r = z/A provides
(C.7)The relation
r = z/A provides
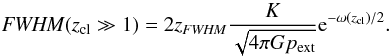 (C.8)As noted in
Sect. 3.5, in the limit of high overpressure
(zcl ≫ 1) the FWHM for constant T and
pext decreases inversely proportional to the square root of
the overpressue
pc/pext.
Replacing the central pressure by the mass surface density through the centre gives
finally for zcl ≫ 1 the asymptotic behaviour
(C.8)As noted in
Sect. 3.5, in the limit of high overpressure
(zcl ≫ 1) the FWHM for constant T and
pext decreases inversely proportional to the square root of
the overpressue
pc/pext.
Replacing the central pressure by the mass surface density through the centre gives
finally for zcl ≫ 1 the asymptotic behaviour 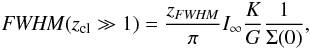 (C.9)so that
FWHM ∝ KΣ-1(0). For high overpressure the
relation FWHM-Σ(0) does not depend on the external pressure.
(C.9)so that
FWHM ∝ KΣ-1(0). For high overpressure the
relation FWHM-Σ(0) does not depend on the external pressure.
Appendix D: On combining power laws
Here, we discuss the main properties of the function used to fit the relation of the FWHM
and the central column density NH(0). Call these
y and x, respectively. There are asymptotic limits
relating these for small and large mass ratios (e.g., the power laws in Eqs. (31) and (29) for cylinders). We assume that two power laws
 with
a > 1 and
b > −1, can be combined in an interpolating
formula
with
a > 1 and
b > −1, can be combined in an interpolating
formula  (D.3)where we have introduced
(D.3)where we have introduced
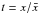 and where
and where 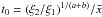 .
As can be verified, the equation provides the correct limits for
t ≪ t0 and
t ≫ t0. The parameter γ
describes the smoothness of the transition and is adjusted to optimize the fit. For
γ → ∞ the function becomes a simple broken power law. The maximum lies
at
.
As can be verified, the equation provides the correct limits for
t ≪ t0 and
t ≫ t0. The parameter γ
describes the smoothness of the transition and is adjusted to optimize the fit. For
γ → ∞ the function becomes a simple broken power law. The maximum lies
at ![\appendix \setcounter{section}{4} \begin{equation} t_{\rm max}=t_0\sqrt[\gamma]{\frac{a-1}{b+1}}, \end{equation}](/articles/aa/full_html/2012/06/aa18961-12/aa18961-12-eq317.png) (D.4)with
(D.4)with
![\appendix \setcounter{section}{4} \begin{equation} y_{\rm max} = \sqrt[a+b]{\xi_1^{b+1}\xi_2^{a-1}}\sqrt[\gamma]{\frac{(a-1)^{a-1}(b+1)^{b+1}}{(a+b)^{a+b}}}\cdot \end{equation}](/articles/aa/full_html/2012/06/aa18961-12/aa18961-12-eq318.png) (D.5)If we identify
(D.5)If we identify
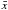 as the value where the function y reaches its maximum we have
as the value where the function y reaches its maximum we have
![\appendix \setcounter{section}{4} \begin{eqnarray} t_0 & = & \sqrt[\gamma]{\frac{b+1}{a-1}},\\ \bar x &=& \sqrt[a+b]{\xi_2/\xi_1} \sqrt[\gamma]{\frac{a-1}{b+1}}\cdot \end{eqnarray}](/articles/aa/full_html/2012/06/aa18961-12/aa18961-12-eq320.png) We
find that the combined function can be written as
We
find that the combined function can be written as
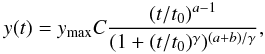 (D.8)with
(D.8)with
![\appendix \setcounter{section}{4} \begin{equation} C^{-1} = \sqrt[\gamma]{\frac{(a-1)^{a-1}(b+1)^{b+1}}{(a+b)^{a+b}}}\cdot \end{equation}](/articles/aa/full_html/2012/06/aa18961-12/aa18961-12-eq322.png) (D.9)In the special case
a = 2, b = 0 as for the relation between FWHM and Σ(0)
for cylinders or in good approximation for a sphere we have
(D.9)In the special case
a = 2, b = 0 as for the relation between FWHM and Σ(0)
for cylinders or in good approximation for a sphere we have
![\appendix \setcounter{section}{4} \begin{eqnarray} t_0 &=& 1, \\ y_{\rm max} &=& \sqrt{\xi_1 \xi_2}/C,\\ C &=& \sqrt[\gamma]{4},\\ \bar x &=& \sqrt{\xi_2/\xi_1}. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18961-12/aa18961-12-eq325.png)
Appendix E: Analytic approximations of the length and time scales of perturbations
The derived dependence of the perturbation lengths λcr and
λm and the initial growth time
τm on the mass ratio and the magnetic field strength are
based on the work of Nagasawa (1987) who presented
calculations for fcyl = 0.01, 0.5, and 1.0. We assumed that
the mass ratio dependence of the time scale given in units
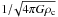 and the ratio of the disturbance length to the FWHM of the cylinder for non-magnetized
cylinders can be described through a fourth-order polynomial function
and the ratio of the disturbance length to the FWHM of the cylinder for non-magnetized
cylinders can be described through a fourth-order polynomial function
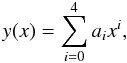 (E.1)in
x = fcyl with vanishing derivatives for low
and high mass ratios
(y′(0) = y′(1) = 0). The curves
reproduce the theoretical values at fcyl = 0, 0.5, and 1.0.
The disturbance lengths can be transferred to absolute lengths using a fifth-order
polynomial approximation for the FWHM in units of the characteristic length
(E.1)in
x = fcyl with vanishing derivatives for low
and high mass ratios
(y′(0) = y′(1) = 0). The curves
reproduce the theoretical values at fcyl = 0, 0.5, and 1.0.
The disturbance lengths can be transferred to absolute lengths using a fifth-order
polynomial approximation for the FWHM in units of the characteristic length
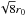 given by
given by
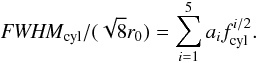 (E.2)The approximation
is 1% accurate and provides the correct asymptotes at low and high
fcyl. The coefficients
ai for the polynomial representations are
given in Table E.1.
(E.2)The approximation
is 1% accurate and provides the correct asymptotes at low and high
fcyl. The coefficients
ai for the polynomial representations are
given in Table E.1.
To estimate the dependence of the magnetic field on the parameters
λcr, λm, and
τm we used at low mass ratios the dispersion relation for an
incompressible self-gravitating cylinder which has been shown to be a valid representation
for fcyl → 0. The relation is given by (Nagasawa 1987)
![\appendix \setcounter{section}{5} \begin{equation} \frac{\omega^2}{4\pi G\rho_{\rm c}} = \frac{\xi I_{1}(\xi)}{I_0(\xi)}\left[K_0(\xi)I_0(\xi)-\frac{1}{2}\right]-\frac{p^2}{8f_{\rm cyl}} \frac{\xi}{I_{0}(\xi)K_1(\xi)}, \end{equation}](/articles/aa/full_html/2012/06/aa18961-12/aa18961-12-eq336.png) (E.3)where
Iν(ξ) and
Kν(ξ) are modified Bessel
functions,
p2 = B2/(4πρcK),
ξ = (2π/λ)R,
and ω = 1/τ. The behaviour at larger
fcyl we described through a fourth-order polynomial function
where we have chosen
(E.3)where
Iν(ξ) and
Kν(ξ) are modified Bessel
functions,
p2 = B2/(4πρcK),
ξ = (2π/λ)R,
and ω = 1/τ. The behaviour at larger
fcyl we described through a fourth-order polynomial function
where we have chosen 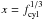 for τm and
for τm and 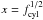 for
the disturbance lengths λcr and
λm. To the analytical function at low mass ratios we produced
a smooth transition and assumed a vanishing derivative at
fcyl = 1. The curves were chosen to reproduce the values of
Nagasawa (1987) at
fcyl = 0.5 and fcyl = 1. For
strong magnetic fields the left boundary for the polynomial approximation is set to a
value were we obtain at high mass ratios essentially a flat curve. The corresponding
curves only show qualitatively at which fcyl the parameters
are affected by the magnetic field.
for
the disturbance lengths λcr and
λm. To the analytical function at low mass ratios we produced
a smooth transition and assumed a vanishing derivative at
fcyl = 1. The curves were chosen to reproduce the values of
Nagasawa (1987) at
fcyl = 0.5 and fcyl = 1. For
strong magnetic fields the left boundary for the polynomial approximation is set to a
value were we obtain at high mass ratios essentially a flat curve. The corresponding
curves only show qualitatively at which fcyl the parameters
are affected by the magnetic field.
Constants of polynomial approximations.
All Tables
All Figures
 |
Fig. 1 Central density of an isothermal self-gravitating molecular cylinder (black) and sphere (grey), for fixed values of the ambient pressure. pext/k = 2 × 104 K cm-3 and cloud temperature T = 10 K. The dotted line is the value achieved by a critical stable sphere. This same central density (or overpressure) is reached in a cylinder with fcyl = 0.733 (filled black circle). |
| In the text | |
 |
Fig. 2 Like Fig. 1, but for the radius of an isothermal self-gravitating cylinder (black) and sphere (grey). |
| In the text | |
 |
Fig. 3 Pressure profiles of isothermal self-gravitating cylinders (black) and spheres (grey), for various overpressures pc/pext from 2 to 20. The dashed curves show density profiles for simple power laws normalized at the cloud boundary. |
| In the text | |
 |
Fig. 4 Like Fig. 1, but for the central column density (left panel) and mean column density (right panel) through an isothermal self-gravitating cylinder (black) and sphere (grey), as a function of mass fraction f. The dashed line in the left-hand plot is the approximation given in Eq. (19). The dashed lines in the right-hand plot echo the central column densities from the left-hand plot for comparison. The horizontal dotted lines give the values achieved by a critical stable sphere. The values for a cylinder with that overpressure, mass fraction 0.733, are shown as filled black circles. |
| In the text | |
 |
Fig. 5 Column density profiles of isothermal self-gravitating cylinders (black lines) and spheres (grey lines) for several central extinction values from AV = 1 mag to AV = 8 mag. The clouds are pressurized by pext/k = 2 × 104 K cm-3. |
| In the text | |
 |
Fig. 6 Pressure profiles (density profiles) for the column density profiles shown in Fig. 5. Recall that profiles for the same overpressure are compared in Fig. 3. |
| In the text | |
 |
Fig. 7 Like Fig. 2, but for the FWHM of an isothermal self-gravitating cylinder (black line) and sphere (grey line). The dashed line gives the asymptotic behaviour of the FWHM of an isothermal self-gravitating cylinder for high f (Eq. (23)). The vertical dashed-dotted lines mark the mass fraction of the maxima of FWHM (Eq. (25)). The horizontal dotted line shows the FWHM of a critical stable sphere. The FWHM of a cylinder with this overpressure 14.04 (fcyl = 0.733) is shown as the filled black circle (FWHMcyl = 0.0812 pc). |
| In the text | |
 |
Fig. 8 Relation of the FWHM and the central column density NH(0) through an isothermal self-gravitating cylinder (black) and sphere (grey). The cloud temperature is 10 K and the external pressure is 2 × 104 K cm-3, except for the long-dashed curve where half the pressure is assumed. The column densities corresponding to the maxima in the FWHM are marked with vertical dashed-dotted lines. The asymptotic behaviour for low and high overpressure is shown by short-dashed curves. The dotted curves (almost hidden by the solid curves) are approximations using Eq. (32). The values for a cloud with the overpressure of a critical stable sphere are shown as filled circles. |
| In the text | |
 |
Fig. 9 Physical parameters of an isothermal self-gravitating cylinder (left panel) and sphere (right panel) with fixed pext/k = 2 × 104 K cm-3 as a function of cloud temperature. Plotted are the cloud diameter (2rcl, dotted line, scale on left axis), the central density (dashed line, right axis), and the column density through the cloud centre (solid line, right axis). The values given for the size and the density depend on the minimum temperature Tmin assumed to be 10 K. For spherical clouds the parameters are shown for all physical solutions including the supercritical ones characterized through an overpressure larger than pc/pext ≈ 14.04. The grey dashed-dotted line in the left hand figure gives the temperature ratio for fcyl = 0.75. |
| In the text | |
 |
Fig. 10 FWHM-NH(0) relation of filaments.
Observed values in Polaris (dark grey
symbols), IC 5146 (black symbols), and
Aquila (light grey symbols), from Fig. 7 of
Arzoumanian et al. (2011). Note that we are
plotting the column density of H nucleons rather than H2. We also lowered
their values by 2.33/2.8 to correct for the value of
|
| In the text | |
 |
Fig. 11 Length and time scales relevant to fragmentation as a function of
fcyl, in units of the FWHM (left axis) and
|
| In the text | |
 |
Fig. 12 Like Fig. 11, but with lengths and time scales expressed in physical units. The molecular cylinders are assumed to have temperatures of Tcl = 10 K and to be pressurized by a medium with pext/k = 2 × 104 K/cm3. Also shown is the corresponding FWHM (see Fig. 7). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.