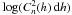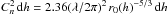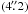| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201218844 | |
| Published online | 24 May 2012 | |
Profiles of the daytime atmospheric turbulence above Big Bear solar observatory
1 Big Bear Solar Observatory, 40386 North Shore Lane, Big Bear City, CA 92314-9672, USA
e-mail: kellerer@bbso.njit.edu
2 National Solar Observatory PO Box 62, Sunspot, NM 88340, USA
3 Center for Solar-Terrestrial Research, New Jersey Institute of Technology, Newark, NJ 07012, USA
Received: 18 January 2012
Accepted: 18 April 2012
Context. Space weather has become acutely critical for today’s global communication networks. To understand its driving forces we need to observe the Sun with high angular-resolution, and within large fields-of-view, i.e. with multi-conjugate adaptive optics correction.
Aims. The design of a multi-conjugate adaptive optical system requires the knowledge of the altitude distribution of atmospheric turbulence. We have therefore measured daytime turbulence profiles above the New Solar Telescope (NST), on Big Bear Lake.
Methods. To this purpose, a wide-field wavefront sensor was installed behind the NST. The variation of the wavefront distortions with angular direction allows the reconstruction of the distribution of turbulence.
Results. The turbulence is found to have three origins: 1. a ground layer (<500 m) that contains 55–65% of the turbulence, 2. a boundary layer between 1–7 km comprises 30–40% of the turbulent energy, 3. and the remaining ~5% are generated in the tropopause, which is above 12 km in summer and between 8 and 12 km in winter.
Conclusions. A multi-conjugate adaptive optical system should thus aim at correcting the ground turbulence, the center of the boundary layer at roughly 3 km altitude and, eventually, the upper boundary layer around 6 km altitude.
Key words: instrumentation: adaptive optics / atmospheric effects / Sun: general
© ESO, 2012
1. Introduction
The New Solar Telescope (NST) in Big Bear Lake, California, is located on the lake, which is characterized by a daytime westerly wind over 3 km of cool water. The telescope has a 1.6 m off-axis primary mirror and is equipped with a 97 element adaptive-optics (AO) system, see Goode et al. (2010a) and Cao et al. (2010). Diffraction limited resolution is attained in the visible after speckle reconstruction. Without speckle reconstruction, and under good atmospheric conditions, the resolution approaches the diffraction limit in the infrared. However, with a single deformable mirror, the atmospheric turbulence is fully corrected only inside the isoplanatic patch. Measurements of daytime isoplanatic angles are sparse. Irbah et al. (1993) measured values up to 6′′ at Calern observatory, France, and Aristidi et al. (2005) indicate a median value of 6 8 at Dome C, Antarctica. No values had yet been measured at Big Bear Lake, but Denker et al. (2007) had analyzed AO corrected images obtained with the now replaced 65 cm solar telescope: the usable AO corrected field had diameters between 10′′ and 25′′, and was thus larger by factors 2–5 than the expected isoplanatic angle ( < 5′′).
8 at Dome C, Antarctica. No values had yet been measured at Big Bear Lake, but Denker et al. (2007) had analyzed AO corrected images obtained with the now replaced 65 cm solar telescope: the usable AO corrected field had diameters between 10′′ and 25′′, and was thus larger by factors 2–5 than the expected isoplanatic angle ( < 5′′).
Parameters of the S-DIMM+ as installed on the NST.
Sunspots and active regions extend over roughly 1′−2′. To attain the diffraction-limit over such field sizes, multi-conjugate adaptive optics (MCAO) applies a wavefront correction that varies inside the field. At the NST, we will use two, eventually three deformable mirrors to correct for the atmospheric turbulence inside a 60′′ × 60′′ (lower limit) to 90′′ × 90′′ (upper limit) field. This will be done in two stages: in summer 2012, a 357 actuator AO system should yield diffraction limited resolution in the visible, over the isoplanatic patch. A second, and eventually a third, deformable mirror will be installed in 2013 and the wavefront distortions will be corrected inside an extended field of view.
The design of an MCAO system requires knowledge of the altitude distribution of atmospheric turbulence. Atmospheric profiles have been measured at Big Bear Lake in the context of the Advanced Technology Solar Telescope (ATST) site testing campaign (Socas-Navarro et al. 2005; Hill et al. 2006; Denker & Verdoni 2006; Verdoni & Denker 2007). The profiles – obtained in terms of the SHAdow BAnd Ranger (SHABAR) (Beckers 2001) – are precise up to 100 m altitude. In addition, the ATST team estimated profiles up to 3.5 km from a combination of SHABAR and Solar Differential IMage Monitor (SDIMM) data.
This article characterizes the daytime atmospheric turbulence at Big Bear Lake, from the ground up to 20 km altitude, with ~1 km resolution. The profiles are determined with a wide-field wavefront sensor, as suggested by Scharmer & van Werkhoven (2010). A total of 550 data sequences were collected on 26 days between June 20th and September 28th 2011 – the height of the observing season at Big Bear Lake. Another set of 311 sequences was acquired during the winter season, between January 31st and February 23rd 2012. Section 2 describes the instrument and the data analysis. A validation of the analysis through simulated data is presented in Sect. 3. Section 4 characterizes the turbulence distribution above Big Bear Lake, and estimates isoplanatic angles with and without MCAO correction.
2. The method
A wide-field Shack-Hartmann (SH) wavefront sensor is installed in the Coudé focus of the NST. Figure 1 is a mechanical view of the instrument: a diaphragm in a focal plane limits the field of view to 66.5′′ × 66.5′′, and prevents overlapping of adjacent sub-aperture images on the detector. A neutral-density filter reduces the flux before the beam is sent on to the SH lenslet. The instrument’s characteristics are listed in Table 1.
Our instrument is a slightly adapted version of the S-DIMM+ described in Scharmer & van Werkhoven (2010): the phase distortions are not measured over the whole pupil but only along its diameter (see Fig. 2). This setup was chosen in view of our future plan to acquire images at high frequency (several hundred Hertz) in order to measure the atmospheric coherence-time. Such a fast read-out requires a small enough region-of-interest on the detector. An image recorded with the conventional S-DIMM+ carries more redundant information. This is helpful to increase the signal-to-noise ratio. In our set-up, we insure data redundancy by recording at least 100 images per sequence. The minimum number of 100 was determined via simulations (see Sect. 3).
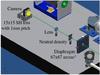 |
Fig. 1 Mechanical layout of the wide-field wavefront sensor. |
 |
Fig. 2 Layout of the 15 sub-apertures over the NST primary mirror (D = 1.6 m, without central obstruction). |
2.1. Image analysis
The data analysis includes the following steps (see Figs. 4 and 5 for a graphic summary):
-
1.
The 15 sub-aperture images are located on the detector andstored in a matrix.
-
2.
We were careful to use approximately 80% of the detector’s full well capacity to maximize the signal-to-noise ratio, while avoiding saturation. Acquisitions that are nevertheless saturated or under-illuminated are disregarded.
-
3.
Each image-sequence is calibrated with a dark and a flat-field image.
-
4.
Under-illuminated sub-apertures at the pupil border are discarded. This accounts for drifts in the pupil-position.
-
5.
The wavefront slopes are measured in the pupil plane with a SH sensor. There are Si ≤ 15 sub-pupils of size 135 × 135 pixels. The 5 pixels at the border of each sub-aperture image are disregarded, and the effective image size is thus 125 × 125 pixels. On each sub-aperture image the wavefront slope is determined with an angular sampling step s. The value of s is determined via the simulations discussed in Sect. 3.
-
6.
NR images with good contrast are selected from the ensemble of Si × I images (I = 100 − 300: number of acquisitions per sequence). These images serve as references for the image-shift calculations. The optimal number of reference images is determined from simulations (Sect. 3).
-
7.
For each of the field points (i0,j0), a wavefront slope is determined by measuring the shift of a Nc × Nc sub-image centered on (i0,j0). The optimal value of Nc is likewise determined in Sect. 3. The shift of the sub-image, S, relative to the reference, R, is obtained through a minimization of the squared intensity-difference between the image and the reference:
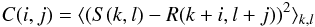 (1) ⟨ ⟩ denotes averaging over the Nc × Nc sub-image. The point (i,j) that minimizes C sets the image shift with pixel precision. i and j are made to vary between − 6 and +6 pixels, and larger image shifts are therefore underestimated. The full-width at half maximum of a long exposure image equals θ0 = 4/π·λ/r0. For r0 = 5 cm, θ = 3.4″ = 7 pixels, hence [−6, +6] pixels is a sufficiently large interval even under strong atmospheric turbulence. The computation of the squared difference is computationally slow, but yields better results than other cross-correlation algorithms – especially in the regime of large shifts values, see Löfdahl (2010). The precision is further improved to 0.1 pixel by a 2-dimensional quadratic interpolation:
(1) ⟨ ⟩ denotes averaging over the Nc × Nc sub-image. The point (i,j) that minimizes C sets the image shift with pixel precision. i and j are made to vary between − 6 and +6 pixels, and larger image shifts are therefore underestimated. The full-width at half maximum of a long exposure image equals θ0 = 4/π·λ/r0. For r0 = 5 cm, θ = 3.4″ = 7 pixels, hence [−6, +6] pixels is a sufficiently large interval even under strong atmospheric turbulence. The computation of the squared difference is computationally slow, but yields better results than other cross-correlation algorithms – especially in the regime of large shifts values, see Löfdahl (2010). The precision is further improved to 0.1 pixel by a 2-dimensional quadratic interpolation:  where
where ![\begin{eqnarray} a_2&=&[C(i+1,j)-C(i-1,j)]/2\\ a_3&=&[C(i+1,j)-2\,C(i,j)+C(i-1,j)]/2\\ a_4&=&[C(i,j+1)-C(i,j-1)]/2\\ a_5&=&[C(i,j+1)-2\,C(i,j)+C(i,j-1)]/2\\ a_6&=&[C(i+1,j+1)-C(i-1,j+1) \nonumber \\ && -C(i+1,j-1)+C(i-1,j-1)]/4 \end{eqnarray}](/articles/aa/full_html/2012/06/aa18844-12/aa18844-12-eq44.png) NR shift estimates are obtained in terms of NR reference images.
NR shift estimates are obtained in terms of NR reference images. -
8.
Static aberrations are determined on a set of 400–1200 images and are removed from each wavefront estimate.
-
9.
The structure functions of the wavefront slopes (along the x- and y-directions, see Fig. 2) are determined for each image sequence:
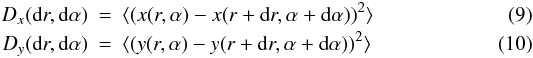 dr is the pupil separation along the axis of the lenslet array (i.e. along the x-axis), dα denotes the angular separation in the vertical plane that contains the x-axis (see Fig. 2).
dr is the pupil separation along the axis of the lenslet array (i.e. along the x-axis), dα denotes the angular separation in the vertical plane that contains the x-axis (see Fig. 2). -
10.
The noise is removed from the structure function, as described in Sect. 2.2.
-
11.
The structure functions are the sum of structure functions contributed by layers at different altitudes:
![\begin{eqnarray} D_s({\rm d\/}r,{\rm d}\alpha) &\,=\,& \left\langle\left[\sum_h s_h(r\!+\!h \alpha)\! -\!\!\sum_h s_h(r\!+\!{\rm d}r \!+\! h (\alpha\!+\!{\rm d}\alpha))\!\right]^2\right\rangle~~~~ \\ &=& \sum_h \langle[s_h(r+h\,\alpha)\! -\! s_h(r+{\rm d\/}r \!+\! h (\alpha\!+\!{\rm d\/}\alpha))]^2\rangle~~ ~~\\ &=& \sum_h D_{h,s} ({\rm d\/}r + h\,{\rm d\/}\alpha) \end{eqnarray}](/articles/aa/full_html/2012/06/aa18844-12/aa18844-12-eq50.png) where s is the wavefront slope in either the x- or y-direction. Dh,s is the structure-function of the wavefront slope at altitude h. The wavefront slopes are averaged over square sub-apertures of size de × de, where de = d + Nc αp h. d = D/16 = 0.1 m is the size of SH sub-apertures, Nc equals the number of pixels used for the cross-correlation (typically 16),
where s is the wavefront slope in either the x- or y-direction. Dh,s is the structure-function of the wavefront slope at altitude h. The wavefront slopes are averaged over square sub-apertures of size de × de, where de = d + Nc αp h. d = D/16 = 0.1 m is the size of SH sub-apertures, Nc equals the number of pixels used for the cross-correlation (typically 16), 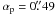 denotes the angular size of a pixel. Sarazin & Roddier (1990) give approximate expressions for the structure functions of wavefront slopes measured over circular apertures of diameter, d:
denotes the angular size of a pixel. Sarazin & Roddier (1990) give approximate expressions for the structure functions of wavefront slopes measured over circular apertures of diameter, d: 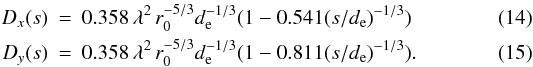 This expression is valid for s > de/2. We determined modified coefficients for square apertures in terms of 1000 simulated Kolmogorov phase-screens with infinite outer scale. We also adjusted the expressions to extend their validity to s < de/2:
This expression is valid for s > de/2. We determined modified coefficients for square apertures in terms of 1000 simulated Kolmogorov phase-screens with infinite outer scale. We also adjusted the expressions to extend their validity to s < de/2: ![\begin{eqnarray} D_x(s) &=& 0.32\,\lambda^2\,r_0^{-5/3}d_{\rm e}^{-1/3}\,\left(1-\frac{0.70}{(s/d_{\rm e}+0.70^3)^{1/3}} \right)\\[3mm] D_y(s) &=& 0.32\,\lambda^2\,r_0^{-5/3}d_{\rm e}^{-1/3}\,\left(1-\frac{0.82}{(s/d_{\rm e}+0.82^3)^{1/3}} \right)\cdot \end{eqnarray}](/articles/aa/full_html/2012/06/aa18844-12/aa18844-12-eq61.png) These structure-functions are used to fill the matrix M that converts the turbulent energy as a function of altitude, r0(h) − 5/3, into the structure function measured at the telescope pupil, Ds(dr,dα). This matrix is shown in Fig. 3.
These structure-functions are used to fill the matrix M that converts the turbulent energy as a function of altitude, r0(h) − 5/3, into the structure function measured at the telescope pupil, Ds(dr,dα). This matrix is shown in Fig. 3. -
12.
The pseudo-inverse, M ∗ , of the matrix M converts the measured structure-functions into profile estimates. This typically results in some layers with negative turbulent energy. These negative values are moved into adjacent layers iteratively, until all layers have either positive or zero energy content: if r0(hi)5/3 < 0, then
![\begin{eqnarray} r_0(h_{i-1})^{5/3} &=& r_0(h_{i-1})^{5/3} - 0.5\, r_0(h_{i})^{5/3} \\[1.5mm] r_0(h_{i+1})^{5/3} &=& r_0(h_{i+1})^{5/3} - 0.5\, r_0(h_{i-1})^{5/3} \\[1.5mm] r_0(h_i)^{5/3} &=& 0 \end{eqnarray}](/articles/aa/full_html/2012/06/aa18844-12/aa18844-12-eq67.png) with proper modification when hi is at the border of the height grid: the negative energy at altitude h1 (resp. hN) is entirely transferred to h2 (resp. hN − 1). This solution is used as an initial guess for a non-linear fit by the Levenberg-Marquardt method.
with proper modification when hi is at the border of the height grid: the negative energy at altitude h1 (resp. hN) is entirely transferred to h2 (resp. hN − 1). This solution is used as an initial guess for a non-linear fit by the Levenberg-Marquardt method. -
13.
Residual noise in the structure function translates into a high-altitude component in the profile estimates ( > 20 km), which we set to zero. This empirical solution is validated on simulated images.
 |
Fig. 3 The matrix M that converts the turbulent energy at altitude h, r0(h) − 5/3 [m−5/3], into the structure functions of wavefront slopes, Dx and Dy [arsec2]. The contrast of the structure functions decreases with altitude, because the slopes are computed through a cross-correlation over a field of finite size, and are thus averaged over larger surfaces with increasing altitude. |
 |
Fig. 4 On each of the Si ≤ 15 sub-aperture images wavefront shifts are determined every sampling step, s. This yields Sα × Sα = ((N − 10 − Nc)/s)2 angular sampling points. The optimal values of s and Nc are determined from simulated images in Sect. 3. |
 |
Fig. 5 Each sequence of 100–300 images yields two structure-functions (of the x- and y-wavefront slopes) in dependence on pupil separation, dr, and angular separation, dα. See also Fig. 2. |
2.2. Noise removal
The measured structure-functions equal: 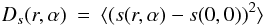 (21)where s is the slope estimate in either x or y-direction. It is the sum of the actual wavefront slope, plus a noise contribution:
(21)where s is the slope estimate in either x or y-direction. It is the sum of the actual wavefront slope, plus a noise contribution: 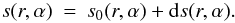 (22)Since the slopes and the noise are uncorrelated,
(22)Since the slopes and the noise are uncorrelated, 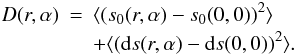 (23)The noise-free structure function, D0(r,α), thus equals:
(23)The noise-free structure function, D0(r,α), thus equals: 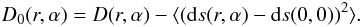 (24)The slope estimates are the average of the measurements obtained with NR reference images:
(24)The slope estimates are the average of the measurements obtained with NR reference images: 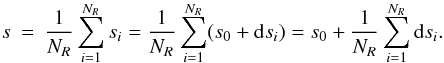 (25)Hence,
(25)Hence, 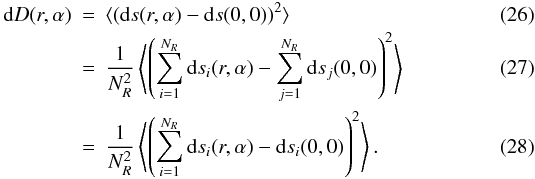 This is because ⟨ (dsi(r,α) − dsj(0,0))2 ⟩ = 0 for any i ≠ j, except when (x,α) = (0,0). The zero point of the structure function, however, does not need noise subtraction since D(0,0) = 0. Equation (28) rewrites as:
This is because ⟨ (dsi(r,α) − dsj(0,0))2 ⟩ = 0 for any i ≠ j, except when (x,α) = (0,0). The zero point of the structure function, however, does not need noise subtraction since D(0,0) = 0. Equation (28) rewrites as: 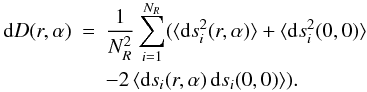 (29)The cross-term ⟨ dsi(r,α) dsi(0,0) ⟩ differs from zero when α = 0: the two slopes si(r,0) and si(0,0) are then determined in terms of the same reference image and the measurement errors dsi(r,0) and dsi(0,0) are correlated.
(29)The cross-term ⟨ dsi(r,α) dsi(0,0) ⟩ differs from zero when α = 0: the two slopes si(r,0) and si(0,0) are then determined in terms of the same reference image and the measurement errors dsi(r,0) and dsi(0,0) are correlated.
We use the NR slope estimates, to quantify the three terms in Eq. (29): 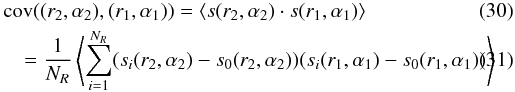
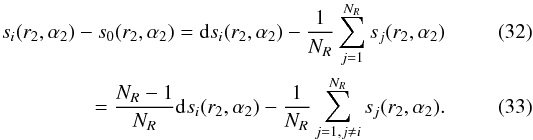 It follows that the covariance is
It follows that the covariance is 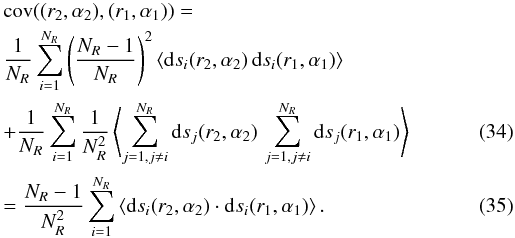 This is because ⟨ dsi(r,α)·dsj(r,α) ⟩ = 0 when i ≠ j and (r,α) ≠ (0,0). From Eqs. (24), (29) and (35), we conclude:
This is because ⟨ dsi(r,α)·dsj(r,α) ⟩ = 0 when i ≠ j and (r,α) ≠ (0,0). From Eqs. (24), (29) and (35), we conclude: ![\begin{eqnarray} D_0(r,\alpha) &\!=\!& D(r,\alpha) \!-\! \frac{1}{N_R-1} [{\rm cov\/} ((r,\alpha),(r,\alpha))\! +\!{\rm cov\/} ((0,0),(0,0)) \nonumber \\ &&-2\,{\rm cov\/} ((r,\alpha),(0,0))]. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18844-12/aa18844-12-eq102.png) (36)
(36)
3. Simulations
S-DIMM+ images were independently simulated by Jose Marino. They were then used to test the data analysis and to set constraints on parameter values in a series of hounds and hares exercises.
3.1. Description of the simulations
The optical parameters – telescope aperture, wavelength, parameters of the SH sensor – are chosen to be identical to the experimental set-up (see Table 1).
 |
Fig. 6 An S-DIMM+ image is used as input to generate the simulated data. |
-
1.
An image recorded with our instrument is used as input for the simulation code (Fig. 6). This is done to ensure a realistic image contrast, and hence a realistic precision on the shift estimates.
-
2.
A phase screen is generated for each layer of the atmospheric model. The phase screens have different sizes to accommodate for the field of view at different heights. The pixel size on the phase screens is 6.25 mm.
-
3.
A grid of 50 × 50 field points covering 80′′ × 80′′ is generated. For each point in the grid, the phase seen along that direction is computed and the resulting shifts are calculated. It is equivalent to a zero field-of-view wavefront sensor that is pointed at different directions in the sky. In that way image shifts are obtained for each sub-aperture along each of the field-points in the grid.
-
4.
This process is repeated I = 200 times. The consecutive phase screens are not correlated, which accounts for the time lags between two S-DIMM+ acquisitions (dt = 103/60 = 16.7 ms) being much larger than the coherence time of daytime turbulence (τ0 ≤ 5 ms).
-
5.
Once the shifts are known, we go through each sub-aperture in each step and distort the object image (see Fig. 6) according to the shifts. The central 66.5′′ × 66.5′′ of the distorted image is clipped and resampled to a pixel array size of 135 × 135.
-
6.
Photon noise is added into the distorted images.
3.2. Simulation results
The S-DIMM+ measurements were done around 0.65 μm wavelength. To ease the comparison with data from the literature, we characterize the atmospheric turbulence at 0.55 μm: if not otherwise mentioned, the Fried parameter, r0, the turbulent energy, 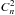 and the isoplanatic angle, θ0, are indicated at 0.55 μm throughout this article.
and the isoplanatic angle, θ0, are indicated at 0.55 μm throughout this article.
We have generated data-sequences for a series of two-layer profiles (see Table 2). The best-guess profiles are shown in Fig. 7. The estimated r0 equals (8.3 ± 0.2) cm and is in good agreement with the input 8.2 cm (this corresponds to r0 = 10 cm at the observing wavelength λ = 0.65 μm).
 |
Fig. 7 Profiles retrieved on simulated data-sequences. The input profiles are described in Table 2. The color indicates the value of |
Input profiles.
We then simulated a data-sequence corresponding to continuously distributed turbulence: 23 layers with same turbulent strength, located at altitudes 0.25 i [km], i = 0.22. The best-guess profiles are shown in Fig. 8.
 |
Fig. 8 Simulation of continuously distributed turbulence: 23 layers of equal intensity between 0 and 5.5 km (black line). Red: best-guess profile. The parameter-values for the analysis are listed in Table 3. |
Two cross-correlation algorithms were tested for the analysis – the squared difference function detailed in Sect. 2 and a cross-correlation in the Fourier-domain: 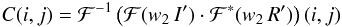 (37)ℱ and ℱ-1 are the Fourier and inverse Fourier transforms. ∗ stands for the complex conjugate. I′ = I − ⟨ I ⟩ and R′ = R − ⟨ R ⟩ , where ⟨ ⟩ denotes averaging over the Nc × Nc pixels. w2 is a 2-dimensional Hamming window as recommended by Löfdahl (2010):
(37)ℱ and ℱ-1 are the Fourier and inverse Fourier transforms. ∗ stands for the complex conjugate. I′ = I − ⟨ I ⟩ and R′ = R − ⟨ R ⟩ , where ⟨ ⟩ denotes averaging over the Nc × Nc pixels. w2 is a 2-dimensional Hamming window as recommended by Löfdahl (2010): 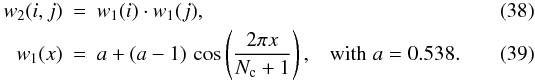 The point (i,j) that maximizes the covariance function sets the image shift with pixel precision. The sub-pixel precision is obtained through a 2D quadratic interpolation (see Sect. 2).
The point (i,j) that maximizes the covariance function sets the image shift with pixel precision. The sub-pixel precision is obtained through a 2D quadratic interpolation (see Sect. 2).
The advantage of the cross-correlation in the Fourier-domain is its speed. We find, however that the Fourier-based algorithm strongly underestimates large shifts values. This agrees with results by Löfdahl (2010). For our purpose – (1) no adaptive optics correction, i.e. large shifts values, and (2) no need of a real-time data analysis – the least-squares based cross-correlation algorithm is thus preferable.
We have further tested the dependence of the analysis on five parameters, and we conclude the following:
-
The turbulent layers are correctly retrieved provided that thecross-correlation is done on images of at least16 × 16 pixels. Since the altitude resolution drops with increasing image size, Nc, we adopt the lower 16 × 16 pixel limit for the rest of the analysis.
-
The angular sampling step, s, should be smaller than 20 pixels =
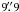 . We use 15 pixels =
. We use 15 pixels = 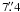 for our analysis. This correspond to a sampling point every 72 cm at the highest altitude considered (20 km).
for our analysis. This correspond to a sampling point every 72 cm at the highest altitude considered (20 km). -
At least Si = 12 sub-apertures need to be correctly illuminated.
-
Each sequence should contain at least I = 100 images.
-
A minimum of NR = 6 reference images is required to retrieve profiles under strong turbulence (r0 ~ 5 cm).
The turbulence is underestimated when r0 < 4 cm. This is due to the algorithm used for the image-shift calculation: the optimal shift is searched within [ − 6,6] pixels, larger shifts are underestimated (see point 7 in Sect. 2.1).
The final parameter-values used for the analysis of the S-DIMM+ images are summarized in Table 3.
Parameter-values for the analysis of simulated S-DIMM+ data.
4. The atmosphere above Big Bear Lake
The NST is situated at 2 km altitude. It is located on Big Bear Lake, 200 m from the shore line. Its topography and climate are described in Zirin & Mosher (1988) and Verdoni & Denker (2007). A main characteristic is a stable ground-layer turbulence throughout the day, due to the low lake temperatures. This is particularly effective for the typical westerly winds, as the air is then cooled over 3 km of open water, and passes NST in a cool, laminar airflow.
4.1. Fried parameter
Figure 9 traces the cumulative distributions of the Fried parameter derived from the S-DIMM+ measurements. The summer and winter distributions frame the results of the ATST survey (Socas-Navarro et al. 2005). The distributions equal 0 for r0 < 4 cm: as already predicted through simulations, lower values are over-estimated by our analysis (see Sect. 3.2).
 |
Fig. 9 Cumulative distributions of the Fried parameter, r0: the straight line is obtained from the 550 summer values (June–Sept. 2011), the dashed line corresponds to the 311 winter measurements (Jan.–Feb. 2012). The circles represent the values obtained by the ATST survey (Socas-Navarro et al. 2005). All values refer to 0.55 μm wavelength. |
We measure r0 = (9.1 ± 3.3) cm in summer and r0 = (5.5 ± 0.8) cm in winter. Accordingly, a diffraction-limited AO correction at 0.55 μm wavelength requires D/r0 = 18 (29) actuators per pupil diameter on a typical summer (winter) day. This compares to 11 and 20 actuators for the current 97-actuator AO system and the future upgrade to 357 actuators. In summer, the 357 actuator system will allow to obtain diffraction-limited images in the G-band, around 0.48 μm, where r0 = (0.48/0.55)6/5(9.1 ± 3.3) cm = (7.7 ± 2.8) cm.
Figure 10 traces the Fried parameter against local observing-time: no correlation exists, neither in summer nor winter. This stability confirms previous results by e.g. the ATST site-testing campaign: on mountain sites the seeing is best in the morning hours, it then degrades around midday and slightly improves again in the late afternoon. In contrast, there is little or no variation over the day on lake sites like Big Bear. If anything, our summer values show an improved r0 around noon and after 2 pm. We typically started the S-DIMM+ measurements either at 10:30 AM (start of the observing day) or after the midday break (observations need to be halted for a few minutes due to a limitation of the telescope mount). The improved r0 around noon and after 2 PM shows that we’d be eager to get more data on days with good seeing, while we’d likely stop the measurements if the turbulence were strong.
 |
Fig. 10 r0 as a function of local time. The red lines indicate the average value and root-mean square deviation of r0 over 5 time intervals of equal length. At mountain sites the turbulence is strongest around noon. Over Big Bear Lake there is no clear evolution of turbulent strength over the day. |
4.2. Turbulence profiles
Figure 11 shows the profiles measured on a summer- and on a winter-day: on August 29th, the turbulence is mainly generated in a large boundary layer that extends up to 5–6 km. On February 10th, it originates from a strong ground layer ( ≤ 2 km) and from a separate, higher-altitude layer.
 |
Fig. 11 Atmospheric profiles on Aug. 29th, 2011 (top) and Feb. 10th, 2012 (bottom). The average Fried parameter (isoplanatic angle) equals 9.9 cm |
The number of layers per profile is represented in Fig. 12: in summer, there are typically 2 strong layers with r0 ≤ 0.3 m, and 1–4 weaker layers with r0 ≤ 1.0 m. In winter, the turbulence is mostly contained in 3–4 strong layers (r0 ≤ 0.3 m) and 3 − 5 weaker layers (r0 ≤ 1.0 m).
 |
Fig. 12 Red (resp. blue): Percentage of profiles with N layers of r0 ≤ 0.3 m (resp. 0.3 m < r0 ≤ 1.0 m). |
As seen in Fig. 13, summer profiles consist of a ground layer (<500 m) and an extended boundary layer (≤6−7 km). There is almost no turbulence above 8 km. In winter, the ground layer extends up to 2 km. Additional turbulence is generated between 4 and 7 km and in a third layer between 8 and 14 km. In summary, summer profiles show more ground layer turbulence, while winter profile have relatively more turbulence at the tropopause ( ≥ 8 km). These results are summarized in Table 4.
 |
Fig. 13 Red (resp. blue): percentage of profiles where the layer at altitude h has r0 ≤ 0.3 m (resp. 0.3 m < r0 ≤ 1.0 m). |
Average percentage of turbulent energy in different altitude-slabs and resulting Fried parameters – for the 550 summer- and 311 winter-profiles.
Meteorological data confirm the seasonal evolution of the layer at the tropopause. The northern hemisphere jet-streams move to lower latitudes in winter, and are then right above Big Bear. In summer, they are to the North of Big Bear (Fig. 14). The stronger winds in winter are also confirmed by upper-air soundings at the Vandenberg Air Force Base (Fig. 15, right panel), which is located 325 km to the west of Big Bear on the Pacific coast. The tropopause is lower in winter (Fig. 15, left panel): 11 − 12 km, against 16–18 km in summer, which converts to 9–10 km and 14–16 km above Big Bear. These facts are in good agreement with Fig. 13.
 |
Fig. 14 Jet streams on Aug. 29th 2011 (top) and Feb. 10t 2012 (bottom). The jet streams are generally right above Big Bear (red circle) in winter. Maps available at http://virga.sfsu.edu/ |
 |
Fig. 15 Upper air sounding at the Vandenberg Air Force Base, 325 km to the west of Big Bear lake along the Pacific coast. Left panel: the tropopause lies 17 km above sea level on Aug. 29th, 2011 (green) and 12 km above sea level on Feb. 10th, 2012 (red). Right panel: the high-altitude winds are stronger in winter. Data from http://weather.uwyo.edu/upperair/sounding.html |
4.3. Consequences for multi-conjugate adaptive optics
An isoplanatic angle is estimated from each profile in terms of the following relation – see the definition on page 323 of Roddier’s review (1981): 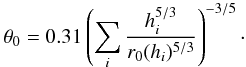 (40)The average isoplanatic angle derived from the 550 summer profiles equals 6″ at 0.55 μm wavelength. This means that a long-exposure AO corrected image is diffraction-limited inside a 6″ diameter field-of-view, in average. The current remedy at NST consists in recording bursts of 70 short-exposure images. These are then combined after image post-processing. The resulting usable scientific field is a factor 2–5 larger than the isoplanatic angle, see Denker et al. (2006). In winter the average isoplanatic angle decreases to 2″.
(40)The average isoplanatic angle derived from the 550 summer profiles equals 6″ at 0.55 μm wavelength. This means that a long-exposure AO corrected image is diffraction-limited inside a 6″ diameter field-of-view, in average. The current remedy at NST consists in recording bursts of 70 short-exposure images. These are then combined after image post-processing. The resulting usable scientific field is a factor 2–5 larger than the isoplanatic angle, see Denker et al. (2006). In winter the average isoplanatic angle decreases to 2″.
We estimate isoplanatic angles after MCAO correction by setting to zero different high-altitude layers in our profiles. The turbulent layer at 500 m is likewise set to zero under the assumption that it is corrected by the ground-layer deformable mirror (DM). Note that the intensity of the ground-layer (h = 0) does not affect the isoplanatic angle (see Eq. (40)).
Figure 16 traces the average isoplanatic angle, without AO correction, with a ground layer AO, and with two and three-mirror MCAO systems. The conjugation heights of the high-altitude mirrors are set to the center and to the upper limit of the boundary layer: 3 and 6 km (see Table 4). The mirrors are assumed to correct the turbulence in a 2 km wide interval centered around the conjugation height.
With a two mirror MCAO system that corrects the ground and the center of the boundary layer, the isoplanatic angle gets extremely large if the turbulence is confined to the ground. The reverse – a high-altitude layer with no turbulence close to the ground – rarely happens. Accordingly, correcting the center of the boundary layer secures excellent isoplanatic angles on days without high-altitude turbulence: 20% of our summer profiles yield θ0 > 100′′. With a three mirror MCAO system the average isoplanatic-angle equals 43″ in summer (blue curve in Fig. 16, left panel). Note that these values are obviously optimistic since they assume a perfect MCAO correction.
In summer, the average Fried parameters measured in the ground layer (0–500 m), the extended ground layer (1–2 km) and the boundary layer (3–7 km) equal 12, 23 and 32 cm. These values reduce to 10, 20 and 27 cm in the G-band, around 0.48 μm. At 3 km altitude, the meta-pupil (the surface that contains all wavefront-footprints inside the field-of-view) of a 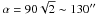 diameter field equals Dm = (D + h·α) = 3.5 m. It equals 5.4 m at 6 km. The deformable mirrors of an MCAO system should thus have of the order of Dm/r0 = 16; 18; 20 actuators per diameter at conjugation heights 0; 3; 6 km.
diameter field equals Dm = (D + h·α) = 3.5 m. It equals 5.4 m at 6 km. The deformable mirrors of an MCAO system should thus have of the order of Dm/r0 = 16; 18; 20 actuators per diameter at conjugation heights 0; 3; 6 km.
At BBSO the plan is to start with two 357 actuator DMs (20 actuators over the pupil diameter), and to eventually install a third DM after one observing season. We conclude that the conjugation heights of the initial, two-mirror system should be 0 and 3 km – the ground and the center of the boundary layer. This will ensure excellent isoplanatic angles on days without jet-streams.
 |
Fig. 16 Average isoplanatic angle without AO correction (black), with a ground-layer AO that corrects turbulence up to 500 m altitude (green), a two mirror MCAO (red) and a three mirror MCAO (blue). The conjugation heights correspond to the center and to the upper limit of the boundary layer (see Table 4). We consider the subset of profiles with best isoplanatic angles: the x-axis indicates the percentage of profiles considered. |
5. Discussion and conclusions
The S-DIMM+ method proposed by Scharmer & van Werkhoven (2010) has been used at the NST to obtain profiles of the atmospheric turbulence from the ground up to 20 km altitude. The instrument was modified to record only a single line of SH sub-apertures: this allows detector read-outs of several hundred Hertz, and we can use this feature to measure the coherence times of the atmospheric layers. Starting in summer 2012, an upgrade will permit simultaneous S-DIMM+ and science observations.
On 550 data sequences obtained between June 20th and Sept. 28th 2011 the Fried parameter at 0.55 μm wavelength equals (9.1 ± 3.3) cm. The actuator spacing of our future 357 DM equals 8 cm on the NST primary mirror, and this system should thus provide diffraction-limited images at 0.55 μm under typical summer conditions. 310 sequences recorded between Jan. 31st and Feb. 23rd 2012 yield r0 = (5.5 ± 0.8) cm and suggest that winter conditions will be a challenge to our future AO system.
In the G-band – around 0.48 μm – the Fried parameter scales to r0 = (7.7 ± 2.8) cm in summer: diffraction limited resolution should be attained under good atmospheric conditions. This is essential for observations of bright points in the inter-granular lanes of the solar photosphere. With the current 97 actuator system, G-band observations lack the necessary resolution and the bright points are instead observed in the TiO band at 0.71 μm. These observations have already challenged our previous picture of granular lanes organized in sheet-like structures, see Goode et al. (2010b). The upgrade to 357 actuators will permit diffraction-limited observations in the G-band, thereby increasing the resolution by a factor 2. It will be intriguing to monitor the structure and intensity of the lanes, and to set new constraints on the formation process of flux tubes. The increased correction will also permit the discrimination of intensity fluctuations caused by magnetic field changes and by seeing variations.
Our profiles show three main origins for the daytime turbulence in summer:
-
1.
On average, 63% of the turbulence are contained within500 m of the ground.
-
2.
The boundary layer extends up to 7 km altitude and contains 34% of the turbulent energy.
-
3.
The reaming 3% of the energy are located above 8 km.
The profiles measured by Scharmer & van Werkhoven (2010) above the Swedish Solar Telescope (La Palma, Canary Islands) on June 26th, 2009 in terms of 20 data sequences revealed an average 67, 13 and 19% of the energy content in the 0–0.5, 1.5–6 and 9.5–30 km altitude slabs, respectively (see their Fig. 11). Roughly, the turbulence profiles at La Palma and BBSO are similar with La Palma showing relatively more turbulence in the tropopause and less at the boundary layer.
The average isoplanatic angle on our 550 summer sequences equals 6″ at 0.55 μm wavelength, and reduces to 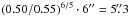 at 0.50 μm. This compares favorably to
at 0.50 μm. This compares favorably to 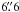 measured
measured
at 0.50 μm over the highly-regarded site of Dome C on the Antarctic plateau, see Aristidi et al. (2005).
During the summer season, our average 6″ increases to 26″ with a two mirror MCAO system conjugated to the ground and to the center of the boundary layer (3 km). The isoplanatic angle exceeds 100′′ on the 20% of sequences with weakest turbulence at the tropopause. Accordingly, with our future two-mirror MCAO, wide-field G-band observations should be scheduled on days where no jet-streams are forecasted over Big Bear. This shall allow to observe remote, but related events in the field of view of a solar flare, and should provide new insights on the fine temporal and spatial structure of flares, the so called “elementary bursts”. The increased field of view will also heighten the chances of finding the rare events that give us new insights into questions such as: how are flux-tubes formed and how do they evolve? How do they interact with the turbulent flows in the photosphere and what is their lifetime?
Acknowledgments
Thanks to John Varsik and Sergey Shumko for assistance throughout the project, and to Göran Scharmer for numerous and patient explanations. The National Science Foundation is gratefully acknowledged for funding this research through grant NSF-AST-0079482. This article has been considerably improved by the referee’s careful review.
References
- Aristidi, E., Agabi, A., Fossat, E., et al. 2005, A&A, 444, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beckers, J. M. 2001, Exp. Astron., 12, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, W., Gorceix, N., Coulter, R., et al. 2010, Astron. Nachr., 331, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Denker, C., & Verdoni, A. 2006, SPIE, 6267, 62670 [Google Scholar]
- Denker, C., Deng, N., Rimmele, T., Tritschler, A., & Verdoni, A. 2007, Sol. Phys., 241, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Goode, P. R., Coulter, R., Gorceix, N., Yurchyshyn, V., & Cao, W. 2010a, Astron. Nachr., 331, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Goode, P. R., Yurchyshyn, V., & Cao, W. 2010b, ApJ, 714, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, F., Beckers, J., Brandt, P., et al. 2006, SPIE, 6267 [Google Scholar]
- Irbah, A., Borgnino, J., Laclare, F., & Merlin, G. 1993, A&A, 276, 663 [NASA ADS] [Google Scholar]
- Löfdahl, M. 2010, A&A, 524, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roddier, F. 1981, Progress in Optics XIX, ed. E. Wolf [Google Scholar]
- Sarazin, M., & Roddier, F. 1990, A&A, 227, 294 [NASA ADS] [Google Scholar]
- Scharmer, G., & van Werkhoven, T. 2010, A&A, 513, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H., Beckers, J., Brandt, P., et al. 2005, PASP, 117, 1296 [NASA ADS] [CrossRef] [Google Scholar]
- Verdoni, A., & Denker, C. 2007, PASP, 119, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Zirin, H., & Mosher, J. 1988, Sol. Phys., 115, 183 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Average percentage of turbulent energy in different altitude-slabs and resulting Fried parameters – for the 550 summer- and 311 winter-profiles.
All Figures
 |
Fig. 1 Mechanical layout of the wide-field wavefront sensor. |
| In the text | |
 |
Fig. 2 Layout of the 15 sub-apertures over the NST primary mirror (D = 1.6 m, without central obstruction). |
| In the text | |
 |
Fig. 3 The matrix M that converts the turbulent energy at altitude h, r0(h) − 5/3 [m−5/3], into the structure functions of wavefront slopes, Dx and Dy [arsec2]. The contrast of the structure functions decreases with altitude, because the slopes are computed through a cross-correlation over a field of finite size, and are thus averaged over larger surfaces with increasing altitude. |
| In the text | |
 |
Fig. 4 On each of the Si ≤ 15 sub-aperture images wavefront shifts are determined every sampling step, s. This yields Sα × Sα = ((N − 10 − Nc)/s)2 angular sampling points. The optimal values of s and Nc are determined from simulated images in Sect. 3. |
| In the text | |
 |
Fig. 5 Each sequence of 100–300 images yields two structure-functions (of the x- and y-wavefront slopes) in dependence on pupil separation, dr, and angular separation, dα. See also Fig. 2. |
| In the text | |
 |
Fig. 6 An S-DIMM+ image is used as input to generate the simulated data. |
| In the text | |
 |
Fig. 7 Profiles retrieved on simulated data-sequences. The input profiles are described in Table 2. The color indicates the value of |
| In the text | |
 |
Fig. 8 Simulation of continuously distributed turbulence: 23 layers of equal intensity between 0 and 5.5 km (black line). Red: best-guess profile. The parameter-values for the analysis are listed in Table 3. |
| In the text | |
 |
Fig. 9 Cumulative distributions of the Fried parameter, r0: the straight line is obtained from the 550 summer values (June–Sept. 2011), the dashed line corresponds to the 311 winter measurements (Jan.–Feb. 2012). The circles represent the values obtained by the ATST survey (Socas-Navarro et al. 2005). All values refer to 0.55 μm wavelength. |
| In the text | |
 |
Fig. 10 r0 as a function of local time. The red lines indicate the average value and root-mean square deviation of r0 over 5 time intervals of equal length. At mountain sites the turbulence is strongest around noon. Over Big Bear Lake there is no clear evolution of turbulent strength over the day. |
| In the text | |
 |
Fig. 11 Atmospheric profiles on Aug. 29th, 2011 (top) and Feb. 10th, 2012 (bottom). The average Fried parameter (isoplanatic angle) equals 9.9 cm |
| In the text | |
 |
Fig. 12 Red (resp. blue): Percentage of profiles with N layers of r0 ≤ 0.3 m (resp. 0.3 m < r0 ≤ 1.0 m). |
| In the text | |
 |
Fig. 13 Red (resp. blue): percentage of profiles where the layer at altitude h has r0 ≤ 0.3 m (resp. 0.3 m < r0 ≤ 1.0 m). |
| In the text | |
 |
Fig. 14 Jet streams on Aug. 29th 2011 (top) and Feb. 10t 2012 (bottom). The jet streams are generally right above Big Bear (red circle) in winter. Maps available at http://virga.sfsu.edu/ |
| In the text | |
 |
Fig. 15 Upper air sounding at the Vandenberg Air Force Base, 325 km to the west of Big Bear lake along the Pacific coast. Left panel: the tropopause lies 17 km above sea level on Aug. 29th, 2011 (green) and 12 km above sea level on Feb. 10th, 2012 (red). Right panel: the high-altitude winds are stronger in winter. Data from http://weather.uwyo.edu/upperair/sounding.html |
| In the text | |
 |
Fig. 16 Average isoplanatic angle without AO correction (black), with a ground-layer AO that corrects turbulence up to 500 m altitude (green), a two mirror MCAO (red) and a three mirror MCAO (blue). The conjugation heights correspond to the center and to the upper limit of the boundary layer (see Table 4). We consider the subset of profiles with best isoplanatic angles: the x-axis indicates the percentage of profiles considered. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.