| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201218786 | |
| Published online | 05 June 2012 | |
Observations and simulations of longitudinal oscillations of an active region prominence
1 School of Astronomy and Space Science, Nanjing University, 210093 Nanjing, PR China
2 Key Lab of Modern Astronomy and Astrophysics (Ministry of Education), Nanjing University, PR China
e-mail: chenpf@nju.edu.cn
3 Center for Plasma Astrophysics, K.U. Leuven, Celestijnenlaan 200B, 3001 Heverlee, Belgium
Received: 8 January 2012
Accepted: 12 April 2012
Context. Filament longitudinal oscillations have been observed in Hα observations of the solar disk.
Aims. We intend to find an example of the longitudinal oscillations of a prominence, where the magnetic dip can be seen directly, and examine the restoring force of this type of oscillations.
Methods. We carry out a multiwavelength data analysis of the active region prominence oscillations above the western limb on 2007 February 8. In addition, we perform a one-dimensional hydrodynamic simulation of the longitudinal oscillations.
Results. Our analysis of high-resolution observations performed by Hinode/SOT indicate that the prominence, seen as a concave-inward shape in lower-resolution extreme ultraviolet (EUV) images, consists of many concave-outward threads, which is indicative of magnetic dips. After being injected into the dip region, a bulk of prominence material started to oscillate for more than 3.5 h, with the period of 52 min. The oscillation decayed with time, on the decay timescale 133 min. Our hydrodynamic simulation can reproduce the oscillation period, but the damping timescale in the simulation is 1.5 times as long as the observations.
Conclusions. The results clearly show the prominence longitudinal oscillations around the dip of the prominence and our study suggests that the restoring force of the longitudinal oscillations might be the gravity. Radiation and heat conduction are insufficient to explain the decay of the oscillations. Other mechanisms, such as wave leakage and mass accretion, have to be considered. The possible relation between the longitudinal oscillations and the later eruption of a prominence thread, as well as a coronal mass ejection (CME), is also discussed.
Key words: Sun: filaments, prominences / Sun: oscillations / methods: observational / methods: numerical
© ESO, 2012
1. Introduction
Solar prominences are cold (~104 K) and dense (1010−1011 cm-3) plasma suspended in the hot corona. They appear to be dark filaments in the Hα images on the solar disk (Tandberg-Hanssen 1995). Prominences (or filaments) are formed above the magnetic polarity inversion lines (Zirker 1989; Martin 1998; Berger et al. 2008; Ning et al. 2009). It can be formed within several hours, starting from a hot plasma and then undergoing cold condensation (Liu et al. 2012). It is generally thought that the equilibrium of the prominences is maintained by the force balance between the gravity of prominence and the magnetic tension force of the dip-shaped field lines, although prominences have seldom been observed to have a dipped shape. Theoretical models suggest that dips exist in two types of magnetic configurations, one of which is normal-polarity (Kippenhahn & Schlüter 1957), and the other inverse-polarity (Kuperus & Raadu 1974). The first type can be formed in sheared arcades with a weak twist (Antiochos et al. 1994; 1999; DeVore & Antiochos 2000; Aulanier & Schmieder 2002; Karpen & Antiochos 2008; Luna et al. 2012), and the second type has a helical flux rope with a stronger twist that may either emerge from the subsurface (Lites 2005) or be formed in the corona by magnetic reconnection (van Ballegooijen & Martens 1989; Amari et al. 2000).
Many prominences end up with a final eruption to become coronal mass ejections (CMEs). The eruption is generally triggered by photospheric motions, emerging magnetic flux, or internal reconnection (see Forbes et al. 2006; Chen 2011, for reviews). Whatever mechanism is involved in triggering the eruption, the triggering process, as a kind of perturbation, should generate waves and oscillations in the prominence. Therefore, based on this line of thought and spectroscopic observations of an oscillating prominence prior to eruption, Chen et al. (2008) proposed that long-time prominence oscillations can be considered as one of the precursors of CME eruptions. A prominence oscillation prior to eruption was also observed by Bocchialini et al. (2011), and the oscillation was even able to be sustained until the eruption phase (Isobe & Tripathi 2006; Gosain et al. 2009). The restoring force in this kind of transverse oscillations was generally thought to be the magnetic tension force.
 |
Fig. 1 Panel a) Hα image at 08:11 UT on 2007 February 6, showing a filament near active region 0940. Panel b) Hinode/SOT Ca ii H image showing that the filament appeared above the western limb as a prominence on February 8. The rectangle indicates a wide slice used for Fig. 3. Panel c) STEREO/EUVI 171 Å image at 17:35 UT on February 8. Panel d) STEREO/EUVI 304 Å image at 17:22 UT on February 8. |
In addition to the transverse oscillations that have been widely investigated (e.g., Lin et al. 2007), prominences may also have longitudinal oscillations. Jing et al. (2003) for the first time found that, initiated by a subflare, a filament started to oscillate along its axis. They mentioned several possible origins of the restoring force in the oscillations, including the gravity and a reflecting Alfvén wave package. Vršnak et al. (2007) studied a similar event, attributing the restoring force to magnetic pressure gradient along the field lines. With radiative hydrodynamic simulations, Luna & Karpen (2012) claimed that the projected gravity along the flux tube should act as the restoring force. One issue with the past observations is that the longitudinal oscillations were observed on the solar disk, where the shape of the flux tube cannot be detected, so it is impossible to check whether the field-aligned gravity component can explain the observed oscillation period. Therefore, it would be of interest to investigate the longitudinal oscillations along a prominence, where the shape of the flux tube can be inferred from the high-resolution observations. It is also interesting to check whether longitudinal oscillations may precede the eruption of the prominence.
In this paper, we report the longitudinal oscillations of an active region prominence, which was observed by the Hinode (Kosugi et al. 2007) satellite with a high resolution. The data processing is described in Sect. 2, and the analysis is presented in Sect. 3. In Sect. 4, we perform a one-dimensional (1D) hydrodynamic numerical simulation to reproduce the damped oscillations of the prominence. Discussions and a summary are presented in Sects. 5 and 6, respectively.
2. Observations and data processing
On 2007 February 6, there was a filament located in the active region 0940 (S05W71). The filament was seen to be slightly offset from the north-south direction in the Hα images observed by Kanzelhöhe Solar Observatory as shown in Fig. 1a. It measured ~300′′ in length and 15′′−20′′ in width. The southern part of the filament resided in the active region, while the northern part extended far into the quiescent region along the magnetic polarity inversion line. On February 8, as the Sun rotated, the filament became a prominence and was monitored by the Ca ii H channel of the broadband filtergraph onboard the Hinode satellite, which carries three instruments: Solar Optical Telescope (SOT; Tsuneta et al. 2008), X-Ray Telescope (XRT; Golub et al. 2007), and EUV Imaging Spectrometer (EIS; Culhane et al. 2007). Owing to the limited field of view of SOT (111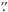 5 × 111
5 × 111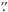 5), only a segment of the prominence was observed, which is shown in Fig. 1b. The pixel size and time cadence of the SOT observations are 0
5), only a segment of the prominence was observed, which is shown in Fig. 1b. The pixel size and time cadence of the SOT observations are 0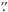 08 and 8 s, respectively. The observations started from 15:01 UT and stopped at 21:24 UT. From ~17:20 UT, a bulk of dense material was injected from the south into the SOT field of view. The dense plasma began to oscillate for 3.5 h until the end of the observations. The raw SOT data were calibrated using the standard Solar Software program fg_prep.pro. We note that a data gap exists from 18:00 UT to 18:14 UT.
08 and 8 s, respectively. The observations started from 15:01 UT and stopped at 21:24 UT. From ~17:20 UT, a bulk of dense material was injected from the south into the SOT field of view. The dense plasma began to oscillate for 3.5 h until the end of the observations. The raw SOT data were calibrated using the standard Solar Software program fg_prep.pro. We note that a data gap exists from 18:00 UT to 18:14 UT.
The prominence was also observed by the Extreme UltraViolet Imager (EUVI; Newmark et al. 2007) on board the Solar TErrestrial RElations Observatory (STEREO-A; Kaiser 2005) spacecraft from a slightly different viewing angle. The 171 Å and 304 Å are shown in panels (c) and (d) of Fig. 1, where we can see that the prominence was straddled by much higher coronal loops that are much hotter than the prominence. The pixel size and time cadence of the EUV observations are 1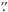 6 and 10 min, respectively. Its data calibration was conducted using the program secchi_prep.pro. In addition, the deviation of STEREO north-south direction from the solar rotation axis was corrected.
6 and 10 min, respectively. Its data calibration was conducted using the program secchi_prep.pro. In addition, the deviation of STEREO north-south direction from the solar rotation axis was corrected.
We note that a faint limb CME was captured by the Large Angle and Spectrometric Coronagraph (LASCO; Brueckner et al. 1995) onboard SOHO, as well as the COR1 coronagraph onboard STEREO-A. It was registered by the CDAW CME catalog1 with a propagation speed of 480 km s-1. The flare accompanying the CME was registered as C1.2-class by the GOES satellite. The data from the coronagraphs were collected to investigate a possible connection between the observed prominence dynamics and the CME.
3. Observational results
As displayed in Fig. 1, the prominence looked slightly different in the chromospheric line Ca ii H and the EUVI 304 Å line observations. While the lower-resolution 304 Å image shows that the prominence was a concave-inward structure at −100″ < y < 0″, the higher-resolution Ca ii H image indicates that the prominence consists of a bunch of concave-outward threads. To indicate the dipped structure in Ca ii H more clearly, we perform the top-hat transform of the Hinode image, which can greatly enhance the detailed structures. Figure 2 displays the processed Hinode Ca ii H image at 18:41 UT, where prominence threads, as well as their oscillations, are found to be aligned with the dipped trajectories. Since the Ca ii H thread originates from the core material of the prominence, which should trace the local magnetic field, the concave-outward structure is strongly indicative of the existence of magnetic dip along the prominence thread. The white dashed line traces one single dipped thread, with point A located at one shoulder and point B at the trough of an expected field line. The shape of this expected field line is used for numerical simulations in Sect. 4.
 |
Fig. 2 Hinode/SOT Ca ii H image at 18:41 UT on 2007 February 8, which is processed with the top-hat transform. Points A and B mark the shoulder and the trough of a dipped prominence thread. Note that the image is rotated counterclockwise by 90°. North is to the left. |
 |
Fig. 3 Time-slice plot of the Ca ii H intensity along the vertical direction of the rectangle in Fig. 1b. The intensity is averaged along the horizontal direction. The superposed dashed line is a damped sine function for fitting the main oscillation, whereas the dotted line represents the weak prominence oscillation prior to the plasma injection. A data gap exists between 18:00 UT and 18:14 UT. |
At ~17:00 UT, the prominence was activated somehow. To show the dynamics of the prominence activation, in Fig. 3 we plot the temporal evolution of the Ca ii H intensity along a wide slice. The slice is along the prominence axis in the south-north direction, with a width of 20′′ as indicated in Fig. 1b. From Fig. 3, it can be seen that at ~17:00 UT a plasma clump formed near y = −30″, and then spread bi-directionally. During 17:10 UT–17:45 UT, a bulk of dense plasma moved from south to north with a velocity of ~40 km s-1. After a short interval, a denser plasma structure moved to north. Although there was a data gap between 18:00 UT and 18:14 UT, it is still discernible that whereas some of the dense plasmas moved outside the northern edge of the Hinode/SOT field of view, the other part of them remained in the field of view, and started to oscillate with an initial amplitude of ~30′′. The amplitude of the oscillation decreased with time, but nearly four periods are visible in the observation slot. To describe the prominence oscillation quantitatively, we fit the oscillating pattern in Fig. 3 with a decayed sine function with respect to time, i.e.,
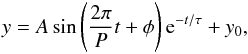 (1)where A is the initial amplitude, P the period, τ the decay timescale, φ the phase, t the time lapse since 18:00 UT, and y0 the equilibrium position of the prominence. By trial and error, we found that with A = 24 Mm, φ = −π/2, P = 52 min, and τ = 133 min, the analytical function fits the oscillating pattern very well, as overplotted in Fig. 3 with the dashed curve. The ratio of the decay timescale to the period is 2.6, which is very similar to the results in Jing et al. (2003) and Vršnak et al. (2007).
(1)where A is the initial amplitude, P the period, τ the decay timescale, φ the phase, t the time lapse since 18:00 UT, and y0 the equilibrium position of the prominence. By trial and error, we found that with A = 24 Mm, φ = −π/2, P = 52 min, and τ = 133 min, the analytical function fits the oscillating pattern very well, as overplotted in Fig. 3 with the dashed curve. The ratio of the decay timescale to the period is 2.6, which is very similar to the results in Jing et al. (2003) and Vršnak et al. (2007).
We note that even before the bulk of dense plasma was injected into the SOT field of view, as indicated by the dotted line in Fig. 3, the less dense prominence material near y = 5′′ was already oscillating with almost the same period as the main oscillations described above, which implies that the oscillation period was mainly determined by the magnetic configuration, rather than the mass of the prominence, as claimed by Luna & Karpen (2012).
4. Numerical simulations
4.1. Simulation setup
Jing et al. (2003) proposed several origins of the restoring force of the oscillation, including the gravity and a reflecting Alfvén wave package, where the gravity acting as the restoring force was backed by Luna & Karpen (2012). On the other hand, Vršnak et al. (2007) attributed the restoring force to a magnetic pressure gradient. Here, that the oscillation was centered around the magnetic dip reminds us of an alternative explanation, i.e., the restoring force might be gravity. In order to explain the dynamics of a prominence after being disturbed, we performed a 1D radiative hydrodynamics simulation in this section. The geometry of the dipped magnetic field line is taken from the observation in Fig. 2, as marked by the white dashed line. Since the prominence was inclined to the local meridian by θ = 8° as implied by Fig. 1a when the prominence was observed on the solar disk as a filament, the length of the dipped field line is 1/cos(θ + 10°) times the apparent value assuming that the fine threads of the Hα filament is 10° with respect to the filament axis. The reconstructed magnetic loop is depicted in Fig. 4, where the magnetic dip is 8.1 Mm in depth and 107.3 Mm in length.
 |
Fig. 4 Magnetic field configuration used for the 1D radiative hydrodynamic simulation of the prominence oscillation. Note that the horizontal and the vertical sizes are not to scale. |
The simulation setup was described in detail in Xia et al. (2011; 2012), and briefly explained as follows: a background heating is imposed to sustain the corona-chromosphere structure. As an extra localized heating is added at the chromosphere symmetrically at two footpoints of the magnetic loop, cool plasmas are heated up and evaporated into the corona. At a critical stage, thermal instability is triggered in the corona, and the evaporated mass cools down to form a condensation (or prominence segment). As the localized heating is switched off, the condensation will relax to a quasi-static state. To simulate the oscillation of the condensation, an impulsive momentum is imposed on the plasma condensation, which makes the plasma to move with an initial velocity of 40 km s-1.
The 1D radiative and conductive hydrodynamic equations, as listed in Xia et al. (2011), are numerically solved with the Message Passing Interface-Adaptive Mesh Refinement Versatile Advection Code (MPI-AMRVAC, Toth & Odstrcil 1996; Keppens et al. 2012). The Total Variation Diminishing Lax-Friedrichs (TVDLF) scheme using linear reconstruction and a Woodward limiter are selected for the spatial differentiation, while the predictor-corrector two-step explicit scheme is utilized for the time progressing. Mesh refinement with six levels in a block-based approach is applied.
4.2. Simulation results
 |
Fig. 5 Time evolutions of the density (top) and the temperature (bottom) distributions along the magnetic loop, which indicate that the prominence experiences a damped oscillation subjected to a perturbation. |
As the initial conditions for the simulation in this paper, a prominence thread formed by the thermal instability stays in a quasi-static state, with the density being ~2.0 × 1011 cm-3, the temperature being ~1.8 × 104 K, and the length being 27.8 Mm. A velocity perturbation with an amplitude of 40 km s-1 is introduced into the prominence thread, which decreases to zero smoothly near the prominence-corona transition layer.
Subjected to the velocity perturbation, the prominence thread begins to oscillate along the dip. The time evolutions of the density and temperature of the plasma along the magnetic loop are displayed in Fig. 5, which shows that the prominence thread oscillates with a damping amplitude. Using a formula similar to Eq. (1), we fit the displacement of the prominence from the center of the dip as a function of time. It turns out that the initial amplitude is A = 18.6 Mm, the period is P = 56 min, and the damping timescale is τ = 202 min. We note that the oscillation period in the 1D simulation, i.e., 56 min, is very close to the real observations. However, the decay timescale, 202 min, is ~1.5 times as long as the real observations between 18:00 UT and 21:24 UT.
Since the magnetic field line is fixed here in the 1D simulation, the restoring force candidates in the simulation are the field-aligned component of the gravity and the gas pressure gradient. After comparing the two forces in the simulation results, we found that the gravity component is much stronger than the gas pressure gradient. Therefore, the result that the simulated period is similar to the observed one indicates that the gravity component along the field line nicely accounts for the restoring force of the longitudinal oscillation of the prominence. Our results are consistent with the conclusion of Luna & Karpen (2012) that the main restoring force is the projected gravity in the flux tube dips where the threads oscillate. The energy-losing mechanisms in our simulation include thermal radiation and heat conduction. That the decay timescale of the oscillation in our simulation is 1.5 times as long as the observed one implies that some other energy loss mechanisms should be taken into account, such as the wave leakage (e.g., Stenuit et al. 1999) and mass accretion (e.g., Luna & Karpen 2012).
5. Discussions
5.1. Identification of the longitudinal oscillations
Even a quiescent prominence is full of significant dynamical motion. The typical motion inside prominences is counter-streamings (Zirker et al. 1998). These bidirectional motions have been observed in quiescent region filaments (Lin et al. 2005; Schmieder et al. 2010), as well as in active region prominences (Okamoto et al. 2007). The counter-streaming can be easily discerned in Fig. 3 of this paper. Especially near t = 21:00 UT, counter-streamings are clearly seen around y = −70′′. With this background of counter-streamings, a distinct feature in Fig. 3 is that a bulk of prominence began to oscillate with a period of 52 min. The oscillation decayed with a timescale of 133 min. The oscillations might indeed be an artificial pattern due to the superposition of the ongoing counter-streamings along the line of sight. We tend to discard such a possibility and favor the oscillation explanation for several reasons: (1) the counter-streamings are often random, and it is rare, if possible, for them to form a coherent periodic oscillation pattern for >3.5 h; (2) the oscillation was centered around the dip of the prominence, whereas counter-streamings appear everywhere along the prominence axis; (3) the prominence oscillations in Fig. 3 decayed in a steady way. It is a little hard to understand how the superposition of counter-streamings could evolve in such a systematic way; (4) it is seen that even before the injection of the bulk of plasma, the less dense prominence material near the dip was already oscillating with an identical period to the main oscillations; (5) more importantly, with the shape of the magnetic flux tube inferred from observations, we performed radiative hydrodynamic simulations, and the simulated oscillation period is close to the observed value, which strongly supports that the observed pattern in Fig. 3 represents evidence of prominence longitudinal oscillations, and the gravity serves as the restoring force for the longitudinal oscillations.
We note that only the portion of the prominence between y = −40′′ and y = −20′′ was oscillating, which is probably because only some threads of the prominence were involved in the oscillation, and the other threads remained unaffected by the perturbation.
 |
Fig. 6 The running-difference images of EUVI 171 Å channel at 21:45 UT (left) and 304 Å channel at 21:52 UT (right) showing that only a thread of the prominence erupted. The white cross in the left panel marks the location of a microflare, which occurred at 18:00 UT. |
 |
Fig. 7 Top: STEREO/COR1 running-difference images showing the early propagation of a CME; bottom-left: running-difference image from LASCO/C2 coronagraph at 23:54 UT; bottom-right: Fe ix/x 171 Å image at 22:55 UT showing a C1.2-class flare associated with the CME. |
5.2. Possible connection with the later CME/flare
No Hinode/SOT observations were available after 21:24 UT, while the prominence oscillation should still be ongoing. Then, around 21:52 UT, a thread of the prominence erupted, as illustrated by the EUVI 171 Å and 304 Å running-difference images in Fig. 6. In association with that, a faint CME first appeared in the field of view of the STEREO/COR1 coronagraph above the western limb at 22:53 UT, as illustrated by the top panels of Fig. 7. The faint CME was later observed by the LASCO coronagraph, which showed that the CME was deflected toward south as seen in the bottom-left panel of Fig. 7. In association with the CME, a C1.2-class flare appeared just below the prominence, starting around 22:55 UT, as indicated by the bottom-right panel of Fig. 7. We note that despite the large-scale CME eruption, the major part of the prominence remained at the original place. Although the available observations did not cover the evolutions of the prominence eruption and the CME continuously, we speculate on the possible connection between the erupting prominence thread, the flare, and the CME: first, none of active regions or filaments existed west to AR0940 before February 9. Hence, the CME could not originate from any filament eruption on the backside of the Sun near the western limb. There was another long filament in AR0941 east of AR0940. However, the He I 304 Å movie reveals that the filament did not erupt before the CME. Second, the central position angle of the CME is close to the latitude of the erupting thread of the prominence. Finally, as displayed below, the timing of all the components closely fits the standard CME/flare model, i.e., a prominence is somehow triggered to rise with the formation of a current sheet. The reconnection of the current sheet leads to a flare and the acceleration of the CME.
The timeline of the whole event is illustrated in Fig. 8. It is seen that the prominence oscillation preceded the CME and the accompanying C1.2 flare. Despite a data gap existing after 21:24 UT, we suspect that the longitudinal prominence could continue to oscillate for a few cycles more. Since only one thread of the prominence was seen to erupt with the major part remaining in the low corona, this should be a partial prominence eruption event, which might be consistent with the rupture model (Sturrock et al. 2001), where part of the flux rope struggle out of the overlying field lines, pushing some of them aside on the way, as simulated by Fan (2005).
This paper might provide another example to illustrate that long-time prominence oscillation can be regarded as a precursor for CME eruptions, as proposed by Chen et al. (2008). However, the eruption in this paper is different from theirs in the sense that their prominence oscillation was transverse, whereas ours is along the prominence axis, i.e., it is a longitudinal oscillation, although both of the prominence oscillations were probably triggered by magnetic reconnection between emerging flux and the pre-existing field lines. Caveat should be taken that many of the CME precursors are neither sufficient nor necessary conditions for the CME eruption (Chen 2011). In both Jing et al. (2003) and Vršnak et al. (2007), it also seems that no CME followed the longitudinal oscillation of the prominence.
Interestingly, an A7.0 microflare peaked around 18:00 UT near the prominence, as seen from the GOES light curve in Fig. 8. The location of the microflare is marked by the cross in the left panel of Fig. 6. The microflare might be due to the reconnection between emerging flux and the prominence magnetic field, which led to the second prominence oscillation. However, there are a number of caveats. First, this is a limb event, so the microflare, which seemed to be close to the prominence in the image might be far from the prominence. Second, the oscillation of the massive prominence started ~30 min before the microflare, hence seems unlikely that the microflare triggers the prominence oscillation.
 |
Fig. 8 Timeline of the whole event, where the flare is indicated by the GOES 1 − 8 Å SXR light curve (solid line), the prominence oscillation is represented by the insertion of the time-slice plot of Fig. 3, and we also show the CME heights observed by different instruments, i.e., STEREO/COR1 (squares), LASCO/C2 (stars), and LASCO/C3 (diamonds), respectively. |
6. Summary
We have carried out a multiwavelength data analysis and a radiative hydrodynamic simulation of longitudinal oscillations of an active region prominence along the axis on 2007 February 8. The main results are summarized as follows:
-
1.
Despite the overall shape of the prominence being concave-inward, the high-resolution observations by Hinode/SOT indicate that the prominence consists of many threads that are actually concave-outward. The concave-outward structures are strongly indicative of the magnetic dips that support the heavy prominence materials suggested by previous theoretical models.
-
2.
After being injected, a bulk of dense prominence plasma was seen to oscillate along the prominence main axis, i.e., a longitudinal oscillation could be discerned. The period and the damping timescale are 52 min and 133 min, respectively. The oscillations continued for more than 3.5 h, and no further observations were taken.
-
3.
To determine the underlying mechanisms of restoring force and amplitude decay in the prominence oscillations, we have performed a 1D hydrodynamic numerical simulation with the geometry of the dipped magnetic loop inferred from observations. The oscillation period derived from the simulation is nearly identical to the observed values, indicating that gravity might serve as the restoring force for the prominence longitudinal oscillations, as mentioned by Jing et al. (2003) and Luna & Karpen (2012). However, the decay timescale of the oscillation in the simulation, 202 min, is 1.5 times as long as the observed value, 133 min, suggesting that mechanisms other than thermal radiation and heat conduction, say the wave leakage and mass accretion, might be more relevant to the energy loss during the prominence longitudinal oscillations.
-
4.
With the main body of the prominence remaining undisturbed, a thread from the prominence was seen to erupt, leading to a CME and a C1.2-class flare. We tentatively propose that the prominence longitudinal oscillations studied in this paper might be a precursor of the CME/flare, which is related to the triggering process of the eruption, as proposed by Chen et al. (2008).
Acknowledgments
The authors thank the anonymous referee for valuable comments and suggestions that helped to improve the quality of this paper. Q. M. Zhang appreciates Z. J. Ning, M. D. Ding, C. Fang, and B. Vršnak for discussions and suggestions on this work. The Hα data were obtained from the Global High Resolution Hα Network operated by the Big Bear Solar Observatory, New Jersey Institute of Technology. Hinode is a Japanese Mission, with NASA and STFC (UK) as international partners. STEREO/SECCHI data are provided by a consortium of US, UK, Germany, Belgium, and France. The CME catalog is generated and maintained at the CDAW Data Center by NASA and The Catholic
University of America in cooperation with the Naval Research Laboratory. The research is supported by the Chinese foundations NSFC (11025314, 10878002, and 10933003) and 2011CB811402. PFC thanks UCL/MSSL for the hospitality during his stay.
References
- Amari, T., Luciani, J. F., Mikic, Z., & Linker, J. 2000, ApJ, 529, L49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Antiochos, S. K., Dahlburg, R. B., & Klimchuk, J. A. 1994, ApJ, 420, L41 [Google Scholar]
- Antiochos, S. K., MacNeice, P. J., Spicer, D. S., & Klimchuk, J. A. 1999, ApJ, 512, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Aulanier, G., & Schmieder, B. 2002, A&A, 386, 1106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, T. E., Shine, R. A., Slater, G. L., et al. 2008, ApJ, 676, L89 [Google Scholar]
- Bocchialini, K., Baudin, F., Koutchmy, S., Pouget, G., & Solomon, J. 2011, A&A, 533, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F. 2011, Liv. Rev. Sol. Phys., 8, 1 [Google Scholar]
- Chen, P. F., Innes, D. E., & Solanki, S. K. 2008, A&A, 484, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19 [Google Scholar]
- DeVore, C. R., & Antiochos, S. K. 2000, ApJ, 539, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2005, ApJ, 630, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, T. G., Linker, J. A., Chen, J., et al. 2006, Space Sci. Rev., 123, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Golub, L., Deluca, E., Austin, G., et al. 2007, Sol. Phys., 243, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gosain, S., Schmieder, B., Venkatakrishnan, P., Chandra, R., & Artzner, G. 2009, Sol. Phys., 259, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, H., & Tripathi, D. 2006, A&A, 449, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jing, J., Lee, J., Spirock, T. J., et al. 2003, ApJ, 584, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, M. L. 2005, Adv. Space Res., 36, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., & Antiochos, S. K. 2008, ApJ, 676, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., Meliani, Z., van Marle, A. J., et al. 2012, J. Comp. Phys., 231, 718 [Google Scholar]
- Kippenhahn, R., & Schlüter, A. 1957, ZAp, 43, 36 [NASA ADS] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kuperus, M., & Raadu, M. A. 1974, A&A, 31, 189 [NASA ADS] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L., Wiik, J. E., & Berger, T. E. 2005, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L. H. M., & van Noort, M. 2007, Sol. Phys., 246, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W. 2005, ApJ, 622, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Berger, T. E., & Low, B. C. 2012, ApJ, 745, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., & Karpen, J. 2012, ApJ, 750, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Karpen, J. T., & DeVore, C. R. 2012, ApJ, 746, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F. 1998, Sol. Phys., 182, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Newmark, J. S., Cook, J. W., & Moses, J. D. 2007, Proc. SPIE, 6689 [Google Scholar]
- Ning, Z., Cao, W., & Goode, P. R. 2009, ApJ, 707, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, T. J., Tsuneta, S., Berger, T. E., et al. 2007, Science, 318, 1577 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schmieder, B., Chandra, R., Berlicki, A., & Mein, P. 2010, A&A, 514, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenuit, H., Tirry, W. J., Keppens, R., & Goossens, M. 1999, A&A, 342, 863 [NASA ADS] [Google Scholar]
- Sturrock, P. A., Weber, M., Wheatland, M. S., & Wolfson, R. 2001, ApJ, 548, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Tandberg-Hanssen, E. 1995, Science, 269, 111 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Toth, G., & Odstrcil, D. 1996, J. Chem. Phys., 128, 82 [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- van Ballegooijen, A. A., & Martens, P. C. H. 1989, ApJ, 343, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Vršnak, B., Veronig, A. M., Thalmann, J. K., & Žic, T. 2007, A&A, 471, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xia, C., Chen, P. F., Keppens, R., & van Marle, A. J. 2011, ApJ, 737, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, C., Chen, P. F., & Keppens, R. 2012, ApJ, 748, L26 [Google Scholar]
- Zirker, J. B. 1989, Sol. Phys., 119, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Zirker, J. B., Engvold, O., & Martin, S. F. 1998, Nature, 396, 440 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Panel a) Hα image at 08:11 UT on 2007 February 6, showing a filament near active region 0940. Panel b) Hinode/SOT Ca ii H image showing that the filament appeared above the western limb as a prominence on February 8. The rectangle indicates a wide slice used for Fig. 3. Panel c) STEREO/EUVI 171 Å image at 17:35 UT on February 8. Panel d) STEREO/EUVI 304 Å image at 17:22 UT on February 8. |
| In the text | |
 |
Fig. 2 Hinode/SOT Ca ii H image at 18:41 UT on 2007 February 8, which is processed with the top-hat transform. Points A and B mark the shoulder and the trough of a dipped prominence thread. Note that the image is rotated counterclockwise by 90°. North is to the left. |
| In the text | |
 |
Fig. 3 Time-slice plot of the Ca ii H intensity along the vertical direction of the rectangle in Fig. 1b. The intensity is averaged along the horizontal direction. The superposed dashed line is a damped sine function for fitting the main oscillation, whereas the dotted line represents the weak prominence oscillation prior to the plasma injection. A data gap exists between 18:00 UT and 18:14 UT. |
| In the text | |
 |
Fig. 4 Magnetic field configuration used for the 1D radiative hydrodynamic simulation of the prominence oscillation. Note that the horizontal and the vertical sizes are not to scale. |
| In the text | |
 |
Fig. 5 Time evolutions of the density (top) and the temperature (bottom) distributions along the magnetic loop, which indicate that the prominence experiences a damped oscillation subjected to a perturbation. |
| In the text | |
 |
Fig. 6 The running-difference images of EUVI 171 Å channel at 21:45 UT (left) and 304 Å channel at 21:52 UT (right) showing that only a thread of the prominence erupted. The white cross in the left panel marks the location of a microflare, which occurred at 18:00 UT. |
| In the text | |
 |
Fig. 7 Top: STEREO/COR1 running-difference images showing the early propagation of a CME; bottom-left: running-difference image from LASCO/C2 coronagraph at 23:54 UT; bottom-right: Fe ix/x 171 Å image at 22:55 UT showing a C1.2-class flare associated with the CME. |
| In the text | |
 |
Fig. 8 Timeline of the whole event, where the flare is indicated by the GOES 1 − 8 Å SXR light curve (solid line), the prominence oscillation is represented by the insertion of the time-slice plot of Fig. 3, and we also show the CME heights observed by different instruments, i.e., STEREO/COR1 (squares), LASCO/C2 (stars), and LASCO/C3 (diamonds), respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


