| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118274 | |
| Published online | 04 June 2012 | |
The position of β Pictoris b position relative to the debris disk⋆,⋆⋆
1 Institut de Planétologie et d’Astrophysique de Grenoble, Université Joseph Fourier, CNRS, BP 53, 38041 Grenoble, France
e-mail: anne-marie.lagrange@obs.ujf-grenoble.fr
2 LESIA-Observatoire de Paris, CNRS, UPMC Univ. Paris 06, Univ. Paris-Diderot, 92195 Meudon, France
3 Max Planck Institut fur Astronomie Königstuhl 17, 69117 Heidelberg, Germany
4 Department of Astronomy and Department of Planetary Sciences, The University of Arizona, 933 N Cherry Avenue, Tucson, AZ 85718, USA
5 ESO Vitacura Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago de Chile 19, Chile
Received: 14 October 2011
Accepted: 16 January 2012
Context. We detected in 2009 a giant, close-by planet orbiting β Pic, a young star surrounded by a disk that has been extensively studied for more than 20 years. We showed that if the planet were located on an inclined orbit, this could account for several peculiarities of the β Pictoris system. However, the available data did not permit us to measure the inclination of β Pic b with respect to the disk, and in particular to establish in which component of the disk – either the main, extended disk or the inner inclined component/disk – the planet was located. Comparison between the observed planet position and the disk orientation measured using previous imaging data was not an option because of potential biases in the measurements.
Aims. Our aim is to measure precisely the planet location with respect to the dust disk using a single high-resolution image, and correcting for systematics or errors that degrade the precision of the disk and planet relative-position measurements.
Methods. We gathered new NaCo data in the Ks band, with a set-up optimized to derive simultaneously the orientation(s) of the disk(s) and the planet projected position.
Results. We show that the projected position of β Pic b is above the midplane of the main disk. With the current data and knowledge of the system, this implies that β Pic b cannot be located in the main disk. The data instead suggest that the planet is located in the inclined component.
Key words: planetary systems / planet-disk interactions / planets and satellites: detection / planets and satellites: formation / instrumentation: adaptive optics
Based on observations collected at the European Southern Observatory, Chile, ESO; run 086.C-0341(A).
Appendices A and B are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Understanding planetary system formation and evolution has become one of the most exciting challenges in astronomy, since the imaging of a resolved debris disk around the young star β Pictoris, in the 80’s and the discovery of the first exoplanet around the solar-type star 51 Peg in the 90’s. While more than 500 planets (mostly giants, hereafter GPs) closer than a few AU have been identified with radial velocity (RV) and transit techniques, very few have been imaged and definitely confirmed around stars, at separations comparable to those of our Solar System giants (Marois et al. 2008; Lagrange et al. 2010). The planets imaged so far orbit young stars; indeed the young planets are still hot and the planet-star contrasts are compatible with the detection limits currently achievable, in contrast to similar planets in older systems (we exclude here planetary mass objects detected around brown dwarfes, whose origins are still debated). Noticeably, the stars are of early-types, and surrounded by debris disks, i.e. disks populated at least by small grains with lifetimes so short that they must be permanently produced, probably by the destruction (evaporation, collisions) of larger solid bodies.
Apart from these still rare cases of imaged planets, several of these debris disks have now been resolved at optical or near-IR wavelengths, with sometimes peculiar structures (rings, gaps) that could indicate the presence of yet unseen planets. These debris disks, and especially those with already imaged planets, are ideal places to study planet-disk interaction and early ages. Among these systems, the young (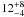 Myr; Zuckerman et al. 2001) and close (19.3 ± 0.2 pc; Crifo et al. 1997) disk around the A5V star β Pictoris has been considered as a prototype of young planetary systems. We detected with NaCo (Lenzen et al. 2003; Rousset et al. 2003) on the Very Large Telescope a companion to β Pic orbiting between 8 and 15 AU from the star (Lagrange et al. 2009). Using the models of Lyon group (Baraffe et al. 2003) and the observed L′ magnitude, we derived from the available photometry a temperature of ~ 1500 K and a mass of 9 ± 3 MJup. These parameters were later confirmed by new observing techniques at 4.0 μm (resp. Quanz et al. 2010), and at Ks band (Bonnefoy et al. 2011)1. As the brightness-mass relationships predicted by these models at young ages are still influenced by uncertain initial conditions, we furthermore used RV data to directly constrain its true mass to be less than ≃ 10–25 MJup (Lagrange et al. 2012), for orbital separations of 8–12 AU. Additional astrometric data obtained in 2010–2011 show finally that the planet semi-major axis is in the range 8–10 AU (Chauvin et al. 2012), and its eccentricity less than 0.12. Hence, β Pic b is today the closest planet ever imaged around a star.
Myr; Zuckerman et al. 2001) and close (19.3 ± 0.2 pc; Crifo et al. 1997) disk around the A5V star β Pictoris has been considered as a prototype of young planetary systems. We detected with NaCo (Lenzen et al. 2003; Rousset et al. 2003) on the Very Large Telescope a companion to β Pic orbiting between 8 and 15 AU from the star (Lagrange et al. 2009). Using the models of Lyon group (Baraffe et al. 2003) and the observed L′ magnitude, we derived from the available photometry a temperature of ~ 1500 K and a mass of 9 ± 3 MJup. These parameters were later confirmed by new observing techniques at 4.0 μm (resp. Quanz et al. 2010), and at Ks band (Bonnefoy et al. 2011)1. As the brightness-mass relationships predicted by these models at young ages are still influenced by uncertain initial conditions, we furthermore used RV data to directly constrain its true mass to be less than ≃ 10–25 MJup (Lagrange et al. 2012), for orbital separations of 8–12 AU. Additional astrometric data obtained in 2010–2011 show finally that the planet semi-major axis is in the range 8–10 AU (Chauvin et al. 2012), and its eccentricity less than 0.12. Hence, β Pic b is today the closest planet ever imaged around a star.
Two particularities of the β Pic disk are: 1) the warping of its inner (less than 80 AU) parts, observed with HST and from the ground with adaptive optics since the late nineties (Mouillet et al. 1997; Heap et al. 2000; Golimowski et al. 2006; Boccaletti et al. 2009), and 2) several asymmetries in more external parts of the disk observed earlier-on (Kalas & Jewitt 1995). We attributed the observed warp to the gravitational perturbation of a massive body located on an inclined orbit, on a disk of planetesimals, and the outer asymmetries to the distribution of the small grains released by collisions among the perturbed planetesimals, and immediately blown away by the stellar radiation pressure (Mouillet et al. 1997; Augereau et al. 2001). Golimowski et al. (2006) interpreted this inner part as a secondary, inclined disk2. We showed in Lagrange et al. (2010) that given its observed properties and the earlier modeling results, if β Pic b were indeed located in the warped part of the disk (or close to it), several of these asymmetries could be accounted for. However, the error bars in the position of β Pic b with respect to the star, and in particular, its position angle (hereafter PA) did not allow us to determine whether it is located within the main, outer disk or the inner, warp component.Both components are indeed separated by only 2–5°, very close to the uncertainty in the measured projected PA of the planet. This rather large uncertainty on the planet PA is in part caused by our inability to reliably measure the star center positions in the heavily saturated images we use to achieve the high contrast necessary to detect planets. The star center position is obtained from a fit to the low-flux level wings of the saturated image, which happens to be very variable in shape and display significant asymmetries that, we believe, cannot be corrected for (see below). Currie et al. (2011) claimed that β Pic b was located in the main disk rather than in the inclined/warped disk. However, we believe for the following four reasons that these results have to be taken with care. First, the data were calibrated using platescales and orientations measured on data taken more than one month (L′ data) and almost one year (M′ data) after the data presented in their paper. Second, the uncertainties associated with these measurements, between 1.2 and 1.9 degrees, are only the uncertainties associated with the planet centroiding estimates. We show in the following that this uncertainty is by far not the largest source of uncertainty. Third, the comparison between the planet and disk PA relies on a PA of the main disk measured in low spatial resolution data (Kalas & Jewitt 1995) acquired years before, and does not take into account any error bars in the disk PA, while revised values were published by our group far more recently (Boccaletti et al. 2009). Fourth, the authors did not discuss that the observed position angle of the planet with respect to the disk is affected by possible projection effects if, as proposed earlier, the disk(s) is(are) inclined with respect to the line of sight. Following the results of Currie et al., Dawson et al. (2011) developed dynamical simulations involving three scenarios: 1) β Pic b is on an inclined orbit as described above, and is responsible for the warp; 2) β Pic b orbits within the main disk, and an additional planet is responsible for the warp; and 3) β Pic b was initially on an inclined orbit, responsible for the warp, and then moved back into the main disk through inclination damping. Interestingly, the second scenario was not found to be viable.
Accurate measurements of the disk or planet absolute PA are not straightforward to obtain, and require precise calibrations of detector orientation. Aware of these uncertainties, we decided to obtain new data of the β Pic system that would allow us to measure directly the position of the planet with respect to the disk, using data that would show at the same time the main and warped component, as well as β Pic b, so as to mimimize as much as possible the instrumental systematics and associated uncertainties. In Sect. 2, we describe the data, the reduction procedures, and we provide the resulting images. We present in Sect. 3 (resp. Sect. 4) the methods used to measure the disk (resp. planet) orientations and the associated results. We note that as we are interested in finding the relative position of β Pic b with respect to the disk, we do not a priori need to measure the planet and disk absolute PAs and associated uncertainties (detailed in Appendices A and B). In particular, the planet position relative to the disk will not be influenced by systematics that affect the planet and disk PAs in the same way, such as, for instance, the absolute detector orientation on the sky. In contrast, all effects that impact differently the planet and disk positions have to be quantified in detail. As the disk and planet absolute PAs may nonetheless be interesting information for other purposes, we address these issues in Sects. 3 and 4. We then discuss the relative (projected) position of β Pic b relative to the disk. Finally, in Sect. 5, we constrain the de-projected position of the planet, hence its location within the dusty disk.
2. Data and reduction procedures
In our VLT/NACO follow-up program of β Pic b, we focused mainly on the determination of the planet orbital parameters. Several images were taken at different epochs. However, the data were either obtained in L′ band where the disk is much fainter, and/or with a dithering pattern (different positions of the star on the detector, referred hereafter to as the different “offsets”) to reduce the background (sky and above all detector) noise but limiting the FoV to ≃4′′ (80 AU); such a limited field of view therefore prevented an unambiguous measurement of the main disk component because of the presence of the inner warped component. Without dithering offsets, a much larger field can be obtained, allowing us to detect the disk at larger distances, where the main component dominates (the warp component contribution drastically declines longwards of 80 AU). As a drawback, the background removal is expected to be more critical.
2.1. The data
To achieve our goal of measuring the position angle of the planet with respect to the disk using a single set of data, we decided to acquire VLT/NACO images at Ks in which the star was located at a single offset on the detector. The observations were carried out on 2010 Nov. 16, with the S27 camera. All data considered here were recorded in pupil tracking mode (angular differential imaging, ADI, Marois et al. 2006), consisting in a sequence of saturated images (several datacubes), both followed and preceded by a series of un-saturated PSF images, with a measured FWHM = 2.98 pixels = 80.49 mas, used to estimate the PSF shape for calibration purposes (photometry, shape), and fake planet simulation (see below). In the present context, we are not so much interested in the photometry but rather the PSF shape (which is used to inject fake planets, see below). Immediately after the last saturated image had been acquired, the telescope was offset and images with detector integration times (DITs) similar to those of the saturated data were taken, to estimate the sky/background. We tried to observe β Pic at parallactic angles such that the telescope spiders did not overlap the disk. Finally, the detector plate scale was measured on five stars located in an Orion field, using HST astrometric data, to be 27.01 ± 0.05 arcsec per pixel, and the north orientation offset (=absolute PA – PA measured on the detector) was measured to be − 0.25 ± 0.07°. These 5 stars are those we use regularly for our astrometric calibrations (Chauvin et al. 2012). If, instead of using these 5 stars, we use 15 stars in the same field, we find the same offset (within the error bars): − 0.29°, but with an increased dispersion (0.3°). We attribute this discrepancy in the dispersions to possible systematics due for instance to the limited precision of the HST astrometric data, which serve as references for the stars positions, and also to the fact that we use in the second approach fainter targets, for which the centroid measurements may be less precise. This shows in any case how difficult it is to get precise absolute PAs and further inforces the relevance of our present approach, which allows us to get rid of these uncertainties.
 |
Fig. 1 β Pic disk at Ks obtained on November, 16th: Ks, S27 data, with a 27 mas/pixel sampling. Northeast side is to the left and southwest is to the right. We show the images of the same data reduced with cADI, cADI-disk, sADI, rADI and LOCI. Notes: 1) the color codes are not identical for the different images; 2) the radial thin and bright structures are due to an imperfect removal of the telescope spiders. |
 |
Fig. 2 Isophotes (from 0. to 1. ADU) of the image of the β Pic disk at Ks obtained on November, 16th (cADI-disk). Northeast side is to the left and southwest is to the right. β Pic b is not visible with the present brightness scale, but the white circle, with a radius of 15 pixels indicates the approximate separation of β Pic b. |
2.2. Data reduction
As a first step, the data were reduced with different procedures, which we name cADI, cADI-disk, sADI, rADI, and LOCI. All ADI reduction procedures indeed induce biases that may have different impacts on the disk or the final planet positions; they are then important to know in the present context, to identify the best methods and derive the associated error bars.
The cADI, sADI, and LOCI procedures were previously described in Lagrange et al. (2010). They differ basically in the way in which they estimate the star halo (that we refer to as “PSF” hereafter) that has to be subtracted from the data to allow planet detection. Briefly, in cADI, the PSF is taken as the mean or median of all individual recentered ADI saturated images3; all individual images are then subtracted from this PSF and the residuals thus obtained are derotated and combined (mean or median) to produce the final image. sADI computes “PSFs” for each individual image, using a given number of images taken before or after the considered image, with a field rotation larger than a given angle expressed in FWHM at a given separation (the angle is then constant for all separations). The residuals thus obtained are then derotated and combined to produce the final image. The rADI procedure (identical to Marois et al. 2006, ADI) is a generalization of the sADI procedure, which at each radius, and for each image, once corrected from the median of all images, selects a given number of images recorded at parallactic angles separated by a given value in FWHM (the same value in FWHM for each separation), to build a PSF to be subtracted from the considered image. In the LOCI approach, for each given image and at each given location in the image, we compute “parts” of “PSFs”, using linear combinations of all available data, with coefficients that allow us to minimize the residuals in a given portion of the image. Finally, cADI-disk is a variation of the cADI procedure that after cADI reduction, subtracts from the initial PSF a rotated image of the residuals, in order to remove as much as possible the contribution of the disk to the so-called “PSF”. The disk-corrected PSF is then subtracted from the individual images; the individual residuals are then derotated and stacked (median or average) to get the final image. This procedure was designed mainly to check the impact of the self-subtraction with the cADI procedure.
In practice, we fixed some parameters of the sADI, rADI, and LOCI procedures:
-
LOCI: Δr = 2 × FWHM (radial extent of the subtraction zones); g = 1 (radial to azimuthal width ratio), NA = 300 × FWHM (surface of the optimization zone); separation criteria between 1.25, 1.50, and 2.00 × FWHM;
-
rADI: separation criteria: 1., 1.25, and 1.5 × FWHM; number of images used to compute each “PSF” : 10. We note that the criteria that are optimal for the planet detection and the disk detection are not the same (see below);
-
sADI: the separation criteria was 1.3, 1.5, and 1.8 × FWHM at a separation of 12, 13, 15, and 19 pixels; the number of images used to compute each “PSF” was between 10 and 20.
2.3. Disk and planet images
The non-offsetted images reduced with the different methods are shown in Fig. 1. The disk is well-detected out to 130 (SW) and 140 (NE) AU from the star. This allows us to identify both the main and warped components. Figure 2 shows the isophotes in the case of the cADI-disk image.
The images show a circular pattern located NE of the star; this is an artefact that we attribute to the combination of pupil tracking observations, PSF saturation, and sky removal. This feature strongly affects the detection of the disk at radii shorter than ~2.7′′ (~50 AU) at the NE, while the disk is clearly seen to the SW at radii twice as short (see Fig. 2). We then consider this part as unusable in the following. The artifact is stronger in the non-offsetted images than in the offsetted ones, owing to a comparatively less efficient background correction.
If we now compare the disk images produced by the different methods, we see that the disk appears slightly thinner when reduced with sADI, and significantly thinner with rADI than with cADI (or even more cADI-disk). The limited impact of sADI on the disk height is caused by the separation criterium (1.5 × FWHM) being set at a short separation, and the corresponding angular separation is kept for all separations, hence the disk self-subtraction at large separations ( ≥ 50 AU) is very limited. This is in contrast to the case of rADI data, where the criterium separation is set at all separations. Disk self-subtraction can in principle be at least partly reduced by choosing larger separation criteria, but in such a case, the image would not be adapted to the planet imaging and position measurement. In the case of LOCI, the disk appears much fainter, and the inclined component is no longer detectable. This is due to a large amount of self-subtraction, in particular of the inner disk. As a result, we consider in the following only the cADI and sADI methods to ensure that the disk (and in particular its warped component) is less affected by the ADI procedures.
3. Disk orientation(s)
3.1. Main disk orientation: measurements
We describe here the different approaches that we adopted to measure the disk(s) orientation(s). An important issue is obviously the uncertainties associated with the measured values. We address this issue in detail in the next subsection.
3.1.1. Maximum-spine fit to the main disk
To estimate the PA of the main disk, we first computed its spine and measured its position angle at separations large enough to ensure that the considered region is dominated by the main disk and that the warp contribution is comparatively smaller. This happens longwards ≃ 80 AU in the present data. The HST data (Heap et al. 2000; Golimowski et al. 2006) show that the warped component is indeed about four times fainter than the main disk at separations ≥ 80 AU. In our data, which have a lower signal-to-noise ratio (S/N) at large separations, such a contribution is close to the level of noise. The considered baseline region for the main disk is then between ≃ 80 and 120 AU (160–230 pixels; the outer limit being conservatively set by the quality of the data at large radii).
Ks data used in this paper.
Main disk position angle (NE/SW), as measured with the various methods described in the text,for cADI, sADI, and rADI (based on averages of resp. 3, 3, and 1 reduced images).
To define the spine, we first simply identified the brightest pixel in the disk at each radius (“spine-maximum” approach), and measured the PA of the curve obtained in the 160–230 pixels region. To measure this PA, we first took it as a free parameter and derotated the disk around a roughly estimated PA value (29° and 209° resp. for the NE and SW sides, see below) with a step of 0.01°. For each given derotation, we computed the slope of the spine curve; the adopted PA is the angle of rotation for which the slope is null (within ± 0.01°). The PA obtained for the NE and SW sides of the disk are given in Table 2 for the cADI data4, together with the associated uncertainties described in Appendix A. With the rough maximum-spine method, we found with cADI a PA of 29.33°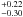 and 209.10°
and 209.10°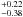 for the NE side and SW sides respectively, assuming an uncertainty of 0.07° for the true north position. We found very similar results with the median data. We also note that the values found are close to those derived by eye from the isophotes extrema in the same region of the disk, namely 29.2° and 208.9° when considering the isophotes between 160 and 230 pixels. Table 2 also provides similar measurements derived from the sADI and rADI data, together with their associated uncertainties. The sADI data give quite similar values, which is consistent with the fact that given the parameters adopted, the sADI process is not very different from the cADI process at large separations. The rADI data lead to lower values (yet coherent with the others derived, given the error bars). We recall that the disk is far more affected by the rADI process than by either the cADI or the sADI ones (with the parameters adopted).
for the NE side and SW sides respectively, assuming an uncertainty of 0.07° for the true north position. We found very similar results with the median data. We also note that the values found are close to those derived by eye from the isophotes extrema in the same region of the disk, namely 29.2° and 208.9° when considering the isophotes between 160 and 230 pixels. Table 2 also provides similar measurements derived from the sADI and rADI data, together with their associated uncertainties. The sADI data give quite similar values, which is consistent with the fact that given the parameters adopted, the sADI process is not very different from the cADI process at large separations. The rADI data lead to lower values (yet coherent with the others derived, given the error bars). We recall that the disk is far more affected by the rADI process than by either the cADI or the sADI ones (with the parameters adopted).
3.1.2. Lorentzian fit to the main disk
In a second approach, which had been expected to be more precise, we fitted the vertical profile of the derotated disk at each radius, with a weighted Lorentzian profile, with a weight proportional to the fourth power of the flux, to enhance the maximum of the profile. We then proceeded as in the spine-maximum approach. Again the results are given in Table 2 for the cADI, sADI and rADI data, together with associated uncertainties (see Appendix A). They appear to be quite consistent with the ones obtained with the spine-maximum approach, with yet slightly improved error bars.
3.1.3. Hybrid fit to the main disk
Previous works have fitted the observed disk by a two-component Lorentzian profile. This implicitely assumes that the observed disk can be decomposed into two distinct disks5. We therefore assumed that the vertical profile of the disk can be fitted by two Lorentzian profiles as done in previous works (see e.g. Golimowski et al. 2006), corresponding to the main disk on the one side, and to another inclined disk on the other side. We measured the orientations of both components as follows: we considered different rotations of the disk with values close to the main disk PA, and in steps of 0.01°. For each rotation angle, we fitted the vertical profile by two Lorentzians; we determined the rotation angle that nulls the slope of the vertical distance to the midplane of the main disk in the considered reference region, [160–230] pixels (see above). We found for the NE (resp. SW) side a PA of ≃ 29.1° and 209.0° for the NE and SW sides of the main disk on the cADI data (see Table 2). These values are close to the ones found previously, which confirms that the warp component only marginally effects the disk orientation at large separations. Once the PA of the main disk was known, we determined the slope of the second component, which gives the tilt of the inclined disk relative to the main disk. An example of a decomposition of the vertical profile by two Lorentzians at r = 80 AU is given in Fig. 3. The values are found to be very similar, but slightly lower ( ≃ 0.3°) than those derived with the weighted Lorentzian and the spine-maximum methods. We attribute this discrepancy to a small contribution of the warp component in the 160–230 pixels region that impact the results obtained with these last two methods. This is in qualitative agreement with the difference found when considering the isophotes either between 160 and 230 pixels, or further away (between 200 and 240 pixels): 0.4° and 0.3° for the NE and SW sides of the disk. This is also in agreement with the values found with the weighted Lorentzian fit to the disk between 200 and 240 pixels: in such a case,the PA is smaller by 0.2° than the PA measured between 160 and 230 pixels. Finally, sADI data provide similar results, and rADI data do not allow such a fitting, due to the important self-subtraction of the warped component.
 |
Fig. 3 Fit to the vertical profile of the disk (see text) at r = 80 AU (NE) by two Lorentzians. |
As a summary, Fig. 4 shows the warp position relative to the main disk, obtained with the different methods. The overall agreement between the three methods is clear; the impact of the warp contribution on the main disk Lorentzian or spine fit is also visible shortwards of 80 AU.
 |
Fig. 4 Warp position as estimated with the three different approaches (cADI data). NE is to the left and SW to the right. For clarity purpose, we show here the average of five consecutive data points along the disk. |
3.1.4. Simultaneous fit to the NE and SW sides
For all the approaches above, it appears that the NE and SW sides of the main disk are aligned with each other within the error bars. We then made a last estimate of the main disk PA by performing a linear regression considering both sides of the disk at the same time, hence without assuming a priori a given center for the star. For the cADI data, when averaging the Lorentzian and two-component fit results, we found a PA of 29.17° (mean or median), to be compared to 29.18° (mean) and 29.17 (median) when considering the NE side of the disk alone, and 209.17 (mean or median) when considering the SW side. The sADI measurements are within 0.04° of the cADI ones. The star center appears to be offset by less than 0.05° ( ± 0.1°) from the disk main plane (all error bars included, true north corrected).
3.2. Main disk orientation: uncertainties and systematics
The different identified sources of uncertainties in the measurement of the disk position angle and their estimations are described in Appendix A. In brief, we identified two main classes of uncertainties. The first class is related to the data reduction and calibration, and contains in particular, uncertainties associated with (1) the imperfect determination of the star center in the heavily saturated images, (2) the way in which the “PSF” subtracted during the ADI reduction is estimated, (3) the disk self-subtraction, and (4) the true north (hereafter TN) position (which is important only for absolute measurements). The second class is related to the PA measurements themselves: the fitting of the disk, and the region considered for the PA determination. Finally, we found rather small error bars, of approximately ± 0.2–0.5 degree (see Table 2). We recall nevertheless that an absolute calibration of the TN would increase the error bars by an additional 0.3°.
3.3. Warped component orientation: measurements and associated uncertainties
We first fitted the vertical profile of the disk with a two-component profile as described above. However, to optimize the measurement of the warp PA, we chose regions where the warp contribution is more significant than previously: [130–160] and [130–180] pixels, i.e. ≃ [68–83] and [68–94] AU. We then averaged the results (PA values averaged and uncertainties quadratically added) of the different reduced images for each method. The obtained values are ≃ 3.5–4°.
The measurement of the tilt between the warp and main components is free from most of the errors associated with the data reduction and calibrations and with the ADI process (assuming, realistically, that they impact similarly the main and warp components). The main sources of uncertainty in this case are related to 1) the determination of the warp itself with the two-Lorentzian profile fitting or the symmetry approach, 2) the impact of disk self-subtraction, and 3) the assumptions taken to compute the final image (mean/median). The last source of uncertainty was found to be negligible. We performed simulations of a two-component fitting using two fake disks and found that 1) the two-component fitting approach underestimates the inclination of the warp component by 0.5° and 2) that the ADI treatment also underestimates the inclination by another 0.1°. Hence, the measured inclination is probably underestimated by 0.6°. These values have been taken into account in the error bars provided in Table 2. We note that we chose to consider them as errors rather than offsets, as the present estimation probably depends on the assumptions about the disk geometries.
In a second, exploratory approach (referred to as “warp symmetry”), we tried to separate the warp contribution from the main disk one. To do so, for the NE (resp SW) side of the disk, we isolated the contribution of the disk above (resp. below) the midplane and symetrize it to build an estimate of the main disk. We then subtracted this estimate of the main disk from the observed disk to get an estimate of the warp contribution. An illustration of the method is given in Fig. 5, and the results obtained are given in Fig. 4. The inclination of the warp thus reconstructed was measured in the [130–160] and [130–180] pixel regions, with the maximum-spine method or with a Lorentzian fit. The obtained values range between 3.6° and 4.6° (cADI, sADI), in agreement with the values obtained with the two-component fit. However, as we do not have a proper way of estimating the biases introduced by this method, we believe that this method should be regarded only as illustrative.
 |
Fig. 5 An estimate of the warp. Top: initial image. Middle: estimated main disk. Bottom: subtraction of the first two images, to reconstruct the warp. |
3.4. Conclusions about the disk(s) orientation(s)
3.4.1. Adopted values for the disk orientations
Taking into account the results given in Table 2, we conservatively deduce a PA of 29.3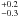 degrees for the NE side of the main disk and 209.2
degrees for the NE side of the main disk and 209.2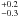 degrees for its SW side. We assume an uncertainty of 0.07° for the true north position. We furthermore adopt an inclination of 3.5–4.6° between the warp disk/component and the main disk.
degrees for its SW side. We assume an uncertainty of 0.07° for the true north position. We furthermore adopt an inclination of 3.5–4.6° between the warp disk/component and the main disk.
3.4.2. Comparison with previous results
There are very few published data on the position angle of the disk observed in the optical or near-IR6. In particular, to our knowledge, no value of the main disk PA has been published for HST ACS or STIS data. Kalas & Jewitt (1995) reported a PA of 30.1° and 211.4° for, respectively, the NE and SW sides. The values vary within a 1° to 2.5° range. Noticeably, the data used to measure the PA traced only the outer part of the disk, hence they correspond to the main disk PA. More recently, we proposed a revised lower value of 29.5° for the position of the main component (Boccaletti et al. 2009). Our measurements are then compatible with the values found by Boccaletti et al. (2009) and slightly marginally compatible with those found by Kalas & Jewitt (1995). The present associated error bars are much smaller. Finally, we note that HST data (Golimowski et al. 2006) indicate that the NE and SW sides are not perfectly aligned, with a difference of about 0.9° (see also their Fig. 10). The present data analysis does not seem to support this result, but we note that given the uncertainty associated with the difference in PA of the NE and SW sides, ≃ 0.5°, one may consider that this conclusion is weak. In addition, part of the discrepancy might be due to the reference regions used by Golimowski et al. (2006) and by ourselves to make the hybrid fit being different, respectively 80–250 AU and ≃ 80–120 AU (see above).
The tilt between the warp component and the main disk was mesured by HST, with values of ≃ 3° (Mouillet et al. 1997) using ESO/T3.6 m AO ground-based data, and 4–5° (Heap et al. 2000), ≃ 5° (Golimowski et al. 2006) both using HST, higher-SN data. The tilts measured here ( ≃ 4°) are then compatible with previous estimates. However, the comparison is probably not entirely meaningful as we, in contrast to Golimowski et al. (2006), constrained the center of both disks to be identical, which then affects the measured tilt. For instance, it seems, from their Fig. 9, that constraining both centers to be identical would lower the PA of the NE side, without significantly changing the PA of the SW side. Golimowski et al. (2006) also found that the SW part is less tilted (4.7 ± 0.3°) than the NE side (5.9 ± 0.6° ). The present analysis does not allow us to either confirm or disprove these results. Finally, Weinberger et al. (2003) derived a PA of 33.3 ± 2 degrees from mid-IR data. In addition, Wahhaj et al. (2003) appeared to adopt the value of Kalas & Jewitt (1995) for the main disk PA, but found the 82 AU radius clump is offset from the main midplane by about two degrees. We must bear in mind that these mid-IR data correspond to thermal emission from the dust where as the near-IR data correspond to scattered light.
 |
Fig. 6 Top: zoom of β Pic b position with respect to the disk main component and warp component (mean cADI image), together with associated error bars for a pessimistic case. Left: mean cADI; right: median cADI. Bottom: idem for rADI images. |
4. Planet position
4.1. β Pic b position: measurements
To measure the planet position, we used the same images (obtained with the same reduction procedures and parameters, and using the positive parts of the residuals) as those used to compute the disk PA.
Position of bPic b on the different images.
We determined the position of the planet with a centroid calculation using either a two-dimensional Gaussian fitting or Moffat fitting of the observed signal. The results are provided in Table 3, together with the associated uncertainties resulting from the analysis of all identified sources of errors (see Appendix B). Note that as in the case of the disk, the values given here are the average of measurements performed on images obtained with different reduction softwares (three different measurements for the cADI data, three for the sADI data, and one for for the rADI data). The planet position is found to be (sep, PA) ≃ (14.2 pix; 212.3°) on the cADI mean. The (sep; PA) values obtained with the cADI and sADI methods differ, but they remain nevertheless compatible given the error bars. The rADI measurements depend significantly on the separation criterium chosen (1.0, 1.2, 1.5, 1.75, or 2 × FWHM); this is because when the separation criterium is small, the planet self-subtraction is very large and the residual signal becomes comparable to the noise on the one hand, and when the separation criterium is high, several frames lack comparison frames to build the PSFs, hence the number of frames effectively used to build the final image becomes prohibitively small. The derived (sep; PA) are slightly lower than the cADI and sADI values, but still compatible given the error bars.
We note that the various disk PA measurements have a smaller dispersion than the measurements of the planet position; this is because the measured planet position is very sensitive to the residuals in the final images, whereas the disk, located much further away, is unaffected by these residuals.
In a second step, we inserted negative fake planets with variable fluxes and positions (separations and PA) and processed the data to find the position and flux values that minimize the residuals at the β Pic b location. This method was described in Lagrange et al. (2010) and also used in Bonnefoy et al. (2011); it is potentially efficient in the sense that it intrinsically takes into account the planet self-absorption during the process (see Appendix B). It appeared that depending on the choice of the unsaturated PSF (either the one taken prior to or the one taken after the record of the unsaturated data) used to generate the fake planet signal, the values obtained differ by up to (0.1pix; 0.7°) in cADI and up to (0.05 pix; 1.25°) in sADI. Such high differences then preclude the use of this method in the present set of data owing to the large PSF temporal variations that took place during the recording of the saturated images.
 |
Fig. 7 Top: position of β Pic b together with errors bars measured on 3 different cADI images (mean of the residuals). The full lines correspond to mean cADI data, the dashed lines correspond to measurements on median cADI data. Dashed horizontal lines shows the min and max PAs of the main disk and dotted ones the min and max PAs of the warp component. Conservative error bars have been taken into account. Middle: idem for sADI data. Bottom: idem for rADI data. |
4.2. β Pic b position: uncertainties
The uncertainties associated with the measurements are described and estimated in Appendix A. They are dominated by the uncertainty in the star position, and by the impact of the low S/N of the planet signal. They are larger than those associated with the disk PA, because a) the planet lies within the halo of speckles and b) is close to the star, so the measurements are very sensitive to the uncertainty in the star position.
5. Position of β Pic b relative to the circumstellar disk
5.1. Planet projected position with respect to the disk
The measurements given in the previous section take into account all systematics and uncertainties. The relative position of β Pic b with respect to the disk is unaffected by the common systematics when a given reduced image is considered (e.g. the uncertainty associated with the true north). In addition, the uncertainties depend on the images considered (for instance, cADI, sADI, mean, median, etc.). To explore the planet position relative to the disk, we considered then for each reduced image, the measured disk and planet positions and the associated uncertainties, except the uncertainty associated with the TN. An example is shown in Fig. 6 where we show, for a cADI mean image, a zoomed image of the planet projected position with respect to the main disk and warped component directions. We note that the warped component orientation is the average of the spine-weighted Lorentzian fit and the two-component fit results. The β Pic b projected position is clearly above the main disk midplane. In Fig. 7, we summarize all measured individual relative positions in the individual mean (left) and median (right) cADI images, in addition to sADI and rADI images (note that for rADI, we do not have any value of warp inclination). We see that even though some differences occur from one reduction to the other, all data agree that β Pic b projected position is above the main disk mid-plane.
5.2. Implication of the position of β Pic b relative to the disk
Our aim is now to use the information about the projected position to constrain the de-projected position of β Pic b with respect to the disk(s), taking into account the disk(s) orientations. According to Olofsson et al. (2001), the gaseous disk rotates towards us on the SW side and away from us on the NE side. We assume that this is also true for the solid component and the planet. In addition, we assume, taking into account the imaging data, that the planet orbits with a semi-major axis between 8 AU and 12 AU from the star (the most probable value being 9 AU; Chauvin et al. 2012), and has not yet reached the quadrature, i.e. its maximum projected separation from the star. We also assume that the main disk is inclined by 2 to 5 degrees with respect to the line of sight (Kalas & Jewitt 1995; Golimowski et al. 2006), and that the nearest-to-Earth part of the disk is tilted above the main disk mid-plane (Golimowski et al. 2006). Under these conditions, if β Pic b were located within the main disk midplane, its projected position would be between 0.9 and 2.2° (r = 8 AU), 1.4° and 3.7° (r = 9 AU) and 1.9° and 4.7° (r = 10 AU) below the observed midplane, which is inconsistent with the present observations.
We now assume that the warp component has the same inclination with respect to line of sight. In such a case, if the planet were located within the warped component, its projected position would be a few degrees below its midplane, hence between four (for a tilt of two degrees between the warp component and the main disk) and one degree (for a five degree tilt) above the main disk midplane. This is compatible with the present data. Given the number of degrees of freedom for the warp characteristics (inclination with respect to the disk, with respect to line of sight, and inclination with respect to line of nodes), we consider that it is impossible to more reliably constrain the planet position. We note that the MCMC fitting of the astrometric orbit (Chauvin et al. 2012) provides ranges of 30–34 degrees for the PA of the planet orbit and 0–3 degrees with respect to the main disk midplane for its inclination. These ranges agree with our present results.
Overall, these results do not confirm the results of Currie et al. (2011) who claim that β Pic b is located within the main disk. However, as already mentionned, these results were based on the comparison of the measurements of the planet PA with published values of the disk PA (with undefined error bars). The comparison was then affected by different, and probably important systematics.
6. Summary and future prospects
Using a single Naco Ks image, we have measured the relative projected position of β Pic b with respect to the disk. Since both the disk and the planet projected PA were measured simultaneously, some possible systematics were removed, such as the absolute detector orientation, which in turn significantly reduces the uncertainties associated with these difficult measurements. We show that β Pic b projected position is located above the main disk midplane, and actually closer to the warped component. Taking into account our knowledge on the system, we conclude that β Pic b does not orbit within the main disk, and that the data available today are compatible with an orbital motion within the inclined/warped component. Consequently, β Pic b may be responsible for the inner disk inclination as described in
Mouillet et al. (1997), Augereau et al. (2001) and more recently in Dawson et al. (2011). Future similar observations will be very important in helping us to confirm this result, which has important consequences for the disk-planet dynamical interactions. We note that forthcoming high contrast imagers on 8-m class telescopes such as VLT/SPHERE or GEMINI South/GPI, will allow us to measure the planet position much more precisely, hence to refine its orbital properties, but given their relatively small FoV, they will not be well-adapted for a precise measurement of the main disk PA.
Online material
Appendix A: Main disk orientation: uncertainties and systematics
We describe here the different identified sources of uncertainties and how we estimated them. To do so, we either used our actual disk data, or, when needed to get rid of the noise limitations and isolate the impact of a given effect, simulated disk data, with shapes and brightness profiles similar to that of β Pic disk7.
We quantified the impact of the various effects on the cADI, sADI, and rADI data (mean/median), whenever the uncertainties depended on the way in which the images were obtained.
A.1. Uncertainties and systematics related to data reduction and calibration
We first considered the uncertainty associated with the imperfect knowledge of the star center in the saturated images. This is caused by the NaCo PSFs not being perfectly axisymmetrical and the position of the star center in the saturated images cannot therefore be straightforwardly retrieved from the center of the PSF wings. Ideally (for a perfectly stable PSF), the offset between the true center and the one estimated from the PSF wings should be treated as an offset (bias). However, owing to the observed variations between the unsaturated PSFs images taken prior to and after the saturated images, we conservatively assume that it is an uncertainty. This uncertainty impacts both the recentering offsets that have to be applied to each saturated frame; hence the center of derotation of the PT images (which is also the center of reference for the PA measurement) and finally the measurement of the PA. To estimate the impact on the measured PA, we used a bright fake disk. We first estimated the error associated with the star center position. To do so, we computed the star center (Moffat fitting) in the unsaturated PSFs recorded just prior and after the set of saturated images, once scaled (through the DITs and neutral density filter) to the same flux levels as the saturated PSFs, using either the whole flux range of the PSF, or using only its wings up to varying levels up to 14 000 ADU (which is the level of saturation with the given observing mode). It appears that for levels between 5000 ADU and 8000 ADU (which frame the 6500 ADU threshold used for our saturated PSF fitting), the centers offsets are in the range [−0.026; 0.26] pixel on the x-axis, and [−0.011; 0.18] on the y-axis. To estimate the impact of this uncertainty in the star center on the final PA measurements, we used simulated bright fake disks that we added to the actual datacubes (hence in PT mode), and processed these data assuming that the actual star center is shifted by values of between −0.26 and +0.026 pixel on the detector x axis and between −0.18 and 0.011 pixel on the y axis; we then measured the resulting disk PA as described above. We found that the impact on the PA is rather small, less than −0.05° and 0.03°.
 |
Fig. A.1 Measured star center on the x-axis (diamonds) and y-axis (triangles) on the detector when considering the whole unsaturated PSFs taken before (red) and after (blue) the saturated images and when considering various radius as thresholds (see text). |
 |
Fig. A.2 Impact of the considered regions for the estimation of the main disk PA (cADI images, see text). Three regions are considered: [130; 230] pixels [65–115] AU, [160; 230] pixels [80–115] AU, [200; 240] pixels [100–120] AU. Blue: two-component fit. Red = spine, maximum. Yellow: weighted Lorentzian. |
We then considered the uncertainty associated with the way in which we estimate the “PSF” is subtracted (either the mean or median of the saturated images). This uncertainty was measured on the real data. No detectable impact on the PA measurement was found, which is coherent with the fact that the measurements are performed at large separations.
We proceeded to study the uncertainty associated with the self-subtraction of the disk in the ADI procedure. This error can be estimated using bright fake disks; it was found to be smaller than 0.01° in cADI and sADI, and larger (0.04°) in rADI (1.2 and 1.5 × FWHM), but the latter value strongly depends on the rADI parameters and on the considered region.
Finally, we considered the uncertainty associated with the determination of the true north (absolute calibration) on the detector. This error was estimated to be 0.07° when considering five stars in the field of view. As mentioned before, using all stars led to a larger dispersion, 0.3°. In Table 2, the error considered was 0.07°, which has to be kept in mind.
A.2. Uncertainties and systematics related to the PA measurements
We examined first the uncertainty associated with the fitting of the main disk. For the disk PA, we first estimated the noise level (as a function of star distance) in a disk free, 10° angular region. For the maximum method, for each vertical profile, we defined the error in pixel of the brightest pixel as the largest vertical distance between pixels having a flux greater than the maximum flux – the noise rms level. For the Lorentzian fit, the use of weights prevented us from performing a linear fit to the data associated with errors. We then conservatively considered a +/−0.5 pixel error in the center measurement. Finally, for the two-component fit, we took the following approach: for each pixel of a given vertical profile, we associated an error in ADU with the noise rms level at the appropriate distance to the star. In a second step, we derived the error in pixels associated with the position of the center of the main used to compute the slopes (hence the disk(s) PA) and associated errors. The estimates were of course made on the real data. Typically, the errors were found to be less than 0.08°.
Systematics associated with the region considered for the PA determination: we performed several measurements of the disk PA with reference regions variable in size and positions (within realistic values). For the cADI data (real data), we considered two other reference regions, one from the range 130–230 pixels, and one from 200–240 pixels, in addition to the former one of from 160 to 230 pixels. With the 130–230 pixel region, we found a somewhat higher value for the PA than with the reference region, when assuming a single component disk and a similar value when considering a two-Lorentzian fit (Fig. A.2). This is because this region is more contaminated by the warped contribution than the [160–230] pixel range. When using the 200–240 pixel region, we again found a similar value with the two-Lorentzian model, and values slightly lower (0.05°) when considering a single component. The values adopted to build up the error budget are those derived from the comparison of the [160–230] pixel and [200–240] pixel regions only.
Appendix B: β Pic b position: associated uncertainties
B.1. Uncertainties related to the data reduction and calibration
To estimate the uncertainties/systematics, we procedeed as for the disk (see above), using bright fake planets positioned at the β Pic b location instead of bright simulated disks, or using the data themselves. The fake planets were created using the unsaturated PSFs8 properly scaled in flux.
To determine the uncertainty associated with the imperfect knowledge of the star center in the saturated images (see above for a detailed description), we used bright fake planets injected at the β Pic b position to measure this uncertainty, and assumed the same star center offsets as for the disk. The impact on the planet position was found to be quite significant, up to 0.3 pixels for the separation, and 0.6° for the PA. This contrasts with the low impact on the disk PA and is explained by the fact that the planet is much closer to the star than the disk.
We considered the uncertainty associated with the recentering of the individual saturated images with respect to each other within a cube. This occurred in only one reduction where the
data were intentionally not recentered within each cube, but were directly collapsed. We found an error of 0.1° (resp. 0.3°) for the measured PA for cADI (resp. sADI).
Another uncertainty is associated with the estimation of the “PSF” to be subtracted (either mean or median of the saturated images). When bright fake planets are considered, the impact is found to be very small (smaller than 0.01 pix for the separation and 0.08° for the PA) for all data.
Next, we studied the uncertainty associated with the self-subtraction of the planet in the ADI procedure. We found that the impact on a bright fake planet is quite limited for the cADI data; less than 0.1° for the PA. The effect on fainter fake planets would be larger as the signal would be closer to the noise. We therefore consider this uncertainty below.
The uncertainty associated with the residual noise is the most difficult to measure. Ideally it should be measured at the location of the planet. We could not find a way to do so because of the presence of the planet. We therefore considered several fake planets, with a flux and a separation identical to those of β Pic b, at different PA. We then measured the dispersion in the errors between the position of the injected planets and the actually measured locations after reduction. This leads to quite large uncertainties, of up to (0.3 pix; 0.5°) in cADI and (0.3 pix; 0.7°) in sADI. These values are probably conservative as we consider different directions, and in particular regions that are not free of spider signatures, which induce higher levels of noise.
We finally considered the uncertainty associated with the determination of the true north (absolute calibration) on the detector. The conclusions are the same as for the disk. We note that we considered here an 0.07° uncertainty.
B.2. Uncertainties related to the PA measurement
We also investigated the uncertainty associated with the fitting of β Pic b. We first checked that using either Gaussian or Moffat fitting does not induce significant differences. For Moffat fitting, we made several measurements using apertures of different sizes (from 5 to 7 pixels in diameters), and we positioned the center of the aperture at variable positions, within 1 pixel of the β Pic b estimated center. We found differences of up to (0.1 pix; 0.2°).
Currie et al. (2011) published a detection in M band. The photometric information should however be interpreted with extreme care: owing to the lack of an unsaturated β Pic PSF image (necessary to estimate the flux level of the planet in the saturated images), the authors used a photometric reference that had been observed 2 years prior to the actual observations. This, we believe, is unsuitable in the case of ground-based imaging, moreover at IR.
Note that this may not be the case if the warp is indeed produced by a planet as the warped component shape would not be disk-like (see e.g. Augereau et al. 2001).
Early sub-mm (850 μm) data found a disk PA of 32 ± 4° at outer distances (Holland et al. 1998), while recent 1.3 mm observations indicate a PA of about 34°, but without error bars (Wilner et al. 2011).
We assumed a radial profile density that follows a power-law distribution given by ∝ r-4.5 further than 102 AU, ∝ r-2 in the 30–102 AU region, and ∝ r2 within 30 AU. The vertical structure of the disk is given by
where the height scale 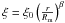 is 2 AU at 102 AU, and the disk flare coefficient is β = 1.5. The disk brightness was normalized to K = 11.5 at 100 AU, corresponding to a disk ten times brighter than the actual β Pic disk, to avoid any error due to the limited S/N of the real data, and reliably identify the bias caused by the procedure only. Finally, the disk was slightly inclined (i = 87.7°), but this inclination has no consequence on the results. The simulated disk was added to the actual data, at a PA similar to the measured main disk PA, but significantly brighter.
is 2 AU at 102 AU, and the disk flare coefficient is β = 1.5. The disk brightness was normalized to K = 11.5 at 100 AU, corresponding to a disk ten times brighter than the actual β Pic disk, to avoid any error due to the limited S/N of the real data, and reliably identify the bias caused by the procedure only. Finally, the disk was slightly inclined (i = 87.7°), but this inclination has no consequence on the results. The simulated disk was added to the actual data, at a PA similar to the measured main disk PA, but significantly brighter.
Acknowledgments
We acknowledge financial support from the French Programme National de Planétologie (PNP, INSU) and from the French National Research Agency (ANR) through the GuEPARD project grant ANR10-BLANC0504-01. This research was also supported in part by the NASA Origins of Solar Systems Program (NNX11AG57G). We thank D Golimowski, G. Schneider, and P. Delorme for fruitful discussions about the β Pic disk and/or the ADI reduction. We finally thank the referee for his/her careful reading of the paper and comments.
References
- Augereau, J.-C., Nelson, R. P., Lagrange, A. M., et al. 2001, A&A, 370, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Lagrange, A. M., Chauvin, G., et al. 2011, A&A, 528, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Augereau, J.-C., Baudoz, P., et al. 2009, A&A, 495, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2005a, A&A, 438, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005b, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A. M., Beust, H., et al. 2012, A&A, 542, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crifo, F., Vidal-Madjar, A., Lallement, R., Ferlet, R., & Gerbaldi, M. 1997, A&A, 320, L29 [NASA ADS] [Google Scholar]
- Currie, T., Thalmann, T., Matsumura, S., et al. 2011, ApJ, 736, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., Murray-Clay, R. A., & Fabricky, D. C. 2011, ApJ, 743, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Golimovski, D. A., Ardila, D. R., Krist, J. E., et al. 2006, AJ, 131, 3109 [NASA ADS] [CrossRef] [Google Scholar]
- Heap, S. R., Lindler, D. J., Lanz, T. M., et al. 2000, ApJ, 539, 435 [Google Scholar]
- Holland, W. S., Greaves, J. S., Zuckerman, B., et al. 1998, Nature, 392, 788 [Google Scholar]
- Kalas, P., & Jewit, D. 1995, AJ, 110, 794 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lafrenière, D., Jayawardhana, R., & van Kerkwijk, M. H. 2010, ApJ, 719, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A.-M., Backman, D., & Artymowicz, P. 2000, in PPiv (Univ. of Arizona Press), 639 [Google Scholar]
- Lagrange, A. M., Desort, M., Galland, F., et al. 2009, A&A, 495, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A. M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A. M., De Bondt, K., Meunier, N., et al. 2012, A&A, 542, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, SPIE, 4841, 944 [Google Scholar]
- Marois, C., Lafreniere, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., MacIntosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A. M. 1997, MNRAS, 292, 896 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Olofsson, G., Liseau, R., & Brandeker, A. 2001, ApJ, 563, 770 [Google Scholar]
- Quanz, S. P., Meyer, M. R., Kenworthy, M., et al. 2010, ApJ, 722, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, SPIE, 4839, 140 [Google Scholar]
- Wahhaj, Z., Koerner, D. W., Ressler, M. E., et al. 2003, ApJ, 584, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberger, A., Becklin, E. E., & Zuckerman, B. 2003, ApJ, 584, L33 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wilner, D. J., Andrews, S. M., & Hughes, A. M. 2011, ApJ, 727, 42 [Google Scholar]
- Zuckerman, B., Song, I., Bessel, M. S., & Webb, R. A. 2001, ApJ, 562, L87 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Main disk position angle (NE/SW), as measured with the various methods described in the text,for cADI, sADI, and rADI (based on averages of resp. 3, 3, and 1 reduced images).
All Figures
 |
Fig. 1 β Pic disk at Ks obtained on November, 16th: Ks, S27 data, with a 27 mas/pixel sampling. Northeast side is to the left and southwest is to the right. We show the images of the same data reduced with cADI, cADI-disk, sADI, rADI and LOCI. Notes: 1) the color codes are not identical for the different images; 2) the radial thin and bright structures are due to an imperfect removal of the telescope spiders. |
| In the text | |
 |
Fig. 2 Isophotes (from 0. to 1. ADU) of the image of the β Pic disk at Ks obtained on November, 16th (cADI-disk). Northeast side is to the left and southwest is to the right. β Pic b is not visible with the present brightness scale, but the white circle, with a radius of 15 pixels indicates the approximate separation of β Pic b. |
| In the text | |
 |
Fig. 3 Fit to the vertical profile of the disk (see text) at r = 80 AU (NE) by two Lorentzians. |
| In the text | |
 |
Fig. 4 Warp position as estimated with the three different approaches (cADI data). NE is to the left and SW to the right. For clarity purpose, we show here the average of five consecutive data points along the disk. |
| In the text | |
 |
Fig. 5 An estimate of the warp. Top: initial image. Middle: estimated main disk. Bottom: subtraction of the first two images, to reconstruct the warp. |
| In the text | |
 |
Fig. 6 Top: zoom of β Pic b position with respect to the disk main component and warp component (mean cADI image), together with associated error bars for a pessimistic case. Left: mean cADI; right: median cADI. Bottom: idem for rADI images. |
| In the text | |
 |
Fig. 7 Top: position of β Pic b together with errors bars measured on 3 different cADI images (mean of the residuals). The full lines correspond to mean cADI data, the dashed lines correspond to measurements on median cADI data. Dashed horizontal lines shows the min and max PAs of the main disk and dotted ones the min and max PAs of the warp component. Conservative error bars have been taken into account. Middle: idem for sADI data. Bottom: idem for rADI data. |
| In the text | |
 |
Fig. A.1 Measured star center on the x-axis (diamonds) and y-axis (triangles) on the detector when considering the whole unsaturated PSFs taken before (red) and after (blue) the saturated images and when considering various radius as thresholds (see text). |
| In the text | |
 |
Fig. A.2 Impact of the considered regions for the estimation of the main disk PA (cADI images, see text). Three regions are considered: [130; 230] pixels [65–115] AU, [160; 230] pixels [80–115] AU, [200; 240] pixels [100–120] AU. Blue: two-component fit. Red = spine, maximum. Yellow: weighted Lorentzian. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.