| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117985 | |
| Published online | 25 May 2012 | |
Constraints on planets around β Pic with Harps radial velocity data⋆,⋆⋆
1 Institut de Planétologie et d’Astrophysique de Grenoble, Université Joseph Fourier, CNRS, BP 53, 38041 Grenoble, France
e-mail: anne-marie.lagrange@obs.ujf-grenoble.fr
2 ESO, Karl Schwarzschild St 2, 85748 Garching, Germany
Received: 31 August 2011
Accepted: 24 January 2012
Context. The β Pictoris system with its debris disk and a massive giant planet orbiting at ≃9 AU represents an ideal laboratory for studying giant planet formation and evolution as well as planet-disk interactions. β Pic b can also help in testing brightness-mass relations at young ages. Other planets, yet undetected, may of course be present in the system.
Aims. We aim at directly constraining the mass of β Pic b and at searching for additional jovian planets on orbits closer than typically 2 AU.
Methods. We used high-precision Harps data collected over eight years since 2003 to measure and analyse β Pic radial velocities.
Results. We show that the true mass of β Pic b is less than 10, 12, 15.5, 20, and 25 MJup if orbiting at 8, 9, 10, 11, and 12 AU, respectively. This is the first direct constraint on the mass of an imaged planet. The upper mass found is well in the range predicted by brightness-mass relations provided by current “hot start” models. We also exclude the presence of giant planets more massive than 2.5 MJup with periods less than 100 days (hot Jupiters), more massive than 9 MJup for periods in the range 100−500 days. In the 500−1000 day range, the detection limit is in the brown dwarf domain. Beyond the intrinsic interest for β Pic, these results show the possibilities of precise RV measurements of early-type, rapidly rotating stars.
Key words: planets and satellites: detection / planets and satellites: individual:βPic / techniques: radial velocities
RV data is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/542/A18
© ESO, 2012
1. Introduction
Since the imaging of a circumstellar debris disk in the eighties, the young (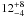 Myr; Zuckerman et al. 2001) and close (
Myr; Zuckerman et al. 2001) and close (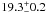 pc; Crifo et al. 1997) A5V star β Pictoris has been considered as a prototype of young planetary systems. Together with the other debris disks imaged since, this system allows us to study the physical and chemical characteristics of sites of on-going or just completed planetary formation. Recently, we were able to detect a companion orbiting the star at a distance ranging between 8 and 15 AU (Lagrange et al. 2009a). Its L′ = 11.2 approximate apparent magnitude translates into a temperature of ~1500 K and a mass of ~8 MJup according to Lyon’s group models (Baraffe et al. 2003). Similar masses were later found from images at Ks (Bonnefoy et al. 2011), and at 4 μ (Quanz et al. 2010). If it were orbiting on a slightly inclined orbit, the companion could explain most morphological (asymmetries) and dynamical peculiarities of the β Pictoris dust system, as well as the “falling evaporating bodies” (FEB) phenomenon at the origin of the replenishment of the disk gas phase. In particular, it could explain the characteristics of the warp observed within the inner part of the disk (Lagrange et al. 2010, and ref. therein). Additional data now show that the planet semi-major axis is probably in the range 8−12 AU (see Chauvin et al. 2012, and references there-in). Interestingly in the present context of planet formation theories, β Pic b is located in the region where, according to the Kennedy & Kenyon (2008) models, and given the star age and mass, giant planets can have formed in situ by core-accretion, in contrast to the few other planets imaged so far (Marois et al. 2008, 2010; Kalas et al. 2008; Lafreniere et al. 2010; Chauvin et al. 2005a,b), which are located farther away from their parents.
pc; Crifo et al. 1997) A5V star β Pictoris has been considered as a prototype of young planetary systems. Together with the other debris disks imaged since, this system allows us to study the physical and chemical characteristics of sites of on-going or just completed planetary formation. Recently, we were able to detect a companion orbiting the star at a distance ranging between 8 and 15 AU (Lagrange et al. 2009a). Its L′ = 11.2 approximate apparent magnitude translates into a temperature of ~1500 K and a mass of ~8 MJup according to Lyon’s group models (Baraffe et al. 2003). Similar masses were later found from images at Ks (Bonnefoy et al. 2011), and at 4 μ (Quanz et al. 2010). If it were orbiting on a slightly inclined orbit, the companion could explain most morphological (asymmetries) and dynamical peculiarities of the β Pictoris dust system, as well as the “falling evaporating bodies” (FEB) phenomenon at the origin of the replenishment of the disk gas phase. In particular, it could explain the characteristics of the warp observed within the inner part of the disk (Lagrange et al. 2010, and ref. therein). Additional data now show that the planet semi-major axis is probably in the range 8−12 AU (see Chauvin et al. 2012, and references there-in). Interestingly in the present context of planet formation theories, β Pic b is located in the region where, according to the Kennedy & Kenyon (2008) models, and given the star age and mass, giant planets can have formed in situ by core-accretion, in contrast to the few other planets imaged so far (Marois et al. 2008, 2010; Kalas et al. 2008; Lafreniere et al. 2010; Chauvin et al. 2005a,b), which are located farther away from their parents.
The mass determination of β Pic b as well as those of all other imaged planets, however, relies on the model-dependant brightness-mass relation provided by the so-called hot-start models. In these models, the giant planet is formed by the collapse of a gaseous cloud and the released energy is entirely transferred into heat. The young planet is therefore quite hot during its first 100 Myr, which may allow a direct detection of planets around young stars with current imagers. Recently, however, Fortney et al. (2008) have developed an alternative model, which is expected to provide brightness-mass relation for core-accretion. In their model (“cold-start” model), a significant amount of energy is lost during the accretion process of gas onto a solid core. As a result of this energy loss, their model predicts planets much fainter than the hot-start model predictions at young ages at a given mass: for instance, a 10-Jupiter mass planet aged 10 Myr is ≃5−6 mag fainter. Under these assumptions, and except during the very short accretion phase, young planets would not be detectable with current instruments. We note that the discrepancy between both models decreases with time, but remains significant up to 100 Myr. Returning to β Pic b, the observed magnitude is compatible with a planet formed under the hot-start model, but not under the cold-start model, as presently developed. In particular, this cold-start model does not predict any planet with this luminosity at 10 Myr. However, it would be prematurate to conclude that β Pic b did not form by core-accretion based on these brightness-mass considerations, because these models 1) probably represent two extreme situations in between which actual processes at work during giant planet formation take place, and 2) were not calibrated so far by means of observations. Calibrations require independant measurements of the mass of the planets, i.e. dynamical masses, derived from astrometric or RV measurements1. This is why detecting and characterizing planets, in particular young ones, is so badly needed.
Another important matter is the presence of other planets around β Pictoris. The example of HR 8799 (Marois et al. 2010) and the radial velocities (hereafter RV) study of solar-type stars (http://www.exoplanet.eu) show that multiple planetary systems are indeed very common. Also, gaps have been reported in the β Pic disk in the mid-IR (Okamoto et al. 2008; Wahhaj et al. 2003; Telesco et al. 2005) that were sometimes attributed to planets (Freistetter et al. 2007). Our available images do not show evidence of planets more massive than ~5 MJup at separations of 10−20 AU (Lagrange et al. 2010). Because current imagers are unable to put constraints on the presence of planets closer than typically 5−6 AU from the parent stars, other methods are needed to get information on the presence of planets in the inner 5 AUs. An analysis of 120 spectra obtained with Coralie in 1998−1999 as well as 258 Harps spectra obtained between November 2003 and July 2004 allowed us earlier to exclude the presence of an inner giant planet with a mass larger than 2 MJup at a distance to the star of 0.05 AU, and 9 MJup at 1 AU (Galland et al. 2006). In this paper, we analyse more than 1000 Harps spectra recorded between 2003 and 2011 (described in Sect. 2) to search for additional, closer planets (Sect. 3) and to constrain even more the β Pic b mass (Sect. 4).
2. Data
We have now gathered 1098 Harps spectra from the ESO Archive or obtained them during our observing runs. These data span a period of time from October 2003 to February 2011. Exposure times of individual spectra are between typically 60 and 120 s, and typical signal-to-noise ratio (S/N) vary between 150 at 250 at 400 nm.
All data were reduced and analysed with our SAFIR software (Galland et al. 2005), which we developed to measure RVs of early-type stars to detect planets. These stars are usually rapid rotators and show much fewer lines than solar-type stars; they are then not adapted to mask-based technics. The method consists of correlating in the Fourier space each spectrum and a reference spectrum built by summing-up all available spectra for this star to measure its RV.
The RVs thus obtained are shown in Fig. 1. The most obvious feature are high frequency (HF) variations, already described in Coralie and Harps spectra (Galland et al. 2006) at 47.4 0.01 cycle/day (period of 30.4 min) and 39.05
0.01 cycle/day (period of 30.4 min) and 39.05 0.01 cycle/day (period of 36.9 min) and part of a complex pattern of pulsations described in Koen et al. (2003). Before 2008, each pointing (referred to as a visit) consisted generally of two consecutive exposures, and lasted typically 5−10 min, including overheads. Starting from March 2008, we adopted an observational strategy aimed at attenuating these HF variations. The duration of the visits was increased to ≃ 2 h, during which we recorded several 1−2 min consecutive exposures, to average out the HF variations as much as possible. Examples of the RVs obtained during these two-hour-visits are provided in Fig. 2. The period between March 2008 (JD 2454542) and February 2011 (JD 2455597, referred to as “set 1”; 810 spectra over ≃ 1000 days) defines a much more homogeneous set of data than the whole set of data. The impact of this strategy on the RV curve is illustrated in Fig. 3, where we show the data once averaged over 0.5 day and 1 day. The improvement is also clear when we consider the rms of the data (see Table 1), which is significantly decreased once the data have been averaged.
0.01 cycle/day (period of 36.9 min) and part of a complex pattern of pulsations described in Koen et al. (2003). Before 2008, each pointing (referred to as a visit) consisted generally of two consecutive exposures, and lasted typically 5−10 min, including overheads. Starting from March 2008, we adopted an observational strategy aimed at attenuating these HF variations. The duration of the visits was increased to ≃ 2 h, during which we recorded several 1−2 min consecutive exposures, to average out the HF variations as much as possible. Examples of the RVs obtained during these two-hour-visits are provided in Fig. 2. The period between March 2008 (JD 2454542) and February 2011 (JD 2455597, referred to as “set 1”; 810 spectra over ≃ 1000 days) defines a much more homogeneous set of data than the whole set of data. The impact of this strategy on the RV curve is illustrated in Fig. 3, where we show the data once averaged over 0.5 day and 1 day. The improvement is also clear when we consider the rms of the data (see Table 1), which is significantly decreased once the data have been averaged.
 |
Fig. 1 Top: RV data of β Pic between 2003 and 2011. Bottom: associated periodogram. |
 |
Fig. 2 Examples of high-frequency RV variations. |
 |
Fig. 3 RV data of β Pic between 2003 and 2011, averaged over 0.5 (red) and 1 (green) day. For comparison, the unaveraged data are also given in blue. Averaged data were vertically shifted for clarity. |
3. Search for short-period planets
3.1. rms-based detection limits
Our SAFIR software provides estimates of the detection limits. These limits are computed in the following way: for a given planet (mass, period), we computed the induced RVs at the same observing dates as the real observations and the rms of these simulated RVs, for several (typically 1000) values of orbital phase. The distribution of the obtained rms is Gaussian. The planet is detected if the rms of the observed RVs (which we call hereafter RV-jitter) is lower than the average of the rms distribution of the simulated RVs. The level of confidence (detection probability) is computed by comparing the standard deviation of the simulated distribution and the gap between the observed rms and the average value of the simulated distribution. We showed in Lagrange et al. (2009a) that when the signal is adequately sampled, the detection limit is close to the one that corresponds, for a given period, to a planet that would produce an RV amplitude equal to 3 × RV-jitter. This computation of the detection limits is very fast; however, it does not take into account the temporal structure of the stellar noise. Because the β Pic variations are mainly HF variations (Fig. 1), this method tends to overestimate the detection limits for periods longer than one day (unless, when the data sampling allows it, temporal averaging can be performed). We therefore developed additional alternative methods that take into account the frequency structure of the stellar noise. These approaches will be described in Sect. 3.2.
The detection limits (99.7% probability) as computed on the whole set of data are provided in Fig. 4. Typical values obtained for P ≃ 5, 10, 100, 500, and 1000 days are 7, 10, 16, 62, and 70 MJup, respectively (all computed masses given in this sub-section are rounded to the next integer or integer/2 mass). Because the system is seen edge-on, within a few degrees at most, the detection limits derived are not affected by the sin(i) indetermination (i = 90 degrees) if we assume that the planets orbit within the debris disk.
When averaging the RV over one day, we find detection limits of 4.5, 5.5, 13.5, 29 and 53 MJup (see also Fig. 4). Hence, averaging over one day significantly improves the detection limits. This is consistent with the measured RV rms being dominated by the HF variations (see Table 1).
rms (m/s) of all RV measurements between 2003 and 2011 and rms of the uncertainties (m/s) associated to the RV measurements.
 |
Fig. 4 rms-based detection limits for periods in the range 1−1000 days. Blue: all data, no average; red: all data, averaged over 1 day; green: set 1 data, averaged over 1 day. |
Finally, if we now consider set 1 data (no average), we obtain detection limits of 7, 8, and 16 MJup for periods of 5, 10, 100 days, comparable to the limits found using the whole set of data, when short periods are considered (limits for periods longer than typically 200 days are not meaningful given the comparatively shorter duration of set 1). This similarity arises because the rms associated are comparable (see Table 1). Finally, when averaging the data over one day, we find lower detection limits: 3, 4 and 6.5 MJup for the same periods. These values are comparitively better than those obtained after averaging the whole set of data, even though the time span is shorter and there are fewer data. This illustrates the usefullness of our adopted observing strategy, which naturally averages the stellar jitter.
3.2. Periodogram-based detection limits
Here we provide a brief description of the alternative approaches we developed to take into account the structure of the stellar noise, and the associated results. We refer to a forthcoming paper (Meunier et al., in prep.) for a detailed study of these approaches, and of their respective merits, depending on the available data.
3.2.1. Highest peak-based estimates
For a given planetary mass and a given period, we computed the RV induced by the planet at the same observing dates as for the real data. We added this planet-induced RV signal to the observed one. We then identified the five highest peaks in the planet periodogram2. The mean power of the five highest peaks outside the window defined in the footnote was then compared to the power of the planet peak. For each planet mass and period, we simulated 1000 realisations with different orbital phase between 0 and 2π. The planet was declared detectable if in 99.9 percent of the simulations, the planet peak was higher than the mean of the five highest peaks. Given the steps adopted, the calculated detection limit has an accuracy of 0.5 MJup (set by the step taken in the computations)3.
The detection limits obtained are shown in Fig. 5. Typical values obtained for P ≃ 5, 10, 100, and 500 days are 2.4, 3.8, 8.0, and 9.0 MJup, respectively (99.9% probability), hence in general significantly better than the rms-jitter-based ones when using un-averaged data; the difference is not so important when compared to the set 1, rms-jitter-based data averaged over 1 day. This is consistent with the reduced jitter obtained once averaging set 1 data. For a 1000 day-period, the detection limit is higher than 50 MJup.
 |
Fig. 5 Detection limits found with the peak-based approach (5 peaks, blue dashed/diamonds), and the correlation approach (red full line/stars). |
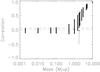 |
Fig. 6 Correlations for 100 realisations at each planet mass versus the planet mass (in MJup) for a period of 10 days. The solid line shows the mean for each mass. The dashed line indicates the threshold (determined from the maximum correlation at very low planet mass) and the arrow shows the detection limit. |
3.2.2. Correlation-based estimates
In a second approach, we compared the periodogram of the planet alone to the periodogram corresponding to the total radial velocities (i.e. the observed + planet-induced RV). We computed the correlation between those two periodograms again for 1000 realisations corresponding to the same planet mass, and the same planet period, and 1000 different orbital phases. In Fig. 6, the obtained correlation values are shown as a function of the planet mass for a given period (here 10 days). We see that for low planetary masses, the upper limits of the correlations for a given planet mass remain constant (i.e. do not depend on the planet mass). The same holds for the maximum and minimum values at each mass. At these low masses, the planet is certainly not detected and consequently the correlation values there correspond to a “no detection”-case. We defined the detection limit as the lowest planet mass for which the lowest correlation value is higher than the threshold determined by the maximum correlation at the very low mass of 0.002 MJup. Hence the detection limit is the lowest mass for which 99.9% of the realisations have a correlation above that threshold.
The detection limits obtained are shown in Fig. 5. Typical values obtained are 2.9, 1.8, 2.5, and 28.7 MJup for P ≃ 5, 10, 100, and 500 days, respectively (99.7% probability). Again they are better than the rms-based detection limits (no averaging), and comparable (and even slightly better) to those obtained by the highest peak-based estimates.
3.3. Planets with periods shorter than 1000 days: conclusions
From the above study, we conclude that there are no planets with masses larger than 2.5 MJup and periods shorter than 100 days around β Pic. This consequently excludes massive hot Jupiters around β Pic, whereas the star has certainly been surrounded by a massive protoplanetary disk and at least one outer planet has formed out of this disk. For planets with periods in the range 100−500 days, the detection limit is in the range 2.5−9 MJup. Finally, for planet periods in the 500−1000 day range, the detection limit is in the brown dwarf domain. These are the best detection limits found around this star but also around any early-type, rapidly rotating star, and these results clearly show the tremendous, yet sofar largely underestimated, possibilities of precise RV measurements of these stars. More RV data on β Pic will help constraining the detection limit at periods in the range 100−1000 days evenmore, and of course, also constraining the presence of planets at even larger periods. The present study shows that given the temporal structure of the stellar noise, two-hour-visits per year can in the future allow us to improve significantly the present detection limits for periods ≥ 200 day. Even more, planets with periods as long as 1000 days or longer could be tested. Coupled with other observing techniques such as interferometry (Absil et al. 2011), aperture masking (Lacour et al. 2011) and AO imaging (Lagrange et al. 2010), this would allow us to obtain for the first time a complete coverage of the mass-separation plane for giant planets and for a separation as small as a few tenths of AU to several AU.
3.4. Direct constraints on β Pic b mass
 |
Fig. 7 Plots of the statistical distribution of the simulated radial velocity slope using the model developed in Chauvin et al. (2012), for three different masses: 1.2 MJup (red line), 9 MJup (green line) and 24 MJup (blue line) and semi-major axis in the range 8.5 − 8.5 AU (left) and 11.5 − 12.5 AU (right). The vertical grey/black bar shows the measured slope value, which is also the 3σ upper limit of the slope. |
The present data cover only eight years, and therefore do not allow us to estimate detection limits for periods longer than typically 1000 days, i.e. farther than 2.5 AU. However, these data can be very useful to constrain the β Pic b mass because we have additional information on the planet position between 2003 and 2011. According to present knowledge, the planet semi-major axis is probably between 8 and 12 AU, with the most probable orbit at 9 AU. Its eccentricity is low (≤0.17) and its longitude of periastron (computed for instance from the line of sight) is only poorly constrained. Very importantly, in 2003, β Pic b was close to a quadrature, moving away from us to pass behind the star, and in 2011, close to the other quadrature, coming towards us (Lagrange et al. 2010; Chauvin et al. 2012). This is a very favourable situation because we can expect β Pic RV variations induced by β Pic b to be close to the maximum amplitude at both dates. Knowing the companion positions in 2003 and 2011, using the fact that its orbital plane is seen edge-on, the RV data provide us with direct constraints on its mass, conversely to imaging, which yields model-dependent (through brightness-mass relation) estimates.
To quantify an upper limit on β Pic b mass, we proceeded as follows:
-
First, we measured the slope of the observed RV; the value found is 3.1e-5 km s-1/day, with a fitting error of 1.4 e-6 km s-1/day. To estimate the actual error on the slope, we performed 1000 bootstraps of the data and measured the slopes obtained for each bootstrap. The average of the 1000 slopes is found to be 5.7 e-8 km s-1/day (i.e. close to 0, as expected), and the dispersion is σ = 1.02e-5 km s-1/day, a value unsurprisingly much higher than the error associated to the fitting process. We note that, as expected, this dispersion is identical to that obtained on 1000 realisations of random noise with an rms of 275 m/s with the same calendar. This shows that the measured slope is detected at a level of 3-sigma.
-
Then, we computed the detection limit for a planet with orbital characteristics similar to those of β Pic b. We assumed that the planet was at quadrature early in January 2003, the currently most probable date (Chauvin et al. 2012). We then considered a planet with a given semi-major axis (we assumed a circular orbit), and a mass between 0.1 and 25 MJup (steps of 0.1 MJup), and computed the RV induced by this planet on a 1.75 solar mass star at the dates of the actual data. We added random noise with an rms of 275 m/s (corresponding to the jitter measured on β Pic RV data), and performed a linear fit of these simulated RV, taking into account the error bars measured at each date on β Pic data, to estimate the slope of the variations together with associated error bars. An example of the RV variations is shown in Fig. 8 for a 30 MJup planet located on a 9 AU (P = 7400 d period): even though the sinusoidal shape of the variations is not obvious because of the high level of jitter, a significant positive drift is observed, that is not present in the β Pic RV (Fig. 1). For each planet mass, we repeated this operation for 1000 different noise realisations to fully take into account the impact of the jitter noise. The values of the slopes thus obtained are shown in Fig. 9 for a 9 AU orbit (in this figure, we took steps of 0.5 MJup instead of 0.1 MJup for clarity). We considered that a planet is detected if the slopes obtained are steeper than 3 × σ = 3 × 1.02e-5 km s-1/day in 99% of the realisations4.
-
We then explored the impact of the date of quadrature, assuming a range of −70; +130 days with respect to the most probable date, following Chauvin et al. (2012). The impact on the planet mass is found to be 0.5−2 MJup, for a semi-major axis in the range 8−12 AU.
Table 2 gives the upper limits for a semi-major axis of 8, 9, 10, 11, and 12 AU.
Constraints on β Pic b mass. See text.
To improve these upper limits, we performed a similar analysis using data averaged over 10 and 30 days. The upper limits found are not improved, which is because the jitter is still high (100 m/s or more), owing to the poor sampling of the data taken prior to 2008.
To test the robustness of these results and the impact of the planet eccentricity, we considered the statistical orbit distribution obtained from our MCMC analysis in Chauvin et al. (2012). For each model in this distribution, we computed the expected radial velocities at the observing dates, assuming a given planetary mass and eccentricities up to 0.17 following Chauvin et al. (2012). We then computed the statistical distribution of the slopes after fitting the RV curve with a linear fit. The slope depends on the assumed mass of β Pic b of course. This allows us a compatible mass range, assuming that the measured slope must fall within the computed distribution; the slopes are then compared to the 3σ limit. The results agree with those deduced from the previous analysis. This is illustrated in Fig. 7 where the slope distribution is plotted for three masses (1.2, 9 and 24 MJup) and for semi-major axis in the ranges 8.5−9.5 AU (left) and 11.5−12.5 AU (right). In the left figure, which corresponds to a ≃9 AU, the distribution of slopes for a 24 MJup mass is noticeably shifted compared to the 3σ limit, whereas the one corresponding to a 9 MJup is a better match. For a value of ≃12 AU, the slope distribution with a 24 MJup mass is closer to the 3σ limit.
Finally, we address the question whether these data also give constraints on the minimum mass of the planet. Assuming that the minimum slope is indeed equal to 3e-5 km s-1/day, we can, as an exploratory exercice, derive a tentative lower limit to the mass of the planet if this is responsible for the slopes. Proceeding with a similar reasoning as above, and exploring again different dates of quadratures, we find lower masses in the range 1−2 MJup for a semi-major axis between 8 and 12 AU. These conclusions are also compatible with the second approach described above, because distributions for e.g. 1.2 MJup are below the measured slope (see Fig. 7). The present values should be considered only as an illustration of the potential of the present approach however and not as definite results because the slope is so close to the limit; more data with optimized temporal sampling are necessary to derive more reliable estimates of the β Pic minimum mass.
 |
Fig. 8 RV induced by a 30 MJup planet with a 7400-day-period (9 AU sep.) located at the position of β Pic b in 2003, when using the actual data sampling: grey crosses: without jitter noise, black squares: with a noise of 275 m/s. The grey line indicates the slope derived from the linear fitting of RV variations, and the black line indicates the slope of the β Pic real data deduced from linear fitting. |
 |
Fig. 9 Slopes of the RV induced by a planet with different masses with a 7400-day-period when using the actual data sampling (steps of 0.5 MJup); the horizontal lines indicate the 3-sigma upper level derived from β Pic data. |
3.5. Conclusion on the β Pic b mass
The present data allowed us to directly constrain the β Pic b mass to be less than 10, 12, 15.5, 20.0, and 25 MJup if orbiting at 8, 9, 10, 11, and 12 AU, respectively. For the most probable
orbit, 9 AU, the upper limit is in the planetary mass regime, which means that the detected source is definitively not a more massive object (brown dwarf). This is the first time an imaged extra-solar planet mass is directly constrained, and does not depend only on model-dependant brightness-mass relationships. The β Pic b upper mass falls nicely in the range predicted by the brightness-mass relations provided by the hot-start models. In contrast, current cold-start models fail to explain a giant planet with the observed brightnesses at the Ks (Bonnefoy et al. 2011), L′ (Lagrange et al. 2010) and M (Quanz et al. 2010) bands. In the future, especially in the next years, new data with optimized sampling should allow us to improve our estimate of the β Pic b mass. The present combination of RV and high contrast data on exoplanets is a pioniering one; it will be more generalized in the future, when more young planets will be imaged at short separations from their stars, which will be a precious opportunity to test brightness-mass predictions.
In practice, the simulated periodogram is affected by the injection of the planet not only at the planet period but also close to the planet period: several peaks, induced by the planet, are present close to the planet period. Therefore, we have to exclude these peaks; to do so, we computed the periodogram corresponding to a planet with period = Ppla for the same observing dates, and computed the associated median m and standard deviation s (Meunier et al., in prep.). We then identified the peaks that are above a threshold of m + 4s and located within  10% Ppla from Ppla. We note Pf the period of the peak that is the farthest from Ppla. The window size is then defined by min (10% Ppla; Pf).
10% Ppla from Ppla. We note Pf the period of the peak that is the farthest from Ppla. The window size is then defined by min (10% Ppla; Pf).
Acknowledgments
We acknowledge financial support from the French Programme National de Planétologie (PNP, INSU). We also acknowledge support from the French National Research Agency (ANR) through project grant ANR10-BLANC0504-01. We also thank Julien Milli for fruitfull discussions and the referee for his/her comments.
References
- Absil, O., Le Bouquin, J.-B., Berger, J.-P., et al. 2011, A&A, 535, A68 [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Lagrange, A. M., Boccaletti, A., et al. 2011, A&A, 528, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2005a, A&A, 438, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005b, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A. M., Beust, H., et al. 2012, A&A, in press, DOI: 10.1051/0004-6361/201118346 [Google Scholar]
- Crifo, F., Vidal-Madjar, A., Lallement, R., Ferlet, R., & Gerbaldi, M. 1997, A&A, 320, L29 [NASA ADS] [Google Scholar]
- Fortney, J. J., Marley, M. S., Saumon, D., & Lodders, K. 2008, ApJ, 683, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Freistetter, F., Krivov, A. V., & Loehene, T. 2007, A&A, 466, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2005, A&A, 443, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2006, A&A, 452, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., Balona, L. A., Khadaroo, K., et al. 2003, MNRAS, 344, 1250 [NASA ADS] [CrossRef] [Google Scholar]
- Lacour, S., Tuthill, P., Amico, P., et al. 2011, A&A, 532, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lafrenière, D., Jayawardhana, R., & van Kerkwijk, M. H. 2010, ApJ, 719, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A. M., Desort, M., Galland, F., et al. 2009a, A&A, 495, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A. M., Gratadour, D., Chauvin, G., et al. 2009b, A&A, 493, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A. M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., MacIntosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Okamoto, Y. K., Kataza, H., Honda, M., et al. 2008, Nature, 431, 660 [Google Scholar]
- Telesco, C. M., Fisher, R. S., Wyatt, M. C., et al. 2005, Nature, 433, 133 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Quanz, S. P., Meyer, M. R., Kenworthy, M. A., et al. 2010, A&A, ApJ, 722, L49 [Google Scholar]
- Wahhaj, Z., Koerner, D. W., Ressler, M. E., et al. 2003, ApJ, 584, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Song, I., Bessel, M. S., & Webb, R. A. 2001, ApJ, 562, L87 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
rms (m/s) of all RV measurements between 2003 and 2011 and rms of the uncertainties (m/s) associated to the RV measurements.
All Figures
 |
Fig. 1 Top: RV data of β Pic between 2003 and 2011. Bottom: associated periodogram. |
| In the text | |
 |
Fig. 2 Examples of high-frequency RV variations. |
| In the text | |
 |
Fig. 3 RV data of β Pic between 2003 and 2011, averaged over 0.5 (red) and 1 (green) day. For comparison, the unaveraged data are also given in blue. Averaged data were vertically shifted for clarity. |
| In the text | |
 |
Fig. 4 rms-based detection limits for periods in the range 1−1000 days. Blue: all data, no average; red: all data, averaged over 1 day; green: set 1 data, averaged over 1 day. |
| In the text | |
 |
Fig. 5 Detection limits found with the peak-based approach (5 peaks, blue dashed/diamonds), and the correlation approach (red full line/stars). |
| In the text | |
 |
Fig. 6 Correlations for 100 realisations at each planet mass versus the planet mass (in MJup) for a period of 10 days. The solid line shows the mean for each mass. The dashed line indicates the threshold (determined from the maximum correlation at very low planet mass) and the arrow shows the detection limit. |
| In the text | |
 |
Fig. 7 Plots of the statistical distribution of the simulated radial velocity slope using the model developed in Chauvin et al. (2012), for three different masses: 1.2 MJup (red line), 9 MJup (green line) and 24 MJup (blue line) and semi-major axis in the range 8.5 − 8.5 AU (left) and 11.5 − 12.5 AU (right). The vertical grey/black bar shows the measured slope value, which is also the 3σ upper limit of the slope. |
| In the text | |
 |
Fig. 8 RV induced by a 30 MJup planet with a 7400-day-period (9 AU sep.) located at the position of β Pic b in 2003, when using the actual data sampling: grey crosses: without jitter noise, black squares: with a noise of 275 m/s. The grey line indicates the slope derived from the linear fitting of RV variations, and the black line indicates the slope of the β Pic real data deduced from linear fitting. |
| In the text | |
 |
Fig. 9 Slopes of the RV induced by a planet with different masses with a 7400-day-period when using the actual data sampling (steps of 0.5 MJup); the horizontal lines indicate the 3-sigma upper level derived from β Pic data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


