| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201016046 | |
| Published online | 04 June 2012 | |
Really focused stellar winds in X-ray binaries
1 Astronomical Institute, Academy of Sciences, Boční II 1401, 14131 Praha 4, Czech Republic
e-mail: had@sunstel.asu.cas.cz
2 Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
e-mail: cechura@astro.cas.cz
Received: 2 November 2010
Accepted: 23 March 2012
Aims. We investigate the anisotropy of stellar winds in binaries to improve the models of accretion in high-mass X-ray binaries.
Methods. We model numerically the stellar wind from a supergiant component of a binary in radial and three-dimensional radiation hydrodynamic approximation taking into account the Roche potential, Coriolis force, and radiative pressure in the continuum and spectral lines.
Results. The Coriolis force influences substantially the mass loss and thus also the accretion rate. The focusing of the stellar wind by the gravitational field of the compact companion leads to the formation of a gaseous tail behind the companion.
Key words: accretion, accretion disks / hydrodynamics / methods: numerical / stars: winds, outflows / X-rays: binaries
© ESO, 2012
1. Introduction
Roche-lobe overflow and an isotropic radial stellar wind have traditionally been considered as two competing scenarios to explain the mass loss from a companion star that can feed an accretion disc around a compact object, particularly in interacting binaries and X-ray binaries – cf., e.g. Shakura & Sunyaev (1973). One of us thus developed a model of an evaporative radial stellar wind modulated by the effective Roche potential to overcome this dichotomy (Hadrava 1980). This model revealed that there is a smooth transition between the outflow from a narrow stream around the inner Lagrangian point L1 for small ratios of thermal to escape velocities, to an almost isotropic wind for high values of this ratio. The distribution of mass-loss rates on the surface of the companion is modulated depending also on the mass ratio of the system. In some cases, the mass loss in the vicinity of the L2 point exceeds that around L1. Kříž (1980, priv. comm.) raised an objection to this model based on the argument that it neglects the Coriolis force and thus artificially enhances the outflow by an unrealistic centrifugal force. Because of this criticism, the model was not published until Hadrava (1987, cf. the Appendix). In the meantime, a similar model of a radiatively driven wind was published by Friend & Castor (1982). This model of a so-called focused stellar wind is now widely used to explain the behaviour of X-ray binaries. However, the above-mentioned objection is also valid for this model and the Coriolis force should be taken into account to improve the model of stellar wind anisotropy. This may significantly influence the interplay between the mass loss from the donor star, its accretion by the compact component, and the consequent ionization of the donor’s wind and atmosphere illuminated by the X-ray radiation – cf. Gies et al. (2008).
Here we present our first preliminary results of our revised calculations of the anisotropic stellar wind in binaries achieved by Čechura (2010). In Sect. 2, we summarize our calculations of the radial wind based on the Friend-Castor approximation. To reveal the role of the Coriolis force, we then numerically modelled on a three-dimensional (3D) grid the radiation hydrodynamics of the stellar wind taking into account the same expressions for the radiative pressure in the lines – cf. Sect. 3. These calculations showed the formation of a gaseous tail behind the compact companion, which resembles Bondi-Hoyle-Lyttleton accretion (Hoyle & Lyttleton 1939) – cf. Sect. 4. As discussed in Sect. 5, this feature actually deserves to be denoted as a gravitational focusing of the wind rather than the slight tidal modulation of the wind’s root.
2. Radial stellar wind
Our present model of anisotropic radial stellar wind is based on a modified version of the line-driven wind theory of Castor, Abbott, and Klein (Castor et al. 1975, CAK hereafter), where the wind material is predominantly accelerated by the line absorption of the star’s radiation field. In this work, the authors solved the equation of radiative transfer in the stellar wind under the assumption of the Sobolev approximation (Castor 1974) and found that the line force could be approximated by a power law in optical depth 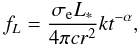 (1)where t is the optical depth parameter defined by
(1)where t is the optical depth parameter defined by 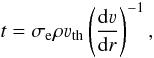 (2)and k and α are parameters of the CAK model that depend on the effective temperature of the star. Physically speaking, k is a measure of the number of driving lines, and α is a measure of the relative distribution of optically thick to optically thin lines. We chose the values of α = 0.7 and k = 1/30 in our model. These values should provide a reasonable approximation of the line force corresponding to a star with an effective temperature of around 30 000 K (cf. CAK). The quantity σe is the electron scattering coefficient, L∗ is the luminosity of the primary star, ρ is the density of the wind material, and νth is the thermal velocity of the ions in the wind.
(2)and k and α are parameters of the CAK model that depend on the effective temperature of the star. Physically speaking, k is a measure of the number of driving lines, and α is a measure of the relative distribution of optically thick to optically thin lines. We chose the values of α = 0.7 and k = 1/30 in our model. These values should provide a reasonable approximation of the line force corresponding to a star with an effective temperature of around 30 000 K (cf. CAK). The quantity σe is the electron scattering coefficient, L∗ is the luminosity of the primary star, ρ is the density of the wind material, and νth is the thermal velocity of the ions in the wind.
In the case of an isothermal radial outflow, the equation of momentum conservation is given by 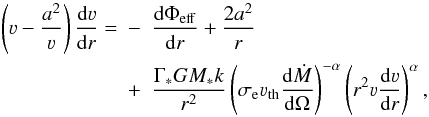 (3)where a = (dPg/dρ)1/2 is the isothermal sound speed, M∗ is the mass of the primary star, and Γ∗ is the ratio of the primary star luminosity to the Eddington luminosity
(3)where a = (dPg/dρ)1/2 is the isothermal sound speed, M∗ is the mass of the primary star, and Γ∗ is the ratio of the primary star luminosity to the Eddington luminosity 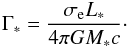 (4)To include the effects of the compact companion on the wind dynamics, we have replaced the spherically symmetric gravitational potential of the mass-losing star by the Roche potential Φeff, i.e. both the tidal force and the centrifugal force due to a rotation synchronized with the circular orbital motion of the companion are taken into account. In a spherical coordinate system, a new effective potential is given by
(4)To include the effects of the compact companion on the wind dynamics, we have replaced the spherically symmetric gravitational potential of the mass-losing star by the Roche potential Φeff, i.e. both the tidal force and the centrifugal force due to a rotation synchronized with the circular orbital motion of the companion are taken into account. In a spherical coordinate system, a new effective potential is given by ![\begin{eqnarray} \Phi_{\rm eff}\left(r,\phi,\theta\right) = &-&\frac{GM_\ast}{D}\left\{\frac{D\left(1-\Gamma_\ast\right)}{r}\right. \nonumber \\ &+&\frac{q\left(1-\Gamma_{x}\right)}{\left[1-2\left(r/D\right)\lambda+\left(r/D\right)^2\right]^{1/2}} \nonumber \\ &-&\left.q\left(\frac{r}{D}\right)\lambda + \frac{1}{2}\left(1+q\right)\left(\frac{r}{D}\right)^2\left(1-\mu^2\right)\right\}, \label{MOD5} \end{eqnarray}](/articles/aa/full_html/2012/06/aa16046-10/aa16046-10-eq7.png) (5)where the variables λ and μ are defined by
(5)where the variables λ and μ are defined by 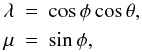 (6)in terms of the latitude φ and the longitude θ on the surface of the mass-losing star, D is the separation of the components of the binary, q is the ratio Mx/M∗, where Mx is the mass of the compact companion, and φ = 0 and θ = 0 determines the line-of-centres of the two stars in the orbital plane.
(6)in terms of the latitude φ and the longitude θ on the surface of the mass-losing star, D is the separation of the components of the binary, q is the ratio Mx/M∗, where Mx is the mass of the compact companion, and φ = 0 and θ = 0 determines the line-of-centres of the two stars in the orbital plane.
The radiation pressure in the continuum caused by the Thomson scattering of the photons emitted by both component stars on free electrons is also involved by means of the Eddington factors Γ∗ and Γx, which are chosen as free parameters for both stars (for which we use the values 0.26 and 0.31, respectively).
These forces cause a shift in the critical point of the outflow that varies across the surface of the mass-losing star and they distort the spherical symmetry of the wind. The mass-loss rate becomes a strong function of the size of the primary component relative to its critical potential lobe. In this radial approximation, we still ignore the tangential forces caused by the pressure gradients between the neighbouring flux-tubes, as well as the Coriolis force, which should be taken into account when computing in the non-inertial reference frame co-rotating with both stars. The streamlines of the wind are strictly radial and the material is confined within a selected cone, hence the mass continuity equation becomes 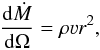 (7)where dṀ/dΩ is the mass-loss rate per unit solid angle. The outflow of the wind is artificially reinforced by an unrealistic centrifugal force. We expect this approximation to have little influence on the deep highly subsonic layers of the wind, although it must lead to a completely unrealistic model in the supersonic circumstellar region.
(7)where dṀ/dΩ is the mass-loss rate per unit solid angle. The outflow of the wind is artificially reinforced by an unrealistic centrifugal force. We expect this approximation to have little influence on the deep highly subsonic layers of the wind, although it must lead to a completely unrealistic model in the supersonic circumstellar region.
 |
Fig. 1 Distribution of stellar wind intensity on the surface of the optical component of Cyg X-1 in the radial approximation (CAK model – the uppermost panel), the radial approximation of the radiation-hydrodynamic model in 3D Cartesian grid (the second panel), the non-radial radiation-hydrodynamic solution without the Coriolis force (the third panel) and the full radiation-hydrodynamic solution with the Coriolis force included (the bottom panel). The direction to the L1-point and the companion has the sidereographic longitude 0°, the longitude 180° is directed towards the L2-point. The number in the lower right corner of each panel gives the overall outflow of the material from the supergiant in M⊙ yr-1. |
The results of this radial numerical model are presented in the upper panel of Fig. 1, where we display the directional dependence of the stellar wind intensity (i.e. the mass-loss rate per unit solid angle). We have chosen values of these parameters that are appropriate for the high-mass X-ray binary system Cygnus X-1 and its primary O star supergiant HDE 226868. The orbital period is 5.6 days and the masses of the supergiant and the black hole have been chosen to be equal to 24. and 8.7 M⊙, resp., within the still wide region of the observational limits 23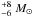 and 11
and 11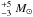 found by Caballero-Nieves et al. (2009). These values result in a distance of 42.4 R⊙ between the component centres. The critical Roche lobe of this system has a mean radius of 20 R⊙: the L1-point is at a distance of 25.6 R⊙, while the intersection of the critical equipotential with the rotational axis is 18.7 R⊙ from the supergiant centre. We have set the surface of the donor star to a mean radius 18 R⊙ (i.e. at the equipotential of size 19.9 R⊙ towards the companion and 17.3 R⊙ towards the pole). The gravity acceleration g varies across this equipotential from 1.5 to 3.1 × 103 cm s-2 towards the L1 and the pole, resp., i.e. the mean value log g = 3.3 is close to the observational limit 3.00 ± 0.25 found by Caballero-Nieves et al. (2009). Similarly, the temperature 30.0 kK, which we have taken from the values for which CAK gives the parameters k and α in Eq. (1), roughly corresponds to the value 28.0 ± 2.5 kK determined in Caballero-Nieves et al. (2009).
found by Caballero-Nieves et al. (2009). These values result in a distance of 42.4 R⊙ between the component centres. The critical Roche lobe of this system has a mean radius of 20 R⊙: the L1-point is at a distance of 25.6 R⊙, while the intersection of the critical equipotential with the rotational axis is 18.7 R⊙ from the supergiant centre. We have set the surface of the donor star to a mean radius 18 R⊙ (i.e. at the equipotential of size 19.9 R⊙ towards the companion and 17.3 R⊙ towards the pole). The gravity acceleration g varies across this equipotential from 1.5 to 3.1 × 103 cm s-2 towards the L1 and the pole, resp., i.e. the mean value log g = 3.3 is close to the observational limit 3.00 ± 0.25 found by Caballero-Nieves et al. (2009). Similarly, the temperature 30.0 kK, which we have taken from the values for which CAK gives the parameters k and α in Eq. (1), roughly corresponds to the value 28.0 ± 2.5 kK determined in Caballero-Nieves et al. (2009).
The proximity of the black-hole companion and the assumed synchronous rotation of the mass-losing supergiant obviously disturb the spherical symmetry of the wind and the most intensive outflow of the material is concentrated in the equatorial plane. The highest intensity can be found at a point directly facing the black hole. However, more interestingly, another significant local maximum is situated on the completely opposite side of the star. According to our model, the total mass-loss rate Ṁ of HDE 226868 is close to 2.23 × 10-6 M⊙ yr-1. The total outflows from the facing and opposite hemispheres are almost comparable and their ratio depends on the system parameters. These results qualitatively agree with the earlier works of Friend & Castor (1982) and Hadrava (1987). It should, however, be noted that there is a significant quantitative difference between the tidal modulation of the evaporative and line-driven winds. The typical thermal velocity is approximately 22 km s-1 for the temperature 30 kK, which, compared to the critical rotational velocity 500 km s-1, gives a ratio of the thermal to the binding potential energy of the order of 10-3. The Parker’s evaporative wind is thus highly concentrated in the vicinity of the L1-point (cf. the Appendix A.2, Fig. A.4). However, if the CAK-radiative drag enhances the wind and the radiation of the star is assumed to be isotropic, the tidal modulation of the wind intensity is partly smeared out. The distribution of mass-loss rate is then sensitive to the choice of the surface level.
3. Radiation hydrodynamic model of the wind
3.1. Equations of motion
To deal with the previously mentioned objection to the radial approximation, we also created a numerical model of the stellar wind based on the radiation hydrodynamics calculated in a 3D Eulerian coordinate grid. In this case, a new equation of motion is given by 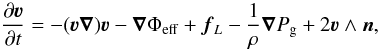 (8)which has to be solved together with the continuity equation
(8)which has to be solved together with the continuity equation 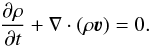 (9)The constant orbital angular velocity n is given by the third Kepler’s law (n2D3 = (1 + q)GM∗). Our present model uses the purely Newtonian approach to handle the gravity and the dynamics. We can naturally expect that relativistic effects are important in the close vicinity of the compact companion in the X-ray binary, which is either a neutron star or a black hole. However, the grid we use for our numerical solution is sparse in order to achieve a reasonable computational time. A typical dimension of one cell corresponds to several thousands of Schwarzschield radii and we are unable to distinguish structures that are smaller than this typical length. It is therefore reasonable to assume that at such a distance, relativistic effects will be negligible.
(9)The constant orbital angular velocity n is given by the third Kepler’s law (n2D3 = (1 + q)GM∗). Our present model uses the purely Newtonian approach to handle the gravity and the dynamics. We can naturally expect that relativistic effects are important in the close vicinity of the compact companion in the X-ray binary, which is either a neutron star or a black hole. However, the grid we use for our numerical solution is sparse in order to achieve a reasonable computational time. A typical dimension of one cell corresponds to several thousands of Schwarzschield radii and we are unable to distinguish structures that are smaller than this typical length. It is therefore reasonable to assume that at such a distance, relativistic effects will be negligible.
We have assumed that the radiative pressure fL in the lines, which is a main source of the repulsive force, is radial and that its value is also given by Eq. (1). The gravity and continuum radiation pressure of both components of the binary have also been included in terms of the effective potential Φeff given by Eq. (5). In addition, new effects are taken into account, such as the tangential components of the gas-pressure gradient and the Coriolis force. The gas pressure Pg was taken from the equation of state of an ideal gas whose temperature is fixed to the effective temperature of the star in the present version of our code. This is a simplifying approximation that we will improve in future versions of the model, although it may not be too inaccurate in the case of a rarefied gas in thermodynamic equilibrium with the radiation of both stars. To develop a self-consistent radiation-hydrodynamical model, the radiative transfer should also be solved, whereas in our present model the radiation field is prescribed. In the subsequent paragraph, we briefly discuss the possible consequences of this simplification.
3.2. The radiation field
In his referee report to this paper Gayley raised additional objections to the Friend-Castor approximation used to describe the radial line-driven wind in binaries. On the basis of their investigations of the stellar winds of early-type fast rotators and the problem of the (non-)existence of wind-compressed disks (Owocki et al. 1996, 1998; Gayley & Owocki 2000) Gayley suggested that both the non-radial components of the radiative force and the anizotropy of the supergiant radiation due to the gravity darkening may substantialy influence the structure of the wind in binaries. To verify whether this suggestion is indeed valid, we would need to create a sophisticated model that exceeds the possibilities of our current numerical model and intentions of this work. We thus give here only our preliminary estimates of the possible influence of these effects.
The non-radial components of the radiative force in supersonic axisymmetric flows were studied by Grinin (1978). In a differentially rotating medium such as a Keplerian disk, they are due to the asymmetry of the velocity gradients in directions skewed forward and backward with respect to the radial direction and the consequent difference in the depletion or enhancement of the line radiation intensities. As for either the Poynting-Robertson effect (Robertson 1937) or the reflection of radiation by rotating disks (Hadrava et al. 1997), this radiative torque can transfer the energy and angular momentum from the medium to the radiation and stimulate a fall down of the flow. Gayley & Owocki (2000) found that this effect may decrease the angular-momentum loss of the fast rotators by the wind to about 30% or 40%.
However, in the case of the synchronously rotating component of a binary with a non-negligible mass of the companion, the rotation is safely subcritical (even if the component fills its Roche lobe, which is restricted by the tides). In the particular case of our present model, the rotational velocity of the supergiant is approximately 160 km s-1, while the critical velocity is 500 km s-1. Consequently, the influence of the non-radial components of line-driven radiative force is also smaller than in the case of critically rotating stars.
While these non-radial components of the radiative force may to some extent influence the motion of the circumstellar matter in the supersonic region, where a non-local coupling can also take place, their role is even more questionable in the subcritical region where the surface distribution of the wind intensity is determined. In this quite narrow slab of the atmosphere, the tangential component of the wind velocity increases only slowly due to the Coriolis force, hence the optical depths in the skewed directions given by Eq. (2) cannot differ significantly.
A more substantial objection to the Friend-Castor model is the possible role of gravity darkening. According to von Zeipel’s theorem (von Zeipel 1924), the distribution of the radiative flux F and the effective temperature Teff across the tidally or rotationally distorted surface of a star should be given by the local gravity acceleration g as 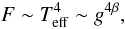 (10)where β ≡ 0.25 in the standard von Zeipel’s formula. Because the radiative force fL given by Eq. (1) is proportional to the flux, it may enhance the wind more in the polar region of the star, where g reaches its highest value, than in the equator and especially in the line joining the component stars, where it has its smallest value. For the values of parameters chosen in our calculations, g is higher by 23% at the poles and lower by 15% and 40% in the directions towards the L2 and L1, resp., than its value in the perpendicular direction. This effect is thus the opposite of the direct modulation of the wind by the effective potential. In the region, where the distance from the star is comparable to its radius, this effect is additionally enhanced by the ellipticity of the star.
(10)where β ≡ 0.25 in the standard von Zeipel’s formula. Because the radiative force fL given by Eq. (1) is proportional to the flux, it may enhance the wind more in the polar region of the star, where g reaches its highest value, than in the equator and especially in the line joining the component stars, where it has its smallest value. For the values of parameters chosen in our calculations, g is higher by 23% at the poles and lower by 15% and 40% in the directions towards the L2 and L1, resp., than its value in the perpendicular direction. This effect is thus the opposite of the direct modulation of the wind by the effective potential. In the region, where the distance from the star is comparable to its radius, this effect is additionally enhanced by the ellipticity of the star.
To determine the outcome of these mutually competitive effects, one would need to develop a reliable model of the gravity darkening. The above-mentioned original von Zeipel’s formula is widely used owing to its simplicity, but it is neither physically self-consistent nor confirmed by observations, which mostly indicate that the actual gravity darkening is smaller, as expected from a more detailed theoretical treatment. Lucy (1967) reinvestigated the problem of gravity darkening asuming a convective instead of a radiative equilibrium arriving to a generalized formula in Eq. (10) in which the exponent β = 0.08. The classical von Zeipel’s formula is based on the solution of radiative transfer in the diffusion approximation only, assuming hydrostatic equilibrium and hence the homogeneity of the atmosphere on equipotential surfaces (cf. Appendix A.1). The simplified treatment of radiative transfer neglects both the dilution of the radiative flux in the parts of sub-surface layers with higher curvature, which enhances the gravity darkening, and the tangential diffusion of the radiation, which decreases its effect, (cf. Hadrava 1992). However, even more importantly, the resulting gravity darkening violates the homogeneity and the hydrostatic equilibrium, which are the starting assumptions of von Zeipel’s theorem, and gives rise to meridional circulations. The Coriolis force acting on these flows may then also break the mirror symmetry of the advancing and recessing hemispheres of the star and hence the simple picture of the flux given by the local value of g (cf. Gayley et al. 2007). Our detailed solution of radiative transfer in plane-parallel grey atmosphere in exact hydrostatic equilibrium yields β ≃ 0.13 for small variations in g and a more complex dependence F = F(g) for its larger variations (cf. Hadrava 1987, and Appendix A.1, particularly Fig. A.2). Yet another value β ≃ 0.19 was obtained by Claret (2012), who also gives references to several observational results confirming that the actual gravity darkening parameter β has a scatter and is usually smaller than the von Zeipel’s value of 0.25.
 |
Fig. 2 Distribution of the stellar wind intensity in dependence on gravity darkening. The radial approximation for the same parameters as in Fig. 1 is calculated for radiation modulated according to Eq. (10) and values of the parameter β from the top to the bottom of 0.0, 0.125, 0.1875, and 0.25. |
On the referee’s suggestion, we recalculated the outflow in the radial approximation described in Sect. 2, assuming the gravity darkening given by Eq. (10) with several values of the parameter β (cf. Fig. 2). For the medium value β = 0.125, the tidally enhanced outflows in the directions of the L1- and L2-points can really be diminished due to the decrease of the radiative drag. For even higher values of β, our calculations show a formation of local minima of the wind intensity in these directions, although the local minima caused by the potential barrier in polar regions persist and the maximum of the wind intensity appears at moderate latitudes. This is, however, an upper estimate based on a model with several inconsistencies.
Because the starting assumption of hydrostatic equilibrium is violated from the very beginning in the case of strong stellar winds, we have not included the von Zeipel’s formula for gravity darkening in our 3D models. To achieve a really self-consistent radiative-hydrodynamic solution, the 3D radiative transfer should be included in the procedure, which would be computationally much more demanding even in the simpler case of axially symmetric rotating stars. In the current approximation, we include in the hydrodynamic modelling the radiative forces from the given purely radial and isotropic radiation of the components and postpone the treatment of radiative transfer in the circumstellar matter to a future study.
3.3. Numerical model
The results of the previously computed radial model, i.e. the spatial distribution of density ρ and the Cartesian components of the velocity vector ν, were used as initial conditions for the corresponding quantities in the new 3D hydrodynamic simulation of the time evolution of the wind and circumstellar matter. They were also used to define the inner boundary conditions for the gas outflow in the photosphere of the donor star, which is nearly in hydrostatic equilibrium and the effects of the additional terms could thus be neglected there.
An equidistant Cartesian coordinate grid was chosen in the co-rotating reference frame. The values of ρ and ν found from the radial-wind model were interpolated onto this grid and kept fixed inside a Roche equipotential chosen to correspond to the surface of the donor star in order to define the inflow boundary condition for the Eulerian radiation-hydrodynamic solution. The outer boundary condition at the edge of the grid is a simple outflow boundary condition with derivatives of all variables set equal to 0. The time derivatives of the density and components of the velocity vector were calculated from the equations of the mass and momentum conservation, resp. The small corrections corresponding to a sufficiently short time-step Δt were then added to the initial values. Repeating this process, the initial stationary solution of the radial model adapted to satisfy the conditions of the new model. A new stationary solution was achieved after a relatively quick convergence of all quantities. The sum of time steps typically corresponds to a small number of orbital periods of the system (cf. Fig. 3). This is obviously a consequence of the wind velocity at the critical point given by the sound speed a being comparable to the orbital velocity nD in our investigated cases when the mass loss by stellar winds is substantial. The convergence could be much slower in the sub-sonic layers of the wind, if the inner boundary conditions were chosen on a deep equipotential where the density is high and outflow velocity low. However, to avoid the steep density gradients in these layers, which could not be represented with sufficient accuracy in the limited space-resolution of the grid, we had to choose this layer closely below the surface of critical points. The convergence of the numerical model was thus accelerated by the numerical viscosity within a few grid cells around the inner boundary surface.
A value of time step Δt, which is constant for the whole grid, was subjected to the Courant-Friedrichs-Lewy condition, specifically 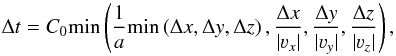 (11)where Δx, Δy, and Δz are the distances between the neighbouring grid nodes in the x, y, and z-directions, resp. The Courant number C0 is a safety factor, which in this case is taken to be 0.5.
(11)where Δx, Δy, and Δz are the distances between the neighbouring grid nodes in the x, y, and z-directions, resp. The Courant number C0 is a safety factor, which in this case is taken to be 0.5.
 |
Fig. 3 Evolution of the density distribution in the equatorial plane computed with the radiation hydrodynamic model during the convergence process towards a new stationary solution. The uppermost left panel represents the state close to the conditions set up by the radial model. The bottom right panel captures the nearly steady-state solution corresponding to the newly included forces – the Coriolis force and the tangential forces caused by the pressure gradients. The white index in the upper right corner of each panel indicates an evolutionary time expressed in the units of the orbital periods. The red cross and asterisk show the position of the black hole and the centre of the supergiant, resp. |
We chose a combination of the forward-time central-space scheme (FTCS hereafter) and the Lax-Friedrichs numerical integration scheme in our computations. This combination allowed us to exploit all of the advantages of both schemes, in addition to suppressing most of their drawbacks. The FTCS is a very simple and computationally fast integration scheme, which is unfortunately always unstable. To overcome this instability, we introduced a correctional mechanism to prevent random numerical peaks. On the other hand, the Lax-Friedrichs scheme is stable in all cases when the Courant stability condition is satisfied and therefore it serves as a stabilizing component in our model. However, the Lax-Friedrichs scheme is characterized by a high numerical viscosity, which results in a high level of diffusion. For a large number of integration steps, this feature would lead to smearing of all steep gradients, even those that are physically interesting. This is why we applied the Lax-Friedrichs scheme as infrequently as possible, specifically only once in every 25 integration steps. If we had included the Lax-Friedrichs scheme with a lower frequency, the numerical simulation would have become unstable in the long term.
The additional averaging of the density and the velocity in the outer boundary of the integration area was added to prevent oscillations and numerical instabilities within the stationary solution. This averaging is responsible for less accurate results in this area. Nevertheless, the density is very low at the border of the integration area and therefore should not have a measurable impact on the solution in the inner regions.
The evolution of the density distribution in the equatorial plane during the convergence process towards a new stationary solution is captured in Fig. 3. The initial state corresponds to the conditions set up by the radial approximation. The integration process was stopped when a nearly steady-state solution corresponding to the newly included forces – the Coriolis force and the tangential forces caused by the pressure gradients – was reached. The white index in the upper right corner of each panel indicates an evolutionary time expressed in the units of the orbital periods. The red cross and the asterisk show the position of the black hole and the centre of the supergiant, resp. The patch at the centre of each panel represents the supergiant component of the binary. More specifically, it is an intersection of the volume defined by an equipotential surface and the equatorial plane. The convergence to a new stationary solution is relatively quick: at the time index equal to 3.0, the changes of studied quantities in one time step are less than 10-4 of their initial values. As indicated in Fig. 3, the originally radial distribution of density becomes strongly influenced by the presence of the compact companion. We can see a gradual formation of a density tail behind the compact component, which is diverted by the Coriolis force. It is also apparent that the density increases with time throughout the entire modeled space. The reason for this increase is that we reduced the centrifugal force by allowing the wind to be diverted by the Coriolis force. Therefore, the repulsive net force is weakened, leading to the slowdown of the radial component of the wind velocity and hence due to the equation of mass continuity also to the increase in the wind density.
A modified directional distribution of the stellar-wind intensity is traced back to the roots of the streamlines on the Roche equipotential surface at the centre, which was selected to represent a surface of the supergiant. The result for the same stellar parameters corresponding to the system Cyg X-1 is shown in the bottom panel of Fig. 1.
To distinguish the role of the different numerics and the physical effects involved in the new model, we also calculated two artificial intermediate models: the radial model in the 3D Cartesian grid and a non-radial model with tangential gradients and velocity components included but for which the Coriolis force had been neglected (cf. the second and the third panel of Fig. 1, resp.).
The second panel of Fig. 1 represents results of the 3D hydrodynamical simulation where the non-radial components of velocity were suppressed in each step of the computing process. We thus allowed the wind material to move in the radial direction only and forced it to reach a stationary solution independently in each radial cone. Consequently, this solution should correspond to the radial approximation depicted in the uppermost panel. However, the numerical results show a considerably higher intensity of the stellar wind all across the surface of the supergiant with a particularly enhanced outflow in the direction of the L1-point and the integrated outflow increase to 2.52 × 10-6 M⊙ yr-1. This difference between the two physically equivalent models is obviously due to numerical errors caused by the insufficient spatial resolution of the 3D-grid in the inner region of the computing area where we meet a steep density gradient. As a result, we experience an increase in the density all across this region and consequently a higher level of intensity of the stellar wind. To achieve certain qualitative conclusions about the role of the non-radial motion of the wind and the Coriolis force in real binaries, we have to compare the subsequent results of our 3D hydrodynamical model with this normalized radial approximation solution.
In the third panel of Fig. 1, the results of the midway hydrodynamic simulation are presented. In this model, we also take into account the tangential forces caused by the pressure gradients between the neighbouring flux-tubes. We set no additional conditions on the velocity so the streamlines of the wind can bend into non-radial directions though the Coriolis force is still excluded. We note that the overall intensity of the wind has increased compared to the normalized radial approximation solution in the second panel. The directional distribution of the outflow has also changed. The intensity in the equatorial plane has increased, in contrast to the drop-off that has occured in the polar regions. Allowing the non-equatorial streamlines to deviate from the radial direction, they can perceive the centrifugal force and are slightly bent towards the plane of the orbital motion of the binary. The most significant increase in the outflow at the primary maximum happens because the streaming of gas through the Roche potential window around the L1-point is more effective if non-radial velocities are allowed. A larger amount of material is transported in the direction with the lower effective potential barrier and the overall intensity of the outflow increases to 2.72 × 10-6 M⊙ yr-1.
3.4. Results of the computations
The final solution of the 3D hydrodynamical model including the Coriolis force is shown in the bottom panel of Fig. 1. Comparing it with the results of the previously described model in the third panel we note a slight shift in the primary and secondary maxima counter-clockwise in the equatorial plane. This effect can naturally be expected if we introduce the Coriolis force into our problem – most of the matter escapes along the streamlines that pass through the L1 or L2 points or their vicinities and originate in deeper layers shifted in the direction of the orbital rotation. Another important feature of the new stationary solution is that the mass-loss rate at the primary maximum is lower than the value of the same quantity in the previous model. We note that there is an even more significant decrease in the intensity at the secondary maximum on the opposite hemisphere from the black-hole companion. The overall intensity has decreased and the integrated mass-loss rate for the entire star has dropped to 2.50 × 10-6 M⊙ yr-1. This effect is also caused predominantly by the Coriolis force – the flux tubes originating in parts of the stellar surface where the gravity is most significantly reduced by the tidal force must overcome a higher barrier of the Roche potential, while the actual maximum of the outflow around the Lagrange points is less enhanced by the tides. In other words – we now allow streamlines of the stellar wind to curve and not to co-rotate with the orbital motion. In consequence, we reduce the centrifugal force, which repulses the material from the star, and therefore we may expect that the overall mass-loss rate be lower than in the hydrodynamical simulation in which the Coriolis force is not included, as predicted by Kříž. The effects of the non-radial flowing and the Coriolis force practically cancel each other in our present calculation. However, they may be in a different proportion in other systems and with the temperature structure taken into account. The classical models of radial stellar winds in binaries should thus be revised to achieve reliable quantitative results.
 |
Fig. 4 Hydrodynamic solution of the wind-fed circumstellar matter. The white cross shows the position of the black-hole companion, the black crosses mark the positions of the points L1 and L2. The distance scale on the x-axis is labelled in units of the separation between both components of the binary. The right-hand-side colour-scale corresponds to the distribution of the wind density in the equatorial plane. The left-hand-side colour-scale describes the directional dependence of the intensity of the stellar wind projected onto the surface of the supergiant. The red lines represent the streamlines of the stellar wind and the black contour-lines labelled by the corresponding numbers in km s-1 mark the absolute values of the stream velocity in the orbital plane. |
The flow of the circumstellar matter in the wider vicinity of the mass-losing star can be seen in Fig. 4, which represents the density, velocity, and streamlines in the orbital plane. The colour map on the projection of the tidally distorted disk of the star reflects the wind density shown in Fig. 2 projected from the direction of the rotational axis (its minimum in the polar region and the maxima shifted with respect to the region below the Lagrangian points can be clearly seen). The colour-map outside the stellar surface represents the density distribution, the approximately concentric isocontours show the values of the velocity, while the radial curves show the streamlines in the equatorial plane. In general, the density of the stellar wind decreases while the velocity increases with the distance from the supergiant. The distortion of the streamlines by the Coriolis force is obvious and its role in bringing the mass ejected around the L2-point into the vicinity of the compact companion can be estimated. (The significance of this effect argued by Gies depends on the parameters of the system and the regime of the radiative acceleration.)
The most spectacular feature in this Fig. 4, is the dense tail that appears behind the compact companion (the position of the companion is marked by the cross). The growth of this tail can be seen in Fig. 3. Its source is obvious from the streamlines of the wind. The flow of the wind is focused by the intense gravity field of the black hole, and the mass density increases in the tail as the streamlines passing the black hole at larger distances join it. This effect, which is naturally beyond of scope of the models of radial wind, is obviously a version of the Bondi-Hoyle-Lyttleton (BHL hereafter) accretion (with differences described in the next section). In an approximation of free-particle motion, this effect is analogous to the gravitational focusing of photons and the formation of high-density caustics. Our isothermal model facilitates the condensation of the tail, although a similar increase in the mass density behind the companion star can be seen in the results of many numerical models of mass exchange in binaries.
An important characteristic of the BHL accretion investigated already in the original papers of its discoverers but often neglected in more recent papers is its instability. There is no unique steady-state solution with a strict boundary between the region of the tail that falls on the accretor and which escapes to infinity. The accumulation of the mass in the tail and the variability of the accretion rate with time may play an important role in triggering the transitions of X-ray binaries between the radiatively high/soft and low/hard regimes of the accretion. Our computations also indicate that there are some instabilities in the tail, although an increase in the spatial resolution and a sophistication of the physical model will be needed to verify or disprove these results.
The close proximity of a luminous X-ray source could influence the dynamics of the line-driven wind by producing a change in the temperature and ionization structure of the wind material. The X-ray heating and photoionization can inhibit the wind acceleration by reducing population of electron levels available to absorb the momentum of the radiation flux from the primary. In the case of a very strong X-ray flux, the photoionization radius can reach the photosphere of the primary causing the line-driven wind to never achieve the escape velocity. It may then cease to supply the accretion process with material. Although the calculations of the ionization structure were not included in the present version of the code, we were able to simulate the above-mentioned effect by the assumption that the k parameter from Eq. (1) is artificially set to 0 for the wind material, which leaves the part of the photosphere facing the X-ray source. If the CAK line-driven mechanism is a main source of the repulsive force acting on the wind material, by cancellation of the line force, the wind material loses its support and starts falling back onto the primary. The situation is captured in Fig. 5. The initial state (the uppermost left panel) corresponds to the steady-state solution depicted in Fig. 4. There is an apparent steep increase in the density in the region where the line force has been artificially switched off. This is caused by the slowdown of the wind velocity in this region and also by the higher layers of the wind material failing to achieve the escape velocity and falling back onto the photosphere.
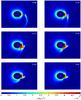 |
Fig. 5 Evolution of the density distribution in the equatorial plane computed with the radiation hydrodynamic model after the line-driven force from the companion-facing hemisphere was artificially switched off. The initial state (the uppermost left panel) corresponds to the steady-state solution depicted in Fig. 4. The bottom right panel captures the new nearly steady-state solution. The white index in the upper right corner of the each panel indicates an evolutionary time expressed in the units of the orbital periods. The red cross and asterisk show the position of the black hole and the centre of the supergiant, resp. |
4. Bondi-Hoyle-Lyttleton accretion
The standard theory of BHL accretion assumes that the accreting object moves through a homogeneous static gas (cf. Hoyle & Lyttleton 1939; Bondi & Hoyle 1944; or Edgar 2004, for a review). This means that the initial velocities of the incident gas elements are parallel, while the stellar wind diverges. This difference is essential because the divergence limits the mass rate of the accretion into the formed tail (cf. Hadrava & Karas 1984). Moreover, for an accretor moving in either a perpendicular or skewed direction with respect to the source of the wind, the axial symmetry of the flow is broken.
To modify the calculation of BHL accretion in the case of the gravitational interaction of a radial stellar wind with an orbiting satellite, the boundary conditions must be modified. We define 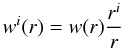 (12)to be the unperturbed velocity of the wind and Ri(t) to be the track of the satellite. The relative velocity of the wind in the instantaneous inertial system of the satellite can be expanded in variable x ≡ r − R up to linear terms as
(12)to be the unperturbed velocity of the wind and Ri(t) to be the track of the satellite. The relative velocity of the wind in the instantaneous inertial system of the satellite can be expanded in variable x ≡ r − R up to linear terms as 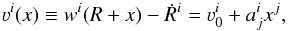 (13)where
(13)where 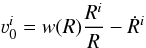 (14)is the velocity of the wind in the rest frame of the satellite colliding with it head-on, and
(14)is the velocity of the wind in the rest frame of the satellite colliding with it head-on, and 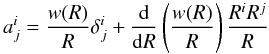 (15)is a symmetric matrix describing the dilution of the unperturbed wind in the space around the satellite with respect to its rest frame. Its projection to the plane perpendicular onto ν0
(15)is a symmetric matrix describing the dilution of the unperturbed wind in the space around the satellite with respect to its rest frame. Its projection to the plane perpendicular onto ν0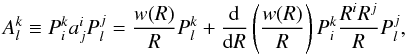 (16)where the projector
(16)where the projector 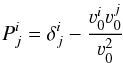 (17)yields the apparent divergence of the wind streamlines. For a vector z that is perpendicular to the orbital plane (i.e. (zR) = (zṘ) = (zν0) = 0 and consequently Pz = z), we get
(17)yields the apparent divergence of the wind streamlines. For a vector z that is perpendicular to the orbital plane (i.e. (zR) = (zṘ) = (zν0) = 0 and consequently Pz = z), we get 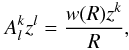 (18)which means that the dilution of streamlines in this plane corresponds to the proper distance R of their source. On the other hand, for a vector y in the orbital plane perpendicular to ν0, i.e.
(18)which means that the dilution of streamlines in this plane corresponds to the proper distance R of their source. On the other hand, for a vector y in the orbital plane perpendicular to ν0, i.e. ![\begin{equation} y^{l} =c \left[R^{l}\left(\dot{R}^{2}-\frac{w(R)}{R}(R\dot{R})\right)+\dot{R}^{l}(Rw(R)-(R\dot{R}))\right], \label{BH8} \end{equation}](/articles/aa/full_html/2012/06/aa16046-10/aa16046-10-eq73.png) (19)(for which (yν0) = 0 and hence Py = y, but
(19)(for which (yν0) = 0 and hence Py = y, but ![\hbox{$(y\dot{R})=(yR)\frac{w(R)}{R} =\frac{cw(R)}{R}[R^{2}\dot{R}^{2}-(R\dot{R})^{2}]\neq 0$}](/articles/aa/full_html/2012/06/aa16046-10/aa16046-10-eq76.png) ), we get
), we get ![\begin{eqnarray} A^{k}_{l}y^{l} \!=\! \left[\frac{w(R)}{R} +\frac{R^{2}\dot{R}^2-(R\dot{R})^{2}}{Rw^{2}(R)-2(R\dot{R})w(R)+R\dot{R}^{2}} \frac{{\rm d}}{{\rm d}R}\left(\frac{w(R)}{R}\right)\right]y^{k}. \label{BH9} \end{eqnarray}](/articles/aa/full_html/2012/06/aa16046-10/aa16046-10-eq77.png) (20)In particular, when the satellite moves perpendicularly to the wind (i.e. (RṘ) = 0) and the wind is not accelerated (
(20)In particular, when the satellite moves perpendicularly to the wind (i.e. (RṘ) = 0) and the wind is not accelerated (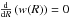 ), the apparent divergence of streamlines in the orbital plane is reduced as if the distance of their source is increased by the square of the ratio of the apparent (ν0) to the true (w) wind velocity
), the apparent divergence of streamlines in the orbital plane is reduced as if the distance of their source is increased by the square of the ratio of the apparent (ν0) to the true (w) wind velocity 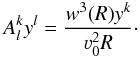 (21)
(21)
 |
Fig. 6 Gravitational focusing of the wind in the satellite’s co-moving frame in the approximation of free-particle motion. The thin black lines show asymptotes of the Keplerian hyperbolic trajectories. Owing to an aberration of the initial velocities, the trajectories with the same impact-parameter in the orbital plane (x,y) (red in the electronic version) reach the x-axis closer to the gravitating body (placed in the coordinate centre) than those in (x,z)-plane (blue lines). The particles moving out of these planes (violet lines) collide mutually in the (x,z)-plane before reaching the x-axis |
As a consequence, the streamlines in the equatorial plane (x,y in Fig. 6) are focused on the x-axis more efficiently than the streamlines in the perpendicular plane (x,z). The streamlines passing the satellite out of both these planes cross the x,z-plane earlier than the orbital plane and are thus not focused exactly on the x-axis; the focusing is astigmatic. This conclusion agrees with the results of numerical models described in the previous section, which show that the cross-section of the tail is elongated in the direction perpendicular to the orbital plane. The more complicated structure of the tail will thus need to be treated using detailed 3D hydrodynamic modelling to study the time variability of the accretion rate.
5. Discussion and conclusions
The increasingly high quality data available owing to improved observational techniques at various wavelengths now enable the more detailed investigation of the circumstellar matter in the interacting binaries. An accurate interpretation of these observations requires more sophisticated theoretical models to get more precise predictions of the observable quantities and test observationally the viability of the models and their underlying assumptions.
To yield physically self-consistent and quantitatively reliable results, our numerical model of the 3D radiation hydrodynamics of stellar winds in high-mass X-ray binaries (cf. Negueruela 2010, for a recent review) presented here needs to be improved in terms of several aspects of physics (first of all to model the radiative transfer of the X-rays from the companion and their interaction with the wind) and numerical properties (higher resolution). However, even in its present form it shows that non-radial models are necessary to derive quantitative information about the angular modulation of the wind and the mass-loss and accretion rates with an accuracy of about ten percents. The preliminary results of our calculations in which the radiative pressure in lines is scaled to account qualitatively for the ionization of the wind by X-ray illumination in different states of the compact companion show the significant non-linear response of the wind strength to the radiative drag.
The formation of narrow gaseous tails (or “wakes”) behind compact objects can be seen in our numerical hydrodynamic models of high-mass binaries. Similar results have also been found in several previous hydrodynamic simulations of isothermal flows – e.g. Ishii et al. (1993), while the adiabatic flows tend to form wider shock cones – cf. Matsuda et al. (1991). (Note that the equations of motion (3) and (2.2), resp., are incorrectly typed in these papers.) The physics of the formation of this tail is a modification of the BHL-accretion, i.e. a gravitational focusing of the wind that is basically similar to the gravitational lensing of photons. Unlike the axially symmetric case of the classical BHL-accretion, the stellar wind from a supergiant has spatial gradients of both the velocity and the density when reaching the orbit of the companion object and its accretion must thus be non-axisymmetric. The violation of the symmetry is more pronounced if the wind speed does not significantly exceed the orbital velocity of the companion. In this asymmetric case, the classical approximation of the BHL accretion rate is less accurate (Walder 1997) and the accretion is unstable (Ruffert 1997, 1999). There are sophisticated general-relativistic radiation- or magneto-hydrodynamic models (cf., e.g., Zanotti et al. 2011,and references therein) of the BHL-accretion. These models are needed to treat in detail the accretion in the close vicinity of the compact component and the generation of the X-ray radiation. The present models, however, mostly assume the homogeneity of the incident flow. An inhomogeneity in the flow may significantly influence the angular momentum of the accreted matter, hence both the size of the inner accretion disc and its luminosity. The inhomogeneity of the wind in the neighbourhood of the companion depends on its tidal modulation in the subsonic region of the donor star and its non-radial flow in the space between the components. These effects have thus to be taken into account in self-consistent models of the accretion.
The existence of these gaseous tails in interacting binaries is confirmed observationally – cf. Dumm et al. (2000) or Dhawan et al. (2006). The deposition of the mass focused into the tail and the well-known instability of BHL accretion (Foglizzo et al. 2005) may influence the interplay between the variability of the wind mass-loss from the donor star, the hydrodynamics of the circumstellar matter, and its accretion onto the compact object. It may thus be responsible for different kinds of time variability for these objects – cf., e.g., Blondin & Pope (2009).
Acknowledgments
The authors are grateful to J. Dale, K. G. Gayley, J. Kubát, and R. Wünsch for useful comments and suggestions. This work has been done in the framework of the Center for Theoretical Astrophysics (ref. LC06014) with a support of grants GAČR 202/09/0772 and 205/09/H033, GAUK 139810 and SVV-265301.
References
- Blondin, J. M., & Pope, T. C. 2009, ApJ, 700, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero-Nieves, S. M., Gies, D. R., Bolton, C. T., et al. 2009, ApJ, 701, 1895 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I. 1974, MNRAS, 169, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Čechura, J. 2010, Particle motion in the vicinity of compact stellar objects, Diploma Thesis, Charles Univ., Czech Rep. [Google Scholar]
- Claret, A. 2012, A&A, 538, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dhawan, V., Mioduszewski, A., & Rupen, M. 2006, in VI Microquasar Workshop: Microquasars and Beyond [Google Scholar]
- Dumm, T., Folini, D., Nussbaumer, H., et al. 2000, A&A, 354, 1014 [NASA ADS] [Google Scholar]
- Edgar, R. 2004, New A Rev., 48, 843 [CrossRef] [Google Scholar]
- Foglizzo, T., Galletti, P., & Ruffert, M. 2005, A&A, 435, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friend, D. B., & Castor, J. I. 1982, ApJ, 261, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Gayley, K. G., & Owocki, S. P. 2000, ApJ, 537, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Gayley, K. G., Townsend, R., Parsons, J., & Owocki, S. 2007, in Massive Stars in Interactive Binaries, ed. N. St.-Louis, & A. F. J. Moffat, ASP Conf. Ser., 367, 393 [Google Scholar]
- Gies, D. R., Bolton, C. T., Blake, R. M., et al. 2008, ApJ, 678, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Grinin, V. P. 1978, Astrofizika, 14, 537 [NASA ADS] [Google Scholar]
- Hadrava, P. 1980, Kinetic theory of extended stellar atmospheres, Ph.D. Thesis, Astron. Inst. Acad. Sci., Czechoslovakia [Google Scholar]
- Hadrava, P. 1987, Publ. Astron. Inst. Czechoslovak Acad. Sci., 70, 263 [NASA ADS] [Google Scholar]
- Hadrava, P. 1992, A&A, 256, 519 [NASA ADS] [Google Scholar]
- Hadrava, P., & Karas, V. 1984, Bull. Astron. Inst. Czechoslovakia, 35, 343 [NASA ADS] [Google Scholar]
- Hadrava, P., Bao, G., & Ostgaard, E. 1997, ApJ, 480, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Lyttleton, R. A. 1939, in Proc. Cambridge Philosophical Society, 34, 405 [Google Scholar]
- Ishii, T., Matsuda, T., Shima, E., et al. 1993, ApJ, 404, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1967, ZAp, 65, 89 [NASA ADS] [Google Scholar]
- Matsuda, T., Sekino, N., Sawada, K., et al. 1991, A&A, 248, 301 [NASA ADS] [Google Scholar]
- Negueruela, I. 2010, in ASP Conf. Ser. 422, ed. J. Martí, P. L. Luque-Escamilla, & J. A. Combi, 57 [Google Scholar]
- Owocki, S. P., Cranmer, S. R., & Gayley, K. G. 1996, ApJ, 472, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Cranmer, S. R., & Gayley, K. G. 1998, Ap&SS, 260, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, H. P. 1937, MNRAS, 97, 423 [NASA ADS] [Google Scholar]
- Ruffert, M. 1997, A&A, 317, 793 [NASA ADS] [Google Scholar]
- Ruffert, M. 1999, A&A, 346, 861 [NASA ADS] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Walder, R. 1997, in Accretion Phenomena and Related Outflows, ed. D. T. Wickramasinghe, G. V. Bicknell, & L. Ferrario, IAU Colloq., 163, ASP Conf. Ser., 121, 822 [Google Scholar]
- Zanotti, O., Roedig, C., Rezzolla, L., & Del Zanna, L. 2011, MNRAS, 417, 2899 [NASA ADS] [CrossRef] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Model atmospheres of binary components
We now reproduce in a language corrected form the parts of Hadrava (1987) relevant to our present study. Figure captions missing in the original paper because of lack of space are added here.
The models of stellar atmospheres are based on the assumption of either their plane-parallel or spherical symmetry. The violation of either of these assumptions by tides and rotation in close binaries leads to the incompatibility of hydrostatic and radiative equilibria. An improvement in the model atmospheres in this respect is desirable for simulating both the light curves and line profile changes. Moreover, the atmospheres of the contact components of interacting binaries determine the initial conditions of dynamics of gaseous streams and in this way influence the behaviour of the binary system.
A.1. Hydrostatic equilibrium
It is well-known that the stellar configuration in hydrostatic equilibrium must be homogeneous across each equipotential. This follows from the vector nature of the equation of the hydrostatic equilibrium 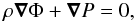 (A.1)because the pressure P and density ρ must be functions only of the potential Φ, and following the equation of state
(A.1)because the pressure P and density ρ must be functions only of the potential Φ, and following the equation of state 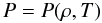 (A.2)the same must be valid for the temperature T = T(Φ). The temperature distribution is determined by the energy balance, driven mainly by radiative transfer. The solution of radiative transfer is the main problem in modelling symmetric (i.e. plane-parallel or spherical) atmospheres, where the tangential components of Eq. (A.1) are trivial and both Eqs. (A.1) and (A.2) can be simply integrated. However, if the symmetry is violated e.g. by either rotation or tides, the homogeneity imposes an a priori restriction on the radiation field across different parts of stellar surface. This restriction cannot generally be satisfied. This can be seen from Fig. A.1, where the source function S is plotted (full line) for the grey atmosphere. If g is increased, the hot inner layers are shifted to lower optical depths (dashed line), which in agreement with von Zeipel’s theorem corresponds to an increase in the effective temperature (dotted line). On the other hand, the surface temperature (for τ → 0) remains constant and is thus incompatible with the radiation coming from the interior. When the surface layers are heated by absorbing this radiation, the hydrostatic equilibrium is violated in the tangential direction and tangential radiative transfer takes place. The latter of these generally also appears as a consequence of the different radiation dilution caused by the variable curvature of the equipotentials. The incompatibility of the hydrostatic and radiative equilibria should give rise to meridional circulations in the atmosphere. The construction of model atmospheres as a mosaic of one-dimensional (especially plane-parallel) models can thus be accepted only as a first approximation. Another violation of hydrostatic equilibrium is caused by the existence of stellar wind, which is discussed in Sect. A.2. Additional complications arise when the binary component does not rotate synchronously with the orbital motion, particularly when the orbit is eccentric. Despite the aforementioned objections, the hydrostatic equilibrium is a valuable approximation, at least for the inner layers of atmospheres. It is thus advantageous to choose a coordinate system that fits the corresponding shape of the atmosphere for the further investigation. This is achieved using Roche coordinates, where the first coordinate ξ1 is the effective potential and the surfaces ξ2,3 = const. are perpendicular to the equipotentials (but generally not mutually perpendicular). The generalisation of a Roche potential to a finite mass concentration is also possible, but fortunately not essential.
(A.2)the same must be valid for the temperature T = T(Φ). The temperature distribution is determined by the energy balance, driven mainly by radiative transfer. The solution of radiative transfer is the main problem in modelling symmetric (i.e. plane-parallel or spherical) atmospheres, where the tangential components of Eq. (A.1) are trivial and both Eqs. (A.1) and (A.2) can be simply integrated. However, if the symmetry is violated e.g. by either rotation or tides, the homogeneity imposes an a priori restriction on the radiation field across different parts of stellar surface. This restriction cannot generally be satisfied. This can be seen from Fig. A.1, where the source function S is plotted (full line) for the grey atmosphere. If g is increased, the hot inner layers are shifted to lower optical depths (dashed line), which in agreement with von Zeipel’s theorem corresponds to an increase in the effective temperature (dotted line). On the other hand, the surface temperature (for τ → 0) remains constant and is thus incompatible with the radiation coming from the interior. When the surface layers are heated by absorbing this radiation, the hydrostatic equilibrium is violated in the tangential direction and tangential radiative transfer takes place. The latter of these generally also appears as a consequence of the different radiation dilution caused by the variable curvature of the equipotentials. The incompatibility of the hydrostatic and radiative equilibria should give rise to meridional circulations in the atmosphere. The construction of model atmospheres as a mosaic of one-dimensional (especially plane-parallel) models can thus be accepted only as a first approximation. Another violation of hydrostatic equilibrium is caused by the existence of stellar wind, which is discussed in Sect. A.2. Additional complications arise when the binary component does not rotate synchronously with the orbital motion, particularly when the orbit is eccentric. Despite the aforementioned objections, the hydrostatic equilibrium is a valuable approximation, at least for the inner layers of atmospheres. It is thus advantageous to choose a coordinate system that fits the corresponding shape of the atmosphere for the further investigation. This is achieved using Roche coordinates, where the first coordinate ξ1 is the effective potential and the surfaces ξ2,3 = const. are perpendicular to the equipotentials (but generally not mutually perpendicular). The generalisation of a Roche potential to a finite mass concentration is also possible, but fortunately not essential.
 |
Fig. A.1 The dependence of source function S in a grey atmosphere on the optical depth τ (the full line). In the parts of atmosphere with a higher gravity g, layers with a given temperature are shifted to lower optical depths (the dashed line). This corresponds to increase of the radiative flux in large optical depths (the dotted line), which gives, however, a temperature incompatible at low depths with the homogeneity on equipotential. The actual value of emergent flux H for different shifts of S in g is shown in Fig. A.2. |
 |
Fig. A.2 The dependence of radiative flux H from an inhomogeneous grey atmosphere in exact hydrostatic equilibrium on the local gravity g (in units of its mean unperturbed value). |
A.2. Stellar wind
The density of a gas in thermodynamic equilibrium is an exponential function of the potential. This is why it decreases to zero and the mass (or optical) depth is finite in upper layers of plane-parallel atmosphere, where Φ → ∞. However, Φ → 0 at infinity for a spherical (or other finite) configuration and consequently ρ → ρ∞ > 0 and the mass depth becomes infinite for such a configuration in equilibrium with its surroundings. If a real star is immersed into vacuum, it must evaporate. Equation (A.1) of hydrostatic equilibrium must then be thus replaced by the equation of motion 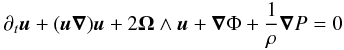 (A.3)and the equation of continuity
(A.3)and the equation of continuity 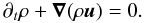 (A.4)This system of partial differential equations can be simplified for a stationary flow (∂t = 0), if the stream lines
(A.4)This system of partial differential equations can be simplified for a stationary flow (∂t = 0), if the stream lines 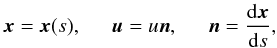 (A.5)are known (e.g. if they are radial for spherically symmetric problem). Equation (A.4) then becomes
(A.5)are known (e.g. if they are radial for spherically symmetric problem). Equation (A.4) then becomes 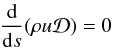 (A.6)and its solution is
(A.6)and its solution is 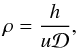 (A.7)where h is the flow of gas, which is constant along the stream line, and
(A.7)where h is the flow of gas, which is constant along the stream line, and 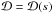 is the cross-section of stream-tube, determined by the dilution of the stream lines
is the cross-section of stream-tube, determined by the dilution of the stream lines 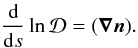 (A.8)The component of Eq. (A.3) parallel to n reads
(A.8)The component of Eq. (A.3) parallel to n reads 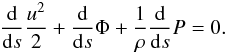 (A.9)The density can be substituted here from Eq. (A.7), and if the thermal regime of the flow is known (e.g. where there is a polytropic expansion or T = T(s)), the equation for u = u(s) is obtained. It can be simply integrated in the form
(A.9)The density can be substituted here from Eq. (A.7), and if the thermal regime of the flow is known (e.g. where there is a polytropic expansion or T = T(s)), the equation for u = u(s) is obtained. It can be simply integrated in the form ![\appendix \setcounter{section}{1} \begin{eqnarray} f(u)&=&\frac{u^{2}_{k}-u^{2}}{2}+\frac{kT}{m}{\rm ln}\frac{u}{u_{k}} \nonumber\\[3mm] &=&-\frac{kT}{m}\ln \mathcal{D}+\Phi-\Phi_{k}=\Phi_{\rm eff}(s)-\Phi_{k} \label{Eq19} \end{eqnarray}](/articles/aa/full_html/2012/06/aa16046-10/aa16046-10-eq113.png) (A.10)
(A.10)
 |
Fig. A.3 Evaporative wind in an effective Roche potential – the left and right upper panels give the left and right sides of Eq. (A.10), i.e. the effective potential Φeff as a function of u and s, resp. The bottom panel gives the solution u = u(s), the full line corresponds to the wind solution, and the dashed line to accretion. |
 |
Fig. A.4 Angular distribution of wind strengths for several values of θ and q. Full lines mark the isocontours of the mean wind intensity (dashed lines show values for one and two orders higher and lower) in spherical coordinates with poles towards the L1 and L2 points. The latitude ϕ is drawn in a linear scale on the horizontal axis; the longitude λ measured from the intersection with the orbital plane scaled by cosϕ increases upward up to the rotational axis at the top of each drawing. |
for an idealised problem of isothermal flow (Φk is an integration constant). There are two solutions 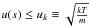 and u(s) ≥ uk of this equation – see Fig. A.3. The former is asymptotically hydrostatic, while the latter corresponds to a free fall for Φeff → − ∞. An important feature is that the dilution of the stream lines acts as a repulsive force (nozzle) through the first term on the r.h.s. of Eq. (A.10). The above-mentioned solution can be matched at the critical point sk, where Φeff reaches its maximum Φeff(sk) = Φk, and u(sk) = uk. Its position can be influenced or even dominated by the presence
and u(s) ≥ uk of this equation – see Fig. A.3. The former is asymptotically hydrostatic, while the latter corresponds to a free fall for Φeff → − ∞. An important feature is that the dilution of the stream lines acts as a repulsive force (nozzle) through the first term on the r.h.s. of Eq. (A.10). The above-mentioned solution can be matched at the critical point sk, where Φeff reaches its maximum Φeff(sk) = Φk, and u(sk) = uk. Its position can be influenced or even dominated by the presence
of another repulsive force such as radiative pressure or centrifugal force. The latter is combined with the tidal force in binaries. A critical point thus depends on the Roche potential along a particular stream line. It determines the velocity in deep layers, where the hydrostatic equilibrium is approached and the density is the same exponential function of potential for each stream line. The flow of mass is thus 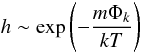 (A.11)in different directions. The results for a radial wind are shown in Fig. A.4 for several values of the mass ratio q and ratio
(A.11)in different directions. The results for a radial wind are shown in Fig. A.4 for several values of the mass ratio q and ratio 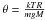 of thermal kinetic to gravitational potential energy of a gas particle. The Roche potential is thus a potential barrier to the cool gas, that can flow only in the vicinity of the L1-point, although the anisotropy of the stellar wind decreases with increasing surface temperature. In any case, the Roche-lobe overflow and mass loss by stellar winds are not independent processes as often assumed, but only two extreme pictures of the same physical process – an anisotropic stellar wind.
of thermal kinetic to gravitational potential energy of a gas particle. The Roche potential is thus a potential barrier to the cool gas, that can flow only in the vicinity of the L1-point, although the anisotropy of the stellar wind decreases with increasing surface temperature. In any case, the Roche-lobe overflow and mass loss by stellar winds are not independent processes as often assumed, but only two extreme pictures of the same physical process – an anisotropic stellar wind.
All Figures
 |
Fig. 1 Distribution of stellar wind intensity on the surface of the optical component of Cyg X-1 in the radial approximation (CAK model – the uppermost panel), the radial approximation of the radiation-hydrodynamic model in 3D Cartesian grid (the second panel), the non-radial radiation-hydrodynamic solution without the Coriolis force (the third panel) and the full radiation-hydrodynamic solution with the Coriolis force included (the bottom panel). The direction to the L1-point and the companion has the sidereographic longitude 0°, the longitude 180° is directed towards the L2-point. The number in the lower right corner of each panel gives the overall outflow of the material from the supergiant in M⊙ yr-1. |
| In the text | |
 |
Fig. 2 Distribution of the stellar wind intensity in dependence on gravity darkening. The radial approximation for the same parameters as in Fig. 1 is calculated for radiation modulated according to Eq. (10) and values of the parameter β from the top to the bottom of 0.0, 0.125, 0.1875, and 0.25. |
| In the text | |
 |
Fig. 3 Evolution of the density distribution in the equatorial plane computed with the radiation hydrodynamic model during the convergence process towards a new stationary solution. The uppermost left panel represents the state close to the conditions set up by the radial model. The bottom right panel captures the nearly steady-state solution corresponding to the newly included forces – the Coriolis force and the tangential forces caused by the pressure gradients. The white index in the upper right corner of each panel indicates an evolutionary time expressed in the units of the orbital periods. The red cross and asterisk show the position of the black hole and the centre of the supergiant, resp. |
| In the text | |
 |
Fig. 4 Hydrodynamic solution of the wind-fed circumstellar matter. The white cross shows the position of the black-hole companion, the black crosses mark the positions of the points L1 and L2. The distance scale on the x-axis is labelled in units of the separation between both components of the binary. The right-hand-side colour-scale corresponds to the distribution of the wind density in the equatorial plane. The left-hand-side colour-scale describes the directional dependence of the intensity of the stellar wind projected onto the surface of the supergiant. The red lines represent the streamlines of the stellar wind and the black contour-lines labelled by the corresponding numbers in km s-1 mark the absolute values of the stream velocity in the orbital plane. |
| In the text | |
 |
Fig. 5 Evolution of the density distribution in the equatorial plane computed with the radiation hydrodynamic model after the line-driven force from the companion-facing hemisphere was artificially switched off. The initial state (the uppermost left panel) corresponds to the steady-state solution depicted in Fig. 4. The bottom right panel captures the new nearly steady-state solution. The white index in the upper right corner of the each panel indicates an evolutionary time expressed in the units of the orbital periods. The red cross and asterisk show the position of the black hole and the centre of the supergiant, resp. |
| In the text | |
 |
Fig. 6 Gravitational focusing of the wind in the satellite’s co-moving frame in the approximation of free-particle motion. The thin black lines show asymptotes of the Keplerian hyperbolic trajectories. Owing to an aberration of the initial velocities, the trajectories with the same impact-parameter in the orbital plane (x,y) (red in the electronic version) reach the x-axis closer to the gravitating body (placed in the coordinate centre) than those in (x,z)-plane (blue lines). The particles moving out of these planes (violet lines) collide mutually in the (x,z)-plane before reaching the x-axis |
| In the text | |
 |
Fig. A.1 The dependence of source function S in a grey atmosphere on the optical depth τ (the full line). In the parts of atmosphere with a higher gravity g, layers with a given temperature are shifted to lower optical depths (the dashed line). This corresponds to increase of the radiative flux in large optical depths (the dotted line), which gives, however, a temperature incompatible at low depths with the homogeneity on equipotential. The actual value of emergent flux H for different shifts of S in g is shown in Fig. A.2. |
| In the text | |
 |
Fig. A.2 The dependence of radiative flux H from an inhomogeneous grey atmosphere in exact hydrostatic equilibrium on the local gravity g (in units of its mean unperturbed value). |
| In the text | |
 |
Fig. A.3 Evaporative wind in an effective Roche potential – the left and right upper panels give the left and right sides of Eq. (A.10), i.e. the effective potential Φeff as a function of u and s, resp. The bottom panel gives the solution u = u(s), the full line corresponds to the wind solution, and the dashed line to accretion. |
| In the text | |
 |
Fig. A.4 Angular distribution of wind strengths for several values of θ and q. Full lines mark the isocontours of the mean wind intensity (dashed lines show values for one and two orders higher and lower) in spherical coordinates with poles towards the L1 and L2 points. The latitude ϕ is drawn in a linear scale on the horizontal axis; the longitude λ measured from the intersection with the orbital plane scaled by cosϕ increases upward up to the rotational axis at the top of each drawing. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


