| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201118765 | |
| Published online | 06 April 2012 | |
Stabilization of radiation pressure dominated accretion disks through viscous fluctuations
1 Center for Theoretical Physics, Polish Academy of Sciences, Al. Lotnikow 32/46, 02-668 Warsaw, Poland
e-mail: agnes@cft.edu.pl
2 Inter-University Centre for Astronomy and Astrophysics, Pune 41107, India
e-mail: rmisra@iucaa.ernet.in
Received: 31 December 2011
Accepted: 28 February 2012
Aims. The standard thin accretion disk model has successfully explained the soft X-ray spectra of Galactic black hole systems and perhaps the UV emission of active galactic nuclei. However, radiation pressure dominated disks are known to be viscously unstable and should produce high-amplitude oscillations that are typically not observed. Instead, these sources exhibit a stochastic variability that may naturally arise through viscous fluctuations in a turbulent disk. Here we investigate whether these aperiodic viscous fluctuations can stabilize the inner radiation pressure dominated disks and hence maybe the answer to a forty-year old problem in accretion disk theory.
Methods. The structure and evolution of a time-dependent accretion disk around a black hole is solved numerically. We incorporated fluctuations in the disk by considering stochastic variations in the viscous parameter α on the local viscous time-scale. We studied both locally stable disks where the viscous stress scales with the gas pressure and locally unstable disks where the stress scales as the total pressure. We considered steady state disk parameters pertaining to both stellar and supermassive black holes.
Results. For locally stable disks, the power spectra of the luminosity variations are found to inversely scale with frequency, i.e., P(f) ∝ 1/f as expected from analytical studies of linear viscous fluctuations. For unstable disks, where the viscous stress scales with the total pressure, the standard oscillatory solutions are seen when the viscous fluctuation amplitude is low. Increasing the fluctuation amplitude decreases the amplitude of these oscillations until for a sufficiently high (near unity) fluctuation amplitude, the oscillatory behavior disappears and the luminosity variation of the disk becomes stochastic. This study may explain why many accreting black holes, although they show sufficiently high accretion rates to develop the radiation pressure instability, do not exhibit high-amplitude regular outbursts, or, like the micro-quasar GRS 1915+105, produce diminished versions of these outburst only in some specific spectral states.
Key words: accretion, accretion disks / hydrodynamics / instabilities / galaxies: active / X-rays: binaries
© ESO, 2012
1. Introduction
The standard accretion disk model (Shakura & Sunyaev 1973) has been the basic framework in which the accretion process around black holes is understood. The model, which is also referred to as the α-disk model, assumes a thin Keplerian accretion disk where the unknown turbulent viscosity is parametrized such that the viscous torque is proportional to the total pressure, i.e., Trφ = αPtot. The model predicts that for supermassive black holes the peak radiation will be emitted in the ultraviolet and this is often identified with the “big blue bump” in active galactic nuclei (AGN). For stellar mass black holes, the emission peaks in soft X-rays and a thermal soft emission like this is indeed observed in Galactic black hole binaries.
Galactic black hole binaries exhibit different spectral states (see, e.g., for a review Done et al. 2007). In the hard/low state the spectra are dominated by a hard X-ray power-law that extends to ~100 keV and a weaker soft black-body-like component. The soft component is generally modeled as a truncated standard accretion disk and the primary hard power-law is believed to arise from a hot inner disk (e.g., Shapiro et al. 1976). In the soft state, the spectrum is dominated by the thermal emission from the standard accretion disk. For X-ray novae the luminosity changes by several orders of magnitude, yet the inferred inner radius of the standard accretion disk remains constant, as expected from the standard disk theory. Indeed, spectral computation based on the standard theory, but incorporating general relativistic effects, and detailed radiative transfer have been successfully used to fit the soft component. This analysis can constrain the mass and spin of the black holes and opens up the possibility of testing General Relativity in the strong field limit. Therefore, while there may be some ambiguity regarding the origin of the hard X-ray emission from black hole binaries, there is a near consensus that the soft component originates in a standard accretion disk, which allows a detailed and unprecedented understanding of these sources.
There has been the long-standing concern that in the standard accretion disk model the disk is both thermally and viscously unstable when radiation pressure is dominant (Lightman & Eardley 1974). This occurs in the inner regions of the disk around a ten-solar-mass black hole, when its luminosity exceeds ≳3 × 1037 erg/s. X-ray binaries can typically exceed this luminosity, which is substantially lower than the Eddington limit of ~1039 erg/s. For AGNs, which harbor 107 M⊙ black holes, the disk should be unstable for luminosities exceeding ≳5 × 1043 erg/s, which is significantly less than the Eddington limit of ~1045 erg/s. Consequently, the standard accretion disk is unstable and not applicable for typical black hole binaries and AGNs.
The extension of the radiation pressure dominated part of the disk depends on the accretion rate, the black hole mass, and the viscosity. The parameter regions of the radiation pressure dominated disks in Galactic black holes and AGN were shown recently in Janiuk & Czerny (2011); the approximate fitting formula for this dependence is
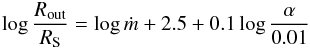 (1)for a Galactic black hole of 10 M⊙ at accretion rates above log ṁcrit = −1.5 where ṁ = Ṁ/ṀEdd and RS = 2GM/c2. For a supermassive black hole of 108 M⊙ at accretion rates above log ṁcrit = −2.5, the radial range is
(1)for a Galactic black hole of 10 M⊙ at accretion rates above log ṁcrit = −1.5 where ṁ = Ṁ/ṀEdd and RS = 2GM/c2. For a supermassive black hole of 108 M⊙ at accretion rates above log ṁcrit = −2.5, the radial range is 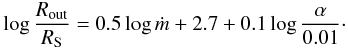 (2)Initially it was postulated that the unstable inner regions of the standard disk may become converted into a hot two-temperature region (Shapiro et al. 1976). The hot inner disk could then be the source of the hard X-ray emission and is a consistent model for Galactic black holes in the hard state. However, in the soft state, where the luminosity could be even higher than in the hard state, there is a soft thermal-like emission indicating that the standard disk somehow survives the instability caused by the radiation pressure instability. Moreover, time-dependent numerical evolution of the unstable disk shows that instead of the disk becoming transformed into a hot one, it undergoes cyclic behavior, which results in high-amplitude oscillations in luminosity. These strong variations in luminosity have not been observed.
(2)Initially it was postulated that the unstable inner regions of the standard disk may become converted into a hot two-temperature region (Shapiro et al. 1976). The hot inner disk could then be the source of the hard X-ray emission and is a consistent model for Galactic black holes in the hard state. However, in the soft state, where the luminosity could be even higher than in the hard state, there is a soft thermal-like emission indicating that the standard disk somehow survives the instability caused by the radiation pressure instability. Moreover, time-dependent numerical evolution of the unstable disk shows that instead of the disk becoming transformed into a hot one, it undergoes cyclic behavior, which results in high-amplitude oscillations in luminosity. These strong variations in luminosity have not been observed.
Attempts have been made to stabilize the disk, or to at least reduce the destabilizing effect, by accounting for the fraction of power that may be transferred to an overlying corona or jet. This indeed increases the critical accretion rate above which the instability occurs by a factor of few, nevertheless, the instability persists and the model predicts high-amplitude oscillations at high luminosities. Furthermore, assuming that there is a vertical height dependence on the energy dissipated in the disk, where a significant fraction of the energy is dissipated near the photosphere and not the mid-plane, does not completely stabilize the disk either. Finally, one can question the form of the viscous stress chosen in the standard model, where the stress is taken to be proportional to the total pressure, Trφ = αPtot. Indeed, if the viscous stress scales with only the gas pressure Trφ = αPgas, the disk would be unconditionally stable. However, it is not clear why this ad hoc prescription would be physical. If the turbulence length scales with the height of the disk, but the eddy speed scales with the gas sound speed, 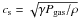 (instead of the total sound speed
(instead of the total sound speed 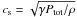 ), the viscous stress would be
), the viscous stress would be 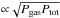 . However, even for this prescription the disk is not stable, but undergoes luminosity oscillations with diminished amplitude. A combination of this viscous prescription and the assumption that a fraction of the power is transferred to a corona may explain the variability of the micro-quasar GRS 1915+105, in certain spectral states (Janiuk & Czerny 2011). GRS 1915+105 is not typical, and the apparent stability of other bright X-ray binaries and even for GRS 1915+105 in its stable states remains a puzzle (see e.g., Neilsen et al. 2011).
. However, even for this prescription the disk is not stable, but undergoes luminosity oscillations with diminished amplitude. A combination of this viscous prescription and the assumption that a fraction of the power is transferred to a corona may explain the variability of the micro-quasar GRS 1915+105, in certain spectral states (Janiuk & Czerny 2011). GRS 1915+105 is not typical, and the apparent stability of other bright X-ray binaries and even for GRS 1915+105 in its stable states remains a puzzle (see e.g., Neilsen et al. 2011).
Instead of showing high-amplitude oscillatory behavior, black hole binaries and AGNs exhibit stochastic variability with a high-frequency cutoff (Nowak et al. 1999). In the hard state of the X-ray sources, the photons from the disk are upscattered through the Comptonization in the hot plasma. The dispersion of the scattering times may lead to the attenuation of the observed variability amplitude. Also, the dependence of the power density spectrum (PDS) with energy may be caused by direct fluctuations in the Comptonizing medium (Nowak et al. 1999). In the soft state, the observed radiation comes mainly from the accretion disk, whose dynamical variability may be coupled to the emission processes in a non-linear way. Also, the effect of reflection of the hard X-rays from the disk surface may lead to a feedback effect and influence the variability amplitude (Uttley & McHardy 2005). For some sources, gravitational light bending may also be affecting the variability of the source (NGC-6-30-15; see Miniutti & Fabian 2004). In any case, the amplitude of the observed variability in both Galactic black holes and AGN is on the order of 30%.
One of the models for the physical origin of the disk variability are stochastically driven damped harmonic oscillations at the local epicyclic frequency (Misra & Zdziarski 2008).
Alternatively, or additionally, the variability may be caused by variations in the local viscous stress, which induces local accretion rate fluctuations, which in turn induces and adds to the variability downstream at smaller radii (Lyubarskii 1997). The model predicts a 1/f like variability for the inner disk accretion rate and a cutoff at the frequency corresponding to the viscous time-scale of the inner region. Indeed, the observed power spectra of black hole binaries and AGNs can be explained in terms of this viscous fluctuation models (e.g., Churazov et al. 2001; Uttley et al. 2005; Titarchuk et al. 2007; Ingram & Done 2011). More interestingly, since in this model the disturbance travels from the outer to the inner regions and if higher energy photons are preferentially produced in the inner regions, there would be a time-lag between high- and low-energy photons. The cylindrical geometry would make this time-lag inversely proportional to frequency (Misra 2000). The observed time-lags in black hole binaries and AGNs has this frequency dependence (Nowak et al. 1999), which gives strong credibility to the viscous fluctuation model, which otherwise would be difficult to explain. Theoretically too, one expects that a turbulent viscous stress, perhaps arising from the magneto-hydrodynamic rotational instability, should show high-amplitude variability as indicated by numerical simulations. Magneto-hydrodynamic simulations of radiation pressure dominated accretion disks use however the shearing box geometry, and hence they do not provide information about the nature of the viscous instability (Hirose et al. 2009).
It is interesting to study which effect the viscous stress fluctuations will have on the overall stability of radiation pressure dominated disks. If the viscous fluctuation amplitude is low, a linear analysis would naturally show that the unstable mode and viscous fluctuations would be uncoupled and the variability will simply be their sum. In other words, the perturbations in the linear regime would grow because of the unstable mode and would not be affected by the viscous fluctuations. However, when the viscous fluctuation amplitudes are high, there may be non-trivial and non-linear coupling between the two, perhaps leading to interesting results. This may especially be true when the systems evolves due to the instability and the viscous time-scale on which the fluctuations occur changes in the disk. Therefore, to properly understand these effects, we undertake here a numerical computation to simulate the time-dependent behavior of a standard accretion disk with viscous fluctuations.
The article is organized as follows. In Sect. 2 we describe our model for the viscosity fluctuations, giving also the references to a series of previous work where our radiation pressure instability numerical model was presented and developed. In Sect. 3 we present the results, showing first (Sect. 3.1) the case of stable accretion disk models with viscosity fluctuations, and second (Sect. 3.2) the case of unstable models with fluctuations. In Sect. 4 we discuss the results and their implications.
2. The numerical scheme
We used the 1(+1)-D hydrodynamical code developed and described first by Janiuk et al. (2002) for the time-dependent evolution of an accretion disk. Depending on the mean accretion rate, the disk may become unstable due to the radiation pressure domination. The code has been generalized to incorporate two phase flows taking into account mass exchange between the disk and an overlying corona (Janiuk & Czerny 2005) and the possibility of a fraction of the power being transmitted to the a jet/outflow (e.g., Kunert-Bajraszewska et al. 2010). As in the standard model, the code assumes that the flow is Keplerian but allows for the possibility of energy advection to smaller radii.
We here adopted the kinematic viscosity of Shakura & Sunyaev (1973) as less than, or equal to, the sound speed times the disk vertical scaleheight, via the dimensionless proportionality parameter α. We incorporated viscous fluctuations in the disk by considering the time-varying α parameter given by (see Lyubarskii 1997) ![\begin{equation} \alpha(r,t) = \alpha_{0} [1+\beta(r,t)], \label{eq:alphart} \end{equation}](/articles/aa/full_html/2012/04/aa18765-11/aa18765-11-eq28.png) (3)where α0 is a standard constant value on the order of 0.01 − 0.1, and the small factor β(r,t) accounts for the fluctuating part. whose time variation is assumed to follow the Markov chain process:
(3)where α0 is a standard constant value on the order of 0.01 − 0.1, and the small factor β(r,t) accounts for the fluctuating part. whose time variation is assumed to follow the Markov chain process: 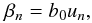 (4)where b0 is a parameter and
(4)where b0 is a parameter and 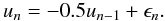 (5)The factor 0.5 in the above equation ensures that the Markov chain does not diverge for large n. In general, the modulus of this factor should be less than 1.0, and its value governs the number of series steps between the peaks, N, as well as the amplitude of the oscillations, var u. For a factor 0.5, we have N ≈ 2.6 and var u = 0.75 var ϵ (see e.g. King et al. 2004; Janiuk & Czerny 2007). The random variable ϵn is generated with a uniform distribution between − 1 and 1. The timescale of the fluctuation is given by the local viscous time-scale at that radius r expressed in terms of the Schwarzschild radius 2GM/c2, as
(5)The factor 0.5 in the above equation ensures that the Markov chain does not diverge for large n. In general, the modulus of this factor should be less than 1.0, and its value governs the number of series steps between the peaks, N, as well as the amplitude of the oscillations, var u. For a factor 0.5, we have N ≈ 2.6 and var u = 0.75 var ϵ (see e.g. King et al. 2004; Janiuk & Czerny 2007). The random variable ϵn is generated with a uniform distribution between − 1 and 1. The timescale of the fluctuation is given by the local viscous time-scale at that radius r expressed in terms of the Schwarzschild radius 2GM/c2, as 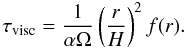 (6)Here H is the height, Ω the Keplerian angular velocity and
(6)Here H is the height, Ω the Keplerian angular velocity and 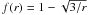 is the boundary condition to ensure that the torque vanishes at the last stable orbit, which also implies that the density in the disk becomes zero at its inner edge. The coherent length over which α varies is assumed to be the local height H, which is calculated from the total pressure as H = cs/Ω.
is the boundary condition to ensure that the torque vanishes at the last stable orbit, which also implies that the density in the disk becomes zero at its inner edge. The coherent length over which α varies is assumed to be the local height H, which is calculated from the total pressure as H = cs/Ω.
The computations are numerically expensive and were performed with the message-passing-interface technique on multi-CPU Linux computer cluster machines. We had to restrict the number of radius bins to about 200. For typical parameters used in this work, this translates into a bin size Δr ~ H0(r)/3, where H0(r) is the height of the steady state disk. This radial grid was kept fixed through the time-evolution, i.e., we did not adaptively change the radial grid. However, the α variability is taken to be coherent over a region ~H in the model, where H is the height at a given time. We took this into account by incorporating a multiplicative factor on β of 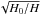 , which is typically small. This factor increases/decreases the viscous variability when the coherent length scale is shorter/longer than the grid size bin. This scheme is similar to the one used by Mayer & Pringle (2006) to model magnetic dynamo evolution.
, which is typically small. This factor increases/decreases the viscous variability when the coherent length scale is shorter/longer than the grid size bin. This scheme is similar to the one used by Mayer & Pringle (2006) to model magnetic dynamo evolution.
3. Results
3.1. Stable accretion disk models with viscosity fluctuations
We first studied the effect of viscous fluctuations on stable accretion disks. Ideally, one should analyze accretion disks where the accretion is low, such that the disk is not radiation pressure dominated. However, for these disks the height H ≪ r and hence the numerical computation would require very many radial bins to incorporate the viscous fluctuations correctly. Hence, we considered disks in which the viscous stress scales only with gas pressure, i.e., Trφ = αPgas.
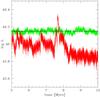 |
Fig. 1 Lightcurves of models for stable disks in which the viscous stress scales only with the gas pressure. The green (red) line shows the model with viscous fluctuation amplitude b0 = 0.6 (0.99), and the thick black line shows the model with b0 = 0.0. The mean viscosity parameter α0 = 0.1, the mean accretion rate is ṁ = 0.33, and the black hole mass is 3 × 108 M⊙. |
 |
Fig. 2 Power density spectra of the luminosity fluctuations for stable disks in which the viscous stress scales only with the gas pressure. The models have flickering parameters of b0 = 0.6, b0 = 0.99, b0 = 1.5 and b0 = 2.0 shown with green, red, magenta, and blue points, respectively. The mean viscosity parameter α0 = 0.1, the mean accretion rate is ṁ = 0.33, and the black hole mass is 3 × 108 M⊙. |
 |
Fig. 3 Lightcurves of models for stable disks in which the viscous stress scales only with the gas pressure with flickering parameter b0 = 0.3, 0.6 and 0.99, marked with magenta, green and red lines, respectively, and the thick black line shows the model with b0 = 0.0 The mean viscosity parameter α0 = 0.1, the mean accretion rate is ṁ = 0.33, and the black hole mass is 10 M⊙. |
 |
Fig. 4 Power density spectra of the luminosity fluctuations for stable disks in which the viscous stress scales only with the gas pressure. The models have flickering parameters of b0 = 0.1, b0 = 0.3, b0 = 0.6, b0 = 0.99 and b0 = 2.0 shown with cyan, magenta, green, red and blue points, respectively. The mean viscosity parameter α0 = 0.1, the mean accretion rate is ṁ = 0.33, and the black hole mass is 10 M⊙. |
In the presence of viscous fluctuations the luminosity of the disk varies, as shown in Fig. 1, where we plot the lightcurves of a disk around a 3 × 108 M⊙ black hole with accretion rate ṁ = 0.33 in Eddington units and α0 = 0.1. As expected, as the flickering amplitude b0 increases, so does the variability of the luminosity. It is more illustrative to see the power density of the luminosity fluctuations that are shown in Fig. 2. For small variations in the viscous fluctuations, the variation in the luminosity can be estimated to have a power spectrum of roughly ∝ 1/f (Lyubarskii 1997). This is qualitatively consistent with the power spectra shown in Fig. 2, especially for small b0, i.e., the power spectrum is roughly ∝ 1/f such that f × power is nearly independent of the frequency. For higher values of b0 there is a significant increase of power in low frequency. The reason for this behavior is more evident when we plot the light curves for a disk around a 10 M⊙ black hole in Fig. 3 and the corresponding power spectra in Fig. 4. The lightcurves show that for large b0 apart from increased stochastic variability, there are also long time-scale “jumps” in the luminosity. These low-frequency variations, which occur in the viscous time-scale of the outer radii, may indeed be caused by outer boundary conditions that are imposed in the numerical scheme. The outer disk radius for the computations was taken to be ~1000 Schwarzschild radii. Increasing the outer radii incorporates a large cost in computation time, especially since the total simulation time has to be increased to be longer than the viscous time-scale of the outer radius.
While the low-frequency variability at large b0 may be an artifact of the outer boundary conditions, we note that it will not effect the results of our primary study, which is the effect of fluctuations on unstable disks. Here the instability time-scale is the viscous time-scale of the inner accretion disk region, which is significantly shorter than the viscous time-scale of the outer radius.
Therefore, our numerically computed luminosity variations of the viscous fluctuations are in general consistent with those expected from analytical estimates that predict power spectra ∝ 1/f.
3.2. Unstable accretion disk models with viscosity fluctuations
After verifying that the results of our numerical code are generally consistent with those expected for a stable accretion disk where analytical results are possible, we considered the more physically consistent situation where the viscous stress scales with the total pressure. Our primary result is illustrated in Fig. 5. For low values of viscous fluctuation amplitude b0 = 0.66, the disk is unstable and shows periodic very high amplitude outbursts as expected.
It can be seen from the plot that the strong fluctuations in the luminosity occur when the flux level of the source is high. This is because during these “high” flux states, the disk is thicker and hence the stochastic viscous fluctuations occur over a wider coherent range. Moreover, the viscous time-scale is shorter and hence the effects of viscous fluctuations are more pronounced.
Increasing b0 = 0.99 causes the oscillations to become irregular, and the duration of the bursts also changes. Further increase of b0 = 2.0 decreases the amplitude of the bursts, and the lightcurve becomes more “chaotic” in nature. Finally for a large b0 = 2.5, after a transient beginning phase, the lightcurve becomes stochastic and there is no evidence for any cyclic bursts.
The time-averaged accretion rate in all simulations shown in Fig. 5 is equal to the external accretion rate supplied to the disk (ṁ = 0.33). When the radiation pressure instability operates, the disk luminosity cannot be constant, corresponding to this average acretion rate, but switches between the low and high luminosities, corresponding to the stages when the accretion rate onto the black hole is either much higher or much lower than the average value. When the instability is suppressed by the viscous fluctuations, there are no longer any “low” or “high” states.
For stellar mass black holes, we find similar results with the disk showing an oscillatory behavior for low values of b0 and stochastic behavior for higher values (see Fig. 6). The disks stabilize at a lower value of b0 ≈ 1 compared to b0 ≥ 1.5 for AGN disks. This may be related to the fact that at the same Eddington rate an AGN disk is more radiation pressure dominated than that for a stellar mass black hole.
 |
Fig. 5 Lightcurves in the five models of accretion disk oscillations caused by the radiation pressure instability limit-cycle. The results are shown for the alpha flickering models with parameters b0 = 0.0, b0 = 0.6, b0 = 0.99, b0 = 2, and b0 = 2.5, from top to bottom, respectively (the quiescent period between thew outbursts in b0 = 0.0 model is about 0.6 Myr). The model parameters are black hole mass of 3 × 108 M⊙, accretion rate of ṁ = 0.33 in Eddington units, α0 = 0.1. The model includes no jet. |
 |
Fig. 6 Lightcurves in the five models of accretion disk oscillations caused by the radiation pressure instability limit-cycle. The results are shown for the alpha flickering models with parameters b0 = 0.0, b0 = 0.3, b0 = 0.6, b0 = 0.99, and b0 = 2.0, from top to bottom, respectively. The model parameters are black hole mass of 10 M⊙, accretion rate of ṁ = 0.33 in Eddington units, α0 = 0.1. The model includes no jet. |
We also considered the effect of power being transferred to a jet. Specifically, we parametrized the jet (cf. Janiuk & Czerny 2011) by including an additional term in the energy equation 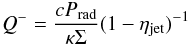 (7)where the fraction ηjet is assumed to depend on time and distance from the black hole via the local accretion rate
(7)where the fraction ηjet is assumed to depend on time and distance from the black hole via the local accretion rate 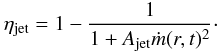 (8)with Ajet being a parameter of the model. The physical meaning of this parametrization is that at the Eddington accretion limit there would be equipartition between the jet and disk radiation for Ajet = 1. We adopted a value of Ajet = 5 or = 10, which means a moderately strong jet. Without viscous fluctuations,the disk undergoes cyclic oscillations even for these moderately strong jets, but with a reduced amplitude. The inclusion of comparatively low viscous fluctuations b0 = 0.3 stabilizes the disk for both values of Ajet. Thus a moderately strong jet decreases the amount of viscous fluctuation that are required for stability.
(8)with Ajet being a parameter of the model. The physical meaning of this parametrization is that at the Eddington accretion limit there would be equipartition between the jet and disk radiation for Ajet = 1. We adopted a value of Ajet = 5 or = 10, which means a moderately strong jet. Without viscous fluctuations,the disk undergoes cyclic oscillations even for these moderately strong jets, but with a reduced amplitude. The inclusion of comparatively low viscous fluctuations b0 = 0.3 stabilizes the disk for both values of Ajet. Thus a moderately strong jet decreases the amount of viscous fluctuation that are required for stability.
In Table 1 we present the summary of the models we calculated. In summary, high-amplitude viscous fluctuations stabilize the disk against the radiation pressure instability. The strength of the viscous fluctuation required to stabilize the disk is slightly lower for stellar mass black hole systems than AGNs and decreases when there is an effective jet in the system. The table also shows the normalized rms variability of the luminosity. Note that for locally stable disks (i.e., when τrφ ∝ Pgas), the rms increases with b0, while for locally unstable disks (i.e. when τrφ ∝ Ptot), it generally decreases. This is because the viscous fluctuations stabilize the disk and high-amplitude oscillations disappear.
Summary of the time-dependent disk models.
We defer a detailed comparison of these results with the observations of a particular source to future work. This may be conducted for the various states of the microquasar GRS 1915+105 (Belloni et al. 2000). Another good candidate may be the recently studied source IGR J17091-3624, which also exhibits the so-called “heartbeat” states for luminosity variations in some spectral states, as well as stochastic fluctuations (Altamirano et al. 2011). The detailed modeling would require a proper determination of the Eddington ratio as well as an estimation of the fraction of energy going into jet power from radio observations.
4. Summary
Our numerical simulations show that high-amplitude viscous fluctuations can stabilize radiation pressure dominated standard accretion disks. This may explain why even at luminosities close to the Eddington limit, black hole systems exhibit spectral signatures of a standard accretion disk that do not show high-amplitude cyclic behavior. Instead, they show stochastic variation that may be caused by viscous fluctuations that stabilize the disk.
At low luminosities, the disk would be gas pressure dominated and hence intrinsically stable. Here, viscous fluctuations may produce variability in the luminosity. However, since it is likely that the coherent length of the viscous variability scales as the height of the disk, which is much smaller than the radius for low accretion rate systems, the net effect on the total luminosity should be weak. In other words, since H/R ≪ 1 for these sources, the viscous fluctuations at different radii will incoherently add to give a diminishing effect on the total luminosity of the disk. This may explain why the standard disk component in some low-luminosity systems are found to be steady with little variability.
While in this work we considered some general characteristics of Galactic black holes and AGNs, a more detailed comparison with data of one or two specific sources may provide both qualitative and quantitative insights. In particular, the time-varying spectra and not just the integrated luminosity from these numerical simulations should be compared with data from some chosen sources. The model should be confronted with the variability as a function of energy as well as frequency-dependent time-lags.
In the light of the results of this work, it will also be interesting to re-examine the models for GRS 1915+105 for cases
with or without oscillations. Detailed comparison between the expected and observed lightcurves may reveal whether the viscous variability amplitude changes between the different states or is the fraction of energy going into the jet. The study may finally reveal the distinguishing feature of the source compared to other black hole systems.
Finally, a more comprehensive numerical analysis needs to be undertaken with different boundary conditions and assumptions, which may identify the crucial conditions necessary for the unstable disk to be stabilized by viscous fluctuations. An adaptive radial grid will be particularly useful. The rotating disk may also give rise to non-trivial effects, which can be studied only by a full 3D hydrodynamic code. Indeed, what seems to be important is that the non-linear effect of high-amplitude perturbations, which can be captured only by numerical simulations, can give rise to non-trivial results such as stabilization of a system that is locally highly unstable.
Acknowledgments
We thank Bozena Czerny for helpful discussions. Part of this work was done thanks to the hospitality of the Inter University Center for Astronomy and Astrophysics, Pune, India. Partially this work was supported by grant NN 203 512638 from the Polish National Science Center. A part of the numerical computations have been performed on the computer cluster machines in the Copernicus Astronomical Center of PAS in Warsaw.
References
- Altamirano, D., Belloni, T., Linares, M., et al. 2011, ApJ, 742, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T., Klein-Wolt, M., Méndez, M., van der Klis, M., & van Paradijs, J. 2000, A&A, 355, 271 [NASA ADS] [Google Scholar]
- Czerny, B., & Janiuk, A. 2007, A&A, 464, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churazov, E., Gilvanov, M., & Revnivtsev, M. 2001, MNRAS, 321, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Gierlinski, M., & Kubota, A. 2007, A&AR, 15, 1 [Google Scholar]
- Hirose, S., Krolik, J. H., & Blaes, O. 2009, ApJ, 691, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., & Done, C. 2011, MNRAS, 415, 2323 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., & Czerny, B. 2005, MNRAS, 356, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., & Czerny, B. 2007, A&A, 466, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janiuk, A., & Czerny, B. 2011, MNRAS, 414, 2186 [Google Scholar]
- Janiuk, A., Czerny, B., & Siemiginowska, A. 2002, ApJ, 576, 908 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Pringle, J. E., West, R. G., & Livio, M. 2004, MNRAS, 348, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kunert-Bajraszewska, M., Janiuk, A., Gawronski, M., & Siemiginowska, A. 2010, ApJ, 718, 1345 [NASA ADS] [CrossRef] [Google Scholar]
- Lightman, A. P., & Eardley, D. M. 1974, ApJ, 187, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarskii, Yu. E. 1997, MNRAS, 292, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, M., & Pringle, J. E. 2006, MNRAS, 368, 379 [NASA ADS] [Google Scholar]
- Misra, R. 2000, ApJ, 529, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Misra, R., & Zdziarski, A. A. 2008, MNRAS, 387, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Miniutti, G., & Fabian, A. C. 2004, MNRAS, 349, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Nowak, M. A., Vaughan, B. A., Wilms, J., Dove, J. B., & Begelman, M. C. 1999, ApJ, 510, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Neilsen, J., Remillard, R. A., & Lee, J. C. 2011, ApJ, 737, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N., & Sunyaev, R. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shakura, N., & Sunyaev, R. 1976, MNRAS, 175, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. L., Lightman, A. P., & Eardley, D. M. 1976, 204, 187 [Google Scholar]
- Titarchuk, L., Shaposhnikov, N., & Arefiev, V. 2007, ApJ, 660, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., & McHardy, I. M. 2005, MNRAS, 363, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., McHardy, I. M., & Vaughan, S. 2005, MNRAS, 359, 345 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Lightcurves of models for stable disks in which the viscous stress scales only with the gas pressure. The green (red) line shows the model with viscous fluctuation amplitude b0 = 0.6 (0.99), and the thick black line shows the model with b0 = 0.0. The mean viscosity parameter α0 = 0.1, the mean accretion rate is ṁ = 0.33, and the black hole mass is 3 × 108 M⊙. |
| In the text | |
 |
Fig. 2 Power density spectra of the luminosity fluctuations for stable disks in which the viscous stress scales only with the gas pressure. The models have flickering parameters of b0 = 0.6, b0 = 0.99, b0 = 1.5 and b0 = 2.0 shown with green, red, magenta, and blue points, respectively. The mean viscosity parameter α0 = 0.1, the mean accretion rate is ṁ = 0.33, and the black hole mass is 3 × 108 M⊙. |
| In the text | |
 |
Fig. 3 Lightcurves of models for stable disks in which the viscous stress scales only with the gas pressure with flickering parameter b0 = 0.3, 0.6 and 0.99, marked with magenta, green and red lines, respectively, and the thick black line shows the model with b0 = 0.0 The mean viscosity parameter α0 = 0.1, the mean accretion rate is ṁ = 0.33, and the black hole mass is 10 M⊙. |
| In the text | |
 |
Fig. 4 Power density spectra of the luminosity fluctuations for stable disks in which the viscous stress scales only with the gas pressure. The models have flickering parameters of b0 = 0.1, b0 = 0.3, b0 = 0.6, b0 = 0.99 and b0 = 2.0 shown with cyan, magenta, green, red and blue points, respectively. The mean viscosity parameter α0 = 0.1, the mean accretion rate is ṁ = 0.33, and the black hole mass is 10 M⊙. |
| In the text | |
 |
Fig. 5 Lightcurves in the five models of accretion disk oscillations caused by the radiation pressure instability limit-cycle. The results are shown for the alpha flickering models with parameters b0 = 0.0, b0 = 0.6, b0 = 0.99, b0 = 2, and b0 = 2.5, from top to bottom, respectively (the quiescent period between thew outbursts in b0 = 0.0 model is about 0.6 Myr). The model parameters are black hole mass of 3 × 108 M⊙, accretion rate of ṁ = 0.33 in Eddington units, α0 = 0.1. The model includes no jet. |
| In the text | |
 |
Fig. 6 Lightcurves in the five models of accretion disk oscillations caused by the radiation pressure instability limit-cycle. The results are shown for the alpha flickering models with parameters b0 = 0.0, b0 = 0.3, b0 = 0.6, b0 = 0.99, and b0 = 2.0, from top to bottom, respectively. The model parameters are black hole mass of 10 M⊙, accretion rate of ṁ = 0.33 in Eddington units, α0 = 0.1. The model includes no jet. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


