| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 15 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201118139 | |
| Published online | 12 April 2012 | |
Long-term magnetic field monitoring of the Sun-like star ξ Bootis A⋆,⋆⋆
1 Université de Toulouse, UPS-OMP, Institut de Recherche en Astrophysique et Planétologie, Toulouse, France
e-mail: amorgent@ast.obs-mip.fr; petit@ast.obs-mip.fr
2 CNRS, Institut de Recherche en Astrophysique et Planétologie, 14 avenue Edouard Belin, 31400 Toulouse, France
3 Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA
4 Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
5 Dublin Institute for Advanced Studies, School of Cosmic Physics, 31 Fitzwilliam Place, Dublin 2, Ireland
6 Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
7 Centre for Astronomy, School of Engineering and Physical Sciences, James Cook University, 4811 Townsville, Australia
8 SUPA, School of Physics & Astronomy, University of St Andrews, North Haugh, St Andrews KY16 9SS, UK
9 Instituto de Astronomia, Universidad Nacional Autonoma de Mexico, 04510 Coyoacan, DF, Mexico
10 Institut d’Astrophysique et de Géophysique, Université de Liège, Allée du 6 Août 17, 4000 Liège, Belgium
Received: 23 September 2011
Accepted: 23 February 2012
Aims. We aim to investigate the long-term temporal evolution of the magnetic field of the solar-type star ξ Bootis A, both from direct magnetic field measurements and from the simultaneous estimate of indirect activity indicators.
Methods. We obtained seven epochs of high-resolution, circularly-polarized spectra from the NARVAL spectropolarimeter between 2007 and 2011, for a total of 76 spectra. Using approximately 6100 photospheric spectral lines covering the visible domain, we employed a cross-correlation procedure to compute a mean polarized line profile from each spectrum. The large-scale photospheric magnetic field of the star was then modelled by means of Zeeman-Doppler Imaging, allowing us to follow the year-to-year evolution of the reconstructed magnetic topology. Simultaneously, we monitored the width of several magnetically sensitive spectral lines, the radial velocity, the line asymmetry of intensity line profiles, and the chromospheric emission in the cores of the Ca II H and Hα lines.
Results. During the highest observed activity states, in 2007 and 2011, the large-scale field of ξ Bootis A is almost completely axisymmetric and is dominated by its toroidal component. The toroidal component persists with a constant polarity, containing a significant fraction of the magnetic energy of the large-scale surface field through all observing epochs. The magnetic topologies reconstructed for these activity maxima are very similar, suggesting a form of short cyclicity in the large-scale field distribution. The mean unsigned large-scale magnetic flux derived from the magnetic maps varies by a factor of about 2 between the lowest and highest observed magnetic states. The chromospheric flux is less affected and varies by a factor of 1.2. Correlated temporal evolution, due to both rotational modulation and seasonal variability, is observed between the Ca II emission, the Hα emission and the width of magnetically sensitive lines. The rotational dependence of polarimetric magnetic measurements displays a weak correlation with other activity proxies, presumably due to the different spatial scales and centre-to-limb darkening associated with polarimetric signatures, as compared to non-polarized activity indicators. Better agreement is observed on the longer term. When measurable, the differential rotation reveals a strong latitudinal shear in excess of 0.2 rad d-1.
Key words: stars: activity / stars: atmospheres / stars: chromospheres / stars: imaging / stars: solar-type / stars: magnetic field
Based on observations obtained at the Bernard Lyot Telescope (TBL, Pic du Midi, France) of the Midi-Pyrénées Observatory, which is operated by the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique of France.
Tables 3–6 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
It is generally accepted that the regular succession of magnetic minima and maxima observed in the Sun and in many cool stars is the result of an astrophysical dynamo, triggered by the combined presence of an outer convection layer and stellar rotation (e.g. Brandenburg & Subramanian 2005). Using chromospheric emission as a magnetic proxy, observations of stellar cyclicity have been conducted for several decades, revealing a richness in the temporal behaviour of solar-type dwarfs (e.g. Baliunas et al. 1995; Saar & Brandenburg 1999; Lockwood et al. 2007; Oláh et al. 2009; Metcalfe et al. 2010). More recently, spectropolarimetric observations of cool dwarfs have become sufficiently accurate to enable the direct detection of magnetic fields on low-activity stars (e.g. Petit et al. 2008), further expanding our insight into magnetic variability through the ability to monitor the long-term evolution of magnetic vectorial topologies, instead of the disc-averaged chromospheric or photospheric fluxes.
For most targets, the time-base of spectropolarimetric observations is still restricted to a few years. This limited time span can only offer a fragmentary view of magnetic cycles, except for cycle periods much shorter than solar. A few dwarfs have already been observed to undergo at least one global polarity switch (e.g. Petit et al. 2009), or to complete a full magnetic cycle (Fares et al. 2009; Morgenthaler et al. 2011). Following the temporal evolution of large-scale stellar magnetic topologies provides important constraints for numerical simulations of stellar dynamos, particularly now that the magnetic cycles of cool stars can be investigated through 3-D MHD simulations (Brown et al. 2010, 2011; Ghizaru et al. 2010).
Systematic comparisons between the temporal evolution of the large-scale magnetic field and other activity proxies (photospheric or chromospheric) are still largely unexplored. Such studies are of interest because different measurable quantities related to magnetic activity can carry complementary information about the magnetic field generation in cool stellar objects, in particular through the different spatial scales to which they relate. As a step in this direction, we concentrate here on the solar-type star ξ Bootis A. This active star is a main-sequence dwarf with an effective surface temperature of 5600 K and a surface gravity log g = 4.65 (Valenti & Fischer 2005). As a visual binary system, the masses of ξ Bootis A and B have been determined from astrometry to be 0.85 and 0.72 M⊙ , respectively (Wielen 1962). The very high magnetic activity of ξ Bootis A (Baliunas et al. 1995) has allowed early magnetic field detections (Robinson et al. 1980) and is linked to a fast rotation period of 6.43 d (Toner & Gray 1988). Given a low vsini of 3 km s-1 (Gray 1984) and a stellar radius of about 0.8 R⊙ (Petit et al. 2005), the short rotation period implies a low stellar inclination angle of about 28°.
In this article, we simultaneously investigate the seasonal evolution of various activity proxies of ξ Bootis A using (a) the large-scale surface magnetic topology, along with its short-term distortion through latitudinal differential rotation, (b) the Zeeman broadening of high Landé factor spectral lines, (c) the Ca II H and Hα core emission and (d) the radial velocity of intensity profiles, together with their asymmetry. We first describe the instrumental setup and spectropolarimetric time-series used in this study and the procedure employed to extract Zeeman signatures. We then detail the reconstruction of the large-scale magnetic topology of the star at seven different epochs, followed by the extraction, from the same data sets, of a number of classic activity tracers. We finally discuss the results derived from our measurements.
2. Instrumental setup, data reduction, and multi-line extraction of Zeeman signatures
 |
Fig. 1 Normalized Stokes V profiles (V/Ic) of ξ Boo A for 2007.59, 2008.09, 2009.46, 2010.04, 2010.48, 2010.59 and 2011.07 (from left to right and top to bottom), after correction for the mean radial velocity of the star (the radial velocity values are listed in Table 2). Black lines represent the data and red lines correspond to synthetic profiles of our magnetic model. Successive profiles are shifted vertically for display clarity. Rotational phases of observations are indicated in the right-hand part of the plot and error bars are illustrated on the left side of each profile. |
The data sets were collected with the NARVAL spectropolarimeter at the Telescope Bernard Lyot (Observatoire du Pic du Midi, France) whose instrumental setup is identical to the one described by Petit et al. (2008). The échelle spectrograph has a resolution of 65 000 and covers the whole optical wavelength domain from near-ultraviolet (370 nm) to near-infrared (1000 nm) in one exposure, with 40 orders on the CCD. NARVAL provides simultaneous recordings of the intensity spectrum (Stokes I) and one polarized spectrum (linear or circular). Here we deal with circular polarization (Stokes V parameter). Seven sets of spectra were obtained between 2007 and 2011 (see Tables 3 and 4). They each contain between 7 and 19 spectra (in 2011.07 and 2008.09, respectively), obtained over 15 to 62 consecutive days (in 2007.59 and 2010.04, respectively).
The raw data were processed using LibreEsprit, an automatic reduction software developed for NARVAL, based on the algorithm detailed by Donati et al. (1997). For the reduced spectra of ξ Bootis A, the maximum signal-to-noise ratio (S/N) is achieved at a wavelength of about 730 nm. The S/N value depends on the adopted exposure time and weather conditions above the Pic du Midi Observatory, with typical values varying between 450 and 700. The S/N drops in the blue part of the spectrum, with a usual value of about 100 around the Ca II H&K lines. The situation is better in the near-infrared, with a S/N close to 500 in the neighbourhood of FeI@846.8404 used later in this study.
The S/N of the polarized spectra is not sufficient to detect Zeeman signatures in individual spectral lines, even for photospheric lines with high Landé factors. To achieve a sufficiently low noise level, we used the reduced spectrum to calculate a single, cross-correlated photospheric line profile using the least square deconvolution (LSD) multi-line technique (Donati et al. 1997; Kochukhov et al. 2010). We employed a line-list of about 6100 spectral lines matching a stellar photospheric model for the spectral type of ξ Bootis A (G8V). This line-list is the same as the one previously used by Petit et al. (2005). Thanks to this cross-correlation approach, the noise level of the mean Stokes V line profiles is reduced by a factor of about 30 with respect to the initial spectrum, so that the resulting noise level lies in the range 3.0 × 10-5−1.6 × 10-4Ic, where Ic denotes the continuum intensity.
Figure 1 shows the seven sequences of Stokes V LSD line profiles corresponding to the seven observing runs. The rotational phases, indicated in the right-hand part of the plot and listed in Tables 3 and 4, were calculated according to the ephemeris of Petit et al. (2005), who adopted a rotational period of 6.43 d (Toner & Gray 1988) and a Julian date for zero rotational phase equal to 2 452 817.41. This rotation period is longer than the equatorial period derived from the modelling of the surface differential rotation (see Sect. 3.2), because it better represents the rotation period of the higher stellar latitudes that are expected to dominate the disc-integrated activity tracers, owing to the star’s low inclination angle. The rotational modulation of most activity proxies investigated in this study is more pronounced when using the adopted period of 6.43 d.
Polarized features in the profile core, interpreted as Zeeman signatures, are detected for a large fraction of the observations, with amplitudes comfortably exceeding the noise level. It can already be seen in Fig. 1 that the signal amplitudes are higher in 2007.59 than in the following years. If we take a closer look at the shape of the signatures, we note that the majority of them are antisymmetric about the line centre (e.g., the rotational phase 1.959 in 2007.59). A few of them are almost symmetric (phase 3.203 in 2007.59, 4.04 in 2008.09, and 10.172 in 2010.04). We note also that the sign of the signatures (symmetric or antisymmetric) is the same throughout the observations.
Magnetic quantities derived from the set of magnetic maps.
Mean values of the activity tracers.
3. Photospheric magnetic field
 |
Fig. 2 Magnetic maps of ξ Bootis A, derived from 2007.59, 2008.09, 2009.46, 2010.04, 2010.48, 2010.59, and 2011.07 observations (from left to right and top to bottom). For each data set, the three charts illustrate the field projection onto one axis of the spherical coordinate frame with, from top to bottom, the radial, azimuthal, and meridional field components. The magnetic field strength is expressed in Gauss. |
 |
Fig. 3 Four sets of six subplots, each set corresponding to one epoch (from top to bottom, 2007.59, 2008.09, 2009.46, and 2010.04). For each set, the left subplots contain, from top to bottom, the NHα-index (filled circles and left axis) and NCaIIH-index (crosses and right axis of the top panel of each set), the FeI@846.8404 magnetic line widths (km s-1), Bl (Gauss). The right subplots, from top to bottom, correspond to the velocity spans (km s-1) obtained from the profile bisectors (Sect. 4.2), the radial velocity (km s-1), and the mean unsigned magnetic strength of the total (full line), radial (dashes), azimuthal (dot-dashes) and meridional (dots) magnetic field components extract from the ZDI maps. Error bars are not included whenever they are smaller than the symbol size. |
3.1. Longitudinal magnetic field
Using the LSD line profiles in the Stokes parameters I and V, we can derive the longitudinal component Bl of the surface magnetic field, as averaged over the visible hemisphere of the star. To do so, we used the centre-of-gravity method described by Rees & Semel (1979), through the equation 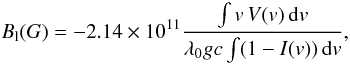 (1)where v (km s-1) is the radial velocity in the stellar rest-frame, λ0 (nm) the mean wavelength of the line mask used to compute the LSD profile (538 nm in our case), g the mean effective Landé factor of the line list (equal to 1.21), and c (km s-1) the velocity of light in vacuum. The integration window covers a velocity range of ±16 km s-1 around the line centre.
(1)where v (km s-1) is the radial velocity in the stellar rest-frame, λ0 (nm) the mean wavelength of the line mask used to compute the LSD profile (538 nm in our case), g the mean effective Landé factor of the line list (equal to 1.21), and c (km s-1) the velocity of light in vacuum. The integration window covers a velocity range of ±16 km s-1 around the line centre.
The Bl values are listed in Tables 5 and 6, and the averaged values for each epoch are recorded in Table 1. We note that for Stokes V profiles with the same amplitude, longitudinal fields derived using the centre-of-gravity technique are a maximum when the Stokes V signature is anti-symmetric about the line centre. This is often not the case in our observations, because ξ Bootis A has a large-scale toroidal field component (see Petit et al. 2005, and Sect. 3.2). If a profile has a higher redshift for the zero-crossing velocity, for example, phase 6.148 in 2010.48, this can result in a lower Bl value, in spite of a high Stokes V amplitude.
The rotational dependence of Bl (Figs. 3 and 4) is visible at several epochs, and is especially obvious in 2007.59 and 2010.59. The phase dependence is generally more complex than a sine curve, indicating that the surface magnetic geometry is not limited to a simple dipole. A long-term trend is also observed in the averaged Bl values (Fig. 6), with a strength of 8.7 G (with a dispersion of 7.1) in 2007.59 and a much lower average value of 4.6 G (with a dispersion of 3.1) in 2008.09. This global decrease can readily be seen in the decreased amplitude of the Stokes V profiles between the two epochs. Most of the later measurements have a similar or higher Bl value to that in 2007.59, with the exception of 2010.04, which has a value similar to that in 2008.09.
3.2. Magnetic maps
The rotational modulation observed in the line-of-sight projection of the magnetic field (Fig. 1) indicates a complex surface distribution of magnetic fields. We can model this complex field topology using a tomographic approach.
We employed Zeeman-Doppler Imaging (ZDI) to reconstruct the surface distribution of the magnetic vector from the time-series of Stokes V LSD profiles at each observing epoch. This method, first proposed by Semel (1989), was implemented and tested by Donati & Brown (1997). The version of the ZDI code used here assumes that the field geometry is projected onto a spherical harmonics frame (Donati et al. 2006). In this inversion procedure, the time series of Stokes V LSD profiles is compared to a set of synthetic Stokes V line profiles computed for the same rotational phases as the observed profiles. Synthetic Stokes profiles are calculated from an artificial star whose surface is divided into a grid of pixels. Each surface pixel is associated with a local Stokes I and V profile. Assuming a given magnetic field strength and orientation for each pixel, local Stokes V profiles are calculated under the weak-field assumption, where Stokes V is proportional to 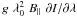 , with λ0 representing the average wavelength of the LSD profile, B ∥ the line-of-sight projection of the local magnetic field vector and g the effective Landé factor of the LSD profile.
, with λ0 representing the average wavelength of the LSD profile, B ∥ the line-of-sight projection of the local magnetic field vector and g the effective Landé factor of the LSD profile.
We furthermore assumed that there are no large-scale brightness inhomogeneities over the stellar surface, so that all synthetic Stokes I profiles are locally the same everywhere. The limitation of this assumption will be illustrated by the observed variations in radial velocity and profile bisectors (Sect. 4.2), providing us with evidence that Stokes I profiles do vary as a function of the rotational phase, due to starspots or plages. The restriction of the reconstructed magnetic topology to the global-scale component of the surface magnetic field is probably limiting the consequences of these model inaccuracies, which should affect mainly smaller, unresolved spatial scales. In the present model, the Stokes I profiles are assumed to possess a Gaussian shape, with a depth and width adjusted to achieve a good match between synthetic and observed Stokes I line profiles. We assumed a projected rotational velocity (vsini) of 3 km s-1 and an inclination angle equal to 28°, both of these values were previously used in the forward modelling of the field topology made by Petit et al. (2005). We also assumed the limb-darkening to be linear with μ = cos(θ), where θ is the limb angle, with a coefficient equal to 0.75. We finally restricted the spherical harmonics expansion to ℓmax ≤ 10, since no improvement to the fits, between modelled and observed LSD profiles, is noticed for values of ℓmax greater than 5.
Because each data set was collected over several weeks, we assumed that the magnetic geometry might be distorted by latitudinal differential rotation over the timespan of the data collection. We therefore included a two-parameter differential rotation law in our stellar model, with the form 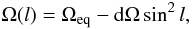 (2)
(2)
where Ω(l) is the rotation rate at latitude l, Ωeq the rotation rate of the equator and dΩ the difference in rotation rate between the poles and equator. Following the method of Petit et al. (2002), a grid of magnetic inversions was calculated for a range of values of the quantities Ωeq and dΩ. The values listed in Table 1 correspond to the χ2 minimum in the parameter plane, whenever this minimum exists and is unique in the scanned Ωeq -dΩ area.
One first limitation of this indirect imaging procedure is the roughness of the underlying stellar model, which, combined with the sparse phase sampling and uneven S/N ratio, may be the source of inaccuracies in the reconstructed magnetic geometry (see, e.g., Donati & Brown 1997). One other limitation of the maximum-entropy algorithm is the absence of error bars on the resulting maps. To limit the consequences of these two restrictions as much as possible, we do not discuss here the finest details of the magnetic topology (i.e., individual magnetic spots), but rather concentrate on a set of quantities derived from the largest spatial scales of the field geometry (e.g., its low-order multipolar expansion), as listed in Table 1. As an attempt to evaluate the uncertainties on these global magnetic quantities, we then reproduce the approach of Petit et al. (2008) and compute several magnetic maps, each of which is calculated using different values of the input parameters of ZDI (within the error bars on individual parameters). The dispersion of the resulting magnetic values are considered as error bars. As for other solar-like stars presented by Petit et al. (2008), we generally note that the resulting dispersion is dominated by the uncertainty on the inclination angle of ξ Bootis A.
The fits from our tomographic modelling are illustrated in Fig. 1 and the magnetic maps are given in Fig. 2. The modelled data were fitted to the observed ones with a reduced χ2 (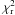 hereafter) of between 1.3 and 4.8 (see Table 1), showing that the fit accuracy never reached the noise level. The fit is not significantly improved by simple changes in the local line profile model, e.g. by the replacement of the Gaussian local Stokes I profile by a Lorentzian one (in an attempt to slightly improve the fitting of the profile wings), or the implementation of an ad-hoc asymmetry in local Stokes V profiles, as previously proposed by Petit et al. (2005). A possible cause for the repeated mismatch may be the residual effect of blended lines (Kochukhov et al. 2010) which could be larger than the noise level. Another likely cause is the intrinsic evolution of the magnetic topology during data collection, if this evolution is not entirely caused by latitudinal differential rotation, or if the latitudinal shear is following a different law than the simple formula used here. Fast evolution of the magnetic geometry is observed between 2010.48 and 2010.59, but the field configuration seems to be more stable at other epochs, for instance in 2010.04, where a 62 d timespan produced a magnetic inversion with
hereafter) of between 1.3 and 4.8 (see Table 1), showing that the fit accuracy never reached the noise level. The fit is not significantly improved by simple changes in the local line profile model, e.g. by the replacement of the Gaussian local Stokes I profile by a Lorentzian one (in an attempt to slightly improve the fitting of the profile wings), or the implementation of an ad-hoc asymmetry in local Stokes V profiles, as previously proposed by Petit et al. (2005). A possible cause for the repeated mismatch may be the residual effect of blended lines (Kochukhov et al. 2010) which could be larger than the noise level. Another likely cause is the intrinsic evolution of the magnetic topology during data collection, if this evolution is not entirely caused by latitudinal differential rotation, or if the latitudinal shear is following a different law than the simple formula used here. Fast evolution of the magnetic geometry is observed between 2010.48 and 2010.59, but the field configuration seems to be more stable at other epochs, for instance in 2010.04, where a 62 d timespan produced a magnetic inversion with 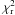 = 1.3.
= 1.3.
The limited lifetime of magnetic tracers is especially of concern in the measurement of surface differential rotation. In the ideal situation of a magnetic topology progressively distorted by a surface shear, the 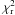 landscape in the Ωeq -dΩ plane takes the shape of a 2D paraboloid (Petit et al. 2002). This is never the case here, except for 2008.09. At other epochs, iso-
landscape in the Ωeq -dΩ plane takes the shape of a 2D paraboloid (Petit et al. 2002). This is never the case here, except for 2008.09. At other epochs, iso-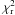 contours are sometimes not ellipsoidal (2009.46, 2010.48, 2010.59), delimit at least two local
contours are sometimes not ellipsoidal (2009.46, 2010.48, 2010.59), delimit at least two local 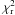 minima of similar depth (2011.07), or display no minimum (2007.59 and 2010.04). Therefore the apparent temporal variations of the shear shown in Table 1 should be taken with caution, even when the observed differences are above the statistical error bars. In particular, we note that modifying the number of profiles used to model the surface shear (for instance, by removing the first or last profile of a time-series) often has a significant impact on the measured dΩ, suggesting that intrinsic magnetic variability is affecting some of our differential rotation measurements. Whenever a unique
minima of similar depth (2011.07), or display no minimum (2007.59 and 2010.04). Therefore the apparent temporal variations of the shear shown in Table 1 should be taken with caution, even when the observed differences are above the statistical error bars. In particular, we note that modifying the number of profiles used to model the surface shear (for instance, by removing the first or last profile of a time-series) often has a significant impact on the measured dΩ, suggesting that intrinsic magnetic variability is affecting some of our differential rotation measurements. Whenever a unique 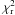 minimum was not identified, the differential rotation parameters of 2008.09 were adopted in the inversion process.
minimum was not identified, the differential rotation parameters of 2008.09 were adopted in the inversion process.
The magnetic maps show the reconstructed geometry of the large-scale photospheric field. Over the years, the most recognizable feature is the azimuthal field component, organized in a fragmented or complete ring encircling the rotation axis at a latitude of about 40°, showing a large-scale toroidal magnetic component at the stellar photosphere. The toroidal component contains most of the magnetic energy, except in 2008.09 and 2010.48 (Table 1), and its dominant polarity is constant for all data sets. The poloidal magnetic component is dominated by a dipole, with the dipole tending to host a larger fraction of the magnetic energy when the toroidal field component is strongest, i.e., in 2007.59 and 2011.07. The fraction of the axisymmetric field (fraction of magnetic energy stored in spherical harmonics modes with ℓ = 0) is also evolving in correlation with the strength of the toroidal field.
3.3. Zeeman broadening
To investigate the photospheric magnetic field of ξ Bootis A in even greater, we looked at the broadening of several spectral lines with high magnetic sensitivity. This approach, successfully applied to ξ Bootis A in the past (Robinson et al. 1980), is complementary to the Zeeman-Doppler Imaging strategy, because Zeeman broadening is sensitive to the total magnetic flux, while the polarized Zeeman signatures carry selective information about the large-scale component of the magnetic field (owing to signal cancellation for close-by regions of opposite magnetic polarity). Here, we monitored the temporal fluctuations of the Zeeman broadening. To achieve this goal, we adopted a very rough tracer of the magnetic broadening by simply following the time evolution of the line width. To do so, we first used a cubic spline algorithm to modify the wavelength sampling of the line to obtain a grid of spectral bins offering points of equal intensity on both wings of the line profile. We then evaluated the width at various depths in the line, and finally retained the depth (0.33Ic above the normalized intensity of the line centre) at which the rotational modulation is the most obvious. The measured width is therefore not a standard FWHM.
We have mainly focused on the FeI@846.8404 line, which offers a high Landé factor (g = 2.493) and an infrared wavelength, which both enhance the Zeeman broadening effect. Other advantages of using this specific line are the relatively high S/N obtained in this part of the NARVAL spectra (close to 500) and the clean surrounding continuum, which is mostly free from telluric or photospheric lines, which ensures accurate continuum normalization. The line width measurements are listed in Table 5 and plotted in Figs. 3 and 4. A complex phase dependence of the line width is obvious at several epochs. A correlated evolution is sometimes observed with Bl (e.g. in 2010.48), but this occasional similarity cannot be taken as a general trend, as illustrated by the anti-correlation observed only about a month later, in 2010.59. In addition to the rotational modulation in line width, a long-term trend is observed, with a significant decrease in the line width between 2007.59 and the following data sets. This variability is larger than the rotational variability observed at individual epochs (Fig. 6). This decrease agrees with the trend in decreasing magnetic field strength seen in the magnetic maps (Table 1).
The line width was also monitored using two other magnetically sensitive lines (FeI@549.75, g = 2.26 and FeI@550.68, g = 2.00). The variations described above are consistently recovered using these lines, although the correlation with chromospheric emission (see Sect. 4.1) is generally worse than for the infrared line. We also studied three lines with a weak Landé factor (FeI@481.78, g = 0.48, FeI@592.74, g = 0.43 and FeI@840.14, g = 0.51) which, as expected, did not exhibit any significant temporal evolution in their width.
4. Other activity tracers
4.1. Chromospheric activity
Using our Stokes I spectra we monitored the evolution of the chromospheric flux between each set of observations and also across the stellar rotation cycle. A simple comparison of the core of the Ca II H line for two different years (Fig. 5) reveals the variability of the chromospheric activity, with the core emission stronger in 2007.59 than in 2010.04. We constructed two emission indexes to quantify the emission changes, using the Ca II H and Hα lines, respectively. Our method is described below.
 |
Fig. 5 Ca II H line for August 2 2007 (solid line) and for January 18 2010 (dashed line). |
 |
Fig. 6 Top three rows: long-term evolution of the average values (calculated over individual observing runs) and dispersion (vertical bars) of the activity proxies presented in Fig. 3 and 4. Bottom two rows: temporal evolution of magnetic quantities listed in Table 1. |
4.1.1. NCaIIH-index
Before computing the index itself, the continuum normalization in the spectral region around Ca II H&K was adjusted. The very dense distribution of photospheric spectral lines in this part of the spectrum prevented the standard reduction pipeline of LibreEsprit from defining a reliable continuum level, resulting in local normalization inaccuracies of the order of 20%. To improve the situation, we took as a reference a synthetic normalized spectrum from the POLLUX database (Palacios et al. 2010) with Teff and log (g) values close to those of ξ Boo A. First, we interpolated the synthetic spectrum on the NARVAL wavelength grid, we then defined by hand a number of reference points around the Ca II H&K lines and used them to estimate the local ratio between the NARVAL spectrum and the synthetic spectrum. The series of ratios were then fitted by a fourth-order polynomial and, finally, the region of interest in the NARVAL spectrum was divided by the polynomial. We achieved a good continuum level using this method, without the need to rotationally broaden the synthetic spectrum. This confirms that rotational broadening can be ignored in the process, at least for a star like ξ Bootis A that has a low vsini .
Afterwards, we calculated a NCaIIH-index following the method outlined in Duncan et al. (1991), who defined S-values from Mount Wilson observations. We used two triangular bandpasses H and K with a FWHM of 0.1 nm to determine the flux in the line cores. Two 2 nm-wide rectangular bandpasses R and V, centred on 400.107 and 390.107 nm, respectively, were used for the continuum flux in the red and blue sides of the H and K lines. Although results from this adapted S index are generally good, one concern was the location of Ca II K in an order overlap in the 2007.59 data set (later on, the order overlap was slighlty shifted, so that the line core fell outside the overlap region). This unfortunate position in the spectrum generates additional difficulties in obtaining a reliable continuum normalization and increases the uncertainties in the computed values (since the S/N ratio decreases rapidly towards the edge of an order). After multiple trials, we chose to use only the Ca II H line because it gave the most reliable results. Finally, in the same way as Wright et al. (2004) defined an L-index for Lick observations, we defined a NCaIIH-index for our NARVAL spectra as follows: 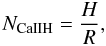 (3)where H and R are the same as described above.
(3)where H and R are the same as described above.
To match the Mount Wilson values, we transformed the NCaIIH-index as 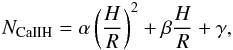 (4)
(4)
where α, β and γ are relative weights to be determined. To estimate them, we chose 31 cool stars simultaneously present in the NARVAL archive and in Wright et al. (2004), and ensured that all selected NARVAL observations had an S/N above about 100 around the Ca II H line. We then performed a least-squares fitting between the chromospheric activity values of the two stellar samples and found an optimal value of –0.972 for α, 1.803 for β and –0.051 for γ. Using the result of this calibration, some residual scatter is still observed between our measurements and Wright’s values. These differences are probably due to the different dates of observation between the two studies, bearing in mind that the chromospheric emission of cool active stars display long-term fluctuations. The observed scatter, which is not associated to any systematic bias, is similar to that between Wright’s estimates and older Mount Wilson measurements.
The NCaIIH-index is shown in Figs. 3 and 4, and the mean values for each set appear in Table 2. Random errors are about 10-3 for individual observations. Occasional repeated observations of ξ Boo A during a single night (twice each night on 2008 Jan. 18 and 23) enabled us to obtain another estimate of uncertainties, assuming that the chromospheric activity is fairly constant over the few minutes that separate successive spectra. The typical difference in the NCaIIH-index between these close-by observations is about 4 × 10-3.
A rotational modulation in NCaIIH is visible in most data sets, and is particularly evident in 2008.09. A longer-term evolution is also seen (Fig. 6), with differences between the years being larger than the fluctuations observed during a single rotation cycle. In individual data sets, a correlation between the rotational modulation of NCaIIH and the width of FeI@846.84 is sometimes observed (e.g., 2008.09) but is much less pronounced at other epochs (e.g., 2009.46). A possible reason for this partial mismatch is the different centre-to-limb behaviour of the two magnetic field tracers. Stokes I for FeI@846.84 will be affected by changes in the central, unsplit π component of the line (increasing towards the limb) as well as changes in the split σ components (decreasing towards the limb). The combination of the two types of Zeeman components gives a different centre-to-limb variation than for the chromospheric lines, for which a limb brightening is expected if there are faculae/plages contributing to the Ca II emission (Ortiz et al. 2002). The correlation between NCaIIH and FeI@846.84 is more easily seen on the longer term (Fig. 7).
4.1.2. NHα-index
In the same manner as for NCaIIH, we defined a quantity to measure the variability in Hα. We used the same rectangular bandpasses that Gizis et al. (2002) defined around the Hα line. The red-side continuum is taken to be between 656.62 and 656.84 nm, the blue-side continuum between 655.77 and 656.0 nm, and the line core between 656.10 and 656.46 nm. By defining the flux values in the continuum bandpasses as Cred and Cblue and the flux in the line as FHα, our index was constructed as follows: 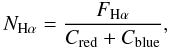 (5)note that the higher S/N around Hα, as well as the better continuum normalization in this spectral region, allowed us to skip the renormalization procedure adopted for Ca II H. The results obtained for each year are given in Figs. 3 and 4, and the mean values are listed in Table 2. Random errors are about 10-4 for a single observation. Using the two nights for which repeated observations are available, as we did for NCaIIH, the empirical uncertainty was measured to be around 7 × 10-4.
(5)note that the higher S/N around Hα, as well as the better continuum normalization in this spectral region, allowed us to skip the renormalization procedure adopted for Ca II H. The results obtained for each year are given in Figs. 3 and 4, and the mean values are listed in Table 2. Random errors are about 10-4 for a single observation. Using the two nights for which repeated observations are available, as we did for NCaIIH, the empirical uncertainty was measured to be around 7 × 10-4.
Most conclusions drawn for the NCaIIH index are also valid for NHα, given the correlation of the two indexes illustrated in Fig. 7. Again, rotational variability is observed for most epochs, as well as a year-to-year trend. The changes seen between the observing epochs are higher than the rotationally induced variations.
4.2. Radial velocities and profile bisectors
 |
Fig. 7 Correlation between NCaIIH and NHα (top), and between the widths of the FeI@846.84 line and NCaIIH (bottom). |
Even for the low Doppler broadening of spectral lines suffered by ξ Bootis A (vsini = 3km s-1), surface inhomogeneities (cool spots or plages) can be expected to modify the shapes of the Stokes I LSD profiles. During its transit across the visible hemisphere of the star, a cool spot changes the depth of one wing of the profile when it gets closer to the stellar limb (so that its spectral counterpart gains significant Doppler shift). This effect may be detected as a change in the radial velocity of the line centroid, or as a modification of the profile bisector. The typical profile asymmetry produced by convective flows (Toner & Gray 1988) may also be locally modified by strong magnetic fields, resulting in a temporary change of the profile bisector. In this section, we propose to investigate these effects for ξ Bootis A.
Radial velocities (RV hereafter) were calculated from our Stokes I LSD profiles by applying a Gaussian fit to the line profiles and using the centroid of the resulting Gaussian function as a radial velocity estimate. Using a (symmetric) Gaussian fit may be thought inadapted for asymmetric Stokes I LSD profiles observed for ξ Bootis A. We note, however, that the level of asymmetry is generally low compared to radial velocity fluctuations derived below (Table 2). Detailed measurements can be found in Table 5 and phase-folded results are shown in Figs. 3 and 4. The typical error for a single measure of RV, using NARVAL in polarimetric mode, was estimated by Moutou et al. (2007) and is of the order of 0.015–0.030 km s-1. Several data sets display rotationally modulated variations in RV, with amplitudes sometimes in excess of 0.1 km s-1 (see for instance 2009.46). Most of the time, this activity proxy is acting differently from other tracers.
We also used the Stokes I LSD profiles to construct profile bisectors. After adjusting the sampling of the intensity line profile with a cubic spline procedure, we computed the bisector using a method similar to Toner & Gray (1988). The phase-dependence of the bisector shape is plotted in Fig. 8 for the observations of 2008.09. We note that the bisectors never display the typical redshift near the continuum that they exhibited most of the time in previous studies of Toner & Gray (1988) and Petit et al. (2005). This shape difference is due to the spectral range (covering the whole visible domain) used to derive the LSD profiles. Using various sub-sets of our line-list to compute LSD profiles in narrower spectral regions, we note that the shape reported by Toner & Gray (1988) is typical of the red- and near-infrared domains, while a mirror shape (with a blueshift close to the continuum) is observed for the bluest parts of the NARVAL spectral range.
We note that strong and weak individual spectral lines (which are expected to have different bisector shapes) are mixed together in the computation of a LSD profile. If the resulting bisector shape is still a tracer of photospheric convective flows (Gray 1980, 1981, 1982; Dravins 1987), any direct comparison with individual line bisectors should be taken with caution. When adopting the exact line list of Toner & Gray (1988) to compute LSD profiles (eight lines close to 625 nm), we indeed derived bisectors similar to theirs, but here again the comparison is of limited relevance, since it might be affected by the difference in spectral resolution and time of observation.
To quantify the changes in the bisector shape, we calculated the velocity span associated to each bisector, as defined by Toner & Gray (1988). Here, we take the difference in radial velocity between a point near the top of the line profile (I/Ic = 0.95) and a point near the bottom (the I/Ic minimum value plus 0.01). Uncertainties in the bisector span were derived using the approach of Povich et al. (2001), yielding error bars of 20–30 m s-1. Repeated measurements within a few minutes, obtained at two occurrences in 2008.09, provided us with variations of the velocity span within the calculated uncertainties. The bisector fluctuations are shown in Figs. 3 and 4, with numerical quantities listed in Table 5. Variations with the rotational phase are visible for most epochs of observation, and sometimes follow a complex pattern (e.g. 2008.09). Most of the time, no obvious correlation can be found with other magnetic or activity proxies. In contrast to most other tracers, a long-term trend of the bisector span is not detected above its typical dispersion level (Fig. 6).
 |
Fig. 8 Bisectors of Stokes I LSD profiles as a function of the rotational phase for 2008.09. Dashes represent observations taken a few minutes apart from the overplotted solid-line bisector. |
5. Discussion and conclusions
We have used spectropolarimetric observations to derive a time-series of magnetic field maps and activity proxies covering almost four years in the life of ξ Bootis A. In doing so we combined observational approaches that are often investigated separately.
5.1. Magnetic topology
In spite of its rapid rotation rate, the spectral lines of ξ Bootis A are not significantly affected by Doppler broadening. The low vsini of the star is due to the combined effect of a low inclination angle and a relatively small radius. When applied to stars with low rotational broadening, ZDI selectively reconstructs only the largest spatial scales of the surface magnetic field. The reconstructed magnetic maps of ξ Bootis A show a surface-averaged field strength of the order of 30–100 G. These values are significantly lower than the previous estimate of Petit et al. (2005), derived from observations taken during the summer of 2003, both for the poloidal and toroidal field components. This difference is possibly the consequence of a long-term magnetic trend, however, we emphasize that the instrumental setup and modelling methods are different in the two studies (direct modelling in Petit et al. 2005, inverse tomography in the present study), which may account for part of the apparent decrease. Both methods agree on the existence of a strong toroidal field component on ξ Bootis A, which is dominating the energy budget in the results of Petit et al. (2005), and also in most of the ZDI magnetic field reconstructions in the present study, except in 2008.09 and 2010.48 (for which the poloidal field component dominates the surface magnetic energy).
The properties of the large-scale field of ξ Bootis A can also be compared to that of other ZDI studies of solar-type dwarfs, as long as the selected stars also exhibit a low vsini , so as to ensure that all stars used for the comparison are affected by a same low-pass spatial filtering of their magnetic geometry. As far as mass is concerned, the closest available neighbour is HD 189733 (Fares et al. 2010). The average surface field strength recovered for this star is lower than that derived for ξ Bootis A, which is likely a consequence of the slower rotation rate of HD 189733 (with a rotation period of 12 d). In spite of this difference, both stars have a significant fraction of their surface magnetic energy reconstructed in a toroidal field component.
A small number of main-sequence stars of higher mass can also serve as comparisons. The average field strength of ξ Bootis A is consistent with the large-scale field strength measured for 1 M⊙ stars with rotation periods slower than about 10 d (Petit et al. 2008). The prominent toroidal component of the large-scale magnetic geometry, observed for each year except for 2008.09 and 2010.48, agrees with the assertion, derived from both observations and numerical simulations of stellar dynamos, that surface magnetic geometries become predominantly toroidal for solar-type dwarfs with rotation periods as short as a few days, whereas a mainly poloidal surface field is a common feature of slow rotators (Petit et al. 2008; Brown et al. 2010).
5.2. Magnetic variability
If ξ Bootis A seems to obey the above-mentioned trends, the temporal fluctuations of its magnetic properties demonstrate that magnetic variability will induce some scatter around any average behaviour, because the global field strength, the fraction of energy in the toroidal field, and the field axisymmetry all vary with time. While relative fluctuations observed in the chromospheric emission are limited to about 20% (although Baliunas et al. 1995, suggest that longer-term variations of up to 60% can be observed), simultaneous variations by a factor of about 2 are observed in the mean large-scale field strength, and reach a factor of about 5 in the fraction of energy reconstructed in the axisymmetric field component and a factor of 3 in the fraction of energy stored as a toroidal component. Assuming that these sharp variations are too important to simply reflect intrinsic limitations of our magnetic model (Sect. 3.2), they suggest that the large-scale field structures seen in polarimetry are more sensitive to dynamo fluctuations than the smaller-scale structures that contribute to the chromospheric flux. The difference in behaviour between the activity tracers and the large-scale field is also visible on the shorter term, e.g., between the close-by epochs of 2010.48 and 2010.59, when a fast evolution of the global magnetic topology (similar in its short timescale to previous observations by Petit et al. 2005) has no clear counterpart in other activity proxies.
Several possibilities can be proposed to account for the low agreement between the Stokes V and Stokes I activity indicators. Firstly, Zeeman broadening and chromospheric emission are expected to trace a wider range of spatial scales than the polarized Zeeman signatures, which are missing a significant fraction of the total magnetic flux of the star. Secondly, the different limb visibility of the various proxies is expected to result in different temporal evolutions. Thirdly, the flux in chromospheric indicators tends to saturate with increasing magnetic flux (Schrijver et al. 1989; Loukitcheva et al. 2009), so that strong magnetic field variations may result in more gentle Ca II variations.
The complex long-term magnetic variations of ξ Bootis A, previously noted by Baliunas et al. (1995), are reminiscent of the behaviour of high-activity, very rapidly-rotating dwarfs (Donati et al. 2003b; Jeffers et al. 2011; Marsden et al. 2011). There is obvious magnetic field evolution over the four years of observations, but it does not take the simple form of fast global polarity switches observed on other rapidly-rotating sun-like stars (Fares et al. 2009; Petit et al. 2009; Morgenthaler et al. 2011). Instead, the main variability observed is a drop of the average field strength from 2008 to early 2010, encompassed by epochs associated with stronger field. This evolution is also observed in most of the activity proxies. We note that the toroidal field component is relatively weaker whenever the global field strength is close to its minimum value, and observe a more axisymmetric field structure in high-activity states. The magnetic topologies of 2007.59 and 2011.07 are very similar, suggesting that the repeated observation of this magnetic pattern may be related to a type of magnetic cycle that does not imply a global polarity switch. Based on our data sets, the large-scale magnetic variability of ξ Bootis A may seem chaotic, however, we stress that not all relevant temporal scales are explored here, so that a longer monitoring or a denser temporal sampling may help reveal other patterns.
5.3. Differential rotation
Some of the short-term changes in the magnetic topology can be taken into account in our model, assuming that they obey a simple differential rotation law. The measurement of the rotational shear was not conclusive at every epoch, presumably because of the fast emergence/disappearance of magnetic spots, which affects the tracking accuracy of the magnetic tracers used to determine the shear (a source of error already mentioned by Petit et al. 2002). Whenever measurable, the values of the differential rotation parameters are consistent with a strong surface shear, with dΩ from five to ten times the solar value. As mentioned in Sect. 3.2, part of this observed scatter is likely generated by fast changes in the surface topology, but this random effect is not expected to result in systematic biases of dΩ measurements. The dΩ values are far above some measurements obtained for very rapidly rotating dwarfs in this temperature domain (see Barnes et al. 2005, who report a drop of differential rotation for stars cooler than the Sun). It is, however, reminiscent of the strong shear observed on the T Tauri star v2247 Oph, in spite of a spectral type as late as M2 (Donati et al. 2010). An increase in dΩ with rotation is also consistent with other observational studies (Donahue et al. 1996; Saar 2009) and with the models of Brown et al. (2008) and Ballot et al. (2007).
The high latitudinal shear of ξ Bootis A also suggests that in spite of the high activity level of the star, Maxwell stresses are still inefficient at forcing solid-body rotation as proposed, e.g., for active M dwarfs (Morin et al. 2008; Browning 2008), but also for very rapidly rotating sun-like stars (Henry et al. 1996; Reiners & Schmitt 2003). If such an extreme state is not reached by ξ Bootis A, the sharp apparent fluctuations of the shear level, if real, may indicate that a feedback of the magnetic field onto the large-scale flows is probably active in the convective layers and is affecting the differential rotation, as suggested for other high-activity dwarfs (Donati et al. 2003a) and from dynamo models of Brun et al. (2005).
Online material
Journal of observations for 2007.59, 2008.09, and 2009.46.
Activity tracers of ξ Bootis A derived from the Stokes I profiles for each observation for 2007.59, 2008.09, and 2009.46.
Acknowledgments
This research made use of the POLLUX database (http://pollux.graal.univ-monpt2.fr) operated at LUPM (Université Montpellier II – CNRS, France, with support of the PNPS and INSU). We are grateful to the staff of TBL for their efficient help during the many nights dedicated to this observing project. We are grateful to an anonymous referee for a number of constructive comments that helped to clarify this article. This long-term magnetic monitoring was undertaken in the framework of the Bcool project.
References
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Ballot, J., Brun, A. S., & Turck-Chièze, S. 2007, ApJ, 669, 1190 [Google Scholar]
- Barnes, J. R., Collier Cameron, A., Donati, J.-F., et al. 2005, MNRAS, 357, L1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, B. P., Browning, M. K., Brun, A. S., Miesch, M. S., & Toomre, J. 2008, ApJ, 689, 1354 [CrossRef] [Google Scholar]
- Brown, B. P., Browning, M. K., Brun, A. S., Miesch, M. S., & Toomre, J. 2010, ApJ, 711, 424 [Google Scholar]
- Brown, B. P., Miesch, M. S., Browning, M. K., Brun, A. S., & Toomre, J. 2011, ApJ, 731, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Browning, M. K. 2008, ApJ, 676, 1262 [Google Scholar]
- Brun, A. S., Browning, M. K., & Toomre, J. 2005, ApJ, 629, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, R. A., Saar, S. H., & Baliunas, S. L. 1996, ApJ, 466, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J., & Brown, S. F. 1997, A&A, 326, 1135 [NASA ADS] [Google Scholar]
- Donati, J., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Collier Cameron, A., & Petit, P. 2003a, MNRAS, 345, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Collier Cameron, A., Semel, M., et al. 2003b, MNRAS, 345, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J., Howarth, I. D., Jardine, M. M., et al. 2006, MNRAS, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Skelly, M. B., Bouvier, J., et al. 2010, MNRAS, 402, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Dravins, D. 1987, A&A, 172, 211 [NASA ADS] [Google Scholar]
- Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Fares, R., Donati, J., Moutou, C., et al. 2009, MNRAS, 398, 1383 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fares, R., Donati, J.-F., Moutou, C., et al. 2010, MNRAS, 406, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Ghizaru, M., Charbonneau, P., & Smolarkiewicz, P. K. 2010, ApJ, 715, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Gizis, J. E., Reid, I. N., & Hawley, S. L. 2002, AJ, 123, 3356 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1980, ApJ, 235, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1981, ApJ, 251, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1982, ApJ, 255, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1984, ApJ, 281, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, T. J., Soderblom, D. R., Donahue, R. A., & Baliunas, S. L. 1996, AJ, 111, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffers, S. V., Donati, J.-F., Alecian, E., & Marsden, S. C. 2011, MNRAS, 411, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Henry, G. W., et al. 2007, ApJS, 171, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Loukitcheva, M., Solanki, S. K., & White, S. M. 2009, A&A, 497, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsden, S. C., Jardine, M. M., Ramírez Vélez, J. C., et al. 2011, MNRAS, 413, 1922 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Basu, S., Henry, T. J., et al. 2010, ApJ, 723, L213 [NASA ADS] [CrossRef] [Google Scholar]
- Morgenthaler, A., Petit, P., Morin, J., et al. 2011, Astron. Nachr., 332, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2008, MNRAS, 390, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Moutou, C., Donati, J., Savalle, R., et al. 2007, A&A, 473, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ortiz, A., Solanki, S. K., Domingo, V., Fligge, M., & Sanahuja, B. 2002, A&A, 388, 1036 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palacios, A., Gebran, M., Josselin, E., et al. 2010, A&A, 516, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, P., Donati, J.-F., & Collier Cameron, A. 2002, MNRAS, 334, 374 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Petit, P., Donati, J., Aurière, M., et al. 2005, MNRAS, 361, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Petit, P., Dintrans, B., Morgenthaler, A., et al. 2009, A&A, 508, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Povich, M. S., Giampapa, M. S., Valenti, J. A., et al. 2001, AJ, 121, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, D. E., & Semel, M. D. 1979, A&A, 74, 1 [NASA ADS] [Google Scholar]
- Reiners, A., & Schmitt, J. H. M. M. 2003, A&A, 398, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robinson, R. D., Worden, S. P., & Harvey, J. W. 1980, ApJ, 236, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H. 2009, in Solar-Stellar Dynamos as Revealed by Helio- and Asteroseismology: GONG 2008/SOHO 21, ed. M. Dikpati, T. Arentoft, I. González Hernández, C. Lindsey, & F. Hill, ASP Conf. Ser., 416, 375 [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Cote, J., Zwaan, C., & Saar, S. H. 1989, ApJ, 337, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
- Toner, C. G., & Gray, D. F. 1988, ApJ, 334, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wielen, R. 1962, AJ, 67, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2004, ApJS, 152, 261 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Activity tracers of ξ Bootis A derived from the Stokes I profiles for each observation for 2007.59, 2008.09, and 2009.46.
All Figures
 |
Fig. 1 Normalized Stokes V profiles (V/Ic) of ξ Boo A for 2007.59, 2008.09, 2009.46, 2010.04, 2010.48, 2010.59 and 2011.07 (from left to right and top to bottom), after correction for the mean radial velocity of the star (the radial velocity values are listed in Table 2). Black lines represent the data and red lines correspond to synthetic profiles of our magnetic model. Successive profiles are shifted vertically for display clarity. Rotational phases of observations are indicated in the right-hand part of the plot and error bars are illustrated on the left side of each profile. |
| In the text | |
 |
Fig. 2 Magnetic maps of ξ Bootis A, derived from 2007.59, 2008.09, 2009.46, 2010.04, 2010.48, 2010.59, and 2011.07 observations (from left to right and top to bottom). For each data set, the three charts illustrate the field projection onto one axis of the spherical coordinate frame with, from top to bottom, the radial, azimuthal, and meridional field components. The magnetic field strength is expressed in Gauss. |
| In the text | |
 |
Fig. 3 Four sets of six subplots, each set corresponding to one epoch (from top to bottom, 2007.59, 2008.09, 2009.46, and 2010.04). For each set, the left subplots contain, from top to bottom, the NHα-index (filled circles and left axis) and NCaIIH-index (crosses and right axis of the top panel of each set), the FeI@846.8404 magnetic line widths (km s-1), Bl (Gauss). The right subplots, from top to bottom, correspond to the velocity spans (km s-1) obtained from the profile bisectors (Sect. 4.2), the radial velocity (km s-1), and the mean unsigned magnetic strength of the total (full line), radial (dashes), azimuthal (dot-dashes) and meridional (dots) magnetic field components extract from the ZDI maps. Error bars are not included whenever they are smaller than the symbol size. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 for 2010.48, 2010.59 and 2011.07. |
| In the text | |
 |
Fig. 5 Ca II H line for August 2 2007 (solid line) and for January 18 2010 (dashed line). |
| In the text | |
 |
Fig. 6 Top three rows: long-term evolution of the average values (calculated over individual observing runs) and dispersion (vertical bars) of the activity proxies presented in Fig. 3 and 4. Bottom two rows: temporal evolution of magnetic quantities listed in Table 1. |
| In the text | |
 |
Fig. 7 Correlation between NCaIIH and NHα (top), and between the widths of the FeI@846.84 line and NCaIIH (bottom). |
| In the text | |
 |
Fig. 8 Bisectors of Stokes I LSD profiles as a function of the rotational phase for 2008.09. Dashes represent observations taken a few minutes apart from the overplotted solid-line bisector. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


