| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 7 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201118222 | |
| Published online | 24 February 2012 | |
Type Ia supernovae in globular clusters: observational upper limits
1 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
e-mail: rvoss@science.ru.nl
2 Institute for Astronomy, K.U. Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
Received: 7 October 2011
Accepted: 28 November 2011
Aims. In the dense stellar environment of globular clusters it is expected that compact binaries can be produced dynamically. This in turn would mean that the fraction of type Ia supernovae that will explode in globular clusters will be higher than would be expected from the mass of stars present. Therefore we wish to determine observational constraints on the number of supernovae type Ia explosions in globular clusters as a means to constrain the number of dynamically formed binary systems.
Methods. We searched for globular clusters at the positions of observed type Ia supernovae. We used archival HST images and literature data that cover the positions either before the supernovae exploded, or sufficiently long after the supernovae to have faded below the luminosities of globular clusters.
Results. We did not find evidence for globular clusters at any of the supernova positions. For 18 type Ia supernovae, the observations are sensitive enough that any globular cluster would have been detected, and for another 17 type Ia supernovae, the brighter globular clusters would have been detected. Correcting for incompleteness, we derive a 90% upper limit of 0.09 for the fraction of type Ia supernovae that explode in globular clusters for the full sample and 0.22 for the sample of supernovae in late-type galaxies. This allows us to limit enhancements per unit stellar mass for a coeval population ηco ≲ 50 (100) with 90% (99%) confidence. We find that by observing the positions of a sample of less than 100 type Ia supernovae in the outer parts of early-type galaxies, it will be possible to probe the currently favoured range of ηco ~ 1−10.
Key words: supernovae: general / galaxies: star clusters: general
© ESO, 2012
1. introduction
Type Ia supernovae (SNIa) are believed to be thermonuclear explosions of white dwarfs (e.g. Hillebrandt & Niemeyer 2000). The two main scenarios for bringing the white dwarfs above the critical explosion mass MC (similar but not equal to the Chandrasekhar mass) are (1) the single-degenerate (SD) scenario, in which a white dwarf accretes from a non-degenerate companion star (Whelan & Iben 1973; Nomoto 1982), and (2) the double degenerate (DD) scenario, in which the merger of two white dwarfs with a total mass exceeding MC causes the explosion (Iben & Tutukov 1984; Webbink 1984). Both scenarios requires binaries with white dwarfs in orbits close enough that mass transfer occurs at some point during the evolution of the binary.
Globular clusters (GCs) are known to harbour large populations of compact binaries. Best known are the bright low-mass X-ray binaries (LMXBs) with a specific density per unit mass 100 times higher than in the field (Clark 1975). The population of millisecond pulsars (Lyne et al. 1987; Lorimer 2005) and blue stragglers (Sandage 1953) have also been found to be strongly enhanced. Particularly interesting for type Ia supernovae is the relatively recent observational evidence that the populations of white dwarf systems are also enhanced (e.g. Heinke et al. 2005; Dieball et al. 2007; Maccarone & Knigge 2007; Knigge et al. 2008; Henze et al. 2009). The enhancement of tight binaries in globular clusters is a consequence of the very high stellar densities found there (up to 106 M⊙ pc-3). With these high densities, dynamical encounters that create or modify binaries are frequent, and the higher mass of the binaries makes them sink to the center, where the encounter rates are highest.
It is therefore reasonable to expect that both SD and DD SNIa progenitors will be enhanced in globular clusters. The few theoretical studies that have investigated this have indeed found such an enhancement in their models (Ivanova et al. 2006; Shara & Hurley 2006). However, the magnitude of this enhancement is highly uncertain. Not only are we ignorant of which systems do lead to supernova explosions and how these systems evolve outside globular clusters, there is also a very large uncertainty caused by the difficulties of modelling and observing exotic binary populations in globular clusters.
The most massive globular clusters with the highest collision rates are bright and are therefore visible up to far distances (~50 − 100 Mpc). It is therefore feasible to derive limits on the fraction of type Ia supernovae that explode in globular clusters by identifying these in deep pre- or post-explosion images of the supernova positions (Pfahl et al. 2009). Despite this prediction, no such observational survey has been carried out to date.
We performed a survey using archival observations and literature data to place observational constraints on the fraction of SNIae in globular clusters. We first discuss the theoretical estimates in Sect. 2, then we discuss our methodology in Sect. 3. In Sect. 4 we describe and analyse the literature and archival data, and in Sect. 5 we discuss the results and perspectives for future surveys.
2. Theoretical expectations
It is clear from both observations and theory that compact binaries can be formed efficiently through dynamical interactions in the dense stellar environment of globular clusters. However, the picture of the formation and evolution of these compact binaries remains vague because of the many unconstrained physical processes involved, and because of the computational expense of globular cluster models that include binary evolution. Modelling the formation of SNIa progenitors is even more problematic, given their unknown nature. It is therefore not surprising that only few studies have attempted this.
The enhancement of compact binaries in a globular cluster is expected to be proportional to the rate of interactions Γ (e.g. Hut & Verbunt 1983; Pooley et al. 2003; Pooley & Hut 2006). While Γ can be estimated for nearby globular clusters, based on their structural parameters, the estimates are not very reliable (Maccarone et al. 2011), and it is not possible to measure the parameters accurately outside the Galaxy. For this reason we used the commonly employed average enhancement factor for a galactic population of N globular clusters 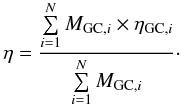 (1)Single-degenerate progenitors were considered in the study of Ivanova et al. (2006), who found an enhancement factor (per unit stellar mass) of η = 1 − 7 compared to a field population with solar metallicity. The authors found no single-degenerate SNIa in a population of stars with the same properties as the globular clusters but with interactions turned off. Shara & Hurley (2006) found a small enhancement ≲ 2 in the production rate of accreting white dwarfs, but in their globular cluster models, the accreting white dwarfs are heavier, which makes them more likely to be SNIa progenitors. Other studies have predicted higher numbers of accreting white dwarfs (Di Stefano & Rappaport 1994; Davies & Benz 1995), corresponding to η = 5, but did not consider SNIa progenitors specifically. Shara & Hurley (2006) found no enhancement of double white dwarf binaries, but this study does not discuss SNIa progenitors specifically either. Ivanova et al. (2006) find an enhancement of merging double white dwarfs above the Chandrasekhar mass of η = 3 − 13 compared to a field population with the same metallicity and age as the population in the globular clusters, but no significant enhancement (η = 0.3 − 1.2) when compared to field population with solar metallicity.
(1)Single-degenerate progenitors were considered in the study of Ivanova et al. (2006), who found an enhancement factor (per unit stellar mass) of η = 1 − 7 compared to a field population with solar metallicity. The authors found no single-degenerate SNIa in a population of stars with the same properties as the globular clusters but with interactions turned off. Shara & Hurley (2006) found a small enhancement ≲ 2 in the production rate of accreting white dwarfs, but in their globular cluster models, the accreting white dwarfs are heavier, which makes them more likely to be SNIa progenitors. Other studies have predicted higher numbers of accreting white dwarfs (Di Stefano & Rappaport 1994; Davies & Benz 1995), corresponding to η = 5, but did not consider SNIa progenitors specifically. Shara & Hurley (2006) found no enhancement of double white dwarf binaries, but this study does not discuss SNIa progenitors specifically either. Ivanova et al. (2006) find an enhancement of merging double white dwarfs above the Chandrasekhar mass of η = 3 − 13 compared to a field population with the same metallicity and age as the population in the globular clusters, but no significant enhancement (η = 0.3 − 1.2) when compared to field population with solar metallicity.
An alternative approach is to compare the SD scenario to observations of similar systems. This is not possible for the DD scenario because of the lack of observational systems to compare it to. With their accreting massive white dwarfs, SD SNIa progenitors are somewhat similar to cataclysmic variables (CVs) and LMXBs in their formation and evolution. The bright LMXB population in globular clusters is quite well studied because they can be observed at large distances with Chandra, and they have been found to be over-abundant by a factor of ~100 (Clark 1975; Sarazin et al. 2003; Jordán et al. 2007; Voss et al. 2009). The CV population is much less understood because they are much harder to identify. Only a small sample has been found in recent years, consistent with an over-production by a factor of ~few (e.g. Pooley & Hut 2006; Dieball et al. 2007; Knigge et al. 2008), but completeness is a serious problem, and higher enhancement factors are therefore not ruled out. Observations of novae in M31 suggest an enhancement factor of ~10 (Henze et al. 2009). The SD SNIa progenitors have white dwarfs with masses near MC, more similar to the masses of neutron stars than to those of most CVs. They therefore sink to the center more easily and experience more dynamical encounters than more typical white dwarf systems, which leads to a higher expected enhancement.
From the discussion above we conclude that η is most likely greater than one and lower than 10. However, the results are clearly very poorly constrained, and models with η outside this range cannot be discarded. It is therefore important to find constraints for this fraction from observations.
In addition to η, the fraction of SNIae that explodes in globular clusters also depends on the fraction of stellar mass that resides in the globular clusters, FM,GC = MGC/MF, where MGC is the total mass of the population of globular clusters and MF is the total mass of all other stars. For a sample of N SNIae, the expected number that explodes in globular clusters is then 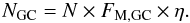 (2)The mass fraction FM,GC varies strongly between galaxies. The Milky Way has a low abundance of globular clusters, with FM,GC ~ 0.1% (e.g. the catalogue of Harris 1996). Therefore only ~10% of the Milky Way LMXBs (see e.g. Liu et al. 2007), and based on the considerations above, probably ~1% of the CVs, are found in globular clusters. This is in stark contrast to many elliptical galaxies with rich globular cluster systems, where in some cases FM,GC can be higher than 1% (e.g. Harris 2009), and the majority of bright LMXBs are found in globular clusters (Angelini et al. 2001). Correspondingly, if the SNIa enhancement is a factor of 10, about 10% of the SNIae in these galaxies must be formed in globular clusters. Averaging over the population of nearby galaxies yields a fraction of SNIae in globular clusters of ~1−3 × 10-3η (Pfahl et al. 2009), most likely a few per cent.
(2)The mass fraction FM,GC varies strongly between galaxies. The Milky Way has a low abundance of globular clusters, with FM,GC ~ 0.1% (e.g. the catalogue of Harris 1996). Therefore only ~10% of the Milky Way LMXBs (see e.g. Liu et al. 2007), and based on the considerations above, probably ~1% of the CVs, are found in globular clusters. This is in stark contrast to many elliptical galaxies with rich globular cluster systems, where in some cases FM,GC can be higher than 1% (e.g. Harris 2009), and the majority of bright LMXBs are found in globular clusters (Angelini et al. 2001). Correspondingly, if the SNIa enhancement is a factor of 10, about 10% of the SNIae in these galaxies must be formed in globular clusters. Averaging over the population of nearby galaxies yields a fraction of SNIae in globular clusters of ~1−3 × 10-3η (Pfahl et al. 2009), most likely a few per cent.
A complicating factor that was not taken into account in previous studies is that the rate of type Ia supernovae RSNIa decreases with age for a coeval population of stars. In general the distribution of globular cluster ages is different from that of the field stars. Therefore 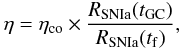 (3)where tGC is the age of the globular clusters and tf is the age of the field stars. For early-type galaxies tGC ~ tf, whereas the bulk of the field population of late-type galaxies tends to be significantly younger than the globular cluster population. ηco is the globular cluster enhancement per unit stellar mass, compared to a field population of the same age. The exact shape of the delay-time distribution (DTD, the SNIa rate as a function of time for a coeval population of stars) is not known, but it has been shown to decrease strongly by a factor of >10 from young environments <1 Gyr to older environments ~10 Gyr (e.g. Maoz et al. 2010). Therefore ~50−85% of all type Ia supernovae explode within the first Gyr after star formation (e.g. Maoz et al. 2010). However, the current star-formation density is much lower than at redshifts 1, and comparing the local rate of star formation (Hanish et al. 2006) to the stellar mass density (Salucci & Persic 1999; Cole et al. 2001) leads to a fraction of ~2% of stars in the local universe that were formed less than 1 Gyr ago. Despite the high percentage of prompt SNIae for a coeval population of stars, the local population will therefore be dominated by the tardy component. Combining the fractions found by Sullivan et al. (2006) with the local rate of star formation (Hanish et al. 2006) and stellar mass density (Salucci & Persic 1999; Cole et al. 2001), only ≲ 20 per cent of the local SNIae are expected to belong to the prompt component.
(3)where tGC is the age of the globular clusters and tf is the age of the field stars. For early-type galaxies tGC ~ tf, whereas the bulk of the field population of late-type galaxies tends to be significantly younger than the globular cluster population. ηco is the globular cluster enhancement per unit stellar mass, compared to a field population of the same age. The exact shape of the delay-time distribution (DTD, the SNIa rate as a function of time for a coeval population of stars) is not known, but it has been shown to decrease strongly by a factor of >10 from young environments <1 Gyr to older environments ~10 Gyr (e.g. Maoz et al. 2010). Therefore ~50−85% of all type Ia supernovae explode within the first Gyr after star formation (e.g. Maoz et al. 2010). However, the current star-formation density is much lower than at redshifts 1, and comparing the local rate of star formation (Hanish et al. 2006) to the stellar mass density (Salucci & Persic 1999; Cole et al. 2001) leads to a fraction of ~2% of stars in the local universe that were formed less than 1 Gyr ago. Despite the high percentage of prompt SNIae for a coeval population of stars, the local population will therefore be dominated by the tardy component. Combining the fractions found by Sullivan et al. (2006) with the local rate of star formation (Hanish et al. 2006) and stellar mass density (Salucci & Persic 1999; Cole et al. 2001), only ≲ 20 per cent of the local SNIae are expected to belong to the prompt component.
For most local galaxies, the ratio 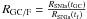 will therefore be higher than what could be expected from the DTD. It is typically in the range ~0.1−1. For early-type galaxies, the typical age of the field population is similar to the age of the globular clusters, and therefore RGC/F ~ 1. Late-type galaxies can have significant populations of young stars for which the SNIa rate is more than a magnitude higher than for the old population of stars in their globular clusters. However, the vast majority of late-type galaxies also have older stellar components, and RGC/F will therefore almost always be higher than 0.1.
will therefore be higher than what could be expected from the DTD. It is typically in the range ~0.1−1. For early-type galaxies, the typical age of the field population is similar to the age of the globular clusters, and therefore RGC/F ~ 1. Late-type galaxies can have significant populations of young stars for which the SNIa rate is more than a magnitude higher than for the old population of stars in their globular clusters. However, the vast majority of late-type galaxies also have older stellar components, and RGC/F will therefore almost always be higher than 0.1.
3. Exclusion of cluster origins for a sample of type Ia supernovae
The association of type Ia supernovae with globular clusters relies on the spatial coincidence. If a type Ia supernova is found to have exploded at the same position as a globular cluster, it may have exploded inside the globular cluster. If not, then a globular cluster origin is definitely excluded. However, the GC luminosities are widely distributed and many observations are only sensitive to the bright end of the GC luminosity function. Pfahl et al. (2009) showed that for η = 10 approximately 1% of all SNIa should explode in globular clusters, corresponding to one supernova in a globular cluster within 100 Mpc every year, and that a dedicated HST programme would be able to find the connection, if each SNIa were observed a few years after the explosion. With the assumptions of Pfahl et al. (2009) such a programme would require deep HST observations of ~100 fields every year. They did not consider the fact that some SNIa suffer from significant extinction and that observations inside galaxies where there is a high background are much less sensitive than in the field. These effects are difficult to model for the full sample of type Ia supernovae, and it is therefore unclear if the proposed observational programme would be succesful despite the high costs.
We therefore used the currently available HST data to observe or put limits on the fraction of SNIae in globular clusters, and to be able to estimate the sensitivity that can be achieved with a dedicated observational programme.
3.1. Globular cluster completeness
To be able to exclude a GC origin, it is necessary to know the observable properties of the GCs. Because they are old stellar systems, there are only relatively small variations in the mass-to-light ratios of different clusters, with the main difference being related to the globular cluster metallicity. However, the mass distribution of globular clusters is wide, with several orders of magnitude difference between the brightest and the faintest clusters (e.g. Harris 1991; Jordán et al. 2007). In the more distant galaxies or in shallow observations it will not be possible to observe the faint clusters and it is necessary to calculate the incompleteness caused by this.
The most straightforward way to do this is to use the observed luminosity function of globular clusters (Pfahl et al. 2009). However, while the definition of η as the enhancement per unit mass is a useful measure, it is misleading in terms of the physical interpretation, because the number of compact binaries does not scale linearly with the mass of the globular cluster. Instead it is related to the stellar encounter rate Γ inside the clusters. The distribution of structural parameters (and hence Γ) of clusters is not well known. Since the exact processes of compact binary formation are poorly also constrained, it is therefore not possible to make theoretical estimates of the relation between GC mass and the probability of hosting SNIa progenitors.
We instead attempted to do this on an empirical basis. The only compact binaries that have been surveyed in large samples of GCs are LMXBs. We used the results of Peacock et al. (2010) and Sivakoff et al. (2007) to estimate the mass distribution of GCs that contribute to the population of compact binaries, and thereby to estimate four completeness levels, CL25, CL50, CL75 and CL100, meaning the GC masses/luminosities above which 25%, 50%, 75% and 100% of the compact binaries are expected to reside. We strongly caution that this is based on observations of LMXBs alone, and that it is very possible that SNIa progenitors could have a different mass-dependence. However, currently there are no models that predict a different behaviour, and the populations of faint X-ray sources in Galactic GCs do seem to follow the distribution of bright LMXBs.
To estimate the completeness masses, we used the K-band data of Peacock et al. (2010) and the z-band data of Sivakoff et al. (2007). We give the completeness values for the K-band observations of M31 and z-band observations of Virgo in Table 1. To compare these results and extrapolate them to other wavelengths we used the integrated simple stellar population magnitudes of Girardi et al. (2000); Marigo et al. (2008). The values agree well, assuming a 12 Gyr stellar population with a Chabrier initial mass function and a metallicity of 0.012. We also provide estimates of the corresponding (initial) globular cluster masses, using the K-band magnitudes and two different metallicities. These are then used to find the colours in all the different bands used in the following analysis. Because the metal-rich GCs are redder, they are fainter than the metal-poor GCs in the used bands for a given K-band luminosity. We therefore used the calculations for z = 0.012 to determine the confidence limits in all bands, noting that in this way the confidence limits will be underestimated, decreasing our sensitivity somewhat. Younger clusters would be brighter for a given stellar mass, similarly leading to an underestimation of the confidence limits. The magnitudes for CL100 are given in Table 2. HST magnitudes are given in the VEGA photometric system. From Table 1 it can be seen that subtracting 1.5, 2.5, and 3.0 from these magnitudes yields CL75, CL50, and CL25, respectively.
Empirical completeness levels (absolute magnitudes) of globular clusters with LMXBs and the corresponding globular cluster masses.
Assumed absolute magnitudes for CL100.
Faintest observed BVRI magnitudes or upper limits from late-time observations of type Ia supernovae in the literature.
Additional published optical limits on SNIa in GCs.
4. Results
The observations of globular clusters at the positions of type Ia supernovae can be performed before the explosions, but also after, because the light of the globular clusters is provided by stars that are not affected by the explosion. Because the luminosity of the SNIae is very high shortly after the explosion, it is necessary to wait until it has become fainter than a globular cluster. This typically takes less than two years, although SNIae with light-echoes might be bright enough to hide globular clusters for a longer time.
4.1. Literature survey
SNIae for which we were able to exlude a globular cluster origin based on archival HST observations.
To facilitate comparisons and thereby the use of type Ia supernova as standard candles in cosmology, their lightcurves are observed using BVRI photometry. While most studies are limited to less than ~100 days, a number of SNIae have published late-time data. We have surveyed the litterature to compile a sample of 19 such SNIa. None of the published results show signs of a constant component expected from a host cluster. We list these in Table 3. The table also lists the faintest observed magnitudes in the BVRI bands, as well as the distance to the host galaxy and an estimate of the extinction towards the supernovae. We used these to find the intrinsic absolute magnitude of the faintest observation in each band and compared them with the values given in Tables 1 and 2, to find the confidence level (CL) at which we can exclude globular clusters on the basis of these light-curves. In Table 3 we left out four SNIae (SN1991T, SN2000E, SN2000cx, and SN2001el) for which useful late-time lightcurves exist, because more constraining limits are found in the analysis below.
In Table 4 we compiled a second more heterogenous literature sample. This consists of two old SNIae that were observed before the definition of the BVRI photometry (SN1937C and SN1972E), one where the magnitude was reported using HST with the VEGA magnitude system (SN2000cx), and five where upper limits were published based on pre-supernova HST images. Similar to Table 3 we derived completeness limits for these supernovae.
Upper limits on the fraction of type Ia supernovae in globular clusters.
4.2. HST observations
In addition to the literature survey, we searched for archival HST data at the positions of all known SNIa within 100 Mpc. We analysed the data to either find observations where the supernova is faint enough to exclude a GC origin, or where the supernova was not observed and an interesting upper limit could be inferred. One problem is the positional accuracy of the sources, because the fields of external galaxies can be crowded. Therefore positions of sub-arcsec precision are needed. Unfortunately, many supernova positions are relatively poorly determined, because the only published coordinates are from the original detections with small telescopes, when the supernovae were very bright, and the coordinates are provided without error estimates. Where several groups have published coordinates, the distance between the positions can be considerable. Unfortunately, most supernova observations are not publicly available, making it impossible to verify the positions.
We therefore only report results from supernovae where we are confident that the positions are well-determined. In a few cases, the limits were obtained from images where the supernova is still seen at a luminosity below that of globular clusters. In some cases, the positions were found from other HST images taken when the supernova was visible, which were then matched to the image from which the limit was determined. Where the positions could not be determined from HST images, we used the positions listed in Hicken et al. (2009), who performed careful astrometry of a large sample of supernovae. We compared their positions to HLA HST images, where the HST astrometry was already corrected using either 2MASS, GSC or SDSS as reference. We also used these catalogues to confirm the astrometry, because the HLA astrometry is done automatically. We furthermore searched for ground-based observations of the supernovae, through which we found the positions of seven additional SNIae.
To find the upper limit in an individual observation, we used the background counts in a number of circular regions near the supernova position (excluding point sources) to estimate the count rate of a 3-sigma fluctuation C3σ. The upper limit CUL on the supernova counts were then calculated by subtracting the median Cμ of the background fields CUL = C3σ − Cμ. The radius of the circular regions were chosen in the range 0.15 − 0.5 arcsec, depending on the local density of point sources and the gradient of the host galaxy light. From this we calculated the upper limit in the VEGA magnitude system using the standard count-rate to magnitude conversions from the HST data handbook, including PSF corrections for the aperture size. We tested our method against the method used in Nelemans et al. (2008) and Voss & Nelemans (2008), where fake sources were inserted in the images and the upper limit was based on the detection of these, and we found good agreement.
The results are listed in Table 5 for the supernovae whose upper limits provide constraints on the globular cluster connection.
4.2.1. Notes on individual sources
Some parts of the analysis of individual sources needs more explanation. SN1998bu and SN1991T have light echoes that are seen in all HST observations. For these sources we used the last F814W observations and we measured their flux within an aperture of 0.2 arcsec radius from the central source position. For both SNIae, the flux from this region is low enough that the existence of globular clusters at these positions can be excluded.
For many of the SNIae in Table 5 the position cannot be found from HST data. Four positions (SN2002bo, SN2002fk, SN2005el, and SN2005hk) are from Hicken et al. (2009), and another seven were found from ground-based data that we matched to the HST images. Four SNIae, SN1994ae, SN2001el, SN2005df, and SN2007af were identified in images taken with the NTT (SN1994ae) and VLT (SN2001el, SN2005df, and SN2007af) obtained from the ESO archive. Three more SNIae positions were found from ground-based images provided by Weidong Li. SN1999gh and SN1999gd were observed with KAIT and SN1998aq with a 1.2 m CfA telescope.
4.3. Derived upper limits
The results above constitute the first observational survey of the connection between globular clusters and type Ia supernovae. We have fully or partially excluded a connection for 35 SNIae, and no SNIa with possible globular counterparts has been found. Considering that faint globular cluster counterparts would still be possible for some of the SNIae in our sample, this allows us to derive PCL = 90% and 99% upper limits on the fraction of SNIae in globular clusters FUL. If a fraction FSNIa of SNIae explodes in globular clusters, the probability of not finding a globular cluster at the position of SNIa number i is 1 − FSNIa × CLi, where CLi is the globular cluster completeness level (which for our sample can take the values 0.25, 0.5, 0.75, and 1.0, see Sect. 3.1). The probability of finding no globular clusters for the entire sample of N SNIae is the product of finding no globular clusters for each SNIae and FUL, the upper limit on FSNIa, can therefore be found by solving 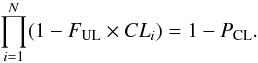 (4)Table 6 lists the derived limits. The table lists the sum of the completeness (CL) for each SNIa in the sample. FUL,90% and FUL,99% are the upper limits on the fraction of SNIae in globular clusters derived from the sample, ⟨ RGC/F ⟩ and ηco,90% are the ranges of assumed values of the fraction of stellar mass in the globular clusters and the SNIa rate ratio for the age of the globular clusters compared to the field, respectively. ηco,90% and ηco,90% are the upper limits on the values on the coeval enhancement of the SNIa rate in globular clusters per unit stellar mass, ηco.
(4)Table 6 lists the derived limits. The table lists the sum of the completeness (CL) for each SNIa in the sample. FUL,90% and FUL,99% are the upper limits on the fraction of SNIae in globular clusters derived from the sample, ⟨ RGC/F ⟩ and ηco,90% are the ranges of assumed values of the fraction of stellar mass in the globular clusters and the SNIa rate ratio for the age of the globular clusters compared to the field, respectively. ηco,90% and ηco,90% are the upper limits on the values on the coeval enhancement of the SNIa rate in globular clusters per unit stellar mass, ηco.
Table 6 lists the limits for the full sample and for two subsamples. The first subsample consists of all the normal SNIae, which follow the same standard lightcurve evolution. This sample was chosen to eliminate those with peculiar lightcurves, because they are more likely to have been studied in detail and therefore can bias our sample by being over-represented. Furthermore, their origin might differ from the normal SNIae. We note that the peculiar label is subjective and some of them could belong to the normal population, making the normal sample overly conservative. Our second subsample consists of all SNIae in early-type (elliptical and S0) galaxies. These have old stellar populations that are similar to the populations found in globular clusters, and are therefore particularly useful for comparison.
The 90% upper limit from the full sample is very close to our expectation that a few per cent of type Ia supernovae could explode in globular clusters, and it is therefore useful for constraining theoretical models. From Eqs. (2) and (3), the upper limits on FUL corresponds to upper limits on η: 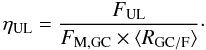 (5)For the full sample, the average stellar population is significantly younger than in the globular clusters, and we therefore assume ⟨ RGC/F ⟩ ~ 0.2−0.4. Because the fraction of globular clusters is small in the late-type galaxy part of the sample, FM,GC ~ 0.1−0.3%. With these assumption we obtain a result of ηco < 75−450. The ages of stars in the sample of early-type galaxies are similar to the ages of the globular clusters and therefore ⟨ RGC/F ⟩ ~ 1. Furthermore, the globular cluster mass fraction is higher, and we assume an average value of 0.3 − 0.6%. This leads to a more constraining limit of ηco < 37−73.
(5)For the full sample, the average stellar population is significantly younger than in the globular clusters, and we therefore assume ⟨ RGC/F ⟩ ~ 0.2−0.4. Because the fraction of globular clusters is small in the late-type galaxy part of the sample, FM,GC ~ 0.1−0.3%. With these assumption we obtain a result of ηco < 75−450. The ages of stars in the sample of early-type galaxies are similar to the ages of the globular clusters and therefore ⟨ RGC/F ⟩ ~ 1. Furthermore, the globular cluster mass fraction is higher, and we assume an average value of 0.3 − 0.6%. This leads to a more constraining limit of ηco < 37−73.
5. Discussion
We have derived upper limits on the enhancement per unit stellar mass ηco of SNIae in globular clusters. The limits are above the favoured theoretical expectations by almost an order of magnitude, but are well below the observed enhancement of LMXBs, ηLMXB > 100. We discussed the effect of the decline of the SNIa DTD on the observations. Owing to the older age of globular clusters compared to the field population in late-type galaxies, this decreases the value of the parameter η (which can be seen as the average enhancement over the whole population of galaxies), which is predominantly used in the literature (see Eq. (3)). For this reason we find that the sample of SNIae in early-type galaxies is more constraining than the full sample, despite containing only ≲ 1/3 of the supernovae. Because this effect of the DTD will be sample-dependent, we suggest that it is more appropriate to use ηco, which is the direct measure of the enhancement factor. However, we note that it is possible that ηco is also time-dependent, because early and late SNIae progenitors are likely to have different evolutionary histories, and because the structure of globular clusters evolve.
In this pilot study we only included supernovae with available HST images, and for which we were able to identify the position with high accuracy. This sample constitutes only a fraction of the total number of SNIae within distances at which it is possible to observe globular clusters (~100 Mpc). Because no globular clusters were detected at the position of the supernovae, and because we have managed to probe enough SNIae positions that we are starting to constrain theory, it is clearly interesting to extend the sample. To reach the values currently favoured by theory, it will be necessary to expand the sample by a factor of a few.
There are several ways to proceed. Because new supernovae are discovered continuously, and more galaxies are being observed with HST, it is possible to simply wait and let the sample expand. However, it is clear that from the current sample that only a few SNIae will be added every year, and it will therefore take decades before we can reach the goal of a factor of a few more supernovae. Another option is to use archival data from other telescopes. Because none of these are as sensitive to globular clusters as HST, it will only be possible to probe more nearby SNIae, but the advantage is that many more galaxies will be covered by useful observations. This study will be tedious, because data from many different telescopes will have to be processed, and it is unlikely that a factor of a few can be reached.
A third option is to conduct a dedicated obsertional programme to observe the positions of known SNIae. Enough are known that it will be possible to reach the goal of increasing the sample by a factor of a few. The most effective way of reaching it would be to launch a joint programme with a medium-sized ground-based telescope for the nearest SNIae, and HST for the more distant ones. Our experience from this pilot project tells us that it is very difficult to obtain useful limits for sources well inside the galaxies because the background there is bright and inhomogenous. While the number of SNIae will be lower if one excludes sources in the inner parts of the galaxies, it will be possible to be complete to farther distances, ~25−30 Mpc with ground-based telescopes and 100 Mpc with HST.
From our results it is obvious that targetting early-type galaxies will provide much stronger constraints owing to the lower difference between the ages (and hence SNIa rate) of the field and globular cluster populations, and this effect is being enhanced by the higher incidence of globular clusters in these galaxies. Specifically targetting SNIae at larger radii can additionally reduce the number of observations needed. This is because the globular clusters have shallower radial density profiles than the stars in the galaxies. For this reason, FM,GC can be several times higher when only considering the outer parts of galaxies. It can therefore be possible to probe values of ηco ~ few with less than 100 positions.
6. Conclusions
We have searched for globular clusters at the position of observed type Ia supernovae, using archival HST observations and literature data. We did not find evidence for globular clusters at any of the SNIa positions, and our analysis showed that for 18 SNIae the observations were sensitive enough that any globular cluster should have been detected if it had been there. For the positions of another 17 SNIae, bright globular clusters would have been detected. For the latter sample, we developed a new empirical method to estimate the incompleteness based on samples of globular clusters with bright X-ray sources in nearby galaxies. The sample of non-detections allows us to derive upper limits on the fraction of type Ia supernovae that take place in globular clusters. For the full sample the 90% and 99% upper limits on the fraction of type Ia supernovae are 9% and 16%. This is higher than the currently favoured estimates of ≲ 1%, but within the range allowed by theory. The sample of early-type galaxies provides the best limits for the enhancement factor per unit stellar mass for a coeval population ηco ≲ 50 (90% confidence). We argue that a dedicated survey, combining ground-based observations of nearby SNIa positions with HST observations of more distant SNIa positions would be able to probe the favoured theoretical estimates.
Acknowledgments
This research is supported by NWO Vidi grant 016.093.305. We thank Weidong Li for help with finding supernova images. Based on observations made with the NASA/ESA Hubble Space Telescope, obtained from the data archive at the Space Telescope Institute. STScI is operated by the association of Universities for Research in Astronomy, Inc. under the NASA contract NAS 5-26555.
References
- Angelini, L., Loewenstein, M., & Mushotzky, R. F. 2001, ApJ, 557, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Baade, W., Burbidge, G. R., Hoyle, F., et al. 1956, PASP, 68, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. J., Roming, P. W. A., Milne, P., et al. 2010, ApJ, 721, 1608 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., Mazzali, P. A., Benetti, S., et al. 1997, A&A, 328, 203 [NASA ADS] [Google Scholar]
- Clark, G. W. 1975, ApJ, 199, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Norberg, P., Baugh, C. M., et al. 2001, MNRAS, 326, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, M. B., & Benz, W. 1995, MNRAS, 276, 876 [NASA ADS] [Google Scholar]
- Di Stefano, R., & Rappaport, S. 1994, ApJ, 423, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Dieball, A., Knigge, C., Zurek, D. R., et al. 2007, ApJ, 670, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Elias-Rosa, N., Benetti, S., Cappellaro, E., et al. 2006, MNRAS, 369, 1880 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Rest, A., Stritzinger, M., et al. 2010, AJ, 140, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996, AJ, 112, 2408 [Google Scholar]
- Hanish, D. J., Meurer, G. R., Ferguson, H. C., et al. 2006, ApJ, 649, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 2009, ApJ, 703, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Heinke, C. O., Grindlay, J. E., Edmonds, P. D., et al. 2005, ApJ, 625, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., et al. 2009, A&A, 500, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hicken, M., Challis, P., Jha, S., et al. 2009, ApJ, 700, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P., & Verbunt, F. 1983, Nature, 301, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. Jr., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Heinke, C. O., Rasio, F. A., et al. 2006, MNRAS, 372, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Jha, S., Kirshner, R. P., Challis, P., et al. 2006, AJ, 131, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., Sivakoff, G. R., McLaughlin, D. E., et al. 2007, ApJ, 671, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Kirshner, R. P., & Oke, J. B. 1975, ApJ, 200, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C., Dieball, A., Maíz Apellániz, J., et al. 2008, ApJ, 683, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Phillips, M. M., Stubbs, C., et al. 2001, AJ, 122, 1616 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Marion, G. H., Suntzeff, N. B., et al. 2009, AJ, 138, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Lair, J. C., Leising, M. D., Milne, P. A., & Williams, G. G. 2006, AJ, 132, 2024 [NASA ADS] [CrossRef] [Google Scholar]
- Leloudas, G., Stritzinger, M. D., Sollerman, J., et al. 2009, A&A, 505, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, W., Filippenko, A. V., Gates, E., et al. 2001, PASP, 113, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Bloom, J. S., Podsiadlowski, P., et al. 2011, Nature, 480, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Lira, P., Suntzeff, N. B., Phillips, M. M., et al. 1998, AJ, 115, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2007, A&A, 469, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorimer, D. R. 2005, Liv. Rev. Rel., 8, 7 [Google Scholar]
- Lyne, A. G., Brinklow, A., Middleditch, J., Kulkarni, S. R., & Backer, D. C. 1987, Nature, 328, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Maccarone, T., & Knigge, C. 2007, Astron. Geophys., 48, 050000 [Google Scholar]
- Maccarone, T. J., Kundu, A., Zepf, S. E., & Rhode, K. L. 2011, MNRAS, 410, 1655 [NASA ADS] [Google Scholar]
- Maeda, K., Kawabata, K., Li, W., et al. 2009, ApJ, 690, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Mannucci, F. 2008, MNRAS, 388, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Sharon, K., & Gal-Yam, A. 2010, ApJ, 722, 1879 [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milne, P. A., The, L. S., & Leising, M. D. 1999, ApJS, 124, 503 [Google Scholar]
- Milne, P. A., Brown, P. J., Roming, P. W. A., et al. 2010, ApJ, 721, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Voss, R., Roelofs, G., & Bassa, C. 2008, MNRAS, 388, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1982, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, M. B., Maccarone, T. J., Kundu, A., & Zepf, S. E. 2010, MNRAS, 407, 2611 [NASA ADS] [CrossRef] [Google Scholar]
- Pfahl, E., Scannapieco, E., & Bildsten, L. 2009, ApJ, 695, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Pooley, D., & Hut, P. 2006, ApJ, 646, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Pooley, D., Lewin, W. H. G., Anderson, S. F., et al. 2003, ApJ, 591, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Salucci, P., & Persic, M. 1999, MNRAS, 309, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Salvo, M. E., Cappellaro, E., Mazzali, P. A., et al. 2001, MNRAS, 321, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A. R. 1953, AJ, 58, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., Reindl, B., & Tammann, G. A. 2010, ApJ, 714, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L., Kundu, A., Irwin, J. A., et al. 2003, ApJ, 595, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., & Stanek, K. Z. 2011, ApJ, 733, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., & Hurley, J. R. 2002, ApJ, 571, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., & Hurley, J. R. 2006, ApJ, 646, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Sivakoff, G. R., Jordán, A., Sarazin, C. L., et al. 2007, ApJ, 660, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Sollerman, J., Lindahl, J., Kozma, C., et al. 2004, A&A, 428, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stanishev, V., Goobar, A., Benetti, S., et al. 2007, A&A, 469, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stritzinger, M., Burns, C. R., Phillips, M. M., et al. 2010, AJ, 140, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Le Borgne, D., Pritchet, C. J., et al. 2006, ApJ, 648, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1988, Catalog of Nearby Galaxies [Google Scholar]
- Tully, R. B., Rizzi, L., Shaya, E. J., et al. 2009, AJ, 138, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Turatto, M., Piemonte, A., Benetti, S., et al. 1998, AJ, 116, 2431 [NASA ADS] [CrossRef] [Google Scholar]
- Voss, R., & Nelemans, G. 2008, Nature, 451, 802 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Voss, R., Gilfanov, M., Sivakoff, G. R., et al. 2009, ApJ, 701, 471 [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, I. Jr. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Empirical completeness levels (absolute magnitudes) of globular clusters with LMXBs and the corresponding globular cluster masses.
Faintest observed BVRI magnitudes or upper limits from late-time observations of type Ia supernovae in the literature.
SNIae for which we were able to exlude a globular cluster origin based on archival HST observations.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


