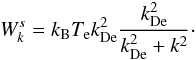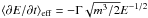| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201118216 | |
| Published online | 22 February 2012 | |
Wave-particle interactions in non-uniform plasma and the interpretation of hard X-ray spectra in solar flares
School of Physics & Astronomy, University of Glasgow, G12 8QQ, UK
e-mail: Eduard.Kontar@glasgow.ac.uk
Received: 6 October 2011
Accepted: 21 December 2011
Context. High-energy electrons accelerated during solar flares are abundant in the solar corona and in interplanetary space. Commonly, the number and energy of non-thermal electrons at the Sun is estimated through hard X-ray (HXR) spectral observations (e.g. RHESSI) and a single-particle collisional approximation.
Aims. We aim to investigate the role of the spectrally evolving Langmuir turbulence on the population of energetic electrons in the solar corona.
Methods. We numerically simulated the relaxation of a power-law non-thermal electron population in a collisional inhomogeneous plasma, including wave-particle and wave-wave interactions.
Results. The numerical simulations show that the long-time evolution of electron population above 20 keV deviates substantially from the collisional approximation when wave-particle interactions in non-uniform plasma are taken into account. The evolution of the Langmuir wave spectrum towards smaller wavenumbers, caused by large-scale density fluctuations and wave-wave interactions, leads to an effective acceleration of electrons. Furthermore, the time-integrated spectrum of non-thermal electrons, which is normally observed with HXR above 20 keV, is noticeably increased because of acceleration of non-thermal electrons through Langmuir waves.
Conclusions. The results show that the observed HXR spectrum, when interpreted in terms of collisional relaxation, can lead to an overestimated number and energy of energetic electrons accelerated in the corona.
Key words: Sun: flares / Sun: X-rays, gamma rays / acceleration of particles / plasmas / turbulence
© ESO, 2012
1. Introduction
Solar flares provide many theoretical challenges for various aspects of electron dynamics, including their acceleration and transport. One of the important aspects of solar flares is the high acceleration efficiency of electrons, seen via their Hard X-ray emission (HXR) in the dense atmosphere footpoints (e.g. Brown et al. 1990; Shibata 1999; Aschwanden 2002; Lin et al. 2003; Lin 2006; Bian et al. 2010; Battaglia et al. 2011; Battaglia & Kontar 2011; Christe et al. 2011; Krucker et al. 2011). It was realized early on that the solar corona can store large amounts of magnetic energy (Sweet 1958; Priest & Forbes 2002), which can be released to increase the kinetic energy of the surrounding plasma. While the exact location and properties of the electron acceleration site are still under debate, spatially resolved HXR observations, notably with RHESSI, point to the coronal origin of electron acceleration and subsequent transport of energetic electrons towards the denser lower corona (e.g. Holman et al. 2011; Kontar et al. 2011, as the most recent reviews). HXR emission from these dense regions is then commonly used as the model-dependent diagnostic of electron acceleration in the corona. The low dynamic range of current hard X-ray instruments is insufficient to observe the evolution of the energetic electron distribution enroute between the coronal and the footpoint parts. The exception to this rule are probably the radio observations of emissions from energetic electrons (e.g. Fleishman et al. 2011).
The propagation of energetic electrons between the coronal and the footpoint sources is often treated as a simple collisional transport. In this approximation the energy of an electron E = mv2/2 decreases with time through binary Coulomb collisions, so that for non-thermal particles v(t) ≫ vTe, one can write 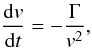 (1)where Γ = 4πe4nlnΛ/m2, n is the number density of the surrounding plasma, e is the electron charge, m is electron mass, vTe is the electron thermal velocity, and lnΛ ≃ 20 is the Coulomb logarithm. This treatment obviously ignores all collective interactions in plasma, but gives a simple relation between the accelerated and the resulting mean electron spectra responsible for the observed HXR spectra (e.g. Brown et al. 2003)1.
(1)where Γ = 4πe4nlnΛ/m2, n is the number density of the surrounding plasma, e is the electron charge, m is electron mass, vTe is the electron thermal velocity, and lnΛ ≃ 20 is the Coulomb logarithm. This treatment obviously ignores all collective interactions in plasma, but gives a simple relation between the accelerated and the resulting mean electron spectra responsible for the observed HXR spectra (e.g. Brown et al. 2003)1.
Realizing the importance of various streaming instabilities and the subsequent wave-particle interactions, a number of models have included the generation of Langmuir waves. Indeed, Langmuir wave turbulence can be effectively generated when the bump on tail distribution is formed (Kaplan & Tsytovich 1973; Tsytovich 1995). Firstly, the initially stable ∂f/∂v < 0 electron distribution function f(v) can be turned unstable i.e. ∂f/∂v > 0, when the fast electrons overtake the slower ones. During collisional relaxation of the electron population, a “gap” distribution can appear from an initially power-law distribution on collisional time-scales because slower particles lose their energy faster, τcol(E) ≃ mv3/(2Γ). This gap distribution of electrons creates a positive slope ∂f/∂v > 0 (Syrovatskii & Shmeleva 1972; Emslie & Smith 1984; Hamilton & Petrosian 1987), which could lead to the growth of Langmuir waves. The beam-plasma instability acts to decrease the gradient of the electron distribution in velocity space, while Coulomb collisions tend to restore it. The net result is a plateau-like distribution with the plateau height slowly decreasing, while energy is lost to the background plasma via collisions. It has been shown (e.g. Hamilton & Petrosian 1987; McClements 1987; Hannah & Kontar 2011) that even for the time-independent injection of electrons into plasma, the electrons should effectively generate Langmuir waves, but the time or space-integrated electron spectrum (to be compared with the HXR observations) is only weakly affected by this process. The overall evolution of the beam-plasma system is complicated by various non-linear processes, which can affect the spectrum of Langmuir turbulence (see Tsytovich 1995, as a review). Owing to these processes, the energy of Langmuir waves can be transferred from one range of phase velocities to another, hence suppressing the growth of Langmuir waves. The removal of Langmuir waves out of resonance with the electron beam can potentially lead to nonlinear stabilization of the beam-plasma instability, e.g., Papadopoulos (1975); Vlahos & Papadopoulos (1979); Rowland & Vlahos (1985); Muschietti & Dum (1991). While these earlier works were predominantly analytical estimates, more recent weakly turbulent treatments (e.g. Ziebell et al. 2001; Kontar & Pécseli 2002; Ziebell et al. 2011) are self-consistent and capture a complex interplay between wave-particle and wave-wave processes in collisionless plasma. For beam relaxation in a plasma, these processes can lead to the appearance of electrons with velocities above the maximum injected. At short scales, beam-plasma interaction Vlasov or PIC simulations (e.g. Karlický & Kašparová 2009; Tsiklauri 2010; Daldorff et al. 2011; Tsiklauri 2011) are particularly useful to capture phase-space effects of beam-plasma interaction at short time-scales. However, the interpretation of solar flare HXR emission requires knowledge of electron evolution at much longer time-scales, which are inaccessible by Vlasov or PIC approaches.
In this paper, we investigate the evolution of non-thermal electrons and Langmuir waves using a weak-turbulence theory in a collisional, inhomogeneous solar coronal plasma. We show that the evolution of the Langmuir wave spectrum caused by plasma inhomogeneities and wave-wave processes leads to effective acceleration of high-energy electrons. The resulting HXR spectrum is found to be strongly affected by the evolution of Langmuir turbulence, so that if the HXR spectrum is interpreted in terms of a collisional model, the accelerated electron spectrum will be overestimated.
2. Weak turbulent evolution of energetic electrons in a collisional plasma
The weakly turbulent collisional relaxation of an energetic electron population is considered in a collisional plasma typical for the solar corona. The evolution of energetic electrons is described using weak turbulence theory including wave-particle and wave-wave interactions in non-uniform plasma. The corresponding equations (Vedenov & Velikhov 1963; Vedenov et al. 1967; Tsytovich 1995) governing the electron distribution function f(v,t) [electrons cm-3 (cm/s)-1] and the spectral energy densities of Langmuir Wk, and ion-sound waves  [erg cm-2] are as in Kontar & Pécseli (2002):
[erg cm-2] are as in Kontar & Pécseli (2002): 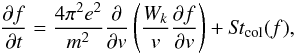 (2)\arraycolsep0pt
(2)\arraycolsep0pt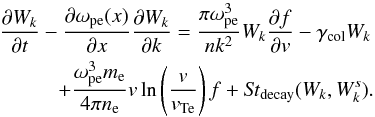 (3)\arraycolsep1.75ptHere,
(3)\arraycolsep1.75ptHere, 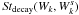 is the integral describing the parametric decay of a Langmuir wave with an ion-sound wave represented by l → l′ + s,
is the integral describing the parametric decay of a Langmuir wave with an ion-sound wave represented by l → l′ + s,![\begin{eqnarray} &&{\it St}_{\rm decay}(W_k,W^s_k)=\alpha\omega_{k}\nonumber\\ &&\hspace*{4mm}\times \int\omega^s_{k^{\prime}}\left[ \left( \frac{W_{k-k^{\prime}}}{\omega_{k-k^{\prime}}}\frac{W^s_{k'}}{\omega^s_{k'}}- \frac{W_k}{\omega_k}\left(\frac{W_{k-k^{\prime}}}{\omega_{k-k^{\prime}}}+ \frac{W^s_{k^{\prime}}}{\omega^s_{k^{\prime}}}\right)\right)\right.\nonumber\\ &&\hspace*{4mm}\times\, \delta (\omega_{k}-\omega_{k-k^{\prime}}-\omega^s_{k^{\prime}})- \left.\left(\frac{W_{k+k^{\prime}}}{\omega_{k+k^{\prime}}}\frac{W^s_{k'}}{\omega^s_{k'}}- \frac{W_k}{\omega_k}\left(\frac{W_{k+k^{\prime}}}{\omega_{k+k^{\prime}}}- \frac{W^s_{k^{\prime}}}{\omega^s_{k^{\prime}}}\right)\right)\right.\nonumber \\ &&\hspace*{4mm}\times \left.\delta(\omega_{k}-\omega_{k+k^{\prime}}+\omega^s_{k^{\prime}}) \right.\biggr] \,{\rm d}k^{\prime} \end{eqnarray}](/articles/aa/full_html/2012/03/aa18216-11/aa18216-11-eq25.png) (4)\arraycolsep1.75ptwith
(4)\arraycolsep1.75ptwith 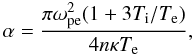 (5)where the spectral energy density is normalized such that
(5)where the spectral energy density is normalized such that 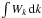 is the energy density of the waves [erg cm-3]. The system of Eqs. (2) − (5) describes the weakly turbulent evolution of electrons and Langmuir waves in the presence of density inhomogeneities and/or ion-sound waves. The spontaneous emission of Langmuir waves has been treated as in Hannah et al. (2009) and Reid et al. (2011), and the system was numerically integrated using a numerical scheme as in Kontar (2001c).
is the energy density of the waves [erg cm-3]. The system of Eqs. (2) − (5) describes the weakly turbulent evolution of electrons and Langmuir waves in the presence of density inhomogeneities and/or ion-sound waves. The spontaneous emission of Langmuir waves has been treated as in Hannah et al. (2009) and Reid et al. (2011), and the system was numerically integrated using a numerical scheme as in Kontar (2001c).
Because we are interested in the evolution of the system at time-scales t ≫ τcol, the collisional operator (e.g. Lifshitz & Pitaevskii 1981) is included to account for the binary collisions 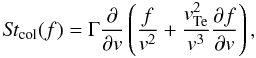 (6)where the first RHS term describes the systematic drag on energetic particles and the second term diffusion in velocity space through binary collisions. We note that the collisional drag is stronger than energy losses caused by spontaneous emission of Langmuir waves [second term in the right hand side of Eq. (2)] by a non-thermal electron in a plasma. In other words, only a small part of the energy lost by an electron with velocity v is transmitted into spontaneously generated Langmuir waves given by Eq. (3). Finally, the collisional damping rate for Langmuir waves
(6)where the first RHS term describes the systematic drag on energetic particles and the second term diffusion in velocity space through binary collisions. We note that the collisional drag is stronger than energy losses caused by spontaneous emission of Langmuir waves [second term in the right hand side of Eq. (2)] by a non-thermal electron in a plasma. In other words, only a small part of the energy lost by an electron with velocity v is transmitted into spontaneously generated Langmuir waves given by Eq. (3). Finally, the collisional damping rate for Langmuir waves 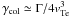 is added to Eq. (3).
is added to Eq. (3).
2.1. Initial electron distribution function
 |
Fig. 1 Collisional relaxation of an electron beam in a plasma. Top and middle panels: the electron distribution function f(v) and the spectral energy density of Langmuir waves (here fixed at the thermal level), respectively. Each coloured line shows the distribution at a different time. Bottom panel: the time-averaged electron flux spectrum [electrons keV-1 cm-2 s-1] plotted against electron energy. The dashed line shows the initial power-law flux. |
Let us consider the evolution of a non-thermal electron population with the initial electron distribution g0(v) in a Maxwellian plasma (Fig. 1): 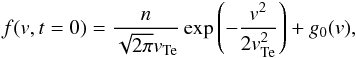 (7)where the non-thermal particle distribution g0(v) is initially a power law f(v,t = 0) ~ v − 2δ for v > vb = 10vTe and flattens at low velocities v < 10vTe;
(7)where the non-thermal particle distribution g0(v) is initially a power law f(v,t = 0) ~ v − 2δ for v > vb = 10vTe and flattens at low velocities v < 10vTe; ![\begin{equation} g_0({v})=\frac{2 n_{b}}{\sqrt{\pi}\, {v}_{b}}\frac{\Gamma(\delta)}{ \Gamma(\delta-\frac{1}{2})} \left[1+({v}/{v}_{b})^2\right]^{-\delta}, \label{eq:g0} \end{equation}](/articles/aa/full_html/2012/03/aa18216-11/aa18216-11-eq38.png) (8)where δ is the power law index for the energetic particles in energy space, nb the number density of non-thermal electrons, nb ≪ n, and Γ(x) denotes the gamma function. The initial electron distribution is normalized to the electron number density [electrons cm-3], so that
(8)where δ is the power law index for the energetic particles in energy space, nb the number density of non-thermal electrons, nb ≪ n, and Γ(x) denotes the gamma function. The initial electron distribution is normalized to the electron number density [electrons cm-3], so that 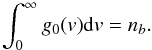 (9)The initial level of Langmuir waves can be calculated assuming an equilibrium with Maxwellian electron distribution function, ignoring all non-linear terms and setting dWk/dt = 0 in Eq. (3)
(9)The initial level of Langmuir waves can be calculated assuming an equilibrium with Maxwellian electron distribution function, ignoring all non-linear terms and setting dWk/dt = 0 in Eq. (3) 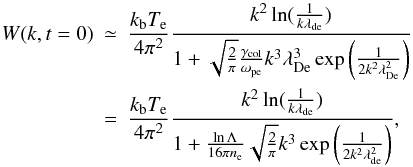 (10)where kb is Boltzmann constant,
(10)where kb is Boltzmann constant, 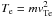 the electron temperature of the plasma, and λDe = vTe/ωpe is the Debye length. Equation (10) can be reduced to
the electron temperature of the plasma, and λDe = vTe/ωpe is the Debye length. Equation (10) can be reduced to 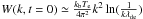 in the collisionless limit for γcol → 0, which is the thermal level of plasma waves in a collisionless Maxwellian plasma (Kaplan & Tsytovich 1973; Tsytovich 1995). For the problem considered, the exact initial level of plasma waves is not important, because the governing equations quickly establish a balanced level, which is a few orders of magnitude lower than the level driven by the instability.
in the collisionless limit for γcol → 0, which is the thermal level of plasma waves in a collisionless Maxwellian plasma (Kaplan & Tsytovich 1973; Tsytovich 1995). For the problem considered, the exact initial level of plasma waves is not important, because the governing equations quickly establish a balanced level, which is a few orders of magnitude lower than the level driven by the instability.
3. Evolution of the electron distribution function
We assume a background plasma similar to the solar corona, with plasma frequency of fpe = ωpe/2π = 2 GHz and an electron and ion temperature of Ti = Te = 1 MK. The corresponding plasma density is then 5.0 × 1010 cm-3 and the collisional timescale is τcol = 1/γcol = 7 × 10-5 s. For the electron beam we take nb/n = 1 × 10-2, and δ = 4, which results in a power-law index of 8 in velocity space above approximately vb.
3.1. Collisional relaxation
Under the influence of Coulomb collisions, the electron distribution function for v ≫ vTe evolves according to 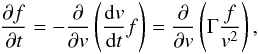 (11)which can be straightforwardly solved for an arbitrary initial distribution function, g0(v), so that f(v,t) = [v/u(v,t)] 2g0(u(v,t)), where u(v,t) = (v3 + 3Γt)1/3. The time-integrated, or mean electron distribution, will be the so-called thick-target electron spectrum. This expression is, as expected, similar to the space-integrated collisional thick-target model (e.g. Dubov 1963; Brown 1971; Brown et al. 2003) and directly corresponds to the electron spectrum responsible for X-ray flux. Figure 1 shows the time evolution of the electron distribution and the time-integrated electron flux spectrum. The time-dependent positive slope ∂f/∂v > 0 is formed for velocities v < (3Γt)1/3 while the tail at v > (3Γt)1/3 is weakly affected by collisions. As time progresses, a wider range of electron velocities shows a distribution function, which grows with velocity.
(11)which can be straightforwardly solved for an arbitrary initial distribution function, g0(v), so that f(v,t) = [v/u(v,t)] 2g0(u(v,t)), where u(v,t) = (v3 + 3Γt)1/3. The time-integrated, or mean electron distribution, will be the so-called thick-target electron spectrum. This expression is, as expected, similar to the space-integrated collisional thick-target model (e.g. Dubov 1963; Brown 1971; Brown et al. 2003) and directly corresponds to the electron spectrum responsible for X-ray flux. Figure 1 shows the time evolution of the electron distribution and the time-integrated electron flux spectrum. The time-dependent positive slope ∂f/∂v > 0 is formed for velocities v < (3Γt)1/3 while the tail at v > (3Γt)1/3 is weakly affected by collisions. As time progresses, a wider range of electron velocities shows a distribution function, which grows with velocity.
 |
Fig. 2 Same as in Fig. 1 but for collisional relaxation including Langmuir wave generation in homogeneous plasma. In the bottom panel, the black line shows the collisions-only case, the blue line includes wave generation. |
3.2. Langmuir wave generation in uniform plasma
For a uniform plasma (∂ωpe/∂x = 0) and for simplicity ignoring all wave-wave terms, the collisionally formed unstable distribution will lead to instability and effective generation of plasma waves (Fig. 2). The generation of Langmuir waves quickly flattens the distribution function and forms a plateau between ~3vTe < v < (3Γt)1/3 (Fig. 2). Over time, more non-thermal electrons are lost through collisions, and the plateau in velocity space becomes wider. As soon as the beam density has dropped, Langmuir waves are no longer generated noticeably, and the evolution of the electron beam again becomes purely collisional. The important aspect is that while the instantaneous distributions of electrons during quasi-linear and collisions-only relaxations are very different, the time-integrated spectra of energetic electrons are almost identical. This confirms the previously published results (Hamilton & Petrosian 1987; McClements 1987; Hannah et al. 2009; Hannah & Kontar 2011) that the quasi-linear interaction weakly affects the time-integrated spectrum. The energy is quickly transferred from electrons to the plasma waves and back, the time-integrated amount of energy for a given resonant velocity is almost constant (e.g. Vedenov & Velikhov 1963; Mel’Nik et al. 1999). The collisional energy loss of Langmuir waves does not facilitate the transfer of energy between different velocities, but simply reduces the energy.
3.3. Spectral evolution of Langmuir turbulence
The Langmuir wave spectrum can quickly evolve in k space, changing the wave energy available at different resonant velocities, v = ωpe/k. Firstly, the nonlinear wave-wave interactions change the distribution of Langmuir wave energy (Vedenov et al. 1967; Papadopoulos et al. 1974; Goldman & Dubois 1982; Bárta & Karlický 2000; Yoon et al. 2005; Fouquet & Pesme 2008; Palastro et al. 2009) and secondly, the waves can be effectively scattered or refracted by inhomogeneous plasma (Ryutov 1969; Breǐzman & Ruytov 1969; Krasovskii 1978; Coste et al. 1975; Nishikawa & Ryutov 1976; Smith & Sime 1979; Asadullin et al. 1980; Melrose & Cramer 1989; Kontar 2001a,b; Li et al. 2006; Ziebell et al. 2011).
3.3.1. Inhomogeneous plasma – constant density gradient
To illustrate the role of the spectral evolution of Langmuir waves on the electron distribution function, we consider the relaxation of energetic electrons in a plasma with a constant density gradient, so that the term describing refraction of Langmuir waves is 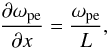 (12)where
(12)where 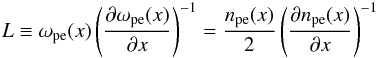 (13)is the characteristic scale of density inhomogeneity. Langmuir waves propagating into the region of higher/lower density experience change in wavenumber to k + Δk, with Δk ≃ ± ωpeΔt/|L|, depending on the sign of the density gradient. This in turn affects the resonant velocity v = ωpe/k, so electrons of lower/higher velocities can now interact with this wave. For electrons propagating into denser regions, the plasma density grows, causing generated Langmuir waves to have a negative shift in k, Δk ≃ − ωpeΔt/|L|. Therefore, Langmuir waves generated at higher k are shifted towards lower k (higher phase velocities), and hence, can be effectively absorbed by faster electrons with ∂f/∂v < 0, which are consequently accelerated. For a density gradient of L ≳ 106 cm, the waves are shifted faster than the characteristic time of collisional relaxation, so for
(13)is the characteristic scale of density inhomogeneity. Langmuir waves propagating into the region of higher/lower density experience change in wavenumber to k + Δk, with Δk ≃ ± ωpeΔt/|L|, depending on the sign of the density gradient. This in turn affects the resonant velocity v = ωpe/k, so electrons of lower/higher velocities can now interact with this wave. For electrons propagating into denser regions, the plasma density grows, causing generated Langmuir waves to have a negative shift in k, Δk ≃ − ωpeΔt/|L|. Therefore, Langmuir waves generated at higher k are shifted towards lower k (higher phase velocities), and hence, can be effectively absorbed by faster electrons with ∂f/∂v < 0, which are consequently accelerated. For a density gradient of L ≳ 106 cm, the waves are shifted faster than the characteristic time of collisional relaxation, so for 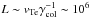 cm, substantial energy can be transferred to higher electron velocities. Figure 3 shows efficient acceleration of energetic electrons above ~ 30vTe because the Langmuir waves shift to higher phase velocities. Importantly, these accelerated electrons are evident in the time-averaged spectrum, hence the resulting hard X-ray spectrum will be affected and the role of Langmuir waves is detectable.
cm, substantial energy can be transferred to higher electron velocities. Figure 3 shows efficient acceleration of energetic electrons above ~ 30vTe because the Langmuir waves shift to higher phase velocities. Importantly, these accelerated electrons are evident in the time-averaged spectrum, hence the resulting hard X-ray spectrum will be affected and the role of Langmuir waves is detectable.
 |
Fig. 3 Same as in Fig. 2, but for a plasma with constant density gradient as in Eq. (12), with L = 106 cm. |
3.3.2. Density fluctuations
However, even without a constant density gradient, the Langmuir wave spectrum is also expected to evolve. For instance, the solar coronal plasma, as any real plasma, has a fluctuating part, n + δn(x,t). For large-scale density perturbations 1/L ≪ ωpe/vb, the resonant conditions for Langmuir wave decay or scattering cannot be satisfied and the Langmuir waves will be scattered with a small change in k (Nishikawa & Ryutov 1976; Goldman & Dubois 1982). Let us consider density fluctuations with ⟨ (δn/n)2 ⟩ ≪ 1, zero mean ⟨ δn ⟩ = 0 and a Gaussian spectrum 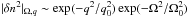 , where q0 and Ω0 are their characteristic wavenumber and frequency. Under the influence of these turbulent density fluctuations, the spectral evolution of Langmuir waves in k becomes diffusive
, where q0 and Ω0 are their characteristic wavenumber and frequency. Under the influence of these turbulent density fluctuations, the spectral evolution of Langmuir waves in k becomes diffusive 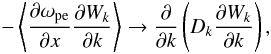 (14)where ⟨ ⟩ denotes ensemble average over density fluctuations. The diffusion coefficient describing this random refraction of waves is
(14)where ⟨ ⟩ denotes ensemble average over density fluctuations. The diffusion coefficient describing this random refraction of waves is 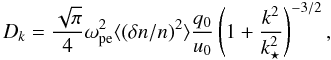 (15)where
(15)where 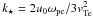 and u0 = Ω0/q0. Assuming a modest level of turbulence δn/n = 10-3, with a characteristic speed close to the speed of sound in the corona u0 = Ω0/q0 ~ 107 cm s-1 and long wavelength 1/q0 ~ 104 cm, this spectral diffusion Dk substantially changes the spectrum of Langmuir waves in a few collisional times. Figure 4 shows the evolution of the electron distribution function and the spectral energy density of Langmuir waves. Langmuir waves diffuse in k-space, from an initial value of k ~ ωpe/vb, so in time the spectrum of Langmuir waves becomes broader with time. The absorption of Langmuir waves by electrons above 20vTe leads to electron acceleration. As in the constant gradient case, the integrated electron flux for the fluctuating density case changes considerably at energies above ~20 keV.
and u0 = Ω0/q0. Assuming a modest level of turbulence δn/n = 10-3, with a characteristic speed close to the speed of sound in the corona u0 = Ω0/q0 ~ 107 cm s-1 and long wavelength 1/q0 ~ 104 cm, this spectral diffusion Dk substantially changes the spectrum of Langmuir waves in a few collisional times. Figure 4 shows the evolution of the electron distribution function and the spectral energy density of Langmuir waves. Langmuir waves diffuse in k-space, from an initial value of k ~ ωpe/vb, so in time the spectrum of Langmuir waves becomes broader with time. The absorption of Langmuir waves by electrons above 20vTe leads to electron acceleration. As in the constant gradient case, the integrated electron flux for the fluctuating density case changes considerably at energies above ~20 keV.
3.3.3. Three-wave interaction of Langmuir waves
For density fluctuations with wavenumber q ~ ωpe/vb the diffusive treatment is no longer valid, and we must individually consider the interactions between Langmuir waves and other modes in the plasma. In particular, we are interested in those modes that may be excited by the high level of Langmuir waves present because of the beam-plasma interaction. Following the treatments in uniform (Ziebell et al. 2001) and inhomogeneous (Kontar & Pécseli 2002; Ziebell et al. 2011) plasmas, we now consider the three-wave process, l ⇄ l′ + s, where l and l′ are Langmuir waves and s is a sound wave. This process efficiently scatters electron-beam-generated waves with wavenumber k, into secondary Langmuir waves with wavenumber k′ ≈ − k. The decay of a Langmuir wave generates an ion-sound wave with q ≈ 2k. Every scattering decreases the absolute value of the Langmuir wave number by 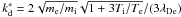 . Hence, repeated wave-wave processes cause Langmuir waves to appear at lower k (higher phase velocities). As in the previous cases, Langmuir waves can be absorbed by the tail of the distribution, leading to acceleration of non-thermal electrons.
. Hence, repeated wave-wave processes cause Langmuir waves to appear at lower k (higher phase velocities). As in the previous cases, Langmuir waves can be absorbed by the tail of the distribution, leading to acceleration of non-thermal electrons.
The simultaneous evolution of both ion-sound waves and Langmuir waves has already been simulated (e.g. Ziebell et al. 2001; Kontar & Pécseli 2002; Ziebell et al. 2011) and does produce the effect outlined in the previous paragraph. Here we limit ourself to a more simple but quite illuminating situation with a fixed level of density fluctuations produced by ion-sound waves. We assume the level of ion-sound waves to be thermal,
The results are presented in Fig. 5. As for the constant density gradient and random density fluctuations, we see a plateau distribution up to ~60vTe at t = 1 s. The nonlinear decay term has a strong impact on the distribution above 50vTe because of the high level of waves for k < kDe/60. Because the wave-wave terms are particularly effective in shifting the Langmuir wave energy to low k, making Langmuir waves more isotropic, the number of accelerated electrons at energies above 100 keV also increases. Below 100 keV, the effect in the time-integrated spectrum is similar to the previous cases.
4. Discussion and conclusions
The above results show the significant effect that Langmuir waves have on the corresponding electron distribution function. A constant density gradient, or random long-wavelength density fluctuations, produce an enhancement of the electron distribution in the range 30−60 vTe. On the other hand, the wave-wave interactions with short wavelength fluctuations q ~ 2k show a more pronounced effect at velocities v ≃ 60vTe. Unlike the case of a uniform plasma, the time-averaged electron spectrum is noticeably different from collisional relaxation. Because the time averaged spectrum is directly related to hard X-ray observations, the role of Langmuir waves in non-uniform plasma is observable. The resulting HXR spectrum above ~20 keV is higher than expected from collisional relaxation, and if interpreted as thick-target relaxation, the number of energetic electrons injected is overestimated.
 |
Fig. 6 Effective energy loss rate of an electron ⟨ ∂E/∂t ⟩ eff using Eq. (17), at 0.5 s. Collisional losses |
Given the evolution of the electron distribution, f(v,t), we can calculate the effective energy change rate. Evidently the actual energy loss/gain rate is given by the kinetic Eqs. (2) − (5), but assuming a single-particle description often used in the literature (e.g. Brown et al. 2009), the effective energy-loss rate ⟨ dE/dt ⟩ eff can be defined as the one satisfying a continuity equation: 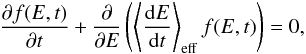 (16)where f(E,t) = mv(E)f(v(E),t) is the energy distribution function. The effective energy loss/gain rate satisfying this equation is
(16)where f(E,t) = mv(E)f(v(E),t) is the energy distribution function. The effective energy loss/gain rate satisfying this equation is 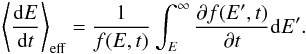 (17)If the evolution of particles is governed by collisions only, the effective loss rate is simply
(17)If the evolution of particles is governed by collisions only, the effective loss rate is simply 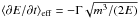 (Fig. 6). The evolving Langmuir wave turbulence notably changes ⟨ ∂E/∂t ⟩ eff, decreasing the effective energy loss at energies of a few keV, increasing the loss rate in the intermediate range near 10 keV, and leading to acceleration and/or reduced energy loss rate at about 20 keV and above. This effective energy change rate increases the flux of electrons above 20 keV by a factor of a few to several tens (shown in Figs. 3 − 5).
(Fig. 6). The evolving Langmuir wave turbulence notably changes ⟨ ∂E/∂t ⟩ eff, decreasing the effective energy loss at energies of a few keV, increasing the loss rate in the intermediate range near 10 keV, and leading to acceleration and/or reduced energy loss rate at about 20 keV and above. This effective energy change rate increases the flux of electrons above 20 keV by a factor of a few to several tens (shown in Figs. 3 − 5).
We emphasize that the acceleration of energetic electrons is caused by spectral evolution of Langmuir waves. The Langmuir wave generation in a uniform plasma only weakly changes the time-integrated HXR spectrum and, hence, is not likely to be detected in current HXR measurements. The important exception is the generation of waves by spatially localized electron beams (e.g. Hannah & Kontar 2011), when electrons are accelerated in bunches and not as a continuous stream, as expected in some acceleration models. The acceleration of energetic electrons in non-uniform plasma is through Langmuir waves generated by the non-thermal electrons themselves and does not increase the total energy of the beam-plasma system. On the contrary, the energetic electrons lose their energy not only via collisions but also via generation of Langmuir waves and their subsequent absorbtion via collisions. Therefore, although the low-energy electrons lose their energy faster, the higher energy electrons are gaining energy and hence can generate HXR emission for a longer time. This “self-acceleration” of some electron population reduces the number of accelerated electrons necessary to explain the observed HXR fluxes. This process also produces a similar effect to a re-acceleration from externally applied electric fields as discussed by Brown et al. (2009), but evidently does not require additional energy input.
A few important comments are due on the application of these results to the interpretation of solar flare X-ray spectrum. The overall effect of electron re-acceleration through evolution of Langmuir turbulence is beam-density dependent. The higher the beam density, the stronger the generation of Langmuir waves, and therefore the effects considered should be more evident in HXR data. Therefore, the stronger the flare, the larger the overestimation of non-thermal electrons, when interpreted by a collisional thick-target model. Furthermore, these simulations need to be extended to account for the spatial transport of energetic electrons in solar flare conditions, a relativistic treatment of the electrons included, and the role of whistlers (e.g. Stepanov & Tsap 2002) and kinetic Alfven waves (e.g. Bian et al. 2010) considered. The relaxation produces an enhanced level of Langmuir waves, which could lead to plasma microwave emission (Emslie & Smith 1984; Hamilton & Petrosian 1987) and needs to be investigated in more detail. However, as the spectrum of Langmuir turbulence evolves with time, the wave-wave and density gradient effects need to be included.
In summary, the evolving Langmuir turbulence spectrum has a noticeable effect on both the instantaneous and time-averaged distribution functions, and leads to the overestimation of electron flux (and hence energy) in non-thermal electrons > 20 keV, if interpreted in terms of a standard collisional thick-target model. Therefore, if Langmuir waves are effectively generated in flares and their spectrum evolves, the number of accelerated electrons could be substantially smaller than inferred from HXR thick-target interpretation.
Acknowledgments
This work is supported by a STFC rolling grant (EPK). Financial support by the European Commission through the HESPE Network is gratefully acknowledged.
References
- Asadullin, F. F., Batanov, G. M., Veriaev, A. A., et al. 1980, Sov. J. Plasma Phys., 6, 137 [NASA ADS] [Google Scholar]
- Aschwanden, M. J. 2002, Space Sci. Rev., 101, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bárta, M., & Karlický, M. 2000, A&A, 353, 757 [NASA ADS] [Google Scholar]
- Battaglia, M., & Kontar, E. P. 2011, A&A, 533, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, M., Kontar, E. P., & Hannah, I. G. 2011, A&A, 526, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, N. H., Kontar, E. P., & Brown, J. C. 2010, A&A, 519, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breǐzman, B. N., & Ruytov, D. D. 1969, Sov. J. Exp. Theor. Phys., 30, 759 [NASA ADS] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Karlicky, M., MacKinnon, A. L., & van den Oord, G. H. J. 1990, ApJS, 73, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Emslie, A. G., & Kontar, E. P. 2003, ApJ, 595, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Turkmani, R., Kontar, E. P., MacKinnon, A. L., & Vlahos, L. 2009, A&A, 508, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christe, S., Krucker, S., & Saint-Hilaire, P. 2011, Sol. Phys., 270, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Coste, J., Reinisch, G., Montes, C., & Silevitch, M. B. 1975, Phys. Fluids, 18, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Daldorff, L. K. S., Pécseli, H. L., Trulsen, J. K., et al. 2011, Phys. Plasmas, 18, 052107 [NASA ADS] [CrossRef] [Google Scholar]
- Dubov, É. E. 1963, Sov. Phys. Doklady, 8, 543 [Google Scholar]
- Emslie, A. G., & Smith, D. F. 1984, ApJ, 279, 882 [NASA ADS] [CrossRef] [Google Scholar]
- Fleishman, G. D., Kontar, E. P., Nita, G. M., & Gary, D. E. 2011, ApJ, 731, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Fouquet, T., & Pesme, D. 2008, Phys. Rev. Lett., 100, 055006 [NASA ADS] [CrossRef] [Google Scholar]
- Goldman, M. V., & Dubois, D. F. 1982, Phys. Fluids, 25, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, R. J., & Petrosian, V. 1987, ApJ, 321, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Hannah, I. G., & Kontar, E. P. 2011, A&A, 529, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hannah, I. G., Kontar, E. P., & Sirenko, O. K. 2009, ApJ, 707, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, G. D., Aschwanden, M. J., Aurass, H., et al. 2011, Space Sci. Rev., 159, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, S. A., & Tsytovich, V. N. 1973, Plasma astrophysics, ed. S. A. Kaplan, & V. N. Tsytovich [Google Scholar]
- Karlický, M., & Kašparová, J. 2009, A&A, 506, 1437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontar, E. P. 2001a, Sol. Phys., 202, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P. 2001b, A&A, 375, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontar, E. P. 2001c, Comp. Phys. Comm., 138, 222 [Google Scholar]
- Kontar, E. P., & Pécseli, H. L. 2002, Phys. Rev. E, 65, 066408 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Brown, J. C., Emslie, A. G., et al. 2011, Space Sci. Rev., 159, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Krasovskii, V. L. 1978, Sov. J. Plasma Phys., 4, 1267 [NASA ADS] [Google Scholar]
- Krucker, S., Hudson, H. S., Jeffrey, N. L. S., et al. 2011, ApJ, 739, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B., Robinson, P. A., & Cairns, I. H. 2006, Phys. Plasmas, 13, 092902 [NASA ADS] [CrossRef] [Google Scholar]
- Lifshitz, E. M., & Pitaevskii, L. P. 1981, Phys. kinetics, ed. E. M. Lifshitz, & L. P. Pitaevskii [Google Scholar]
- Lin, R. P. 2006, Space Sci. Rev., 124, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., & Rhessi Team 2003, Adv. Space Res., 32, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- McClements, K. G. 1987, A&A, 175, 255 [NASA ADS] [Google Scholar]
- Mel’Nik, V. N., Lapshin, V., & Kontar, E. 1999, Sol. Phys., 184, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B., & Cramer, N. F. 1989, Sol. Phys., 123, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Muschietti, L., & Dum, C. T. 1991, Phys. Fluids B, 3, 1968 [NASA ADS] [CrossRef] [Google Scholar]
- Nishikawa, K., & Ryutov, D. D. 1976, J. Phys. Soc. Jap., 41, 1757 [Google Scholar]
- Palastro, J. P., Williams, E. A., Hinkel, D. E., Divol, L., & Strozzi, D. J. 2009, Phys. Plasmas, 16, 092304 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, K. 1975, Phys. Fluids, 18, 1769 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, K., Goldstein, M. L., & Smith, R. A. 1974, ApJ, 190, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Forbes, T. G. 2002, A&ARv, 10, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, H. A. S., Vilmer, N., & Kontar, E. P. 2011, A&A, 529, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rowland, H. L., & Vlahos, L. 1985, A&A, 142, 219 [NASA ADS] [Google Scholar]
- Ryutov, D. D. 1969, Sov. J. Exp. Theor. Phys., 30, 131 [Google Scholar]
- Shibata, K. 1999, Ap&SS, 264, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. F., & Sime, D. 1979, ApJ, 233, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, A. V., & Tsap, Y. T. 2002, Sol. Phys., 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Sweet, P. A. 1958, in Electromagnetic Phenomena in Cosmical Physics, ed. B. Lehnert, IAU Symp., 6, 123 [Google Scholar]
- Syrovatskii, S. I., & Shmeleva, O. P. 1972, AZh, 49, 334 [NASA ADS] [Google Scholar]
- Tsiklauri, D. 2010, Sol. Phys., 267, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiklauri, D. 2011, Phys. Plasmas, 18, 052903 [NASA ADS] [CrossRef] [Google Scholar]
- Tsytovich, V. N. 1995, Lectures on Non-linear Plasma Kinetics, ed. V. N. Tsytovich, & D. ter Haar [Google Scholar]
- Vedenov, A. A., & Velikhov, E. P. 1963, Sov. J. Exp. Theor. Phys., 16, 682 [NASA ADS] [Google Scholar]
- Vedenov, A. A., Gordeev, A. V., & Rudakov, L. I. 1967, Plasma Phys., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahos, L., & Papadopoulos, K. 1979, ApJ, 233, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, P. H., Rhee, T., & Ryu, C.-M. 2005, Phys. Rev. Lett., 95, 215003 [NASA ADS] [CrossRef] [Google Scholar]
- Ziebell, L. F., Gaelzer, R., & Yoon, P. H. 2001, Phys. Plasmas, 8, 3982 [NASA ADS] [CrossRef] [Google Scholar]
- Ziebell, L. F., Yoon, P. H., Pavan, J., & Gaelzer, R. 2011, ApJ, 727, 16 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Collisional relaxation of an electron beam in a plasma. Top and middle panels: the electron distribution function f(v) and the spectral energy density of Langmuir waves (here fixed at the thermal level), respectively. Each coloured line shows the distribution at a different time. Bottom panel: the time-averaged electron flux spectrum [electrons keV-1 cm-2 s-1] plotted against electron energy. The dashed line shows the initial power-law flux. |
| In the text | |
 |
Fig. 2 Same as in Fig. 1 but for collisional relaxation including Langmuir wave generation in homogeneous plasma. In the bottom panel, the black line shows the collisions-only case, the blue line includes wave generation. |
| In the text | |
 |
Fig. 3 Same as in Fig. 2, but for a plasma with constant density gradient as in Eq. (12), with L = 106 cm. |
| In the text | |
 |
Fig. 4 Same as in Fig. 2, but for plasma with random density fluctuations given by Eq. (15). |
| In the text | |
 |
Fig. 5 Same as Fig. 2 but with ion-sound wave interactions as well as density fluctuations. |
| In the text | |
 |
Fig. 6 Effective energy loss rate of an electron ⟨ ∂E/∂t ⟩ eff using Eq. (17), at 0.5 s. Collisional losses |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.