| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118202 | |
| Published online | 20 February 2012 | |
Circumstellar disks in binary star systems
Models for γ Cephei and α Centauri
Institut für Astronomie & Astrophysik, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
e-mail: Tobias_Mueller@twam.info
Received: 4 October 2011
Accepted: 2 December 2011
Context. As of today, over 50 planetary systems have been discovered in binary star systems, some of which have binary separations that are smaller than 20 AU. In these systems the gravitational forces from the binary have a strong influence on the evolution of the protoplanetary disk and hence the planet formation process.
Aims. We study the evolution of viscous and radiative circumstellar disks under the influence of a companion star. We focus on the eccentric γ Cephei and α Centauri system as examples and compare disk quantities such as disk eccentricity and precession rate to previous isothermal simulations.
Methods. We performed two-dimensional hydrodynamical simulations of the binary star systems under the assumption of coplanarity of the disk, host star and binary companion. We used the grid-based, staggered mesh code FARGO with an additional energy equation to which we added radiative cooling based on opacity tables.
Results. The eccentric binary companion perturbs the disk around the primary star periodically. Upon passing periastron, spirals arms are induced that wind from the outer disk towards the star. In isothermal simulations this results in disk eccentricities up to edisk ≈ 0.2, but in more realistic radiative models we obtain much smaller eccentricities of about edisk ≈ 0.04−0.06 with no real precession. Models with varying viscosity and disk mass indicate that disks with less mass have lower temperatures and higher disk eccentricity.
Conclusions. The fairly high disk eccentricities, as indicated in previous isothermal disk simulations, implied a more difficult planet formation in the γ Cephei system caused by the enhanced collision velocities of planetesimals. We have shown that under more realistic conditions with radiative cooling the disk becomes less eccentric and thus planet formation may be made easier. However, we estimate that the viscosity in the disk has to very low, with α ≲ 0.001, because otherwise the disk’s lifetime will be too short to allow planet formation to occur along the core instability scenario. We estimate that the periodic heating of the disk in eccentric binaries will be observable in the mid-IR regime.
Key words: accretion, accretion disks / protoplanetary disks / hydrodynamics / radiative transfer / methods: numerical / planets and satellites: formation
© ESO, 2012
1. Introduction
Presently, about 50 planets are known to reside in binary stars systems. In all systems with solar-type stars the planet orbits one of the stars while the secondary star acts as a perturber, i.e. these are in a so-called S-type configuration (Dvorak 1986). Recently, planets seem to have been detected in evolved binary star systems that are in a circumbinary (P-type) configuration (e.g. Beuermann et al. 2011). The main observational characteristic of the known planets in binary stars system have been summarized by Eggenberger et al. (2004); Raghavan et al. (2006); Desidera & Barbieri (2007). Most planets are in binaries with very large separations with semi-major axis beyond 100 AU, in particular when detected by direct imaging. Observationally, there is evidence for fewer planets in binaries with a separation of less than about 100 AU (Eggenberger et al. 2007), in accordance with the expectation that binarity constitutes a challenge to the planet formation process. Despite this, there are several systems with a quite close binary separation such as γ Cephei (Campbell et al. 1988), Gliese 86 (Queloz et al. 2000; Els et al. 2001), HD 41004 (Zucker et al. 2004), and HD 196885 (Correia et al. 2008).
As known from several theoretical studies, the presence of the secondary renders the planet formation process more difficult than around single stars. Owing to the gravitational disturbance, the protoplanetary disk is hotter and dynamically more excited such that the coagulation and growth process of planetesimals as well as the gravitational instability process in the early phase of planet formation are hindered (Nelson 2000; Thébault et al. 2004, 2006). This is particularly true for the mentioned closer binaries with an orbital separation of about 20 AU. Hence this theoretical challenge has put these tighter binaries into the focus of studies on planet formation in binary stars (Quintana et al. 2007; Paardekooper et al. 2008; Kley & Nelson 2008) and on their dynamical stability (Dvorak et al. 2004; Haghighipour 2006). The most famous example in this category is the γ Cephei system, which has been known for over 20 years to contain a protoplanet (Campbell et al. 1988; Hatzes et al. 2003). In recent years the orbital parameter of this system have been updated (Neuhäuser et al. 2007; Torres 2007) and the basic binary parameters are quoted in Table 2 (below) because γ Cephei is our standard model. At the end of the paper we will briefly discuss the α Centauri system as well.
Because planet formation occurs in disks, their dynamical structure is of crucial importance in estimating the efficiency of planetary growth processes. The prime effect of the secondary star is the truncation of the disk owing to tidal torques (Artymowicz & Lubow 1994). The truncation radius depends on the mass ratio of the binary, its eccentricity and the viscosity in the disk. An additional effect, namely the excitation of eccentric modes in the disk, which has been noticed previously in close binary stars (Whitehurst 1988; Lubow 1991; Kley et al. 2008), has recently drawn attention in studies of planet harboring binary stars as well (Paardekooper et al. 2008; Kley & Nelson 2008). In these studies it was shown that despite the high eccentricity of a γ Cephei type binary the disk became eccentric with an average eccentricity of about edisk ≈ 0.12 and a coherent disk precession (Kley & Nelson 2008). However, this leaves the question of numerical effects (Paardekooper et al. 2008). Subsequently the influence of self-gravity of the disk has been analyzed by Marzari et al. (2009a), who concluded that the inclusion of self-gravity leads to disks with lower eccentricity on average.
Interestingly, there may be observational evidence for tidal interactions between a companion on an eccentric orbit and a circumstellar disk around the primary star (van Boekel et al. 2010), as inferred from variable brightness on longer timescales. The possibility to detect an eccentric disk through spectral line observations has been analyzed recently by Regály et al. (2011).
In all simulations mentioned above, the disk has typically been modeled using a fixed radial temperature distribution. This simplifies the numerics such that no energy equation has to be solved but of course it lacks physical reality. In this work we will extend previous studies and consider a much improved treatment of the energy equation. We will do so within the two-dimensional, flat-disk approximation following D’Angelo et al. (2003) and Kley & Crida (2008). Here, the viscous heating of the disk and the radiative losses are taken into account. We will study the structure and dynamical evolution of disks with different masses and binary parameter, and will analyze the influence of numerical aspects, in particular boundary conditions. Our first target of interest will be the well-studied system γ Cephei and we will present results on the α Centauri system subsequently.
2. Model setup
We assumed that the complete system of primary star, circumstellar disk and secondary star is coplanar. Consequently, in our calculations we assumed a flat two-dimensional disk orbiting the primary. The disk is modeled hydrodynamically, under the assumption that the action of the turbulence can be described by a standard viscous stress tensor.
Details of the various opacity regimes by type, showing the transition temperature and the constants κ0, a and b.
2.1. Physics and equations
We used cylindrical coordinates (r,ϕ,z) centered on the primary star where the disk lies in the equatorial, z = 0 plane. Because our model is two-dimensional (r,ϕ), we solved the vertically integrated versions of the hydrodynamical equations. In this approximation the continuity equation is 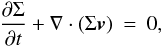 (1)where v = (vr,vϕ) = (v,Ωr) is the velocity, and
(1)where v = (vr,vϕ) = (v,Ωr) is the velocity, and 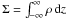 the surface density. As indicated, in the following we will also use v and rΩ for the radial and orbital velocity, respectively. The vertically integrated equation of radial motion is then
the surface density. As indicated, in the following we will also use v and rΩ for the radial and orbital velocity, respectively. The vertically integrated equation of radial motion is then 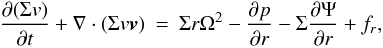 (2)and for the azimuthal component
(2)and for the azimuthal component 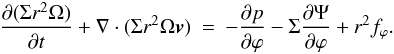 (3)Here p is the vertically integrated pressure, Ψ the gravitational potential of both stars, and fr and fϕ describe the radial and azimuthal forces due to the disk viscosity (Masset 2002). Owing to the motion of the primary star around the center of mass of the binary, the coordinate system is non-inertial, and indirect terms were included in the equations of motion to account for this. These are included in the potential Ψ. The gravitational influence of the disk on the binary is neglected, and the disk in non-self-gravitating. The vertically integrated energy equation reads
(3)Here p is the vertically integrated pressure, Ψ the gravitational potential of both stars, and fr and fϕ describe the radial and azimuthal forces due to the disk viscosity (Masset 2002). Owing to the motion of the primary star around the center of mass of the binary, the coordinate system is non-inertial, and indirect terms were included in the equations of motion to account for this. These are included in the potential Ψ. The gravitational influence of the disk on the binary is neglected, and the disk in non-self-gravitating. The vertically integrated energy equation reads 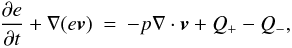 (4)where e is the internal energy density, Q + the heating source term and Q − the cooling source term. To obtain a fully determined system, we additionally used the ideal gas law
(4)where e is the internal energy density, Q + the heating source term and Q − the cooling source term. To obtain a fully determined system, we additionally used the ideal gas law 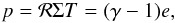 (5)where T is the temperature in the midplane of the disk, γ the adiabatic index and ℛ the universal gas constant divided by the mean molecular mass, which can be calculated by ℛ = kB/(μmu), where kB is the Boltzmann constant, μ the mean molecular weight and mu the unified atomic mass unit.
(5)where T is the temperature in the midplane of the disk, γ the adiabatic index and ℛ the universal gas constant divided by the mean molecular mass, which can be calculated by ℛ = kB/(μmu), where kB is the Boltzmann constant, μ the mean molecular weight and mu the unified atomic mass unit.
The adiabatic sound speed cs within the disk is then given as 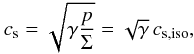 (6)where
(6)where 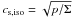 is the isothermal sound speed. The vertical pressure scale height H is then
is the isothermal sound speed. The vertical pressure scale height H is then 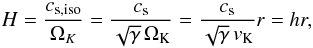 (7)where ΩK denotes the Keplerian angular velocity around the primary and h the aspect ratio.
(7)where ΩK denotes the Keplerian angular velocity around the primary and h the aspect ratio.
For the heating term Q + we assumed that this is solely given by viscous dissipation, and it then is given by ![\begin{eqnarray} Q_+ & = & \frac{1}{2 \nu \Sigma} \left[ \sigma_{rr}^2 + 2 \sigma_{r \varphi}^2 + \sigma_{\varphi \varphi}^2 \right] + \frac{2 \nu \Sigma}{9} (\nabla \vec{v})^2 , \end{eqnarray}](/articles/aa/full_html/2012/03/aa18202-11/aa18202-11-eq72.png) (8)where ν is the kinematic viscosity and σ denotes the viscous stress tensor, to be written in polar coordinates. The viscosity ν is given by ν = αcsH (Shakura & Sunyaev 1973).
(8)where ν is the kinematic viscosity and σ denotes the viscous stress tensor, to be written in polar coordinates. The viscosity ν is given by ν = αcsH (Shakura & Sunyaev 1973).
The cooling term Q − describes the radiative losses from the lower and upper disk surface, which can be written as 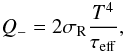 (9)where σR is the Stefan-Boltzmann constant and τeff an effective optical depth. We followed the approach of Kley & Crida (2008) and write, according to Hubeny (1990),
(9)where σR is the Stefan-Boltzmann constant and τeff an effective optical depth. We followed the approach of Kley & Crida (2008) and write, according to Hubeny (1990), 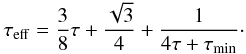 (10)The optical depth follows from τ = ∫ρκdz, that can be approximated by τ ≈ ρκH where ρ and κ(ρ,T) are evaluated at the disk’s midplane. The vertical density profile of a disk is approximately given by a Gaussian and hence
(10)The optical depth follows from τ = ∫ρκdz, that can be approximated by τ ≈ ρκH where ρ and κ(ρ,T) are evaluated at the disk’s midplane. The vertical density profile of a disk is approximately given by a Gaussian and hence 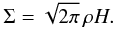 (11)To account for the drop of opacity with vertical height we introduced a correction factor c1 and write finally
(11)To account for the drop of opacity with vertical height we introduced a correction factor c1 and write finally 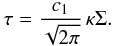 (12)The constant
(12)The constant 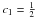 is obtained by comparing two-dimensional disk models with the fully three-dimensional calculations as presented in Kley et al. (2009). For the Rosseland mean opacity κ we adopted power-law dependencies on temperature and density described by Lin & Papaloizou (1985) and Bell & Lin (1994), where
is obtained by comparing two-dimensional disk models with the fully three-dimensional calculations as presented in Kley et al. (2009). For the Rosseland mean opacity κ we adopted power-law dependencies on temperature and density described by Lin & Papaloizou (1985) and Bell & Lin (1994), where 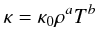 (13)for various opacity regimes. Each opacity regime is described by a minimum temperature Tmin and maximum temperature Tmax, which depends on the density ρ. Table 1 lists the constants κ0, a and b for each regime of the Lin & Papaloizou model. The temperature and density are taken from the midplane, where the density ρ is obtained from Eq. (11).
(13)for various opacity regimes. Each opacity regime is described by a minimum temperature Tmin and maximum temperature Tmax, which depends on the density ρ. Table 1 lists the constants κ0, a and b for each regime of the Lin & Papaloizou model. The temperature and density are taken from the midplane, where the density ρ is obtained from Eq. (11).
In our model we did not consider presently any radiation transport within the disk plane. This contribution is potentially important when strong gradients in temperature and density occur. In our situation this may be the case around the periastron phase of the binary. However, in our simulations the observed contrast did not seem strong enough and we did not expect a large impact on the evolution. In subsequent studies we plan to investigate this question further.
Because we are interested in the global evolution of the disk, we measured the disk eccentricity edisk and the disk periastron ϖdisk by first calculating for each grid cell the eccentricity vector e, which is defined by 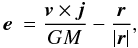 (14)where j = r × v is the specific angular momentum, G the gravitational constant, M the total mass and r the relative vector. In our two-dimensional case the specific angular momentum only has a component in z direction and therefore the eccentricity e and the longitude of periastron ϖ follow as
(14)where j = r × v is the specific angular momentum, G the gravitational constant, M the total mass and r the relative vector. In our two-dimensional case the specific angular momentum only has a component in z direction and therefore the eccentricity e and the longitude of periastron ϖ follow as  The global disk eccentricity edisk and disk periastron ϖdisk is then calculated by a mass-weighted average over the whole disk,
The global disk eccentricity edisk and disk periastron ϖdisk is then calculated by a mass-weighted average over the whole disk, ![\begin{eqnarray} e_\mathrm{disk} &=& \left[ \int_{r_\mathrm{min}}^{r_\mathrm{max}} \int_0^{2 \pi} \Sigma e\,r \,{\rm d}\varphi\,{\rm d}r \right] \times \left[ \int_{r_\mathrm{min}}^{r_\mathrm{max}} \int_0^{2 \pi} \Sigma\,r \,{\rm d}\varphi\,{\rm d}r \right]^{-1} \\ \varpi_\mathrm{disk} &=& \left[ \int_{r_\mathrm{min}}^{r_\mathrm{max}} \int_0^{2 \pi} \Sigma \varpi\,r\,{\rm d}\varphi\,{\rm d}r \right] \times \left[\int_{r_\mathrm{min}}^{r_\mathrm{max}} \int_0^{2 \pi} \Sigma\,r\,{\rm d}\varphi\,{\rm d}r \right]^{-1} \end{eqnarray}](/articles/aa/full_html/2012/03/aa18202-11/aa18202-11-eq104.png) where the integrals are evaluated by summation over all grid cells.
where the integrals are evaluated by summation over all grid cells.
2.2. Numerical considerations
The simulations were performed using the FARGO code (Masset 2000) with modifications from Baruteau (2008). The numerical method used in FARGO is a staggered mesh finite difference method. It uses operator splitting and a first-order integrator to update to velocities with the source terms (potential and pressure gradients, viscous and centrifugal accelerations). The advective terms are treated by a second-order upwind algorithm (van Leer 1977). To speed up calculations the code uses the FARGO algorithm (Masset 2000). The algorithmic details of the FARGO code have been described in Masset (2000). Because the FARGO code is based on ZEUS-2D, the basic techniques are described in Stone & Norman (1992).
 |
Fig. 1 Evolution of the disk within one binary period for the fully radiative standard model. The top labels in the four panels state the current position of the binary (rbin, ϕbin) in polar coordinates. In the first panel the binary companion is at the apastron and has less influence on the disk. The L1 point in this configuration is at about 17.5 AU and therefore far outside the computational domain (gray circles). In the second panel the binary has reduced its distance to about 12.8 AU and the Roche lobe (green curve) has shrunken dramatically and is now entirely within the computational domain. The third panel shows the disk with the binary at periastron. Some of the material in the disk is now outside the Roche lobe and might be lost from the system. In the last panel the binary’s separation increases again, which makes the Roche lobe grow such that it engulfs the disk entirely. The strong tidal forces near periastron induce spiral waves in the disk that will be damped out until the binary is at apastron. |
The position of the secondary star is calculated by a fifth-order Runge-Kutta algorithm. To smooth shocks we used the artificial viscosity described by Stone & Norman (1992) in our simulations.
To test the code we checked that we obtained the same results when using a corotating coordinate system. In addition, several test calculations were made using the RH2D code (Kley 1989, 1999) to assure that we implemented everything correctly.
To avoid numerical problems, we implemented a surface density floor of Σfloor = 10-7 × Σ0 where Σ0 = Σ(1 AU)|t = 0 and a temperature floor of Tfloor = 3 K, which is about the temperature of the cosmic background radiation. In addition to the physical motivation for the floor, very low temperatures only occur in the very outer parts of the disk (see e.g. Fig. 3) where there is only very little mass that influences the dynamics of the disk. For the same reason, these cells do not contribute to the mass weighted average of the disk eccentricity. We performed test simulations with a very low temperature floor and obtained identical results.
For the simulations we typically used two boundary conditions. The open boundary condition allows outflow, but no inflow
of material. It is implemented as a zero-gradient outflow condition, which reads at Rmin as 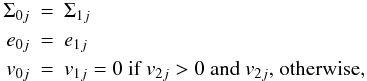 where the index 0 denotes the first inner radial ghost cells, e.g. Σ1j is the first active cell in radial and the jth cell in azimuthal direction. Alternatively, the reflecting boundary condition denies exchange of quantities with the system as is implemented at Rmin as
where the index 0 denotes the first inner radial ghost cells, e.g. Σ1j is the first active cell in radial and the jth cell in azimuthal direction. Alternatively, the reflecting boundary condition denies exchange of quantities with the system as is implemented at Rmin as 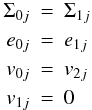 and similarly at Rmax. For the outer radial boundary we always used the standard outflow condition, while at Rmin we typically used the reflecting condition. Below, we will investigate a possible influence of the numerical inner boundary condition.
and similarly at Rmax. For the outer radial boundary we always used the standard outflow condition, while at Rmin we typically used the reflecting condition. Below, we will investigate a possible influence of the numerical inner boundary condition.
3. The standard model
For our simulations we constructed a standard reference model using the physical parameter of the γ Cephei system. The first entries of Table 2 list the orbital parameter of this standard model based on the observations of Neuhäuser et al. (2007) and Torres (2007).
Parameters of the standard model. The top entries refer to the fixed binary parameter.
The disk parameters where chosen to be in a typical range for a possible disk around γ Cephei A, with a total mass that would allow for the formation of the observed planet of about 1.85 MJup (Endl et al. 2011) in the system. Because the tidal forces of the secondary limits the radial extent of the disk to about 6 AU (Artymowicz & Lubow 1994) we chose a slightly larger extent of the computational domain to 8 AU. This reduces artificial boundary effects. The initial density distribution is limited to 6 AU. For the outer boundary condition we always used the zero-gradient outflow boundary condition so that the material that is accelerated during periastron may leave the system freely. The inner boundary in the standard model is typically reflecting. The resolution of the logarithmic grid is trimmed to have quadratic cells (rΔϕ/Δr ≈ 1).
After the initial setup at time zero, the models have to run for several binary orbits until a quasistationary state has been reached, see also Kley & Nelson (2008). This equilibration process typically takes about 15 binary periods, i.e. 1000 years for fully radiative models. Afterward the disk cycles through several states during one orbital period of the binary displayed in Fig. 1. When the binary is at apastron, the the disk is very axisymmetric, but when the binary moves toward its periastron, it starts to perturb the disk. After the binary passes its periastron, two strong tidal spiral arms develop within the disk and wind themselves to the center of the disk. Before the binary reaches its apastron, the disk spiral arms disappear. Periastron passages are also the time when most of the disk mass is lost. During the first periapse the disk looses 4.8% of its mass. This decreases during the next ten periapsis passes to about 0.1%. At the end of the simulation after 200 binary orbits, the disk mass has reduced to 0.0073 M⊙, which is a loss of about 20%.
3.1. Isothermal runs
To check our results and compare them with previous results, we first performed simulations where we kept the initial temperature stratification. In Fig. 2 we present results for constant H/r disks where we did not solve the energy equation. Shown are results for four different values of H/r, which were chosen according to our fully radiative results (see below). The disk reaches an equilibrium state after many (typically several 100) binary orbits, and the magnitude of the final average eccentricity depends on the temperature of the disk. In particular, for the disks with an H/r of about 0.05 the disk eccentricity settles at fairly high values of about 0.2. This seems to be higher than in previous simulations performed by Kley & Nelson (2008), but the parameters used for the γ Cephei system, in particular the mass ratio q = Msecondary/Mprimary of the host star and the binary companion (their q = 0.24 instead of our q = 0.29), and the binary eccentricity ebin (ebin = 0.36 instead of ebin = 0.4) are different. Using the (older) system parameters as given by Kley et al., we were able to reproduce the results nicely (e.g. their Fig. 4).
 |
Fig. 2 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), both sampled at the binary’s apastron, for isothermal simulations of the standard model with different aspect ratios H/r. The disk eccentricity needs quite a long time to reach a quasi-equilibrium and settles at around 0.2 for an H/r of 0.05 and 0.055. High values of H/r result in a lower disk eccentricity. Note that in the lower panel a short time span is displayed for clarity. |
In these isothermal runs it is clear that the two thicker, hotter disks have significantly lower mean eccentricities. The disk with H/r = 0.065 does not even display a coherent disk precession any more (Fig. 2, bottom panel). This drop of edisk with increasing H/r is a consequence of the reduction of the eccentricity growth rate for thicker disks. The growth rate of the disk eccentricity is the lowest for the hottest disk with H/r = 0.065 and increases with decreasing H/r (Fig. 2, top panel), a finding that perfectly agrees with Kley et al. (2008). The hotter disks need therefore much more time to reach an equilibrium state. As the eccentric binary damps the growth of disk eccentricity by tidal interaction (see below), the hotter disks settle into an equilibrium state that has a lower edisk.
Time average of the disk eccentricity ⟨ edisk ⟩ and precession rate 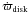 for the four different isothermal models.
for the four different isothermal models.
After about 400 binary periods, i.e. 25 000 years, the time average of the disk eccentricity ⟨ edisk ⟩ reaches a constant value and the disks precess with a nearly constant precession rate 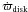 . The values of ⟨ edisk ⟩ and
. The values of ⟨ edisk ⟩ and 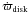 for the four different values of H/r are given in Table 3.
for the four different values of H/r are given in Table 3.
3.2. Fully radiative disks: structure and dynamics
 |
Fig. 3 Radial dependency of surface density (top), midplane temperature (middle) and disk eccentricity (bottom) of the fully radiative standard model for different timestamps. The disk ranges from 0.5 AU to about 5.5–6 AU due to tidal forces of the companion. At t = 0 years the disk is not fully Keplerian and thus edisk > 0. |
 |
Fig. 4 Radial dependency of surface density (top), and disk eccentricity (bottom) of the H/r = 0.05 isothermal model and the fully radiative standard model after 750 binary orbits. |
Now we include all physics, in particular the viscous heating and radiative cooling terms and solve the full set of equations as stated above. For given binary parameter and disk physics (opacity and viscosity) the dynamical state and structure of the disk is completely determined once the disk mass has been specified. The density and temperature distribution cannot be stated freely and hence the power law given in Table 2 refers only to the initial setup.
The radial disk structure is displayed in Fig. 3 where azimuthally averaged quantities of Σ,T and edisk are displayed. The upper panel of Fig. 3 shows the surface density and temperature distribution for five different timestamps. For the initial setup, at t = 0 years, the surface density follows the initial r-1 profile in the inner region (0.5 AU–5 AU) and is lowered to the density floor in the outer region. The temperature follows the initial r-1 profile for the whole computational domain. After about 25 binary orbits a quasistationary state is reached where the profiles show a bend at about r = 1.8 AU. This change in slope, which occurs at a temperature of about 1000 K in the profiles, is a result of a change in the opacity caused by the sublimation of dust grains, which starts at about (ρ g-1 cm3)1/15 × 4.6 × 103 K in the opacity tables (see Table 1) given by Lin & Papaloizou (1985). A second bend occurs at about r = 4.5 AU, which corresponds to the truncation radius of the companion’s tidal forces. In the bottom panel of Fig. 3 the corresponding radial distribution of eccentricity is shown. The eccentricity is low in the inner parts of the disk and increases with larger radii. The highest values for e(r) occur in the outer region r ≳ 5.5 AU, beyond the tidal truncation radius. But these regions do not play an important dynamical role because there is only very little mass left owing to the tidal forces of the secondary star. For example, the disk has a mass-weighted mean overall disk eccentricity of edisk = 0.032 after 100 binary orbits even though more than half of the radial extent of the disk has an eccentricity of ≥0.05. Remarkably the eccentricity is much lower than in the isothermal simulations presented in Sect. 3.1. As a consequence of the lack of eccentricity there is not visible disk precession.
Figure 3 shows the radial dependency of the disk surface density and disk eccentricity of the H/r = 0.05 model in equilibrium after 750 binary orbits compared with the subsequently introduced fully radiative model. The surface density in the isothermal model misses the bend caused by the 1000 K change in the disk opacity and is slightly steeper than the initial r-1 profile. The disk eccentricity in the isothermal case is much more homogeneous with radius, as is to be expected for a coherent structure. This has already been observed by Kley & Nelson (2008).
 |
Fig. 5 Azimuthally averaged surface density (top) and midplane temperature (bottom) profiles for the radiative standard model using two different locations of the inner boundary of the computational domain. Results are displayed at 100 binary orbits (6666 years). In the overlapping region from 0.5–8 AU the profiles match very well and the region from 0.25–0.5 AU in the rmin = 0.25 AU model is a consistent continuation. |
 |
Fig. 6 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), sampled at the binary’s apastron, for two different inner boundary positions. |
To check for numerical dependencies we varied the location of the inner boundary of the computational domain and the grid resolution. First we chose a smaller inner boundary of rmin = 0.25 AU increasing the number of radial grid points such that the spatial grid resolution remained unchanged in the overlap region. In Fig. 5 the radial dependency of the surface density and the midplane temperature at the end of the simulations differs not too much in the overlap region of both simulations, so that the effects of the inner boundary are negligible in this respect. However, the amplitude of the oscillation in the time evolution of the disk eccentricity is nearly gone (see Fig. 6). In the standard model we could see a small oscillation in the disk periastron, which also vanishes in the rmin = 0.25 AU model. The non-existence of a coherent precession is also an indication of very low disk eccentricity in both cases. In additional test simulations (not displayed here), we extended the outer radius to the value of rmax = 12 AU, changing the number of grid cells accordingly to maintain the resolution of the standard model. As expected, this larger radial domain does not change the results.
Then we varied the grid resolution by first doubling the grid cells to 512 × 1150 and doubling it again to 1024 × 2302 grid cells. This change in resolution has basically no impact on the disk’s dynamics. As before, the disk eccentricity settles to a time averaged value of about 0.04. In all three simulations the disk periastron does not reach a state with real precession and the only change caused by the change of resolution is a small shift in time. Consequently our standard resolution of 256 × 574 cells seems to be sufficient to resolve the disk dynamics properly.
4. Variation of physical parameters
To study the influence of the physical conditions on the evolution of the disk, we investigated in particular the impact of the disk mass Mdisk, the viscosity ν, which is determined by α, the opacity κ, and the binary’s eccentricity ebin.
4.1. Disk mass
The first parameter we investigated is the disk mass. In contrast to isothermal simulations our radiative simulations depend on the disk mass as the opacity depends on gas density. To analyze the influence of the disk mass on the disk’s evolution, we ran four simulations with disk masses Mdisk of 0.005 M⊙, 0.01 M⊙, 0.02 M⊙ and 0.04 M⊙ while keeping all other parameters unchanged.
The surface density and temperature profiles after 100 binary orbits for different disk masses is displayed in Fig. 7, where the solid (red) line refers to the standard model displayed in Fig. 3. The profiles can be divided into two regimes that are separated by the 1000 K temperature line caused by the opacity (see Sect. 3.2). In each regime the surface density and temperature profiles follow a simple power-law that depends only weakly on the disk mass, and is given in the caption of Fig. 7.
 |
Fig. 7 Azimuthally averaged surface density (top) and midplane temperature (bottom) profiles after 100 binary orbits (6666 years) for radiative models using different initial disk masses. The profiles can be fitted using power-laws when divided into two regimes: An inner region with temperatures of less than about 1000 K and an outer region with temperatures above 1000 K because of a break in the opacity tables at about 1000 K. The inner region follows Σ ∝ r − 1.49 to −1.51 and T ∝ r − 0.53 to −0.54, whereas the outer region follows Σ ∝ r − 0.82 to −1.67 and T ∝ r − 1.39 to −1.58 for all models. |
 |
Fig. 8 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), sampled at the binary’s apastron, dependency for different disk masses. |
 |
Fig. 9 H/r after 100 binary orbits (6666 years) for different disk masses. |
 |
Fig. 10 Azimuthally averaged surface density (top) and midplane temperature (bottom) profiles after 100 binary orbits (6666 years) using four different values for the viscosity parameter α. The profiles can be fitted using power-laws when divided into two regimes: An inner region with temperatures of less than about 1000 K and an outer region with temperatures above 1000 K, because there is a break in the opacity tables at about 1000 K. The inner region follows Σ ∝ r − 1.48 to −1.53 and T ∝ r-0.53, whereas the outer region follows Σ ∝ r − 0.78 to −0.95 and T ∝ r − 1.45 to −1.53 for all α values. |
Figure 8 shows the time evolution of the disk eccentricity and periastron for different disk masses. The higher the disk mass, the lower the oscillations of the the disk eccentricity, but the time average of the disk eccentricity is in the range of 0.04–0.05 for all disk masses. The disk periastron displays no real precession and with increasing disk mass it settles at about 0. This is in contrast to the isothermal simulations presented in Sect. 3.1 where we obtained a disk eccentricity edisk of 0.2 for an aspect ratio H/r of 0.05 and a real precession of the disk periastron. There is a trend, however, that the eccentricity becomes higher for cooler disks with lower H/r. But one has to be careful here, because the aspect ratio is constant in radius and time for the isothermal simulations, but not for our radiative simulations. Figure 9 shows the aspect ratio of the disk after 100 binary orbits. All models had an initial value of (H/r)initial = 0.05 but end up with different values of H/r depending on the disk mass and the phase in the binary orbit. We note that in all models the mass of the disk reduces with time owing to the mass loss across the outer boundary. In particular, we find that after 100 binary orbits the disks have lost about 27% of their initial mass in the Mdisk = 0.04 M⊙ model, 23% in the Mdisk = 0.04 M⊙ model, 17% in the Mdisk = 0.04 M⊙ and 6% in the Mdisk = 0.005 M⊙ model. Hence, the values quoted in the text and figures always refer to the initial disk masses.
The results for edisk in Fig. 8 show a marginal increase of the disk eccentricity for smaller disk masses. To test if this trend continues, we performed additional simulations for even smaller initial disk masses and found indeed an increased oscillatory behavior of the eccentricity, which settles eventually after about 600 binary orbits to a low eccentric state very similar to the Mdisk = 0.025 model, however. Hence, there does not seem to exist an obvious trend of edisk with disk mass.
4.2. Viscosity
In this section we investigate the influence of the viscosity ν. To study the dependence on ν we varied the α parameter, which determines the viscosity, 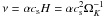 (Shakura & Sunyaev 1973), from our standard model (α = 0.01) and kept all other parameters unchanged. We varied α from 0.005 to 0.04.
(Shakura & Sunyaev 1973), from our standard model (α = 0.01) and kept all other parameters unchanged. We varied α from 0.005 to 0.04.
Figure 10 shows the surface density and temperature profiles after 100 binary orbits. All models started with identical disk mass, and evidently, higher α models lose the disk masses more rapidly. For example, at the displayed time at 100 binary orbits the α = 0.04 model has lost about 71% of its initial mass, while the standard model (α = 0.01) lost only 19%, see also Fig. 12 below. The shape of the surface density and temperature profile seems to be independent of the viscosity in the disk, as expected. Again, the profiles can be divided into two regimes that are separated by the 1000 K temperature line. The power-laws for the surface density and temperature profiles are given in the caption of Fig. 10.
Figure 11 shows the influence of α on the disk eccentricity and periastron. Higher values of α and thus high viscosities result in a calmer disk that does not react fast enough on the disturbances of the binary companion. Therefore the disk shows less oscillations in the disk eccentricity and the disk periastron remains almost constant for the higher values of α. The disk eccentricity in the model with the highest viscosity, α = 0.04, increases to up to 0.25 within 600 binary orbits, and the disk eccentricity in the α = 0.02 model starts to grow slowly after about 200–300 binary orbits. This effect of a rising disk eccentricity is a direct consequence of the increasing viscosity. As shown in Fig. 12, the mass loss of the disk depends on the magnitude of the viscosity, the higher α, the faster the mass loss of the disk. For example, after 500 binary orbits the α = 0.04 disk has lost about 97% of its initial mass. The increased mass loss for higher viscosities is a result of the stronger outward spreading of the disk, i.e. a larger truncation radius. The larger disk makes the outer parts of the disk more susceptible to the tidal perturbations of the secondary, which increase the disk eccentricity dramatically. This is in accordance with the viscosity dependence found in earlier studies, e.g. Kley et al. (2008).
 |
Fig. 11 Global mass-weighted disk eccentricity (top) and periastron (bottom), sampled at the binary’s apastron, as a function of time for different α values for the viscosity. |
 |
Fig. 12 Disk mass evolution for different α values for the disk viscosity. |
4.3. Opacity
The amount of cooling in our radiative model depends on the disk’s opacity. To examine the influence of the opacity model we calculated the standard model with two different opacity models leaving all other parameters unchanged. In the first calculation we used the opacity tables (see Table 1) shown by Lin & Papaloizou (1985), whereas the second calculation uses the opacity tables given by Bell & Lin (1994, their Table 3).
As expected, the opacity plays an important role and the model with the Bell & Lin opacity shows less oscillations in the disk eccentricity, but the time average is about the same as in the model with the Lin & Papaloizou opacity. This is similar to the rmin change in Sect. 3.2. The surface density and midplane temperature profiles at the end of the simulation in the simulation with the Bell & Lin opacity model differ slightly from the one shown in Fig. 3. Both models have a bend at a temperature of about 1000 K but the temperature profile in the model with the Bell & Lin opacity model is flatter and slightly lower in the region below 1000 K and slightly steeper in the region about 1000 K. In exchange, the surface density is slightly steeper and slightly higher in region the below 1000 K and matches the other model in the region above 1000 K very well.
4.4. Binary eccentricity
Another very important factor for the disk’s evolution are the binary parameters. We therefore varied the binary’s eccentricity in our standard model from ebin = 0 to 0.4. Because this also changes the truncation radius of the disk that is caused by the binary’s tidal forces (Artymowicz & Lubow 1994), we extended the computational domain to up to 12.5 AU for the ebin = 0 model. To reach the same resolution in the computational domain of the standard model (0.5–8 AU) we increased the number of cells in radial direction to 295 in the ebin = 0 model. The ebin = 0.05, ebin = 0.1 and ebin = 0.2 models were adjusted accordingly in their computational domain and resolution in radial direction.
Figure 13 shows the time evolution of the disk eccentricity and periastron. Interestingly, the ebin = 0 and ebin = 0.05 models show the highest disk eccentricity. These high values for ebin = 0 seem to agree with Kley et al. (2008). Also, the ebin = 0 and ebin = 0.05 models are the only ones that have a real coherent disk precession with a precession rate of 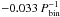 for the ebin = 0 model and
for the ebin = 0 model and 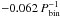 for the ebin = 0.05 model. All other models with ebin ≥ 0.1 show a disk eccentricity of edisk < 0.1 and no precession, which also indicates that the disk is not globally eccentric. For the low eccentric binaries it takes up to about 125 binary orbits to reach the high eccentric quasi-equilibrium disk state, which is long compared to the standard model, which reaches its quasistationary state after only about 15 binary orbits. These timescales agree well with those obtained by Kley et al. (2008) for isothermal disks. The reason why binaries with low ebin tend to have eccentric disks is the larger disk radius in this case. This allows an easier operation of the instability according to the model of Lubow (1991).
for the ebin = 0.05 model. All other models with ebin ≥ 0.1 show a disk eccentricity of edisk < 0.1 and no precession, which also indicates that the disk is not globally eccentric. For the low eccentric binaries it takes up to about 125 binary orbits to reach the high eccentric quasi-equilibrium disk state, which is long compared to the standard model, which reaches its quasistationary state after only about 15 binary orbits. These timescales agree well with those obtained by Kley et al. (2008) for isothermal disks. The reason why binaries with low ebin tend to have eccentric disks is the larger disk radius in this case. This allows an easier operation of the instability according to the model of Lubow (1991).
The surface density and midplane temperature profiles after 100 binary orbits of all five models have the same slope but differ slightly in absolute values. The ebin = 0.4 models is the hottest and densest model and then the temperature and surface density decreases with decreasing binary eccentricity. The ebin = 0 model shows low oscillations in the profiles. As expected, the disk’s truncation radius owing to the binary’s tidal forces is shifted outward in the models with lower binary eccentricity.
 |
Fig. 13 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), sampled at the binary’s apastron, for different binary eccentricities. The low eccentricity (ebin < 0.05) models need much more time to reach their equilibrium state compared to the standard model. These are also the only models that develop a real coherent disk precession. |
5. Brightness variations
To identify possible observable changes in the brightness of the systems caused by perturbations in the disk, we calculated theoretical light curves for our standard model. For that purpose, we examined the time variation of the disk dissipation given by 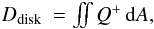 (19)and the disk luminosity given by
(19)and the disk luminosity given by 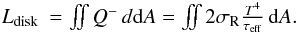 (20)To identify the source of the brightness variations we divided the disk into five rings ranging from 0.5–2 AU, 2–3 AU, 3–4 AU, 4–5 AU and 5–8 AU. In each of these rings the disk dissipation and disk luminosity was calculated. Figure 14 displays the variation of the disk dissipation and disk luminosity of our standard model during one orbital orbit at t = 100 Pbin where the system has already reached its quasistationary state. The periastron occurs at t = 100.5 Pbin, and is indicated by the vertical line.
(20)To identify the source of the brightness variations we divided the disk into five rings ranging from 0.5–2 AU, 2–3 AU, 3–4 AU, 4–5 AU and 5–8 AU. In each of these rings the disk dissipation and disk luminosity was calculated. Figure 14 displays the variation of the disk dissipation and disk luminosity of our standard model during one orbital orbit at t = 100 Pbin where the system has already reached its quasistationary state. The periastron occurs at t = 100.5 Pbin, and is indicated by the vertical line.
 |
Fig. 14 Variation of disk dissipation and disk luminosity during one binary orbit. The dissipation and luminosity are calculated for five different rings ranging from 0.5–2 AU, 2–3 AU, 3–4 AU, 4–5 AU and 5–8 AU. Because the disk is truncated at about 4.5 AU (see Fig. 3), the outmost ring does not contain much mass. The solid (red) curve is the sum of all five rings. The gray line indicates the binary’s periastron passage. |
When the binary is at apastron, the disk is almost uniform (see Fig. 1) and we cannot see any variations in the light curves. However, when the binary passes periastron, it starts to perturb the outer regions of the disk and two spiral arms evolve that wind themselves to the center of the disk. This results in a rise of the luminosity by 2–3 mag in the outer rings of the disk shortly after periastron passage (see Fig. 14) and after a short time also in a smaller rise in the inner rings of the disk. As the binary moves farther away from the disk, the spirals are damped out and the luminosity peak vanishes. These luminosity peaks should be observable as a 2-mag increase in the mid-infrared (MIR) because the main contributions come from the outer rings (3–5 AU) with temperatures between 150 K and 450 K.
Luminosity peaks have already been observed in the mid-infrared in the T Tau S system (van Boekel et al. 2010), a binary system that is not very different from the early stage of the γ Cephei system. Additionally, van Boekel et al. also performed some radiative simulations for the T Tau S system and pointed out that these brightness variations could be caused by the perturbations of the binary companion. However, the brightness variations found in their disk models were very weak.
6. α Centauri
In addition to the γ Cephei system we also performed some calculations for the α Centauri system, because it is of special interest, being the nearest star to our solar system. This system has been investigated for the possibility of planet formation, see e.g. Thébault et al. (2008). Table 4 gives an overview of the parameters of our α Centauri model based on Pourbaix et al. (2002). We tried to keep the disk parameters the same as in the γ Cephei model, so that the main difference are the mass ratio q = Msecondary/Mprimary and the binary’s orbital parameters. In the γ Cephei model we have a mass ratio q of 0.28, an eccentricity ebin of 0.4 and a semi-major axis a of 20 AU, whereas in the α Centauri model we have a mass ratio q of 0.84, an eccentricity ebin of 0.52 and a semi-major axis a of 23.4 AU.
In Sect. 4.4 we saw that for high binary eccentricities the disk eccentricity does not reach very high values, so that we would expect a fairly low disk eccentricity for the α Centauri system. Kley et al. (2008) showed that for isothermal simulations the disk eccentricity in the quasistationary state does not depend heavily on the mass ratio q. Figure 15 shows the evolution of the disk eccentricity and periastron over time. The disk eccentricity settles after about 15 binary orbits at a rather low value of about 0.038 and the disk periastron is also at a nearly constant position.
The surface density and midplane temperature profiles for the α Centauri model can only be fitted in the inner region with r < 1.8 AU as a simple power-law. The surface density can be described by a r-1.49 and the midplane temperature by a r-0.53 power-law. In the outer region the surface density and temperature decreases rather fast to 0 until about 4 AU, where the disk is truncated by the binary’s tidal forces.
Parameters of the α Centauri model.
 |
Fig. 15 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), sampled at the binary’s apastron for the α Centauri model. |
7. Summary and conclusions
We have investigated the dynamics of a protostellar disk in binary star systems using specifically the orbital parameter of γ Cephei and α Centauri. We assumed a coplanar system and used a two-dimensional hydrodynamical code to evolve the non-self-gravitating disk. Extending previous simulations, we included internal viscous heating given by an α-type viscosity prescription, and radiative cooling from the disk surface.
In a first set of simulations we investigated locally isothermal disks for different disk temperatures. We showed that disks in binaries of the γ Cephei type with a standard thickness of H/r = 0.05 become eccentric (edisk ≈ 0.2) showing a coherent disk precession. This agrees well with previous simulations by Kley & Nelson (2008) and Paardekooper et al. (2008). Varying the temperature in the disk, we showed that the magnitude of the disk’s eccentricity becomes lower when the disk thickness increases. For disks with H/r ≳ 0.065 the mean average eccentricity has dropped below 0.08 and the disks do not show a precession anymore.
Then we studied more realistic disks with internal heating and radiative cooling, varying the disk’s mass. In all cases we found relatively low eccentricities and no precession. We attribute the lack of eccentricities firstly to the increased disk height, which is, in particular for the more massive disks, higher than the standard value (see Fig. 9). Secondly, in the full radiative models the disk’s dynamical behavior is more adiabatic compared to the locally isothermal case. Then, through compressional heating (pdV-work), kinetic energy is transferred to internal energy, which leads to a reduced growth of disk eccentricity. We have checked that purely adiabatic models show an even lower disk eccentricity than the radiative models. Hence, the radiative case lies between the adiabatic and isothermal, as expected.
Because the disk’s energy balance is determined via the viscosity, we changed the value of the parameter α ranging from 0.005 to 0.04, all values that are consistent with the results of MHD-turbulent accretion disks. Here, we found that only the disk with the highest α becomes eccentric. The reason for this rise is the larger disk radius, which leads to an enhancement of the tidal torques from the secondary. We note that the disk’s outer radius in our models still lies well inside the 3:1 resonance with the binary. According to the linear instability model by Lubow (1991), the disk eccentricity is excited through the 3:1 resonance and hence, the disk should be sufficiently large, a condition which is fulfilled only for small mass ratios, q = Msecondary/Mprimary. However, as shown by Kley & Nelson (2008), disks in binary star systems with large mass ratios can turn eccentric as well, even though the disks are small, a feature confirmed in our simulations.
The inferred short lifetime of disks with standard viscosities is slightly alarming with respect to planet formation in these systems. In the core-accretion scenario planet formation proceeds along a sequence of many steps that take a few Myr. For disks to persist this long in γ Cephei-type binaries a very low viscosity of α ≲ 10-4 seems to be required. In the gravitational instability scenario the timescale for planet formation is much shorter and hence, this scenario may be favored by our findings. Observationally, several recent studies indeed suggest that the lifetime of disks in young binary stars is significantly reduced compared to disks around single stars (Cieza et al. 2009; Duchêne 2010; Kraus et al. 2012). Dynamically, this behavior is expected, because the perturbation of the companion star leads quite naturally to an increased mass loss of the disk, details depending on the binary separation and eccentricity.
A very critical phase in the core accretion scenario, in particular in binary stars, is the initial growth of meter to km-sized planetesimals. Here, the growth depends on the successful sticking of the two collision partners. Since the relative velocity of the bodies is increased in binary stars, planetary growth will be significantly hindered by the presence of a companion, see e.g. Thébault et al. (2006); Thebault (2011) and references therein. Here our results indicate that planetesimal growth is less negatively influenced because the disk eccentricity is reduced for more realistic radiative disks. As has been shown, eccentric disks tend to increase the mutual relative velocities of embedded objects, in particular of different sizes, because of the misaligned periastrons of the particles (Kley & Nelson 2007; Paardekooper et al. 2008). Hence, a radiative disk with a low viscosity could help to promote planetesimal growth. However, it remains to be seen how the inclusion of stellar irradiation (from both stars) influences the dynamics. Owing to the additional heating of the disk, we expect even more mass loss from the system and possibly higher disk eccentricities because the disks are more isothermal and will have a larger radius.
Previous studies have indicated that in a mutually inclined system planetesimal growth may be enhanced because planetesimals can be size-sorted in differently inclined planes (Xie & Zhou 2009; Marzari et al. 2009b). However, recently Fragner et al. (2011) showed through full 3D hydrodynamical studies that for inclined binaries the relative velocities of different sized planetesimals increases through inclinations effects. They conclude that for inclined systems planetesimal formations can take place only for very distant binary stars with abin ≳ 60 AU. However, the simulations considered only isothermal disks, and it remains to be seen how radiative effects influence the disk. But full 3D radiative simulations are still beyond the present computational possibilities, because thousands of orbital timescales of the disk will have to be calculated.
Acknowledgments
We would like to thank Markus Gyergyovits for useful discussions. Tobias Müller received financial support from the Carl-Zeiss- Stiftung. Most of the simulations were performed on the bwGRiD cluster in Tübingen, which is funded by the Ministry for Education and Research of Germany and the Ministry for Science, Research and Arts of the state Baden-Württemberg. Additionally, we used the cluster of the Forschergruppe FOR 759
“The Formation of Planets: The Critical First Growth Phase” funded by the German Research Society (DFG).
References
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C. 2008, Ph.D. thesis, CEA Saclay [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Buhlmann, J., Diese, J., et al. 2011, A&A, 526, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell, B., Walker, G. A. H., & Yang, S. 1988, ApJ, 331, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L. A., Padgett, D. L., Allen, L. E., et al. 2009, ApJ, 696, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2008, A&A, 479, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., Henning, T., & Kley, W. 2003, ApJ, 599, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Desidera, S., & Barbieri, M. 2007, A&A, 462, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G. 2010, ApJ, 709, L114 [NASA ADS] [CrossRef] [Google Scholar]
- Dvorak, R. 1986, A&A, 167, 379 [NASA ADS] [Google Scholar]
- Dvorak, R., Pilat-Lohinger, E., Bois, E., et al. 2004, in Rev. Mex. Astron. Astrofis. Conf. Ser. 21, ed. C. Allen, & C. Scarfe, 222 [Google Scholar]
- Eggenberger, A., Udry, S., & Mayor, M. 2004, A&A, 417, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, A., Udry, S., Chauvin, G., et al. 2007, A&A, 474, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Els, S. G., Sterzik, M. F., Marchis, F., et al. 2001, A&A, 370, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endl, M., Cochran, W. D., Hatzes, A. P., & Wittenmyer, R. A. 2011, in AIP Conf. Ser. 1331, ed. S. Schuh, H. Drechsel, & U. Heber, 88 [Google Scholar]
- Fragner, M. M., Nelson, R. P., & Kley, W. 2011, A&A, 528, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haghighipour, N. 2006, ApJ, 644, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2003, ApJ, 599, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W. 1989, A&A, 208, 98 [NASA ADS] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Nelson, R. 2007 [arXiv:0705.3421] [Google Scholar]
- Kley, W., & Nelson, R. P. 2008, A&A, 486, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., Papaloizou, J. C. B., & Ogilvie, G. I. 2008, A&A, 487, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., Bitsch, B., & Klahr, H. 2009, A&A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, A. L., Ireland, M. J., Hillenbrand, L. A., & Martinache, F. 2012, ApJ, 745, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1985, in Protostars and Planets II, ed. D. C. Black, & M. S. Matthews, 981 [Google Scholar]
- Lubow, S. H. 1991, ApJ, 381, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Scholl, H., Thébault, P., & Baruteau, C. 2009a, A&A, 508, 1493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marzari, F., Thébault, P., & Scholl, H. 2009b, A&A, 507, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S. 2002, A&A, 387, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, A. F. 2000, ApJ, 537, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Neuhäuser, R., Mugrauer, M., Fukagawa, M., Torres, G., & Schmidt, T. 2007, A&A, 462, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., Thébault, P., & Mellema, G. 2008, MNRAS, 386, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Pourbaix, D., Nidever, D., McCarthy, C., et al. 2002, A&A, 386, 280 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Quintana, E. V., Adams, F. C., Lissauer, J. J., & Chambers, J. E. 2007, ApJ, 660, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., Henry, T. J., Mason, B. D., et al. 2006, ApJ, 646, 523 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Regály, Z., Sándor, Z., Dullemond, C. P., & Kiss, L. L. 2011, A&A, 528, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Thebault, P. 2011, Cel. Mech. Dyn. Astron., 40 [Google Scholar]
- Thébault, P., Marzari, F., Scholl, H., Turrini, D., & Barbieri, M. 2004, A&A, 427, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., Marzari, F., & Scholl, H. 2006, Icarus, 183, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., Marzari, F., & Scholl, H. 2008, MNRAS, 388, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G. 2007, ApJ, 654, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- van Boekel, R., Juhász, A., Henning, T., et al. 2010, A&A, 517, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leer, B. 1977, J. Comput. Phys., 23, 276 [Google Scholar]
- Whitehurst, R. 1988, MNRAS, 232, 35 [NASA ADS] [Google Scholar]
- Xie, J.-W., & Zhou, J.-L. 2009, ApJ, 698, 2066 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, S., Mazeh, T., Santos, N. C., Udry, S., & Mayor, M. 2004, A&A, 426, 695 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
All Tables
Details of the various opacity regimes by type, showing the transition temperature and the constants κ0, a and b.
Parameters of the standard model. The top entries refer to the fixed binary parameter.
Time average of the disk eccentricity ⟨ edisk ⟩ and precession rate 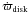 for the four different isothermal models.
for the four different isothermal models.
All Figures
 |
Fig. 1 Evolution of the disk within one binary period for the fully radiative standard model. The top labels in the four panels state the current position of the binary (rbin, ϕbin) in polar coordinates. In the first panel the binary companion is at the apastron and has less influence on the disk. The L1 point in this configuration is at about 17.5 AU and therefore far outside the computational domain (gray circles). In the second panel the binary has reduced its distance to about 12.8 AU and the Roche lobe (green curve) has shrunken dramatically and is now entirely within the computational domain. The third panel shows the disk with the binary at periastron. Some of the material in the disk is now outside the Roche lobe and might be lost from the system. In the last panel the binary’s separation increases again, which makes the Roche lobe grow such that it engulfs the disk entirely. The strong tidal forces near periastron induce spiral waves in the disk that will be damped out until the binary is at apastron. |
| In the text | |
 |
Fig. 2 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), both sampled at the binary’s apastron, for isothermal simulations of the standard model with different aspect ratios H/r. The disk eccentricity needs quite a long time to reach a quasi-equilibrium and settles at around 0.2 for an H/r of 0.05 and 0.055. High values of H/r result in a lower disk eccentricity. Note that in the lower panel a short time span is displayed for clarity. |
| In the text | |
 |
Fig. 3 Radial dependency of surface density (top), midplane temperature (middle) and disk eccentricity (bottom) of the fully radiative standard model for different timestamps. The disk ranges from 0.5 AU to about 5.5–6 AU due to tidal forces of the companion. At t = 0 years the disk is not fully Keplerian and thus edisk > 0. |
| In the text | |
 |
Fig. 4 Radial dependency of surface density (top), and disk eccentricity (bottom) of the H/r = 0.05 isothermal model and the fully radiative standard model after 750 binary orbits. |
| In the text | |
 |
Fig. 5 Azimuthally averaged surface density (top) and midplane temperature (bottom) profiles for the radiative standard model using two different locations of the inner boundary of the computational domain. Results are displayed at 100 binary orbits (6666 years). In the overlapping region from 0.5–8 AU the profiles match very well and the region from 0.25–0.5 AU in the rmin = 0.25 AU model is a consistent continuation. |
| In the text | |
 |
Fig. 6 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), sampled at the binary’s apastron, for two different inner boundary positions. |
| In the text | |
 |
Fig. 7 Azimuthally averaged surface density (top) and midplane temperature (bottom) profiles after 100 binary orbits (6666 years) for radiative models using different initial disk masses. The profiles can be fitted using power-laws when divided into two regimes: An inner region with temperatures of less than about 1000 K and an outer region with temperatures above 1000 K because of a break in the opacity tables at about 1000 K. The inner region follows Σ ∝ r − 1.49 to −1.51 and T ∝ r − 0.53 to −0.54, whereas the outer region follows Σ ∝ r − 0.82 to −1.67 and T ∝ r − 1.39 to −1.58 for all models. |
| In the text | |
 |
Fig. 8 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), sampled at the binary’s apastron, dependency for different disk masses. |
| In the text | |
 |
Fig. 9 H/r after 100 binary orbits (6666 years) for different disk masses. |
| In the text | |
 |
Fig. 10 Azimuthally averaged surface density (top) and midplane temperature (bottom) profiles after 100 binary orbits (6666 years) using four different values for the viscosity parameter α. The profiles can be fitted using power-laws when divided into two regimes: An inner region with temperatures of less than about 1000 K and an outer region with temperatures above 1000 K, because there is a break in the opacity tables at about 1000 K. The inner region follows Σ ∝ r − 1.48 to −1.53 and T ∝ r-0.53, whereas the outer region follows Σ ∝ r − 0.78 to −0.95 and T ∝ r − 1.45 to −1.53 for all α values. |
| In the text | |
 |
Fig. 11 Global mass-weighted disk eccentricity (top) and periastron (bottom), sampled at the binary’s apastron, as a function of time for different α values for the viscosity. |
| In the text | |
 |
Fig. 12 Disk mass evolution for different α values for the disk viscosity. |
| In the text | |
 |
Fig. 13 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), sampled at the binary’s apastron, for different binary eccentricities. The low eccentricity (ebin < 0.05) models need much more time to reach their equilibrium state compared to the standard model. These are also the only models that develop a real coherent disk precession. |
| In the text | |
 |
Fig. 14 Variation of disk dissipation and disk luminosity during one binary orbit. The dissipation and luminosity are calculated for five different rings ranging from 0.5–2 AU, 2–3 AU, 3–4 AU, 4–5 AU and 5–8 AU. Because the disk is truncated at about 4.5 AU (see Fig. 3), the outmost ring does not contain much mass. The solid (red) curve is the sum of all five rings. The gray line indicates the binary’s periastron passage. |
| In the text | |
 |
Fig. 15 Global mass-weighted disk eccentricity (top) and disk periastron (bottom), sampled at the binary’s apastron for the α Centauri model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


