| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014951 | |
| Published online | 20 February 2012 | |
The area asymmetry in bipolar magnetic fields⋆
Solar-Terrestrial Environment Laboratory, Nagoya University,
464-8601
Nagoya,
Japan
e-mail: tyamamot@stelab.nagoya-u.ac.jp
Received: 7 May 2010
Accepted: 21 December 2011
Context. The area asymmetry between the preceding and following regions of opposite magnetic polarity in a bipolar sunspot group has been known since the studies of Hale and his colleagues in the early 20th century. This area asymmetry, however, has not yet been investigated quantitatively using magnetograms.
Aims. We quantitatively define the area asymmetry of bipolar magnetic fields in the photosphere of active regions on the Sun, and investigate correlations between the area asymmetry and other parameters.
Methods. We selected 138 bipolar regions including eleven recurrent regions from magnetograms observed by the Michelson Doppler Imager (MDI) from 23 April 1996 to 2 September 2001. These regions are on the southern hemisphere and around the solar meridian. The area asymmetry (A), tilt angle (θ), and magnetic orientation (M) are investigated separately in the preceding and following polarities of the respective active regions.
Results. It is found that in 37% (51/138) of our events the preceding polarity regions have larger areas than the following polarity regions. The ratio of the area of the preceding and following polarity regions become close to be unity in four recurrent active regions. In the other four regions, the area ratios do not change, and in three regions, the area ratios become far from unity.
Conclusions. Our results quantitatively confirmed our impression that areas of the preceding polarities are lower than those of the following polarities in many bipolar magnetic regions.
Key words: Sun: photosphere / Sun: surface magnetism / sunspots
Table 3 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/539/A13
© ESO, 2012
1. Introduction
It is easily found in magnetograms that there is the area asymmetry between the preceding and following polarities in many bipolar regions. This area asymmetry shows a tendency toward the preceding polarity having more compact and stronger magnetic field than the following polarity. The area asymmetry in magnetograms could be comparable to the morphological asymmetry of sunspots in white-light data, which typically means that the preceding polarity has a large sunspot and the following polarity has small and fragmented ones (see, Fig. 4 of Fisher et al. 2000). This morphological asymmetry is one of well known features in sunspot activities (see, Sect. 10 of Zirin 1988), and has been studied with sunspots’ areas (e.g., Ludmány et al. 1999). In this paper, we quantitatively investigate the area asymmetry of solar bipolar regions with magnetic field data.
Hale et al. (1919) is one of the oldest papers on the morphological asymmetry of sunspots. They classified sunspot groups that appeared from 1915 through 1917 with their proposed sunspot types (Mt. Wilson magnetic classification), and reported in their Table 3 that about 50% of the sunspot groups show principal spots on the preceding polarities, while 10% of the groups show principal spots on the following polarities.
Several previous papers (see Ludmány et al. 1999, and references therein) obtained their results from white-light data. Their issues are morphological asymmetries between the preceding and following sunspots; e.g., Ludmány et al. (1999) attempted to quantify the compactness of the preceding and following sunspots, and studied the sunspots asymmetry derived from their compactness.
In previous numerical simulations of the thin flux tube model, Fan et al. (1993) and Fan & Fisher (1996) showed from their numerical simulations that the area asymmetry, which is comparable to the field strength asymmetry, between the preceding and following polarities could be produced by the Coriolis force during a flux tube’s rising motion in the solar convection zone. However, there is no quantitative study of the area asymmetry that can be compared with the results of Fan et al. (1993) and Fan & Fisher (1996). Fisher et al. (2000) reviewed observed morphological asymmetries of active regions and numerical simulations of flux tube emergence.
Recently Tian & Alexander (2009) reported helicity injection asymmetries and magnetic flux imbalances between the positive and negative polarities on several active regions. Fan et al. (2009) reproduced the area asymmetry in their magnetohydrodynamic simulation, and showed helicity flux asymmetry. They argued that an area asymmetry in their simulations coincides with a magnetic twist asymmetry between the preceding and following flux lopes, and this twist asymmetry results in the helicity flux asymmetry. Our results for the area asymmetry may have relations with these issues.
In this study, we quantitatively estimate the area asymmetry ratio from photospheric magnetograms, and compare this with other parameters described in the later. In Sect. 2 data and parameters are described. We show our results in Sect. 3. Discussions are given in Sect. 4. Our results are summarized in Sect. 5.
 |
Fig. 1 Instances for area asymmetry (A). Red and blue indicate positive and negative polarities, respectively. Rectangles show the areas where morphological parameters are derived. The dynamic range of display is within ±100 G. For emphasis, a region where unsigned field strength is less than 50 G is shown in gray. |
2. Data and parameters
2.1. Data and events
We investigated level 1.5 magnetograms obtained with the Michelson Doppler Imager (MDI; Scherrer et al. 1995) from 1996 April 23 to 2001 September 2. This period is the first half of cycle 23. To retain the homogeneity in our ensemble with minimum sample number, we selected active regions that existed on the southern hemisphere during the first half of cycle 23.
The magnetograms that we checked were observed around 00:00 UT or 01:36 UT on each day. We ignored days on which magnetograms were not observed at these times. These magnetograms covered about 90% of the MDI observation days during our analysis period. The pixel width of the magnetograms is 1.98 arcsec.
To select active regions and to exclude other magnetic field components from their appearances, we arbitrarily set possible smaller rectangle regions including active regions with the following conditions.
-
1.
Isolated bipolar regions are selected, because it is easy to definethe field-weighted positions of the positive and negativepolarities.
-
2.
Regions near the solar meridian are checked only once during its solar passage.
-
3.
Emerging flux regions are not included, because morphological properties of emerging regions sometimes change in a few days.
-
4.
Magnetic flux imbalance (d) between the positive and negative polarities is less than 15% in a rectangle region. The magnetic flux imbalance d is defined as
 where Φ is the unsigned magnetic flux in the rectangle region, subscripts “ + ” and “−” show the positive and negative polarities, and Bz is the longitudinal field strength. To calculate Φ and other morphological parameters described in Sect. 2.2, we selected pixels where unsigned field strength is greater than 50 G. We tried to set rectangle regions to make the magnetic flux balance small.
where Φ is the unsigned magnetic flux in the rectangle region, subscripts “ + ” and “−” show the positive and negative polarities, and Bz is the longitudinal field strength. To calculate Φ and other morphological parameters described in Sect. 2.2, we selected pixels where unsigned field strength is greater than 50 G. We tried to set rectangle regions to make the magnetic flux balance small.
Figure 1 shows examples of selected active regions and rectangles. Finally, we obtained 138 regions including not only active regions but also decaying active regions. The range of total magnetic flux (Φ + + Φ−) is from 7 × 1012 Wb to 6 × 1014 Wb, and that of total area is from 7 × 108 km2 to 3 × 1010 km2. In this selection we excluded much smaller regions and scattered regions that are hardly confirmed in the dynamic range of display (± 1000 G). In our future statistical study, regions will be detected automatically.
To reduce the uncertainty of area asymmetry caused by the magnetic flux imbalance, we selected active regions whose magnetic imbalances are less than 15%. So far, several authors have reported magnetic flux imbalances in active regions (see Sect. 3.6 of Tian et al. 2003, and references therein). From 517 samples, Tian et al. (2003) report that 47% of active regions are in 10% flux imbalance, and 31% in flux imbalance between 10% and 20%. It is easily predicted that a larger magnetic flux imbalance can lead to greater area asymmetry. By excluding larger magnetic flux imbalance, we tried to obtain area asymmetry that does not relate to magnetic flux imbalance. We discuss this uncertainty in Sect. 4.3.
Here we also mention a saturation of field strength measurement by MDI, which cannot observe strong field strength (| Bz| ≥ 2000 G in level 1.5 magnetograms) around sunspot umbrae (e.g., Fig. 6 of Berger & Lites 2003). Liu et al. (2007) report the cause of this saturation. A typical value of our unsigned field strength is 196 G, and the maximum field strength is 2080 G. In seven regions, maximum field strengths are over 1900 G. This saturation may affect estimations of the magnetic flux imbalance, and do not affect measurements active regions areas. As for the calibration status of MDI, see their WEB site1.
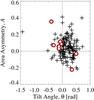 |
Fig. 2 Tilt angle (θ) vs. area asymmetry (A). “+” shows regular orientation regions (M = 1), and white-filled circles shows irregular orientation regions (M = 0). |
 |
Fig. 3 Histograms of area asymmetry (A) and tilt angle (θ). Bin sizes are 0.02 in the upper panel and 0.05 in the lower. Dashed lines show results of the Gaussian fitting. a0–a2 at the top of the both panels are the height, the center, and the width (the standard deviation) of the Gaussian distribution. |
2.2. Morphological parameters
We estimated following morphological parameters of the selected regions; magnetic orientation (M), tilt angle (θ), and area asymmetry ratio (A). If magnetic orientation is consistent with Hale’s polarity rule (Hale et al. 1919), M is set to be 1. Otherwise, M is equal to 0. According to Hale’s polarity rule, negative polarities appeared at the preceding region on the southern hemisphere in solar cycle 23. We decided M from the field-weighted positions (x′, y′) of the preceding and following polarities. These field-weighted positions are calculated as, 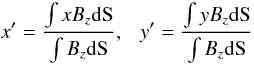 (3)where x and y indicate the solar center coordinate. If x′ of the negative polarity is larger than that of the positive polarity, M is set to be 1.
(3)where x and y indicate the solar center coordinate. If x′ of the negative polarity is larger than that of the positive polarity, M is set to be 1.
The tilt angle θ is estimated from the following equation, 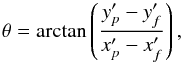 (4)where subscripts p and f shows the preceding and following polarities, respectively.
(4)where subscripts p and f shows the preceding and following polarities, respectively.
The area asymmetry ratio A is defined as, 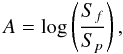 (5)where S is the area of each polarity where unsigned field strength is over 50 G. Therefore, if an area of the preceding polarity is smaller than that of the following polarity, A is greater than zero. The particular choice of the threshold of 50 G is motivated by the noise level of MDI magnetograms of about 20 G (Table 1 of Scherrer et al. 1995).
(5)where S is the area of each polarity where unsigned field strength is over 50 G. Therefore, if an area of the preceding polarity is smaller than that of the following polarity, A is greater than zero. The particular choice of the threshold of 50 G is motivated by the noise level of MDI magnetograms of about 20 G (Table 1 of Scherrer et al. 1995).
Table 3, available at the CDS, contains a list of the bipolar regions. Columns 1–3 describe the date, Col. 4 shows the MDI daily number of the 96 minutes cadence data set, Cols. 5–8 give the field-weighted position (x′,y′), area, and average field strength of the positive polarity, and Cols. 9–12 show those of the negative polarities. As a result of our region selection, these parameters were obtained from magnetograms observed around 00:00 UT.
Number of events between θ, M, and A.
 |
Fig. 4 Temporal evolutions of A in recurrent regions. |
Temporal evolutions of A in the recurrent regions.
3. Results
3.1. Statistical results
Here we show results of A. Figure 2 shows a scatter plot between θ and A. Figure 3 shows histograms of θ and A. Table 1 shows number of regions between θ, M, and A. It is found that A in Fig. 2 distributes between −0.2 and 0.4. From the Gauss fitting shown in Fig. 3, the average value of A is found to be 0.03, and the standard deviation is 0.11. The average value of tilt angle θ is 0.15 radian, and the standard deviation is 0.23 radian. Table 1 shows that area asymmetry is negative in 37% (51/138) of the analyzed regions. There is no correlation between A and θ in Fig. 2.
Here we point out irregular orientation regions (M = 0). Table 1 shows that irregular orientation regions are 6% (8/138) of the analyzed regions. This value is similar to previous results obtained from white light data (e.g., Richardson 1948; Khlystova & Sokoloff 2009). We cannot give a clear reason for irregular orientation regions distributed in certain parameter regions ([A ≤ 0 and θ > 0] or [A > 0 and θ ≤ 0]) in Fig. 2. This is a subject of our future statistical study.
We also investigated dependencies of θ and A on the magnetic flux and latitude. We cannot, however, find any clear dependencies on these parameters. Magnetic fluxes and latitudes that we used are the average ones derived from the positive and negative polarities. This may be due to how few events we have. Fisher et al. (1995) analyzed 24 701 sunspot groups, while we analyzed 138 regions. Figure 1 of Fisher et al. (1995) shows the weak latitude dependency of tilt angles with large dispersion. Statistical study of A with large sample number is our future subject.
 |
Fig. 5 Histograms of field strength within the rectangle region of the upper-right panel of Fig. 1. Red and blue lines show results of the linear fitting (50. ≤ |Bz| ≤ 300.) in the positive and negative polarities, respectively. The lower panel shows a zoom of the middle part of the upper panel for low field strengths. |
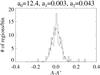 |
Fig. 6 Histogram of A − A′. |
3.2. Temporal evolution of A
In our samples, number of decay-phase regions is 25. A decay-phase region is defined as a region that appeared more than one month ago. These decay-phase regions show a narrower range of A, −0.15–0.14, than shown in Fig. 2. As for the latitude, a range of the decay-phase regions are equal to the one in Fig. 2. From this result, we expected that the area asymmetry would come closer to zero as a region decays.
In our samples, we could compare values of A in eleven recurrent regions. Table 2 and Fig. 4 show temporal evolutions of A in these recurrent regions. The intervals of the recurrent regions are almost 28 days. Column 6 in Table 2 shows variations in A. Values of A come closer to zero in four regions. Variation amplitudes of A in these regions are larger than the typical uncertainty of A (0.043, discussed in Sect. 4.1). In four regions values of A are almost retained, and in three regions the values of A get farther from zero.
We checked temporal evolutions of average values of unsigned magnetic fluxes. (Unsigned magnetic fluxes between the positive and negative polarities are almost balanced in our samples. See Sect. 2.1.) Column 7 in Table 2 shows magnetic flux evolutions. In seven regions, unsigned magnetic fluxes decreased, at least by 10%. In three regions, unsigned magnetic fluxes increased by 60% in one region and at most by 20% in two regions. In one region, the variation of unsigned magnetic fluxes is less than 10%. We cannot find a clear correlation between variations of A and those of averaged magnetic fluxes.
We also checked area variations in the positive and negative polarities. There is, however, no clear tendency between variations of A and those of areas.
4. Discussions
4.1. Uncertainties of the area asymmetry
Here we try to estimate uncertainties of the area asymmetry. As shown by Eq. (5), an uncertainty of the area asymmetry originates in the uncertainties of area measurements in the positive and negative polarities. There are two error sources of area measurements: 1) whether (rectangle) regions that we set properly include active regions or not; 2) unsigned field strengths below the threshold value (50 G).
Rectangle regions would not be the best way to select active regions, although rectangle regions that we set in this study can contain major components of the active regions (e.g., Fig. 1). One of our future subjects is a more appropriate selection of an active region area.
In the following, we estimate a typical uncertainty of area asymmetry due to lower field strengths. With an assumption, we estimate areas of lower field strengths, and calculated A′ as, 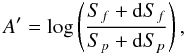 (6)where dSp and dSf are the areas of lower field strengths in the preceding and following polarities, respectively.
(6)where dSp and dSf are the areas of lower field strengths in the preceding and following polarities, respectively.
 |
Fig. 7 The lower panels show recurrent regions of those shown in the upper panels. |
To obtain dSf and dSp, we assume that number of pixels of lower field strengths are continuously distributed from that of higher field strengths. The upper panel of Fig. 5 shows a histogram of field strength in a rectangle region (the upper-right panel of Fig. 1). Red and blue lines show results of the linear fitting in the positive and negative polarities, respectively. The linear fittings are calculated within 50 ≤ |Bz| ≤ 300. The lower panel of Fig. 5 shows a zoom of the middle part of the upper panel for low field strengths. From these fitting results, we obtained number of pixels of lower field strengths.
Figure 6 show a histogram of A − A′. From the Gauss fitting, we find that standard deviation of A − A′ is 0.043. Therefore, if we can lower field strength than the threshold field strength, our results would change around ±0.043. We also calculated area asymmetry A′′ with lower threshold value, 20 G. As a result, from the Gauss fitting, standard deviation of A − A′′ is found to be 0.037.
4.2. Origins of the area asymmetry
In Sect. 3, we found that the area asymmetry (A) distributes between −0.2 and 0.4. This is the quantitative result of what Hale et al. (1919) found. So far, only Fan et al. (1993) has explained a mechanism for positive area asymmetry (A > 0) in their Sect. 3.2. In their calculations, during flux tube emergence, plasma gases in the preceding side of a flux tube are transferred into the following side by the Coriolis force along the flux tube axis. Governed by the balance of the gas and the magnetic field pressure in a flux tube, the cross-sectional area of the following side of the flux tube increases, and that of the preceding side decreases. This produces the positive area asymmetry between the preceding and following polarities. This mechanism, however, cannot qualitatively explain negative area asymmetries (A ≤ 0) shown in the lower panels of Fig. 1 and temporal evolution of A shown in Fig. 4.
About the negative area asymmetry, one may consider that this asymmetry is explained by kinking a flux tube whose original area asymmetry is positive (e.g., the left part of Fig. 1 of López Fuentes et al. 2000). López Fuentes et al. (2000) report a rotation motion of an irregular orientation region, and interpret this rotating motion as counter kink motion (see their Fig. 1). We, however, confirmed that some regions of the negative area asymmetry did not show any rotating motions. Figure 7 shows magnetic field maps for two recurrent regions. As is shown in this figure, these recurrent regions did not rotate. Therefore, the area asymmetry in these regions cannot be explained only by kinking a flux tube.
From another point of view, the decay process of active regions may relate to temporal evolution of A. It is believed that magnetic field in an active region spreads during its decay phase as small magnetic elements (e.g., moving magnetic features; Kubo et al. 2008), and some small elements vanish by colliding with the opposite polarity elements (e.g., magnetic flux cancellation; Chae et al. 2004). Some fraction of the decaying magnetic fields are believed to be transported into the poleward by the meridional circulation flow (e.g., Dikpati & Charbonneau 1999). More precise analysis in active regions is needed.
4.3. Magnetic flux imbalance
As introduced by the previous authors (e.g., Tian et al. 2003), there are magnetic flux imbalances in analyses of longitudinal field magnetograms. One can easily imagine that larger magnetic flux imbalance can produce larger area asymmetry. In the following, we show a histogram of the magnetic flux imbalance and a relation between the magnetic flux imbalance and the area asymmetry.
Figure 8 shows a histogram of the magnetic flux imbalance. Added to the 138 events, this figure shows another 37 events whose unsigned magnetic flux imbalances greater than 15%. This histogram can be approximated by the Gaussian distribution. Samples of the negative magnetic flux imbalance are more than those of the positive magnetic flux imbalance. We cannot judge whether this difference in our samples is significant or not. Tian et al. (2003) show a histogram of the magnetic flux imbalance in their Fig. 7, and its shape seem to be distorted from the Gaussian distribution.
Figure 9 shows a scatter plot between the magnetic flux imbalance and the area asymmetry. As is shown in this figure, samples of larger flux imbalance (“ + ”) tend to show greater area asymmetry. On the other hand, those of smaller flux imbalance (“◇”) are distributed in lower correlation with the area asymmetry. Therefore, here we conclude that the area asymmetry is not strongly correlated to the magnetic flux imbalance in our 138 events.
 |
Fig. 8 Histogram of the magnetic flux balance. |
Positions of active regions are one of imaginable reasons of the magnetic flux imbalance in longitudinal magnetogram analysis. We, however, found that there is no correlation between magnetic flux imbalances and distances from the solar center in our samples. Quantitative study of the magnetic flux imbalance is one of our future subjects.
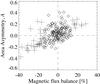 |
Fig. 9 Area asymmetry vs. magnetic flux balance. “+” and “◇” show samples whose unsigned magnetic flux imbalance is more than and less than 15%, respectively. |
5. Summary
In this paper, we quantitatively studied the area asymmetry of the 138 bipolar regions that appeared from 1996 April 23 to 2001 September 2. It is found in Fig. 2 that the area asymmetry ratio (A) distributes between −0.2 and 0.4, and the average value of A is 0.03. We show in Table 1 that the negative area asymmetry is shown in 37% (51/138) of our events, and the irregular orientation (M = 0) in 6% (8/138) of our regions. We cannot find any dependencies of A on the latitude, tilt angle, and magnetic flux. Temporal evolutions of A are also found in
eleven recurrent regions (Fig. 4). In four regions, values of A close to zero. In other four regions, values of A are retained. In three regions, a value of A becomes far from zero. It is difficult to qualitatively explain temporal evolution of A and negative area asymmetry only with the processes considered by Fan et al. (1993). Additional processes are needed to reproduce the area asymmetry.
Acknowledgments
We are grateful to the editor and the anonymous referee for their constructive and helpful comments. This work has been supported by the GEMSIS project of Solar-Terrestrial Environment Laboratory, Nagoya University. This work has also been supported by the Nobeyama Solar Radio Observatory. We thank the MDI consortia for providing data. SoHO is a mission of international cooperation between ESA and NASA.
References
- Berger, T. E., & Lites, B. W. 2003, Sol. Phys., 213, 213 [Google Scholar]
- Chae, J., Moon, Y.-J., & Pevtsov, A. A. 2004, ApJ, 602, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Dikpati, M., & Charbonneau, P. 1999, ApJ, 518, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y., & Fisher, G. H. 1996, Sol. Phys., 166, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y., Fisher, G. H., & Deluca, E. E. 1993, ApJ, 405, 390 [Google Scholar]
- Fan, Y., Alexander, D., & Tian, L. 2009, ApJ, 707, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Fan, Y., & Howard, R. F. 1995, ApJ, 438, 463 [Google Scholar]
- Fisher, G. H., Fan, Y., Longcope, D. W., Linton, M. G., & Pevtsov, A. A. 2000, Sol. Phys., 192, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, G. E., Ellerman, F., Nicholson, S. B., & Joy, A. H. 1919, ApJ, 49, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Khlystova, A. I., & Sokoloff, D. D. 2009, Astron. Rep., 53, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Kubo, M., Lites, B. W., Shimizu, T., & Ichimoto, K. 2008, ApJ, 686, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Norton, A. A., & Scherrer, P. H. 2007, Sol. Phys., 241, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Ludmány, A., Baranyi, T., Mezö, G., & Tóth, L. 1999, Mag. Fields Sol. Proc., 448, 613 [NASA ADS] [Google Scholar]
- López Fuentes, M. C., Demoulin, P., Mandrini, C. H., & van Driel-Gesztelyi, L. 2000, ApJ, 544, 540 [Google Scholar]
- Magara, T., & Longcope, D. W. 2003, ApJ, 586, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, R. S. 1948, ApJ, 107, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Tian, L., & Alexander, D. 2009, ApJ, 695, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, L., Liu, Y., & Wang, H. 2003, Sol. Phys., 215, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Zirin, H. 1988, Astrophysics of the Sun (Cambridge: Cambridge Univ. Press) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Instances for area asymmetry (A). Red and blue indicate positive and negative polarities, respectively. Rectangles show the areas where morphological parameters are derived. The dynamic range of display is within ±100 G. For emphasis, a region where unsigned field strength is less than 50 G is shown in gray. |
| In the text | |
 |
Fig. 2 Tilt angle (θ) vs. area asymmetry (A). “+” shows regular orientation regions (M = 1), and white-filled circles shows irregular orientation regions (M = 0). |
| In the text | |
 |
Fig. 3 Histograms of area asymmetry (A) and tilt angle (θ). Bin sizes are 0.02 in the upper panel and 0.05 in the lower. Dashed lines show results of the Gaussian fitting. a0–a2 at the top of the both panels are the height, the center, and the width (the standard deviation) of the Gaussian distribution. |
| In the text | |
 |
Fig. 4 Temporal evolutions of A in recurrent regions. |
| In the text | |
 |
Fig. 5 Histograms of field strength within the rectangle region of the upper-right panel of Fig. 1. Red and blue lines show results of the linear fitting (50. ≤ |Bz| ≤ 300.) in the positive and negative polarities, respectively. The lower panel shows a zoom of the middle part of the upper panel for low field strengths. |
| In the text | |
 |
Fig. 6 Histogram of A − A′. |
| In the text | |
 |
Fig. 7 The lower panels show recurrent regions of those shown in the upper panels. |
| In the text | |
 |
Fig. 8 Histogram of the magnetic flux balance. |
| In the text | |
 |
Fig. 9 Area asymmetry vs. magnetic flux balance. “+” and “◇” show samples whose unsigned magnetic flux imbalance is more than and less than 15%, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


