| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117948 | |
| Published online | 13 February 2012 | |
Comparison of synthetic maps from truncated jet-formation models with YSO jet observations
II. The effect of varying inclinations⋆
1 Institute of Astronomy and Astrophysics, Section Computational Physics, Eberhard Karls Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
e-mail: matthias.stute@tat.physik.uni-tuebingen.de
2 High Performance Computing Center Stuttgart (HLRS), Universität Stuttgart, 70550 Stuttgart, Germany
Received: 25 August 2011
Accepted: 22 November 2011
Context. Analytical radially self-similar models are the best available solutions describing disk-winds, but they need several improvements. In a previous article, we introduced models of jets from truncated disks, i.e. evolved in time numerical simulations based on a radially self-similar MHD solution but including the effects of a finite radius of the jet-emitting disk, hence the outflow. In Paper I of this series, we compared these models with available observational data by varying the jet density and velocity, the mass of the protostar, and the radius of this truncation.
Aims. In Paper I, we assumed that the jet lies in the plane of the sky. In this paper, we investigate the effect of different inclinations of the jet.
Methods. To compare our models with observed jet widths inferred from recent optical images taken with HST and AO, we again created emission maps in different forbidden lines, and from such emission maps determined the jet width as the full-width half-maximum of the emission.
Results. We can reproduce the jet width of DG Tau and its variations very well, and the derived inclination of 40° is in excellent agreement with literature values of 32–52°. In CW Tau we overestimate the inclination in our best-fit model. In the other objects, we cannot find appropriate models that reproduce the variations in the observed jet widths. Only the average jet width itself is well modeled.
Conclusions. We conclude that truncation – i.e. taking the finite radius of the jet launching region into account – is needed to reproduce the observed jet widths, and our simulations limit the possible range of truncation radii. The effects of inclination are important for modeling the intrinsic variations seen in observed jet widths. Our models can be used to infer the inclinations in the observed sample independently; however, a parameter study with a finer grid of parameters is needed.
Key words: methods: numerical / magnetohydrodynamics (MHD) / stars: pre-main sequence / ISM: jets and outflows
Appendices are only available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Astrophysical jets and disks (Livio 2009) seem to be inter-related, notably in the case of young stellar objects (YSOs), wherein jet signatures are well correlated with the infrared excess and accretion rate of the circumstellar disk (Cabrit et al. 1990; Hartigan et al. 2004). Disks provide the plasma that is flowing into the jets, while jets in turn provide the disk with the needed angular momentum removal so that accretion in the protostellar object takes place (Hartmann 2009). On the theoretical front, the most widely accepted description of this accretion-ejection phenomenon (Ferreira 2007) is based on the interaction of a large-scale magnetic field with an accretion disk around the central object. Then, plasma is channeled and magneto-centrifugally accelerated along the open magnetic field lines threading the accretion disk, as first described in Blandford & Payne (1982). Several works have extended this study either by semi-analytic models using radially self-similar solutions of the full magnetohydrodynamics (MHD) equations with the disk treated as a boundary condition (Vlahakis & Tsinganos 1998), or, by selfconsistent numerical treatment of the disk-jet system (e.g. Zanni et al. 2007).
List of numerical models.
The original Blandford & Payne (1982) model, however, has serious limitations for a meaningful comparison of its predictions with observations. Singularities exist at the jet axis, the outflow is not asymptotically superfast, and most important, the disk has no intrinsic scale with the result that the jet formally extends to radial infinity, to mention just a few problems. The singularity at the axis can be easily taken care of by numerical simulations extending the analytical solutions close to this symmetry axis (Gracia et al. 2006, GVT06 hereafter). The outflow speed at large distances may be tuned to cross the corresponding limiting characteristic, with the result that the terminal wind solution is causally disconnected from the disk, so that perturbations downstream of the superfast transition (as modified by self-similarity) cannot affect the whole structure of the steady disk-wind outflow (Vlahakis et al. 2000, V00 hereafter), which has also been shown to be structurally stable (Matsakos et al. 2008, M08 hereafter). The next step has been undertaken in a previous paper (Stute et al. 2008) by introducing a scale in the disk, wherein we presented numerical simulations of truncated flows whose initial conditions are based on analytical self-similar models.
To test our truncated models, we then applied our simulations to observations (Stute et al. 2010, Paper I hereafter). In recent years, many NIR and optical data have become available for exploring the morphology and kinematics of the jet-launching region (e.g. Dougados et al. 2000; Ray et al. 2007; Dougados 2008, and references therein). HST and adaptive optics observations give access to the innermost regions of the wind, where the acceleration and collimation occurs (Ray et al. 1996; Dougados et al. 2000; Woitas et al. 2002; Hartigan et al. 2004). Since YSO jets emit in a number of atomic (and molecular) lines, we use a synthetic emission code to create emission maps in different forbidden lines, which were used by other authors to extract the jet width from images. In Paper I, we compared the observed jet widths with those extracted from our synthetic images. A similar study has been done by Ferreira (1997), Casse & Ferreira (2000), Garcia et al. (2001), and Dougados et al. (2004), but using untruncated disk wind models.
In Paper I, however, we always assumed the inclination of the jet to be 90°. The influence of varying inclinations on the derived synthetic jet widths is now examined in this paper.
The remainder of the paper is organized as follows. We briefly review the initial set-up of the numerical simulations and describe our procedure for the comparison with observations in Sect. 2. The results of our studies are presented in Sect. 3. In Sect. 4 we describe our best-fit models for each object in the sample and compare derived inclinations with the literature values. Finally, we conclude with the implications of the results in terms of the structure of the disk and the respective launching radii of the jets in YSOs. In Appendix A, we present the extracted line widths for all models, runs, and inclinations for the sake of completeness. Jet velocities derived from synthetic position-velocity diagrams are given in Appendix B.
2. The models
This work is based on the results of our numerical simulations discussed in Stute et al. (2008) and two new models already added in Paper I (Table 1). We solved the MHD equations with the PLUTO code1 (Mignone et al. 2007) starting from initial conditions set according to a steady, radially self-similar solution as described in V00, which crosses all three critical surfaces. At the symmetry axis, the analytical solution was modified as described in GVT06 and M08.
To study the influence of the truncation on the analytical solution, we divided our computational domain up into a jet region and an external region, separated by a truncation field line αtrunc. For lower values of the normalized magnetic flux function, i.e. α < αtrunc – or conversely smaller cylindrical radii – our initial conditions are fully determined by the solution of V00 and the modification of GVT06 and M08 close to the axis. In the outer region, we modified all quantities and initialized them with another analytical solution but with modified parameters (models with outer truncation; SC1a–g, SC2, SC4). In models SC1a–g we varied the truncation radius and within models SC1a, SC2 and SC4, we probed different modifications in the outer region. Two simulations were performed with inner truncation (SC3, SC5), i.e. the analytical solution with modified quantities is inside the original analytical solution. For further details, we refer the reader to Stute et al. (2008).
2.1. Synthetic emission maps and jet width extraction
We used the synthetic emission code OpenSESAMe v0.1 to produce synthetic observations from our simulations in different consecutive stages. The first stage approximates the chemical composition of the plasma by locally solving a chemical network under the assumption of stationarity. The second stage calculates the statistical equilibrium of level populations for each ion of interest as a function of temperature and density and yields the emissivity for individual transitions of interest. Further stages take care of integration along the line-of-sight and projection. Finally, the ideal maps are convolved with a Gaussian point-spread-function (PSF) to mimic the finite spatial resolution of a given instrument. These synthetic emission maps are then quantitatively analyzed with similar techniques to those used on real observed maps.
We compared the width of jets measured from HST and AO observations (Dougados et al. 2000; Ray et al. 2007; Dougados 2008, and references therein) to synthetic emission maps calculated from our MHD models. We convolved the maps with a Gaussian with an FHWM of 15 AU (σ = 6.37 AU) throughout this paper, equivalent to HST’s resolution of 0.1′′ at a distance of 150 pc. We used a sample of eight jets: DG Tau, HN Tau, CW Tau, UZ Tau E, RW Aur, HH34, HH30 and HL Tau (Fig. 1). To determine the width of the jets in our models, we used a method that is as close as possible to the one applied by the observers. We created convolved synthetic maps for the emission in the [SII] λ6731 and [OI] λ6300 lines for each numerical model and each run of OpenSESAMe and determined the jet width from the map’s full-width half-maximum (FWHM) as a function of distance along the axis.
 |
Fig. 1 Variation in jet width (FWHM) derived from [SII] and [OI] images as a function of distance from the source. Data points are from CFHT/PUEO and HST/STIS observations of DG Tau (diamonds), HN Tau (plus signs), CW Tau (squares), UZ Tau E (crosses), RW Aur (circles), HH 34 (one triangle). Data are taken from Ray et al. (2007) for distances below 200 AU and Dougados et al. (2000) beyond this distance. |
 |
Fig. 2 Synthetic emission maps of the [OI] λ6300 line, convolved with a Gaussian PSF with an FWHM of 15 AU, for run (500, 1000, 0.5) and the untruncated model ADO (top) and the model SC1a with outer truncation (middle) and for run (500, 100, 0.2) and model SC3 with inner truncation (bottom). The inclinations are 30°, 40°, 60°, 70°, and 90° (from left to right). The flux is in units of erg s-1 cm-2. |
 |
Fig. 3 Same as Fig. 2, but normalized by the intensity on the jet axis for each row. Also plotted is the contour line where I/Iaxis = 0.5, i.e. the position of the FWHM. |
2.2. Normalizations
To compare our results with observations, i.e. to run OpenSESAMe correctly, we have to scale the dimensionless quantities in which PLUTO performs its calculations (Stute et al. 2008) to physical units by providing scaling factors for density ρ0, pressure p0, velocity v0, magnetic field strength B0, a length scale R0, and a mass scale ℳ. However, in terms of the normalizations used in the PLUTO code, only three of those quantities are indepedent. A possible choice is the mass of the central object, velocity scale, and density scale, while the remaining factors are calculated from these. The PLUTO domain is set from (0, 6) to (50, 100), and the physical scale of the jet in AU is simply the PLUTO domain multiplied with a length scale R0. In the solution of V00, the length scale R0 is connected to the mass of the central object and to the velocity normalization via 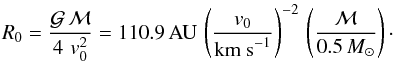 (1)From the velocity and density normalization the normalizations for the magnetic field and pressure directly follow as
(1)From the velocity and density normalization the normalizations for the magnetic field and pressure directly follow as 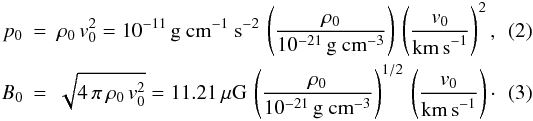 The mass of the central object only affects the length scale R0. The pressure and temperature of the jet, and thus the synthetic emission maps, are only affected by the density and velocity scales ρ0 and v0.
The mass of the central object only affects the length scale R0. The pressure and temperature of the jet, and thus the synthetic emission maps, are only affected by the density and velocity scales ρ0 and v0.
As typical jet velocities in YSOs, we assumed in Paper I values of 100, 300, 600, and 1000 km s-1, as typical masses of T Tauri stars 0.2, 0.5, and 0.8 M⊙ (Hartigan et al. 1995), and as jet number densities values of 125, 500, 1000, and 5 × 104 cm-3. We adopted the nomenclature for our runs as e.g. (500, 600, 0.5) with njet in cm-3, vjet in km s-1 and M in M⊙.
For numerical reasons, the density shows a steap increase close to the jet axis. This artifact had to be corrected, therefore we applied the following corrections before running OpenSESAMe, as in Paper I. We limited the temperature to 104 K, the density around the axis by setting the density inside 1 FHWM to its value at 1 FHWM for each z and the fraction xe = ne/ntot to 0.1. These values of xe and T are typical of those deduced from analyses of line ratios in jets (e.g. Bacciotti & Eislöffel 1999; Lavalley-Fouquet et al. 2000).
With the same requirement that the FWHM of the Gaussian of 15 AU is sampled by a reasonable number of pixels (see Paper I), the only valid runs are
-
(..., 600, 0.2), (..., 600, 0.5), (..., 1000, 0.5), (..., 1000, 0.8) for models ADO, SC1a–b, SC2, SC4;
-
(..., 600, 0.2), (..., 600, 0.5), (..., 1000, 0.2), (..., 1000, 0.5), (..., 1000, 0.8) for models; SC1c–f;
-
(..., 600, 0.2), (..., 1000, 0.2), (..., 1000, 0.5), (..., 1000, 0.8) for model SC1g;
-
(..., 100, 0.2) for model SC3;
-
no valid runs for model SC5.
At first sight, the required velocities of 600 and 1000 km s-1 in our models with outer truncation SC1a–g, SC2, and SC4 seem to be chosen too high in comparison with observed values in typical YSO jets. We have to note that the velocity vjet is a formal parameter of the model and corresponds to a physical velocity component only very close to the source, i.e. is not the asymptotic velocity of the flow.
The observed velocities of YSO jets are usually inferred from either proper motions of jet knots (i.e. pattern speeds, not flow speeds) or position-velocity diagrams that show the velocities along the line of sight convolved with emissivity. In our simulations, proper motions cannot be measured because patterns are missing. In Fig. 4, we show a synthetic position-velocity diagram for the model SC1a, run (500, 1000, 0.8) and an inclination of 40° – which will be our best-fit model for DG Tau – and the observed map of DG Tau from Lavalley-Fouquet et al. (2000). We chose a velocity resolution like the one in the observations, and the dynamical range is similar in both plots. We can directly see that high velocities around vjet are only detectable close to the jet source, the velocity of the jet at distances over 0.5′′ is 220 km s-1 and thus in the range of the observed value of 280 km s-1. In Appendix B, we list the velocities of the jet for most of our models derived from the synthetic position-velocity diagrams.
 |
Fig. 4 Top: synthetic position-velocity diagram of the [OI] λ6300 line for model SC1a, run (500, 1000, 0.8), and an inclination of 40°, where we assumed a distance to the jet of 150 pc. Bottom: observed position-velocity map of DG Tau for [OI] λ6300 (black thin lines) and [NII] λ6583 (green thick lines) from Lavalley-Fouquet et al. (2000). The dynamical range is similar in both plots. |
3. Results
Naturally the inclination plays a crucial role for the way the jet is seen in synthetic emission maps. This is even more pronounced in the truncated jet solutions (Fig. 2).
3.1. Synthetic jet widths
We extracted the jet width from a ratio of intensities by using the FWHM, i.e. we divided the maps by the intensity on the axis and checked where the ratio is 0.5. Since in all models we have densities below the critical density the emissivity is proportional to ρ2 in the whole domain, therefore the factor ρ2 should cancel out. In Paper I, we already found this behavior, where the absolute value of the jet density is not important for the extracted jet widths. The same is present in this study, so we show mainly results with a jet density of 500 cm-3 throughout this paper.
A second result is that the setup of the external solution is not important; i.e., the extracted jet widths of models SC1a, SC2, and SC4 are very similar. The only important parameters for our study are indeed the truncation radius and the inclination, when the jet velocity and mass of the central object are fixed by observations.
In Paper I, we found that all untruncated ADO models give jet widths that are too large compared to the observations of T Tauri jets. This result is not changed when varying the inclination. We again conclude that we need an additional effect that reduces the derived jet width, to be able to reproduce all jets in our sample.
We already found that the extracted jet width does not follow any directly apparent feature in either the density or temperature maps or the emissivity map. A property of the extracted jet width, which was and still is intrinsic in all our runs, is the overall structure with at least one maximum. The position of maxima is generally only obvious in the normalized emission maps, i.e. after dividing by the intensity on the jet axis (Fig. 3). In Paper I, we ignored this maximum and compared the synthetic jet widths with the observed ones only for long distances along the jet axis. Since the observed jet widths, however, also show a bumpy profile, it may be worth investigating the origin of the maxima in our simulations further and taking them into account for fitting the observations.
The distance of the first maximum from the jet source increases for increasing mass of the central object and decreasing velocity of the jet. It also increases for increasing degree of truncation. In several models, a second maximum appears whose distance decreases for increasing degree of truncation.
 |
Fig. 5 Jet widths in AU derived from synthetic [OI] images as a function of distance from the source in model SC1c and for run (500, 1000, 0.8). Overlaid are the data points of Fig. 1. |
In the model SC3 with inner truncation, the derived jet width is almost constant. The effects of varying inclination are therefore only marginal when ignoring the geometrical effect mentioned above (Fig. 6).
 |
Fig. 6 Jet widths in AU derived from synthetic [OI] images as a function of distance from the source in model SC3 and for run (500, 100, 0.2). Overlaid are the data points of Fig. 1. |
3.2. Origin of variations in the extracted jet widths
The maxima were already present in our runs in Paper I, i.e., in those with an inclination of 90°. This shows that we have to differentiate intrinsic variations and variations due to geometrical effects. First, we have to note again that maxima in the extracted jet width are not necessarily connected with e.g. density knots. In Stute et al. (2008), we found that the model with inner truncation SC3 collapses toward the jet axis leading to knots in the density maps. In Paper I and also in Fig. 2 (bottom), we find in the corresponding synthetic emission map in [OI] two areas of enhanced emission whose position, however, is not the same as that of the density knots. Furthermore, the extracted jet width is almost constant despite these areas.
To find an physical origin of the variations, it is useful not to focus on the first maximum but on the minimum directly behind it. One common feature in all our MHD simulations is the fast magnetosonic separatrix surface (FMSS, Stute et al. 2008). This surface is a weak shock causally disconnecting the subfast flow from the superfast one. Its position in Z direction increases monotonically with increasing R value. Both density and pressure along the flow line show a jump at the FMSS. As mentioned above, we convolve our map with a Gaussian of 15 AU and modify the density inside 15 AU from the jet axis. We find that the minimum in the extracted jet width is at the same position, where the FMSS has a radius of 15 AU and enters this region. For inclinations different from 90°, the two crossing points of FMSS with the Gaussian both in front of the jet and behind the jet are visible as local minima in the extracted jet widths.
Beyond physical origins of the maxima, another origin is the geometry of the system, i.e. the finiteness of our computational domain. To quantify this aspect, we calculated the emission maps and extracted the jet width for a domain with constant density and temperature. Thus also the emission is constant across the domain. If seen with an inclination of 90°, the extracted jet width is constant as expected; however, if the inclination is 40°, the extracted jet width is almost constant only between about 15 and 68 R0 (Fig. 7). These values are dependent on the aspect ratio of the computational domain and the tangent of the inclination. In our models, this geometrical effect leads to another maximum in extracted jet widths whose position moves to shorter distances with decreasing inclination (Fig. 5) and has to be corrected when comparing our models to observations. We used this test case with constant emission for quantifying the area in which our extracted jet widths are not affected by it.
 |
Fig. 7 Normalized emission map of the [OI] λ6300 line for a computational domain with constant density and temperature. The inclination is 40° (left) and 90° (right). Also plotted is the contour line where I/Iaxis = 0.5, i.e. the position of the FWHM. |
4. Best-fit models
In Paper I, we found best-fit models for the jets in the observed sample. We always ignored there the first maximum in the synthetic jet widths and focused on longer distances from the source. Now we can include the effects of inclination, use the position of the maxima in our synthetical jet width variations for estimating the inclination, and compare the derived inclination with values from the literature.
4.1. DG Tau
The observed mass of DG Tau (Fig. 1) is 0.67 M⊙ (Hartigan et al. 1995), so we have to focus on the runs (500, 1000, 0.8), and perhaps also on runs (500, 600, 0.5) and (500, 1000, 0.5). The best-fit model is between ADO and SC1a, implying a truncation radius larger than 0.22 AU. DG Tau can be reproduced quite well with model SC1a, the run (500, 1000, 0.8), and an inclination of 40° (Fig. 8). This inclination is in excellent agreement with the literature values of 32–52° (Eislöffel & Mundt 1998; Bacciotti et al. 2002; Pyo et al. 2003).
 |
Fig. 8 Best-fit model for DG Tau: model SC1a, run (500, 1000, 0.8), and inclination of 40°. The red part is not reliable due to the geometric effect discussed in Sect. 3.2. |
4.2. CW Tau
The mass of CW Tau is the highest in our sample, 1.03 M⊙ (Hartigan et al. 1995). Using the runs (500, 1000, 0.8), the best-fit model was SC1b or SC1c. The truncation radius is thus between 0.25–0.3 AU. CW Tau may be modeled best with simulation SC1c, run (500, 1000, 0.8), and an inclination of 60° (Fig. 9). The literature value, however, is about 41° (Coffey et al. 2007).
 |
Fig. 9 Best-fit model for CW Tau: model SC1c, run (500, 1000, 0.8), and inclination of 60°. The red part is not reliable due to the geometric effect discussed in Sect. 3.2. |
4.3. RW Aur
The measured mass of RW Aur (circles) is 0.85 M⊙ (Hartigan et al. 1995), so we had to focus on runs (500, 1000, 0.8). We needed a very high degree of truncation as in models SC1e-g, thus a truncation radius on the order of 0.04 AU, which seems to be unphysical. For these models, however, the influence of inclination is only marginal. We find literature values of 42° (Lay et al. 1997).
4.4. HN Tau and UZ Tau E
HN Tau (plus signs) has a mass of 0.72 M⊙ (Hartigan et al. 1995), thus again the runs (500, 1000, 0.8) were favored. When we ignore the first maximum, we can interpolate the jet shape at greater distances and find a best-fit model between ADO and SC1a, so the truncation radius is again larger than 0.34 AU. However, this result is highly uncertain, and this procedure contradicts our present approach of taking the maxima into account.
UZ Tau E (crosses) has the lowest mass in our sample, only 0.18 M⊙ (Hartigan et al. 1995), so we used the runs (500, 600, 0.2). Again we have to interpolate the jet width from longer distances and could in principle choose model SC1a as best-fit model. The truncation radius would be about 0.26 AU.
Over all, we cannot find best-fit models, since our numerical resolution very close to the jet source is not sufficient. The inclination of HN Tau is not known (Hartigan et al. 2004). For the inclination of UZ Tau E we find literature values of 60–70° (Jensen et al. 1996; Prato et al. 2002).
5. Summary and conclusions
In Paper I, we showed as a proof of concept that jet widths derived from numerical simulations extending analytical MHD jet formation models can be very helpful for understanding recently observed jet widths from observations with adaptive optics and space telescopes. Here we investigated the influence of different inclinations qualitatively. We examined the origin of variations in the extracted jet widths and identified physical and geometrical effects. We showed in which range our results are reliable and not affected by numerical artifacts.
We found that the distance of the first maximum from the jet source increases for increasing mass of the central object and decreasing velocity of the jet. It also increases for increasing degree of truncation. In several models, a second maximum appears whose distance decreases for increasing degree of truncation. The most noticeable effect of a decreasing inclination is a change in the position of the maxima in the synthetic jet widths. In all cases, the distance of the first maximum from the jet source decreases for decreasing inclination. The lower the inclination, the higher the number of maxima in the jet width.
We compared our synthetic jet widths with observations of our sample including the position of maxima in the jet width variations as diagnostics for the inclination. Only for DG Tau and CW Tau could we unambiguously find models that fitted the observed jet widths. For the former, the derived inclination is perfectly consistent with values found in the literature; for the latter, our derived inclination is higher than commonly measured (60° compared to 41°).
In a future work, we have to refine our grid of models for reproducing the observed jet widths and their variations even more accurately. These models have to be done with higher numerical resolution in order to give significant results in terms of synthetic emission maps even within a few AU to the jet source. Furthermore, we have to extend the dimensions of our computational domain to avoid the described geometrical artefacts.
Online material
Appendix A: Extracted line widths for all models and runs
Here we present the extracted line widths derived from synthetic [OI] λ6300 images for all models, runs, and inclinations for the sake of completeness.
 |
Fig. A.1 Jet widths in AU derived from synthetic [OI] images as a function of distance from the source in model ADO and for runs (500, 600, 0.2), (500, 600, 0.5), (500, 1000, 0.5), (500, 1000, 0.8). Overlaid are the data points of Fig. 1. |
Appendix B: Velocities of the jet derived from the synthetic position-velocity diagrams
Velocities of the jet derived from the synthetic position-velocity diagrams for model ADO.
Acknowledgments
The authors would like to thank the referee for suggestions and comments that improved this paper.
References
- Anderson, J. M., Li, Z.-Y., Krasnopolsky, R., & Blandford, R. D. 2003, ApJ, 590, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Bacciotti, F., & Eislöffel, J. 1999, A&A, 342, 717 [NASA ADS] [Google Scholar]
- Bacciotti, F., Ray, T. P., Mundt, R., et al. 2002, ApJ, 576, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S., Edwards, S., Strom, S. E., & Strom, K. M. 1990, ApJ, 354, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, F., & Ferreira, J. 2000, A&A, 353, 1115 [NASA ADS] [Google Scholar]
- Coffey, D., Bacciotti, F., Ray, T. P., et al. 2007, ApJ, 663, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Combet, C., & Ferreira, J. 2008, A&A, 479, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dougados, C. 2008, in Jets from Young Stars II: Clues from High Angular Resolution Observations, ed. F. Bacciotti, E. Whelan & L. Testi (Berlin, Heidelberg: Springer-Verlag), Lecture Notes in Physics, 742 [Google Scholar]
- Dougados, C., Cabrit, S., Lavalley, C., & Menard, F. 2000, A&A, 357, L61 [NASA ADS] [Google Scholar]
- Dougados, C., Cabrit, S., Ferreira, J., et al. 2004, Ap&SS, 293, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Eislöffel, J., & Mundt, R. 1998, AJ, 115, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 1997, A&A, 319, 340 [NASA ADS] [Google Scholar]
- Ferreira, J. 2007, in Jets from Young Stars: Models and Constraints, ed. J. Ferreira, C. Dougados & E. Whelan (Berlin Heidelberg: Springer-Verlag), Lecture Notes in Physics, 723 [Google Scholar]
- Garcia, P. J. V., Cabrit, S., Ferreira, J., & Binette, L. 2001, A&A, 377, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gracia, J., Vlahakis, N., & Tsinganos, K. 2006, MNRAS, 367, 201 (GVT06) [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Edwards, S., & Ghandour, L. 1995, ApJ, 452, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Edwards, S., & Pierson, R. 2004, ApJ, 609, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L. 2009, in Protostellar Jets in Context, ed. K. Tsinganos, T. P. Ray & M. Stute (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Jensen, E. L. N., Koerner, D. W., & Mathieu, R. D. 1996, AJ, 111, 2431 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalley-Fouquet, C., Cabrit, S., & Dougados, C. 2000, A&A, 356, L41 [NASA ADS] [Google Scholar]
- Lay, O. P., Carlstrom, J. E., & Hills, R. E. 1997, ApJ, 489, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M. 2009, in Protostellar Jets in Context, ed. K. Tsinganos, T. P. Ray, & M. Stute (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Matsakos, T., Tsinganos, K., Vlahakis, N., et al. 2008, A&A, 477, 521 (M08) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsakos, T., Massaglia, S., Trussoni, E., et al. 2009, A&A, 502, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Najita, J. R., Carr, J. S., Glassgold, A. E., & Valenti, J. A. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt & K. Keil (Tucson: University of Arizona Press), 507 [Google Scholar]
- Prato, L., Simon, M., Mazeh, T., et al. 2002, ApJ, 579, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Pyo, T.-S., Kobayashi, N., Hayashi, M., et al. 2003, ApJ, 590, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Ray, T. P., Mundt, R., Dyson, J. E., Falle, S. A. E. G., & Raga, A. C. 1996, ApJ, 468, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Ray, T. P., Dougados, C., Bacciotti, F., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt & K. Keil (Tucson: University of Arizona Press), 231 [Google Scholar]
- Stute, M., Tsinganos, K., Vlahakis, N., Matsakos, T., & Gracia, J. 2008, A&A, 491, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stute, M., Gracia, J., Tsinganos, K., & Vlahakis, N. 2010, A&A, 516, A6 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlahakis, N., & Tsinganos, K. 1998, MNRAS, 298, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahakis, N., Tsinganos, K., Sauty, C., & Trussoni, E. 2000, MNRAS, 318, 417 (V00) [NASA ADS] [CrossRef] [Google Scholar]
- Woitas, J., Ray, T. P., Bacciotti, F., Davis, C. J., & Eislöffel, J. 2002, ApJ, 580, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Zanni, C., Ferrari, A., Rosner, R., Bodo, G., & Massaglia, S. 2007, A&A, 469, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Velocities of the jet derived from the synthetic position-velocity diagrams for model ADO.
All Figures
 |
Fig. 1 Variation in jet width (FWHM) derived from [SII] and [OI] images as a function of distance from the source. Data points are from CFHT/PUEO and HST/STIS observations of DG Tau (diamonds), HN Tau (plus signs), CW Tau (squares), UZ Tau E (crosses), RW Aur (circles), HH 34 (one triangle). Data are taken from Ray et al. (2007) for distances below 200 AU and Dougados et al. (2000) beyond this distance. |
| In the text | |
 |
Fig. 2 Synthetic emission maps of the [OI] λ6300 line, convolved with a Gaussian PSF with an FWHM of 15 AU, for run (500, 1000, 0.5) and the untruncated model ADO (top) and the model SC1a with outer truncation (middle) and for run (500, 100, 0.2) and model SC3 with inner truncation (bottom). The inclinations are 30°, 40°, 60°, 70°, and 90° (from left to right). The flux is in units of erg s-1 cm-2. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but normalized by the intensity on the jet axis for each row. Also plotted is the contour line where I/Iaxis = 0.5, i.e. the position of the FWHM. |
| In the text | |
 |
Fig. 4 Top: synthetic position-velocity diagram of the [OI] λ6300 line for model SC1a, run (500, 1000, 0.8), and an inclination of 40°, where we assumed a distance to the jet of 150 pc. Bottom: observed position-velocity map of DG Tau for [OI] λ6300 (black thin lines) and [NII] λ6583 (green thick lines) from Lavalley-Fouquet et al. (2000). The dynamical range is similar in both plots. |
| In the text | |
 |
Fig. 5 Jet widths in AU derived from synthetic [OI] images as a function of distance from the source in model SC1c and for run (500, 1000, 0.8). Overlaid are the data points of Fig. 1. |
| In the text | |
 |
Fig. 6 Jet widths in AU derived from synthetic [OI] images as a function of distance from the source in model SC3 and for run (500, 100, 0.2). Overlaid are the data points of Fig. 1. |
| In the text | |
 |
Fig. 7 Normalized emission map of the [OI] λ6300 line for a computational domain with constant density and temperature. The inclination is 40° (left) and 90° (right). Also plotted is the contour line where I/Iaxis = 0.5, i.e. the position of the FWHM. |
| In the text | |
 |
Fig. 8 Best-fit model for DG Tau: model SC1a, run (500, 1000, 0.8), and inclination of 40°. The red part is not reliable due to the geometric effect discussed in Sect. 3.2. |
| In the text | |
 |
Fig. 9 Best-fit model for CW Tau: model SC1c, run (500, 1000, 0.8), and inclination of 60°. The red part is not reliable due to the geometric effect discussed in Sect. 3.2. |
| In the text | |
 |
Fig. A.1 Jet widths in AU derived from synthetic [OI] images as a function of distance from the source in model ADO and for runs (500, 600, 0.2), (500, 600, 0.5), (500, 1000, 0.5), (500, 1000, 0.8). Overlaid are the data points of Fig. 1. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but in model SC1a. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1, but in model SC1b. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1, but in model SC1c. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.1, but in model SC1d. |
| In the text | |
 |
Fig. A.6 Same as Fig. A.1, but in model SC1e. |
| In the text | |
 |
Fig. A.7 Same as Fig. A.1, but in model SC1f. |
| In the text | |
 |
Fig. A.8 Same as Fig. A.1, but in model SC1g. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


