EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 538 (February 2012) A&A, 538 (2012) A152 Full HTML
Free Access
Issue
A&A
Volume 538, February 2012
Article Number A152
Number of page(s) 10
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201117946
Published online 17 February 2012

© ESO, 2012

1. Introduction

Since the first detection of an extragalactic H2O maser towards M 33 (Churchwell et al. 1977), 22 GHz (λ = 1.3 cm) H2O maser surveys have covered  ~3000 galaxies, with reported detections from 85 objects (e.g., Zhang et al. 2006; Braatz & Gugliucci 2008; Greenhill et al. 2008; Darling et al. 2008). With respect to their physical origin, these maser sources can be subdivided into two classes: (1) those associated with star-forming regions (hereafter SF-masers), which are similar to the stronger sources in the Galaxy; and (2) those associated with active galactic nuclei (hereafter AGN-masers). The majority of the extragalactic H2O masers are believed to belong to the latter class, mainly because among the small number of interferometrically studied sources, all of the masers with isotropic luminosities  >10 L⊙ are found to be associated with AGN. With their exceptional luminosities, far surpassing those of any galactic maser, these molecular lighthouses are termed “megamasers”. Among AGN maser sources, a large portion (~40%) has been identified as disk maser candidates (Kondratko et al. 2006; Zhang et al. 2010). Their maser spots are located within the central few pc, forming parts of a molecular accretion disk around the nuclear engine. In addition to “systemic” features, “high velocity” components are also found, representing the approaching and receding edges of the disks, which are viewed approximately edge-on. Systematic studies of such disk masers have become a promising tool for addressing a wide variety of astrophysical problems, using both high resolution VLBI (Very Long Baseline Interferometry) imaging and spectral line monitoring of maser spots (Braatz et al. 2009).

Observations show that H2O megamasers are mostly associated with the nuclear regions of Seyfert 2 and LINER (low ionizing nuclear emission regions) galaxies, which are commonly heavily obscured (gas column density NH > 1023 cm-2) (Braatz et al. 1997; Zhang et al. 2006; Greenhill et al. 2008). AGN are considered to be the ultimate energy source of H2O megamasers (e.g., Lo 2005), so we may expect some kind of correlation between maser power and the nuclear radio luminosity (for its definition, see Sect. 2.1). On the one hand, the nuclear radio continuum luminosity has been established as a useful isotropic luminosity indicator of AGN power (Giuricin et al. 1990; Diamond-Stanic et al. 2009). On the other, H2O line emission may be produced by amplifying the nuclear radio emission, which can provide “seed” photons for masers located on the front side of the nucleus or an associated nuclear jet (Braatz et al. 1997; Henkel et al. 1998).

In this paper, we compile radio measurements from the literature for the entire sample of reported H2O maser host galaxies with luminosity distances D > 0.5 Mpc in order to investigate their radio properties and probe possible correlations between H2O megamasers and the nuclear radio emission. The maser sample, as well as an unbiased comparison sample with no detected 22 GHz H2O emission but good upper limits, is presented in Sect. 2. In Sect. 3, we analyze their radio properties. Their properties are compared, emphasizing 6 cm and 20 cm nuclear radio flux distributions and spectral indices. Furthermore, correlations between maser emission and nuclear radio power are explored. These results are summarized in Sect. 4.

Table 1

A comparison of nuclear radio luminosities of maser and nonmaser galaxies (for details, see Sect. 3.2).

2. Samples and data

2.1. The H2O maser sample

All 85 galaxies with luminosity distances D > 0.5 Mpc and reported H2O maser emission are presented in Table 2. They include 66 AGN-masers, ten SF-masers (isotropic luminosity LH2O < 10   L⊙, known as “kilomasers”), and additional low-luminosity sources, which are still awaiting interferometric observations to identify their nature (for details of their classification and activity types, see Zhang et al. 2010). For radio continuum measurements of this maser galaxy sample, we have used the NASA Extragalactic Database (NED; http://nedwww.ipac.caltech.edu), the NVSS (NRAO VLA Sky Survey), and FIRST (Faint Images of the Radio Sky at Twenty-centimeters) catalogs. Since H2O maser galaxies are mostly Seyfert 2s or LINERs, their radio continuum tends to be weak and is dominated by the circumnuclear region (Braatz et al. 1997). Most sources have been measured at 6 cm and 20 cm, while just a few sources have been observed at other wavelengths. Therefore we have collected the 6 cm and 20 cm data and use them as nuclear radio output.

The nuclear radio properties of maser host galaxies were already studied by Braatz et al. (1997). There were only 16 maser sources known at that time and just nine sources with available radio continuum data, inhibiting any detailed statistical analysis. Therefore, the current maser sample provides a drastic improvement. In Braatz et al. (1997), 6 cm VLA data measured in the A and B configurations were taken to ensure that only the small-scale flux was considered. For our current larger sample, there are no VLA observations for some sources and many sources were observed by different telescopes with different beam size. When multiple data were available, measurements were selected according to the following criteria.

  • (1)

     Observations with smaller beam sizes arepreferred, in order to isolate the nuclear from the large scaleemission of the host galaxy (Diamond-Stanic et al.2009). This might cause missing flux when selectinginterferometric data. However, the best VLA resolution at6 cm is  ~0.4 arcsec, which corresponds to a linear size of  ~20 pc for a source at distance 10 Mpc. This size and the corresponding highest VLA resolution at 20 cm,  ~2 arcsec, is much larger than that of the maser spots observed on sub-pc scales (e.g., Miyoshi et al. 1995; Reid et al. 2009) and that of potentially associated nuclear continuum sources.

  • (2)

    Both 6 cm and 20 cm data should have similar beam size. The most stringent requirement would be that data for a given source were obtained from high resolution VLA observations. Six centimeter data from the B configuration and 20 cm data from the A configuration would be optimal.

Overall, we got 6 cm data for 57 sources and 20 cm data for 79 sources. There are 55 sources with 6 cm and 20 cm data, including 41 sources with both flux densities from the same telescope. For those 41 sources, 27 have been measured with the VLA at both frequencies. Among these, 11 belong to the ideal case, with A-array 20 cm and B-array 6 cm data. For those sources with 6 cm and 20 cm data from different telescopes, the 20 cm data were taken from the VLA-D array and the 6 cm data from the Green Bank 91 m (7), the Parkes 64 m (6), or the MERLIN array (1). All data with the corresponding telescopes and, if necessary, the configuration, are presented in Table 2. Below, these data are used determine the nuclear radio fluxes and corresponding luminosities.

2.2. The nonmaser sample

Table 2

Radio properties of H2O maser host galaxies.*

As mentioned before, the detection rate of extragalactic H2O masers is rather low (commonly  <10%, e.g., Henkel et al. 2005), and it is reasonable to ask whether H2O maser galaxies have “special” intrinsic properties, relative to apparently similar galaxies without detected maser emission. Diamond-Stanic et al. (2009) have compiled a complete sample of 89 nearby Seyfert galaxies, drawn from the unbiased revised Shapley-Ames catalog (with a limiting magnitude of BT < 13 mag) (Maiolino & Rieke 1995; Ho et al. 1997). This sample is unique in that it covers mostly Seyfert 2s (like our H2O maser sample), that it is complete, that the galaxies are rather nearby, and that sensitive H2O measurements have been obtained toward all these targets. The distance of all those sources is less than 200 Mpc, which is comparable to that of our H2O maser galaxies (except for the two quasar sources, SDSS J0804+3607 with z ~ 0.66 and MG J0414+0534 with z ~ 2.64, detected by Barvainis & Antonucci 2005; and Impellizzeri et al. 2009, respectively).

There are 19 maser and 70 nonmaser sources in the Seyfert comparison sample, the latter providing a useful comparison. This nonmaser sample (its sources have been targeted in H2O maser surveys, but have not been detected) includes 16 Seyfert 1s (type 1–1.5) and 54 Seyfert 2s (type 1.8–2.0), which is similar to our maser-host Seyfert sample (most Seyfert 2s, just five Seyfert 1s (type 1–1.5), NGC 2782, UGC 5101, NGC 235A, NGC 4051 and NGC 4151). Upper limits to their maser luminosity were estimated from the rms value (taken from the Hubble Constant Maser Experiment (HoME1) and the Megamaser Cosmology Project (MCP2)), assuming a characteristic linewidth of a spectral feature of 20 km s-1 and a 5σ detection threshold (e.g., Bennert et al. 2009).

The 6 cm and 20 cm radio flux densities are collected from the literature. There are 61 sources with 6 cm data and 32 sources with 20 cm data. For complementary 20 cm data, the NVSS and FIRST catalogs were also used, and we found additional 20 cm data for 17 sources and upper limits for 12 sources (with relatively low angular resolution). The nonmaser sample and corresponding data are presented in Table 3.

3. Analysis and discussion

3.1. Radio properties of H2O maser galaxies

For our H2O maser galaxies with available data, the distributions of nuclear radio luminosities at 6 cm and 20 cm are plotted in Fig. 1. The upper panel shows the histogram of 6 cm luminosities for both the entire sample of 57 sources and the subsample of 43 AGN-masers. For the entire sample, the distribution of log L6 cm peaks around 29 (here and throughout the article, L6 cm and L20 cm are given in units of erg s-1 Hz-1) and the mean value is 28.8 ± 0.2 (Throughout the paper, given errors are the standard deviation of the mean). The mean values are 29.0 ± 0.2, 27.2 ± 0.4, and 28.5 ± 0.3 for AGN-masers, SF-masers, and masers without known type, respectively. The distribution of the 20 cm luminosity is presented in the lower panel, also for all of the 79 sources and for the subsample of 56 AGN-masers, respectively. The mean value of log L20 cm is 29.1 ± 0.2 for the entire sample and the mean values are 29.3 ± 0.2, 27.4 ± 0.5, and 28.9 ± 0.2 for AGN-masers, SF-masers, and masers without known type, respectively. The subsample of AGN-disk-maser galaxies (29 sources; not shown separately, but see Sect. 3.3) shows nuclear radio luminosities consistent with those of the entire AGN-sample. Comparing the subsamples of AGN-masers and SF-masers, a striking difference can be found between their luminosities at both 6 cm and 20 cm, i.e., AGN-masers are detected toward galaxies with higher nuclear radio luminosities. This important point is discussed further in Sect. 3.3.

Table 3

Radio properties of Seyfert galaxies without detected H2O maser.*

To study the radio properties of our H2O maser galaxies, radio spectral indices were derived for those sources for which 6 cm and 20 cm flux densities were measured. Assuming a power-law dependence for the continuum flux density given by S ∝ ν−α, the spectral index can be calculated by

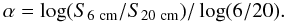The spectral index (α) is obtained for 55 sources including 42 targets hosting AGN-masers, six objects exhibiting SF-masers, and seven sources with unknown maser type (see the second last column of Table 2). Figure 2 plots the distribution of the spectral index for those 55 maser sources and the subsamples of AGN- and SF-masers. The spectral index for the majority of sources lies in the 0.5–1.0 bin, with a mean value of 0.66 ± 0.07. Since H2O maser emission is mostly detected in Seyfert 2 systems, it agrees with the fact that Seyfert 2 galaxies are always steep spectrum sources. If targets with spectral index α ≥ 0.3 are defined as steep spectrum sources (Ho & Ulvestad 2001), 80% (44/55) of our maser sources belong to this category. For the subsamples of AGN-masers and SF-masers, the mean spectral indices are 0.66 ± 0.07 and 0.61 ± 0.27, respectively. No significant difference between both distributions can be found. However, in view of the small number of SF-masers, statistical constraints are not very stringent. In addition, we note that the spectral index might be overestimated for those 12 sources with 6 cm data from single-dish telescopes and 20 cm data from the VLA-D array. Eliminating these sources, the mean spectral index for the remaining 32 AGN-maser sources is 0.65 ± 0.07, while the three remaining SF sources do not justify a statistical evaluation. For the 11 sources with “optimal” data (9 AGN-masers and 2 targets of unknown type observed at 6 cm with the VLA-B and at 20 cm with the VLA A-array), the continuum appears to be flatter with a mean index value of 0.38 ± 0.12.

3.2. Comparison of radio properties of maser and nonmaser galaxies

For the entire nonmaser sample (see Sect. 2.2; all targets are Seyfert galaxies), the mean log L6 cm and log L20 cm luminosities (in units of erg s-1 Hz-1) are 27.7 ± 0.2 and 28.2 ± 0.2, respectively. For all our maser Seyferts, the mean values are log L6 cm = 28.8 ± 0.2 and log L20 cm = 29.1 ± 0.1, respectively (see Table 1). The difference in nuclear radio luminosity between nonmaser and maser Seyferts is obvious. Considering that extragalactic H2O masers are mostly found in Seyfert 2s, we can further compare the nuclear radio luminosities between the nonmaser Seyfert 2 subsample (36 sources) and our maser Seyfert 2 sources (41 sources). The mean values of log    L6 cm and log    L20 cm (again in units of erg s-1 Hz-1) are 27.5 ± 0.2 and 28.0 ± 0.2 for nonmaser Seyfert 2s and 28.8 ± 0.2 and 29.1 ± 0.2 for maser Seyfert 2s, respectively. It shows the same trend, i.e., maser Seyfert 2s have higher nuclear radio luminosities than the nonmaser Seyfert 2s. The difference seems to amount to slightly more than an order of magnitude, roughly corresponding to factors of  ~10–20.

To visualize the difference, we plot 6 cm versus 20 cm luminosities for both the nonmaser Seyfert sample and our maser Seyfert sample (Fig. 3). The trend is apparent. Most nonmaser sources are distributed in the lower left, while maser galaxies are mostly located in the central and upper right regions. However, there is also overlap, and there are a few maser Seyferts with low nuclear radio luminosities. This indicates that there is no strict radio continuum luminosity threshold for individual sources.

So far, we have not yet discussed a potential distance bias for the samples considered here. If measurements are very sensitive and signals strong, different distances should not play a major role with respect to detection rates. If one is, however, near the limit of sensitivity, typical luminosities of observed and classified sources should increase with the distance squared. While the average distances of the maser and nonmaser Seyfert samples show a similar range (the two distant quasars detected in H2O by Barvainis & Antonucci 2005; and Impellizzeri et al. 2009 do not belong to any of the Seyfert samples), we find for the mean values 66.4 ± 7.5 and 31.5 ± 2.6 Mpc, respectively. Therefore, this may introduce a bias of order (66.4/31.5)2 ~ 4. Even fully accounting for this effect, however, a luminosity ratio of order four still remains between the maser and the nonmaser samples.

thumbnail Fig. 1

The luminosity distributions of the 6 cm (log L6 cm, upper panel) and 20 cm (log L20 cm, lower panel) continuum emission in units of erg s-1 Hz-1 for the entire maser sample, the AGN-maser subsample (shaded regions), the star formation (SF-) maser subsample (diagonal lines), and masers of unknown type (white).

In the nonmaser sample, there is just one source with distance  >71 Mpc, while there are 20 such sources in our maser Seyfert sample. Eliminating all sources with distances  >71 Mpc, the mean distances of the maser and nonmaser sample become similar (31.9 ± 3.4 Mpc versus 29.9 ± 2.1 Mpc). The mean luminosities are then log L6 cm = 28.4 ± 0.3 and log L20 cm = 28.7 ± 0.2 for our maser sample and log L6 cm = 27.7 ± 0.2 and log L20 cm = 27.9 ± 0.2 for the nonmaser sample (units: erg s-1 Hz-1). The difference in their nuclear radio luminosities is still apparent (ratios of about 5 and 6 at 6 cm and 20 cm, respectively).

The luminosity ratio between the 16 H2O detected galaxies (three additional sources show SF-related H2O or H2O emission of unknown type) and the 70 H2O undetected sources in the entire Seyfert comparison sample is not affected by the Malmquist bias. Both subsamples have similar mean distances (27.5 ± 7.7 and 31.5 ± 2.6 Mpc, respectively). The mean nuclear radio luminosity of the 16 sources comprising the maser subsample (log L6 cm = 28.2 ± 0.3 and log L20 cm = 28.4 ± 0.2) is about two to three times higher than that of the 70 non-detections. The Seyfert 2 sources among these two subsamples include 15 AGN-related H2O detections and 54 non-detections with mean distances of 28.5 ± 7.4 Mpc and 29.8 ± 2.3 Mpc, respectively. The mean luminosities on an erg s-1 Hz-1 scale are log    L6 cm = 28.2 ± 0.3 and log    L20 cm = 28.5 ± 0.3 for the first and log    L6 cm = 27.5 ± 0.2 and log    L20 cm = 28.0 ± 0.2 for the second sample. The luminosity ratio is of order four (five at 6 cm and three at 20 cm). With all this evidence we thus conclude that a nuclear radio continuum luminosity ratio greater than unity is real. For a summary, see Table 1.

thumbnail Fig. 2

Number distribution of the radio spectral index between 6 cm and 20 cm. The shaded region of the histogram represents the subsample of AGN masers. The area with diagonal lines denotes SF-masers, while the remaining masers are of unknown type.

thumbnail Fig. 3

Distribution of the 6 cm against the 20 cm luminosity of both the maser (filled symbols) and the nonmaser Seyfert sample (open symbols). Circles and triangles show Seyfert 2s and Seyfert 1s, respectively. Units for L6 cm and L20 cm are erg s-1 Hz-1.

thumbnail Fig. 4

Distribution of the 6 cm (log L6 cm, upper panel) and 20 cm luminosities (log L20 cm, lower panel) in units of erg s-1 Hz-1 for the sample of nearby Seyfert galaxies without detected maser emission and its subsample of Seyfert 2s (shaded regions). For comparison, the distributions for our maser Seyfert 2s are also presented (areas filled with diagonal lines).

To visualize this result, 6 cm and 20 cm luminosity distributions are plotted for the entire nonmaser sample and its subsample comprised of Seyfert 2s in Fig. 4. For comparison, the luminosity distributions for our maser Seyfert 2s are also presented. The differences are significant for the two Seyfert 2 samples and a Kolmogorov-Smirnov (KS) test shows probabilities of 0.005% at 6 cm and 0.01% at 20 cm that both Seyfert 2 samples are drawn from the same parent population.

Similar to our maser sample, spectral indices were calculated for those 48 sources of the comparison sample (including 16 sources with 20 cm data from the NVSS or FIRST) with both 6 cm and 20 cm flux density data. The mean values of the index are 0.84 ± 0.12 and 0.83 ± 0.12 for the entire sample (48 sources) and for the Seyfert 2 subsample (36 sources). However, as mentioned before, 16 sources have low-resolution 20 cm data (from NVSS or FIRST) and high-resolution 6 cm data. This results in overestimated spectral indices for these sources, even including extremely high values (e.g., 3.47 for NGC 1097 and 2.89 for NGC 2992). After excluding those 16 sources, the mean values become 0.52 ± 0.09 for the entire sample (32 sources) and 0.55 ± 0.10 for the Seyfert 2 subsample (24 sources). Figure 5 plots the distribution of the spectral index for the nonmaser Seyfert sample (without including those 16 sources). Compared with maser host galaxies (dashed lines in Fig. 5), no significant difference can be found between the spectral index distributions. A KS test results in a probability of 79.2% that maser and nonmaser Seyfert 2 samples are drawn from the same parent distribution.

thumbnail Fig. 5

The distributions of the spectral index between 6 cm and 20 cm for the nearby Seyfert sample without detected maser emission and its subsample of Seyfert 2s (shaded regions). For comparison, the distribution of Seyfert 2s with maser detections is also presented (areas filled with diagonal lines).

thumbnail Fig. 6

H2O maser luminosities (logarithmic scale, in L⊙) against the nuclear radio luminosity (logarithmic scale, in erg s-1 Hz-1) of maser host galaxies at 6 cm (upper panel) and 20 cm (lower panel). Squares, triangles, and circles represent AGN-masers, star formation-masers, and masers of unknown type, respectively. Pentacles inside squares indicate potential or confirmed disk-maser sources, which are presented in boldface in Table 2. The solid lines show linear fits to the AGN-maser sources.

3.3. H2O maser power vs. nuclear radio power

Here we study possible correlations between H2O maser line strength and AGN power. For the SF-masers alone we do not expect a correlation between the nuclear radio emission and maser power, since these maser spots are found in star-forming regions well displaced from the nuclei.

Maser luminosities, assuming here and elsewhere isotropic emission, and nuclear radio continuum fluxes are given in Table 2. In Fig. 6, these maser luminosities are plotted against 6 cm (upper panel) and 20 cm continuum luminosities (lower panel). For both panels, a correlation can be found, i.e., rising maser luminosity with increasing nuclear radio luminosity. SF-maser sources (LH2O < 10 L⊙) tend to be located in the lower left and AGN-masers (mostly LH2O > 10 L⊙) in the upper right hand corners of Fig. 6, i.e., AGN-maser galaxies tend to have higher nuclear radio luminosities relative to SF-masers (see also Sect. 3.2).

For the 6 cm continuum and 1.3 cm AGN-maser line luminosity (upper panel of Fig. 6, 41 sources), a weak correlation is apparent. A linear least-square fit shows log LH2O = (−7.7 ± 3.1) + (0.3 ± 0.1)log L6 cm, with Spearman’s rank correlation coefficient R = 0.51 and a chance probability P = 5.1 × 10-4. For the 20 cm continuum and maser line luminosities (lower panel, 61 sources), our linear fitting gives log LH2O = (−7.3 ± 2.7) + (0.3 ± 0.1)log    L20 cm, with the fitting parameters R = 0.41 and P = 1.0 × 10-3. As already mentioned, for many sources, the 6 cm and 20 cm data were obtained with different beam sizes (for details, see Table 2). It is thus necessary to consider this effect on the correlation. For the nine AGN-masers among those 11 sources with “ideal” observational data (i.e., 6 cm data from the VLA-B and 20 cm data from the VLA-A configuration), the correlation becomes log LH2O = (−8.1 ± 6.0) + (0.3 ± 0.2) log    L6 cm, with the fitting parameters R = 0.51 and P = 0.16. While they are too few sources for a reliable fit, the tendency toward higher continuum flux densities associated with more luminous masers is still apparent.

thumbnail Fig. 7

H2O maser luminosity (logarithmic scale, in L⊙) versus 20 cm luminosity (logarithmic scale in erg s-1 Hz-1) for AGN-masers (squares). The solid (red) and the dashed (black) lines show linear fits without and with considering the Malmquist effect, respectively. The non-detection sample is also plotted displaying the upper 5σ limits (see Sect. 2.2) of the maser luminosity (triangles).

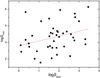thumbnail Fig. 8

Integrated H2O flux densities (logarithmic scale, in Jy km s-1) versus 6 cm luminosity (logarithmic scale in Jy) for AGN-masers (squares). The red line shows a very tentative linear fit.

As a subsample of the AGN maser sources, disk maser candidates are also shown in Fig. 6. These masers originate in the innermost few parsec, which might suggest a particularly close connection between their maser emission and the AGN-power. A correlation seems again to be apparent (R = 0.37 and P = 0.13), but the small number of disk-maser sources mean the statistical evidence is still quite weak.

We have not yet considered the Malmquist bias caused by different mean distances of galaxies comprising the samples for the luminosity-luminosity correlations. Thus we reanalyzed the relation between nuclear radio continuum and maser luminosities, using the method of partial correlation coefficients (e.g., Darling & Giovanelli 2002; Kandalyan & Al-Zyout 2010). Since both luminosities are correlated with the variable distance, the correlations should be subtracted when we analyze the correlation between two luminosities. This type of correlation is known as a partial correlation coefficient. Figure 7 plots H2O maser luminosity against the 20 cm nuclear radio luminosity for our AGN-maser subsample, and shows linear fits without and with considering the Malmquist effect. The correlation becomes weaker after taking the Malmquist effect into account. The correlation coefficient changes from  ~0.3 to  ~0.2 and the fitting becomes flatter with a slope of  ~0.2 instead of  ~0.3.

For comparison, our non-detection sample with upper limits to the maser luminosity is also presented in Fig. 7. The upper limits were obtained from the individual rms values of H2O maser data (see details in Sect. 2.2 and Table 3). A few overlaps in maser luminosity can be found, along with H2O undetected sources located in the lower left hand region well below the fitting line. This is consistent with the trend described in Sect. 3.2, i.e., maser activity tends to weaken with decreasing nuclear radio power.

For the AGN-maser subsample, we also correlated integrated line and continuum flux densities (for the 6 cm continuum, see Fig. 8). A linear fit yields log (SH2O × ΔV) = (0.3 ± 0.1) log    S6 cm + (2.8 ± 0.3) (41 sources) and log (SH2O × ΔV) = (0.2 ± 0.1)log    S20 cm + (3.0 ± 0.2) (56 sources), respectively, with Spearman’s rank coefficients amounting to R = 0.32 and 0.19 and chance probabilities of P = 0.03 and 0.16.

There may be a variety of causes for our statistically marginal correlations between maser and nuclear radio continuum. In the case of unsaturated H2O maser emission only a part of the nuclear continuum may be amplified (see, e.g., the situation in NGC 4258, Herrnstein et al. 1998). For saturated maser emission, no direct correlation with the background continuum will appear. In addition, the AGN-maser sample presented here is inhomogeneous. It includes disk masers and jet masers (masers related to the interaction of nuclear radio jets with ambient molecular clouds or to the amplification of the jet’s seed photons by suitably located foreground clouds), and perhaps also additional so far not yet identified maser types. The absorbing column densities along the lines of sight also differ. Among 31 AGN-masers with available data, about 60% are Compton-thick (Zhang et al. 2010). Moreover, 6 cm or 20 cm measurements as indicators of intrinsic nuclear power may introduce some uncertainties. The observed nuclear radio luminosity may depend on the geometry of the system, such as shielding by the torus. And large uncertainties may be produced from isotropically calculated H2O maser luminosities, since maser beam angles are often poorly constrained and may be quite small due to source geometry and propagation effects (Kartje et al. 1999). Lastly, uncertainties in the nuclear radio luminosity can be introduced from radio data including measurements with different resolution and sensitivity. In view of all these uncertainties, the presence of a correlation would hint at the possibility that a higher degree of activity may be able to heat up a larger volume to temperatures suitable for 22 GHz H2O maser emission (Neufeld et al. 1994). More detailed interferometric studies are therefore required to obtain a larger sample of “ideal” data for deeper insight.

4. Summary

In this paper, the entire extragalactic 22 GHz H2O maser sample published so far has been studied, with the notable exception of the Magellanic Clouds. Radio continuum data were analyzed to better understand the properties of the AGN associated with H2O masers. For comparison, a complementary Seyfert sample without detected maser emission was also compiled. The main results are summarized in the following.

  • (1)

    For the entire H2O Seyfert maser sample, the mean 6 cm and 20 cm nuclear radio luminosities are log    L6 cm = 28.8 ± 0.2 and log    L20 cm = 29.1 ± 0.2, respectively (L6 cm, L20 cm in units of erg s-1Hz-1). For the comparison sample of Seyferts without detected maser emission, the mean values of log L6   cm and log L20 cm are 27.7 ± 0.2 and 28.2 ± 0.2, respectively. Comparisons of corresponding subsamples also show the difference, i.e., H2O maser sources tend to be more luminous than nonmaser sources. After considering a potential distance bias, we converged on a luminosity ratio of order five.

  • (2)

    For the H2O maser sample and the sample of Seyferts devoid of detected H2O emission, spectral indices were derived from the 6 cm and 20 cm data. There is no significant difference for the distributions of the spectral indices between our H2O maser sources and the H2O undetected sources. The mean value of the index is 0.66 ± 0.07 for our H2O maser sample and 0.52 ± 0.09 for the comparison sample.

  • (3)

    For the subsample of AGN-masers, a correlation seems to be present between H2O maser isotropic luminosity and nuclear radio power of the host galaxy. However, the correlation is significantly affected by the Malmquist bias so that no definite conclusion can be drawn right now.

  • (4)

    Based on the results outlined above, the nuclear radio luminosity may provide a clear signature of AGN-masers, possibly providing suitable constraints for future H2O megamaser surveys.

Acknowledgments

This work is supported by the Natural Science Foundation of China (No. 11043012, 11178009) and China Ministry of Science and Technology under State Key Development Program for Basic Research (2012CB821800). We made use of the NASA Astrophysics Data System Bibliographic Services (ADS) and the NASA/IPAC extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with NASA.

References

  1. Baan, W. A., & Klöckner, H. R. 2006, A&A, 449, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Barvainis, R., & Antonucci, R. 2005, ApJ, 628, L89 [NASA ADS] [CrossRef] [Google Scholar]
  3. Becker, R. H., White, R. L., & Edwards, A. L. 1991, ApJS, 75, 229 [NASA ADS] [CrossRef] [Google Scholar]
  4. Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bennert, N., Barvanis, R., Henkel, C., & Antonucci, R. 2009, ApJ, 695, 276 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bordalo, V., Plana, H., & Telles, E. 2009, ApJ, 696, 1668 [NASA ADS] [CrossRef] [Google Scholar]
  7. Braatz, J. A., & Gugliucci, N. E. 2008, ApJ, 678, 96 [NASA ADS] [CrossRef] [Google Scholar]
  8. Braatz, J. A., Wilson, A. S., & Henkel, C. 1997, ApJS, 110, 321 [NASA ADS] [CrossRef] [Google Scholar]
  9. Braatz, J. A., Condon, J. J., Henkel, C., Lo, K.-Y., & Reid, M. J. 2009, in Astro2010: The Astronomy and Astrophysics Decadal Survey, Science White Papers, No. 23 [Google Scholar]
  10. Bransford, M. A., Appleton, P. N., Heisler, C. A., Norris, R. P., & Marston, A. P. 1998, ApJ, 497, 133 [NASA ADS] [CrossRef] [Google Scholar]
  11. Churchwell, E., Witzel, A., Huchtmeier, W., et al. 1977, A&A, 54, 969 [NASA ADS] [Google Scholar]
  12. Condon, J. J. 1983, ApJS, 53, 459 [NASA ADS] [CrossRef] [Google Scholar]
  13. Condon, J. J., Helou, G., Sanders, D.B. & Soifer, B.T. 1996, ApJS, 103, 81 [NASA ADS] [CrossRef] [Google Scholar]
  14. Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
  15. Condon, J. J., Cotton, W. D., & Broderick, J. J. 2002, AJ, 124, 675 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cooper, N. J., Lister, M. L., & Kochanczyk, M. D. 2007, ApJS, 171, 376 [NASA ADS] [CrossRef] [Google Scholar]
  17. Darling, J., Brogan, C., & Johnson, K. 2008, ApJS, 685, 39 [NASA ADS] [CrossRef] [Google Scholar]
  18. Diamond-Stanic, A. M., Rieke, G. H., & Rigby, J. R. 2009, ApJ, 698, 623 [NASA ADS] [CrossRef] [Google Scholar]
  19. Filho, M. E., Barthel, P. D., & Ho, L. C. 2006, A&A, 451, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gallimore, J. F., Axon, D. J., O’Dea, C. P., Baum, S. A., & Pedlar, A. 2006, AJ, 132, 546 [NASA ADS] [CrossRef] [Google Scholar]
  21. Giuricin, G., Mardirossian, F., Mezzetti, M., & Bertotti, G. 1990, ApJS, 72, 551 [NASA ADS] [CrossRef] [Google Scholar]
  22. Greenhill, L. J., Tilak, A., & Madejski, G. 2008, ApJ, 686, L13 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gregory, P. C., & Condon, J. J. 1991, ApJS, 75, 1011 [NASA ADS] [CrossRef] [Google Scholar]
  24. Griffith, M. R., Wright, A. E., Burke, B. F., & Ekers, R. D. 1995, ApJS, 97, 347 [NASA ADS] [CrossRef] [Google Scholar]
  25. Guo, Q., Zhang, J. S., & Fan, J. H. 2009, IJMPD, 1809, 1367 [NASA ADS] [CrossRef] [Google Scholar]
  26. Haschick, A. D., Baan, W. A., Schneps, M. H., et al. 1990, ApJ, 356, 149 [NASA ADS] [CrossRef] [Google Scholar]
  27. Henkel, C., Wang, Y.-P., Falcke, H., Wilson, A. S., & Braatz, J. A. 1998, A&A, 335, 463 [NASA ADS] [Google Scholar]
  28. Henkel, C., Peck, A. B., Tarchi, A., et al. 2005, A&A, 436, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Herrnstein, J. R., Greenhill, L. J., Moran, J. M., et al. 1998, ApJ, 497, L69 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ho, L. C., & Ulvestad, J. S. 2001, ApJS, 133, 77 [NASA ADS] [CrossRef] [Google Scholar]
  31. Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997, ApJS, 112, 31 [Google Scholar]
  32. Impellizzeri, C. M. V., McKean, J. P., Castangia, P., et al. 2008, Nature, 456, 927 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  33. Kandalyan, R. A., & Al-Zyout, M. 2010, Astrophys., 53, 475 [Google Scholar]
  34. Kartje, J. F., Königl, A., & Elitzur, M. 1999, ApJ, 513, 180 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kobulnicky, H. A., & Johnson, K. E. 1999, ApJ, 527, 154 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kondratko, P. T., Greenhill, L. J., & Moran, J. M. 2006, ApJ, 638, 100 [NASA ADS] [CrossRef] [Google Scholar]
  37. Lo, K. Y. 2005, ARA&A, 43, 625 [NASA ADS] [CrossRef] [Google Scholar]
  38. Maiolino, R., & Rieke, G. H. 1995, ApJ, 454, 95 [NASA ADS] [CrossRef] [Google Scholar]
  39. Miyoshi, M., Moran, J., Herrnstein, J., et al. 1995, Nature, 373, 127 [NASA ADS] [CrossRef] [Google Scholar]
  40. Morganti, R., Tsvetanov, Z. I., Gallimore, J., & Allen, M. G. 1999, A&AS, 137, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Neff, S. G., & Hutchings, J. B. 1992, ApJ, 103, 1746 [Google Scholar]
  42. Neff, S. G., Ulvestad, J. S., & Teng, S. H. 2004, ApJ, 611, 186 [NASA ADS] [CrossRef] [Google Scholar]
  43. Neufeld, D. A., Maloney, P. R., & Conger, S. 1994, ApJ, 436, L127 [NASA ADS] [CrossRef] [Google Scholar]
  44. Oosterloo, T. A., Morganti, R., Sadler, E. M., van der Hulst, T., & Serra, P. 2007, A&A, 465, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Reid, M. J., Braatz, J. A., Condon, J. J., et al. 2009, ApJ, 695, 287 [NASA ADS] [CrossRef] [Google Scholar]
  46. Sadler, E. M., Slee, O. B., Reynolds, J. E., & Roy, A. L. 1995, MNRAS, 276, 1373 [NASA ADS] [Google Scholar]
  47. Sandqvist, A., Joersaeter, S., & Lindblad, P. O. 1995, A&A, 295, 58 [Google Scholar]
  48. Schmitt, H. R., Ulvestad, J. S., Antonucci, R. R. J., & Kinney, A. L. 2001, ApJS, 132, 199 [NASA ADS] [CrossRef] [Google Scholar]
  49. Slee, O. B., Sadler, E. M., Reynolds, J. E., & Ekers, R. D. 1994, MNRAS, 269, 928 [NASA ADS] [CrossRef] [Google Scholar]
  50. Tarchi, A., Castangia, P., Henkel, C., Surcis, G., & Menten, K. M. 2011, A&A, 525, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Taylor, G. B., Peck, A. B., Henkel, C., et al. 2002, ApJ, 574, 88 [NASA ADS] [CrossRef] [Google Scholar]
  52. Thean, A., Pedlar, A., Kukula, M. J., et al. 2000, MNRAS, 314, 573 [Google Scholar]
  53. Ulvestad, J. S., & Wilson, A. S. 1984a, ApJ, 278, 544 [NASA ADS] [CrossRef] [Google Scholar]
  54. Ulvestad, J. S., & Wilson, A. S. 1984b, ApJ, 285, 439 [NASA ADS] [CrossRef] [Google Scholar]
  55. Ulvestad, J. S., & Wilson, A. S. 1989, ApJ, 343, 659 [NASA ADS] [CrossRef] [Google Scholar]
  56. Vila, M. B., Pedlar, A., & Davies, R. D. 1990, MNRAS, 242, 379 [NASA ADS] [CrossRef] [Google Scholar]
  57. White, R. L., & Becker, R. H. 1992, ApJS, 79, 331 [NASA ADS] [CrossRef] [Google Scholar]
  58. Wilson, A. S., Pooley, G. G., Clements, E. D., & Willis, A. G. 1980, ApJ, 237, 61 [NASA ADS] [CrossRef] [Google Scholar]
  59. Wright, A., & Otrupcek, R. 1990, PKSCAT90 [Google Scholar]
  60. Wright, A. E., Griffith, M. R., Burke, B. F., & Ekers, R. D. 1994, ApJS, 91, 111 [NASA ADS] [CrossRef] [Google Scholar]
  61. Wright, A. E., Griffith, M. R., Hunt, A. J., et al. 1996, ApJS, 103, 145 [NASA ADS] [CrossRef] [Google Scholar]
  62. Zhang, J. S., Henkel, C., Kadler, M., et al. 2006, A&A, 450, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Zhang, J. S., Henkel, C., Guo, Q., Wang, H. G., & Fan, J. H. 2010, ApJ, 708, 1528 [NASA ADS] [CrossRef] [Google Scholar]
  64. Zijlstra, A., Pottasch, S. & Bignell, C. 1990, A&AS, 82, 273 [NASA ADS] [Google Scholar]

All Tables

Table 1

A comparison of nuclear radio luminosities of maser and nonmaser galaxies (for details, see Sect. 3.2).

In the text
Table 2

Radio properties of H2O maser host galaxies.*

In the text
Table 3

Radio properties of Seyfert galaxies without detected H2O maser.*

In the text

All Figures

thumbnail Fig. 1

The luminosity distributions of the 6 cm (log L6 cm, upper panel) and 20 cm (log L20 cm, lower panel) continuum emission in units of erg s-1 Hz-1 for the entire maser sample, the AGN-maser subsample (shaded regions), the star formation (SF-) maser subsample (diagonal lines), and masers of unknown type (white).
In the text
thumbnail Fig. 2

Number distribution of the radio spectral index between 6 cm and 20 cm. The shaded region of the histogram represents the subsample of AGN masers. The area with diagonal lines denotes SF-masers, while the remaining masers are of unknown type.
In the text
thumbnail Fig. 3

Distribution of the 6 cm against the 20 cm luminosity of both the maser (filled symbols) and the nonmaser Seyfert sample (open symbols). Circles and triangles show Seyfert 2s and Seyfert 1s, respectively. Units for L6 cm and L20 cm are erg s-1 Hz-1.
In the text
thumbnail Fig. 4

Distribution of the 6 cm (log L6 cm, upper panel) and 20 cm luminosities (log L20 cm, lower panel) in units of erg s-1 Hz-1 for the sample of nearby Seyfert galaxies without detected maser emission and its subsample of Seyfert 2s (shaded regions). For comparison, the distributions for our maser Seyfert 2s are also presented (areas filled with diagonal lines).
In the text
thumbnail Fig. 5

The distributions of the spectral index between 6 cm and 20 cm for the nearby Seyfert sample without detected maser emission and its subsample of Seyfert 2s (shaded regions). For comparison, the distribution of Seyfert 2s with maser detections is also presented (areas filled with diagonal lines).
In the text
thumbnail Fig. 6

H2O maser luminosities (logarithmic scale, in L⊙) against the nuclear radio luminosity (logarithmic scale, in erg s-1 Hz-1) of maser host galaxies at 6 cm (upper panel) and 20 cm (lower panel). Squares, triangles, and circles represent AGN-masers, star formation-masers, and masers of unknown type, respectively. Pentacles inside squares indicate potential or confirmed disk-maser sources, which are presented in boldface in Table 2. The solid lines show linear fits to the AGN-maser sources.
In the text
thumbnail Fig. 7

H2O maser luminosity (logarithmic scale, in L⊙) versus 20 cm luminosity (logarithmic scale in erg s-1 Hz-1) for AGN-masers (squares). The solid (red) and the dashed (black) lines show linear fits without and with considering the Malmquist effect, respectively. The non-detection sample is also plotted displaying the upper 5σ limits (see Sect. 2.2) of the maser luminosity (triangles).
In the text
thumbnail Fig. 8

Integrated H2O flux densities (logarithmic scale, in Jy km s-1) versus 6 cm luminosity (logarithmic scale in Jy) for AGN-masers (squares). The red line shows a very tentative linear fit.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.