| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 14 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201117872 | |
| Published online | 30 January 2012 | |
Optimization of synthetic galaxy spectra⋆
Application to ESA’s Gaia mission
1 Department of Astrophysics, Astronomy & MechanicsFaculty of Physics, University of Athens, 15783 Athens, Greece
e-mail: ankaramp@phys.uoa.gr
2 Institut d’Astrophysique de Paris, 98bis Bd Arago, 75014 Paris, France
3 Université de Paris-Sud XI, IAS, 91405 Orsay Cedex, France
4 Institute for Astronomy and Astrophysics, National Observatory of Athens, PO Box 20048, 11810 Athens, Greece
5 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
Received: 11 August 2011
Accepted: 9 November 2011
Aims. We present an optimized library of synthetic galaxy spectra that are to be used for the Gaia satellite observations of unresolved galaxies. These galaxy spectral templates are useful for the optimal performance of the unresolved galaxy classifier (UGC) software. The UGC will assign spectral classes to the observed unresolved galaxies by Gaia (classification) and estimate some of their intrinsic astrophysical parameters, which were used to create the synthetic library (parametrization). We present the new optimized synthetic library of galaxy spectra and the classification and parametrization results using the Gaia-simulated version of this library.
Methods. To optimize our synthetic library, we applied the principal component analysis (PCA) method to our synthetic spectra and studied the influence of the star-formation rate parameters on the spectra, and how these agree with some typical characteristics of the galaxy spectral types. We used support vector machines (SVM) to classify and parametrize the optimal simulated spectra.
Results. The library of synthetic galaxy spectra was optimized. In this new set of synthetic spectra, overlaps in spectral energy distributions and colors are highly suppressed, while the results of UGC classification are improved.
Key words: methods: statistical / methods: data analysis / galaxies: fundamental parameters
The optimum synthetic galaxy spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/538/A38
© ESO, 2012
1. Introduction
ESA’s cornerstone Gaia mission is going to repeatedly observe a billion astrophysical objects of the entire sky during the next few years. The faintest objects that are expected to be observed will have approximately a G = 20 Gaia magnitude (unfiltered light), which corresponds to a limit of V = 20−25 mag, depending on the spectral type (Jordi et al. 2006). The final observational data will include low-resolution spectrophotometry of millions of unresolved galaxies. This will be performed with Gaia’s spectrophotometer, a slitless prism spectrograph with a blue (BP) and a red (RP) channel over the wavelength range between 330 nm and 1000 nm (Jordi et al. 2010). The classification of these galaxies into spectral classes and the prediction of some of their significant astrophysical parameters (Kontizas et al. 2011) are among the goals of the Gaia mission.
A corresponding software package (unresolved galaxy classifier, UGC) to accomplish this task is under development (Bellas-Velidis et al. 2010). The UGC uses Gaia-simulated synthetic galaxy spectra as templates, learning to successfully predict their spectral classes (classification) and the values of some significant astrophysical parameters (regression). Classification and regression is performed by support vector machines (SVM, Vapnik 1995).
An extended library of synthetic galaxy spectra has already been produced (Tsalmantza et al. 2009) with the PÈGASE.2 model (http://www.iap.fr/pegase) of galaxy spectral evolution (Fioc & Rocca-Volmerange 1997; Fioc & Rocca-Volmerange 1999; Le Borgne & Rocca-Volmerange 2002). This model uses the stellar evolutionary tracks of the Padova group, extended to the thermally pulsating asymptotic giant branch (AGB) and post-AGB phases (Groenewegen & de Jong 1993), and the BaSeL 2.2 library of stellar spectra, to produce low-resolution (R ~ 200) ultraviolet to near-infrared synthetic spectra of galaxies. Each spectrum represents a specific evolutionary scenario, the latter including a star formation rate (SFR) law, an initial mass function (IMF), etc.
The spectral library produced corresponds to four spectral types (early type, spiral, irregular and QSFG – quenched star-forming galaxies) at various random redshift values. The synthetic spectra satisfactorily cover the (g − r) – (r − i) color–color diagram of the DR4 SDSS galaxies. They have also been simulated for Gaia’s BP and RP photometers (description in Sordo & Vallenari 2009), with the addition of reddening, using the extinction law by Fitzpatrick (1999) and noise, for three G-band magnitude values (G = 15, G = 18.5, and G = 20). Support vector machines have been applied to the simulated spectra. Currently, an extensive comparison of the synthetic spectra with observed SDSS spectra is under development, leading to a semi-empirical library of galaxy spectra (Tsalmantza et al. 2012), combining real SED with information about galaxy parameters from galaxy evolution modeling.
All these numerous multi-parameter models have to be tested additionally for overlaps and for how well they represent realistic spectral classes. The quality of these spectra directly affects the efficiency of the UGC. The principal components analysis (PCA) method is able to compress the valuable information and reveal the significant correlations among the data entries in these huge databases. This is the reason why the PCA has become a very popular tool for determining the abundance of large-extent observations or simulations.
Section 2 briefly describes the structural characteristics of the synthetic spectra library and the complexity of handling it. Section 3 presents the PCA technique and its application to the synthetic spectra. The PCA results were analyzed in the context of the corresponding evolutionary scenario of each spectral type, presented in Sect. 4. Section 5 deals with the impact of the optimization on the Gaia-simulated version of our library, which is being used by the UGC. Discussion and conclusions are provided in Sect. 6.
2. The library of synthetic galaxy spectra
The synthetic spectra have been constructed by using two different star-formation law (SFL) scenarios: exponential star-formation rate (SFR) for early-type galaxies, and SFR proportional to the mass of the gas for spiral galaxies, irregular galaxies, and QSFG. These SFL were then modeled by varying the corresponding SFR parameters (p1, p2 for the exponential SFR and p1, p2, p3, tinfall for SFR proportional to the mass of the gas), at a fixed galaxy age (13 Gyr for early-type and spirals, 9 Gyr for irregulars and QSFG). The parameters p1 and p2 of the exponential SFR scenario do not correspond to the parameters p1 and p2 of the SFR scenario that is proportional to the mass of the gas. Their range was determined in a way to produce realistic synthetic spectra. For more details about the library of synthetic galaxy spectra, see Tsalmantza et al. (2009).
For the purposes of the UGC, the synthetic library should contain a considerable variety of spectra, which should be as typical as possible and, at the same time, as realistic as possible. This way, the relevant software would be able to classify and parametrize the spectra of unknown galaxies that Gaia will observe in a more efficient way.
This library contains spectra with realistic colors. However, a wide range of SFR parameters for different SFL and ages were used to produce SEDs with a huge variety of continua shapes and emission line strengths. Moreover, it is not clear how the simultaneous variation of two, three, or even four SFR parameters affects the shape of the produced SED, for example:
-
a)
two different sets of SFR parameters of the same SFL can resultin similar spectra;
-
b)
this similarity in spectra could possibly also occur for two different sets of SFR parameters assuming two different SFL, i.e. a spiral galaxy similar to an early type one;
-
c)
the various spectral types could contain a considerable amount of non-normal galaxy spectra.
To optimize the spectral library and use it for the purposes of a learning-based algorithm like UGC, it is important to know how the various sets of SFR parameters affect the shape of the resulting spectra. This information could be used to identify duplicated spectra of the same spectral type, spectral overlaps between different spectral types, and non-normal spectra. The corresponding suppression of these spectra could improve the classification and regression efficiency of UGC. Additionally, a better understanding of the modeling would be obtained for the relation between input parameters and output spectra. This would ensure a more productive future usage of the PÈGASE code.
Of course, in reality spectral overlaps between different spectral types as well as more complex cases such as mergers, are to be expected, which will make the classification and parametrization more difficult and challenging. However, such a puzzling task would be better addressed with a simple and realistic set of spectral templates.
Each galaxy spectrum can be considered as a point in a multidimensional space, with as many axes as the number of its wavelength bins. In each axis, this galaxy will have the flux value of its corresponding bin. Because a plot like this would be impossible to draw, other methods are required to reduce the dimensionality to just two or three principal dimensions to gain an overview of all spectra simultaneously and analyze the whole library of synthetic galaxy spectra at once. This can be done with the principal components analysis method, as we show in the next section.
3. Principal components analysis for the study of the synthetic spectra
3.1. Outline
The principal components analysis is part of a family of methods called unsupervised methods. Unsupervised methods are used to visualize data, usually to indicate groups (clustering), or to classify data. They apply when no classes, such as spectral types, are defined a priori or when existing classes are to be confirmed. The PCA provides a linear orthogonal transformation of a data set (e.g. galaxy spectra) into a new base, where a particular characteristic of interest (e.g. the variance of the original data) is preferentially highlighted. The new set of axes onto which the original data are being projected is called the principal components (PCs).
Amongst the numerous relevant publications, we refer the reader to the PCA applications on stellar spectra from the Michigan Spectral Survey (Bailer-Jones et al. 1998) and the SDSS/SEGUE project (Re Fiorentin et al. 2007), and on galaxy spectra from SDSS (Yip et al. 2004), DEEP2 Redshift Survey (Madgwick et al. 2008), the 2dF Galaxy Redshift Survey (Folkes et al. 1999) and the Spitzer Infrared Spectrograph (Wang et al. 2010). The PCA has also been applied to spectroscopic imaging observations (Heyer et al. 1997; Steiner et al. 2009), where spatial information is available. Steiner and collaborators managed to discover the existence and the location of an active nucleus of very low luminosity in the NGC 4736 galaxy. Finally, Ronen et al. (2008) analyzed synthetic galaxy spectra, including PÈGASE spectra, with different ages, star-formation histories and metallicities, while Tsalmantza et al. (2007) visualized PÈGASE spectra corresponding to Hubble types.
3.2. Usage
For a (n spectra si) × (m wavelength bins) data set, the PCA applies as follows:
-
(a)
either the correlation matrix (standardized PCA) or thevariance-covariance matrix (unstandardized PCA) ofthe data is computed;
-
(b)
the eigenvalues λ and the eigenvectors (eigenspectra) u (principal components) of either the correlation matrix or the variance-covariance matrix are calculated. If n ≥ m, then m eigenvalues and m corresponding eigenvectors are computed;
-
(c)
the eigenvalues are sorted in decreasing order. The first principal component, u1 (PC1), corresponds to the first (higher value) eigenvalue λ1 and accounts for the maximum amount of the total variance of the data. The second principal component, u2 (PC2), corresponds to the second eigenvalue λ2, is orthogonal to PC1 and accounts for the second highest variance fraction. Lower-order principal components are found the same way.
Thus, each original spectrum si is decomposed onto the new set of axes u (eigenspectra) as
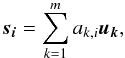 where ak,i is the admixture coefficient (the projection of the ith spectrum onto the kth principal component). In many cases, the first few principal components account for practically the total variance of the original spectra. This means that the most significant PCs can be used to reconstruct the original spectra with high accuracy, thus providing an efficient data compression. The reduced reconstruction s(r)i of si by using the r most significant PCs is
where ak,i is the admixture coefficient (the projection of the ith spectrum onto the kth principal component). In many cases, the first few principal components account for practically the total variance of the original spectra. This means that the most significant PCs can be used to reconstruct the original spectra with high accuracy, thus providing an efficient data compression. The reduced reconstruction s(r)i of si by using the r most significant PCs is
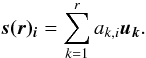 If r ≤ 3 is satisfactory, then the data set can be visualized by two- or three-dimensional plots and be further analyzed. The reduced reconstruction can be also used to remove noise and identify unusual spectra. For this reason, the PCA can preprocess data before they are analyzed by a classifier (Bailer-Jones et al. 1998). The above denote the main advantages of PCA: data compression and dimensionality reduction.
If r ≤ 3 is satisfactory, then the data set can be visualized by two- or three-dimensional plots and be further analyzed. The reduced reconstruction can be also used to remove noise and identify unusual spectra. For this reason, the PCA can preprocess data before they are analyzed by a classifier (Bailer-Jones et al. 1998). The above denote the main advantages of PCA: data compression and dimensionality reduction.
3.3. Application to the synthetic spectra
We applied the PCA method to the library of 28 885 synthetic galaxy spectra with z = 0. Because we aim to retain the relative strengths of the spectral features of the synthetic spectra, we used the unstandardized PCA procedure (see also Steiner et al. 2009). We computed the variance-covariance matrix, where the diagonal elements represent the variances of the flux bins and the off-diagonal elements the covariances between them.
The amount of the total variance and the corresponding cumulative variance of the five most significant eigenvectors are listed in Table 1. Figure 1 shows the first three principal components of the synthetic galaxy spectra. The first eigenvector is a “red” spectrum with emission lines, probably related to the brightness of the synthetic spectra. The linear Pearson correlation coefficient between the total fluxes of the spectra and the admixture coefficients of PC1 is 0.998. The second and the third eigenvectors are “bluer” with more dominant emission lines. The most prominent ones are OII (372.7 nm), OIII (500.7 nm), Hα (656.2 nm), and SIII (906.9 nm).
 |
Fig. 1 First (upper), second (middle) and third (lower) eigenvectors of the synthetic library of galaxy spectra. |
Amount of the total variance of the five most significant eigenvectors, the cumulative variance, and the corresponding reconstruction error for the synthetic galaxy spectra.
Amount of the total variance of the two most significant eigenvectors for randomly selected subsamples of the spectral library.
The reconstruction error that corresponds to the use of up to a specific eigenvector is listed in Table 1. This error is the mean absolute percentage error in the total normalized flux. Figure 2 illustrates the reconstruction error for each spectral type. The first eigenvector seems to favor the efficient reconstruction of the early-type and spiral galaxies. The second and the third eigenvectors, which have more dominant emission lines (Fig. 1), preferably fix the irregulars and the QSFG.
 |
Fig. 2 Reconstruction error for the whole sample and for each spectral type. Because this error drops very quickly, this plot shows the contribution of only the first four eigenvectors. |
 |
Fig. 3 Projection of the early-type synthetic galaxy spectra on the first and the second principal components. Light gray points show emission-line spectra, black points show non-emission line spectra, while dark gray points show non-emission line low-SFR spectra. |
 |
Fig. 4 Mean QSFG spectra for various ranges of the p3 SFR parameter. |
Therefore it is sufficient to consider the first two principal components to accurately analyze the whole library of synthetic galaxy spectra and use them in UGC, because we have a low error of 2% (on average) in spectral reconstruction and a 99% inclusion of the total variance. The data dimensionality is vastly reduced, apparently without significant loss of information.
Table 2 presents the results of the tests carried out to investigate the stability of the principal components. The PCA method was applied to randomly selected subsamples of the spectral library, ten times for each subsample. The amount of the total variance of the two most significant PCs was calculated. Table 2 lists the corresponding mean and standard deviation values for each subsample. The eigenvectors remain practically unchanged.
Figure 5 shows the sampling effect in terms of selected galaxy type, confirming the stability of the PCs. A PCA was carried out separately for each type. The first principal component (PC1) reflects the main variance for the selected spectral type, and is different in each case (see also Ronen et al. 2008), which reflects the major differences in their SEDs. Spiral galaxies appear to have strong absorption lines in PC1 rather than emission ones, but the sign of the PCs is arbitrary. Because these lines have the same relative sign, spirals are similar to the other types in this aspect. The second principal component (PC2) practically remains unchanged.
Figure 6 shows the projection of the synthetic galaxy spectra on the first and the second principal components. The representation of all the galaxies on the plane of the first two principal components can help us investigate a) among which spectral types there are overlaps and b) which sets of SFR parameters cause these overlaps. This investigation can help us optimize the existing library of synthetic galaxy spectra by suitably adjusting the SFR parameters space, and define the context of a future extension through a better knowledge of the modeling. However, this approach has to be implemented in a way that the optimum set of synthetic spectra is still realistic.
In Fig. 6, early-type galaxies are distributed toward the lower part of this plot, where the emission-line dominant PC2 is of less importance. The majority of them has negative PC2 values, which decreases the emission line strengths of the PC1 contribution. On the other hand, irregulars and QSFG tend to be distributed toward the upper left part of the diagram, where PC2 is more significant than in the previous case. Spirals show a broader variety of PC1-PC2 combinations.
This rough distinction together with overlaps between the various spectral types up to some reasonable level are to be expected. However, this figure shows that the overlaps are quite extended. Spiral galaxies are highly overlapped with early type galaxies and QSFG, while QSFG are also highly overlapped with irregular galaxies. Less overlap occurs between spirals and irregulars and between QSFG and early-type galaxies. No overlap exists between early-type and irregular galaxies.
4. Optimization of the library of synthetic galaxy spectra
The findings of the previous section could explain the classification performance of the scientific tests for the UGC software, using the Gaia-simulated version of the synthetic library. For example, most of the misclassified early-type galaxies are classified as spirals, while not a single early-type galaxy is misclassified to the irregular spectral class. An optimized version of the synthetic library of galaxy spectra with less overlaps could increase the spectral type classification and the parameters regression performance of UGC (Sect. 5). The results of the PCA application to the synthetic galaxy spectra are analyzed in the next paragraphs for each specific spectral type, and main conclusions for all analyzed galaxy types are summarized in Sect. 4.5.
 |
Fig. 5 First and the second eigenvectors when the PCA is applied separately for each spectral type. |
 |
Fig. 6 Projection of the synthetic galaxy spectra (Tsalmantza et al. 2009) on the first (PC1) and the second (PC2) principal components for each spectral type. |
 |
Fig. 7 Investigation of the properties of synthetic early-type spectra, corresponding to the presence or not of emission lines and the SFR intensity. First row: the diagram of the p1 vs. p2 SFR parameters used to produce the early-type synthetic galaxy spectra for each selected group of spectra. The thick black line separates the non-emission line from the emission line spectra. Non-emission line spectra are represented by the points to the left of this line. Second row: the corresponding (g − r) − (r − i) color–color diagram of these spectra (dense area of black points) overplotted on the colors of the SDSS spectra (black dots) and the synthetic spiral spectra (dense area of gray points). Third row: the corresponding mean spectra that characterize each selected group of early-type galaxies. Fourth row: an example of the evolution of the SFR of one galaxy for each selected group. |
 |
Fig. 8 Normalized SFR for various combinations of the SFR parameters for the spirals (left) and the irregulars (right). The examples illustrate the effect of varying the p1 (upper), p2 (middle) and tinfall (lower) SFR parameters to the SFR. |
4.1. Early-type galaxies
The synthetic early-type galaxy spectra were constructed using an exponential SFL with SFR
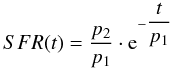 by varying the SFR parameters p1 and p2 until the age of 13 Gyr. The available mass is normalized to 1 M⊙. This SFL mainly aims to produce galaxies that have undergone a strong episode of star formation during the first years of their life. At present time (t = 13 Gyr) star formation should have practically stopped. In this context, an intense and rapidly decreasing SFR should be desirable. Note that the aim was to produce typical red galaxies and not to include the special cases of ellipticals that produce stars at a low rate at present or interact with other galaxies and become enriched with gas.
by varying the SFR parameters p1 and p2 until the age of 13 Gyr. The available mass is normalized to 1 M⊙. This SFL mainly aims to produce galaxies that have undergone a strong episode of star formation during the first years of their life. At present time (t = 13 Gyr) star formation should have practically stopped. In this context, an intense and rapidly decreasing SFR should be desirable. Note that the aim was to produce typical red galaxies and not to include the special cases of ellipticals that produce stars at a low rate at present or interact with other galaxies and become enriched with gas.
However, the range of the SFR parameters p1 and p2 arithmetically allows long-lived star formation (high p1 values) or inefficient SFR right from the first years of a galaxy’s life (low p2/p1 ratio). In the first case, present star formation is relatively high because the exponential SFR drops slowly, and emission lines will appear in the spectrum (Karampelas et al. 2010). In the second case, an unreal scenario will take place, with very inefficient and rapidly decreasing SFR.
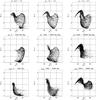 |
Fig. 9 Projection of the spiral galaxies on the first and the second principal components for various ranges of the p1 (first row), p2 (second row) and tinfall (third row) SFR parameters. |
 |
Fig. 10 Projection of the irregular galaxies on the first and the second principal components for various ranges of the p1 (first row), p2 (second row) and tinfall (third row) SFR parameters. |
Figure 7 shows how the initial choice of p1 and p2 parameters affects the SFR, the final SEDs, and the corresponding colors. Three different groups of spectra were investigated, as mentioned above: 1) non-emission line spectra; 2) non-emission line low-SFR spectra; and 3) emission line spectra. The first group (first column of Fig. 7), defined by p1 < 2000 Myr and p2 > 0.5 M⊙, includes the desirable SEDs and SFRs, with a low color–color overlap with spirals. The second group (second column of the same figure), defined by p1 < 2000 Myr and p2 < 0.5 M⊙, has weak star formation and a noticeable color–color overlap with spirals. The third group (third column of the same figure), defined by p1 > 2000 Myr, corresponds to active star formation, resulting in spectra with strong emission lines, whose colors heavily coincide with those of spirals. The corresponding boundaries of the SFR parameters were determined both from the examination of the actual SEDs and the distribution of their colors in the (g − r) − (r − i) color–color diagram.
The PCA findings (Sect. 3.3) agree with the above, because they reveal an extended overlap between early-type galaxy spectra and spiral ones (Fig. 6). They also reveal a less extended overlap between early-type and QSFG spectra. Figure 3 shows the distribution of the synthetic early-type galaxies on the first two principal components, corresponding to the presence or not of emission lines and the SFR intensity, as in Fig. 7. In agreement with the above analysis, we suppressed the early-type galaxies with p1 > 2000 Myr and p2 < 0.5 M⊙ (the second and the third group as described in the previous paragraph), which correspond to emission line spectra and very low SFR spectra, respectively, which selects typical red spectra.
 |
Fig. 11 Projection of the QSFG on the first and the second principal components for various ranges of the p1 (first row), p2 (second row), p3 (third row) and tinfall (fourth row) SFR parameters. |
 |
Fig. 12 Projection of the optimized synthetic galaxy spectra on the first (PC1) and the second (PC2) principal components for each spectral type. |
4.2. Spiral galaxies
The synthetic spiral galaxy spectra were constructed using an SFR that is proportional to the mass of the gas Mgas(t) at a given time t:
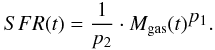 At t = 0 the model assumes that the galaxy has no mass and it is starting to be formed by accretion of gas with a total normalized mass of 1 M⊙. The accretion rate AR is
At t = 0 the model assumes that the galaxy has no mass and it is starting to be formed by accretion of gas with a total normalized mass of 1 M⊙. The accretion rate AR is
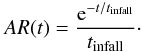 These galaxies were produced by varying the SFR parameters p1, p2 and tinfall until the age of 13 Gyr. Several experiments were carried out to investigate the effect of varying the SFR parameters on the SFR. This was made by executing the PÈGASE.2 code for various values of a specific SFR parameter, while keeping the other two parameters constant. The same procedure was repeated for the other two parameters, too. The results are illustrated in the left part of Fig. 8. Evidently, the SFR in spirals is increasing at first until it reaches a maximum, and then starts decreasing. Indeed, when the galaxy starts to be formed, low amounts of gas are available to form stars. Star formation is still poor, because it is proportional to the mass of the gas. Subsequently, SFR is increased as accreted, unused and returned gas from the death of fast-evolving higher-mass stars is accumulated. Then, as gas accretion is decreasing exponentially and SFR continues, the available mass of the gas is reduced, resulting in lower SFR. The parameters p1, p2 and tinfall adjust the maximum value of SFR (efficiency of star formation) and the age of the galaxy that this happens (timescale of star formation). These, in addition to the selected age of spiral galaxies (13 Gyr), modulate the final spectrum.
These galaxies were produced by varying the SFR parameters p1, p2 and tinfall until the age of 13 Gyr. Several experiments were carried out to investigate the effect of varying the SFR parameters on the SFR. This was made by executing the PÈGASE.2 code for various values of a specific SFR parameter, while keeping the other two parameters constant. The same procedure was repeated for the other two parameters, too. The results are illustrated in the left part of Fig. 8. Evidently, the SFR in spirals is increasing at first until it reaches a maximum, and then starts decreasing. Indeed, when the galaxy starts to be formed, low amounts of gas are available to form stars. Star formation is still poor, because it is proportional to the mass of the gas. Subsequently, SFR is increased as accreted, unused and returned gas from the death of fast-evolving higher-mass stars is accumulated. Then, as gas accretion is decreasing exponentially and SFR continues, the available mass of the gas is reduced, resulting in lower SFR. The parameters p1, p2 and tinfall adjust the maximum value of SFR (efficiency of star formation) and the age of the galaxy that this happens (timescale of star formation). These, in addition to the selected age of spiral galaxies (13 Gyr), modulate the final spectrum.
Figure 9 illustrates the effect of varying the p1, p2 and tinfall SFR parameters on the PC1-PC2 distribution. Higher p1, p2 and tinfall values define weaker and longer-timescale star formation, producing spectra similar to QSFG and irregulars. The projection of the spiral galaxies on the PC1-PC2 plane shows that particularly the high values of p2 shift the spectra toward these spectral types. In agreement with the above analysis, we suppressed the spiral galaxies with p2 > 5000 Myr/M⊙.
4.3. Irregular galaxies
The synthetic irregular galaxy spectra were constructed with the same SFR and AR as for spirals, but until an age of 9 Gyr. The SFR of irregulars follows the trend of spirals, but it stops at an “earlier” time. Additionally, the p1, p2 and tinfall SFR parameters can be much higher than those of spirals, resulting in some cases in extremely weak SFR. The right part of Figs. 8 and 10 illustrate the effect of varying the SFR parameters to the SFR and the PC1-PC2 distribution of the irregular galaxies, respectively. Very high p2 and tinfall values (p2 > 40 000 Myr/M⊙,tinfall > 20 000 Myr) tend to construct very weak SEDs, highly mixed with QSFG, that are crowded toward the origin of the PC1-PC2 plot, despite the wide SFR parameter range. Consequently, the SEDs are not very sensitive to the variation of high p2 and tinfall values, which is not desirable when producing a spectral library, because of the risk of creating duplicates. In agreement with the above analysis, we suppressed the irregular galaxies with p2 > 40 000 Myr/M⊙ and tinfall > 20 000 Myr.
4.4. QSFG
The quenched star-forming galaxies can be thought of as irregulars that have stopped forming stars since 1–250 Myr. The p3 parameter value defines this timescale. This means that SFR = 0 for (9000 − p3) Myr ≤ t ≤ 9000 Myr. The choice p3 = 0 Myr would produce irregular galaxies. The SFR is the same like spirals and irregulars, while the p1, p2 and tinfall parameters span the same range as irregulars.
Figure 11 illustrates the effect of varying the SFR parameters on the PC1-PC2 distribution of the QSFG. We show no SFR examples because of the similarity with the corresponding diagrams of the irregular galaxies. Again, very high p2 and tinfall values tend to construct very weak SEDs, highly mixed with irregulars, toward the origin of the PC1-PC2 plot. Additionally, p3 > 10 Myr values characterize spectra that significantly mix with spirals and early-type galaxies. Figure 4 shows that these spectra do not have emission lines, because the massive stars have already died. In agreement with the above analysis and the corresponding analysis of the irregular galaxy spectra, we suppressed QSFG with p2 > 40 000 Myr/M⊙, p3 > 10 Myr and tinfall > 20 000 Myr.
4.5. Selection of optimum spectra
The analysis of the previous section implies to truncate a) emission line early-type galaxies that resemble spirals; b) non-emission line low-SFR early-type galaxies; c) spiral galaxies with high p2 values that resemble QSFG and irregulars; d) irregulars and QSFG with extremely high p2 and tinfall values, similar to each other; and e) QSFG without emission lines that resemble spirals. Table 3 lists the optimized range of the library of synthetic galaxy spectra.
The PCA method was applied to the library of the optimal spectra to investigate the changes it has undergone. The most significant components of the optimum spectra are almost identical to the corresponding PCs of the original library. Figure 12 illustrates the distribution of the optimum spectra to the two most significant PCs, which have a corresponding error of 1% in spectral reconstruction and a 99% inclusion of the total variance. Because the PCs did not change much, the distribution of the optimum spectra on them reveals similar trends like those illustrated in Fig. 6. However, the optimization results are evident. Early-type galaxies form a distinct group, separately from spirals, with a desired SFR, and the spiral-irregular and spiral-QSFG overlaps have been limited to a relatively narrow region. Additionally, the high concentration of late-type galaxies in the lower left part of this plot has been reduced. A notable overlap between irregulars and QSFG is present in the optimized data. This is not surprising, because the corresponding spectra do have many common characteristics. In any case, overlaps between the various spectral types are to be expected in real data.
Clearly, it is not necessarily correct to have galaxy spectra anywhere in a PC1-PC2 diagram. Physical constraint limit the possible spectral diversity, and a robust spectral decomposition like the one provided by the PCA method must reflect these limitations.
 |
Fig. 13 (g − r) − (r − i) color–color coverage of real (SDSS) spectra (black dots) from the synthetic ones (dense areas of dots), before (left) and after (right) the optimization. |
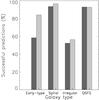 |
Fig. 14 Classification performance of UGC for the noisy, reddened, and redshifted simulated spectra, for each spectral type. Each pair of columns demonstrates the successful predictions of the corresponding spectral type, before (left column) and after (right column) the optimization. |
 |
Fig. 15 Regression performance of UGC for the “clean” spectra for each parameter. Each pair of columns gives the median values of the absolute percentage errors, derived from the comparison between real and predicted values of the corresponding parameter, before (left column) and after (right column) the optimization. The listed parameters are (from left to right): p1, p2 of early-type galaxies, p1, p1, tinfall of spiral galaxies, p1, p1, tinfall of irregular galaxies, p1, p1, p3, tinfall of QSFG, redshift, and reddening. |
Figure 13 presents the (g − r) − (r − i) color–color coverage of real (SDSS) spectra from the synthetic ones, both before and after the optimization. The suppression of overlaps in spectral colors follow the corresponding suppression in spectra. Note especially the distinct group of early-type galaxies in (g − r) > 0.8, and the elimination of the extended overlap between spirals and QSFG in 0.5 < (g − r) < 0.6. The good coverage of observations (SDSS galaxies) was retained.
Optimized range of SFR parameters for each galaxy spectral type.
5. UGC and optimum Gaia-simulated spectra
It is important for the development of the unresolved galaxy classifier to investigate the impact of optimizing the library of synthetic galaxy spectra to its performance. The UGC uses the Gaia-simulated version of the synthetic library. It is an algorithm that is based on the implementation of the supervised learning method SVM. These SVMs (Vapnik 1995) can be used for data classification through the definition of an optimum hyperplane that separates the members of the various classes that describe the data. For this purpose, a set of training data is used to train the SVMs and prepare it to classify data of unknown class. The SVMs can also be used for parameter regression. Again, a set of training data is necessary to train the SVMs and prepare them to predict the parameter values of data that lack this information.
The SVMs are trained to predict the spectral type (classification) and the SFR parameters p1, p2, p3 and tinfall values, together with extinction and redshift values (regression). We applied this procedure to two sets of simulated data, the first containing “clean” spectra without any addition of noise, extinction, or redshift, and the second containing noisy, reddened, and redshifted (“realistic”) spectra, for G = 15 Gaia magnitude.
The classification efficiency (percentage of successful predictions) for the “clean” spectra before and after the optimization is ~100%. The corresponding results for the noisy, reddened, and redshifted spectra are shown in Fig. 14. Spectral type predictions of these spectra are quite successful. Spectral optimization in general improved the classification efficiency of UGC, especially for the early-type galaxies, where the predictions where about 25% more successful. Spirals and irregulars are slightly better classified (~3%), while the optimization practically left the QSFG classification efficiency unchanged, which was already high. These results reflect the suppression of the overlaps between the various spectral types achieved through the optimization of the spectral library.
The results of the parameter regression before and after optimization for the “clean” spectra are shown in Fig. 15. They are given in terms of the median values of the absolute percentage errors, derived from the comparison between real and predicted parameter values. Although the prediction efficiency of some parameters did not improve or worsened, most of them were predicted more accurately. For a few cases of a close-to-zero parameter value, the predicted value could be negative, although the SFR parameters, redshift, and reddening are always positive. In these cases the predicted value was set to zero. The inclusion of an acceptable treatment of unrealistic predicted values in the UGC code is under development (Bellas-Velidis et al. 2010).
6. Discussion and conclusions
The main trend when using the current version of the unresolved galaxy classifier code to predict the various parameters of the synthetic spectra is that optimization in general improves the prediction efficiency (Fig. 15). However, it is not straightforward to fully interpret these errors, especially to compare between different estimated parameters. Because varying the SFR parameters does not linearly affect the corresponding spectrum, comparisons should be made cautiously.
For example, if a spectrum is not very sensitive to the variation of a specific SFR parameter, then even a high error value on the prediction of this parameter could be acceptable. Additionally, the spectral optimization could reject spectra that can be unique compared to other spectra, affecting the efficiency of the SVM. This is obvious in the prediction of the p1 SFR parameter of the early-type galaxies. Although the rejection of the high p1 values that produce emission lines is desirable, the variety of spectra has been reduced, because the range fell from 10 Myr < p1 < 30 000 Myr to 10 Myr < p1 < 2000 Myr. Spectra are more realistic but less unique, making it harder for the SVM method to “learn” how the p1 variation is linked with the final SED. Moreover, a relatively low number of available galaxy spectra could also affect the quality of the training and, consequently, the prediction error. At the same time, advances
in the code itself, such as training the simulated spectra in different ranges of redshift and extinction, could limit the errors even more. First results are encouraging (Bellas-Velidis et al., in prep.).
To conclude, we optimized the library of synthetic galaxy spectra, which was produced with PÉGASE.2 code (Tsalmantza et al. 2009), setting new boundaries in the space of the galaxy parameters. The application of the principal component analysis method to this extended library vastly reduced its dimensionality without any significant loss of information and revealed spectral overlaps. It also provided ways to a better understanding of how the multi-parameter modeling affects the final shape of a synthetic spectrum. Additionally, the investigation of the various star-formation laws used in the modeling helped to trace some non-normal synthetic spectra. This investigation led to a set of more realistic synthetic spectra, where overlaps between spectra and spectral colors were highly suppressed. The findings could be used to define the context of a future extension of this spectral library, because a better understanding of the modeling was achieved.
The Gaia-simulated version of this optimum set of spectra was used for training the unresolved galaxy classifier code, which will be part of the Gaia satellite software. The training was performed by applying the support vector machines method. The classification efficiency was in general improved. Advances in the code itself, which is currently under development, could limit the errors even more.
Acknowledgments
The authors are grateful to the referee J. M. Carrasco for his constructive suggestions that improved this paper. This work was partially supported by the Special Account for Research Grants of the National and Kapodistrian University of Athens (ELKE), the EC FP6 RTN ELSA (MRTN-CT-2006-033481) and the Institut d’Astrophysique de Paris.
References
- Bailer-Jones, C. A. L., Irwin, M., & von Hippel, T. 1998, MNRAS, 298, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Bellas-Velidis, I., Kontizas, M., Livanou, E., & Tsalmantza, P. 2010, ASPC, 424, 256 [NASA ADS] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1999, A&A, 351, 869 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Folkes, S., Ronen, S., Price, I., et al. 1999, MNRAS, 308, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., & de Jong, T. 1993, A&A, 267, 410 [NASA ADS] [Google Scholar]
- Heyer, M. H., & Schloerb, P. F. 1997, ApJ, 475, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Høg, E., Brown, A. G. A., et al. 2006, MNRAS, 7, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karampelas, A., Kontizas, E., Tsalmantza, P., et al. 2010, ASPC, 424, 252 [NASA ADS] [Google Scholar]
- Kontizas, M., Bellas-Velidis, I., Rocca-Volmerange, B., et al. 2011, EAS, 45, 337 [Google Scholar]
- LeBorgne, D., & Rocca-Volmerange, B. 2002, A&A, 386, 446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madgwick, D. S., Coil, A. L., Conselice, C. J., et al. 2003, ApJ, 599, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Re Fiorentin, P., Bailer-Jones, C. A. L., Lee, Y. S., et al. 2007, A&A, 467, 1373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ronen, S., Aragon-Salamanca, A., & Lahav, O. 1999, MNRAS, 303, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Sordo, R., & Vallenari, A. 2009, GAIA-C8-DA-OAPD-RS-004, http://www.rssd.esa.int/llink/livelink/open/2936253 [Google Scholar]
- Steiner, J. E., Menezes, R. B., Ricci, T. V., & Oliveira, A. S. 2009, MNRAS, 395, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Tsalmantza, P., Kontizas, M., Bailer-Jones, C. A. L., et al. 2007, A&A, 470, 761 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsalmantza, P., Kontizas, M., Rocca-Volmerange, B., et al. 2009, A&A, 504, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsalmantza, P., Karampelas, A., Kontizas, M., et al. 2012, A&A, 537, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vapnik, V. 1995, The Nature of Statistical Learning Theory (New York: Springer-Verlag Inc.) [Google Scholar]
- Wang, L., Farrah, D., Connolly, B., et al. 2011, MNRAS, 411, 1809 [NASA ADS] [CrossRef] [Google Scholar]
- Yip, C. W., Connolly, A. J., Szalay, A. S., et al. 2004, AJ, 128, 585 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Amount of the total variance of the five most significant eigenvectors, the cumulative variance, and the corresponding reconstruction error for the synthetic galaxy spectra.
Amount of the total variance of the two most significant eigenvectors for randomly selected subsamples of the spectral library.
All Figures
 |
Fig. 1 First (upper), second (middle) and third (lower) eigenvectors of the synthetic library of galaxy spectra. |
| In the text | |
 |
Fig. 2 Reconstruction error for the whole sample and for each spectral type. Because this error drops very quickly, this plot shows the contribution of only the first four eigenvectors. |
| In the text | |
 |
Fig. 3 Projection of the early-type synthetic galaxy spectra on the first and the second principal components. Light gray points show emission-line spectra, black points show non-emission line spectra, while dark gray points show non-emission line low-SFR spectra. |
| In the text | |
 |
Fig. 4 Mean QSFG spectra for various ranges of the p3 SFR parameter. |
| In the text | |
 |
Fig. 5 First and the second eigenvectors when the PCA is applied separately for each spectral type. |
| In the text | |
 |
Fig. 6 Projection of the synthetic galaxy spectra (Tsalmantza et al. 2009) on the first (PC1) and the second (PC2) principal components for each spectral type. |
| In the text | |
 |
Fig. 7 Investigation of the properties of synthetic early-type spectra, corresponding to the presence or not of emission lines and the SFR intensity. First row: the diagram of the p1 vs. p2 SFR parameters used to produce the early-type synthetic galaxy spectra for each selected group of spectra. The thick black line separates the non-emission line from the emission line spectra. Non-emission line spectra are represented by the points to the left of this line. Second row: the corresponding (g − r) − (r − i) color–color diagram of these spectra (dense area of black points) overplotted on the colors of the SDSS spectra (black dots) and the synthetic spiral spectra (dense area of gray points). Third row: the corresponding mean spectra that characterize each selected group of early-type galaxies. Fourth row: an example of the evolution of the SFR of one galaxy for each selected group. |
| In the text | |
 |
Fig. 8 Normalized SFR for various combinations of the SFR parameters for the spirals (left) and the irregulars (right). The examples illustrate the effect of varying the p1 (upper), p2 (middle) and tinfall (lower) SFR parameters to the SFR. |
| In the text | |
 |
Fig. 9 Projection of the spiral galaxies on the first and the second principal components for various ranges of the p1 (first row), p2 (second row) and tinfall (third row) SFR parameters. |
| In the text | |
 |
Fig. 10 Projection of the irregular galaxies on the first and the second principal components for various ranges of the p1 (first row), p2 (second row) and tinfall (third row) SFR parameters. |
| In the text | |
 |
Fig. 11 Projection of the QSFG on the first and the second principal components for various ranges of the p1 (first row), p2 (second row), p3 (third row) and tinfall (fourth row) SFR parameters. |
| In the text | |
 |
Fig. 12 Projection of the optimized synthetic galaxy spectra on the first (PC1) and the second (PC2) principal components for each spectral type. |
| In the text | |
 |
Fig. 13 (g − r) − (r − i) color–color coverage of real (SDSS) spectra (black dots) from the synthetic ones (dense areas of dots), before (left) and after (right) the optimization. |
| In the text | |
 |
Fig. 14 Classification performance of UGC for the noisy, reddened, and redshifted simulated spectra, for each spectral type. Each pair of columns demonstrates the successful predictions of the corresponding spectral type, before (left column) and after (right column) the optimization. |
| In the text | |
 |
Fig. 15 Regression performance of UGC for the “clean” spectra for each parameter. Each pair of columns gives the median values of the absolute percentage errors, derived from the comparison between real and predicted values of the corresponding parameter, before (left column) and after (right column) the optimization. The listed parameters are (from left to right): p1, p2 of early-type galaxies, p1, p1, tinfall of spiral galaxies, p1, p1, tinfall of irregular galaxies, p1, p1, p3, tinfall of QSFG, redshift, and reddening. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


