| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201117424 | |
| Published online | 10 February 2012 | |
Monte Carlo Markov chain DEM reconstruction of isothermal plasmas
1 Department of Atmospheric, Oceanic and Space Sciences, University of Michigan, Ann Arbor, MI 48109, USA
e-mail: elandi@umich.edu
2 Dipartimento di Scienze Fisiche ed Astronomiche, Sezione di Astronomia, Universita’ di Palermo, Piazza del Parlamento 1, 90134, Italy
3 INAF-Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
4 Smithsonian Astrophysical Observatory, 60 Garden St., Cambridge MA 02138, USA
Received: 6 June 2011
Accepted: 12 December 2011
Context. Recent studies carried out with SOHO and Hinode high-resolution spectrometers have shown that the plasma in the off-disk solar corona is close to isothermal. If confirmed, these findings may have significant consequences for theoretical models of coronal heating. However, these studies have been carried out with diagnostic techniques whose ability to reconstruct the plasma distribution with temperature has not been thoroughly tested.
Aims. In this paper, we carry out tests on the Monte Carlo Markov chain (MCMC) technique with the aim of determining: 1) its ability to retrieve isothermal plasmas from a set of spectral line intensities, with and without random noise; 2) to what extent can it discriminate between an isothermal solution and a narrow multithermal distribution; and 3) how well it can detect multiple isothermal components along the line of sight. We also test the effects of 4) atomic data uncertainties on the results, and 5) the number of ions whose lines are available for the DEM reconstruction.
Methods. We first use the CHIANTI database to calculate synthetic spectra from different thermal distributions: single isothermal plasmas, multithermal plasmas made of multiple isothermal components, and multithermal plasmas with a Gaussian DEM distribution with variable width. We then apply the MCMC technique on each of these synthetic spectra, so that the ability of the MCMC technique at reconstructing the original thermal distribution can be evaluated. Next, we add a random noise to the synthetic spectra, and repeat the exercise, in order to determine the effects of random errors on the results. We also we repeat the exercise using a different set of atomic data from those used to calculate synthetic line intensities, to understand the robustness of the results against atomic physics uncertainties. The size of the temperature bin of the MCMC reconstruction is varied in all cases, in order to determine the optimal width.
Results. We find that the MCMC technique is unable to retrieve isothermal plasmas to better than Δlog T ≃ 0.05. Also, the DEM curves obtained using lines calculated with an isothermal plasma and with a Gaussian distribution with FWHM of log T ≃ 0.05 are very similar. Two near-isothermal components can be resolved if their temperature separation is Δlog T = 0.2 or larger. Thus, DEM diagnostics has an intrinsic resolving power of log T = 0.05. Atomic data uncertainties may significantly affect both temperature and peak DEM values, but do not alter our conclusions. The availability of small sets of lines also does not worsen the performance of the MCMC technique, provided these lines are formed in a wide temperature range.
Conclusions. Our analysis shows the present limitations in our ability to identify the presence of strictly isothermal plasmas in stellar and solar coronal spectra.
Key words: methods: data analysis / techniques: spectroscopic / Sun: corona / Sun: UV radiation
© ESO, 2012
1. Introduction
Detailed measurements of the temperature distribution of the plasma of solar and stellar coronae are of critical importance to understand how they are heated to multimillion degree temperatures, so it is no surprise that the thermal structure of the solar corona has been studied ever since the publication of the seminal paper of Edlen (1942), who discovered its high temperature for the first time. These studies have known a revival in recent years, thanks to the availability of a large body of observations obtained with the new instrumentation carried on board the SOHO, TRACE, STEREO, Hinode and SDO satellites.
Plasma loops are a fundamental component of the solar corona, since they are ubiquitous both in quiet and active solar plasmas. Steady-state models of loops predict that the temperature of these structures varies along the loop (Rosner et al. 1978), and that loops with different length can have very different temperatures; nanoflare-based models predict finely-structured loops filled with multithermal plasma all along their length (Patsourakos & Klimchuk 2005). A consequence of these models is that quiet coronal plasmas observed outside the solar limb should be multithermal because they are the sum of a multitude of loops with different lengths and temperatures along the line of sight. The question of clearly distinguishing between multithermal and isothermal plasma along the line of sight is thus very important in the framework of coronal heating models (e.g. Klimchuk 2006; Reale 2010). However, recent measurements have provided increasing evidence of a nearly isothermal nature of both coronal hole and quiet Sun plasmas when they are observed above the solar limb, contrary to model predictions. Several authors (e.g. Feldman et al. 1998, 1999; Warren 1999; Doschek et al. 2001; Landi 2008) reported single-temperature determinations which are remarkably similar even if taken with different instruments and at different times during the solar cycle. A constant temperature was also found to characterize an entire streamer by Landi et al. (2006). Even a complex active region, when observed at the solar west limb, seemed to be composed by three near isothermal plasmas (Landi & Feldman 2008). Further studies carried out with Hinode/EIS observations, on the contrary, provided evidence that the quiescent solar corona is not strictly isothermal, but it is characterized by a rather narrow temperature structure with a tail that extends to higher temperatures (Warren & Brooks 2009; Brooks et al. 2009; Hahn et al. 2011). The aim of the present paper is to assess how reliable such isothermal plasma claims are.
These measurements have been carried out either with the emission measure (EM) loci technique or with traditional differential emission measured (DEM) techniques (see Feldman & Landi 2008, and references therein). The former allows to determine the temperature and the total emission measure (EM) of an isothermal plasma, and it has been the technique used in most of the studies that resulted in the isothermal corona results. This technique, while useful in the case of strictly isothermal plasmas, fails at providing an assessment of the uncertainty of its results. Traditional DEM techniques rely on several different methods to reconstruct the thermal structure of multithermal plasmas determining the DEM curve. However, most of them rely on assumptions on the smoothness of the distribution, that make it very difficult to study isothermal or near-isothermal plasmas.
Landi & Klimchuk (2010) carried out tests aimed at evaluating the ability of the EM loci technique to discriminate between isothermal and multithermal plasmas, when the spectral line intensities used for the reconstruction included uncertainties. They also developed a quantitative method to determine how multithermal could a plasma distribution be in order to be compatible with a set of observed line intensities that was also compatible with an isothermal condition.
In the present work we extend the Landi & Klimchuk (2010) study to the application of DEM diagnostic techniques to spectral line intensities. In particular, we aim at: 1) determining the ability of such techniques to retrieve isothermal plasma from a set of spectral line intensities, with and without random noise; 2) understanding to what extent are DEM diagnostic techniques able to discriminate between a truly isothermal plasma and a multithermal plasma with a narrow distribution; 3) quantifying how well can such technique detect and resolve multiple isothermal components along the lines of sight; 4) investigate the effects of atomic data uncertainties on the results; and 5) study how DEM reconstructions are affected by the number of ions whose lines are available.
Similar studies with different goals were recently carried out in preparation for the SDO and Hinode missions by Golub et al. (2004) and Weber et al. (2004). Both studies were focused on determining how well, and with what uncertainties, could a DEM curve known a priori be reconstructed using data from the limited number of broad-band filter intensities provided by Hinode/XRT and narrow-band filters in SDO/AIA. They also discussed how efficiently could DEM curves from the large number of pixels expected from such images be determined and visualized. Unlike the present work, such studies were aimed at imaging instruments and did not use spectral lines intensities; also, no guidelines were provided with regard to the interpretation of almost isothermal results. Further, the results of such tests strongly depend on the specific temperature response function of each instrument, so that they can not be easily extended to other instruments.
Line intensities can potentially provide better constraints on DEM curves due 1) to the better temperature resolution provided by their emissivities; and 2) to the finer sampling of the temperature range of the solar corona provided by the large number of ions included in the spectral range of the available spectrometers (CDS and SUMER on SOHO, EIS on Hinode). In the present work, we focus on spectral lines; given the larger amount of available constraints, we can hopefully obtain further insight on the intrinsic abilities of DEM diagnostic techniques at studying isothermal or near-isothermal plasmas. Our results can be applied to analyses of spectra observed by any of the available spectrometers observing the solar upper atmosphere, such as Hinode/EIS, SOHO/CDS, SOHO/SUMER, SOHO/UVCS, EUNIS, SERTS, HRTS and, to a certain extent, even the lower-resolution SDO/EVE. In fact, different spectrometers working at different wavelength ranges may still observe lines from the same element, so that they will be sampling the same temperature interval regardless of their passband. Thus, our results will be of more general use than Golub et al. (2004) and Weber et al. (2004).
Many different DEM diagnostic techniques have been developed in the past (see the reviews of Phillips et al. 2008; and Harrison & Thompson 1992). Harrison & Thompson (1992) carried out a comparative analysis aimed at determining which, among six different DEM diagnostic techniques, was most successful at reproducing pre-defined DEM curves using a set of emission lines. More recently, Mark Weber and Paul Boerner led a similar study in preparation to the SDO mission (http://www.lmsal.com/~boerner/demtest/), where, however, the results are not clearly discussed and no clear conclusions are drawn; also, such a study does not appear to have been published in the literature. Most importantly, Boerner & Weber did not address the ability at discriminating between isothermal and non-isothermal plasmas, which is the focus of the present work.
After inspecting the material in the Boerner & Weber website, we found that Monte Carlo Markov chain (MCMC) method developed by Kashyap & Drake (1998) provided the most robust and accurate results. Also, this method dispenses from many of the assumptions common to other DEM diagnostic techniques, and provides an assessment of the uncertainties of the final DEM curve. Thus, we chose to focus on this method in the present study. Kashyap & Drake (1998) and Kashyap et al. (2004) briefly described tests made to ensure and assess the robustness and reliability of the MCMC technique, but they did not focus on the ability of the MCMC technique to discriminate between an isothermal and multithermal plasma. Here we also provide a set of empirical guidelines for the choice of the input parameters and for the interpretation of MCMC reconstructions.
Section 2 introduces the main plasma structure diagnostic techniques, including MCMC, and discusses their assumptions; it also explains the methodology we follow in our tests. Section 3 describes the results of our tests for several different ad-hoc distributions, and Sect. 4 reviews the results of this study.
2. Analysis method
2.1. Emission line intensities
Solar coronal plasmas are usually tenuous enough to be optically thin below 2000 Å. The intensity of an optically thin emission line can be written as 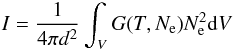 (1)where Ne is the electron density, V is the emitting volume along the line of sight, d is the distance between the emitting source and the observer, and G(T,Ne) is the Contribution Function of the emitting line defined as
(1)where Ne is the electron density, V is the emitting volume along the line of sight, d is the distance between the emitting source and the observer, and G(T,Ne) is the Contribution Function of the emitting line defined as 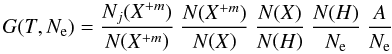 (2)where
(2)where
-
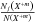 is the relative population of the upper level j and depends on electron temperature and density;
is the relative population of the upper level j and depends on electron temperature and density; -
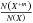 is the relative abundance of the ion X + m (ion fraction); under ionization equilibrium conditions, it depends on the electron temperature;
is the relative abundance of the ion X + m (ion fraction); under ionization equilibrium conditions, it depends on the electron temperature; -
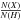 is the abundance of the element X relative to hydrogen;
is the abundance of the element X relative to hydrogen; -
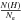 is the hydrogen abundance relative to the electron density ( ≈ 0.83 for fully ionized plasmas);
is the hydrogen abundance relative to the electron density ( ≈ 0.83 for fully ionized plasmas); -
A is the Einstein coefficient for spontaneous emission.
When the plasma is multithermal Eq. (1) can be rewritten by defining the differential emission measure (DEM), 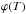 , as
, as 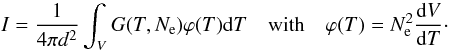 (3)The DEM indicates the amount of material in the plasma as a function of temperature. When the plasma is isothermal at temperature Tc, we can define the emission measure (EM) of the plasma as
(3)The DEM indicates the amount of material in the plasma as a function of temperature. When the plasma is isothermal at temperature Tc, we can define the emission measure (EM) of the plasma as 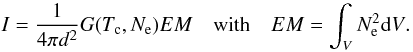 (4)The EM of the plasma is a measure of the total amount of plasma at the temperature Tc.
(4)The EM of the plasma is a measure of the total amount of plasma at the temperature Tc.
2.2. Thermal structure diagnostic techniques
When the plasma is isothermal at the temperature Tc, the EM can be determined from line intensities as: 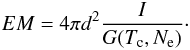 (5)The EM loci diagnostic technique allows to measure simultaneously the plasma EM and Tc values. It consists of calculating for each line the function EM(T) defined as
(5)The EM loci diagnostic technique allows to measure simultaneously the plasma EM and Tc values. It consists of calculating for each line the function EM(T) defined as 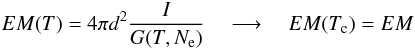 (6)as a function of electron temperature, using the observed line intensities I. Since the plasma EM is the same for all lines, all the EM(T) curves, when displayed as a function of T in the same plot, should cross the same point coordinates (Tc,EM). The presence of this crossing point also confirms that the plasma is isothermal. When the plasma is not isothermal, the EM(T) curves do not cross the same point and the EM loci technique can not be used.
(6)as a function of electron temperature, using the observed line intensities I. Since the plasma EM is the same for all lines, all the EM(T) curves, when displayed as a function of T in the same plot, should cross the same point coordinates (Tc,EM). The presence of this crossing point also confirms that the plasma is isothermal. When the plasma is not isothermal, the EM(T) curves do not cross the same point and the EM loci technique can not be used.
When the plasma is multithermal, the plasma DEM needs to be determined. There are many different types of DEM diagnostic techniques, and they have been reviewed by Phillips et al. (2008). Some techniques rely on the inversion of Eq. (3), others on an iterative procedure; Monte Carlo methods are also available.
The inversion of Eq. (3) is carried out by discretising the temperature interval in bins whose width is chosen by the user. In each bin the DEM is assumed to be constant so that the observed intensity Is of the spectral line s can be written as 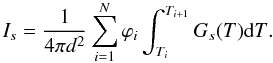 (7)The values of ϕi are determined minimizing via an iterative technique the sum the quantity H = S + χ2, where S is the entropy of the the quantity ϕi and χ2 has the standard definition. In this procedure, each observed line is arbitrarily associated to a temperature value Teff (discussed below), and the results for all lines whose Teff falls in the same bin are combined into a single value. The DEM curve is then determined by fitting the ϕi values of all temperature bins with a polynomial or a spline function.
(7)The values of ϕi are determined minimizing via an iterative technique the sum the quantity H = S + χ2, where S is the entropy of the the quantity ϕi and χ2 has the standard definition. In this procedure, each observed line is arbitrarily associated to a temperature value Teff (discussed below), and the results for all lines whose Teff falls in the same bin are combined into a single value. The DEM curve is then determined by fitting the ϕi values of all temperature bins with a polynomial or a spline function.
Iterative techniques start from an arbitrary initial DEM curve and use each spectral line to calculate a correction C(Teff) associated to a temperature Teff (discussed below). C(Teff) values whose Teff lies in the same temperature bin (whose arbitrary width is chosen by the user) are averaged together. The resulting average corrections for all bins are then interpolated with a polynomial or a spline function and applied to the initial DEM curve to calculate the new curve to be used in the next iteration as initial DEM.
The definition of Teff for each line is rather arbitrary. In many cases Teff is assumed to be Tmax, the temperature of maximum abundance of the ion emitting the line. In other cases, it is defined as some sort of DEM – and Contribution Function – weighted mean of the temperature, such as in Landi & Landini (1997).
2.3. Pitfalls of the diagnostic techniques
Both the inversion and iterative DEM diagnostic methods rely on three main assumptions: 1) the interpolation with a polynomial or a spline function assumes implicitly that the plasma is multithermal and may oversmooth the results; 2) the measured DEM depends on the widths of the temperature bins chosen to group the lines; and 3) with only few exceptions, Teff is arbitrarily chosen as Tmax, regardless of the thermal structure of the plasma.
The first problem makes the DEM analysis unsuitable for determining whether a plasma is isothermal or multithermal, because the DEM analysis implicitly assumes the latter condition. Also, associating each spectral line to a predetermined temperature like Tmax is likely to bias the results against an isothermal solution: in fact, if the plasma has a very narrow temperature distribution, the temperature of the plasma may be very different from the Tmax of most lines in the data set. Associating each line to Tmax results in associating a line to a temperature where there might not be any plasma at all and this leads to an artificially multithermal DEM.
If the width of the temperature bin is chosen too large, variations of the DEM with temperature occurring in temperature intervals smaller than the bin width are averaged out so that the final DEM is oversmoothed. If on the contrary the bin width is too narrow, spurious effects due to problems in individual lines and photon noise can severely affect the solution.
Moreover, the EM and DEM techniques require the use of lines emitted by a large number of different ions whose ion fractions are non-negligible in widely different temperature ranges. The use of only few lines greatly limits the diagnostic capabilities of these techniques, as demonstrated by Judge (2010) and Landi & Klimchuk (2010).
2.4. The Monte Carlo Markov chain DEM diagnostic technique
The problems associated with DEM interpolation and with the definition of Teff do not affect the MCMC technique developed by Kashyap & Drake (1998). This technique is based on a Bayesian statistical formalism that allows the determination of the most probable DEM curve that reproduces the observed line intensities. The heart of this technique relies on the application of the Bayes theorem to line intensities, stating that the probability 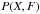 of obtaining a set of observed line intensities
of obtaining a set of observed line intensities 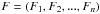 from a DEM characterized by a set of parameters
from a DEM characterized by a set of parameters 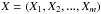 is given by
is given by 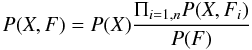 (8)where
(8)where 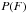 is a normalization factor,
is a normalization factor, 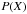 is an a priori probability of the set of parameters X, and
is an a priori probability of the set of parameters X, and 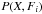 is the probability of obtaining the observed intensity Fi with the set of parameters X and has been defined by Kashyap & Drake (1998) as
is the probability of obtaining the observed intensity Fi with the set of parameters X and has been defined by Kashyap & Drake (1998) as 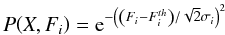 (9)where
(9)where 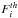 is the intensity of line i calculated with the DEM described by the set of parameters X, and σi is the uncertainty of the observed intensity Fi. This method is implemented by choosing a grid of N temperature bins and assuming that within each bin the plasma is isothermal and can be described by an emission measure value EMi. Once the bin size is chosen, the set of parameters that describe the DEM is thus
is the intensity of line i calculated with the DEM described by the set of parameters X, and σi is the uncertainty of the observed intensity Fi. This method is implemented by choosing a grid of N temperature bins and assuming that within each bin the plasma is isothermal and can be described by an emission measure value EMi. Once the bin size is chosen, the set of parameters that describe the DEM is thus 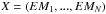 .
.
In order to determine the set of parameters X that provide the maximum probability 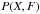 , Kashyap & Drake (1998) adopted a MCMC approach. In this approach, the set of parameters X that describes an initial trial DEM is varied step by step; in each step only one of the parameters in the set X (i.e. one EMi value only) is varied and the others are left unchanged; the change introduced to the varied parameter only depends on the set of parameters X of the previous step. The new set of parameters X′ has a different probability P(X′,F) from the previous one, and is accepted or rejected according to the Metropolis algorithm (Metropolis et al. 1953), based on the change of probability P. This algorithm consists of generating a random number u, such that 0 ≤ u < 1, and a function A(X,X′) defined as
, Kashyap & Drake (1998) adopted a MCMC approach. In this approach, the set of parameters X that describes an initial trial DEM is varied step by step; in each step only one of the parameters in the set X (i.e. one EMi value only) is varied and the others are left unchanged; the change introduced to the varied parameter only depends on the set of parameters X of the previous step. The new set of parameters X′ has a different probability P(X′,F) from the previous one, and is accepted or rejected according to the Metropolis algorithm (Metropolis et al. 1953), based on the change of probability P. This algorithm consists of generating a random number u, such that 0 ≤ u < 1, and a function A(X,X′) defined as ![\begin{equation} A{\left({X,X'}\right)} = \min{\left[{1,{{P{\left({X',F}\right)}}\over{P{\left({X,F}\right)}}}}\right]}\cdot \label{chap5:markow-3} \end{equation}](/articles/aa/full_html/2012/02/aa17424-11/aa17424-11-eq63.png) (10)The new set of parameters is accepted if u < A(X,X′), and rejected otherwise. In this way, not only is a new set of parameters X′ with greater probability than the previous one always accepted (since A(X,X′) = 1), but also a new set with a smaller probability has a finite chance of being accepted. This latter property helps finding the best distribution of parameters X by moving the solution out of local maxima. When the system has found the best solution, the distribution of the EM values in each bin found in all steps is used to determine the confidence interval at each temperature, thus providing an estimate of the uncertainty of the DEM at all temperatures.
(10)The new set of parameters is accepted if u < A(X,X′), and rejected otherwise. In this way, not only is a new set of parameters X′ with greater probability than the previous one always accepted (since A(X,X′) = 1), but also a new set with a smaller probability has a finite chance of being accepted. This latter property helps finding the best distribution of parameters X by moving the solution out of local maxima. When the system has found the best solution, the distribution of the EM values in each bin found in all steps is used to determine the confidence interval at each temperature, thus providing an estimate of the uncertainty of the DEM at all temperatures.
This method dispenses from two of the assumptions common to the other two methods. First, it is not affected by the choice of Teff, since each line contributes to determine the solution in the entire temperature range where its 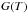 function is defined. Also, no interpolation of the solution is required and no assumption on the smoothness of the solution is made. However, the choice of the bin width is crucial for this technique as it is for the iterative and inversion ones, and it is necessary to assess its effect.
function is defined. Also, no interpolation of the solution is required and no assumption on the smoothness of the solution is made. However, the choice of the bin width is crucial for this technique as it is for the iterative and inversion ones, and it is necessary to assess its effect.
2.5. Methodology of the tests
In order to test the ability of the MCMC method to reconstruct the DEM, we apply this technique to line intensities calculated using known thermal distributions and version 6.0.1 of the CHIANTI database (Dere et al. 1997, 2009) using the Bryans et al. (2009) ion fractions; thus, uncertainties due to the atomic physics do not affect our tests. We assumed a density value of log Ne = 9.0 (Ne in cm-3), typical of moderately active region plasmas. In order to understand how the MCMC diagnostic technique is affected by errors in the data (both in the atomic data used for emissivity calculations as well as observational uncertainties), for each of the synthetic spectra we used we generated five additional datasets; in each additional dataset we have added random errors of up to 20%, i.e. we have randomized each line intensity within a 20% range around the nominal value. Thus, each thermal distribution we have considered will be reconstructed using first the original synthetic line intensities with no errors added, and then each of the five different sets of intensities with random errors. With five different “noisy” datasets, the stability of the solution against errors in the data can be evaluated. As a further test on the effects due to atomic physics only, we repeated the MCMC determinations using the synthetic intensities calculated with version 2 of the CHIANTI database (Landi et al. 1999) and the ion fractions of Mazzotta et al. (1998). The atomic data and ion fractions in the two CHIANTI versions are very different, so that the use of CHIANTI V.2 represents a rather bad case of uncertainties in atomic parameters.
We considered the particularly favorable situation of many lines available for diagnostics: we used lines from 45 different ions, listed in Table 1, that allow to sample very finely the temperature interval 4.6 ≤ log T ≤ 8.0, as shown by Fig. 1. However, above log T = 7.0 and below log T = 5.5 the number of available ions decreases, and thus the MCMC reconstruction is expected to be less accurate.
 |
Fig. 1 Temperature coverage of the ions listed in Table 1. For each ion only the temperature interval where the fractional abundance is larger than 0.01 has been considered. Ion abundances are from Bryans et al. (2009). Top: number of ions emitting in each temperature bin (bin width W = 0.1). Bottom: temperature range covered by the ions of each element. |
Lines used in the present work.
The arbitrary width of the temperature bin has been varied, in order to determine the optimal value that allows us to best reconstruct the initial thermal distribution and its temperature dependence while limiting both the noise and variability due to a too small bin width and the oversmoothing due to a too large width. We run our tests using a grid of width W values: W = 0.01,0.02,0.05,0.1,0.2.
We considered several types of thermal structure:
-
1.
single isothermal plasma;
-
2.
two isothermal plasmas, with variable peak temperature separation and variable relative peak amplitude;
-
3.
a single Gaussian distribution of variable width.
These thermal distributions are aimed at determining 1) to what extent and with what precision is the MCMC diagnostic technique able to detect an isothermal plasma; 2) how capable is it at separating two isothermal components close in temperature; 3) to what extent is it able to discriminate between an isothermal component and a multithermal plasma characterized by a Gaussian distribution; and 4) how do random errors and atomic physics uncertainties affect all the above results.
2.6. Uncertainties of the results
One of the main advantages of the MCMC technique is the ability to provide an estimate of the confidence level of the solution. To determine it, we used the following procedure. Once the best solution is found, we have run additional 50 000 runs of the Markov chain procedure allowing each bin to randomly change by factors up to 6 orders of magnitude. For each change, we calculated the χ2 of the solution and its probability, defined by Eq. (9). We arbitrarily retained only the modified EM distributions with a probability of at least 0.1 × Pbest, where Pbest is the probability of the best solution. Then, for each temperature bin we have calculated the average log EM value and its variance, and taken the value of the latter as an indication of the uncertainty on the EM value of that bin in the best solution.
2.7. Evaluation of the results
The resulting 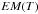 curve is compared to the EM distribution used to calculate the synthetic spectra. The parameters we used to assess the quality of a reconstruction are shown in Table 2. In this table, we report the cases where the plasma is isothermal with log T = 6.0, or made as the sum of two isothermal components with temperatures log T1 = 6.0 and log T2 = log T1 + Δlog T. The temperature distance of the two isothermal components in the multithermal case is chosen to be Δlog T = 0.10,0.15,0.20. A successful fit to the original DEM curve is evaluated using the following criteria:
curve is compared to the EM distribution used to calculate the synthetic spectra. The parameters we used to assess the quality of a reconstruction are shown in Table 2. In this table, we report the cases where the plasma is isothermal with log T = 6.0, or made as the sum of two isothermal components with temperatures log T1 = 6.0 and log T2 = log T1 + Δlog T. The temperature distance of the two isothermal components in the multithermal case is chosen to be Δlog T = 0.10,0.15,0.20. A successful fit to the original DEM curve is evaluated using the following criteria:
-
1.
small χ2;
-
2.
the DEM(T) curve should have a single peak (or two peaks for the multithermal case) at the temperatures log T1 and log T2;
-
3.
there should be no spurious components far from T1 and T2;
-
4.
the peak should be unique, i.e. there should not be spurious peaks anywhere near T1 and T2 (noise in the solution);
-
5.
the width of the peak (taken as the temperature range around T1 and T2 where the EM(T) value is 1/10 of the peak value or larger) should be as small as the temperature bin W.
Performance of the MCMC technique when applied to isothermal plasmas, and to multithermal plasmas composed of two different isothermal components.
3. Results
3.1. Isothermal plasmas
The isothermal plasma was chosen to have log T = 6.0 (in K) and log EM = 43.0 (in cm-3). This temperature was chosen as it allowed us to include lines routinely observed by available spectrometers such as SOHO/CDS, SOHO/SUMER, and Hinode/EIS. Figure 2 shows the EM loci technique applied to the calculated intensities, without random errors included: the original temperature and EM values are recovered without problems. Figure 3 shows the MCMC reconstruction obtained without random errors and varying the bin size W. Results are summarized in Table 2. In all cases the MCMC technique is able to provide an isolated peak several order of magnitude larger than the background. In the case of bin width W = 0.01 the shape of the peak is irregular and one additional satellite peak is present at higher temperatures: this feature is an artifact and it disappears when the bin width increases. In all cases the peak maintains a non-negligible width Δ(log T) ≈ 0.03−0.05 that is approximately constant as the bin width W increases. We interpret this as the ultimate resolution capability of the MCMC technique to resolve a purely isothermal plasma: the result is indistinguishable from a multithermal plasma with a very narrow width. Even if the χ2 of the solution with W = 0.1 is the lowest, the solution with W = 0.05 is to be preferred because the bin width is closer to the apparently intrinsic resolving power of the MCMC technique. In the case with W = 0.05 the two bins at the side of the peak show EM values of ≈ 1% of the peak value, and might be taken as real. Therefore, care should be taken in interpreting such features.
 |
Fig. 2 EM loci technique applied to the single isothermal plasma, without random errors. |
 |
Fig. 3 EM(T) reconstruction of a single isothermal plasma, without random errors. The width of the temperature bin changes from W = 0.01 to 0.10. |
 |
Fig. 4 EM(T) reconstruction of a single isothermal plasma, with random errors within 20% added to line intensities (see text for details). The width of the temperature bin is W = 0.05. All five “noisy” datasets are shown. |
The solutions provided by the MCMC technique always have a background at very low EM values at all temperatures (log EM ≃ 33−37). This background represents the maximum values of the EM at all temperatures outside the isothermal peak that provide contributions to the χ2 smaller than the computer precision. However, this background has no physical significance.
 |
Fig. 5 EM(T) reconstruction of a plasma made of two isothermal components whose peak temperatures are separated by D(log T), which is varied from 0.025 to 0.15. The bin width W, reported in each panel, is chosen to be always smaller than the peak separation D(log T). |
Figure 4 shows how the results change when the random errors are added to the calculated intensities. The plasma EM obtained with W = 0.05 is displayed as a full black line, and the EM curves obtained by the five different “noisy” datasets are shown in red. The main peak remains unaltered, and since the wings, always present, are much lower than the peak value the technique is still able to recover the single peak. However, the background noise now is more significant and secondary peaks, much lower than the one at log T = 6.0, are sometimes present such as those at log T = 6.30 and 6.45.
3.2. Two-component plasmas
Figure 5 displays the results of the reconstruction of the EM(T) curve in the case of two isothermal components with the same EM (log 43.0 each, in cm-3, shown as red diamonds) and with variable temperature separation Δlog T and no random errors. The bin width W in each reconstruction was kept smaller than the temperature separation, and when possible we experimented with increasing W to determine how it affected the ability of the technique to separate the two components. We also studied Δlog T = 0.20 and 0.25, but the results are no different than those obtained with Δlog T = 0.15. Table 2 reports the results for the reconstructions obtained with Δlog T = 0.10,0.15 and 0.20.
Figure 5 shows that even when random errors are absent the MCMC technique is unable to resolve the two components when their temperature separation is smaller than Δlog T = 0.10, and provides a single, very noisy peak with a larger width. Also, small values of the bin width W worsen the noise in the solution, further preventing the separation of the two components. At Δlog T = 0.10 a complete separation of the two peaks can be achieved only when W = 0.05, because noise confuses the result for smaller bin widths and the presence of high EM values in the only bin between the peaks prevents definitive conclusions about separate components. Only when Δlog T = 0.15 the two components can be fully and convincingly resolved with W = 0.05. Noise in the definition of each peak is significant at any value of Δlog T for W < 0.05; the bin W = 0.1 allows us to resolve the two peaks only when Δlog T = 0.20 and causes trouble if the separation is Δlog T = 0.15, providing a large χ2.
 |
Fig. 6 EM(T) reconstruction of a a plasma made of two isothermal components whose peak temperatures are separated by D(log T) = 0.15 (top) and 0.20 (bottom). The bin width W is 0.05. Line intensities have been added a random errors within 20% (see text for details). The reconstruction has been made without (black full curve) and with (red dashed curves) a random errors within 20% to each line intensity. |
The presence of random errors further limits the ability of the MCMC technique to resolve the two components. Figure 6 shows the MCMC reconstruction for Δlog T = 0.15 and 0.20 in the presence of random errors, with W = 0.05. The two peaks are still visible but badly resolved when Δlog T = 0.15, while they are well separated in the other case. Thus, we conclude that Δlog T = 0.20 is a reliable estimate of the smallest temperature distance between two isothermal components which the MCMC technique can realistically resolve when the lines listed in Table 1 are available. If only a smaller number of lines can be used, the minimum Δlog T value may be significantly larger. It is also important to note the spurious components that arise around the two isothermal components when the random errors are present (e.g. at log T = 5.7,5.8,6.35 etc.). Their peak values are significantly lower than the true components, but nevertheless they complicate the interpretation of the result.
The MCMC technique maintains its ability to resolve double peaks even when their relative size is much different. Tests have shown that when the peak separation is Δlog T = 0.20 the two peaks can still be resolved in the presence of random errors even if one of them is a factor 10 or even 100 smaller than the other as shown in Fig. 7 where MCMC reconstructions of a plasma distribution with two isothermal components separated by Δlog T = 0.20 with different heights are shown without (black full lines) and with (red dashed lines) the presence of random errors. The peaks can be recognized because the peak EM values are very close in all reconstructions, while in the other temperature bins the EM values are scattered over a broad EM range.
 |
Fig. 7 EM(T) reconstruction of a plasma made of two isothermal components whose peak temperatures are log T = 6.0 and 6.2. The hotter peak EM is a factor 10 (top) and 100 (bottom) smaller than the colder one. The bin width W is 0.05. The reconstruction has been made without (black full curve) and with (red dashed curves) a random errors within 20% to each line intensity. |
3.3. Gaussian DEM distribution
The reconstruction of the Gaussian EM(T) is shown in Fig. 8. The Gaussian EM(T) curves were defined with a variable FWHM (in log T): 0.05, 0.10, 0.15. The EM(T) curves are also displayed in Fig. 8, starting from top (FWHM = 0.05) to bottom (FWHM = 0.15). The reconstruction was performed with different widths W = 0.01,0.02,0.05. When W < 0.05, the solutions are too noisy to be acceptable in all cases, and also provide a solution too narrow when FWHM = 0.05. When W = 0.05, the reconstruction is smoother and follows more closely the original EM(T) curve.
When FWHM = 0.05, the solution provided by the MCMC technique is very similar to the one provided in the single isothermal plasma component. Figure 9 compares the isothermal results for the isothermal plasma component (black) and the Gaussian EM(T) (red): the two reconstructed curves are almost identical for FWHM = 0.05, while the Gaussian reconstruction is significantly larger than the isothermal one when FWHM = 0.10. This means that the MCMC curve has problems distinguishing an isothermal plasma from a Gaussian plasma when the width of the latter is very small. This result means that the MCMC diagnostic technique is unable to discriminate between isothermal and narrow multithermal distributions. If we combine this limitation with the intrinsic width found in the single, isothermal plasma results, we can state that the MCMC technique is unable to unambiguously detect an isothermal plasma, and that is at best able to determine that a plasma distribution can have a log T width of 0.05 or smaller.
3.4. Effects of a smaller number of ions
 |
Fig. 8 MCMC reconstructions of Gaussian EM(T) distributions. Original curves are also shown. The temperature bin width W is 0.01, 0.02 and 0.05 (left, middle and center column, respectively). The Gaussian FWHM is 0.05 (top row), 0.10 (second row), and 0.15 (bottom row). |
The tests that we have carried out so far included lines from forty-five ions, much more than those usually available in real-case scenarios of high-resolution observations carried out with existing instruments like Hinode/EIS, SOHO/CDS, and SOHO/SUMER. These tests show the intrinsic strengths and weaknesses of the MCMC technique. However, the number of spectral lines and the amplitude of the temperature range they are formed in are also limiting factors in the overall accuracy of DEM diagnostic techniques, as shown by Judge (2010) and Landi & Klimchuk (2010). The question is, how do the results change when a smaller number of ions is available.
 |
Fig. 9 Comparison of MCMC reconstruction of a single isothermal plasma (black) and a Gaussian EM(T) curve (red). The FWHM of the Gaussian is 0.05 (left column) and 0.10 (right column). The temperature bin W is 0.01 (top row), 0.02 (middle row) and 0.05 (bottom row). |
To investigate this, we considered the most recent high-resolution spectrometer available for studies of the solar atmosphere: Hinode/EIS (Culhane et al. 2007). We carried out the same tests described in the previous sections using only lines from the ions that can be observed by EIS. These are marked by asterisks in Table 1, and they are a total of 24 ions; we have omitted Si viii and S viii since their EIS lines are too heavily blended with other species to be used for DEM analysis. On the overall, the results that we have reached in the previous sections are confirmed. Often, even smaller groups of ions than those available in the EIS wavelength range are used. This is due to the fact that when EIS observations are designed and carried out, instrumental or observational constraints usually make it necessary to transmit to the ground only portions of the EIS spectral range, and to sacrifice several ions. A typical dataset is the one used by Brooks et al. (2009), where the ions used were Si vii, Si x, S x, and Fe viii-xv, for a total of 11 ions. Similar numbers are typical of most SOHO/CDS and SOHO/SUMER observations as well. Results obtained from such a restricted dataset do not have significant differences when dealing with plasmas made of one or more isothermal components, and the MCMC technique is able to provide the same results as with larger datasets, provided that the plasma temperature lies inside the range of formation of these ions.
3.5. Effects of inaccuracies in atomic data
 |
Fig. 10 Comparison of EM(T) reconstructions of a plasma made of a single isothermal component (top) and a single Gaussian component (bottom); each reconstructed using two different versions of CHIANTI: version 6.0.1 (red curves) and 2 (blue curves). Thin lines in the top panel indicate the case with random noise added, from Sect. 3.1. |
We test how systematic errors due to uncertainties in atomic physics affect the DEM diagnostics by creating an inconsistency between the generation and the reconstruction of the test DEM. In particular, we use an older version (V.2) of the CHIANTI atomic code to calculate the contribution functions to be used for the DEM reconstruction.
Figures 10 and 11 display (in blue) the results obtained when the emissivities of CHIANTI version 2 are used to determine the EM(T) curves using lines calculated with CHIANTI version 6.0.1. The red lines indicate the results obtained in the previous sections, for comparison purposes. Figure 10 illustrates the isothermal and single-Gaussian (with W = 0.05) cases: a single, almost identical peak is retrieved in both cases, confirming that the DEM method is still unable to distinguish between a true isothermal plasma and one with a narrow Gaussian distribution. However, one difference to be noted is that the peak of the single component is slightly shifted towards lower temperatures. This is mostly due to the Mazzotta et al. (1998) Fe ion abundances used with CHIANTI V.2 being shifted towards lower temperatures than the Bryans et al. (2009) ones used with CHIANTI V.6. The level of noise in the V.2 solution is comparable to that of the datasets with random noise added.
 |
Fig. 11 Comparison of EM(T) reconstructions of a plasma made of two isothermal components separated by Δlog T = 0.15 (top) and Δlog T = 0.2 (bottom); each reconstructed using two different versions of CHIANTI: version 6.0.1 (red curves) and 2 (blue curves). Thin lines in the top panel indicate the case with random noise added, from Sect. 3.1. |
Figure 11 shows the case of two isothermal components, with separation Δlog T = 0.15 and 0.20. In the latter case, the two peaks are fully retrieved and separated, and the level of noise of the solution is comparable to the noise in the solutions obtained when random errors are included in the simulated spectra. When Δlog T = 0.15, the two peaks are less clearly separated. The temperatures of the two peaks are slightly lower than in the original model, but their separation is correct. The only marked difference between the solutions obtained with V.6 and V.2 emissivities lies in the value of the peak EM in the hot isothermal component, since V.2 emissivities underestimate this by a factor 5 and 2 in the Δlog T = 0.15 and 0.20 cases, respectively.
4. Conclusions
In this work we have tested the MCMC diagnostic technique by Kashyap & Drake (1998) in order to: determine its capability to reconstruct a given plasma thermal distribution (isothermal or multicomponent) from a set of individual line intensities; to study how the presence of random errors affects the MCMC reconstructions; to investigate the optimal size of the temperature bin width W as a compromise between retaining as much temperature structure as possible and minimizing the effect of noise in the solution; and to test the effect of different atomic data sets on the final results. We did this by applying the MCMC technique to sets of lines whose intensities were calculated using a known thermal distribution first, and then randomized the intensities within 20% to simulate experimental uncertainties.
Our study shows that the optimal bin width W is W = 0.05, as smaller values cause the MCMC technique to provide spurious results and a high level of noise in the final reconstruction, while larger values oversmooth the results. Even when the emitting plasma is strictly isothermal, the MCMC technique is unable to distinguish between a truly isothermal solution and a Gaussian DEM with FWHM = 0.05; also, the MCMC technique is able to separate multiple near-isothermal EM components only if their separation in temperature is Δlog T = 0.20. Atomic data uncertainties can affect the results by providing less accurate peak EM values and shifting the EM peak temperature, but the Δlog T = 0.20 resolving power of the MCMC technique is unaffected. The number of available ions does not affect the quality of the reconstruction, provided these ions are formed over a temperature range larger than the range where the plasma EM is significant. A smaller ion formation temperature range decreases the temperature resolution achieved by the MCMC technique.
Acknowledgments
The work of Enrico Landi is supported by NASA grants NNX10AM17G and NNX11AC20G. Fabio Reale acknowledges support from Italian Ministero dell’Universitá e Ricerca and from Agenzia Spaziale Italiana (ASI), contract I/015/07/0. Paola Testa was supported by NASA contract NNM07AB07C to the Smithsonian Astrophysical Observatory. We thank the referee for valuable comments that helped us improve the manuscript.
References
- Brooks, D. H., Warren, H. P., Williams, D. R., & Watanabe, T. 2009, ApJ, 705, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Bryans, P., Landi, E., & Savin, D. W. 2009, ApJ, 691, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19 [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&ASS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doschek, G. A., Feldman, U., Laming, J. M., Schühle, U., & Wilhelm, K. 2001, ApJ, 546, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Edlen, B. 1942, Z. Astrophys., 22, 30 [Google Scholar]
- Feldman, U., & Landi, E. 2008, Phys. Plasmas, 15, 056501 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Schühle, U., Widing, K. G., & Laming, J. M. 1998, ApJ, 505, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Doschek, G. A., Schühle, U., & Wilhelm, K. 1999, ApJ, 518, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Golub, L., DeLuca, E. E., Sette, A., & Weber, M. 2004, ASP Conf. Ser., 325, 217 [Google Scholar]
- Hahn, M., Landi, E., & Savin, D. W. 2011, ApJ, 736, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, R. A., & Thompson, A. M. 1992, Intensity integral inversion techniques: a study in preparation for the SOHO mission, RAL-91-092, Rutherford Appleton Laboratory [Google Scholar]
- Judge, P. G. 2010, ApJ, 708, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Kashyap, V. L., & Drake, J. J. 1998, ApJ, 503, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Kashyap, V. L., Lin, L., & Drake, J. J. 2004, Bull. Am. Astr. Soc., 36, 801 [NASA ADS] [Google Scholar]
- Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E. 2008, ApJ, 685, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., & Feldman, U. 2008, ApJ, 672, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., & Klimchuk, J. A. 2010, ApJ, 723, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Landini, M., Dere, K. P., Young, P. R., & Mason, H. E. 1999, A&AS, 135, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landi, E., Feldman, U., & Doschek, G. A. 2006, ApJ, 643, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafransesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [Google Scholar]
- Metropolis, N., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Patsourakos, S., & Klimchuk, J. A. 2005, ApJ, 628, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, K. J. H., Feldman, U., & Landi, E. 2008, Ultraviolet and X-ray Spectroscopy of the Solar Atmosphere, Cambridge Astrophys. Ser., 44 (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Reale, F. 2010, Liv. Rev. Sol. Phys., 7, 5 [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 247, 686 [Google Scholar]
- Warren, H. P. 1999, Sol. Phys., 190, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, H. P., & Brooks, D. H. 2009, ApJ, 700, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M. A., DeLuca, E. E., Golub, L., & Sette, A. L. 2004, Proc. IAU Symp., 223, 321 [Google Scholar]
All Tables
Performance of the MCMC technique when applied to isothermal plasmas, and to multithermal plasmas composed of two different isothermal components.
All Figures
 |
Fig. 1 Temperature coverage of the ions listed in Table 1. For each ion only the temperature interval where the fractional abundance is larger than 0.01 has been considered. Ion abundances are from Bryans et al. (2009). Top: number of ions emitting in each temperature bin (bin width W = 0.1). Bottom: temperature range covered by the ions of each element. |
| In the text | |
 |
Fig. 2 EM loci technique applied to the single isothermal plasma, without random errors. |
| In the text | |
 |
Fig. 3 EM(T) reconstruction of a single isothermal plasma, without random errors. The width of the temperature bin changes from W = 0.01 to 0.10. |
| In the text | |
 |
Fig. 4 EM(T) reconstruction of a single isothermal plasma, with random errors within 20% added to line intensities (see text for details). The width of the temperature bin is W = 0.05. All five “noisy” datasets are shown. |
| In the text | |
 |
Fig. 5 EM(T) reconstruction of a plasma made of two isothermal components whose peak temperatures are separated by D(log T), which is varied from 0.025 to 0.15. The bin width W, reported in each panel, is chosen to be always smaller than the peak separation D(log T). |
| In the text | |
 |
Fig. 6 EM(T) reconstruction of a a plasma made of two isothermal components whose peak temperatures are separated by D(log T) = 0.15 (top) and 0.20 (bottom). The bin width W is 0.05. Line intensities have been added a random errors within 20% (see text for details). The reconstruction has been made without (black full curve) and with (red dashed curves) a random errors within 20% to each line intensity. |
| In the text | |
 |
Fig. 7 EM(T) reconstruction of a plasma made of two isothermal components whose peak temperatures are log T = 6.0 and 6.2. The hotter peak EM is a factor 10 (top) and 100 (bottom) smaller than the colder one. The bin width W is 0.05. The reconstruction has been made without (black full curve) and with (red dashed curves) a random errors within 20% to each line intensity. |
| In the text | |
 |
Fig. 8 MCMC reconstructions of Gaussian EM(T) distributions. Original curves are also shown. The temperature bin width W is 0.01, 0.02 and 0.05 (left, middle and center column, respectively). The Gaussian FWHM is 0.05 (top row), 0.10 (second row), and 0.15 (bottom row). |
| In the text | |
 |
Fig. 9 Comparison of MCMC reconstruction of a single isothermal plasma (black) and a Gaussian EM(T) curve (red). The FWHM of the Gaussian is 0.05 (left column) and 0.10 (right column). The temperature bin W is 0.01 (top row), 0.02 (middle row) and 0.05 (bottom row). |
| In the text | |
 |
Fig. 10 Comparison of EM(T) reconstructions of a plasma made of a single isothermal component (top) and a single Gaussian component (bottom); each reconstructed using two different versions of CHIANTI: version 6.0.1 (red curves) and 2 (blue curves). Thin lines in the top panel indicate the case with random noise added, from Sect. 3.1. |
| In the text | |
 |
Fig. 11 Comparison of EM(T) reconstructions of a plasma made of two isothermal components separated by Δlog T = 0.15 (top) and Δlog T = 0.2 (bottom); each reconstructed using two different versions of CHIANTI: version 6.0.1 (red curves) and 2 (blue curves). Thin lines in the top panel indicate the case with random noise added, from Sect. 3.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


