EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 538 (February 2012) A&A, 538 (2012) A48 Full HTML
Free Access
Issue
A&A
Volume 538, February 2012
Article Number A48
Number of page(s) 15
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201117398
Published online 31 January 2012

© ESO, 2012

1. Introduction

Post-asymptotic giant branch (post-AGB) stars are evolved stars of low and intermediate initial mass (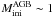–8 M⊙) that have suffered the thermally pulsing asymptotic giant branch (TP-AGB) phase. The star leaves the AGB sequence once strong stellar winds have almost eroded the entire envelope, and rapidly evolves at constant luminosity toward higher temperatures. However, these are not yet hot enough to ionize the circumstellar material and become planetary nebulae (PN) before they evolve through the cooling white dwarf track. For a recent review on post-AGB stars see van Winckel (2003).

The s-process enhancement observed in post-AGB stars is intrinsic, directly synthesized in the C-rich He intershell, the zone between the H shell and the He shell, a small fraction of which is mixed with the envelope by recurrent third dredge-up (TDU) episodes. Therefore, spectroscopic observations in post-AGBs are very useful to test AGB models of nucleosynthesis (e.g., Gallino et al. 2008).

In this work, we analyze the high-resolution spectra of the two post-AGB stars GLMP 334 and IRAS 15482−5741. IRAS 15482−5741 was classified as a post-AGB star by Suarez et al. (2006). In that paper the authors classified it as a star with a spectral type of F7I (Table 4 of Suarez et al. 2006). Indeed, as we shall see, our derived atmospheric parameters correspond to a supergiant star with a temperature close to the spectral values given by these authors. GLMP 334 was first classified as a post-AGB star by García-Lário et al. (1997) based on their IRAS colors. Indeed, the IRAS colors for both GLMP 334 and IRAS 15482−5741 correspond to the locus occupied by the post-AGB stars and PN candidates in the IRAS color–color diagram  [25]–[60]  versus  [12]–[25]  (see Fig. 3 of Suaréz et al. 2006). Table 1 provides some information for these two stars.

Table 1

Basic parameters of the two objects analyzed in this work.

The paper is organized as follows: in Sects. 2 and 3 we provide a discussion of the obtained spectra, data reduction, and abundance patterns observed in these two post-AGB stars. Theoretical interpretations with AGB models are presented in Sect. 4. In Sect. 5 we discuss the chemical peculiarities of GLMP 334 and IRAS 15482 − 5741. A summary of the results is provided in Sect. 6.

2. Observations

The high-resolution spectra of GLMP 334 and IRAS 15482−5741 analyzed in this work were obtained with the FEROS (Fiberfed Extended Range Optical Spectrograph) echelle spectrograph (Kaufer et al. 1999) at the 2.2 m ESO telescope at La Silla (Chile) on the nights of August 3, 2009 (GLMP 334) with two exposures of 3600 s and May 15, 2009 (IRAS 15482−5741) also with two exposures of 3600 s. The FEROS spectral resolving power is R = 48 000, corresponding to 2.2 pixels of 15  μm, and the wavelength coverage goes from 3 800 Å to 9 200 Å. The nominal S / N ratio was evaluated by measuring the rms flux fluctuation in selected continuum windows, and the typical values were S / N = 100–150 for both stars. The spectra were reduced with the MIDAS pipeline reduction package that consists of the following standard steps: CCD bias correction, flat-fielding, spectrum extraction, wavelength calibration, correction of barycentric velocity, and spectrum rectification. Figure 1 shows sample spectra of the programed stars in the 5110–5150 Å region.

thumbnail Fig. 1

Sample spectra of the heavily s-enriched post-AGB stars GLMP 334 and IRAS 15482−5741 compared with the non s-enriched post-AGB star IRAS 19386+0155 analyzed by Pereira et al. (2004). Dotted vertical lines show the transitions of Zr ii 5112.3 Å, La ii 5114.5 Å, Ce ii 5117.2 Å, Y ii 5119.1 Å, and 5123.1 Å, Nd ii 5130.6 Å, and Pr ii 5135.1 Å. Other transitions are shown in the figure.

3. Analysis and results

3.1. Line selection, measurements and oscillator strengths

We identified several absorption lines of Fe i and Fe ii as well as Na i, Mg i, Si i, S i, Ca i, Ti ii, Cr ii and Ni i. Several other transitions caused by the light elements C i, N i and O i were also observed. However, the most interesting aspect of these two post-AGB stars relies on the detection of lines of the heavy-elements (Z  >  26), such as Y ii, Zr ii, Ba ii, La ii, Ce ii, Pr ii, Nd ii, Sm ii and Eu ii. Table 2 lists the Fe i and Fe ii lines employed in the analysis and we also provide the lower excitation potential, χ(eV), of the transitions, the gf-values, and the measurements of the equivalent widths. The last set of measurements were obtained by fitting Gaussian profiles to the observed ones. The gf-values of the Fe i and Fe ii lines were taken from Lambert et al. (1996), Venn et al. (1993) and Castro et al. (1997).

3.2. Determination of the atmospheric parameters

The determination of stellar atmospheric parameters, effective temperature (Teff), surface gravity (log g), microturbulence (ξ), and [Fe/H] (we use the notation [X/H] = log(N(X)/N(H))⋆  −  log(N(X)/N(H))⊙ throughout) are prerequisites for determining the photospheric abundances. The atmospheric parameters were determined by assuming local-thermodynamic-equilibrium (LTE) model atmospheres of Kurucz (1993) using the spectral analysis code MOOG (Sneden 1973).

The solution of the excitation equilibrium used to derive the temperature (Teff) was defined by the zero slope of the trend between the Fe i abundances and the excitation potential of the measured lines. The microturbulent velocity (ξ) was determined by constraining the abundance determined from individual Fe i lines to show no dependence on Wλ / λ. The solution found is in this way unique because it depends only on the set of Fe I, II lines and the atmospheric model employed and yields as a by-product the metallicity of the star [Fe/H]. The final adopted atmospheric parameters are given in Table 3. We found typical uncertainties of σ(Teff) = 150 K, σ(log g) = 0.2 dex, and σ(ξ) = 1.0 km s-1.

Table 3

Atmospheric parameters and radial velocities of GLMP 334 and IRAS 15482 − 5741.

Table 5

Abundances in the log ε(H) = 12.0 scale and in the notation [X/Fe] for GLMP 334 ([Fe/H] =  −0.4) and IRAS 15482−5741 ([Fe/H] =  − 0.5).

thumbnail Fig. 2

Logarithmic surface gravity versus effective temperature diagram showing the location of GLMP 334 and IRAS 15482 − 5741 (red filled triangle) and previously identified post-AGB objects (black filled squares). Data from post-AGB stars were taken from Luck (1993), Reddy et al. (1999, 2002), Reyniers et al. (2004), and van Winckel & Reyniers (2000). HD 172481 (Reyniers & van Winckel 2001) is also shown (red filled square). Post-AGB tracks of Schönberner (1983) and Blöcker & Schönberner (1990) are also shown.

3.3. Abundance analysis

The abundances of chemical elements were determined with LTE model-atmosphere techniques. In brief, equivalent widths are calculated by integration through a model atmosphere and are compared with the observed equivalent widths. The calculation is repeated changing the abundance of the element in question, until a match is achieved. The current version of the line-synthesis code moog (Sneden 1973) was used to carry out the calculations.

Table 4 shows the atomic lines used to derive the abundances of the elements. Table 5 provides the number of lines employed for each species, n, the derived abundances with their respective standard deviations, the [X/Fe] and the total error (σtot) in [X/Fe]. It is known that sodium lines suffer from NLTE effects, which lead to an overestimation of the sodium abundances. To account for NLTE effects we used the theoretical work of Takeda & Takada-Hidai (1994) and Takeda et al. (2003), who calculated the values of the NLTE corrections for several lines using a grid of different atmospheric parameters and equivalent widths of the sodium lines. We found typical corrections of 0.1−0.15 dex for the lines 5682.65 Å  and 5688.22 Å. Therefore we have for GLMP 334 and IRAS 15482−5741, respectively, [Na/Fe] = +0.32 and +0.29. According to Takeda & Takada-Hidai (1995), the nitrogen abundance is also reduced by NLTE corrections: the authors estimated a decrease of [N/Fe] by  ~0.3−0.4 dex by using the 8683.40 Å , 8686.15 Å , 8703.24 Å  and 8718.82 Å  lines. Specifically, we obtained [N/Fe] =  +0.22 for GLMP 334 and +0.43 for IRAS 15482 − 5741.

3.4. Abundance uncertainties

The uncertainties in the derived abundances for the program stars are dominated by the following main sources: the stellar parameters, the equivalent widths measurements, the gf-value effects and the dispersion among the abundance given by the lines used for the abundance determination. This last error is the line-to-line scatter (σltl).

The uncertainties caused by the errors in the gf-values depend upon the particular element. The gf-value uncertainties were discussed in detail in Smith et al. (1995), but they range from 0.02−0.20 dex, and we refer to this paper for a detailed discussion of the individual elements. The abundance uncertainties caused by the errors in the stellar atmospheric parameters Teff, log g, and ξ were estimated by changing these parameters by their standard errors and then computing the changes incurred in the element abundances.

Under the assumption that the errors are independent, they can be combined quadratically so that the total uncertainty is 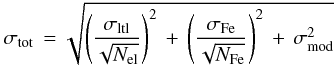(1)where 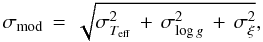(2)and σltl and σFe are the line-to-line scatter on the absolute abundances and on the Fe abundances. Table 5 shows the total error σtot on the mean of the [X/Fe].

4. Discussion

4.1. The position of GLMP 334 and IRAS 15482−5741 in the evolutionary tracks

We were able to locate the two post-AGB stars in log g – log Teff plane with the derived stellar parameters and compared them to post-AGB evolutionary tracks of both Schönberner (1983) and Blöcker & Schönberner (1990). These evolutionary tracks are indicated in Fig. 2 as solid lines for 0.546 M⊙, 0.565 M⊙ and 0.605 M⊙. The position of other post-AGB stars already studied is also given in Fig. 2 (see Sect. 5).

4.2. Comparison with AGB nucleosynthesis models

Asymptotic giant branch stars with low mass (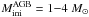) are the main site of carbon and s-process elements during their thermally pulsing phase (TP-AGB). The major neutron source is 13C(α, n)16O, which burns radiatively in a thin region of the He-intershell (the region between the H-shell and the He-shell) during the interpulse period. After the quenching of a thermal instability, the H-shell becomes temporarily inactive and the convective envelope can penetrate the top layers of the He-intershell. This mixing, called third dredge-up (TDU), enriches the surface of the star with 12C and the s-elements synthesized in the inner layers. Moreover, during the TDU few protons are assumed to be diffused in the top layers of the He-intershell. At the activation of the H-shell, the abundant 12C reacts with protons (12C(p, γ)13N(β + ν)13C), forming a thin 13C-rich layer, the 13C-pocket. When the temperature reaches about 0.9 × 108 K, neutrons are released via the 13C(α, n)16O reaction. The second neutron source 22Ne(α, n)25Mg is marginally activated in low-mass AGB stars during the thermal pulses, when a temperature of about  ~3 × 108 K is reached. For exhaustive discussions about the s-process nucleosynthesis in AGB stars see the reviews in Busso et al. (1999), Herwig (2005), Straniero et al. (2006), and Käppeler et al. (2010).

The physical conditions and the mechanisms involved in the formation of the 13C-pocket are not clear yet. Different hypotheses have been advanced, such as algorithm for the treatment of the mixing at the radiative/convective interfaces, models including rotation, magnetic fields or gravity waves (Herwig et al. 1997; Langer et al. 1999; Herwig et al. 2003; Denissenkov & Tout 2003; Siess et al. 2004; Straniero et al. 2006; Cristallo et al. 2009), and it remains one of the more debated questions of AGB models, together with the estimation of the mass loss and the TDU. At present the amount of 13C produced and the mass of the pocket cannot be physically established, therefore we treated the 13C-pocket as a free parameter. We call to “case ST” the 13C-pocket efficiency adopted in low-mass AGB models of half-solar metallicity to reproduce the main component in the solar system (Gallino et al. 1998; Arlandini et al. 1999). Starting from this case, we multiply and divide the amount of 13C and 14N in the pocket by different factors (ST × 2 down to ST/12 for disk stars). More details on the adopted models can be found in Bisterzo et al. (2010).

thumbnail Fig. 3

Theoretical interpretation of the post-AGB star GLMP 334 ([Fe/H] =  −0.4; Teff = 7400 K; log g = 1.4) with = 2 M⊙. Three 13C-pocket efficiencies are shown: cases ST × 2 (solid line), ST × 1.7 (dotted thin line) and ST × 1.3 (dotted thick line). Error bars are shown for elements with more than two detected lines.

thumbnail Fig. 4

Theoretical interpretation of the post-AGB star IRAS 15482–5741 ([Fe/H] =  −0.5; Teff = 7400 K; log g = 1.1) with = 1.4 M⊙. Three 13C-pocket efficiencies are shown: cases ST × 1.3 (dotted thin line), ST (solid line) and ST/2 (dotted thick line). Error bars are shown for elements with more than two detected lines.

The s-process elements are characterized by three peaks that corresponds to the magic neutron numbers, N = 50 (light-s elements, ls = Sr, Y, Zr), N = 82 (heavy-s elements, hs = Ba, La, Ce, Pr, Nd, Sm), and N = 126 (Pb). In Figs. 3 and 4 we show the spectroscopic observations of the two post-AGB stars GLMP 334 and IRAS 15482–5741, respectively, compared with our theoretical interpretations (see below). In both stars, several elements of the first and the second s-process peaks are detected, while no informations are provided for Pb because post-AGB stars have no suitable Pb lines in the optical spectrum at these temperatures and gravities. We define ls as an average between Y and Zr, and hs as an average among La, Nd and Sm (note that different notations may be adopted by various authors). The [ls/Fe] and [hs/Fe] ratios and the s-process indicator [hs/ls], provide essential information about the AGB initial mass and the efficiency of the 13C-pocket. Indeed, by increasing the number of TDUs and then the AGB initial mass, an increasing amount of s-rich material is dredged up in the envelope. Moreover, the relative s-process distribution between the heavy and the light s-elements, the [hs/ls] ratio, depends on the amount of 13C in the pocket: at [Fe/H]  ~  −0.5 and by changing the 13C-pocket efficiency, predicted [hs/ls] covers a range of about 1 dex, from [hs/ls]  ~  −0.5 to +0.5. GLMP 334 shows [ls/Fe] = 1.71 and [hs/Fe] = 1.99, with several detected lines for La (17) and Nd (25), ([hs/ls] = 0.28). IRAS 15482–5741 has [ls/Fe] = 1.48 and [hs/Fe] = 1.64 ([hs/ls] = 0.16). No error bars are shown in the figures for those elements with less than 3 lines available (Na for GLMP 334, Mg, S, Ba, Y, Eu and Hf for GLMP 334).

GLMP 334 is interpreted with an AGB model of initial mass 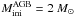, a 13C-pocket ST × 2 (solid line) and half solar metallicity (Fig. 3). Two additional 13C-pockets are displayed to show the behavior of the heavy elements by decreasing the s-process efficiency (cases ST × 1.7, thin dotted line, and ST × 1.3, thick dotted line). While the first case still agrees with the spectroscopic data, case ST × 1.3 predicts a lower [hs/Fe] than observed. This model undergoes 25 thermal pulses with the TDU. A similar behavior is predicted by an AGB model of initial mass 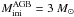. We predict [Pb/Fe]  ~  2.1.

As anticipated in the introduction, we recall that post-AGB stars show an intrinsic s-enhancement that is directly synthesized inside the star and is, therefore, dependent on the AGB initial mass and on the number of TDUs. Therefore, the AGB initial mass is fixed by the [ls,hs/Fe] observed. By decreasing the AGB initial mass, the observed s-elements would be underestimated by theoretical predictions: e.g., a model of 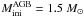that undergoes 19 TDUs at half-solar metallicity shows [ls/Fe]th = 1.4 and [hs/Fe]th = 1.7 (case ST × 2). The occurrence of extra-mixing as “cool-bottom processing” (CBP) may affect the C and N abundances predicted in low-mass AGB stars. The CBP may decrease 12C in the envelope while 14N increases (Wasserburg et al. 1995, 2006; Nollett et al. 2003; Zinner et al. 2006; Busso et al. 2010), consequently the theoretical [C/Fe] would decrease and [N/Fe] increase. However, the exact effect of the CBP on C and N is difficult to estimate with theoretical models, because several physical processes may be involved (e.g., rotation, magnetic fields, thermohaline mixing). In our predictions presented in Figs. 3 and 4, the CBP is not included. However, the sum C+N should be preserved after the CPB. In both stars a decrease of the predicted C to agree with the spectroscopic observations would imply a too high N with respect to the observed one. This is a point on which we do not have solution at present, unless we consider theoretical interpretations with a metallicity higher 0.2 dex higher than observed (see Appendix A, Sect. A.1). The situation is less drastic for other post-AGB stars observed so far at very high resolution, as discussed in Appendix A. Solar Eu is mostly of r-process origin (~95%). In this star, the observed [Eu/Fe] is explained by a pure s-process contribution, for which [La/Eu]s ~ 1 dex.

IRAS 15482–5741 has a slightly lower s-enhancement compared to GLMP 334. In Fig. 4 we present a theoretical interpretation with an AGB model of initial mass 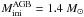, three 13C-pockets (cases ST  ×  1.3, thin dotted line, ST, solid line, ST/2 thick dotted line) and [Fe/H] =  −0.5. The best fit is obtained by a case ST, for which [Pb/Fe]  ~  1.6 is predicted. A range of 13C-pockets is displayed to show the behavior of [hs/Fe] and [Pb/Fe]. This model undergoes 11 thermal pulses with the TDU. Theoretical interpretations with AGB models of lower or higher initial masses are excluded. Indeed, at [Fe/H] =  − 0.5, a 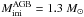model (5 TDUs) reaches maximum values of [ls/Fe]th = 0.6 and [hs/Fe]th = 1.3 (case ST  ×  2). Instead, a 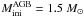model (19 TDUs) predicts [ls/Fe]th = 1.6 and [hs/Fe]th = 1.8 (case ST). Similarly to GLMP 334, the CBP may affect the abundances of [C/Fe] and [N/Fe].

As anticipated in Sect. 4.1 (Fig. 2), the post-AGB tracks by Blöcker & Schönberner (1990) exclude theoretical interpretations with AGB models of intermediate initial mass (IMS, 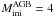to 8 M⊙). Concerning the s-process nucleosynthesis, IMS, have a smaller He-intershell than low-mass AGBs, and a smaller 13C-pocket, and the efficiency of the TDU is reduced accordingly. The 22Ne(α, n)25Mg becomes the main neutron source because of the higher temperatures reached at the bottom of the convective thermal pulses (~3.5 × 108 K), which mainly contributes to the ls elements (Travaglio et al. 2004). Indeed, envelope abundances of AGB models with 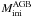= 5 and 7 M⊙ (see Bisterzo et al. 2010, Fig. 3, supplementary material), reach maximum values of [ls/Fe]  ~  1.4 and [hs/Fe]  ~  1 at [Fe/H] =  −0.5, with negative [hs/ls] ratios.

We refer to Appendix A for more details about theoretical predictions with AGB models of different initial masses.

5. Abundances peculiarities in post-AGB stars

As introduced in the previous sections, the C and s-enhance-ments detected in post-AGB stars are intrinsic, which means directly synthesized in the interior of the observed star and therefore dredged-up on the surface through recurrent TDU episodes. Presently, twelve high-resolution post-AGBs showing an s-process enhancement are available in the literature (van Winckel & Reyniers 2000; Reddy et al. 2002; Reyniers et al. 2004, 2007). GLMP 334 and IRAS 15482−5741 belong to this category, even if they show a low [C/Fe]. Note that several post-AGB stars analyzed in the literature are not s-process enriched (e.g., van Winckel 1997; Pereira et al. 2004). This post-AGB dichotomy is widely recognized and confirmed by different authors (van Winckel 2003). A possible explanation may be found in AGB models with no TDU episodes. Indeed, AGB models predict a minimum initial mass for the occurrence of the TDU, depending on the metallicity (e.g., at metallicities close to solar it is 1.3 M⊙; Straniero et al. 2003). Therefore, post-AGB stars with an initial mass below this minimum value do not show any s-enrichment in their envelope.

Another chemical peculiarity observed among the post-AGB stars is observed in those post-AGB stars that are extremely metal-poor and have strong iron depletion, such as [Fe/H] =  −4.9 for HR 4049 (Waelkens et al. 1991). Post-AGB stars that are also binaries show different degrees of depletion of the refractory elements in their photosphere, which means that the elements with a high condensation temperature condense into dust grains. In this binary scenario, the massive AGB wind of the star forms a circumbinary disk under the influence of binary separation. In this disk, dust grains and gas are separated due to radiation pressure so that metals condense into grains while “clean gas”, mainly at the inner disk, will be accreted by the AGB star. This scenario explains not only the strong under-abundance of iron observed in the photosphere of these stars but also the abundance of zinc and other metals in these post-AGB stars (Waelkens et al. 1991; van Winckel et al. 1992, 2009).

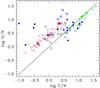thumbnail Fig. 5

Relative abundance O/N versus C/N for several classes of stars (see text for references). Disk carbon stars (green starry points); post-AGB stars enriched in the s-process elements (blue filled triangles); hot post-AGB stars (blue filled squares); post-AGB stars not enriched in the s-process (blue open polygons); Population I supergiants (red plus sign); planetary nebulae (black open squares); HD 172481 (red filled square) and the stars analyzed in this work GLMP 334 and IRAS 15482 − 5741 (red triangles).

5.1. The log C/N – log O/N diagram

Below we discuss the abundance pattern comparing with previous studies for post-AGB stars. In Fig. 5 we show the CNO abundances in plot O/N versus C/N for several classes of objects such as Population I supergiants (Luck & Bond 1989; Luck & Lambert 1985), planetary-nebulae (Kingsburgh & Barlow 1994) and other post-AGB stars. The thick line represents the ratio C/O = 1.0. In this figure we also distinguish the post-AGB stars according to different aspects of their abundance pattern such as those that display the circumstellar feature at 21 μm (van Winckel & Reyniers 2000; Reyniers et al. 2007), another group of post-AGB stars that are not s-process enriched (Luck et al. 1990; van Winckel 1997; Pereira et al. 2004) and four hot post-AGB stars that have effective temperatures around 20 000 K (Thompson et al. 2007; and Ryans et al. 2003). Figure 5 also shows the position of the classical Galactic carbon stars (Lambert et al. 1986).

Figure 5 clearly shows that Pop I supergiants show traces of nitrogen enrichment caused by CNO-cycling. Planetary nebulae are found on both sides of C/O = 1 line. Some of them seem to display only CNO-processed material and are in the same position as Pop I supergiants, while those on the other side of the C/O line show an enhancement of carbon caused by He burning. On the same side as the planetary nebulae with C/O  ≥  1.0 lie the s process enriched post-AGB stars that display the 21 μm feature. Among the post-AGB stars that are not s-process-enriched we see two objects that lie on the side of carbon enrichment. Four hot post-AGB stars present a very high carbon underabundance, as deduced by their position in this diagram. Non-LTE effects are taken into consideration in their abundance determination. The position of the two post-AGB stars analyzed in this work also indicate carbon underabundance as well as some nitrogen enrichment. It is interesting to notice the position of another post-AGB star in this diagram, HD 172481 (red filled square). analyzed by Reyniers & van Winckel (2001). This star does not show carbon enhancement but presents mild s-process enrichment. The authors consider for HD 172481 that an extra-mixing such as the CBP (see Sect. 4.2) is the most likely explanation to account for the high lithium abundance observed in this star and its low-mass nature. As discussed in Sect. 4.2, GLMP 334 and IRAS 15482−5741 are additional examples of the operation of the CBP in AGB stars, needed to reduce the [C/Fe] prediction and to increase [N/Fe]. However, caution about the origin of HD 172481 is suggested (Whitelock & Marang 2001). Note that several uncertainties affect the observations of C and N, as 3D atmospheric models and NLTE corrections (e.g., Asplund 2005; Asplund et al. 2009; Collet et al. 2007; Grevesse et al. 2007; Caffau et al. 2009) as well as the already mentioned CBP that may modify the theoretical AGB predictions.

As far as nitrogen is concerned, the [N/Fe] ratios in both stars show evidence that mixing of CN-cycled material has occurred, which polluted their atmospheres. This can be deduced from their position in the log C/N – log O/N diagram, which is same as that of some Population I supergiants.

5.2. Other elements: Na to Ni

GLMP 334 and IRAS 15482−5741 exhibit a sodium enrichment. In both stars, the observed Na accounting of NLTE corrections is [Na/Fe]  ~  0.3 (Sect. 3.3), slightly exceeding the averaged Na observed in field stars of the same metallicity range ([Na/Fe]field ~ 0; Andrievsky et al. 2007).

Sodium overabundance has been observed in the atmospheres of A-F supergiant stars by (Denissenkov & Ivanov 1987). According to these authors sodium is synthesized in the convective core of main-sequence stars in the NeNa reaction chain. Mixing at the first dredge-up came up to the surface of stars with products of the CNO cycle. Therefore one should expect sodium-enrichment in supergiants and giants rather than in dwarfs. Indeed, Fig. 2 of Boyarchuk et al. (2001) shows that [Na/Fe] is anti-correlated with log g, which is higher for log g = 0.0–0.1 and lower for log g = 2.0–3.0.

The sodium production in post-AGB stars was investigated by Mowlavi (1999). During the AGB phase, sodium is synthesized starting from the 22Ne produced during the He-shell flash via double α capture reactions on 14N (where 14N is left from the ashes of H-burning) through the reaction 22Ne(p, γ)23Na. After a thermal pulse the ashes of hydrogen burning, including sodium, are mixed and brought to the surface (together with 12C) during the third dredge-up. For metallicities close to solar, this is the main reaction chain that produces Na. We recall that by decreasing the metallicity, an additional amount of Na comes from neutron captures on the increasing primary 22Ne (Cristallo et al. 2009, Bisterzo et al. 2010). This reaction is marginal in disk AGB stars as post-AGBs.

The [α/Fe] ratios as given for the elements Mg, Si, S, Ca and Ti is 0.21 ± 0.22 (GLMP 334) and 0.27 ± 0.24 (IRAS 15482 − 5741). Although these stars present a typical value for stars in this metallicity range (Carretta et al. 2002), we may notice that they both display a high standard deviation, the scatter around the mean, of the [α/Fe] ratio. This is caused by the low Mg abundance and to the high Si abundance.

Nickel and chromium show a mean of  ~0.12 for both stars, which agrees with the expectation that these two elements are not synthesized by AGB stars.

6. Conclusions

We have presented high-resolution spectroscopic abundances of two post-AGB stars GLMP 336 and IRAS 15482–5741, with [Fe/H]  ~ −0.5. Both stars show an enhancement in s-process elements, confirmed by several detected lines for Y, Zr, La, Ce, Pr, Nd. The s-enhancement observed in post-AGB stars has an intrinsic origin. It means that the s-elements are directly synthesized in the inner region of the star and, therefore, dredged up to the envelope after recurrent TDU episodes. This provides a useful test for AGB models, and we found a unique theoretical interpretation for GLMP 336 and IRAS 15482–5741.

Theoretical interpretations with AGB nucleosynthesis models of different initial masses and s-process efficiencies were compared with the observations. In the analysis we included AGB models of low and intermediate initial masses (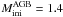, 1.5, 2 and 3 M⊙; 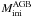= 5 and 7 M⊙). The positive [hs/ls] ratios observed in both post-AGBs suggest that AGB models with low initial mass provide good solutions in the frame of the AGB models presented in Bisterzo et al. (2010). GLMP 334 was interpreted by a model with initial mass M = 2 M⊙ (25 TDUs) and an efficient 13C-pocket (case ST × 2). IRAS 15482−5741 needs a lower initial mass, M = 1.4   M⊙ (11 TDUs), and a case ST. We predict [Pb/Fe]th ~ 2.1 for GLMP 334 and  ~1.6 for IRAS 15482−5741.

The AGB models at the adopted metallicity for both stars predict an amount of [C/Fe] that is too high with respect to that observed in these two post-AGB stars. One may think to apply some sort of extra-mixing or cool-bottom process, which has been introduced in literature to reconcile AGB models and observations (see e.g., Busso et al. 2010, and references therein). However, under the hypothesis of a CBP, a decrease of predicted [C/Fe] that would agree with the spectroscopic observations would imply an [N/Fe] ratio that is too high with respect to that observed for both stars. Indeed, we showed that by increasing the theoretical metallicity by 0.2 dex, which is inside the spectroscopic uncertainty, this major problem is substantially overcome. Moreover, additional uncertainties come from the spectroscopic observations, NLTE effects and 3D atmospherical models. Additional investigation on this topic are strongly needed.

Online material

Table 2

Observed Fe i and Fe ii lines.

Table 4

Other lines studied.

Appendix A: Supplementary material

A.1. GLMP 334 and IRAS 15482–5741

We provide an additional set of figures for both post-AGB stars in this section. We aim to shown the behavior of theoretical predictions by changing the AGB initial mass and 13C-pocket efficiency. The discrepancy between predicted and observed [C, N/Fe] may be improved by increasing the metallicity by 0.2 dex in both stars. This would reduce the predicted [C/Fe] by 0.3 dex with respect to Figs. 3 and 4, while leaving [ls/Fe] and [hs/Fe] unchanged. Indeed, 12C is primarily produced during partial He burning in the convective thermal pulse (independently of the metallicity) and is then dredged-up in the envelope after each TDU. In Figs. A.13 and A.14 we present two special cases modelled for both post-AGB stars. We present a summary of the theoretical interpretations of the two post-AGB stars discussed here compared with other post-AGB stars found in the literature in Sect. A.2.

thumbnail Fig. A.1

GLMP 334: the same as Fig. 3, but showing an additional 13C-pocket (case ST, thin solid line). This figure shows as by further decreasing the s-process efficiency, the observed [hs/Fe] is underestimated by the theoretical prediction.

thumbnail Fig. A.2

GLMP 334: the same as Fig. 3, but for = 3 M⊙ models. Three 13C-pocket efficiencies are shown: cases ST × 2 (solid line), ST × 1.3 (dotted thin line) and ST (dotted thick line). The first two 13C-pockets provide solutions similar to = 2 M⊙ models.

thumbnail Fig. A.3

GLMP 334: the same as Fig. A.2, but for = 1.5 M⊙ models. Owing to the lower number of thermal pulses with TDU (19th), none of the 13C-pockets reach the observed [ls/Fe] value. These solutions were discarded.

thumbnail Fig. A.4

GLMP 334: the same as Fig. A.2, but for = 1.4 M⊙ models (11 TDUs). None of the 13C-pockets reach the observed ls and hs peaks. These solutions were discarded.

thumbnail Fig. A.5

GLMP 334: the same as Fig. A.2, but for = 1.3 M⊙ models (5 TDUs). Even if these solutions perfectly agree with the observed [C/Fe], the low s-process distribution strongly underestimates the observed ls and hs peaks.

thumbnail Fig. A.6

Theoretical interpretation of the post-AGB stars GLMP 334 ([Fe/H] =  − 0.4; Teff = 7400 K; log g = 1.4) with = 5 M⊙ models. Three 13C-pocket efficiencies are shown: cases ST-IMS × 4 (solid line), ST-IMS × 2 (dotted thin line) and ST-IMS (dotted thick line). Note that a different 13C-pocket notation is adopted for IMS stars, because they have a smaller He-intershell than low-mass AGBs, with a smaller 13C-pocket (see Bisterzo et al. 2010). None of these solutions agrees with the observations.

thumbnail Fig. A.7

IRAS 15482–5741: the same as Fig. 4, but showing a different range of 13C-pockets: cases ST × 2 (solid line), ST (dotted thin line) and ST/3 (dotted thick line). This figure shows the behavior of the s-process elements if the 13C-pocket is changed.

thumbnail Fig. A.8

IRAS 15482–5741: the same as Fig. 4, but for = 1.3 M⊙ models. The theoretical [ls/Fe] is about 0.6 dex lower than observed. Even if the predicted [C/Fe] is closer to the low observed value, we discarded this solution.

thumbnail Fig. A.9

IRAS 15482–5741: the same as Fig. 4, but for = 1.5 M⊙ models. These models do not provide good theoretical interpretations for two reasons: first of all, with respect to Fig. 4, a further increase of about 0.2 dex is predicted for [C/Fe], because higher initial masses more TDUs (specifically, 19 instead of 11). Second, no good match is obtained of both ls and hs peaks: [ls/Fe] is perfectly interpreted by a case ST × 2, but [hs/Fe] is too high with respect the observed value. But, case ST/1.3 predicts a [ls/Fe] slightly higher than observed, even if the theoretical [hs/Fe] still lies within the errorbars.

thumbnail Fig. A.10

IRAS 15482–5741: the same as Fig. A.9, but for = 2 M⊙ models. Owing to [C/Fe], [ls/Fe] and [hs/Fe], these solutions were discarded.

thumbnail Fig. A.11

IRAS 15482–5741: the same as Fig. A.9, but for = 3 M⊙ models. Owing to [C/Fe], [ls/Fe] and [hs/Fe], these solutions were discarded.

thumbnail Fig. A.12

Theoretical interpretation of the post-AGB star IRAS 15482–5741 ([Fe/H] =  − 0.5; Teff = 7400 K; log g = 1.1) with = 5 M⊙ models. Three 13C-pocket efficiencies are shown: cases ST-IMS × 4 (solid line), ST-IMS × 2 (dotted thin line) and ST-IMS (dotted thick line). None of these solutions agree with the observations.

thumbnail Fig. A.13

Theoretical interpretation of the post-AGB star GLMP 334 ([Fe/H] =  − 0.4; Teff = 7400 K; log g = 1.4) by assuming a metallicity 0.2 dex higher than that observed. AGB models of initial mass of 1.5 M⊙ (19 TDUs), cases ST × 2 (solid line), ST × 1.7 (dotted thin line) and ST × 1.3 (dotted thick line) are shown. Note that the mass of the pocket was multiplied by a plausible factor of two to obtain 0.2 dex higher abundances in both [ls/Fe] and [hs/Fe]. We modelled these special cases to decrease [C/Fe] predictions with respect to Fig. 3, leaving [ls/Fe] and [hs/Fe] unchanged.

thumbnail Fig. A.14

Theoretical interpretation of the post-AGB star IRAS 154825741 ([Fe/H] =  − 0.5; Teff = 7400 K; log g = 1.1) by assuming a metallicity 0.2 dex higher than that observed. AGB models of initial mass of 1.4 M⊙ (10 TDU), cases ST × 2 (solid line), ST × 1.7 (dotted thin line) and ST × 1.3 (dotted thick line) are shown. Note that the mass of the pocket was multiplied by a plausible factor of two to obtain 0.2 dex higher abundances in both [ls/Fe] and [hs/Fe]. We modelled these special cases to decrease the [C/Fe] predictions with respect to Fig. 4, leaving [ls/Fe] and [hs/Fe] unchanged.

A.2. Comparison with other post-AGB stars presented in the literature.

We provide in Table A.1 a summary of the theoretical interpretations of the post-AGB stars discussed in the literature. Solutions are found within the mass range 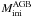= 1.4 to 3 M⊙. The choice of the 13C-pocket efficiency is peaked at ST/1.5, with a spread between ST/3 and ST × 2 (see also Gallino et al. 2008).

Table A.1

Summary of the stellar parameters, metallicities, [ls/Fe], [hs/Fe] and theoretical interpretations of the two post-AGB stars studied in this paper compared with the post-AGB stars discussed in the literature.

Acknowledgments

We thank our referee Hans van Winckel for the suggestions and comments, which substantially improved the manuscript.

References

  1. Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2007, A&A, 464, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Arlandini, C., Käppeler, F., Wisshak, K., et al. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] [Google Scholar]
  3. Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
  4. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2010, MNRAS, 404, 1529 [NASA ADS] [Google Scholar]
  6. Blöcker, T., & Schönberner, D. 1990, A&A, 240, L11 [NASA ADS] [Google Scholar]
  7. Boyarchuk, A. A., Antipova, L. I., Boyarchuk, M. E., & Savanov, I. S. 2001, Astr. Rep., 45, 301 [Google Scholar]
  8. Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] [Google Scholar]
  9. Busso, M., Palmerini, S., Maiorca, E., et al. 2010, ApJ, 717, L47 [NASA ADS] [CrossRef] [Google Scholar]
  10. Caffau, E., Maiorca, E., Bonifacio, P., et al. 2009, A&A, 498, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Carretta, E., Gratton, R., Cohen, J. G., Beers, T. C., & Christlieb, N. 2002, AJ, 124, 481 [NASA ADS] [CrossRef] [Google Scholar]
  12. Castro, S., Rich, R. M., Grenon, M., Barbuy, B., & McCarthy, J. K. 1997, AJ, 114, 376 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cohen, J. G., McWilliam, A., Shectman, S., & Thompson, I. 2006, ApJ, 132, 137 [Google Scholar]
  14. Collet, R., Asplund, M., & Trampedach, R. 2007, A&A, 469, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
  16. Denissenkov, P. A., & Ivanov, V. V. 1987, Soviet Astr. Lett., 13, 214 [NASA ADS] [Google Scholar]
  17. Denissenkov, P. A., & Tout, C. A. 2003, MNRAS, 340, 722 [NASA ADS] [CrossRef] [Google Scholar]
  18. Depagne, E., Hill, V., Spite, M., et al. 2002, A&A, 390, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Drake, J. J., & Smith, G. 1991, MNRAS, 250, 89 [NASA ADS] [Google Scholar]
  20. Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
  21. Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  22. Gallino, R., Bisterzo, S., & Husti, L. 2008, in Evolution and Nucleosynthesis in AGB STARS, ed. R. Guandalini, S. Palmerini, & M. Busso (New York: AIP), AIP Conf. Proc., 1001, 123 [Google Scholar]
  23. García-Lario, P., Manchado, P., Pych, W., & Pottasch, S. R. 1997, A&AS, 126, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Gratton, R. G., & Sneden, C. 1987, A&A, 178, 179 [NASA ADS] [Google Scholar]
  25. Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
  26. Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
  27. Herwig, F., Blöcker, T., Schönberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
  28. Herwig, F., Langer, N., & Lugaro, M. 2003, ApJ, 593, 1056 [NASA ADS] [CrossRef] [Google Scholar]
  29. Käppeler, F., Gallino, R., Bisterzo, S., & Aoki, W. 2011, Rev. Mod. Phys., 63, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
  31. Kingsburgh, R. L., & Barlow, M. J. 1994, MNRAS, 271, 257 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kurucz, R. L. 1993, CD-ROM 13, Atlas9 Stellar Atmosphere Programs and 2 km/s Grid (Cambridge: Smithsonian Astrophys. Obs.) [Google Scholar]
  33. Lambert, D. L., Gustafsson, B., Eriksson, K., & Hinkle, K. H. 1986, ApJS, 62, 373 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lambert, D. L., Heath, J. E., Lemke, M., & Drake, J. 1996, ApJS, 103, 183 [NASA ADS] [CrossRef] [Google Scholar]
  35. Langer, N., Heger, A., Wellstein, S., & Herwig, F. 1999, A&A, 346, L37 [Google Scholar]
  36. Lasker, B., Lattanzi, M. G., McLean, B. J., et al. 2008, AJ, 136, 735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  37. Lawler, J. E., den Hartog, E. A., Labby, Z. E., et al. 2007, ApJS, 169, 120 [NASA ADS] [CrossRef] [Google Scholar]
  38. Luck, R. E. 1993, in Luminous High-Latitude Stars, ed. D. D. Sasselov (San Francisco: ASP), ASP Conf. Ser., 45, 87 [Google Scholar]
  39. Luck, R. E., & Bond, H. 1989, ApJS, 71, 559 [NASA ADS] [CrossRef] [Google Scholar]
  40. Luck, R. E., & Lambert, D. L. 1985, ApJ, 298, 782 [NASA ADS] [CrossRef] [Google Scholar]
  41. Luck, R. E., Bond, H., & Lambert, D. L. 1990, ApJ, 357, 188 [NASA ADS] [CrossRef] [Google Scholar]
  42. Mowlavi, N. 1999, A&A, 350, 73 [NASA ADS] [Google Scholar]
  43. Nollett, K. M., Busso, M., & Wasserburg, G. J. 2003, ApJ, 582, 1036 [Google Scholar]
  44. Norris, J. E., Ryan, S. G., & Beers, T. C. 1996, ApJS, 107, 391 [NASA ADS] [CrossRef] [Google Scholar]
  45. Pereira, C. B., Lorenz-Martins, S., & Machado, M. 2004, A&A, 422, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Preston, G. W., & Sneden, C. 2000, ApJ, 102, 1014 [Google Scholar]
  47. Reddy, B. E., Bakker, E. J., & Hrivnak, B. J. 1999, ApJ, 524, 831 [NASA ADS] [CrossRef] [Google Scholar]
  48. Reddy, B. E., Lambert, D. L., Gonzalez, G., & Yong, D. 2002, ApJ, 564, 482 [NASA ADS] [CrossRef] [Google Scholar]
  49. Reyniers, M., & van Winckel, H. 2001, A&A, 365, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Reyniers, M., van Winckel, H., Gallino, R., & Straniero, O. 2004, A&A, 417, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Reyniers, M., van de Steene, G. C., van Hoof, P. A. M., & van Winckel, H. 2007, A&A, 471, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Ryans, R. S. I., Dufton, P. L., Mooney, C. J., Rolleston, W. R. J., & Keenan, F. P. 2003, A&A, 401, 1119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Schönberner, D. 1983, ApJ, 272, 708 [NASA ADS] [CrossRef] [Google Scholar]
  54. Siess, L., Goriely, S., & Langer, N. 2004, A&A, 415, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Sigut, T. A. A., & Landstreet, J. D. 1990, MNRAS, 247, 611 [NASA ADS] [Google Scholar]
  56. Smalley, B., Smith, K. C., Wonnacott, D., & Allen, C. S. 1996, MNRAS, 278, 688 [NASA ADS] [CrossRef] [Google Scholar]
  57. Smith, V. V., Cunha, K., & Lambert, D. L. 1995, AJ, 110, 2827 [NASA ADS] [CrossRef] [Google Scholar]
  58. Smith, V. V., Cunha, K., Jorissen, A., & Boffin, H. M. J. 1996, A&A, 315, 179 [NASA ADS] [Google Scholar]
  59. Sneden, C. 1973, Ph.D. Thesis, Univ. of Texas [Google Scholar]
  60. Sneden, C., McWilliam, A., Preston, G. W., et al. 1996, ApJ, 467, 819 [NASA ADS] [CrossRef] [Google Scholar]
  61. Straniero, O., Gallino, R., & Cristallo, S. 2006, Nucl. Phys. A, 777, 311 [NASA ADS] [CrossRef] [Google Scholar]
  62. Suárez, O., García-Lario, P., Manchado, A., Manteiga, M., & Ulla, A. 2006, A&A, 458, 137 [Google Scholar]
  63. Takeda, Y., & Takada-Hidai, M. 1994, PASJ, 46, 395 [NASA ADS] [Google Scholar]
  64. Takeda, Y., & Takada-Hidai, M. 1995, PASJ, 47, 169 [NASA ADS] [Google Scholar]
  65. Takeda, Y., Zhao, G., Takada-Hidai, M., et al. 2003, Chin. J. Astron. Astrophys., 3, 316 [Google Scholar]
  66. Thompson, H. M. A., Keenan, F. P., Dufton, P. L., et al. 2007, MNRAS, 378, 1619 [NASA ADS] [CrossRef] [Google Scholar]
  67. Travaglio, C., Gallino, R., Arnone, E., Cowan, J., & Jordan, F. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] [Google Scholar]
  68. van Winckel, H. 1997, A&A, 319, 561 [NASA ADS] [Google Scholar]
  69. van Winckel, H. 2003, ARA&A, 41, 391 [NASA ADS] [CrossRef] [Google Scholar]
  70. van Winckel, H., & Reyniers, M. 2000, A&A, 354, 135 [NASA ADS] [Google Scholar]
  71. van Winckel, H., Mathis, J. S., & Waelkens, C. 1992, Nature, 356, 500 [NASA ADS] [CrossRef] [Google Scholar]
  72. van Winckel, H., Lloyd Evans, T., Briquet, M., et al. 2009, A&A, 505, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Venn, K. A. 1993, ApJ, 414, 316 [NASA ADS] [CrossRef] [Google Scholar]
  74. Waelkens, C., van Winckel, H., Bogaert, E., & Trams, N. R. 1991, A&A, 251, 495 [NASA ADS] [Google Scholar]
  75. Wasserburg, G. J., Boothroyd, A. I., & Sackmann, I.-J. 1995, ApJ, 447, L37 [NASA ADS] [CrossRef] [Google Scholar]
  76. Wasserburg, G. J., Busso, M., Gallino, R., & Nollett, K. M. 2006, Nucl. Phys. A, 777, 5 [NASA ADS] [CrossRef] [Google Scholar]
  77. Wiese, W. L., Smith, M. W., & Miles, B. M. 1969, in Atomic transition probabilities, Sodium through Calcium, A critical data compilation, NSRDS-NBS (Washington, D.C.: US Department of Commerce, National Bureau of Standards), 2 [Google Scholar]
  78. Whitelock, P., & Marang, F. 2001, MNRAS, 323, L13 [NASA ADS] [CrossRef] [Google Scholar]
  79. Zinner, E., Nittler, L. R., Alexander, C. M. O. D., & Gallino, R. 2006, New Astron. Rev., 50, 574 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Basic parameters of the two objects analyzed in this work.

In the text
Table 3

Atmospheric parameters and radial velocities of GLMP 334 and IRAS 15482 − 5741.

In the text
Table 5

Abundances in the log ε(H) = 12.0 scale and in the notation [X/Fe] for GLMP 334 ([Fe/H] =  −0.4) and IRAS 15482−5741 ([Fe/H] =  − 0.5).

In the text
Table 2

Observed Fe i and Fe ii lines.

In the text
Table 4

Other lines studied.

In the text
Table A.1

Summary of the stellar parameters, metallicities, [ls/Fe], [hs/Fe] and theoretical interpretations of the two post-AGB stars studied in this paper compared with the post-AGB stars discussed in the literature.

In the text

All Figures

thumbnail Fig. 1

Sample spectra of the heavily s-enriched post-AGB stars GLMP 334 and IRAS 15482−5741 compared with the non s-enriched post-AGB star IRAS 19386+0155 analyzed by Pereira et al. (2004). Dotted vertical lines show the transitions of Zr ii 5112.3 Å, La ii 5114.5 Å, Ce ii 5117.2 Å, Y ii 5119.1 Å, and 5123.1 Å, Nd ii 5130.6 Å, and Pr ii 5135.1 Å. Other transitions are shown in the figure.
In the text
thumbnail Fig. 2

Logarithmic surface gravity versus effective temperature diagram showing the location of GLMP 334 and IRAS 15482 − 5741 (red filled triangle) and previously identified post-AGB objects (black filled squares). Data from post-AGB stars were taken from Luck (1993), Reddy et al. (1999, 2002), Reyniers et al. (2004), and van Winckel & Reyniers (2000). HD 172481 (Reyniers & van Winckel 2001) is also shown (red filled square). Post-AGB tracks of Schönberner (1983) and Blöcker & Schönberner (1990) are also shown.
In the text
thumbnail Fig. 3

Theoretical interpretation of the post-AGB star GLMP 334 ([Fe/H] =  −0.4; Teff = 7400 K; log g = 1.4) with = 2 M⊙. Three 13C-pocket efficiencies are shown: cases ST × 2 (solid line), ST × 1.7 (dotted thin line) and ST × 1.3 (dotted thick line). Error bars are shown for elements with more than two detected lines.
In the text
thumbnail Fig. 4

Theoretical interpretation of the post-AGB star IRAS 15482–5741 ([Fe/H] =  −0.5; Teff = 7400 K; log g = 1.1) with = 1.4 M⊙. Three 13C-pocket efficiencies are shown: cases ST × 1.3 (dotted thin line), ST (solid line) and ST/2 (dotted thick line). Error bars are shown for elements with more than two detected lines.
In the text
thumbnail Fig. 5

Relative abundance O/N versus C/N for several classes of stars (see text for references). Disk carbon stars (green starry points); post-AGB stars enriched in the s-process elements (blue filled triangles); hot post-AGB stars (blue filled squares); post-AGB stars not enriched in the s-process (blue open polygons); Population I supergiants (red plus sign); planetary nebulae (black open squares); HD 172481 (red filled square) and the stars analyzed in this work GLMP 334 and IRAS 15482 − 5741 (red triangles).
In the text
thumbnail Fig. A.1

GLMP 334: the same as Fig. 3, but showing an additional 13C-pocket (case ST, thin solid line). This figure shows as by further decreasing the s-process efficiency, the observed [hs/Fe] is underestimated by the theoretical prediction.
In the text
thumbnail Fig. A.2

GLMP 334: the same as Fig. 3, but for = 3 M⊙ models. Three 13C-pocket efficiencies are shown: cases ST × 2 (solid line), ST × 1.3 (dotted thin line) and ST (dotted thick line). The first two 13C-pockets provide solutions similar to = 2 M⊙ models.
In the text
thumbnail Fig. A.3

GLMP 334: the same as Fig. A.2, but for = 1.5 M⊙ models. Owing to the lower number of thermal pulses with TDU (19th), none of the 13C-pockets reach the observed [ls/Fe] value. These solutions were discarded.

In the text
thumbnail Fig. A.4

GLMP 334: the same as Fig. A.2, but for = 1.4 M⊙ models (11 TDUs). None of the 13C-pockets reach the observed ls and hs peaks. These solutions were discarded.

In the text
thumbnail Fig. A.5

GLMP 334: the same as Fig. A.2, but for = 1.3 M⊙ models (5 TDUs). Even if these solutions perfectly agree with the observed [C/Fe], the low s-process distribution strongly underestimates the observed ls and hs peaks.

In the text
thumbnail Fig. A.6

Theoretical interpretation of the post-AGB stars GLMP 334 ([Fe/H] =  − 0.4; Teff = 7400 K; log g = 1.4) with = 5 M⊙ models. Three 13C-pocket efficiencies are shown: cases ST-IMS × 4 (solid line), ST-IMS × 2 (dotted thin line) and ST-IMS (dotted thick line). Note that a different 13C-pocket notation is adopted for IMS stars, because they have a smaller He-intershell than low-mass AGBs, with a smaller 13C-pocket (see Bisterzo et al. 2010). None of these solutions agrees with the observations.
In the text
thumbnail Fig. A.7

IRAS 15482–5741: the same as Fig. 4, but showing a different range of 13C-pockets: cases ST × 2 (solid line), ST (dotted thin line) and ST/3 (dotted thick line). This figure shows the behavior of the s-process elements if the 13C-pocket is changed.
In the text
thumbnail Fig. A.8

IRAS 15482–5741: the same as Fig. 4, but for = 1.3 M⊙ models. The theoretical [ls/Fe] is about 0.6 dex lower than observed. Even if the predicted [C/Fe] is closer to the low observed value, we discarded this solution.
In the text
thumbnail Fig. A.9

IRAS 15482–5741: the same as Fig. 4, but for = 1.5 M⊙ models. These models do not provide good theoretical interpretations for two reasons: first of all, with respect to Fig. 4, a further increase of about 0.2 dex is predicted for [C/Fe], because higher initial masses more TDUs (specifically, 19 instead of 11). Second, no good match is obtained of both ls and hs peaks: [ls/Fe] is perfectly interpreted by a case ST × 2, but [hs/Fe] is too high with respect the observed value. But, case ST/1.3 predicts a [ls/Fe] slightly higher than observed, even if the theoretical [hs/Fe] still lies within the errorbars.
In the text
thumbnail Fig. A.10

IRAS 15482–5741: the same as Fig. A.9, but for = 2 M⊙ models. Owing to [C/Fe], [ls/Fe] and [hs/Fe], these solutions were discarded.
In the text
thumbnail Fig. A.11

IRAS 15482–5741: the same as Fig. A.9, but for = 3 M⊙ models. Owing to [C/Fe], [ls/Fe] and [hs/Fe], these solutions were discarded.
In the text
thumbnail Fig. A.12

Theoretical interpretation of the post-AGB star IRAS 15482–5741 ([Fe/H] =  − 0.5; Teff = 7400 K; log g = 1.1) with = 5 M⊙ models. Three 13C-pocket efficiencies are shown: cases ST-IMS × 4 (solid line), ST-IMS × 2 (dotted thin line) and ST-IMS (dotted thick line). None of these solutions agree with the observations.
In the text
thumbnail Fig. A.13

Theoretical interpretation of the post-AGB star GLMP 334 ([Fe/H] =  − 0.4; Teff = 7400 K; log g = 1.4) by assuming a metallicity 0.2 dex higher than that observed. AGB models of initial mass of 1.5 M⊙ (19 TDUs), cases ST × 2 (solid line), ST × 1.7 (dotted thin line) and ST × 1.3 (dotted thick line) are shown. Note that the mass of the pocket was multiplied by a plausible factor of two to obtain 0.2 dex higher abundances in both [ls/Fe] and [hs/Fe]. We modelled these special cases to decrease [C/Fe] predictions with respect to Fig. 3, leaving [ls/Fe] and [hs/Fe] unchanged.
In the text
thumbnail Fig. A.14

Theoretical interpretation of the post-AGB star IRAS 154825741 ([Fe/H] =  − 0.5; Teff = 7400 K; log g = 1.1) by assuming a metallicity 0.2 dex higher than that observed. AGB models of initial mass of 1.4 M⊙ (10 TDU), cases ST × 2 (solid line), ST × 1.7 (dotted thin line) and ST × 1.3 (dotted thick line) are shown. Note that the mass of the pocket was multiplied by a plausible factor of two to obtain 0.2 dex higher abundances in both [ls/Fe] and [hs/Fe]. We modelled these special cases to decrease the [C/Fe] predictions with respect to Fig. 4, leaving [ls/Fe] and [hs/Fe] unchanged.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.