| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117307 | |
| Published online | 27 January 2012 | |
Thermal infrared properties of classical and type II Cepheids
Diffraction limited 10 μm imaging with VLT/VISIR⋆,⋆⋆
1
LESIA, Observatoire de Paris, CNRS UMR 8109, UPMC, Université Paris
Diderot,
5 place Jules Janssen,
92195
Meudon,
France
e-mail: alexandre.gallenne@obspm.fr
2
European Southern Observatory, Alonso de Córdova 3107, Casilla 19001,
Santiago 19,
Chile
Received: 20 May 2011
Accepted: 24 November 2011
We present new thermal infrared (IR) photometry and spectral energy distributions (SEDs) of eight classical Cepheids (type I) and three type II Cepheids, using VISIR thermal IR photometric measurements, supplemented with literature data. We used the BURST mode of the instrument to get diffraction-limited images at 8.59, 11.25, and 11.85 μm. The SEDs show a IR excess at wavelengths longer than 10 μm in ten of the eleven stars. We tentatively attribute these excesses to circumstellar emission created by mass loss from the Cepheids. On the basis of some hypotheses for the dust composition, we estimate a total mass of the envelope ranging from 10-10 to 10-8 M⊙. We also detect a spatially extended emission around AX Cir, X Sgr, W Sgr, Y Oph, and U Car, while we do not resolve the circumstellar envelope (CSE) of the other stars. The averaged circumstellar envelope brightnesses relative to the stellar photosphere are α(AX Cir) = 13.8 ± 2.5%,α(X Sgr) = 7.9 ± 1.4%,α(W Sgr) = 3.8 ± 0.6%,α(Y Oph) = 15.1 ± 1.4%, and α(U Car) = 16.3 ± 1.4% at 8.59 μm. With this study, we extend the number of classical Cepheids with detected CSEs from 9 to 14, confirming that at least a large fraction of all Cepheids are experiencing significant mass loss. The presence of these CSEs may also impact the future use of Cepheids as standard candles at near and thermal infrared wavelengths.
Key words: circumstellar matter / stars: variables: Cepheids / stars: mass-loss / stars: imaging / infrared: stars
Based on observations made with ESO telescopes at Paranal observatory under program ID 081.D-0165(A).
Table 2 is only available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Kervella et al. (2006) discovered in the N and K band a circumstellar envelope (CSE) around ℓ Car using the MIDI and VINCI instruments from the VLTI. Its typical size is 2−3 R ⋆ with a contribution of 4% to the total flux in K. Similar interferometric detections were subsequently reported for other Cepheids (Mérand et al. 2006, 2007), leading to the conclusion that a significant fraction of all Cepheids are surrounded by a CSE. From mid- and far-IR observations with the Spitzer telescope, Barmby et al. (2011) detected extended emission around a significant fraction of their sample of 29 classical Cepheids. The case of δ Cep and its extended emission is discussed extensively in Marengo et al. (2010b). These CSEs have an effect on both the infrared surface brightness technique (IRSB), since the Cepheid appears brighter, and on interferometric measurements, since the star appears larger than it really is. It is therefore necessary to quantify this excess (linked to an extended emission) in order to estimate any bias to the distance. This is particularly important for the James Webb Space Telescope (JWST), which will be able to observe Cepheids in distant galaxies. The distances to these objects could be estimated via the use of IR P–L relations but the presence of an infrared excess would degrade the distance accuracy.
This circumstellar material is also important in the context of Cepheid mass-loss because it may help to explain the Cepheid mass discrepancy (Neilson et al. 2010a, ...). The infrared excess could be linked to a mass-loss mechanism generated by shocks between different layers of the Cepheid’s atmosphere during the pulsation cycle. A correlation between the period and the relative envelope flux (relative to the star flux) was proposed by Mérand et al. (2007), where a Cepheid with a longer pulsation period would have a larger IR excess. In contrast, from photometry on a larger sample of Cepheids, Neilson et al. (2010b) reached a different conclusion. It is thus essential to study these CSEs to quantify their contribution to the overall brightness of Cepheids and understand how they form.
Some relevant parameters of our Cepheids.
To progress with this question, we present new observations of a few classical (type I) and type II Cepheids with the VISIR instrument of the VLT. The mid-IR wavelength coverage of this instrument is well-suited to studying the infrared contribution of the CSEs. The instrument configurations and the data reduction methods are detailed in Sect. 2. In Sect. 3, we present the data analysis using aperture photometry applied to our images and we study the spectral energy distribution (SED) of our sample of stars. We also search for a spatially resolved component using a Fourier technique analysis. Finally we discuss our results in Sect. 4.
2. Observations and data processing
The selected sample of classical Cepheids was chosen based on their brightness, their range of pulsation period (from 4 to 45 days) and their angular size so that they are resolvable by long-baseline interferometry. Y Oph seems to exhibit the brightest CSE detected around a Cepheid (Mérand et al. 2007) and the goal is to explore larger distances from the Cepheid. The type II Cepheids we selected have been extensively studied and are known to have strong IR excesses linked to their CSEs. They were used in our analysis both to compare the properties of their CSEs with those of classical Cepheids, and to validate our modeling approach to estimating the thermal infrared excess (based on the results of previous works on type II Cepheids). We present in Table 1 some relevant parameters for our sample of observed Cepheids.
The observations were performed using the ESO mid-infrared instrument VISIR installed on UT3 at the VLT (Paranal, Chile). This instrument operates in the N (8−13 μm) and Q (16−24 μm) atmospheric windows and provides imaging and long-slit spectroscopy. As we need the highest spatial resolution, we chose the BURST mode (Doucet et al. 2006) of VISIR to overcome the atmospheric seeing. In this mode, short exposure images (i.e. of duration shorter than the atmospheric coherence time) are taken in order to freeze the turbulence. Each short exposure frames then represents one principal speckle. With sets of thousands of short exposure frames, we can apply a shift-and-add process. This enhances the quality of the data and enabled us to reach the diffraction limit of the telescope. To correct for instrumental artefacts and background thermal emission, we applied the classical chop-nod technique.
The raw data of the VISIR BURST mode are data cubes in which the star appears in a different position in the field (the chop-nod positions, perpendicular each other) for each frames. Our first step consisted of a classical subtraction of the chopped and nodded images in order to remove the thermal background and store them in data cubes containing thousands of frames (~20 000). To ensure the highest quality diffraction-limited images, we selected 50% of the best frames according to the brightest pixel (as a tracer of the Strehl ratio). We then proceeded to a precentering (at a integer pixel level), a spatial resampling by a factor of four using a cubic spline interpolation and a fine recentering using a Gaussian fitting (at a precision level of a few milliarcseconds). The resulting cubes were then averaged to get the final image used in the data analysis process (see Sect. 3). This raw data processing had previously been used where its efficiency were proven (see e.g. Kervella & Domiciano de Souza 2007; Kervella et al. 2009; Gallenne et al. 2011).
The observations were carried out on the nights of 2008 May 23–24. Table 6 lists the sequence of our observations including the reference stars that were observed immediately before and after the Cepheids in the same instrumental setup. Series of observations were obtained in three filters: PAH1, PAH2, and SiC (respectively, 8.59 ± 0.42 μm, 11.25 ± 0.59 μm, and 11.85 ± 2.34 μm). We chose the smallest pixel scale of 75 mas/pixel (before resampling) to ensure a proper sampling of the Airy pattern FWHM (average FWHM ~ 4 pixels for the reference stars). For an unknown reason, the nodding position was outside the detector for the observations #15, #17, #19 to #22, #25 to #28 and #31 to #34 but we still have enough frames (~10 000) to correctly subtract the background emission. The observations #23 and #24 were chopped and nodded out of the detector and were not included in the analysis. Owing to the lower sensitivity of VISIR in the SiC filter, we could not recenter the individual VISIR images for the observations #40 and #44. The #4 sequence was not included because its very low signal, maybe caused by some clouds, led to a poor recentering of the individual images.
3. Data analysis
In this section, we first present our study of the evolution of the atmospheric properties (seeing, transparency) during the observations for each night. We then describe the aperture photometry that we applied to our average images. We then combined these measurements with other photometric data we retrieved from the literature to study the SED of each star. By applying a Fourier technique analysis to our average VISIR images, we also searched for the presence of extended emission.
3.1. Atmospheric evolution
We studied the sky transparency evolution using our photometric reference stars. The photometric templates from Cohen et al. (1999) were used to plot the temporal relative atmospheric transmission (relative to the average value of all calibrators observed for each night). We see in Fig. 1 that the atmosphere was pretty stable during the observing nights. In the first night, the relative standard deviation was below 5%, while it was only 3% in the second night.
 |
Fig. 1 Relative atmospheric transmission for our observing nights. Both nights are normalised to the mean value over all calibrators observed. The dotted lines denote a 5% variation. |
3.2. Photometry
We carried out a classical aperture photometry to assess the flux density for each star in each filter. Photometric templates from Cohen et al. (1999) were used to perform an absolute calibration of the flux density taking into account the filter transmission1 using 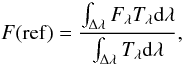 where Fλ is the reference irradiance (from the Cohen et al. templates), Tλ the filter transmission, and Δλ the filter bandpass.
where Fλ is the reference irradiance (from the Cohen et al. templates), Tλ the filter transmission, and Δλ the filter bandpass.
We applied an airmass correction factor 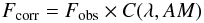 with C(λ,AM) taken from Schütz & Sterzik (2005)
with C(λ,AM) taken from Schütz & Sterzik (2005)![\begin{displaymath} C(\lambda,AM) = 1 + \left[ 0.220 - \frac{0.104}{3}(\lambda - 8.6\,\mu\mathrm{m}) \right] (AM - 1). \end{displaymath}](/articles/aa/full_html/2012/02/aa17307-11/aa17307-11-eq61.png) No aperture correction was required because we kept the same, relatively large, aperture radius (1.3′′) for both the Cepheids and their respective reference stars. We then estimated the flux density of our Cepheid samples
No aperture correction was required because we kept the same, relatively large, aperture radius (1.3′′) for both the Cepheids and their respective reference stars. We then estimated the flux density of our Cepheid samples 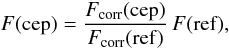 where cep and ref stand for the Cepheid and reference stars.
where cep and ref stand for the Cepheid and reference stars.
The measured flux densities are summarized in Table 3. The uncertainties include the statistical dispersion in the aperture photometry, the dispersion in the calibrator flux densities over the night, and the absolute calibration uncertainty. Some final averaged images of our sample are presented in Fig. 14. The visibility of several diffraction rings reflects the quality of the data.
Measured flux densities of our Cepheid sample.
3.3. Spectral energy distribution of classical Cepheids
We collected additional photometric measurements in the literature from 0.4 μm to 100 μm to analyse the SED of our Cepheids. As they are pulsating stars, their SEDs vary during the pulsation cycle and we have to take into account the phase of pulsation when retrieving the data.
To estimate their magnitudes at our phase of pulsation, we retrieved light curves from the literature when available, which we plotted as a function of phase (all phases were computed with the ephemerides from Table 1). We then applied the Fourier decomposition technique (see e.g. Ngeow et al. 2003) 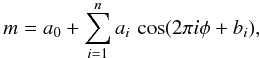 where ai and bi are the Fourier amplitudes and phases for the order i to fit and φ is the pulsation phase. The parameter n depends on the number of data points and the light curve amplitude (higher amplitude require a higher order fit). We used n = 4 for all stars. Examples are shown in Fig. 2 for two stars. The coefficients of the fit were then used to compute the values at our phases. We used this method for the Cepheids FF Aql (in B,V and R bands), AX Cir (B,V), X Sgr (B,V,J,H,K), η Aql (B,V), W Sgr (B,V), Y Oph (B,V), U Car (B,V), and SV Vul (B,V). When data points were not equally spaced in phase, the direct Fourier fit produced unrealistic oscillations, thus we then used a periodic cubic spline interpolation. To evaluate the uncertainty, we used the total standard deviation of the residual values (bottom panels of Fig. 2). The uncertainty was assumed to be the same for all phases. We used this kind of interpolation for the stars η Aql (in J,H,K bands), Y Oph (J,H,K), U Car (J,H,K), SV Vul (J,H,K), and κ Pav (V,J,H,K).
where ai and bi are the Fourier amplitudes and phases for the order i to fit and φ is the pulsation phase. The parameter n depends on the number of data points and the light curve amplitude (higher amplitude require a higher order fit). We used n = 4 for all stars. Examples are shown in Fig. 2 for two stars. The coefficients of the fit were then used to compute the values at our phases. We used this method for the Cepheids FF Aql (in B,V and R bands), AX Cir (B,V), X Sgr (B,V,J,H,K), η Aql (B,V), W Sgr (B,V), Y Oph (B,V), U Car (B,V), and SV Vul (B,V). When data points were not equally spaced in phase, the direct Fourier fit produced unrealistic oscillations, thus we then used a periodic cubic spline interpolation. To evaluate the uncertainty, we used the total standard deviation of the residual values (bottom panels of Fig. 2). The uncertainty was assumed to be the same for all phases. We used this kind of interpolation for the stars η Aql (in J,H,K bands), Y Oph (J,H,K), U Car (J,H,K), SV Vul (J,H,K), and κ Pav (V,J,H,K).
 |
Fig. 2 Examples for the constructed light curves in the V band. Data for FF Aql are from Moffett & Barnes (1984) and for Y Oph from Berdnikov (2008). The resulting light curves are drawn with solid lines. |
There is unfortunately a lack of light curves in the literature for some wavelengths and it was impossible to correct all the data for the phase mismatch. We then chose to use the amplitude of the light curves Aλ as additional uncertainties in the magnitude owing to the phase mismatch. In addition, we know that Aλ decreases with wavelength. Using 51 Galactic Cepheids, Laney & Stobie (1993) plotted the amplitude of the J,H, and K light curves as a function of the pulsation period (their Fig. 8). There are mainly two regions of  with AJ ~ 0.1 mag and log P > 1.0 with AJ ~ 0.2 mag, and these values decrease with wavelength (AK ~ 0.08 mag for
with AJ ~ 0.1 mag and log P > 1.0 with AJ ~ 0.2 mag, and these values decrease with wavelength (AK ~ 0.08 mag for 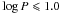 and AK ~ 0.15 mag for log P > 1.0). Therefore, when the collected additional data do not correspond to same phases, we chose the additional uncertainties in the magnitude caused by the phase mismatch to be the values 0.1 mag if
and AK ~ 0.15 mag for log P > 1.0). Therefore, when the collected additional data do not correspond to same phases, we chose the additional uncertainties in the magnitude caused by the phase mismatch to be the values 0.1 mag if  or 0.2 mag if log P > 1.0 for 1 < λ < 3.5 μm and for λ > 3.5 μm we chose 0.05 mag for all periods. We are conscious that this can overestimate the uncertainties but it enables us to completely separate an IR excess detection from a magnitude error in the SED curves. On the other hand, this can also prevent the detection of a small IR excess.
or 0.2 mag if log P > 1.0 for 1 < λ < 3.5 μm and for λ > 3.5 μm we chose 0.05 mag for all periods. We are conscious that this can overestimate the uncertainties but it enables us to completely separate an IR excess detection from a magnitude error in the SED curves. On the other hand, this can also prevent the detection of a small IR excess.
Some of our targets were observed on two different nights and they can have different phases (especially the short periods). We considered the SED corresponding to an intermediate phase between the observations.
The photospheric emission was modeled with tabulated stellar atmosphere models obtained with the ATLAS9 simulation code from Castelli & Kurucz (2003). We chose a grid that was computed for solar metallicity and a turbulence velocity of 2 km s-1. We then interpolated this grid to compute spectra for any effective temperature and any surface gravity. The spectrum was multiplied by the solid angle of the stellar photosphere, 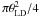 , where θLD is the limb-darkened angular diameter. We adjusted the photometric data to the model taking into account the spectral response of each instrument. We assumed that there is no detectable excess (5% or less) below 2.2 μm and all the photometric measurements bluer than the K band were used to fit the angular diameter and the effective temperature. However, we note that Teff and θLD were correlated variables in this fit. We did not adjust the surface gravity, since the broadband photometry is mostly insensitive to this parameter and its value was derived from the literature.
, where θLD is the limb-darkened angular diameter. We adjusted the photometric data to the model taking into account the spectral response of each instrument. We assumed that there is no detectable excess (5% or less) below 2.2 μm and all the photometric measurements bluer than the K band were used to fit the angular diameter and the effective temperature. However, we note that Teff and θLD were correlated variables in this fit. We did not adjust the surface gravity, since the broadband photometry is mostly insensitive to this parameter and its value was derived from the literature.
All flux densities <3 μm are corrected for interstellar extinction Aλ = Rλ E(B − V) using both the total-to-selective absorption ratios Rλ from Fouqué et al. (2003) and Hindsley & Bell (1989), and the color excess E(B − V) from Fouqué et al. (2007). Fluxes in any other longer wavelengths are not corrected for the interstellar extinction, which we assume to be negligible.
3.3.1. FF Aql
We selected log g = 2.05 from Luck et al. (2008, hereafter L08 as a fixed parameter. The adjusted SED is presented in Fig. 3. The B, V, and R values were taken from the light curves of Berdnikov (2008, hereafter B08 and Moffett & Barnes (1984, hereafter M 84. The J,H, and Ks photometry are from Welch et al. (1984) and correspond to the mean values: there was not a good coverage of phase to estimate accurate light curves, thus we decided to take the mean values and their standard deviations. We also added photometric values from the InfraRed Array Camera (IRAC: 3.6, 4.5, 5.8 and 8 μm) and the Multiband Imaging Photometer (MIPS: 24 μm) installed in the Spitzer space telescope (Marengo et al. 2010a,hereafter M 10). We also used broadband photometry from the Infrared Astronomical Satellite (IRAS: 12 and 25 μm, Helou & Walker 1988), the AKARI satellite IRC point source catalogue (9 and 18 μm, Ishihara et al. 2010) and the Midcourse Space Experiment (MSX: 8.28, 12.13, 14.65, 21.34 μm, Egan & Price 1996; Egan et al. 2003).
Our best-fit model values are presented in Table 4 and plotted in Fig. 3 (black solid curve). This fitted effective temperature is only 3% lower than the value of L08 (6062 ± 43 K) at this phase of pulsation. The angular diameter is in excellent agreement with the 0.86 ± 0.17 mas from Groenewegen (2007).
 |
Fig. 3 Synthetic spectra of the classical Cepheid FF Aql (solid line) with the photometric measurements taken from the literature. The blue triangles are the points used to fit the SED. Our measurements are presented with the red circles, while the black squares are the other photometric data. In the lower panel, we plot the excess flux density relative to the photospheric emission. The green curve represents the flux density model. |
We detected a likely IR emission on the order of 2% (with respect to the stellar flux) in PAH1 and SiC (see Table 3). FF Aql has a more important excess at other wavelengths (8 to 30 μm). The lower panel in Fig. 3 represents the relative flux difference (relative to the model) integrated over the filter bandpass.
We fitted to this star a second component assuming an optically thin envelope that follows an intensity distribution of the form
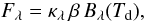 (1)where Bλ(Td) is the Planck function at a dust temperature Td, κλ is the dust opacity, and β is a parameter that is directly proportional to the dust mass (Li 2005)
(1)where Bλ(Td) is the Planck function at a dust temperature Td, κλ is the dust opacity, and β is a parameter that is directly proportional to the dust mass (Li 2005) 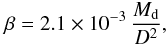 where D is the distance of the star in pc and Md in M⊙.
where D is the distance of the star in pc and Md in M⊙.
The IR excess seems to rise quite sharply around 10 μm and 20 μm in a way that could be linked to silicate/carbon features. We so chose the dust opacity from Ossenkopf & Henning (1994, hereafter O94 for carbon and silicate grains for a MRN size distribution (Mathis et al. 1977).
Best-fit values for our Cepheid sample.
We plotted in Fig. 3 (the green solid curve) our best-fit flux density model with a temperature Td = 539 ± 52 K and β = 3.0 ± 0.7 × 10-19 kg m-2. Using the distance from Benedict et al. (2007, Table 1, this leads to a dust mass of Md = 1.8 ± 0.4 × 10-11 M⊙ and a total mass (gas + dust) of 1.8 ± 0.4 × 10-9 M⊙ (using a gas-to-dust ratio of ~100 typical of circumstellar dust). We note that some of the additional broadband photometric values might be overestimated due to the surrounding interstellar cirrus emission (Barmby et al. 2011).
3.3.2. AX Cir
As AX Cir has almost the same spectral type as FF Aql, we considered a surface gravity of log g = 2.0 noting that a change of ± 0.5 only changes our following estimated values by 0.7%. Fig. 4 shows the SED fit for this Cepheid. The B and V photometric data are from B08 (from light curves) for a color excess index from Tammann et al. (2003). Data were also retrieved from the Deep Near Infrared Survey of the Southern Sky (DENIS) for the J and Ks bands. Beyond 9 μm, data come from MSX, IRC, and IRAS.
Our fitted parameters are presented in Table 4. The diameter agrees with the mean value predicted by Moskalik & Gorynya (2005, hereafter M05.
We did not detect IR emission at 8.6 μm and the value is consistent with the 9 μm measurement from IRC (see Table 3). However, there appears to be an infrared excess at longer wavelengths. We note that the IR excess seems to be larger around 13 μm and could be related to alumina oxide emission. Using an optical constant for amorphous compact alumina (Begemann et al. 1997), we computed κλ from a simple model of homogeneous spheres in the Rayleigh limit of small particles (Bohren & Huffman 1983), with a size distribution from Mathis et al. (1977, for particle sizes from 5 nm to 250 nm as O94 and a density ρ = 2.5 g cm-2. We then used this dust opacity in the model of Eq. (1) to fit a second component (green curve in Fig. 4), assuming that the envelope is mainly composed of amorphous alumina. We obtained β = 1.6 ± 0.4 × 10-19 kg m-2. Table 4 shows the fitted temperature and the total mass of the CSE estimated using a gas to dust ratio of ~100. However, a larger photometric dataset would be necessary to more tightly constrain the CSE parameters and its dust composition.
3.3.3. X Sgr
We retrieve photometric data from both the B,V dereddened magnitudes of Kervella et al. (2004a, hereafter K04 and M 84 (from light curves at an intermediate phase φ = 0.72). The other photometric data come from Feast et al. (2008, from J,H,K light curves, hereafter F08, IRC (9 μm), IRAS (12 μm) and, MSX (8.28, 12.13 and 14.65 μm). These data are plotted in Fig. 5.
For the same surface gravity previously used (log g = 2.0), we found an angular diameter (see Table 4) that is 13% and 3σ smaller than the mean diameter measured by Kervella et al. (2004b, 1.47 ± 0.04 mas, see Table 1. However, the amplitude of the pulsation is ~9% in diameter (M05). Our estimate agrees with θLD = 1.31 ± 0.12 mas assessed from the parallax (Benedict et al. 2007) and the linear diameter at this phase of pulsation (F08). However, K04 used a limb-darkened diameter to model their data and the presence of an extended emission could overestimate the angular diameter.
We detected a likely IR emission on the order of 5–15% (with respect to the stellar flux, see Table 3). We fitted the same flux density model previously used, with the dust opacity from O94 as it seems to have some silicate/carbon features. We obtained β = 5.6 ± 0.9 × 10-19 kg m-2. The other parameters are presented in Table 4.
3.3.4. η Aql
Optical and near-infrared photometry from K04 (B,V,J,H,K), M 84 (B,V), and Barnes et al. (J,H,K, 1997) were used to produce the SED (from light curves at an intermediate phase φ = 0.47). For the longer wavelengths, we retrieved the IRAS fluxes and the Spitzer/IRS spectra (from 5 to 35 μm, Ardila et al. 2010). The result is plotted in Fig. 6. The IRS spectra is plotted in purple. This spectra was acquired at a phase φ = 0.45, which is very close to the intermediate phase of our observations, thus we did not add any uncertainty caused by the phase mismatch. In the lower panel of Fig. 6, we just plotted the spectra for some value (bin of 10 μm) for clarity. The Spitzer flux measurements from M 10 were also added, but are significantly lower than the stellar SED derived from visible and near-IR. A possible explanation of this inconsistency might be the different observing mode used for η Aql with respect to the other Cepheids. η Aql was observed in full-frame mode, while the other stars used in this paper were observed in subarray mode. In the full frame mode, the images of this bright star are heavily saturated. The PSF-fitting method used in M 10 could be incorrect, leading to an underestimation of the photometry. For this reason, we decided not to include them in the fit.
We found that our measured θLD (see Table 4) is in good agreement with the measured diameter from Kervella et al. (2004b, θLD = 1.87 ± 0.03 at this phase and also with the mean angular diameter from Groenewegen (2008, θLD = 1.76 ± 0.09. At an intermediate phase (φ ~ 0.47), Luck & Andrievsky (2004) inferred a surface gravity of log g ~ 1.8 and an effective temperature of about Teff = 5508 ± 40 K, which is only 1% higher than our estimated value.
We can see from the IRS spectra that it is likely that this Cepheid has a small amount of IR emission, starting with a relative excess (still with respect to the photosphere) of 4.7 ± 1.5% at 5.3 μm to 9.2 ± 1.8% at 34.7 μm. We also detected in our VISIR filters an excess of the same order of magnitude (see Table 3).
No strong features of silicate seem to be present in the spectra. We therefore hypothesise that the envelope is composed mainly of amorphous carbon. Using the optical constant for amorphous carbon (Preibisch et al. 1993), we also computed κλ from a simple model of homogeneous spheres in the Rayleigh limit of small particles, with a size distribution from Mathis et al. (1977, for particle sizes from 5 nm to 250 nm as O94 and a density ρ = 2.0 g cm-2. We then used this dust opacity in Eq. (1) to fit the infrared excess (green curve in Fig. 6). We obtained β = 1.6 ± 0.4 × 10-18 kg m-2, which we used to derive the total dust mass presented in Table 4 with the dust temperature.
3.3.5. W Sgr
The B and V photometry are from K04 and B08 (at an intermediate phase φ = 0.48). The other irradiances are from DENIS (J,Ks), Spitzer (3.6, 4.5, 5.8, 8 and 24 μm from M 10), IRC (9 and 18 μm), MSX (8.28, 12.13, 14.65, 21.34 μm), and the 12 μm photometry from IRAS. The SED is plotted in Fig. 7.
Our fitted effective temperature (presented in Table 4) agrees at a 2% level with Teff = 5535 ± 51 K from Luck & Andrievsky (2004) around the same phase with an effective gravity from the same author of 1.7. We found an angular diameter that is about 15% and 2σ smaller than the one measured by interferometry by K04 (1.31 ± 0.04 mas) at this phase of pulsation. In contrast, our estimate agrees with the mean diameter from Bersier et al. (1997), who found 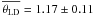 mas based on photometry. However, K04 used a limb-darkened diameter to model their data, and the presence of an extended emission might have them led to overestimate the angular diameter.
mas based on photometry. However, K04 used a limb-darkened diameter to model their data, and the presence of an extended emission might have them led to overestimate the angular diameter.
The measurements obtained for the Spitzer data are consistent with the blackbody radiation adjusted by M 10. However, our VISIR photometry shows an excess of ±15% (see Table 3). The same trend is observed from IRC (at 9 μm) and MSX (at 8.28, 12.13, and 14.65 μm). This could be evidence of a particular dust composition. As no IR emission is detected around 20 μm, we rejected a silicate dust composition and assumed an envelope mainly composed of alumina oxide. We used the same dust opacity model as AX Cir in Eq. (1). The resulting curve is plotted in Fig. 7 and the fitted parameters are listed in Table 4.
3.3.6. Y Oph
We retrieved the B,V data from B08 and M 84. The J,H,K photometry is from Laney & Stoble (1992) (also from light curves at an intermediate phase φ = 0.73) and K04. The plot of the SED is shown in Fig. 8. The other fluxes are from Spitzer (3.6, 4.5, 5.8, 8, and 24 μm from M 10), IRC (9 μm), and the 12 μm and 25 μm photometry from IRAS.
The best-fit model parameters are presented in Table 4 for a found log g ~ 1.8 (L08). L08 also give an effective temperature at this intermediate phase of Teff = 5800 ± 148 K that is in good agreement with our value. Our fitted angular diameter and the value θLD = 1.24 ± 0.01 mas at φ ~ 0.73 measured by Mérand et al. (2007) are also robust.
We detected a likely infrared emission from our photometric measurements (see Table 3). This result is consistent with Mérand et al. (2007), who found a CSE around this star in the K band with a relative contribution of 5.0 ± 2.0%. As some features of silicate/carbon seems to be present around 10 μm and 20 μm, the model of Eq. (1) was fitted with the dust opacity from O94. The best-fitted parameters are presented in Table 4. Y Oph seems to have a hotter circumstellar envelope that might be located close to the star and heated by its radiation.
3.3.7. U Car
We selected the B,V photometry from B08 and Coulson & Caldwell (1985) (from light curves at an intermediate phase φ = 0.63). We also used the J,H,K values from Laney & Stoble (1992, hereafter L92, also from light curves) and mid-IR photometric measurements from IRC (9 and 18 μm), from MSX (8.28, 12.13, 14.65 μm), and Spitzer (3.6, 4.5, 5.8, 8, and 24 μm from M 10). In Fig. 9, we plot the SED.
We list in Table 4 our fitted angular diameter and an effective temperature with a given log g ~ 1.2 from Romaniello et al. (2008), which is given at a phase of 0.49 but as said previously the broadband photometry is almost insensitive to the effective gravity changes. Our estimate of the diameter agrees at a 5% level with the mean angular diameter from Groenewegen (2008, 0.94 ± 0.05. However, our estimated effective temperature is inconsistent with the mean value Teff = 5980 K estimated from the iron abundances by Romaniello et al. (2008). From a color-temperature relation (Fry & Carney 1999), the temperature of the star should be Teff ~ 5000 K, which places in doubt the value of Romaniello et al. (2008). We did not find other measured temperatures in the literature to verify our estimate but we are confident in our value since all photometric data in the SED (<8 μm) look consistent with this effective temperature.
We detected significant IR emission with VISIR (see Table 3). This is also visible at longer wavelengths with an infrared excess of about 20–30%. We also fitted the flux density model (Eq. (1)) with the dust opacity from O94. The results are listed in Table 4. We note that these values could be affected by the interstellar-cirrus background emission in the region of this star (Barmby et al. 2011).
3.3.8. SV Vul
The B,V photometry were retrieved from B08 and M 84 while the J,H,K magnitudes from light curves of Barnes et al. (1997) and Laney & Stoble (1992). Other infrared data are from IRC (9 and 18 μm), MSX (8.28, 12.13, 14.65 μm), and IRAS (12 μm). The SED is presented in Fig. 10.
We took log g ~ 1.4 from Kovtyukh et al. (2005). These authors give an effective temperature around the same phase of Teff = 5977 ± 32 K. We found a temperature that is only 4% and 1.4σ smaller. The angular diameter that we found is 5% smaller than the mean value of Groenewegen (2008, 0.80 ± 0.05, but within 1σ.
We detected an excess both in PAH1 and SiC filters (see Table 3). This excess is also visible at other wavelengths up to 26.7 ± 6.6% at 18 μm with IRC. This indicates that there is circumstellar material.
We fitted the same model previously used (Eq. (1)) for the wavelengths longer than 3 μm and still with the dust opacity from O94. The fitted parameters are listed in Table 4. The uncertainty in the total mass estimate of the envelope is due to the uncertainty in the parallax measurement (Table 1). More photometric data points are necessary to more tightly constrain this SED, and measurements at least between 3 and 8 μm would be useful.
3.4. Spectral energy distribution of type II Cepheids
We use the same methods and models for type II Cepheids as for classical Cepheids.
3.4.1. R Sct
This very irregular pulsator with a large amplitude has been extensively observed and is known to have an infrared excess (see e.g. Goldsmith et al. 1987; Giridhar et al. 2000; De Ruyter et al. 2005). Its irregular pulsation and its large amplitude make it a special case among RV Tauri stars. We retrieved its B,V,J,H,K photometry from Shenton et al. (1994) (at phase 0.48). We also added values from IRC (9 and 18 μm), IRAS (12 μm), and MSX (8.28, 12.13, 14.65, 21.34 μm). We obtained E(B − V) and B − V from Taranova et al. (2010) and Myers et al. (2001), respectively. The SED is plotted in Fig. 11.
We fitted the stellar component (i.e. λ < 3 μm) with an effective gravity of log g = 0.0 given by Giridhar et al. (2000). As expected, we also detected a strong IR emission at our wavelengths (see Table 3). The fitted photospheric curve is shown in Fig. 11 (solid black curve) and its parameters in Table 4. Our temperature is consistent at a 2% level with Giridhar et al. (2000), who gave Teff = 4500 K (at φ = 0.44 using our ephemeris). Shenton et al. (1994) estimated a diameter of about 1.79 ± 0.59 mas (taking d = 431 pc from Hipparcos) and our value is only 3% smaller.
For the circumstellar component, we assumed that the envelope is optically thick and the observed flux density can be fitted by the equation 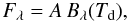 (2)where A is related to the solid angle and the emissivity of the envelope.
(2)where A is related to the solid angle and the emissivity of the envelope.
By looking at the SED, our values seem to be lower than the other measurements and it seems to have two different intensity distributions. As the effective resolution of VISIR is larger than that of the AKARI and IRAS telescopes in the N band, VISIR only detected a compact component located close to the star. We therefore decided to initially fit only our values with a compact component and then to fit a larger component using only the IR data from AKARI and IRAS. The result are presented in Fig. 11. The solid red curve is the possible warmer compact component for which our best-fit model parameters were T = 1486 ± 335 K and A = 4.65 ± 0.83 mas2. For the larger component (the green curve), we found T = 772 ± 83 K and A = 11.2 ± 1.25 mas2 (Table 4). This latter temperature is in the same range as the dust temperature T = 800 ± 50 K modeled by Taranova et al. (2010).
 |
Fig. 11 Synthetic spectra of the type II Cepheid R Sct (solid line) with the photometric measurements taken from the literature. In blue, we plot the points used to fit the SED. Our measurements are presented in red. In the lower panel, we plot the excess flux density relative to the photospheric emission. The red curve represents the flux density model for a compact component, while the green curve denotes the larger one. |
3.4.2. AC Her
AC Her has been studied extensively owing to its strong IR excess caused by thermal emission from circumstellar dust grains (see e.g. De Ruyter et al. 2005). We retrieved B,V,J,H,K band photometric flux from Shenton et al. (1992) (at phase 0.14). The longer wavelength data were taken from IRC (9 and 18 μm), and IRAS (12, 25, 60, 100 μm). Both E(B − V) and B − V were retrieved from Taranova et al. (2010) and Myers et al. (2001), respectively. We have plotted the SED in Fig. 12.
As in De Ruyter et al. (2005), an infrared excess is clearly visible. Our values lie on the maximum of the SED and also show a strong contribution from the circumstellar environment (Table 3). We fitted a two-component spectrum corresponding to the photosphere (still using Kurucz model) and the circumstellar emission. The best-fit model parameters found for the photospheric emission (black solid curve in Fig. 12) with log g = 0.5 from Van Winckel et al. (1998) are in Table 4. The temperature agrees with the one estimated by Taranova et al. (2010) whose mean value was Teff ~ 5400 K where T⊙ = 5800 K. The angular diameter is consistent with Shenton et al. (1992, θLD = 0.31 mas with R = 23.6 R⊙ and d = 750 pc. The second component was fitted with the model of Eq. (2), assuming an optically thick medium (solid green curve in Fig. 12). The fitted temperature is listed in Table 4 with A = 92.0 ± 6.9 mas2. Our estimated temperature is higher than the one of Gielen et al. (2007), who found a black-body temperature of 170 K using a disc model, his model also gave Rin = 50 mas and Rout = 428 mas for the disc (with d = 1400 pc). However, the author assumed that the morphology of the circumstellar material corresponds to a disc. Other values are found from a dust shell model assumed by De Ruyter et al. (2005), who found Rin = 22 mas and Rout = 397 mas. Alcolea & Bujarrabal (1991) also fitted the extended emission with a shell model and found Rin = 76 mas and Rout = 3330 mas with a dust temperature of T = 360 K. We can also note that AC Her was studied using high-resolution imaging with adaptive optics by Close et al. (2003), who did not detect any extended mid-infrared structure larger than 200 mas.
3.4.3. κ Pav
We retrieved the V,J,H,Ks photometric light curves of this target from F08. We used the value of E(B − V) and B − V given by F08. The mid- and far-infrared data were obtained from IRC and IRAS. We plotted the SED in Fig. 13.
We chose a mean effective gravity of log g = 1.2 from Luck & Bond (1989). Our fitted parameters are presented in Table 4. Our diameter estimate is in good agreement with F08 (1.04 ± 0.04 mas at φ = 0.90, with d = 204 ± 6 pc). However, we found an effective temperature that is 9% higher than the mean value estimated by Luck & Bond (1989, Teff ~ 5750 K at φ = 0.94 based on metal abundance analyses. We note that this star is classified as peculiar type II Cepheid, with a distinctive light curve that is brighter than normal type II Cepheid of the same period (see e.g. Matsunaga et al. 2009).
With VISIR, we detected an IR excess on the order of 20%. This excess tends to increase with wavelength leading to the hypothesis of an extended circumstellar envelope. We fitted to the IR photometric data the model of Eq. (1), assuming that the envelope is optically thin. Since some features are present around 10 μm and 20 μm, we also assumed a composition of silicate/carbon grains. We used the dust opacity of O94 to derive the total dust mass, assuming a gas-to-dust ratio of 100. The best-fit model parameters are listed in Table 4.
 |
Fig. 14 Sample of the final VISIR images for our Cepheids and their calibrator. The scale is logarithmic for all images. |
3.5. Spatially resolved emission
We searched for spatially extended emission using a Fourier technique, which is similar in its principle to the calibration technique used in long-baseline interferometry. This method has been previously used and validated by Kervella et al. (2009) and Kervella & Domiciano de Souza (2006). The principle is to divide the Fourier transform modulus of the image of the Cepheid (Icep) by that of the calibrator image (Ical) 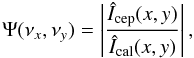 where the hat symbol denote the Fourier transform, (x,y) the sky coordinates, and (νx,νy) the angular spatial frequencies. This equation is related to interferometric observations that provide measurements of the Fourier transform of the intensity distribution of the observed object (Van Cittert-Zernike theorem).
where the hat symbol denote the Fourier transform, (x,y) the sky coordinates, and (νx,νy) the angular spatial frequencies. This equation is related to interferometric observations that provide measurements of the Fourier transform of the intensity distribution of the observed object (Van Cittert-Zernike theorem).
We then computed the ring median of Ψ, i.e. the median for a given spatial frequency radius ν over all azimuths (where 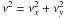 ). The function Ψ(ν) obtained is equivalent to a visibility in interferometry. The error bars in Ψ were estimated as the quadratic sum of the dispersion in the PSF calibrator’s Fourier modulus over the night and the rms dispersion in the calibrated Ψ function over all azimuthal directions for each spatial frequency. A deviation from a central symmetry will not be detected and any departure will be included in the error bars.
). The function Ψ(ν) obtained is equivalent to a visibility in interferometry. The error bars in Ψ were estimated as the quadratic sum of the dispersion in the PSF calibrator’s Fourier modulus over the night and the rms dispersion in the calibrated Ψ function over all azimuthal directions for each spatial frequency. A deviation from a central symmetry will not be detected and any departure will be included in the error bars.
Defining a model of a point-like star surrounded by a Gaussian shaped CSE and taking its Fourier transform, we were able to retrieve the CSE intensity distribution. This type of model was previously used by Kervella et al. (2009) and Kervella & Domiciano de Souza (2006) with the Ψ(ν) function 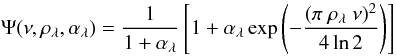
![\begin{displaymath} \Psi (\nu,\rho_\lambda,\alpha_\lambda) = \frac{1}{1 + \alpha_\lambda} \left[ 1 + \alpha_\lambda \exp{\left(-\frac{(\pi\ \rho_\lambda\ \nu)^2}{4\ln{2}} \right) }\right] \end{displaymath}](/articles/aa/full_html/2012/02/aa17307-11/aa17307-11-eq368.png) where the Gaussian CSE is defined with a FWHM ρλ and a relative flux αλ = fcse(λ)/f ⋆ (λ), i.e. the ratio of the flux of the envelope to the photospheric flux. We set V ⋆ = 1 since the star is unresolved by VISIR.
where the Gaussian CSE is defined with a FWHM ρλ and a relative flux αλ = fcse(λ)/f ⋆ (λ), i.e. the ratio of the flux of the envelope to the photospheric flux. We set V ⋆ = 1 since the star is unresolved by VISIR.
We applied the fit using a classical χ2 minimization to all the final images. We did not detect spatially resolved emission for FF Aql, η Aql, U Car (in the SiC filter), SV Vul, R Sct, AC Her, and κ Pav. For the other Cepheids that showed a resolved component, the fitted parameters are presented in Table 5 and the Ψ function are plotted in Fig. 15.
Fitted parameters of the Ψ(ν,ρλ,αλ) function.
 |
Fig. 15 Fit of a Gaussian CSE + unresolved point source model to the Ψ functions of our Cepheids. The dashed curve here represents a reference as an unresolved star. |
For the stars with an undetected envelope, an upper limit of ~265 mas can be set for the extension of the CSE based on the telescope resolution.
That we detected an extended emission around AX Cir and did not in the previous section (Sect. 3.3) can be explained by the lack of J,H,K light curves used to fully constrain the SED at our phase of pulsation. The uncertainties in these bands (0.14 mag in K) are large enough to prevent a detection of a IR excess.
From the distance ρ estimated with this technique, it is possible to assess a lower limit to the mass-loss rate by computing the time t required by a stellar wind to reach this distance. This computation was applied by Marengo et al. (2010b) to the Cepheid δ Cep. Using the escape velocity vesc ~ 100 km s-1 (Welch & Duric 1988) as the minimum wind speed, we found t ~ 12–23 yr. With the total dust mass estimated in Sect. 3.3, we derived a minimum mass loss-rate of Ṁ ~ 7 × 10-11 M⊙ yr-1 for AX Cir and W Sgr, and Ṁ ~ 2 × 10-10 M⊙ yr-1 for X Sgr, Y Oph, and U Car. These values are comparable to the predicted mass-loss rate from Neilson & Lester (2008, ranging from 10-10 to 10-7 M⊙ yr-1 and the measured mass-loss rate from Deasy (1988, ranging from 10-10 to 10-6 M⊙ yr-1.
The Fourier technique gives IR excesses that are comparable to those derived from the SED fitting presented in Sect. 3.3 (except for AX Cir). This convergence of two independent analysis methods instils us with confidence that the derived envelope parameters are reliable.
4. Discussion
Classical and type II Cepheids are two distinct classes of pulsating stars. The former are known to be intermediate-mass stars with regular pulsation periods, evolving as post-main sequence stars in a core He-burning phase. Type II Cepheids are generally associated with lower mass stars with irregular pulsations that undergo post-core He-burning evolution. Therefore, the CSEs surrounding these two classes correspond to different evolutionary stages.
R Sct and AC Her have been observed extensively and are known to have strong IR excesses linked to extended CSEs, that have been interpreted as relics of their strong dusty mass-loss on the asymptotic giant branch. Different models have been applied to constrain the morphology of this surrounding material. De Ruyter et al. (2005) interpreted the SED of these stars using a dust shell model. They found an inner radius Rin = 12.5 AU and an outer radius Rout = 224 AU for AC Her and Rin = 13.4 AU and Rout = 5200 AU for R Sct. From a disc model applied to AC Her, Gielen et al. (2007) found Rin = 35 AU and a smaller external radius Rout = 300 AU. For this star, these results contradict those of Close et al. (2003) who excluded any extended emission larger than 75 AU from high Strehl ratio adaptive optics images in the mid-IR domain. We also did not detect in our filters any extended VISIR emission larger than R = 100 AU.
The case of R Sct is peculiar and this star is often classified as an exception by several authors. Alcolea & Bujarrabal (1991) used a two shell model to interpret both its mid-IR and far-IR data and estimated a temperature for the largest grains of T = 815 K. The estimated radii of the shells were Rin,1 = 30 AU, Rout,1 = Rin,2 = 5 720 AU, and Rout,2 = 12 000 AU (using d = 431 pc), where the indices 1 and 2 denote the inner and outer shells, respectively. We possibly detected the emission of the inner shell from our VISIR photometry but no spatially extended emission larger than R = 100 AU.
κ Pav has been classified as a peculiar type II Cepheid by some authors because of its distinctive light curve. It is significantly brighter than normal type II Cepheids with the same period (see e.g. Matsunaga et al. 2009). This star is not at the same stage of evolution as R Sct and AC Her since it is ascending the Hertzsprung-Russell diagram along the blue horizontal branch to the asymptotic giant branch. During this process, the star undergoes changes in both its core and envelope that could lead to mass loss via pulsation and/or shock mechanisms. An active past and/or ongoing mass loss may explain the large IR excess we have detected.
With classical Cepheids, we are on different scales because the envelope that we have detected until now has a spatial extension of only a few stellar radius. Only a small sample of classical Cepheids is known to host a circumstellar envelopes (ℓ Car, Y Oph, RS Pup, Polaris, δ Cep, S Mus, GH Lup, T Mon and X Cyg; Kervella et al. 2006; Mérand et al. 2006, 2007; Barmby et al. 2011). With this paper, we complement this sample with FF Aql, η Aql, W Sgr, U Car, and SV Vul as probable IR excess Cepheids. The origin of these CSEs is poorly understood. Their presence could be linked to mass loss from the star. It has been suggested that the IR excess is caused by dust formed in a wind from the Cepheids (Kervella et al. 2006). From a radiative-driven wind model including pulsation and shock effects Neilson & Lester (2008) concluded that radiative driving is insufficient to account for the observed IR excesses and proposed that the mass loss could be driven by shocks generated in the atmosphere by the pulsation of the star. Other observational evidence has been provided with IR excess detections from IRAS observations by Deasy (1988), who estimated mass-loss rates ranging from 10-10 to 10-6 M⊙ yr-1.
For the classical Cepheids, Mérand et al. (2007) uncovered a likely correlation between the pulsation period and the CSE flux (relative to the photosphere) in the K band. We have plotted in Fig. 16 the relative CSE flux versus the period at 8.6 μm. It seems that at 8.6 μm the longer periods have larger excesses, as concluded by Mérand et al. (2007) in the K band. Assuming that this excess is linked to a mass-loss phenomena, this correlation shows that long period Cepheids have a larger mass-loss than shorter period, less massive stars. This behavior could be explained by the stronger velocity fields in longer period Cepheids, and the presence of shock waves at certain pulsation phases (Nardetto et al. 2006, 2008).
 |
Fig. 16 Measured relative CSE fluxes at 8.6 μm around Cepheids as a function of the pulsation period. |
5. Conclusion
We presented new thermal IR photometry and SEDs of eight classical Cepheids and three type II Cepheids. We detect extended emission around ten stars in the thermal infrared domain, of which three were previously known. The sample of classical Cepheids with CSEs is extended with five additional stars to a total of nine stars. This confirms that circumstellar material around classical Cepheids is a widespread phenomenon.
A correlation is also found between the pulsation period and the CSE flux in the thermal IR, which confirms the same correlation found in the K band by Mérand et al. (2007). Hence, longer period Cepheids have apparently higher mass-loss rates than shorter periods. Apart from their probable importance to the evolution of Cepheids, the existence of these CSEs may also affect Cepheid distance measurements in the infrared domain, particularly those to be performed with the JWST.
We also point out the need for more optical and near-infrared Cepheid light curves. This is the main source of uncertainty in the SED at a given phase of pulsation. A dedicated J,H,K photometric survey of a few months would be sufficient to derive data with a good coverage in phase and permit any mid- and far-infrared excess detection.
Online material
Log of our VISIR BURST mode observations.
Filter transmission profiles are available on the ESO website http://www.eso.org/sci/facilities/paranal/instruments/visir/inst/index.html
Acknowledgments
We thank the referee for his/her suggestions that led to improvements of this article. We received the support of PHASE, the high angular resolution partnership between ONERA, Observatoire de Paris, CNRS, and University Denis Diderot Paris 7. This work made use of the SIMBAD and VIZIER astrophysical database from CDS, Strasbourg, France and the bibliographic informations from the NASA Astrophysics Data System. Data processing for this work have been done using the Yorick language which is freely available at http://yorick.sourceforge.net/. This research is based on observations with AKARI, a JAXA project with the participation of ESA.
References
- Alcolea, J., & Bujarrabal, V. 1991, A&A, 245, 499 [NASA ADS] [Google Scholar]
- Ardila, D. R., Van Dyk, S. D., Makowiecki, W., et al. 2010, ApJS, 191, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Barmby, P., Marengo, M., Evans, N. R., et al. 2011, AJ, 141, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, III, T. G., Fernley, J. A., Frueh, M. L., et al. 1997, PASP, 109, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Begemann, B., Dorschner, J., Henning, T., et al. 1997, ApJ, 476, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B. E., Feast, M. W., et al. 2007, AJ, 133, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Berdnikov, L. N. 2008, VizieR Online Data Catalog: II/285, originally published in Sternberg Astronomical Institute, Moscow, 2285 (B08) [Google Scholar]
- Berdnikov, L. N., & Caldwell, J. A. R. 2001, J. Astron. Data, 7, 3 [Google Scholar]
- Bersier, D., Burki, G., & Kurucz, R. L. 1997, A&A, 320, 228 [NASA ADS] [Google Scholar]
- Bohren, C. F., & Huffman, D. R. 1983, Absorption and scattering of light by small particles, ed. C. F. Bohren, & D. R. Huffman (New York: Wiley) [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, ed. N. Piskunov, W. W. Weiss, & D. F. Gray (ASP), IAU Symp., 210, 20 [Google Scholar]
- Close, L. M., Biller, B., Hoffmann, W. F., et al. 2003, ApJ, 598, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Coulson, I. M., & Caldwell, J. A. R. 1985, South African Astron. Obs. Circ., 9, 5 [Google Scholar]
- De Ruyter, S., van Winckel, H., Dominik, C., Waters, L. B. F. M., & Dejonghe, H. 2005, A&A, 435, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deasy, H. P. 1988, MNRAS, 231, 673 [NASA ADS] [Google Scholar]
- Doucet, C., Lagage, P., & Pantin, E. 2006, in Visions for Infrared Astronomy, Instrumentation, Mesure, Métrologie, ed. V. Coudé Du Foresto, D. Rouan, & G. Rousset (Paris: Lavoisier), 25 [Google Scholar]
- Egan, M. P., & Price, S. D. 1996, AJ, 112, 2862 [NASA ADS] [CrossRef] [Google Scholar]
- Egan, M. P., Price, S. D., Kraemer, K. E., et al. 2003, VizieR Online Data Catalog: V/114, originally published in: Air Force Research Laboratory Technical Report AFRL-VS-TR-2003-1589 (2003), 5114 [Google Scholar]
- Feast, M. W., Laney, C. D., Kinman, T. D., van Leeuwen, F., & Whitelock, P. A. 2008, MNRAS, 386, 2115 (F08) [NASA ADS] [CrossRef] [Google Scholar]
- Fernie, J. D., Evans, N. R., Beattie, B., & Seager, S. 1995, Inf. Bull. Variable Stars, 4148, 1 [Google Scholar]
- Fouqué, P., Storm, J., & Gieren, W. 2003, in Stellar Candles for the Extragalactic Distance Scale, ed. D. Alloin, & W. Gieren (Berlin: Springer), Lect. Notes Phys., 635, 21 [Google Scholar]
- Fouqué, P., Arriagada, P., Storm, J., et al. 2007, A&A, 476, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fry, A. M., & Carney, B. W. 1999, AJ, 118, 1806 [NASA ADS] [CrossRef] [Google Scholar]
- Gallenne, A., Mérand, A., Kervella, P., & Girard, J. H. V. 2011, A&A, 527, A51 [Google Scholar]
- Gielen, C., van Winckel, H., Waters, L. B. F. M., Min, M., & Dominik, C. 2007, A&A, 475, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giridhar, S., Lambert, D. L., & Gonzalez, G. 2000, ApJ, 531, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, M. J., Evans, A., Albinson, J. S., & Bode, M. F. 1987, MNRAS, 227, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T. 2007, A&A, 474, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2008, A&A, 488, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helou, G., & Walker, D. W. 1988, IRAS catalogue, Vol. 7 (STI) [Google Scholar]
- Hindsley, R. B., & Bell, R. A. 1989, ApJ, 341, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffleit, D., & Jaschek, C. 1991, The Bright star catalogue, ed. D. Hoffleit, & C. Jaschek, 5th revised edition (New Haven: Yale University) [Google Scholar]
- Ishihara, D., Onaka, T., Kataza, H., et al. 2010, A&A, 514, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., & Domiciano de Souza, A. 2006, A&A, 453, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., & Domiciano de Souza, A. 2007, A&A, 474, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Bersier, D., Mourard, D., et al. 2004a, A&A, 428, 587 (K04) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Nardetto, N., Bersier, D., Mourard, D., & Coudé du Foresto, V. 2004b, A&A, 416, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., Perrin, G., & Coudé Du Foresto, V. 2006, A&A, 448, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., & Gallenne, A. 2009, A&A, 498, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovtyukh, V. V., Andrievsky, S. M., Belik, S. I., & Luck, R. E. 2005, AJ, 129, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Laney, C. D., & Stoble, R. S. 1992, A&AS, 93, 93 [NASA ADS] [Google Scholar]
- Laney, C. D., & Stobie, R. S. 1993, MNRAS, 260, 408 [NASA ADS] [Google Scholar]
- Li, A. 2005, in The Spectral Energy Distributions of Gas-Rich Galaxies: Confronting Models with Data, ed. C. C. Popescu, & R. J. Tuffs, AIP Conf. Ser., 761, 123 [Google Scholar]
- Luck, R. E., & Andrievsky, S. M. 2004, AJ, 128, 343 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Luck, R. E., & Bond, H. E. 1989, ApJ, 342, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., Andrievsky, S. M., Fokin, A., & Kovtyukh, V. V. 2008, AJ, 136, 98 (L08) [Google Scholar]
- Marengo, M., Evans, N. R., Barmby, P., et al. 2010a, ApJ, 709, 120 (M10) [NASA ADS] [CrossRef] [Google Scholar]
- Marengo, M., Evans, N. R., Barmby, P., et al. 2010b, ApJ, 725, 2392 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Matsunaga, N., Feast, M. W., & Menzies, J. W. 2009, MNRAS, 397, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Mérand, A., Kervella, P., Coudé Du Foresto, V., et al. 2006, A&A, 453, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Aufdenberg, J. P., Kervella, P., et al. 2007, ApJ, 664, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Moffett, T. J., & Barnes, III, T. G. 1984, ApJS, 55, 389 (M 84) [NASA ADS] [CrossRef] [Google Scholar]
- Moskalik, P., & Gorynya, N. A. 2005, Acta Astron., 55, 247 (M05) [NASA ADS] [Google Scholar]
- Myers, J. R., Sande, C. B., Miller, A. C., Warren, Jr., W. H., & Tracewell, D. A. 2001, VizieR Online Data Catalog: V/109, originally published in Goddard Space Flight Center, Flight Dynamics Division (2002), 5109 [Google Scholar]
- Nardetto, N., Mourard, D., Kervella, P., et al. 2006, A&A, 453, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Groh, J. H., Kraus, S., Millour, F., & Gillet, D. 2008, A&A, 489, 1263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2008, ApJ, 684, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Neilson, H. R., Cantiello, M., & Langer, N. 2010a, 16th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, ed. C. Johns-Krull (San Francisco, CA: ASP), ASP Conf. Ser., in press [arXiv:1011.4391] [Google Scholar]
- Neilson, H. R., Ngeow, C., Kanbur, S. M., & Lester, J. B. 2010b, ApJ, 716, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Ngeow, C., Kanbur, S. M., Nikolaev, S., Tanvir, N. R., & Hendry, M. A. 2003, ApJ, 586, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 (O94) [NASA ADS] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Preibisch, T., Ossenkopf, V., Yorke, H. W., & Henning, T. 1993, A&A, 279, 577 [NASA ADS] [Google Scholar]
- Romaniello, M., Primas, F., Mottini, M., et al. 2008, A&A, 488, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samus, N. N., & Durlevich, O. V. 2009, VizieR Online Data Catalog: B/gcvs, originally published in Institute of Astronomy of Russian Academy of Sciences and Sternberg, State Astronomical Institute of the Moscow State University, 1, 2025 [Google Scholar]
- Schütz, O., & Sterzik, M. 2005, in High Resolution Infrared Spectroscopy in Astronomy, ed. H. U. Käufl, R. Siebenmorgen, & A. Moorwood, Proc. ESO Workshop, held at Garching, Germany, 104 [Google Scholar]
- Shenton, M., Albinson, J. S., Barrett, P., et al. 1992, A&A, 262, 138 [NASA ADS] [Google Scholar]
- Shenton, M., Monier, R., Evans, A., et al. 1994, A&A, 287, 866 [NASA ADS] [Google Scholar]
- Tammann, G. A., Sandage, A., & Reindl, B. 2003, A&A, 404, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taranova, O. G., Shenavrin, V. I., & Tatarnikov, A. M. 2010, Astron. Lett., 36, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Van Winckel, H., Waelkens, C., Waters, L. B. F. M., et al. 1998, A&A, 336, L17 [NASA ADS] [Google Scholar]
- Welch, D. L., & Duric, N. 1988, AJ, 95, 1794 [NASA ADS] [CrossRef] [Google Scholar]
- Welch, D. L., Wieland, F., McAlary, C. W., et al. 1984, ApJS, 54, 547 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Relative atmospheric transmission for our observing nights. Both nights are normalised to the mean value over all calibrators observed. The dotted lines denote a 5% variation. |
| In the text | |
 |
Fig. 2 Examples for the constructed light curves in the V band. Data for FF Aql are from Moffett & Barnes (1984) and for Y Oph from Berdnikov (2008). The resulting light curves are drawn with solid lines. |
| In the text | |
 |
Fig. 3 Synthetic spectra of the classical Cepheid FF Aql (solid line) with the photometric measurements taken from the literature. The blue triangles are the points used to fit the SED. Our measurements are presented with the red circles, while the black squares are the other photometric data. In the lower panel, we plot the excess flux density relative to the photospheric emission. The green curve represents the flux density model. |
| In the text | |
 |
Fig. 4 The same as Fig. 3, but for AX Cir. |
| In the text | |
 |
Fig. 5 The same as Fig. 3, but for X Sgr. |
| In the text | |
 |
Fig. 6 The same as Fig. 3, but for η Aql. The measured spectra were superimposed in purple. |
| In the text | |
 |
Fig. 7 The same as Fig. 3, but for W Sgr. |
| In the text | |
 |
Fig. 8 The same as Fig. 3, but for Y Oph. |
| In the text | |
 |
Fig. 9 The same as Fig. 3, but for U Car. |
| In the text | |
 |
Fig. 10 The same as Fig. 3, but for SV Vul. |
| In the text | |
 |
Fig. 11 Synthetic spectra of the type II Cepheid R Sct (solid line) with the photometric measurements taken from the literature. In blue, we plot the points used to fit the SED. Our measurements are presented in red. In the lower panel, we plot the excess flux density relative to the photospheric emission. The red curve represents the flux density model for a compact component, while the green curve denotes the larger one. |
| In the text | |
 |
Fig. 12 The same as Fig. 11, but for AC Her. |
| In the text | |
 |
Fig. 13 The same as Fig. 11, but for κ Pav. |
| In the text | |
 |
Fig. 14 Sample of the final VISIR images for our Cepheids and their calibrator. The scale is logarithmic for all images. |
| In the text | |
 |
Fig. 15 Fit of a Gaussian CSE + unresolved point source model to the Ψ functions of our Cepheids. The dashed curve here represents a reference as an unresolved star. |
| In the text | |
 |
Fig. 16 Measured relative CSE fluxes at 8.6 μm around Cepheids as a function of the pulsation period. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


