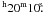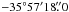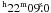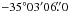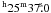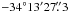EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 538 (February 2012) A&A, 538 (2012) A142 Full HTML
Free Access
Issue
A&A
Volume 538, February 2012
Article Number A142
Number of page(s) 21
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201117299
Published online 16 February 2012

© ESO, 2012

1. Introduction

Star-forming complexes are the main building blocks of the large-scale structure of galaxies and major sites to study how massive stars form. However, in contrast to low-mass stars, the formation of high-mass stars remains poorly understood. In this framework, the Herschel/HOBYS (PI: F. Motte, A. Zavagno, S. Bontemps) Guaranteed Time Key Programme is performing a 75 to 500 μm SPIRE and PACS imaging of a complete sample of molecular complexes more massive than Orion at distance of less than 3 kpc. This sample has been built based on dust extinction images and CO surveys of the Galactic plane and includes NGC 6334 and NGC 6357.

In our Galaxy, NGC 6334 and NGC 6357 are two very active star-forming complexes seen in the optical as two extensive and intensely star-forming H ii regions. The extinction map and the morphology of the 1.2 mm cold dust emission seem to indicate that NGC 6334 and NGC 6357 are connected by a filamentary structure, suggesting that both regions belong to a single complex (Russeil et al. 2010).

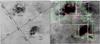thumbnail Fig. 1

a) Hα image (UKST Hα survey, Parker et al. 2005) of the H ii regions NGC 6334 and NGC 6357 (Galactic coordinates). b) Hα image with overplotted the coverage of the VIMOS observations (green) and CTIO observations (red), as well as the zones 1 to 8 (white) discussed in the text. Zones 2, 6, and 8 correspond respectively to NGC 6357, NGC 6334, and GM 24.

The molecular emission associated with NGC 6334 has a mean molecular velocity of VLSR =  −4 km s-1 (Kraemer & Jackson 1999) similar to the value from radio recombination lines, VLSR =  −3.6 km s-1, of NGC 6357 (Caswell & Haynes 1987). These similar velocities for regions located spatially close to each other indicate that they are both at a similar distance. Independant distance determinations of each region are not yet well-established. Owing to their Galactic coordinates close to the Galactic center direction, l,   b = 351.16°, +0.69° and l,   b = 353.01°, +0.89°, respectively, for NGC 6334 and NGC 6357, the kinematic distance is unreliable. The best way to derive their distances is from the determination of the distance to their exciting stars.

As reviewed by Persi & Tapia (2008), NGC 6334 (=Sharpless 8 = RCW 127) contains the H ii regions (Fig. 1) GUM 61, GUM 62, GUM 63, and GUM 64 (Gum 1955) and G351.2+0.5. Roslund (1966), Neckel (1978), Walborn (1982), and Persi & Tapia (2008) computed the distance to NGC 6334 from the distances to the visible early-type stars in these H ii regions and obtained d = 1.45 kpc, 1.74 kpc, 2.30 kpc and 1.61 kpc, respectively. Persi & Tapia (2008) underlined that the discrepancies are due to the different adopted MV calibrations and the adopted extinction law (RV value).

In the optical, NGC 6357 exhibits several bubbles and shell-like regions. The brightest H ii region (G353.2+0.9) shows a sharp boundary facing the massive open cluster Pismis 24. The distance of NGC 6357 is usually established from the distance of Pismis 24 (the exciting cluster of NGC 6357); its most recent determination was that of Massey et al. (2001), who give a value of 2.5 kpc. This distance differs from the 1.7 kpc suggested by Neckel (1978) and Lortet et al. (1984) and the 1.1 kpc and 1.74 kpc derived by Conti & Vacca (1990) and Van der Hucht (2001), respectively, for the Wolf-Rayet star HD 157504 (WR 93).

The distance of NGC 6334 and NGC 6357 has therefore not yet been well-established. However, since the distance is an essential parameter for the determination of the mass, size, and luminosity of the associated young objects (e.g. Russeil et al. 2011), it is essential to evaluate in an homogenous way the distance of the early-type stars in the direction of NGC 6334 and NGC 6357. In this paper, we focus on the content of ionizing OB stars of the star-forming complexes NGC 6334 and NGC 6357 to more tightly constrain their distances, to place them in the Galactic context, and to perform a census of their OB stars.

2. Observations and data extraction

2.1. U, B, and V VIMOS data

We observed NGC 6334, NGC 6357, and GM 24 (GM 1-24, Gyulbudaghian et al. 1977) in U, B, and V bands with the VIMOS camera (ESO-VLT). VIMOS is a visible (360 to 1000 nm) wide field imager and multi-object spectrograph mounted at the Nasmyth focus B of UT3 Melipal. We use VIMOS in its imaging mode. This led to the observation of 67 fields, each composed of 4 quadrants of 7′ × 8′ separated by 2′ gaps. The coverage is presented in Fig. 1. The typical observing method was three exposures of 3 s in B, seven exposures of 4 s in U, and four exposures of 3 s in V. The observations were taken in service mode and delivered flatfielded, bias-corrected and with calculated astrometric and photometric data (zero point, extinction coefficient).

We extracted stellar positions and magnitudes using SExtractor (Bertin & Arnouts 1996). We kept objects a with SExtractor flag  ≤3 (such a condition ensures a good photometry and excludes saturated objects). In addition, we excluded data at the borders of the CCD and in dead columns. All objects brighter than V = 10 mag were typically saturated. As we treated the image independently, we performed a cross-correlation between the extracted U, B, and V data in order to establish a catalogue of stars with U, B, and V magnitudes.

We measured the completeness as in Adami et al. (2006) and Durret et al. (2010). This method adds artificial stars of different magnitudes and at different locations to the original images and then attempts to recover them by running SExtractor again with the same parameters used for object detection and classification on the original images. We investigated the completeness from three typical images located at different parts of the surveyed area with varying levels of background and source crowding. The 90% mean completeness level (Fig. 2) is respectively 21.8, 22.4, and 22.6 mag for U, B, and V filters. Figure 2, shows how the completeness levels vary from CCD to CCD because of the quantum efficiency variations between individual CCDs and because of fluctuations in the diffuse background light.

thumbnail Fig. 2

U a), Bb), and Vc) completeness level in individual CCDs (each dotted curve corresponds to a CCD quadrant, and the black curve is the average of these dotted curves) for the fields centered respectively at 170; (NGC 6334, blue), 17; (green), and 17; (NGC 6357, red).

From a statistical study of the zero-point, we estimated dispersions of 0.09 mag for U, 0.04 mag for B, and 0.03 mag for V. The delivered photometric calibration neglects the color term. Thus we estimated the typical error caused by this assumption about the mean color coefficient estimated for the VIMOS instrument and the mean color of OB stars. This leads to a typical error of 0.017 mag in U and B and 0.006 mag in V. We then estimated the error in the magnitude of a star to be the quadratic sum of the magnitude errors given by SExtractor, the zero-point uncertainty, and the color term uncertainty. This led to typical errors of 0.04 mag, 0.09 mag, and 0.23 mag, respectively, in V, B, and U.

Finally, as some fields overlap, we identified the objects counted twice and retained those located closer to the field center. For the purpose of locating O and B stars, we kept stars with magnitude values in the three (U, B, and V) bands. This provided a sample of 30 388 stars (U, B, and V magnitudes are presented in Appendix, Table A.1).

2.2. R band CTIO images

We obtained R images of NGC 6334, NGC 6357, GM 24, and the more diffuse area between NGC 6334 and NGC 6357 with the MOSAIC camera (Blanco-CTIO). This instrument is an eight CCD mosaic imager with a pixel scale of 0.27′′ mounted at the prime focus of the 4-m Blanco telescope at the Cerro Tololo Inter-American Observatory (CTIO). These observations consist of six fields composed of three exposures of 10 s each. The global coverage is presented Fig. 1. Each field consists of eight quadrants (separated by gaps of  ~13′′ in rows and  ~9.5′′ in columns) covering a 36′ × 36′ field of view. The bias and the flat-field corrections were applied to each of the eight CCD images independently, while the combination of the different exposures, the astrometry, the reconstruction of the final image and the construction of the weight images were done with the modules MissFITS, SCAMP, and SWarp of TERAPIX (Bertin et al. 2002). The photometric calibration was performed using the observation of the Landolt calibration stars S107a, S107b, S104, and S98 (Landolt 2009), giving an extinction coefficient of 0.095 ± 0.043 mag and a zero point of 25.57 ± 0.02 mag. The extraction of the stellar positions and magnitudes was done using SExtractor with the weight images produced by the SWarp module. We kept only objects with a SExtractor flag below 3, and excluded stars in the borders of the CCD and in dead columns. This provided a sample of 53 420 stars (the R magnitudes of which are presented in Appendix, Table A.2). The estimated saturation limit is 11 mag and the typical magnitude uncertainty (quadratic sum of the magnitude errors given by SExtractor, the zero-point uncertainty, and the extinction coefficient uncertainty) is 0.05 mag.

3. Other available data sets

3.1. Near-Infrared data from 2MASS

To complement our optical data, we used data from the Two Micron All Sky Survey (2MASS) point source catalog (Skrutsie et al. 2006). The 2MASS survey scanned the entire sky uniformly in three near-IR bands: J (1.25 μm), H (1.65 μm), and KS (2.17 μm). The 2MASS point source catalog1 (Skrutsie et al. 2006) consists of accurate positions (astrometric accuracy rms better than 200 mas) and brightness information for over 400 million point sources. The point source catalog is more than 99% complete for magnitudes of J < 15.8, H < 15.1, and KS < 14.3 mag. The photometric signal-to-noise ratio is  >10 (i.e. σJ,H,Ks ≤ 0.1 mag) for sources brighter than the completeness limits. The typical magnitude error is 0.05 mag, 0.06 mag, and 0.05 mag, respectively in J, H, and KS.

3.2. DENIS data

The DENIS2 imaging survey (Epchtein et al. 1997) gives a nearly complete overview of the southern sky in three NIR bands: Gunn-I (0.85 μm), J (1.25 μm), and KS (2.15 μm). The images have been taken simultaneously in all three bands, which leads to a very high accuracy in the colors of the objects independent of photometric errors. The DENIS data have a positional accuracy better than 2′′ and the magnitude limits are 18.5 mag, 16.5 mag, and 14 mag in I, J, and KS, respectively. The typical magnitude uncertainty is 0.15 mag, 0.11 mag and 0.10 mag in J, KS, and I, respectively.

3.3. USNO-B1.0 data

USNO-B is an all-sky survey obtained from scans of 7435 Schmidt plates taken for the various optical sky surveys during the past 50 years. The USNO-B1.0 is complete down to V = 21 mag, has an astrometric accuracy of 0.2′′, and a photometric accuracy of 0.3 mag (Monet et al. 2003). From the point source catalog3 we extracted R and I magnitudes.

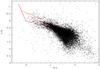thumbnail Fig. 3

Color − color diagram for stars with U, B, and V magnitudes. The red curve is the theoretical unreddened main-sequence and the line is the standard reddening vector, up to AV = 5 mag, for a B3V star (from Schimdt-Kaler 1983).

4. The O-B3 star sample

We selected the young and massive stars (O to B3 stars) based on their U − B and B − V colors. The interstellar reddening affects the intrinsic U − B and B − V colors following the reddening line that has the form: EU − B/EB − V = X + YEB − V. In this equation, EU − B and EB − V are the color excesses, X is the slope of the reddening line, and Y is the curvature term. We used the reddening path EU − B/EB − V = 0.72 + 0.05EB − V (Schmidt-Kaler 1983). To select O to B3 stars from the U − B/B − V color − color diagram, we selected stars above the reddening path of a B3 star (Fig. 3). Following Turner (1996), this corresponds to a normal extinction law (RV = 3.1), while larger RV (as expected for star-forming regions) seem to induce a shallower slope. This does not impact our selection process as stars following a reddening law with a shallower slope will be above the adopted reddening path. In addition the reddening path does not depend strongly on the adopted intrinsic colors. To test this aspect we plot EU − B versus EB − V for stars with known spectra (Table 2) and fitted the EU − B/EB − V = X + YEB − V relationship for the Schmidt-Kaler (1983) and for the most recent Martins et al. (2006) color calibrations of O stars. If our small sample does not allow us to constrain reliably X and Y, the fit results are similar for both calibrations (with a smaller than 1% difference in X and Y). However, Turner (1989) showed that the slope of the UBV reddening line varies from one region of the Milky-Way to another over a range of at least X = 0.62 to 0.80. If the slope is steeper than 0.72, this can cause us to miss some B3 stars.

This provided a sample of 2394 candidate OB stars. We then searched for objects associated with the 2394 candidate OB stars in the DENIS, 2MASS, and USNO catalogues using a 5′′ circular cone search radius. We identified 2148 OB stars with a 2MASS counterpart.

From the O-B3 star sample we discuss, in the next section, the extinction law (Sects. 5.1 and 5.2) in connection with the dust properties (Sect. 5.3), the Galactic structure (Sect. 5.4) and the OB stars census (Sect. 5.5).

Table 1

RV results.

Table 2

Stellar data available in literature for NGC 6357 (Pismis 24) and NGC 6334.

5. Discussion

5.1. Extinction law

The radiation from massive OB stars can modify the interstellar grains present in their immediate vicinity, hence affect the global interstellar extinction law (e.g. Chini & Wargau 1990; Pandey et al. 2000). Any change in the interstellar law will affect the local extinction and thus the photometric distance determination. Many investigations (e.g. Wegner 1994; Whittet & vanBreda 1980; Rieke & Lebofsky 1985) have shown that the normal extinction law (RV = 3.1) is valid nearly everywhere in our Galaxy, although some exceptions are noted especially in the direction of star-forming regions and open clusters, where the RV value is higher (e.g. O’Dell & Wen 1992). Different RV values relate to different environmental conditions and thus different grain-size distributions and compositions, since the extinction depends on the optical properties of the dust grains (e.g. Whittet 2003; Mazzei & Barbaro 2011). In particular low-RV values are expected arise along the lines of sight to smaller grains.

There are four main methods for determining the extinction and the extinction law in a given direction:

  • 1.

    The spectro-photometric method, which is based on thecomparison of the observed energy distribution of a star of knownspectral type with its non-reddened distribution (e.g. Cardelli1989).

  • 2.

    The Paschen-Balmer lines ratio method, which uses the comparison between the predicted and observed Paschen-Balmer line pair ratio emitted by the H ii regions (e.g. Greve 2010).

  • 3.

    The color excess method, which uses two color-excess diagrams of the form E(λ − V) versus E(B − V) (where λ is one of the wavelengths of a broad band filter) of a group of stars and requires the spectral type, hence the intrinsic color, of observed stars to be known (“method A” of Pandey et al. 2003).

  • 4.

    The photometric method, which uses two color diagrams (TCDs) of the form (λ − V) versus (B − V) (where λ is one of the wavelengths of a broad-band filter) of a group of stars and assumes that the observed stars are main sequence stars (“method B” of Pandey et al. 2003). In these plots, the reddening path coincides with the unreddened main sequence causing the stars of different spectral types and extinctions to form a linear relation parallel to the reddening line. The slope of this distribution, relative to the expected slope for the normal reddening path, allows one to derive the value of RV.

As we are performing a statistical study of OB stars in the direction of NGC 6334-NGC 6357 and have no spectral information about the stars, the last method is the most appropriate. To investigate the value of RV in the direction of NGC 6334 – NGC 6357, we used TCDs with λ as one of the wavelengths of the broad band filters (R, I, J, H, K). These TCDs provide an effective method for separating the influence of the normal extinction produced by the diffuse interstellar medium from that of the abnormal extinction. In these diagrams, the slope of the distribution, mobs, is compared to the theoretical slope, mnormal (Pandey et al. 2003). To derive the value of RV, we used the relation (see Samal et al. 2007; Pandey et al. 2000) 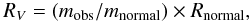(1)where Rnormal = 3.1.

To investigate the RV value in NGC 6334-NGC 6357, we divided the area into eight zones based on the individual region (see Fig. 1) and plotted the TCDs for each zone. Zones 2, 6, and 8 encompass NGC 6357, NGC 6334, and GM24 respectively. Zone 3 is the area between NGC 6357 and NGC 6334. Zones 4 and 1 and zones 5 and 7 are on the eastern and western borders of NGC 6357 and NGC 6334, respectively.

thumbnail Fig. 4

V − K versus B − V for zone 4 a), zone 2 = NGC 6357 b), and zone 6 = NGC 6334 c). The stars identified spectroscopically (see Sect. 5.2) are also overplotted (filled triangles). The small thick segment on the bottom left of the plots is the locus of the unreddened O-B3 stars (from Martins et al. 2006; Koornneef et al. 1983; and Wegner 1994).

Before plotting the TCDs, we adopt the following selection criteria for our sample:

  • 1.

    We removed IR-excess objects based on their 2MASS J − H and H − K colors. Following Hanson et al. (1997), we kept stars with (J − H) − (1.83 × (H − K) + 0.15) ≥ 0.

  • 2.

    We kept only stars with V < 21 mag (to ensure completness) and with B − V uncertainties  < 0.15 mag.

  • 3.

    For CTIO data we retained stars with V − R uncertainties  ≤ 0.15 mag.

  • 4.

    For the 2MASS and DENIS data, we kept stars with magnitude uncertainties  ≤ 0.15 mag and magnitudes brighter than the magnitude limits (see Sects. 3.1 and 3.2).

These criteria helped to minimize the incompleteness problem. For USNO data, we adopted an uncertainty of 0.3 mag for R and I.

In the TCDs, the data were fit using a 1σ-clipping linear regression (see in Appendix B, Figs. B.1 to B.8), and the results are given in Table 1 (the details of the linear regressions and the RV determination are given in Appendix B). To illustrate our results, we present in Fig. 4 some representative color − color diagrams (all the plots are presented in Appendix). In these plots, the majority of the stars follow a linear distribution. Few stars are located above the general trend. Metallicity or age variations cannot explain this result, because a metallicity effect corresponds to a color variation smaller than 0.1 mag (De Grijs et al. 2001) and an age variation can be represented as isochrones parallel to the reddening vector in color − color diagrams (Leitherer 1999). The most likely explanation is the mis-association with near-infrared data. As expected, this effect is more important in crowded areas such as zone 4, which is the closest to the Galactic plane. In the distribution of the stars, we can delineate overdensities (which are clearly illustrated in Fig. 4a). These provide information about the number of the extinction layers present along the line of sight. In the TCD of zone 4, the lowest Galactic latitude zone, we can distinguish up to four extinction layers centered on (B − V) ~ 0.7, 1, 1.3, and 1.75. Stars are mainly located around (B − V) = 1.5 and (B − V) = 1, respectively, in zones 2 (NGC 6357) and 6 (NGC 6334), underlining the small extinction difference between both regions. Finally, in zones 2, 6, and 7 we note the small number of stars around and below (B − V) = 0.5 that depart from the general trend. These stars are probably very nearby foreground stars.

We note that RV varies from zone to zone. From our data we, confirm a higher value of RV in NGC 6357 and NGC 6334 than normal extinction. The value of RV is respectively 3.53 ± 0.08 and 3.56 ± 0.15 for NGC 6357 and NGC 6334, which is very similar for both regions. Neckel & Chini (1981) found a mean value of RV of 3.8 for NGC 6357-NGC 6334 using a similar method. This value comes from (R − V) versus (vs.) (B − V) and (I − V) vs. (B − V) plots (giving RV = 4.08 and 3.64, respectively) only and using stars in both NGC 6357 and NGC 6334. Considering the same plots, the Neckel & Chini (1981) results are consistent with ours (see Table B.3). Bohigas et al. (2004) found that for Pismis 24 (NGC 6357) RV = 3.51, and Pinheiro et al. (2010) found that  ⟨ RV ⟩  = 3.5 for stars in NGC 6334.

The largest value, RV = 3.89 ± 0.09, is found for zone 8 corresponding to GM24. The zones outsides the H ii regions but closer to the Galactic plane (zones 3, 4, and 5) exhibit a similar RV, around 3.43, which is, despite the more diffuse aspect of the interstellar medium expected in these zones, and is higher than the normal value. The zones at higher Galactic latitude (zones 1 and 7) exhibit a closer-to-normal RV with a mean value of 3.25.

5.2. Stars with known spectra

The extinction parameters RV and AV can also be determined for stars of known spectral type. This can then be compared with our pure photometric approach. We compiled in Table 2 from the literature all the O and B stars in NGC 6334 and NGC 6357 with a known spectral type. In this table, Cols. 1 to 3 and 7 give the name, the coordinates, and the spectral type of the stars, while Cols. 4 to 6 and 8 to 10 give the UBVJHK photometric information. Column 11 gives the RV value deduced from Eq. (2) (see below), while the last two columns give the distance and the extinction for each star calculated with the photometric RV value determined in the previous section.

Moffat & Vogt (1973) obtained photometry of 15 stars in Pismis 24, for which 12 are members. Massey et al. (2001) obtained spectroscopy of 11 stars, four of which were not in the list of Moffat & Vogt (1973). They found that two of the cluster stars are of type O3, one of which is a supergiant (HDE 319718 = Pis 24-1) and the other appears to be a giant (Pis 24-17). On the basis of the 10 stars with reliably determined luminosity classes, Massey et al. (2001) inferred a distance modulus of 12.03  ±  0.14 mag. When they used only the six O dwarfs to derive the distance, they computed 11.99 ± 0.05 mag. They adopted a distance modulus of 12.0 mag corresponding to a distance of 2.5 kpc, which is larger than the 1.7 kpc suggested by Neckel (1978) and Lortet et al. (1984). The cluster also contains the Wolf-Rayet star HD 157504 (WR 93), which is of type WC7. Conti & Vacca (1990) described this star as a “WCE + abs” and derived a distance of 1.1 kpc.

In contrast to NGC 6357, NGC 6334 is ionized by a small number of lightly reddened OB stars (Table 2) that are spread about the whole nebula. Persi & Tapia (2008) summarized the available stellar data for early-type stars in the region. NGC 6334 is a grouping of the well-known HII regions GUM 61, GUM 62, GUM 63, and GUM 64. The exciting stars of GUM 61 (HD319703A and HD319703B) and GUM 62 (HD156538) can be clearly distinguished, while the stars HD319702 and CD-35 11484 appear as possible exciting stars of GUM 64.

In GM24, no optical exciting star has been identified. However, a small cluster dominated by a few young massive stars lies at its core (Tapia et al. 1991). On the near-infrared photometry of the cluster stars and extinction considerations, Tapia et al. (1991) deduced a distance of 2 kpc.

Following Samal et al. (2007), one way to estimate the value of RV is to use stars of known spectral type (Table 2). The RV value toward a star can be evaluated using the empirical relationship established by Whittet et al. (1976) 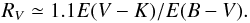(2)Equation (2) is based on the finding that the ratio AV/E(V − K) ≃ 1.1 does not change appreciably with the RV value and across the Galaxy (Whittet & van Breda 1978, 1980). To apply Eq. (2), we transformed the JHKS magnitudes of the stars from the 2MASS system to the Koornneef system (Koornneef 1983) using the relation given by Carpenter (2001). Intrinsic (V − K)0 colors were taken from Koornneef (1983) and intrinsic (B − V)0 colors from Schmidt-Kaler (1983). The results are listed in Table 2. From these results, we note that RV varies from place to place on a typical spatial scale that is smaller than our zone size. In this way, Pismis 24 (NGC 6357) exhibits a mean RV = 3.43, while RV = 3.42 for stars associated with NGC 6334. These results are slightly smaller than, but in agreement with, those obtained from the photometric approach (RV = 3.53 ± 0.08 and 3.56 ± 0.15 in the direction of NGC 6357 and NGC 6334 respectively).

From our photometric determination of RV, we found for NGC 6357 and NGC 6334 a mean distance of 1.93 ± 0.36 kpc and 1.72 ± 0.26 kpc, respectively, and a mean AV of 5.93 ± 0.49 mag (Bohigas et al. 2004, give for Pismis 24 AV = 6.37 mag) and 4.52 ± 0.68 mag, respectively. Fang et al. (2011), from isochrone fitting of O stars in Pismis 24, found a distance of 1.7 ± 0.2 kpc and a median extinction of 5.3 mag. We can then conclude that NGC 6334 and NGC 6357 are at an average distance of 1.75 kpc (weighted mean).

5.3. General dust properties

Small values of RV are generally assumed to relate to a prevalence of small dust grains, which affects the extinction curve at ultraviolet to optical wavelengths (Fitzpatrick 2004). A change in the size distribution naturally explains the variation of RV in different interstellar media. In particular, any change in the distribution of big grains, with a size of between 15 nm and 100 nm, is expected to be directly related to a change in RV. The size distribution of big grains can be altered by shock waves (Jones et al. 2005). High-velocity shocks affect grains through sputtering, which reduces the number of small particles, while in shocks with lower velocities, grain-grain collisions alter the size distribution by increasing the small-to-large grain size ratio (Mazzei & Barbaro 2008). Heiles et al. (1988) proposed that shock velocities of at least  ~30 km s-1 are required to modify the grain size distribution. Seab & Shull (1983) found significant grain destruction only for shock velocities above  ~40 km s-1. They predicted that large grains, with sizes larger than 500 Å (the grains that produce most of the 100 μm radiation), are preferentially affected.

To investigate this finding in terms of the value of RV, we evaluated the average infrared (12, 25, 60, and 100 μm) fluxes (background subtracted) from IRIS4 in the different zones. The MIPSGAL 24 and 70 μm images (Carey et al. 2009) cannot be used because most of the HII regions are saturated. However, IRAS data facilitates the comparison with dust models similar to those of Désert et al. (1990). The IRAS mean fluxes and their uncertainty are measured from the calibrated images within each area using the ds9-“Funtools” tool. The fluxes are corrected from a background value taken at the same location, on the north-west border (to minimize the contribution of the Galactic plane), in every 12 to 100 μm image.

thumbnail Fig. 5

Far infrared dust emission of the 8 zones. The plots are log (I(60)/I(100)) versus log (I(12)/I(25)) a), X1 versus RVb) and X2 versus RVc). Labels 2, 6, and 8 correspond to the regions NGC 6357, NGC 6334, and GM24, respectively.

As expected from Hα emission and OB star content, and based on a large I(60)/I(100) and low I(12)/I(25) ratio corresponding to an increase in the intensity of the radiation field (Boulanger 1988), zones 2, 6, and 8 (corresponding, respectively, to the HII regions NGC 6357, NGC 6334, and GM24) clearly exhibit a stronger radiation field than other zones (Fig. 5). However, NGC 6334 appears to have a higher radiation field than NGC 6357, while NGC 6357 contains more O-type stars (Table 2) and has a higher radio flux than NGC 6334 (see Sect. 4.6).

To characterise the dust properties, we determined the ratios of mid-infrared to far-infrared emission (defined as X1 = νI(12   μm) / [νI(60   μm) + νI(100   μm)] and X2 = νI(25   μm) / [νI(60   μm) + νI(100   μm)]). These ratios are tools for probing the content of small grains such as PAHs (polycyclic aromatic hydrocarbons) and VSGs (very small grains) relative to big grains (Désert et al. 1990). In particular, X1 depends primarily on the abundance of small particles such as the PAHs. Figure 5 presents the variation in X1 and X2 with RV. Both X1 and X2 have values similar to those in Désert et al. (1990) for HII regions.

Globally, X1 shows no trend relative to RV, which is consistent with RV depending on big grains, but also on the radiation field. When we assumed that zone 3 is the most representative of the typical dust properties, as it is the least affected by HII regions and star formation, we found that the zones 1, 4, 6, and 8 are deficient in small particles (PAH and VSG) while zones 7 and 2 are overabundant. NGC 6357 (zone 2) appears to have the highest X1 value suggesting that shocks can act in addition to the photon flux within NGC 6357. This is consistent with morphology (filamentary structures) of NGC 6357 as seen in Hα.

In the X2 versus RV plot, a clear split is observed between HII regions (zones 2, 6, and 8) and other regions. These HII regions exhibit a higher X2, while zones 1, 3, 4, 5, and 7 have similar X2 values of around 0.10 ± 0.02. This relative excess emission at 25 μm could mean that there is an excess of VSGs, that the big grain emissivity has been modified (Désert et al. 1990), and/or that the big grain emission contributes significantly to the 25 μm band flux.

We suggest that there is a global difference between the dust size distributions of NGC 6334 and NGC 6357. The similar RV in both regions suggests that their big grain content is similar, while NGC 6357 contains more very small grains. The OB stars in NGC 6357 seem then to have already re-processed part of the dust, which could be interpreted as a more evolved status for NGC 6357 than for NGC 6334.

5.4. Galactic structure

The relatively large number of OB stars (Table 3) in our sample allowed us to perform a statistical approach to measuring the stellar distance. The zones exhibit similar star-number surface densities, excepts for zone 4, which has a larger value. This is naturally explained by its location pointing towards the Galactic plane, which naturally probes denser stellar regions. Since from photometric data only it is impossible to determine the luminosity class, when determining the distance we assumed that the stars are main-sequence stars and if this is not the case this leads us to underestimate the distance by up to a factor of 0.6 respectively to class III stars. Taking as a starting point the observed colors U − B and B − V, the intrinsic colors (U − B)0 and (B − V)0 and the extinction AV = RV × EB − V are determined following the reddening law and the unreddened main sequence of Schmidt-Kaler (1983). The intrinsic colors are used to determine the spectral type using the main-sequence calibration table of Schmidt-Kaler (1983). The distance is then calculated by adopting the MV-spectral type calibration from Russeil (2003).

The distance uncertainty is evaluated from the photometric uncertainties as σd/d = (ln(10)/5) ×  [σV + RV × σB + RV × σV + σRV × EB − V] . To determine the distance, we adopted the RV value of the area where the stars are lying (Fig. 7a).

We considered the U-band completeness level (see Sect. 2.1), assuming a typical diffuse extinction (AV = 0.7 mag kpc-1, Marshall et al. 2006) and a mean extinction of AV = 5 mag at the distance of NGC 6334 – NGC 6357, and taking the absolute U magnitude for a B3V (Schmidt-Kaler 1983) and a O9.5V (Martins & Plez 2006) star we can estimate that we have a 90% mean completeness level for B3V and O9.5V out to 3300 pc and 5000 pc, respectively. At these distances, we can probe the nearest spiral arm structure.

Table 3

Mean star number and surface density.

In the model of Russeil et al. (2007), the line of sight in the direction of NGC 6334 – NGC 6357, is expected to cross the Sagittarius-Carina arm at  ~1.5 kpc, the Scutum-Crux arm at  ~3 kpc, the Norma arm at  ~4.3 kpc, and a small feature around 6 kpc. For the Hou et al. (2009) model, the distance to the arms are slightly different: 0.82 kpc, 2.9 kpc and 4.7 kpc for the Sagittarius-Carina, Scutum-Crux, and Norma arms. Figure 7a shows peaks at 1 kpc, 1.8 kpc, 2.6 kpc, and 4.6 kpc. Every peak can be associated with a spiral arm.

To estimate the possible impact of our assumptions about the main-sequence type of the stars, we note (Table 2) that 65% are main sequence stars, 17% are type III stars, and 9% are type I stars. We then repeated our determination of the stellar distance distribution (Fig. 7b) considering these proportions of class V and III and adopting an average factor of 1.5 for the distance of class III stars, respectively, to class V stars. We can discern that the features are globally recovered with peaks at distances of around 1.4, 2.6, and 4.6 kpc.

The average distance of the NGC 6334-NGC 6357 complex (1.75 kpc) places it in the Sagittarius-Carina arm, although it appears to be located slightly farther away than the first stellar peak. Such a configuration was already noted for the other Sagittarius-Carina arm HII region RCW108 (Georgelin et al. 1996) at a distance of 1.4 kpc, while the stellar peak of the field stars is at 1.1 kpc. In parallel, Tovmassian et al. (1996), studying an area of about 12°2 centered on l = 297°, b =  −1° find at the distance of the Sagittarius-Carina arm two separate stellar associations at 1.2 and 1.5 kpc. This suggests that there is a possible branch of the arm or a possible age gradient (with HII regions and field stars located at the far and near edge of the arm). It is most probable that there is a non-zero age gradient across the Sagittarius-Carina arm, as Mel’nik et al. (1998) show, because a stratification of stellar ages exists across the Sagittarius-Carina arm, with young objects being located near the inner edge of the arm, while old groupings lie closer to the outer edge.

thumbnail Fig. 6

Hα image (UKST Hα survey, Parker et al. 2005) of the H ii regions NGC 6334 and NGC 6357 (Galactic coordinates). The different regions are labeled. Overplotted are the O-B3 stars in the distance range of 1.5 to 1.95 kpc (red circles) and stellar clusters/groups (yellow symbols and names). Clusters/groups without name are clusters from Bica et al. (2003) and Feigelson et al. (2009).

thumbnail Fig. 7

a) Distribution of distances to OB stars (black histogram). Only stars with distance uncertainties smaller than 400 pc have been considered. The blue dashed histogram is the B star distribution, while the red dashed histogram is the O star distribution. b) Distribution of distances to OB stars assuming a proportion of class V and class III stars of 65% and 17%.

5.5. The OB stars census

Uncertainty about the first phase of high-mass star formation concerns the relative lengths of the lifetimes of high-mass IR-quiet and high-luminosity protostars as well as prestellar sources detected in submm surveys (Motte et al. 2007). To help resolve this uncertainty, we performed a census of massive stars (earlier than B3) in the NGC 6334-NGC 6357 complex, because the statistical lifetime is measured relative to the known age of OB stars.

The 2.7 GHz radio continuum flux of NGC 6334 and NGC 6357 is 439.4 ± 13.5 Jy and 924.1 ± 29.0 Jy, respectively (fluxes estimated from Paladini et al. 2003). These fluxes correspond to ionising photons fluxes (on a logarithmic scale) of 50.04 s-1 and 50.37 s-1. From Table 2, we evaluate the stellar ionising photon flux for both regions using Panagia (1973) and Sternberg et al. (2003). This led to 50.04 s-1 and 50.32 s-1 for NGC 6334 and NGC 6357, respectively, in good agreement with the radio values and suggests that the main ionizing stars are clearly identified. However, to have a complete census of OB stars we must also consider the OB stars that are not optically visible.

In NGC 6357, two open clusters (Fig. 6) were previously identified, the well-known Pismis 24 and AH03J1726-34.4 (Dias et al. 2002). For Pismis 24, Wang et al. (2007) identified 34 O-B3 stars from X-ray studies. The information on the cluster AH03J1726-34.4 is very sparse. AH03J1726-34.4 contains at least 4 OB stars (Neckel 1984; Damke et al. 2006). We were able to count at least 38 OB stars associated with NGC 6357.

For NGC 6334 (Fig. 6), Neckel (1978) found 14 O-B3 stars from optical photometry, and Bica et al. (2003) listed 7 embedded clusters/groups associated with radio sources. Feigelson et al. (2009) show (from a X-ray census of stellar sources in NGC 6334) a complicated spatial pattern with  ~10 distinct star clusters (the heavily obscured clusters are mostly associated with known far-infrared sources and radio H II regions). They also found dozens of likely OB stars, both in clusters, and dispersed throughout the region, suggesting that star formation in the complex has proceeded over millions of years. Tapia et al. (1996) deduced that the young cluster embedded in NGC 6334I has around 93 stars members brighter than K = 16 and that the majority of the observed members are ZAMS stars earlier than B3-B4. Tapia et al. (1996) found 12 faint sources (detected only in K band) centered on the HII region NGC 6334E. They estimated that the ionization of NGC 6334E requires at least an O7.5 ZAMS star or 12-13 B0-B0.5 ZAMS stars. They then proposed that a cluster of B stars is responsible for the ionization of NGC 6334E. Bochum 13, a cluster at the north-west border of NGC 6334, and at the same distance, contains 5 O-B3 stars (McSwain 2005) and a cluster dominated by a few young massive stars (~10) lies in the core of GM24 (Tapia et al. 1991). We then count at least 150 OB stars associated with NGC 6334.

Our UBV data provide an estimate of 40 additional optically visible O-B3 stars at the distance of NGC 6334-NGC 6357 complex (Fig. 6), giving a total count of at least 228 OB stars. We can thus estimate that 230 massive stars (earlier than B3) belong to the entire complex.

In Russeil et al. (2010), we presented a census of high-mass young stellar objects at various evolutionary stages: we identified 1 starless clump, 6 IR-quiet protostars, and 9 high-luminosity IR protostars in NGC 6334-NGC 6357. Since the timescale of the high-mass young objects cannot be derived directly, a statistical method was used. Assuming a steady star formation, the ratio of the number of objects at each stage is proportional to the stage timescale. The unit of time was estimated from the number and age of OB stars. The adopted age of OB stars in NGC 6334-NGC 6357 comes from the age of the cluster Pismis 24, which is between 1.73 Myr (Massey et al. 2001) and 5 ± 3 Myr (Ahumada et al. 2007). This means that from our number of  ~230 OB stars, one high-mass young object corresponds to a statistical lifetime of between  ~7.5 × 103 yr and  ~2.2 × 104 yr. We can then, in NGC 6334-NGC 6357, estimate that the starless and the protostellar phases have a statistical lifetime of 7.5 × 103 − 2.2 × 104 yr and 1.1 × 105 − 3.3 × 105 yr, respectively.

6. Conclusions

The results that we have presented in this paper stress the effectiveness of multicolor optical photometry in the study of the extinction and distance towards HII regions. Our large stellar sample has allowed us to carry out a statistical study of the local structure of the Milky-Way, as well as the census of O-B3 stars in the NGC 6334-NGC 6357 star-forming complex. Spectroscopic information of our large O-B3 stellar sample is now required to confirm the photometric spectral types and improve our distance determinations.

As expected, the total-to-selective extinction coefficient, RV, is higher in a star-forming region such as NGC 6334-NGC 6357 than in the diffuse interstellar medium. Futhermore, this coefficient varies throughout the HII regions, suggesting that there is a variation in the dust properties on the same scale. The RV values we obtained for NGC 6334 and NGC 6357 (3.56 ± 0.15 and 3.53 ± 0.08, respectively) have allowed us to determine more precisely the distance of these regions. We have confirmed that they are located at an average distance of 1.75 kpc. Our census of O-B3 stars in the NGC 6334-NGC 6357 star-forming complex has identified a total of 300 O-B3 stars. This census is important to help us to determine the statistical lifetimes of the different stages of the high-mass star formation in NGC 6334-NGC 6357 that we observe in the infrared with the Herschel satellite (Russeil et al., in prep.).

Online material

Appendix A: Presentation of the data

Tables presenting the data are given in this section.

Table A.1

Stars with U, B, and V magnitudes.

Table A.2

Catalogue of stars: R magnitudes.

Appendix B: The results

We present the results of the fits and all the two-color diagrams for zones 1 to 8. Table B.1 gives the slope of the linear regression for the different filters in the 8 zones. The normal slope is given in the last row. For a few zones and a few wavelengths, it is impossible to determine any reliable slope because of the too small number of data points. Table B.2 gives the correlation coefficient of the fit. Table B.3 gives the RV values deduced from Eq. (1). The last column gives the RV weighted mean value. The small thick segment at the bottom left of the plots is the locus of the unreddened O-B3 stars (from Martins et al. 2006; Koornneef et al. 1983; and Wegner 1994).

Table B.1

Fitted slopes.

Table B.2

Correlation coefficient of the fitted lines.

Table B.3

RV determination.

thumbnail Fig. B.1

Zone 1 two color diagrams.

thumbnail Fig. B.2

Zone 2 two color diagrams.

thumbnail Fig. B.3

Zone 3 two color diagrams.

thumbnail Fig. B.4

Zone 4 two color diagrams.

thumbnail Fig. B.5

Zone 5 two color diagrams.

thumbnail Fig. B.6

Zone 6 two color diagrams.

thumbnail Fig. B.7

Zone 7 two color diagrams.

thumbnail Fig. B.8

Zone 8 two color diagrams.

2

Point source catalog available from http://irsa.ipac.caltech.edu/

4

IRIS (Improved Reprocessing of the IRAS Survey) data are the improved version of the latest IRAS images, followong the second generation processing (or IRAS Sky Survey Atlas, ISSA). These maps have been reprocessed to improve sensitivity and absolute calibration. Compared to the latest version of the IRAS data, these new images have higher quality zodiacal light subtraction, calibration, and zero level adjustments to match the DIRBE data on large angular scales. The IRIS data have a resolution near 4′ in the four wavelengths (12, 25, 60, and 100 μm).

Acknowledgments

Part of this work was supported by the ANR (Agence Nationale pour la recherche) project “PROBES”, number ANR-08-BLAN-0241. Part of this work was completed thanks to SIMBAD and CDS. The authors acknowledge D. Clowe and M. P. Ulmer, respectively PI and Co-I of the NOAO observing time (NOAO 2009A-0137), and L. Guennou for their implication in the NOAO observations.

References

  1. Adami, C., Picat, J. P., Savine, C., et al. 2006, A&A, 451, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  2. Ahumada, A., Claría, J., & Bica, E. 2007, A&A, 473, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bertelli, G., Bressan, A., Chiosi, C., et al. 1994, A&AS, 106, 275 [NASA ADS] [Google Scholar]
  4. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bertin, E., Mellier, Y., & Radovich, M. 2002, ASPC, 281, 228 [Google Scholar]
  6. Bica, E., Dutra, C., & Barbuy, B. 2003, A&A, 397, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bohigas, J., Tapia, M., Roth, M., et al. 2004, AJ, 127, 2826 [NASA ADS] [CrossRef] [Google Scholar]
  8. Boulanger, F., Beuchman, C., Désert, F., et al. 1988, ApJ, 332, 328 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
  10. Carey, S., Noriega-Crespo, A., & Mizuno, D. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
  11. Carpenter, J. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
  12. Caswell, J., & Haynes, R. 1987, A&A, 171, 261 [NASA ADS] [Google Scholar]
  13. Chini, R., & Kruegel, E. 1983, A&A, 117, 289 [NASA ADS] [Google Scholar]
  14. Chini, R., & Wargau, W. 1990, A&A, 227, 213 [NASA ADS] [Google Scholar]
  15. Chini, R., Elsasser, H., & Neckel, T. 1980, A&A, 91, 186 [NASA ADS] [Google Scholar]
  16. Conti, P., & Vacca, W. 1990, AJ, 100, 431 [Google Scholar]
  17. Curti, R., et al. 2003, 2MASS All-Sky Point Sources (Pasadena: NASA/IPAC), http://iras.ipac.caltech.edu/applications/Gator [Google Scholar]
  18. Damke, G., Barba, R., & Morrell, N. 2006, Rev. Mex. Astron. Astrofis., 26, 180 [Google Scholar]
  19. de Grijs, R., O’Connell, R. W., & Gallagher, J. S. 2001, AJ, 121, 768 [NASA ADS] [CrossRef] [Google Scholar]
  20. Désert, F., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
  21. Dias, W., Alessi, B., Moitinho, A., et al. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Durret, F., Laganá, T. F., Adami, C., & Bertin, E. 2010, A&A, 517, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Epchtein, N., de Batz, B., Capoani, L., et al. 1997, Msngr, 87, 27 [Google Scholar]
  24. Fang, X., Storey, P. J., & Liu, X.-W. 2011, A&A, 530, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Feigelson, E., Martin, A., McNeill, C., et al. 2009, AJ, 138, 227 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fitzpatrick, E. L. 2004, ASPC, 309, 33 [Google Scholar]
  27. Georgelin, Y. M., Russeil, D., Marcelin, M., et al. 1996, A&AS, 120, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Greve, A. 2010, A&A, 518, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Gum, C. S. 1955, MmRAS, 67, 155 [NASA ADS] [Google Scholar]
  30. Gyulbudaghian, A., & Maghakian, T. 1977, PAZh, 3, 113 [Google Scholar]
  31. Hanson, M., Howarth, I., & Conti, P. 1997, ApJ, 489, 698 [NASA ADS] [CrossRef] [Google Scholar]
  32. Heiles, C., Reach, W., & Koo, B. 1988, ApJ, 332, 313 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hou, L. G., Han, J. L., & Shi, W. B. 2009, A&A, 499, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Jones, A. 2005, Proc. The dusty and Molecular Universe, ESAP, 577, 239 [NASA ADS] [Google Scholar]
  35. Koornneef, J. 1983, A&A, 128, 84 [NASA ADS] [Google Scholar]
  36. Kraemer, K., & Jackson, J. 1999, ApJS, 124, 439 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
  38. Landolt, A. U. 2009, AJ, 137, 4186 [NASA ADS] [CrossRef] [Google Scholar]
  39. Leitherer, C. 1999, Spectrophotometric Dating of Stars and Galaxies, ed. I. Hubeny, S. Heap, & R. Cornett, ASP Conf. Proc., 192, 3 [Google Scholar]
  40. Lortet, M., Testor, G., & Niemela, V. 1984, A&A, 140, 24 [NASA ADS] [Google Scholar]
  41. Marshall, D. J., Robin, A. C., Reylé, C., et al. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Martins, F., & Plez, B. 2006, A&A, 457, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Massey, P., DeGioia-Eastwood, K., & Waterhouse, E. 2001, AJ, 121, 1050 [NASA ADS] [CrossRef] [Google Scholar]
  44. Mazzei, P., & Barbaro, G. 2008, MNRAS, 390, 706 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mazzei, P., & Barbaro, G. 2011, A&A, 527, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Mel’nik, A., Sitnik, T., Dambis, A., et al. 1998, AstL, 24, 594 [NASA ADS] [Google Scholar]
  47. Moffat, A., & Vogt, N. 1973, A&AS, 10, 135 [NASA ADS] [Google Scholar]
  48. Monet, F., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 98 [Google Scholar]
  49. Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Neckel, T. 1978, A&A, 69, 51 [NASA ADS] [Google Scholar]
  51. Neckel, Th. 1984, A&A, 137, 58 [NASA ADS] [Google Scholar]
  52. Neckel, Th., & Chini, R. 1981, A&AS, 45, 451 [NASA ADS] [Google Scholar]
  53. O’Dell, C. R., & Wen, Z. 1992, ApJ, 387, 229 [NASA ADS] [CrossRef] [Google Scholar]
  54. Paladini, R., Burigana, C., & Davies, R. 2003, A&A, 397, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Panagia, N. 1973, AJ, 78, 929 [NASA ADS] [CrossRef] [Google Scholar]
  56. Pandey, A., Ogura, K., & Sekiguchi, K. 2000, PASJ, 52, 847 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pandey, A., Upadhyay, K., Nakada, Y., et al. 2003, A&A, 397, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Parker, Q., Phillipps, S., Pierce, M., et al. 2005, MNRAS, 362, 689 [NASA ADS] [CrossRef] [Google Scholar]
  59. Persi, P., & Tapia, M. 2008, Handbook of Star Forming Regions, Vol. II: The Southern Sky ASP Monograph Publications, ed. B. Reipurth, 5, 456 [Google Scholar]
  60. Pinheiro, M., Copetti, M., & Oliviera, V. 2010, A&A, 521, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Rieke, G., & Lebofsky, M. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
  62. Roslund, C. 1966, Arkiv. Astr., 4, 101 [Google Scholar]
  63. Russeil, D. 2003, A&A, 397, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Russeil, D., Adami, C., & Georgelin, Y. M. 2007, A&A, 470, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Russeil, D., Zavagno, A., Motte, F., et al. 2010, A&A, 515, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Russeil, D., Pestalozzi, M., Mottram, J. C., et al. 2011, A&A, 526, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Samal, M., Pandey, A., Ojha, D., et al. 2007, ApJ, 671, 555 [NASA ADS] [CrossRef] [Google Scholar]
  68. Schmidt Kaler, Th. 1983, Landolt-Bornstein, New Series, Group VI (Springer), 23, 14 [Google Scholar]
  69. Seab, C., & Shull, J. 1983, ApJ, 275, 652 [NASA ADS] [CrossRef] [Google Scholar]
  70. Skrutskie, M. F., Cutri, R. M., & Stiening, R. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  71. Sternberg, A., Hoffmann, T., & Pauldrach, A. 2003, ApJ, 599, 1333 [NASA ADS] [CrossRef] [Google Scholar]
  72. Tapia, M., Roth, M., Lopez, J., et al. 1991, A&A, 242, 388 [NASA ADS] [Google Scholar]
  73. Tapia, M., Persi, P., & Roth, M. 1996, A&A, 316, 102 [NASA ADS] [Google Scholar]
  74. Tovmassian, H., Navarro, S., & Cardona, O. 1996, AJ, 111, 306 [NASA ADS] [CrossRef] [Google Scholar]
  75. Tovmassian, H., Epremian, R., Hovhannessian, R., et al. 1998, AJ, 115, 1083 [NASA ADS] [CrossRef] [Google Scholar]
  76. Turner, D. 1989, AJ, 98, 2300 [NASA ADS] [CrossRef] [Google Scholar]
  77. Turner, D. 1996, AJ, 111, 828 [NASA ADS] [CrossRef] [Google Scholar]
  78. McSwain, M., & Gies, D. 2005, ApJS, 161, 118 [NASA ADS] [CrossRef] [Google Scholar]
  79. Van der Hucht, K. 2001, NewAR, 45, 135 [NASA ADS] [CrossRef] [Google Scholar]
  80. Walborn, N. 1982, AJ, 87, 1300 [NASA ADS] [CrossRef] [Google Scholar]
  81. Wang, J., Townsley, L., Feigelson, E., et al. 2007, ApJS, 168, 100 [NASA ADS] [CrossRef] [Google Scholar]
  82. Wegner, W. 1993, AcA, 43, 209 [Google Scholar]
  83. Wegner, W. 1994, MNRAS, 270, 229 [NASA ADS] [CrossRef] [Google Scholar]
  84. Whittet, D. C. B 2003, Dust in the Galactic Environment, 2nd edn. (Bristol: Institute of Physics (IOP) Publishing), Series in Astronomy and Astrophysics [Google Scholar]
  85. Whittet, D., & van Breda, I. 1978, A&A, 66, 57 [NASA ADS] [Google Scholar]
  86. Whittet, D., & van Breda, I. 1980, MNRAS, 192, 467 [NASA ADS] [CrossRef] [Google Scholar]
  87. Whittet, D., van Breda, I., & Glass, I. 1976, MNRAS, 177, 625 [NASA ADS] [Google Scholar]

All Tables

Table 1

RV results.

In the text
Table 2

Stellar data available in literature for NGC 6357 (Pismis 24) and NGC 6334.

In the text
Table 3

Mean star number and surface density.

In the text
Table A.1

Stars with U, B, and V magnitudes.

In the text
Table A.2

Catalogue of stars: R magnitudes.

In the text
Table B.1

Fitted slopes.

In the text
Table B.2

Correlation coefficient of the fitted lines.

In the text
Table B.3

RV determination.

In the text

All Figures

thumbnail Fig. 1

a) Hα image (UKST Hα survey, Parker et al. 2005) of the H ii regions NGC 6334 and NGC 6357 (Galactic coordinates). b) Hα image with overplotted the coverage of the VIMOS observations (green) and CTIO observations (red), as well as the zones 1 to 8 (white) discussed in the text. Zones 2, 6, and 8 correspond respectively to NGC 6357, NGC 6334, and GM 24.
In the text
thumbnail Fig. 2

U a), Bb), and Vc) completeness level in individual CCDs (each dotted curve corresponds to a CCD quadrant, and the black curve is the average of these dotted curves) for the fields centered respectively at 170; (NGC 6334, blue), 17; (green), and 17; (NGC 6357, red).
In the text
thumbnail Fig. 3

Color − color diagram for stars with U, B, and V magnitudes. The red curve is the theoretical unreddened main-sequence and the line is the standard reddening vector, up to AV = 5 mag, for a B3V star (from Schimdt-Kaler 1983).
In the text
thumbnail Fig. 4

V − K versus B − V for zone 4 a), zone 2 = NGC 6357 b), and zone 6 = NGC 6334 c). The stars identified spectroscopically (see Sect. 5.2) are also overplotted (filled triangles). The small thick segment on the bottom left of the plots is the locus of the unreddened O-B3 stars (from Martins et al. 2006; Koornneef et al. 1983; and Wegner 1994).
In the text
thumbnail Fig. 5

Far infrared dust emission of the 8 zones. The plots are log (I(60)/I(100)) versus log (I(12)/I(25)) a), X1 versus RVb) and X2 versus RVc). Labels 2, 6, and 8 correspond to the regions NGC 6357, NGC 6334, and GM24, respectively.
In the text
thumbnail Fig. 6

Hα image (UKST Hα survey, Parker et al. 2005) of the H ii regions NGC 6334 and NGC 6357 (Galactic coordinates). The different regions are labeled. Overplotted are the O-B3 stars in the distance range of 1.5 to 1.95 kpc (red circles) and stellar clusters/groups (yellow symbols and names). Clusters/groups without name are clusters from Bica et al. (2003) and Feigelson et al. (2009).
In the text
thumbnail Fig. 7

a) Distribution of distances to OB stars (black histogram). Only stars with distance uncertainties smaller than 400 pc have been considered. The blue dashed histogram is the B star distribution, while the red dashed histogram is the O star distribution. b) Distribution of distances to OB stars assuming a proportion of class V and class III stars of 65% and 17%.
In the text
thumbnail Fig. B.1

Zone 1 two color diagrams.

In the text
thumbnail Fig. B.2

Zone 2 two color diagrams.

In the text
thumbnail Fig. B.3

Zone 3 two color diagrams.
In the text
thumbnail Fig. B.4

Zone 4 two color diagrams.
In the text
thumbnail Fig. B.5

Zone 5 two color diagrams.
In the text
thumbnail Fig. B.6

Zone 6 two color diagrams.

In the text
thumbnail Fig. B.7

Zone 7 two color diagrams.
In the text
thumbnail Fig. B.8

Zone 8 two color diagrams.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.