| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117163 | |
| Published online | 03 February 2012 | |
A deep view on the Virgo cluster core⋆
1
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität
Heidelberg,
Mönchhofstraße 12-14,
69120
Heidelberg,
Germany
e-mail: slieder@ari.uni-heidelberg.de
2
European Southern Observatory, Av. Alonso de Córdova 3107, Vitacura,
Santiago,
Chile
3
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748
Garching bei München,
Germany
4
Universitäts-Sternwarte München, Scheinerstr. 1, 81679
München,
Germany
5
Department of Physics & Astronomy, Youngstown State
University, Youngstown, OH
44555,
USA
Received:
30
April
2011
Accepted:
15
November
2011
Studies of dwarf spheroidal (dSph) galaxies with statistically significant sample sizes are still rare beyond the Local Group, since these low surface brightness objects can only be identified with deep imaging data. In galaxy clusters, where they constitute the dominant population in terms of number, they represent the faint end slope of the galaxy luminosity function and provide important insight on the interplay between galaxy mass and environment. In this study we investigate the optical photometric properties of early-type galaxies (dwarf ellipticals (dEs) and dSphs) in the Virgo cluster core region, by analysing their location on the colour magnitude relation (CMR) and the structural scaling relations down to faint magnitudes, and by constructing the luminosity function to compare it with theoretical expectations. Our work is based on deep CFHT V- and I-band data covering several square degrees of the Virgo cluster core that were obtained in 1999 using the CFH12K instrument. We visually select potential cluster members based on morphology and angular size, excluding spiral galaxies. A photometric analysis has been carried out for 295 galaxies, using surface brightness profile shape and colour as further criteria to identify probable background contaminants. 216 galaxies are considered to be certain or probable Virgo cluster members. Our study reveals 77 galaxies not catalogued in the VCC (with 13 of them already found in previous studies) that are very likely Virgo cluster members because they follow the Virgo CMR and exhibit low Sérsic indices. Those galaxies reach MV = −8.7 mag. The CMR shows a clear change in slope from dEs to dSphs, while the scatter of the CMR in the dSph regime does not increase significantly. Our sample might, however, be somewhat biased towards redder colours. The scaling relations given by the dEs appear to be continued by the dSphs indicating a similar origin. The observed change in the CMR slope may mark the point at which gas loss prevented significant metal enrichment. The almost constant scatter around the CMR possibly indicates a short formation period, resulting in similar stellar populations. The luminosity function shows a Schechter function’s faint end slope of α = −1.50 ± 0.17, implying a lack of galaxies related to the expected number of low-mass dark matter haloes from theoretical models. Our findings could be explained by suppressed star formation in low-mass dark matter halos or by tidal disruption of dwarfs in the dense core region of the cluster.
Key words: galaxies: photometry / galaxies: clusters: general / galaxies: evolution / galaxies: dwarf / galaxies: formation / galaxies: clusters: individual: Virgo
Tables 3 and 4 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The galaxy population of the Virgo cluster is well studied down to a B magnitude of 19 mag by the photographic survey of Binggeli et al. (1985) which resulted in the Virgo cluster catalog (VCC). In addition, Impey et al. (1988), Trentham & Tully (2002), Trentham & Hodgkin (2002) and Sabatini et al. (2003) provided catalogs of (very) low surface brightness objects in this region down to a B magnitude of 21.5 mag. All these studies revealed a faint end slope of the LF in the range −1.1 ≲ α ≲ −1.6. This also holds for different nearby galaxy clusters (Fornax: Ferguson 1988; Mieske et al. 2007, Centaurus: Misgeld et al. 2009, Hydra I: Misgeld et al. 2008, Perseus: Penny & Conselice 2008, Coma: Beijersbergen et al. 2002, Abell 2199: Rines & Geller 2008). However, simulations of Milky Way-sized halos (Klypin et al. 1999; Moore et al. 1999) based on the currently favoured cosmological cold dark matter (ΛCDM) model, in which galaxies form hierarchically (White 1991), show a CDM mass function’s faint end slope of α ≈ −1.8. As deduced by Trentham & Tully (2002), the LF faint end slope has to be steeper than that of the mass function, i.e. α < −1.8. Hence, a large number of DM halos are not observed. On the other hand, Moore et al. (1999) derive a Virgo cluster subhalo mass function by inverting the LF data of Binggeli et al. (1985) using the Tully-Fisher relation (Tully & Fisher 1977). That mass function agrees both in shape and amplitude with the subhalo mass function of their CDM simulations of a Virgo-sized halo. Clearly, reproducing the observed LF is a fundamental test for any viable theory of galaxy formation.
To investigate, from the observational side, the formation history of dEs and dSphs and the impact of mass and environment on their evolution, scaling relations of structure (surface brightness, luminosity, and size) and colour are fundamental tools. For a sample of dEs and Es taken from various environments, Kormendy (1985) reports almost perpendicular sequences of dEs and Es in the diagram of central surface brightness versus luminosity. This behaviour was often interpreted as evidence for different formation processes of dEs and Es. On the other hand, Ferguson (1988) find in their Fornax cluster data that even the brightest galaxies follow the same continuous linear relation as the dwarf galaxies. Graham & Guzmán (2003) show in their analysis that there is no dichotomy between Es and dEs. The different μ0 − M scaling relation of brightest galaxies is due to core evolution and therefore not related to formation mechanism. This is supported by the study of Ferrarese et al. (2006) who see the perpendicular relation for only the cored galaxies in the Virgo cluster but challenged by the galaxy sample presented by Kormendy et al. (2009).
The colour–magnitude relation (CMR) of galaxies is commonly used to interpret the overall stellar population characteristics of galaxies and deduce their formation. Many authors report linear CMRs of early-type galaxies in clusters (e.g. Mieske et al. 2007; Lisker et al. 2008; Misgeld et al. 2008; Smith Castelli et al. 2011; Misgeld et al. 2009), with gradually redder colours at increasing luminosity. This is commonly interpreted as a relation between mass and metallicity, in the sense that more massive galaxies can self-enrich their gas, while dwarf galaxies lose it more easily. This by itself would not imply a different formation process of early-type giant and dwarf galaxies. Recently, however, Ferrarese et al. (2006) reported a curved CMR of 100 Virgo early-type galaxies investigated with the HST ACS Virgo cluster survey (ACS VCS, Côté et al. 2004). From an even larger sample based on homogeneous SDSS photometry, Janz & Lisker (2009) reported an S-shaped Virgo CMR, in which dEs and Es seem offset from each other and connected through a transition region. Yet by comparing the observations to model predictions, Janz and Lisker showed that distinct formation processes between dEs and Es are not necessarily required to explain the nonlinear CMR shape. It is thus still a matter of debate whether dwarf galaxies are merely the faint extension of giant galaxies or whether their origin is different.
Our main goal is to identify and analyse dwarf galaxies in the vicinity of the three giant
ellipticals M 87 and M 86/M 84 in the Virgo cluster core, in a similar manner as it was done
by our group for the Fornax cluster (Hilker et al.
1999, 2003; Mieske et al. 2007) and the Hydra I (Misgeld
et al. 2008) and Centaurus clusters (Misgeld et al.
2009). We aim to investigate the Virgo cluster luminosity function (LF) down to a
V band magnitude of 22, which is approximately two magnitudes lower than
the mentioned Virgo cluster studies. Grebel (2001)
defines the luminosity MV ≈ −17 mag as
dividing parameter between giant and dwarf early-type galaxies. The early-type dwarf
galaxies are commonly subdivided into two classes, the dwarf ellipticals (dEs) and the
fainter dwarf spheroidals (dSphs). The latter are distiguished from the former by a dividing
luminosity of MV ≈ −14 mag (see Grebel 2001). The diameter of the Virgo cluster is
approximately 3 Mpc and its crossing time is 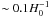 (Tully et al. 1996), so that its galaxies have had
time to interact with each other. But the Virgo cluster is considered as dynamically young
cluster, whereas the dynamically old central region is surrounded by a not virialized but
infalling region (Binggeli et al. 1993). This is
underlined by the irregular structure of at least three subclusters (centered on M 87, M 86
and M 49), suggesting the Virgo cluster might be a complex unrelaxed system (Sabatini et al. 2003).
(Tully et al. 1996), so that its galaxies have had
time to interact with each other. But the Virgo cluster is considered as dynamically young
cluster, whereas the dynamically old central region is surrounded by a not virialized but
infalling region (Binggeli et al. 1993). This is
underlined by the irregular structure of at least three subclusters (centered on M 87, M 86
and M 49), suggesting the Virgo cluster might be a complex unrelaxed system (Sabatini et al. 2003).
 |
Fig. 1 Excerpt of the defective chip to illustrate read-out defects. |
2. Data and visual inspection
From May 1st to May 5th 1999, V- and I-band CFHT wide field imaging data of the central region of the Virgo cluster around M 86 and M 87 were acquired using the CFH12K camera at the Canada-France-Hawaii Telescope (CFHT). The CFH12K camera was a mosaic of 12 CCDs, with a pixel scale of 0.206 arcsec pix-1 and a total areal coverage of 28′ × 42′ per field. However, only 11 of the 12 CCDs were functioning properly – the CCD on the bottom right corner of the layout showed an extended hot region (mostly along the y-axis) and significant read-out defects in the sense that all source detections exhibit a long additional trail in y-direction (see Fig. 1). Thus, data of this chip was excluded from the analysis.
 |
Fig. 2 Coordinate map of the 296 photometrically investigated objects. Filled circles: redshift confirmed cluster members, open triangles: redshift confirmed background galaxies, filled triangles: remaining galaxies catalogued in VCC, stars: no information. The well known giant ellipticals M 86/M 87 are highlighted, rectangles: fields covered by CFH12K instrument. |
A total of 10 fields were obtained, covering a region of ≈1.5 × 2.5 square degrees, as shown in Fig. 2. A small overlap of the fields ensured a complete coverage of the observed Virgo core region. Every field was exposed at least three times with an exposure time of 600 s each. The field, containing M 84/M 86 was exposed four times, the one containing M 87 even five times, resulting in an overall exposure time of 50 min. In case of saturated galaxies in the long exposures additional 60 s exposures were taken. During the four observing nights the median seeing was 0.8 arcsec FWHM.
2.1. Data reduction
The THELI image reduction pipeline (Erben et al. 2005) was used for the preprocessing of the data. All of the CFH12K data were corrected for the bias levels and the dark current, and were flat-fielded using both twilight flats and superflats made from all 33 science images. For the superflat creation we excluded images of CCDs which covered giant galaxies because of the small applied dithering of our data. By defringing the superflats, the brickwall pattern (Martin & Veillet 1999) present in the data was almost completely removed. The astrometric calibration from the THELI reductions is based on cross-correlation with the SDSS catalog of point sources, which also corrected for geometric distortions in the outer most parts of CFH12K fields. After the THELI photometry step, which is based on SExtractor (Bertin & Arnouts 1996), background subtraction was carried out using THELI, except in those cases where extended bright objects were present. In those cases, background subtraction was carried out manually. After the THELI processing, instrumental magnitudes were computed from observations of standard stars taken in all four nights of the observing run, and the photometry calibrated on the Cousins V and I magnitude system of Landolt (1992).
The average noise per pixel for the 30 min exposed fields corresponds to surface brightnesses of μV = 26.5 mag/arcsec2, μI = 25.2 mag/arcsec2 respectively. Hence, the V-band is in general deeper than our I-band observations.
Photometric calibration quantities.
2.2. Visual inspection
All images were carefully inspected visually to detect possible Virgo cluster members. The images in both bands were inspected independently from each other. A first pre-selection was based on the following selection criteria.
-
1.
The depth of the observed data revealed many background objects. While their physical size and luminosity would typically be larger than that of low-mass Virgo galaxies, their apparent size and magnitude can be similar, so that background objects can be mistaken for a Virgo cluster galaxy. Thus, we limited the visual size (at a surface brightness of μV ≈ 26 mag/arcsec2) of objects that are taken into account to a radius ≈ 10 arcsec (see Fig. 4b). This is comparable to the size of the smallest galaxies listed in Binggeli et al.’s (1985) VCC – denoted by D25 – the diameter at a surface brightness of μ ≈ 25 mag/arcsec2 in B.
-
2.
Spiral galaxies were not considered in this work. In the literature very few dwarf spirals are reported (e.g. Schombert et al. 1995; Graham & Guzmán 2003). Therefore we excluded all faint small galaxies with obvious spiral structure, because they are regarded as background galaxies (see Fig. 4c). Since we are using the IRAF ellipse task for photometry, also giant spirals are excluded because of the bad modelling by ellipses. The photmetric errors would be to large.
-
3.
Irregular galaxies were considered as long as their shape has been tolerably elliptical to be modelled with ellipse (see Fig. 4d). Four dIrrs were considered.
3. Photometry
3.1. Photometric analysis
All objects were photometrically analysed using the ellipse task (Jedrzejewski 1987) which is included in the STSDAS package of IRAF. All ellipse fits were performed with fixed parameters for center coordinates, position angle and ellipticity. In some cases like M 86 and M 87 better fitting results were obtained when variable ellipticity was applied. Obvious foreground and background objects were masked using the interactive mode of ellipse.
The ellipse output tables have been used to determine all astronomical quantities which are presented in this study. The extent of a galaxy has been defined to be the isophote at which the intensity falls below 10% of the rms variation of intensity along the isophote1. The flux enclosed by that ellipse is used as total flux f. Using that flux the apparent magnitude of an object is calculated. Finally, the apparent magnitude of an object was corrected for galactic extinction, applying the results of Schlegel et al. (1998).
In Table 1 quantities determined for the photometric calibration are listed. At high luminosities the photometry is limited by the uncertainty of the zeropoint and the atmospheric extiction coefficient κ. The photometrical uncertainties of the dSphs are additionally affected by the sky noise which is then of the same order of magnitude or higher as compared to zeropoint and κ.
3.2. Surface brightness profiles
The half-light radius r50 is determined as the radius enclosing 50% of the total flux. The effective surface brightness μe is defined as the average surface brightness within r50. We note that, due to our above definition of the total flux, r50 differs slightly from the true effective radius, which would enclose 50% of the total flux obtained by integrating the light profile to infinity.
Spectroscopic data are not available for many of the (largely) faint objects in our
sample. As a result, we will need to use the surface brightness profiles of these objects
in order to distinguish true Virgo cluster members from background galaxies (see
Sect. 4). We performed single profile Sérsic fits
(Sersic 1968) to all objects, that is
![\begin{equation} I(r)=I_{\rm e}\exp{\left\{-b_n\left[\left(\frac{r}{R_{\rm e}}\right)^{1/n}-1\right]\right\}}. \end{equation}](/articles/aa/full_html/2012/02/aa17163-11/aa17163-11-eq40.png) (1)Ie
the intensity of the isophote at the effective Re. The
constant bn is defined in terms of the
parameter n which describes the shape of the light profile. As shown by
Caon et al. (1993), a convenient approximation
relating bn to the shape parameter n is
bn = 1.9992n − 0.3271 for
1 ≲ n ≲ 10, which we applied in our calculations. For the Sérsic fit
the inner 3 arcsec were excluded from the fit which is twice the worst seeing with a
FWHM of 1.5 arcsec. For nucleated galaxies only the main body of the
galaxy was fitted. The results of this analysis, displayed in Fig. 3, show that at intermediate magnitudes
(15 ≲ mV ≲ 18 mag) the confirmed
background galaxies (red open triangles) significantly differ in their Sérsic index from
confirmed Virgo cluster members (black filled circles) in the same magnitude range. High
Sérsic indices are typical for Virgo members with
mV ≲ 15 mag. The red open circles in this
plot show a Sérsic index distribution similar to that of the confirmed backgound galaxies,
but exhibiting lower apparent magnitudes. Since those objects have large values of
n (typical for giant ellipticals) we therefore conclude, that these
objects are distant background elliptical galaxies. In the plot the VCC members without
redshift information (black filled triangles) continue the trend given by confirmed
members, resulting in low n (typical for dwarf galaxies). There is a
further group of galaxies with low n (black asterisks) continuing the
trend of the VCC galaxies at lowest luminosities
(mV ≳ 19). We conclude, that these
diffuse objects (characterized by their small n) also belong to the Virgo
cluster. Furthermore there is a noteworthy clean separation between the two groups of
unknown objects (red open circles and black asterisks). Thus, we adopted a membership
criterion of n < 1.5 (for
mV ≳ 15 mag), denoted by the dashed line
in Fig. 3.
(1)Ie
the intensity of the isophote at the effective Re. The
constant bn is defined in terms of the
parameter n which describes the shape of the light profile. As shown by
Caon et al. (1993), a convenient approximation
relating bn to the shape parameter n is
bn = 1.9992n − 0.3271 for
1 ≲ n ≲ 10, which we applied in our calculations. For the Sérsic fit
the inner 3 arcsec were excluded from the fit which is twice the worst seeing with a
FWHM of 1.5 arcsec. For nucleated galaxies only the main body of the
galaxy was fitted. The results of this analysis, displayed in Fig. 3, show that at intermediate magnitudes
(15 ≲ mV ≲ 18 mag) the confirmed
background galaxies (red open triangles) significantly differ in their Sérsic index from
confirmed Virgo cluster members (black filled circles) in the same magnitude range. High
Sérsic indices are typical for Virgo members with
mV ≲ 15 mag. The red open circles in this
plot show a Sérsic index distribution similar to that of the confirmed backgound galaxies,
but exhibiting lower apparent magnitudes. Since those objects have large values of
n (typical for giant ellipticals) we therefore conclude, that these
objects are distant background elliptical galaxies. In the plot the VCC members without
redshift information (black filled triangles) continue the trend given by confirmed
members, resulting in low n (typical for dwarf galaxies). There is a
further group of galaxies with low n (black asterisks) continuing the
trend of the VCC galaxies at lowest luminosities
(mV ≳ 19). We conclude, that these
diffuse objects (characterized by their small n) also belong to the Virgo
cluster. Furthermore there is a noteworthy clean separation between the two groups of
unknown objects (red open circles and black asterisks). Thus, we adopted a membership
criterion of n < 1.5 (for
mV ≳ 15 mag), denoted by the dashed line
in Fig. 3.
 |
Fig. 3 Sérsic indices of all investigated objects versus apparent V-Band magnitude. Black circles: spectroscopically confirmed Virgo members, black triangles: VCC members without redshift information, red triangles: spectroscopically confirmed background objects, red circles: as background considered objects due to their large Sérsic index, black asterisks: as Virgo member considered objects due to their small Sérsic index, red crosses: objects with small Sérsic index but extreme red colour (see Sect. 5.1), dashed line: Virgo cluster membership dividing Sérsic index of 1.5 (for magnitudes fainter than mV ≈ 18 mag). |
 |
Fig. 4 Figures for clarification of selection criteria. |
4. Sample selection and subdivision
During the photometric analysis using ellipse 75 objects (from the initial list of 371 objects) were rejected for any of a number of reasons described below (some of which are illustrated in Fig. 4):
-
1.
The photometry was affected by the presence of either a diffraction spike or bled columns from bright or saturated stars (see Fig. 4e, 2 objects rejected). Masking the spike led to inappropriate ellipse fits.
-
2.
The object was located within the “halo” of a foreground star. An appropriate ellipse fitting was impossible due to the partial overlap of the galaxy with the star’s halo (see Fig. 4f, 5 objects excluded)
-
3.
The subtraction of the best ellipse model from the original image revealed a merger signature. In this case, the light origins from two objects and an ellipse fit is not appropriate for the analysis. (see Figs. 4g and h, 5 objects excluded)
-
4.
The subtraction of the best ellipse model from the original image of small galaxies revealed a slight spiral structure. Since spirals are considered to be giants (see Sect. 2.2), these objects are treated as background galaxies. (see Figs. 4i and j, 27 objects excluded, 12 of which are spectroscopically confirmed background galaxies)
-
5.
Some small galaxies show dust signatures (typical for giant E or S0) but the residual image of the best ellipse model subtraction does not show significant structures. In this case we trust our eyes and classify the galaxies as background. (see Fig. 4k, 11 objects excluded)
-
6.
An object was only taken into account if it was visible in both bands, V and I. (5 objects excluded)
-
7.
Very faint, diffuse galaxies lead to unrobust fits (3 objects excluded)
-
8.
There were too many bad pixels within the object or the object was only partly covered. (3 objects excluded)
-
9.
An appropriate local background subtraction was impossible because of small scale spatial brightness variations. A residual fringe pattern remained on one chip, and some objects were also close to a spiral galaxy or a tail of a merging galaxy, which both could not appropriately be subtracted. (5 objects excluded)
-
10.
Some initially visually selected objects were rejected because closer inspection revealed a too small size (diameter <5 arcsecs; 9 objects excluded)
In the following, we combine the sample of the 41 spectroscopically confirmed Virgo members, the 98 VCC members without redshift information and the 77 probable member galaxies. This combined Virgo cluster sample contains 216 galaxies.
5. Results
Because the data is of higher quality in V-band we present all results related to the according V-band quantity, resulting in smaller errors. Furthermore it is mentioned here, that potential systematic errors due to local background subtraction are not included in our estimates. To convert apparent to absolute magnitudes, we adopt the Virgo cluster distance determined by the ACS VCS (m − M = 31.09 mag, d = 16.5 Mpc, Mei et al. 2007) and use this value for all our galaxies throughout the paper.
 |
Fig. 5 CMD of all investigated objects. Filled circles: spectroscopically confirmed Virgo cluster members, filled circles with surrounding open circle: irregular Virgo galaxies (confirmed), open triangles: spectroscopically confirmed background objects, filled triangles: remaining objects with VCC index, open circles: remaining objects with Sérsic index n > 1.5, asterisks: assumed Virgo cluster members, crosses: excluded from Virgo cluster sample by position in CMD. Thin black line: fit to confirmed cluster members; dashed lines: 5σ confidence interval; thick line: redshift evolution of an E-type galaxy modelled by GALEV (dark grey intercept: Virgo redshift, red: redshifted up to z = 0.65). |
5.1. Colour magnitude diagram
Since spectroscopic data were not available for most of the faint objects, we also
investigated obvious background objects with a comparable apparent magnitude as the Virgo
member galaxies to determine their location in the colour magnitude diagram (CMD). The
resulting CMD for all investigated objects is shown in Fig. 5. The diagram shows a clear distinction between background (red open triangles
and circles) and Virgo objects (black filled circles and triangles). We use that distinct
occupation in the CMD to reject possible background objects from the sample of faint
diffuse objects (asterisks). For the determination of the early-type galaxies’ CMR we
exclude the four irregular galaxies. The CMR of the confirmed Virgo members (black filled
circles) is denoted by the black solid line. Confirmed members, observed in our field of
view, cover a magnitude range of
−22.3 ≲ MV ≲ −13.1 mag. The integrated
colour V − I was determined at the half-light aperture
of each galaxy. This early-type CMR (red sequence) is given by the linear fit
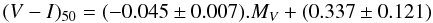 (2)with a rms of
0.098. The obtained CMR is comparable to other studies of the Virgo cluster (see e.g.
Lisker et al. 2008) and other nearby clusters
(see e.g. Misgeld et al. 2008, 2009).
(2)with a rms of
0.098. The obtained CMR is comparable to other studies of the Virgo cluster (see e.g.
Lisker et al. 2008) and other nearby clusters
(see e.g. Misgeld et al. 2008, 2009).
The dashed lines represent the 5σ confidence interval. Four faint diffuse objects (flagged by crosses, see also Fig. 3) are extreme outliers (>5σ) with respect to the CMR of the Virgo cluster galaxies and follow the trend given by the objects with large Sérsic index (red open circles), which are considered to be background objects. Hence, we define them to be background objects.
The CMD of our Virgo cluster sample obviously shows a change in the slope of the CMR at
MV ≈ −14 mag, as can be seen in
Fig. 6. The red solid line indicates the average
trend as found in successive magnitude bins with a width of 1 mag and steps of 0.5 mag,
clipped one time at 3σ as performed in Janz & Lisker (2009). We performed linear fits to both parts of the
sample with MV = −14 mag as dividing
luminosity according to Grebel’s dSph/dE
distinction. The fit of the high luminosity part yields a CMR of
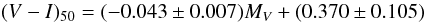 (3)and a rms of 0.090.
The lower luminosity branch yields a CMR of
(3)and a rms of 0.090.
The lower luminosity branch yields a CMR of
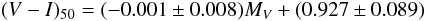 (4)with a rms of
0.117. The slope of the CMR at lower luminosities changes significantly and the scatter
around the relation at lower luminosities increases only slightly. Within the given
uncertainty of the slope, the luminosity does not show a dependency on the
V − I colour in this range. This is illustrated by the
almost vertical red line in Fig. 6 for the dSph
regime. The two solid lines indicate the different slopes of the relation.
(4)with a rms of
0.117. The slope of the CMR at lower luminosities changes significantly and the scatter
around the relation at lower luminosities increases only slightly. Within the given
uncertainty of the slope, the luminosity does not show a dependency on the
V − I colour in this range. This is illustrated by the
almost vertical red line in Fig. 6 for the dSph
regime. The two solid lines indicate the different slopes of the relation.
 |
Fig. 6 CMD of only the early-type Virgo sample is shown. The solid red line is constructed by the average measured in successive magnitude bins (1 mag per bin), the dashed black lines denote the CMR for the MV > −14 mag subsample, MV < −14 mag respectively. The errorbars shown here do not include the systematic uncertainty of the photometric zeropoint, as this would only cause an equal shift of all data points. |
Our sample of background galaxies shows a trend towards redder colours at fainter magnitudes. For the understanding of this behaviour we use the GALEV stellar population models (Kotulla et al. 2009) for illustration purposes. GALEV provides the redshift evolution of the integrated light properties of an E-type galaxy (i.e. an exponentially declining star formation history with decay time of 1 Gyr) of 5 × 1011 M⊙. The thick line in Fig. 5 shows the evolution of the position of this galaxy in the CMD with increasing redshift. The dark grey section of the line indicates the Virgo cluster redshift range, the red section of the line represents the evolution of the galaxy’s position in the CMD with increasing redshift up to z ≈ 0.65. The progessively redder colours of background elliptical galaxies at fainter magnitudes is also shown by the GALEV model.
5.2. Scaling relations
The parameters which are used to distiguish dwarf galaxies from giant galaxies are luminosity and size. Hence, how both parameters scale to each other, or to other physical properties, is of particular interest. A change can be a hint for a different origin of the different types of galaxies – in this case giants, dEs and dSphs – or at least a hint for different evolution. In Fig. 7 we present the common three scaling relations, the luminosity-surface brightness diagram (bottom left panel), the luminosity-size diagram (top left panel) and the size-surface brightness diagram (bottom right panel). Shown are all 213 early-type galaxies which are considered to belong to the Virgo cluster.
 |
Fig. 7 Scaling relations of all Virgo cluster objects (see text). Dashed lines: detection limit of μe,V = 26.5 mag/arcsec2, solid lines: linear fit to all datapoints with MV < −14 mag in the r − M diagram (in μ − M diagram: −18 < MV < −13 mag), dotted black line: 2σ confidence interval, dotted red line: completeness limit of MV = −13.0 mag, filled circles: spectroscopically confirmed Virgo cluster members, filled triangles: remaining objects with VCC index, asterisks: probable Virgo cluster members. |
The dashed line in the two left panels indicates the surface brightness detection limit of μe,V ≈ 26.5 mag/arcsec2. The solid line in the r − M diagram represents the fit to all objects which are brighter than MV = −14 mag. At that magnitude the slope of the CMR changed significantly. In the μe − M diagram the data is fitted to MV ≤ −13 for reasons which are discussed in Sect. 5.3. Furthermore, fitting the data down to that magnitude we are sure not to run into the completeness limit of our data.
Regarding the luminosity-surface brightness diagram, the trend given by the Es and dEs (MV < −14 mag) is obviously continued by the faint galaxies. The scatter around the trend does not seem to change significantly at fainter magnitudes. But the detection limit affects the completeness at fainter magnitudes. We see the same results in the luminosity-size diagram. The faint galaxies seem to continue the trend given by the bright galaxies and the scatter does not seem to increase. Also seen in this plot, the detection limit (dashed line) becomes important at lower luminosities. At faint magnitudes, we expect more galaxies, exhibiting surface brightnesses beyond the detection limit of μe ≈ 26.5 mag. The size-surface brightness diagram does not reveal a trend. But it shows that the uncatalogued galaxies (asterisks) tend to have half-light radii ≲ 10 arcsec, their mean r50 ≈ 4 arcsec corresponds to 320 parsecs while they tend to have on average a lower surface brightness than the previously known member galaxies.
5.3. Completeness
The crucial point in estimating a luminosity down to which the data is complete, is the scatter of the galaxies’ parameters. We do not know whether the scatter remains constant at magnitudes fainter than our completeness limit. Hence, we do not know the full parameter distribution of galaxies, which is why we refrain from creating a sample of artificial galaxies based on that same parameter distribution.
We use the μe − M relation to determine the
completeness of our data. Graham & Guzmán
(2003) used a correlation between the Sérsic index n and
luminosity to transform the linear
μ0 − M relation into a curved
μe − M relation. As a result, we cannot
assume a linear trend over the entire luminosity range. We are not able to give a reliable
curved trend since there are too few datapoints at high luminosities. We therefore
investigate the trend given by all galaxies with luminosities
−18 < MV < −13 mag.
The lower luminosity is chosen to increase the confidence of the trend but not to run into
incompleteness. Regarding Graham & Guzmán’s
Fig. 12 we consider it reliable to linearize the curve in our fitting interval. This trend
is given in the μe − M plot of Fig. 7 and is not valid for higher luminosities, because there
will be a turning point in the curved relation. At lower luminosites we do not expect
large errors because of the asymptotic convergency to the linear
μ0 − M relation. Our linear fit leads to
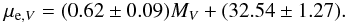 (5)with a rms of = 1.00.
Since we do not observe a change in the scaling relations we assume that the scatter
around the relation also remains constant. We use the scatter around the relation to
determine the completeness of our data sample. In particular, we use the
2σ confidence interval of the luminosity-surface brightness relation to
determine the intersect with the detection limit of 26.5 mag arcsec-2. For all
selected objects the scatter of that scaling relation is given by rms, leading to the
intersect at MV = −13.0 mag. The
2σ interval defines a confidence range of 96%. We expect to miss 2% of
the Virgo objects on the diffuse side at a luminosity of
MV ≈ −13.0 mag. Thus, the data is
rather complete down to that luminosity, given a constant scatter around the
μe − M relation.
(5)with a rms of = 1.00.
Since we do not observe a change in the scaling relations we assume that the scatter
around the relation also remains constant. We use the scatter around the relation to
determine the completeness of our data sample. In particular, we use the
2σ confidence interval of the luminosity-surface brightness relation to
determine the intersect with the detection limit of 26.5 mag arcsec-2. For all
selected objects the scatter of that scaling relation is given by rms, leading to the
intersect at MV = −13.0 mag. The
2σ interval defines a confidence range of 96%. We expect to miss 2% of
the Virgo objects on the diffuse side at a luminosity of
MV ≈ −13.0 mag. Thus, the data is
rather complete down to that luminosity, given a constant scatter around the
μe − M relation.
5.4. Luminosity function
The LF of a cluster is defined as number of galaxies which are found within certain magnitude bins. To determine our V-band LF we choose a bin width of 0.5 mag and created sampling steps every 0.25 mag. Hence, the values are not independent from each other.
Schechter (1976) proposed an analytic
approximation for the LF: 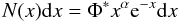 (6)with
(6)with
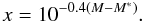 (7)Derivation of the faint
end slope α of the Schechter function is critically dependent on the
completeness of the dataset.
(7)Derivation of the faint
end slope α of the Schechter function is critically dependent on the
completeness of the dataset.
In order to get a reliable LF, we took also into account VCC galaxies which were not investigated in this study. This concerns mainly late-type galaxies, as well as early-type galaxies that were either located close to a star or have been only partly covered. To get information about the early-types, we used SDSS g- and r-band magnitudes. For the late-type galaxies we took g- and r-band photometry of Meyer et al. (in prep., following a similar procedure as in Lisker et al. 2007) based on SDSS data. The g- and r-band magnitudes of the additional 21 VCC galaxies, which are located within our fields, were converted to V-band magnitudes using the transformations from Jester et al. (2005). In Fig. 8 we present the LF of the V-band data. Solid symbols denote our data, open symbols represent datapoints which were corrected by the additionally inserted galaxies.
Due to the specifically selected target area of the Virgo core, encompassing all of the
large ellipticals M 84, M 86 and M 87, we refrain from attempting a fit of the
characteristic magnitude (also see the discussion in Sect. 6.4). Instead of using a Schechter function, we perform a linear fit in the
interval −18.8 ≤ MV ≤ −13.0 mag. The
bright end limit is chosen because of the jump in galaxy counts at
MV = −19 mag. It also corresponds to
the typical division between “dwarf” and “normal” galaxies, and it is still safely away
from typical values of M ∗ in a Schechter luminosity
function. The faint end limit is our completeness limit. We use gnuplot’s implementation of the nonlinear
least-squares Marquardt-Levenberg algorithm to perfom an error weighted linear fit to the
data. That has been done for three different fields and the whole data sample as displayed
in Table 2. It turns out that faint galaxies seem
more concentrated around M 86/M 84. For comparison, in the same fitting interval we also
performed the Schechter function fit with fixed 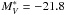 mag, corresponding roughly
to Sandage et al.’s
mag, corresponding roughly
to Sandage et al.’s
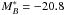 mag. The results are also
shown in Table 2. We find that the faint end slopes
derived with a Schechter fit are slightly shallower in each case, but always lie within
the errors. Figure 8 illustrates that they are almost
indistinguishable from each other.
mag. The results are also
shown in Table 2. We find that the faint end slopes
derived with a Schechter fit are slightly shallower in each case, but always lie within
the errors. Figure 8 illustrates that they are almost
indistinguishable from each other.
 |
Fig. 8 V-band luminosity function of the Virgo cluster sample (bin width:
0.5 mag, sampling step: 0.25 mag). Open symbols denote only early type galaxies,
solid symbols denote datapoints which were corrected by SDSS data. The solid line
indicates a linear fit performed in
−18.8 ≤ MV ≤ −13.0 mag. The
Schechter function fitted in the same interval with fixed
|
Faint end slopes.
Given the areal variation of the faint end slope, we give the overall faint end slope as
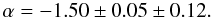 (8)This faint end
slope fits into the range of slopes determined by other Virgo studies (Sandage et al. 1985; Trentham & Hodgkin 2002; Rines &
Geller 2008; Sabatini et al. 2003) and is
also comparable to slopes determined for other nearby clusters (Hilker et al. 2003; Misgeld et al.
2008, 2009; Ferguson 1988; Beijersbergen et al.
2002; Penny & Conselice 2008;
Rines & Geller 2008).
(8)This faint end
slope fits into the range of slopes determined by other Virgo studies (Sandage et al. 1985; Trentham & Hodgkin 2002; Rines &
Geller 2008; Sabatini et al. 2003) and is
also comparable to slopes determined for other nearby clusters (Hilker et al. 2003; Misgeld et al.
2008, 2009; Ferguson 1988; Beijersbergen et al.
2002; Penny & Conselice 2008;
Rines & Geller 2008).
6. Discussion
6.1. Sample selection
The quality of the sample selection is best visible in the colour magnitude diagram in Fig. 5.
The identification of background galaxies by adopting the Sérsic index larger than 1.5 as background criterion at apparent magnitudes fainter than mV ≈ 18 mag excludes all objects with a compact appearance. Doing this, we would remove compact ellipticals3 from the Virgo cluster sample, if they were present. The probability of observing a faint background galaxy with a deVaucouleurs profile at faint magnitudes is much higher than observing a compact dwarf elliptical. This argumentation becomes stronger when regarding the CMD. The sample of objects excluded by their Sérsic index (open circles) continues the trend given by the redshift confirmed background objects (open triangles).
Another hint for dealing with background galaxies is the trend to extreme red colours of these galaxies at apparent magnitudes around mV = 20 mag. This trend can be explained by the colour change of ellipticals with increasing redshift, as shown by GALEV models (red line in the CMD)4.
Also excluded from our Virgo sample are ultra-compact dwarf galaxies (UCDs) since they are very small and did not pass our applied size criterion. When regarding the known UCDs in Virgo (Haşegan et al. 2005; Evstigneeva et al. 2007), we see that there are many other objects which appear similar to UCDs but are obviously unresolved background objects.
Due to the very red colours expected for background elliptical galaxies, we adopted an interval around the CMR inside which objects were considered Virgo cluster members. Of course, this criterion holds only when there is no change in the slope of the CMR at lower luminosities and the scatter remains Gaussian. While both of these conditions are not met (see Sect. 5.1), we have accounted for this (5σ interval) and only four objects were subsequently regarded as background objects.
As seen in Fig. 5, however, there are velocity-confirmed background galaxies that have colours consistent with that of Virgo cluster galaxies. As a result, it is still possible that some of the objects in our sample of 77 probable galaxies are indeed background objects. That there are two objects with a large Sérsic index located in the Virgo member CMD region could be a hint for background objects. On the other hand, these two objects could also be compact Virgo ellipticals. One of them is shown in Fig. 4l. If they are the result of stripped spirals, they should have kept their bulge properties (Chilingarian et al. 2009), including their red colour (Balcells & Peletier 1994). Their colours (V − I ≃ 1) are a bit bluer than M 32 (V − I ≃ 1.2, Lauer et al. 1998). A final statement of this issue can only be made when spectroscopic data of these galaxies are available.
6.2. Colour magnitude relation
There is a change in the slope of the Virgo CMR at MV ≈ −14 mag: at fainter magnitudes, we observe no correlation between colour and magnitude anymore. However, our sample might be biased at faint magnitudes, since the completeness limit is MV = −13.0 mag. In order to assess whether the shallower depth of our I-band images could have preferentially excluded galaxies with blue colours from our sample just below the completeness limit (as we required detection in both bands), we consider the scatter of our galaxies in colour and in surface brightness just above the completeness limit. Due to the relatively large spread in surface brightness and the fact that its faint end governs the completeness limit (Fig. 7), the majority of galaxies around the limit actually has sufficiently high S/N that no colour bias should occur among them. Assuming the colour and surface brightness scatter is similar below the limit, we estimate that down to MV = −11.7 mag we should not have lost more than 6 galaxies that could potentially be bluer than average and thus affect the CMR slope. This number is consistent with the 4 objects that were detected in the V-band only. Thus, while the detection of the faintest targets may be biased towards red colours, no significant bias should be present down to MV = −11.7 mag, giving confidence that the change of the CMR slope at MV ≈ −14 is real.
In the E and dE luminosity range (MV ≲ −14 mag) we observe the commonly known negative slope of the CMR. This is usually explained by the larger potential wells of the more massive galaxies, which made it easier for them to recycle their metal-enriched gas, leading to a higher metallicity and thus redder colour. For the dSphs (MV > −14 mag) no such dependency is seen anymore. However, the intrinsic colour spread of the dSphs is not significantly larger than for the dEs5. This seems to be at odds with an extrapolation of the results of Gavazzi et al. (2002) for Virgo early-type galaxies: fainter galaxies show a more extended star formation history, which should result in a broader colour distribution. However, our data only contains galaxies of Virgo’s core region. It is likely that dwarf galaxies in this region lost all their gas already at an early epoch of the cluster evolution, due to tidal forces from the cluster potential and from massive member galaxies, as well as ram pressure stripping from the intracluster medium. It thus seems plausible that the faint, diffuse dSphs in the Virgo core region have had a similar short period of star formation, leading to similar red colours with small scatter. We speculate that significant enrichment was only possible at magnitudes brightward of the change in slope, which lead to the usual mass-metallicity relation.
6.3. Scaling relations
Regarding the scaling relations of Fig. 7, there are two results to report. First, dSphs seem to continue the trends given by their more luminous counterparts. And second, the detection limit of μe,V = 26.5 mag/arcsec2 in connection with the scatter around the luminosity-surface brightness relation limits the completeness to MV ≲ −13.0 mag.
We excluded high surface brightness objects at lower luminosites from our sample, i.e. excluded all possible cEs and UCDs from our sample. This affects on the one hand the scatter of the found relations, on the other hand it could also affect the relations’s shape itself. Only a dozen of Virgo UCDs are known, not affecting the overall numbers of member galaxies.
A change in the slope of the CMR is observed at MV ≃ −14 mag. The data begins to become incomplete one magnitude fainter, but reaches MV ≃ −9 mag. Hence, the dSphs which differ in their behaviour from the more luminous galaxies (dEs and Es) in the CMR are incomplete, almost over their whole luminosity range. This makes it impossible to prove whether the scaling trends given by the Es and dEs are indeed continued by the dSphs. We can only say: in the face of the scaling relations, the dSphs seem to be the extension of the dE population. In the light of the change in the CMR at MV ≈ −14 mag, this would lead to the argumentation that dSphs and dEs share the same origin (given by the physical parameters) but differ in their evolution (given by the chemical parameter colour).
6.4. Luminosity function and completeness
Due to observation of the Virgo core region, we are unable to independently determine the characteristic magnitude M ∗ of the Virgo cluster. Schechter found that his function is a good fit to the LF of a whole cluster. We fit the Schechter function to a sample which is not representative for the Virgo cluster since our field were chosen such that the three giant ellipticals (M 87 and M 86/M 84) are included. If we shift our field of view in any direction we would have only two or even one of them included, resulting in a more certain estimation of the turning point M ∗ . Because of that uncertain behaviour at the bright end of the LF we performed only a linear fit using a fitting interval which takes into account both the uncertainty at the bright end and at the faint end.
Our estimation of the completeness is rather conservative by using a 2σ confidence interval. Hence, within the fitting interval the data should be complete and therefore the faint end slope reliable. The obtained faint end slope is α = −1.50 ± 0.17 for linear fit and α = −1.43 ± 0.09 for the Schechter function fit respectively. This is in good agreement with the investigation of Sabatini et al. (2003) who found a faint end slope of α = −1.4 ± 0.2 for the central 0.8deg around M 87, hence for the core region. Following Moore et al. (1999) who use the Tully-Fisher relation to calculate the LF of the Virgo cluster from the mass function of their simulations, there is consistency between theory and observations. On the other hand, simulations based on the favoured ΛCDM cosmological model expect a faint end slope of the LF steeper than −1.8 as deduced from the CDM mass function (Trentham & Tully 2002). This observational discrepancy to the theory is often observed. The favoured explanation for the missed observed galaxies is supressed star formation in lowest DM halos. Since we observe the core region of the cluster, disruption should also play a role. Due to the gravitational potential of the most massive galaxies – located in the center of the cluster – we can expect that the less massive galaxies are tidally distorted, some of them might have even been disrupted. This idea was already suggested by Sabatini et al. (2003) supported by their findings of α = −1.8 in the outer regions of the Virgo cluster (distance to M 87 ≥ 1.6deg). The disruption scenario is also supported by Mihos et al. (2005) who find a “complex substructure of Virgo’s diffuse intracluster light”. They discuss in particular four streamers which they relate to ongoing tidal stripping of dwarf galaxies. The tidally distorted galaxies will eventually get stripped by the gravitational potential of their massive counterparts. In this process, the compact nuclei of nucleated dwarf ellipticals might end up as UCDs. Since the fraction of remnant nuclei among the UCD population is unknown – many of them might be just giant globular clusters – we did not consider them in our study. In any case, the progenitor galaxies of remnant nuclei-UCDs in general are in the luminosity range −19 < MV < −15, thus missing some of them does not affect the very faint end of the luminosity function. Also stripped spiral galaxies – ending up as compact ellipticals – are not considered due to their high Sérsic index. Even if there might be undiscovered cEs, their number should be small, since they may originate from giant spiral galaxies. And simulations show, that initially large dark matter halos – containing a giant spiral galaxy which is stripped during its evolution – are rare. Hence, cEs should not contribute tremendously to the faint end of the LF neither. Finally, totally disrupted galaxies can not be observed. The question arises what fraction of partially disrupted/transformed galaxies has been missed by applying our selection criteria.
Due to selection criteria 1, 2, 8, and 9 of Sect. 4 we reject mostly spectroscopically known galaxies. We corrected the LF for the rejected VCC members, but we also reject two uncatalogued galaxies. They might have magnitudes brighter than MV = −13, and therefore, would have had a weak impact on the LF faint end slope. All galaxies rejected by criteria 6 and 7 are candidates for Virgo cluster members, but due to their faintness lie beyond the completeness limit considered for the determination of the faint end slope of the LF.
Furthermore we also miss very low surface brightness objects which are too diffuse to be detected. Due to the applied confidence interval of the completeness determination we assume that we miss only one of these objects (1%). Also the assumption of a constant scatter around the μe − M relation to determine the completeness can be called into question. On the other hand, the faint end slope does not change significantly (α = −1.42) when setting the detection limit to MV = −13.6 mag.
Besides observational biases, also theoretical reasons may explain the lack of dwarf galaxies. Local feedback effects (Dekel & Silk 1986) or the reionization of the Universe (Klypin et al. 1999) could inhibit the collapse of gas into small haloes, leading to DM halos with no visible counterpart. Additionally, Klypin et al. offer a plausible expanation of the missing satellites for a Milky Way-like halo. They argue that high velocity clouds (HVCs) are numerous enough when extrapolating their local (Milky Way) abundance to a larger volume. Whether a dark matter halo hosts a dwarf galaxy or an HVC depends primarily on the circular velocity of the halo. But it is at least questionable if one can simply exend this argumentation to a galaxy cluster with its different evolution.
7. Summary
CFHT V- and I-band data of Virgo cluster’s core region, taken in 1999 with the CFH12K instrument, have been analysed. Applying morphological criteria, 295 galaxies were chosen for photometric investigation. Knowing the redshift of the luminous galaxies, applying a surface brightness criterion at lower luminosities and regarding the location of these galaxies in the CMD, 216 of these galaxies are considered to belong to the Virgo galaxy cluster. 64 of these objects have previously been unknown. The detection limit of the image data is determined at μe,V = 26.5 mag/arcsec2 for the faintest objects at MV = −8.7 mag. In the dSph magnitude regime the detection limit may bias the sample towards redder galaxies.
The CMD of the Virgo cluster sample reveals a change in the slope of the early-type CMR at MV ≈ −14 mag – the distincting luminosity for dEs and dSphs. Provided that the change is real, we conclude that this luminosity corresponds to a specific galaxy mass which is needed to retain its gas. At higher masses, this leads to an extended star formation period and to self-enrichment of the gas, resulting in higher metallicities, and thus in redder colours. We do not observe a significantly increasing scatter around the CMR of dSphs, which we interpret as a comparably short star formation for both types of galaxies, the dEs and the dSphs. The fact that all dSphs have the same V − I colour can be interpreted as a similar metallicity for this galaxy type. Since the cluster’s core region is observed, we conclude that the SFH of these faint galaxies was truncated at a very early epoch of the cluster evolution, resulting in similar V − I colours.
The investigation of the scaling relations (luminosity-size-surface brightness) shows no difference between dEs and dSphs. In the face of this continuing trend, while a definitive conclusion is hampered by the completeness limit of MV = −13.0 mag, dEs and dSphs seem consistent with having the same origin.
Online material
Properties of Virgo cluster objects found in this study but not included in the VCC.
Properties of VCC catalogued galaxies and spectroscopically confirmed cluster members investigated in this study.
The rms value is determined by ellipse, subdividing the isophote into sectors where appropriate (Jedrzejewski 1987). The so determined radii are of the order of 2 to 3 effective radii Re for dSphs and 3 to 4 Re for the dEs.
Binggeli et al. (1985) also included background galaxies and classified them. Our three excluded galaxies were classified as member (2) and possible member (1).
When not considering the uncertainty in the calibration zeropoint, which would apply equally to all galaxies, the rms of our errors is 0.045 mag at these magnitudes, while the observed scatter is 0.117 mag, leading to an intrinsic scatter of 0.108 mag. The same number calculated for the dEs would be 0.090 mag.
Acknowledgments
We thank Hagen Meyer for providing his unpublished photometric measurements for late-type galaxies in our region and Patrick Côté for his comparison of our uncatalogued objects to the Next Generation Virgo cluster Survey (NGVS) data. He confirmed that all our uncatalogued Virgo objects have a matching object in the NGVS data. Special thanks are adressed to Mischa Schirmer for his support on THELI issues with the “old” CFH12K data. S.L. is supported by the ESO Studentship Programme. S.L. and T.L. are supported within the framework of the Excellence Initiative by the German Research Foundation (DFG) through the Heidelberg Graduate School of Fundamental Physics (grant number GSC 129/1). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Balcells, M., & Peletier, R. F. 1994, AJ, 107, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Beijersbergen, M., Hoekstra, H., van Dokkum, P. G., & van der Hulst, T. 2002, MNRAS, 329, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, AApS, 117, 393 [Google Scholar]
- Binggeli, B., Sandage, A., & Tammann, G. A. 1985, AJ, 90, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B., Popescu, C. C., & Tammann, G. A. 1993, A&AS, 98, 275 [NASA ADS] [Google Scholar]
- Caon, N., Capaccioli, M., & D’Onofrio, M. 1993, MNRAS, 265, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I., Cayatte, V., Revaz, Y., et al. 2009, Science, 326, 1379 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Côté, P., Blakeslee, J. P., Ferrarese, L., et al. 2004, ApJS, 153, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Durrell, P. R. 1997, AJ, 113, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Durrell, P. R., Williams, B. F., Ciardullo, R., et al. 2007, ApJ, 656, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Erben, T., Schirmer, M., Dietrich, J. P., et al. 2005, Astron. Nachr., 326, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Evstigneeva, E. A., Gregg, M. D., Drinkwater, M. J., & Hilker, M. 2007, AJ, 133, 1722 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, H. C., & Sandage, A. 1988, AJ, 96 [Google Scholar]
- Ferrarese, L., Côté, P., Jordán, A., et al. 2006, ApJS, 164, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Bonfanti, C., Sanvito, G., Boselli, A., & Scodeggio, M. 2002, ApJ, 576, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., & Guzmán, R. 2003, AJ, 125, 2936 [NASA ADS] [CrossRef] [Google Scholar]
- Grebel, E. 2001, ApSSS, 277 [Google Scholar]
- Haşegan, M., Jordán, A., Côté, P., et al. 2005, ApJ, 627, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Hilker, M., Kissler-Patig, M., Richtler, T., Infante, L., & Quintana, H. 1999, A&AS, 134, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hilker, M., Mieske, S., & Infante, L. 2003, A&A, 397, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Impey, C., Bothun, G., & Malin, D. 1988, ApJ, 330, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Janz, J., & Lisker, T. 2009, ApJ, 696, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Jedrzejewski, R. I. 1987, MNRAS, 226, 747 [Google Scholar]
- Jester, S., Schneider, D. P., Richards, G. T., et al. 2005, AJ, 130, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Kravtsov, A. V., Valenzuela, O., & Prada, F. 1999, ApJ, 522, 82 [Google Scholar]
- Kormendy, J. 1985, ApJ, 295, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Kotulla, R., Fritze, U., Weilbacher, P., & Anders, P. 2009, MNRAS, 396, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Faber, S. M., Ajhar, E. A., Grillmair, C. J., & Scowen, P. A. 1998, AJ, 116, 2263 [NASA ADS] [CrossRef] [Google Scholar]
- Lisker, T., Grebel, E. K., Binggeli, B., & Glatt, K. 2007, ApJ, 660, 1186 [NASA ADS] [CrossRef] [Google Scholar]
- Lisker, T., Grebel, E. K., & Binggeli, B. 2008, AJ, 135, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P., & Veillet, C. 1999, CFHT Bulletin No. 40 [Google Scholar]
- Mei, S., Blakeslee, J. P., Côté, P., et al. 2007, ApJ, 655, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Mieske, S., Hilker, M., Infante, L., & Mendes de Oliveira, C. 2007, A&A, 463, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J., & Morrison, H. 2005, ApJ, 631, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Misgeld, I., Mieske, S., & Hilker, M. 2008, A&A, 486, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misgeld, I., Hilker, M., & Mieske, S. 2009, A&A, 496, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
- Penny, S. J., & Conselice, C. J. 2008, MNRAS, 383, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., & Geller, M. J. 2008, AJ, 135, 1837 [NASA ADS] [CrossRef] [Google Scholar]
- Sabatini, S., Davies, J., Scaramella, R., et al. 2003, MNRAS, 341, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., Binggeli, B., & Tammann, G. A. 1985, AJ, 90, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J. M., Pildis, R. A., Eder, J. A., & Oemler, A., Jr. 1995, AJ, 110, 2067 [NASA ADS] [CrossRef] [Google Scholar]
- Sersic, J. L. 1968, Atlas de galaxias australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Smith Castelli, A. V., Bassino, L. P., Richtler, T., et al. 2008, MNRAS, 386, 2311 [NASA ADS] [CrossRef] [Google Scholar]
- Smith Castelli, A. V., Cellone, S. A., Faifer, F. R., et al. 2011, MNRAS, 1866 [Google Scholar]
- Trentham, N., & Hodgkin, S. 2002, MNRAS, 333, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Trentham, N., & Tully, R. B. 2002, MNRAS, 335, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Tully, R. B., Verheijen, M. A. W., Pierce, M. J., Huang, J., & Wainscoat, R. J. 1996, AJ, 112, 2471 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Frenk, C. 1991, ApJ, 379 [Google Scholar]
All Tables
Properties of Virgo cluster objects found in this study but not included in the VCC.
Properties of VCC catalogued galaxies and spectroscopically confirmed cluster members investigated in this study.
All Figures
 |
Fig. 1 Excerpt of the defective chip to illustrate read-out defects. |
| In the text | |
 |
Fig. 2 Coordinate map of the 296 photometrically investigated objects. Filled circles: redshift confirmed cluster members, open triangles: redshift confirmed background galaxies, filled triangles: remaining galaxies catalogued in VCC, stars: no information. The well known giant ellipticals M 86/M 87 are highlighted, rectangles: fields covered by CFH12K instrument. |
| In the text | |
 |
Fig. 3 Sérsic indices of all investigated objects versus apparent V-Band magnitude. Black circles: spectroscopically confirmed Virgo members, black triangles: VCC members without redshift information, red triangles: spectroscopically confirmed background objects, red circles: as background considered objects due to their large Sérsic index, black asterisks: as Virgo member considered objects due to their small Sérsic index, red crosses: objects with small Sérsic index but extreme red colour (see Sect. 5.1), dashed line: Virgo cluster membership dividing Sérsic index of 1.5 (for magnitudes fainter than mV ≈ 18 mag). |
| In the text | |
 |
Fig. 4 Figures for clarification of selection criteria. |
| In the text | |
 |
Fig. 5 CMD of all investigated objects. Filled circles: spectroscopically confirmed Virgo cluster members, filled circles with surrounding open circle: irregular Virgo galaxies (confirmed), open triangles: spectroscopically confirmed background objects, filled triangles: remaining objects with VCC index, open circles: remaining objects with Sérsic index n > 1.5, asterisks: assumed Virgo cluster members, crosses: excluded from Virgo cluster sample by position in CMD. Thin black line: fit to confirmed cluster members; dashed lines: 5σ confidence interval; thick line: redshift evolution of an E-type galaxy modelled by GALEV (dark grey intercept: Virgo redshift, red: redshifted up to z = 0.65). |
| In the text | |
 |
Fig. 6 CMD of only the early-type Virgo sample is shown. The solid red line is constructed by the average measured in successive magnitude bins (1 mag per bin), the dashed black lines denote the CMR for the MV > −14 mag subsample, MV < −14 mag respectively. The errorbars shown here do not include the systematic uncertainty of the photometric zeropoint, as this would only cause an equal shift of all data points. |
| In the text | |
 |
Fig. 7 Scaling relations of all Virgo cluster objects (see text). Dashed lines: detection limit of μe,V = 26.5 mag/arcsec2, solid lines: linear fit to all datapoints with MV < −14 mag in the r − M diagram (in μ − M diagram: −18 < MV < −13 mag), dotted black line: 2σ confidence interval, dotted red line: completeness limit of MV = −13.0 mag, filled circles: spectroscopically confirmed Virgo cluster members, filled triangles: remaining objects with VCC index, asterisks: probable Virgo cluster members. |
| In the text | |
 |
Fig. 8 V-band luminosity function of the Virgo cluster sample (bin width:
0.5 mag, sampling step: 0.25 mag). Open symbols denote only early type galaxies,
solid symbols denote datapoints which were corrected by SDSS data. The solid line
indicates a linear fit performed in
−18.8 ≤ MV ≤ −13.0 mag. The
Schechter function fitted in the same interval with fixed
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


