| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201116517 | |
| Published online | 09 February 2012 | |
Kinematic properties of the field elliptical NGC 7507⋆,⋆⋆
1 Departamento de Astronomía, Universidad de Concepción, Concepción, Chile
e-mail: rcsave@utu.fi
2 European Southern Observatory, Alonso de Córdova 3107, Santiago, Chile
3 Facultad de Ciencias Astronómicas y Geofísicas de la Universidad Nacional de La Plata and Instituto de Astrofísica de la Plata (CCT La Plata-CONICET-UNLP), Paseo del Bosque S/N, 1900 La Plata, Argentina
4 UCO/Lick Observatory, University of California, Santa Cruz, CA 95064, USA
5 Argelander Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
Received: 14 January 2011
Accepted: 7 November 2011
The dark matter (DM) halos of field elliptical galaxies have not been well-studied and their properties appear controversial in the literature. While some galaxies appear to be nearly devoid of DM, others show clear evidence of its presence. Furthermore, modified Newtonian dynamics (MOND), which has been found to have predictive power in the domain of disk galaxies, has not yet been investigated for isolated elliptical galaxies. We study the kinematics of the isolated elliptical NGC 7507, which has been claimed as a clear example of DM presence in early-type galaxies. We obtained major and minor axis long-slit spectroscopy of NGC 7507 using the Gemini South telescope and deep imaging in Kron-Cousins R and Washington C using the CTIO/MOSAIC camera. Mean velocities, velocity dispersion and higher order moments of the velocity distribution are measured out to ~90′′. The galaxy, although almost circular, has significant rotation along the minor axis and a rapidly declining velocity dispersion along both axes. The velocity dispersion profile is modeled in the context of a spherical Jeans analysis. Models without DM provide an excellent representation of the data with a mass-to-light ratio (M/L) of 3.1 (R-band). The most massive Navarro-Frenk-White (NFW) halo the data allow has a virial mass of only 3.9-2.1+3.1×1011 M⊙, although the data are more consistent with models that have a slight radial anisotropy, which implies the galaxy has an even lower DM halo mass of 2.2-1.2+2.0×1011 M⊙. Modeling of the h4 Gauss-Hermite coefficient is inconclusive but seems to be consistent with mild radial anisotropy. A cored logarithmic DM halo with parameters r0 = 7 kpc and v0 = 100 km s-1 can also reproduce the observed velocity dispersion profile. The MOND predictions overestimate the velocity dispersion. In conclusion, we cannot easily reproduce the previous findings of a predominance of DM in NGC 7507 within a simple spherical model. DM may be present, but only in conjunction with a strong radial anisotropy, for which there are some indications.
Key words: galaxies: individual: NGC 7507 / Galaxy: kinematics and dynamics
Based on observations taken at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the Science and Technology Facilities Council (United Kingdom), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), Ministério da Ciência e Tecnologia (Brazil) and SECYT (Argentina).
Tables 1–3 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The existence of dark matter (DM) in spiral galaxies (or alternatively a law of gravitation that differs from the Newtonian law) remains undisputed. However, the same cannot be said conclusively for all elliptical galaxies. Central galaxies in galaxy clusters such as NGC 6166 (Kelson et al. 2002), NGC 1399 (Richtler et al. 2008; Schuberth et al. 2010), and NGC 3311 (Richtler et al. 2011) are embedded in massive dark halos as is the case of bright non-central cluster ellipticals such as NGC 4636 and NGC 4374 in Fornax (Schuberth et al. 2006; Napolitano et al. 2010). In constrast elliptical galaxies with lower luminosities in sparser environments (NGC 821, 3379, 4494, 4697), whose mass profiles have been studied using planetary nebulae (PNe) kinematics, appear to show only weak evidence of DM (Romanowsky et al. 2003; Douglas et al. 2007; Napolitano et al. 2009; Méndez et al. 2009; Teodorescu et al. 2010; but see Weijmans et al. 2009); although the case of NGC 3379 may be consistent with a normal cold DM halo if a very strong radial anisotropy is present (de Lorenzi et al. 2009).
The comparison of field, and possibly isolated, elliptical galaxies to those in clusters is of great interest. Different formation mechanisms may have led to differences in their dark halo structure, but observationally few properties have been reliably determined. Isolated galaxies may also be good test objects of the modified Newtonian dynamics (MOND, Milgrom 1983; Sanders & McGaugh 2002), since complications arising from the “external field effect” (Milgrom 1983; Wu et al. 2007) should be minimal.
The galaxy NGC 7507 is an elliptical (E0, de Souza et al. 2004) of MV = −21.6, with a distance modulus of 31.83 ± 0.17 based on surface brightness fluctuations (23.22 ± 1.8 Mpc; Tonry et al. 2001,corrected by − 0.16 mag following Jensen et al. 2003); we assume this distance throughout the paper, which implies a scale of 112.5 pc arcsec-1. The galaxy is fairly isolated, forming a probable pair with the SBb galaxy NGC 7513, which lies at a projected distance of 18 arcmin (~130 kpc), but displaying no signs of recent interactions (Tal et al. 2009). Due to its proximity and regular shape, its dynamics have been well studied leading to strikingly different conclusions. Bertin et al. (1994) found no evidence of a DM halo, using major-axis kinematical data out to 66′′. Kronawitter et al. (2000, hereafter K+00) performed dynamical analyses of 21 round elliptical galaxies, including NGC 7507. They concluded that models based on luminous matter could only be ruled out with 95% confidence for only three galaxies, including NGC 7507. Contradicting this finding, Magorrian & Ballantyne (2001) adopted the kinematics of Bertin et al. (1994) and photometry of Franx et al. (1989b) to establish that NGC 7507 has a constant mass-to-light ratio (M/L) profile, i.e. that it does not contain a dark halo.
The most significant difference between these studies appears to be the observational data used and not the modeling approach, which, although different, should not give strongly discrepant results. We decided to obtain new, deeper long-slit spectroscopy using Gemini South. Eight-meter class telescopes have been scarcely used to measure the long-slit kinematics of the unresolved stellar components of elliptical galaxies (e.g. Thomas et al. 2007; Forestell & Gebhardt 2010; Pu et al. 2010; and see Samurović & Danziger 2005, for a review of the work made with 4 m class telescopes). Much effort has been put into kinematic studies of PNe (e.g. Méndez et al. 2009) and globular clusters (e.g. Romanowsky et al. 2009; Schuberth et al. 2010), which can be observed out to much larger galactocentric radii, but provide weaker constraints of their orbital anisotropies.
The paper is organized as follows: we present our observations and reduction procedures in Sect. 2. The photometric properties of the galaxy together with a description of its kinematics are given in Sect. 3. The dynamical modeling is presented in Sect. 4, while the discussion and conclusions can be seen in Sects. 5 and 6, respectively.
2. Observations and data reduction
2.1. CTIO/MOSAIC photometry and photometric calibration
The images used in this study were obtained with the MOSAIC II camera (an 8 CCDs mosaic imager, 16 amplifiers) mounted at the prime focus of the 4-m Blanco telescope at the Cerro Tololo Inter-American Observatory (CTIO, Chile). Observations were carried out during 2005 August 5–6, where the first night was “useful” and the second one “photometric”, according to the CTIO reports. One pixel of the MOSAIC wide-field camera subtends 0.27 arcsec on the sky, which corresponds to a field of 36′ × 36′, i.e. approximately 230 × 230 kpc2 at the distance of NGC 7507.
All fields were imaged in Washington C (λcentral = 3850 Å) and Kron-Cousins R (λcentral = 6440 Å) filters. The R filter was used instead of the original Washington T1, as Geisler (1996) has shown that the Kron-Cousins R filter is more efficient than T1, and that R and T1 magnitudes are closely related, with just a very small colour term and zero-point difference (R − T1 ~ −0.02).
To fill in the gaps between the eight individual MOSAIC chips, the data were dithered taking four images in R with exposure times of 720 s each, and seven images in C with exposures of 1800 s each. To avoid saturation at the galaxy core, additional shorter exposures of 60 s in R and of 300 s in C were also obtained. Sky flats were obtained at the beginning and end of each night.
The MOSAIC data reduction was performed using tasks from the MSCRED package within IRAF. Several tasks were employed to correct for the variable pixel scale across the CCD, which might cause a 4 per cent variability in the point-sources brightness (from the center to the corners). The final combined R image still shows sensitivity variations up to 1.4 per cent, and the final C image up to 3.0 per cent (peak-to-peak). The seeing in these final images is 1.1″ on the R frame, and 1.3″ on the C image.
The photometric calibration was performed with three fields of standard stars selected from the list of Geisler (1996), each containing 7 to 10 standard stars. For these fields, C and R images were obtained in each night, covering an airmass range 1.1 − 2.3. Finally, we used a single set of calibration equations for both nights.
The equations read 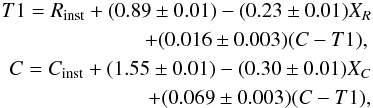 where Cinst and Rinst are instrumental magnitudes and XC and XR are the airmasses.
where Cinst and Rinst are instrumental magnitudes and XC and XR are the airmasses.
The absolute photometric quality of the C-photometry is dubious, hence it is only used for differential analyses. The R-photometry is of high quality, as the comparison of our results with previous photometric data sets of the galaxy reveals. The mean difference from Franx et al. (1989b) is 0.08 mag (Franx et al. is brighter). We also compare with photoelectric aperture measurements given by Poulain & Nieto (1994). In this case, we find that our profile is brighter by 0.15 mag.
2.2. Surface photometry
The surface photometry of the galaxy was perfomed using the IRAF/ELLIPSE task. The shallower images were used to determine the surface brightness profile for the inner ~10″ in the C and R profiles, which were saturated in the longer exposures. The sky brightness in the shallow images was determined by taking the median value of the sky in several 15 × 15 pixel boxes of empty regions further than 5′ from the galaxy center. Since an accurate sky determination is critical in shaping the light profile in the outer parts of a galaxy, a different procedure, similar to the one devised by Dirsch et al. (2003), was adopted for the deep images. First, DAOPHOT (Stetson 1987) was applied to all point sources present in the field. The local sky brightness of each source was determined using the median of the sky value of the pixels between 15 and 25 pixels from each source center. Deviant pixels were rejected using a three-sigma clipping procedure. All the sky values were then ordered according to their distance from the center of NGC 7507. To exclude overestimated sky values (of point sources close to nearby galaxies, bright stars or chip defects), a new iterative 3-sigma clipping was applied to the sky values within radial bins of 100 objects, this time using robust location and scale bi-weight estimators (Beers et al. 1990). At distances larger than 5′ from the center of the galaxy, the value of the sky brightness fluctuates by less than 0.5%. The final value for the sky was then taken as the mean of the sky values between 10′ and 12′ (~78–98 kpc) from the galaxy center and the R sky brightness in mag/arcsec2 was found to be 20.90. The photometry of the galaxy can be seen in Table 1.
2.3. Gemini/GMOS spectroscopy
Long-slit spectra of NGC 7507 were obtained using the Gemini Multi-Object Spectrograph (GMOS) on Gemini South, Cerro Pachón, Chile, in queue mode during the nights of September 19 and 21, 2004 (program GS-2004B-Q-75). The grism was the B600+_G5323 which, in conjunction with a 1′′ slit width, gives a resolution of ~4.7 Å FWHM. Three consecutive exposures of 1800s each were taken for a position angle of 90°, which is close to the major axis (PA = 105°), and for PA = 0°, which is close to the minor axis (PA = 15°). For convenience, these two positions are referred to hereafter as the major and minor axes, respectively. Standard reduction steps (bias subtraction, flat fielding, detectors mosaicing, wavelength calibration) were performed with the Gemini IRAF package (v 1.9.1). Typical wavelength residuals were ~0.05 Å. No cosmic ray cleaning was attempted at this stage because it introduced undesired noise, especially around bright sky lines. Since copper-argon arc spectra were taken during daytime and not immediately either after or before the science exposures, a correction of the zero point of the wavelength solution was necessary and was performed by measuring the position of the bright sky line at 5577.34 Å. This correction typically amounted to 0.1 Å. After that, the three spectra for each position angle were averaged. Sky subtraction was done using the IRAF task background, by averaging 50 rows on opposite sides of each spectra, at around 4.5′ from the galaxy center for the major axis and ~4′ for the minor axis. The two-dimensional (2D) spectra were spatially rebinned to achieve a constant S/N ~ 50/pixel, which is highly desirable when measuring the higher order moments of the line-of-sight velocity distribution (LOSVD). The 4800–5500 Å wavelength range, which contains strong absorption features as Hβ, Mg b, and Fe lines around 5325 Å, was selected for the kinematical analysis.
Mean velocity, velocity dispersion and higher order moment profiles were measured for both long slits by using the Gauss-Hermite pixel fitting code (van der Marel 1994, hereafter vdM code) and the penalized pixel fitting (pPXF) method developed by Cappellari & Emsellem (2004). Both approaches have the advantage of performing their calculations in pixel space instead of Fourier space, thus allowing a more precise masking of undesired zones in the spectra (emission lines, bad columns, etc.). Both methods also parametrize the LOSVD in terms of a Gauss-Hermite series (Gerhard 1993; van der Marel & Franx 1993). The former algorithm measures the mean velocity and the velocity dispersion, and, with these values fixed, fits the higher order terms of the velocity distribution, parametrized by the Gauss-Hermite coefficients h3 and h4. The latter algorithm fits all parameters simultaneously, but can bias the solution to a Gaussian shape when the higher order terms are not sufficiently constrained by the data (Cappellari & Emsellem 2004). An advantage of the pPXF method over the vdM code is that it can perform the fitting process with a linear combination of template spectra, minimizing the effect of template mismatching.
A subset of 22 old and metal-rich single stellar population models from Vazdekis et al. (2010) based on the MILES stellar library (Sánchez-Blázquez et al. 2006) were used as velocity templates for our analysis using the vdM code. These templates were logarithmically rebinned to the same dispersion and convolved with a Gaussian to ensure that they had the same spectral resolution as the science spectra. Final values of mean velocity, velocity dispersion, h3 and h4 parameters were assumed to be the average of the values for the three templates that provided the closest fit (the lowest χ2 values).
In the pPXF analysis, two different sets of spectra were employed as templates to extract the kinematical information, the aforementioned Vazdekis et al. models, but this time the entire library consisting of 350 models, and the full MILES spectral library (Sánchez-Blázquez et al. 2006). Both have a spectral resolution of 2.3 Å FWHM (but see Beifiori et al. 2011). Since we expect to find a population gradient across the galaxy (see Sect. 3), the templates used for each radial bin were not fixed, but freely chosen by pPXF from the MILES library and the Vazdekis models, separately, until the closest model was achieved. For the Vazdekis models, pPXF used typically 3 from the 350 models, while a mean number of 16 template stars from the 985 in the MILES library were used by pPXF for each radial bin. Estimations of the errors for all the calculated values were obtained by performing 100 Monte Carlo simulations in which random noise was added to each science spectrum and then passed again through pPXF (e.g. Cappellari & Emsellem 2004; Bedregal et al. 2006). In this case, only the templates that were previously selected by pPXF were fitted, and not the entire set. The dispersion in the values obtained from the simulations are quoted as the error bars in the measurements from the original spectra.
 |
Fig. 1 Comparison between the different measurements of the velocity dispersion profile of the major axis of NGC 7507 as described in the text. |
The agreement between the results of pPXF using the two sets of templates is very good. However a few remarks are appropriate. Typically pPXF uses much fewer templates from the Vazdekis models (~3) and the χ2 values are always larger than when using MILES. The inclusion of multiplicative Legendre polynomials reduces the χ2, but does not increase the number of templates used. We find a systematic small difference of 3 km s-1 between the velocity dispersion results obtained using the Vazdekis SSP models and the MILES library (Fig. 1, bottom panel). The difference from the values given by the vdM code is somewhat larger: the velocity dispersions derived with vdM are systematically larger. We find a systematic difference of 9 km s-1 (Fig. 1, top panel). Since template mismatching is expected to be far less significant for this method, if not totally negligible, based on previous studies (e.g. Shapiro et al. 2006; Cappellari et al. 2007), we decided to adopt the results obtained using the MILES spectral in all the subsequent kinematic description and dynamical analyses. These measurements can be seen in Tables 2 and 3.
3. Results
3.1. Light and color profile
There is a well-established variety of analytical model light profiles of elliptical galaxies. Since we wish to use the light profile within a spherical Jeans analysis, its analytical form, besides being an excellent representation, should permit a closed analytical deprojection as well as an analytical mass profile. These conditions are fullfilled by the sum of two β profiles (or Hubble-Reynolds profile) 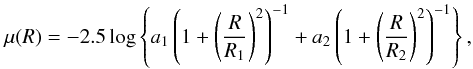 (1)where a1 = 2.052 × 10-8, a2 = 6.452 × 10-7, R1 = 16′′, and R2 = 2.19″, provide an excellent representation of the surface brightness profile between 2′′ and 400′′ (Fig. 2, panel c).
(1)where a1 = 2.052 × 10-8, a2 = 6.452 × 10-7, R1 = 16′′, and R2 = 2.19″, provide an excellent representation of the surface brightness profile between 2′′ and 400′′ (Fig. 2, panel c).
 |
Fig. 2 CTIO/MOSAIC surface photometry of NGC 7507. a) Ellipticity profile. b) C − R color profile. c) R surface brightness profile (black circles) and R surface photometry from Franx et al. (1989b) (filled red squares). The solid red line is the fit of a double β model to our data. Residuals can be seen in panel d). |
Although the β-profile provides an excellent description out to about 50 kpc, the extrapolation to larger radii, which is used in the dynamic modeling, is not a priori justified. It is generally unknown where a galaxy “ends” (but see the remarks in Sect. 4.1). The mass of the β-model diverges for large radii. This raises the concern of whether systematic errors are introduced by extrapolating the profile to larger radii.
We therefore fit the surface brightness profile with the sum of two Sersic profiles 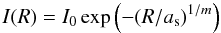 (2)(Sersic 1968; Graham & Driver 2005), since a single Sersic profile fails to accurately reproduce the luminosity in the entire radial range, underestimating the outer ( ≳ 20 kpc) profile. The Sersic parameters are
(2)(Sersic 1968; Graham & Driver 2005), since a single Sersic profile fails to accurately reproduce the luminosity in the entire radial range, underestimating the outer ( ≳ 20 kpc) profile. The Sersic parameters are 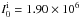 L⊙ pc-2,
L⊙ pc-2, 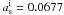 pc, mi = 4.8, for the inner Sersic profile, and
pc, mi = 4.8, for the inner Sersic profile, and 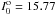 L⊙ pc-2,
L⊙ pc-2, 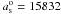 pc, mo = 1.05, for the outer profile; M ⊙ ,R = 4.42 (Binney & Merrifield 1998) was adopted.
pc, mo = 1.05, for the outer profile; M ⊙ ,R = 4.42 (Binney & Merrifield 1998) was adopted.
Both models provide excellent descriptions of the surface density profile from ~200 pc (~1.5′′) until the last photometric point at ~55 kpc, and are practically indistinguishable (see Fig. 3). Differences are seen only in the inner ~200 pc where the double β model underestimates the light profile, while the opposite happens with the double Sersic model and for the extrapolation of the light profile (outside ~55 kpc) where the double β model falls as R-2.0, but the Sersic profile declines more steeply.
The double Sersic profile implies that the effective radius is Re = 75′′. This is significantly larger than the previous estimations of 24′′ (Lauberts & Valentijn 1989), 31′′ (Faber et al. 1989), and 47′′ (de Souza et al. 2004); this is unsurprising given our deep imaging. For example, the value of Faber et al. is taken from the RC2 (de Vaucouleurs et al. 1976) where the total galaxy brightness is defined as the brightness within an isophote with a surface brightness in the B-band of 25 mag arcsec-2 which we found for NGC 7507 occurs at a distance of about 150′′.
 |
Fig. 3 Surface brightness profile of NGC 7507. The green dots indicate the R photometry in units of L⊙ pc-2. The dashed blue lines represent the two Sersic profiles, while the solid blue line is their sum. The red solid line represents the double β model. |
The color profile was evaluated as the difference between the two models in C and R (Fig. 2, panel b). The inner core (within 10″) declines by 0.3 mag with radius to bluer colors, followed by a radial interval of more or less constant color. The color then gets redder again at about 50″, and remains practically unchanged out to 200″. The outer gradient to bluer colors might exist, but owing to the large uncertainties cannot be claimed convincingly. Color profiles for the inner 50″ were given by Franx et al. (1989b) and Goudfrooij et al. (1994). The inner strong gradient is apparent in both of them, but the gradient of almost 0.5 mag in B − I between 30″ and 60″ seen by Goudfrooij et al. (1994) is not found in our color profile.
 |
Fig. 4 C − R color image of NGC 7507 based on the short exposures. Image has been median smoothed in 3 × 3 pixel boxes. Image size is 2′ × 2′. |
It is interesting to consider a 2D color image of the inner region. Figure 4 was obtained by dividing the short C by the R exposures. It is apparent that the “color field” is not spherically symmetric but tends to have bluer colors along the E-W axis. One could therefore interpret the plateau with C − R = 2.0 between 10″ and 50″ as a result of averaging along isophotes, before the color gets redder again. We are unable to determine, however, whether diffuse dust or population effects or both are responsible.
3.2. Ellipticity and higher isophote moments
 |
Fig. 5 Major axis kinematics of NGC 7507, as extracted with pPXF (see text). a) Hermite coefficient h4 profile, b) h3 profile, both panels show a dashed line at the zero level for comparison, c) velocity dispersion. The horizontal error bars show the regions across which the spatial binning was done (shown only in this panel, but valid for all four). The vertical dashed strip indicates a gap between the detectors in which no measurements are possible, d) rotation profile. For all panels, open black circles are our data, red solid squares are from K+00, solid green circles are from Franx et al. (1989a), and blue open squares come from Bertin et al. (1994). |
As all previous studies have pointed out, the galaxy in projection is very round. We find ⟨ ϵ ⟩ = 0.045 ± 0.008, where the mean is taken over the inner 2′, avoiding the innermost 2″ which are affected by seeing. Beyond 2′ the ellipticity slightly increases, partly due to the difficulty in masking a bright 11th mag star, located ~6′ SE of the galaxy (Fig. 2, panel a).
The Fourier coefficient a4 describes the isophote’s boxiness or diskyness (negative: boxy; positive:disky). It is zero out to 2′. The slight boxiness at larger radii may also be caused by the bright star. A table with the photometry, including ellipticities, PA, and a4 is available in Table 1.
3.3. Irregular features
A small, slightly off-centered dip in the light can be seen in the shallow R image. It is not apparent in the shallow C image, which has poorer seeing. We interpret this as a dust lane already detected by Franx et al. (1989b).
Tal et al. (2009) found evidence of a faint shell north of the galaxy. However, when the smoothed 2D model created with IRAF\BMODEL task is subtracted from the galaxy light, we see thi shell in neither the C nor in the R images. No substructure was detected either in the shallower images analyzed by de Souza et al. (2004).
3.4. Stellar kinematics
The kinematics along the major axis of NGC 7507 have been measured by several groups (Bertin et al. 1994; Franx et al. 1989a, K+00); but along the minor axis only by Franx et al. (1989a) and higher order moments only by K+00. We extended the radial coverage of Franx et al. (1989a) by a factor of 1.5 for the major axis and 2.5 for the minor axis.
3.4.1. Rotation
The major axis rotation is very low (Fig. 5, panel d), consistent with no rotation, with a formal amplitude of −1 ± 6 km s-1 within the inner 30′′. In the 30–60′′ range, the amplitude slightly increases to a value of −13 ± 7 km s-1, which is consistent with the aforementioned previous studies. The outermost measured bin, at a mean distance of 97′′ shows a significant increase in the rotation with respect to the center (−68 ± 8 km s-1). This may be partly due to the misalignment of the slit direction and the photometric major axis but perhaps also a hint that the kinematic properties of the galaxy suffer a change at large radii, as seen for example in NGC 821 and NGC 1400 (Proctor et al. 2009).
The minor axis rotation is pronounced and slightly asymmetric with amplitudes of 30 ± 7 km s-1 in the west direction and −43 ± 7 km s-1 in the east direction inside the range 5–50′′ (Fig. 6, panel d). Franx et al. (1989a) measured an amplitude of 36 ± 5 km s-1 in the range 5–30′′, without detecting any asymmetry. In the outermost east and west bins, around 60′′, the mean velocity is consistent with no rotation. This rotation profile closely resembles the major axis rotation of NGC 3379 (Statler & Smecker-Hane 1999; Weijmans et al. 2009, their Fig. 4).
Summarising, the isophote shapes are sufficiently undisturbed and the projected rotation amplitude is small enough to justify the use of a non-rotating, spherical mass model.
3.4.2. Velocity dispersion
The major axis velocity dispersion rapidly declines in the inner 30′′ and undergoes a slower decline at larger radii. The dispersion values of K+00 deviate strongly, not only from our values, but also from Franx et al. (1989a) and Bertin et al. (1994) (Fig. 5, panel c). While the difference at the center of the galaxy is roughly within errors (9.7 ± 4.8 km s-1), and it can be easily explained by the spectra being taken under different seeing conditions; at 27′′ from the center, the difference amounts to 70 ± 14 km s-1 in the sense that K+00 values are larger than ours.
 |
Fig. 6 Minor axis kinematics of NGC 7507. The vertical dashed strips show the positions of the gaps between detectors and two interloping background galaxies, which were masked in the spatial binning process. Symbols are the same as in Fig. 5. |
The minor axis velocity dispersion profile shows a similar rapid decline in the inner 30″ but a less steep decline at larger radii (Fig. 6, panel c). As in the case of the major axis, the difference from Bertin et al. (1994) is minimal and amounts to 14 ± 24 km s-1, where the uncertainty is caused almost entirely by the Bertin et al. (1994) values.
A kinematic classification of early-type galaxies, based on an angular momentum proxy was introduced by Emsellem et al. (2007). They defined 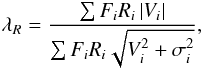 (3)where Fi is flux, Ri is distance to the center of the galaxy, and Vi and σi are the mean velocity and velocity dispersion. Emsellem et al. (2007) found that early-type galaxies can be separated into two classes of slow and fast rotators, depending on whether they have λR values below (slow) or above (fast) 0.1 inside Re. Even though this parameter was introduced for the SAURON 2D data, it can been applied to long-slit measurements in order to help us to compare with the original definition, once a proper scaling factor of 0.57 is applied (Cappellari et al. 2007; Coccato et al. 2009). In that case the sum is over the quantities along the slit.
(3)where Fi is flux, Ri is distance to the center of the galaxy, and Vi and σi are the mean velocity and velocity dispersion. Emsellem et al. (2007) found that early-type galaxies can be separated into two classes of slow and fast rotators, depending on whether they have λR values below (slow) or above (fast) 0.1 inside Re. Even though this parameter was introduced for the SAURON 2D data, it can been applied to long-slit measurements in order to help us to compare with the original definition, once a proper scaling factor of 0.57 is applied (Cappellari et al. 2007; Coccato et al. 2009). In that case the sum is over the quantities along the slit.
We calculated the λR parameter separately for each long slit position. For both axes, the parameter mildly increases inside Re reaching 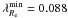 and
and 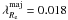 , staying basically flat beyond that radius. This is consistent with the mild rotation of the galaxy. NGC 7507 can be classified as a slow rotator, sharing also the kinematic misalignment which is often seen in these galaxies, although it has a rapidly declining velocity dispersion profile which is more common amongst fast rotators (Coccato et al. 2009).
, staying basically flat beyond that radius. This is consistent with the mild rotation of the galaxy. NGC 7507 can be classified as a slow rotator, sharing also the kinematic misalignment which is often seen in these galaxies, although it has a rapidly declining velocity dispersion profile which is more common amongst fast rotators (Coccato et al. 2009).
3.4.3. Higher order moments
The Gauss-Hermite coefficient h3, which measures the asymmetric deviation from a Gaussian, is consistent with being zero along the major axis. Along the minor axis within 20″, it appears to have a gradient which would be consistent with its rotation (Fig. 6, panels b and d).
The coefficient h4, which indicates symmetric deviations from a Gaussian profile, is positive for both the major and minor axis spectra. The sign agrees with the measurements of K+00, who also found slightly positive values of h4, although their values were somewhat smaller (Fig. 5, panel a). We return to this result when discussing any possible anisotropies.
4. Dynamical modeling
4.1. The stellar mass profile
To obtain the (spherical) stellar mass profile we have to deproject the surface brightness profile after correcting for Galactic absorption (AR = 0.128; Schlegel et al. 1998). In the case of the double-β profile this is achieved by applying the Abel deprojection formula, which for the β profile has an analytical description ![\begin{equation} \label{eq:light2} j(r)=\frac{C_R}{2}\sum_{i=1}^2\frac{a_i/R_i}{[1+(r/R_i)^2]^{3/2}}, \end{equation}](/articles/aa/full_html/2012/02/aa16517-11/aa16517-11-eq97.png) (4)where ai and Ri come from Eq. (1), and CR = 2.5 × 1010 is the factor used to transform to units of L⊙ pc-2, adopting M ⊙ ,R = 4.42 (Binney & Merrifield 1998). The enclosed stellar mass can be obtained by integrating this light density
(4)where ai and Ri come from Eq. (1), and CR = 2.5 × 1010 is the factor used to transform to units of L⊙ pc-2, adopting M ⊙ ,R = 4.42 (Binney & Merrifield 1998). The enclosed stellar mass can be obtained by integrating this light density
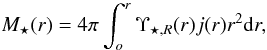 (5)where Υ ⋆ ,R is the stellar M/LR. For constant M/LR, this integral has the exact solution
(5)where Υ ⋆ ,R is the stellar M/LR. For constant M/LR, this integral has the exact solution 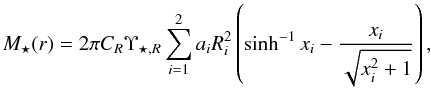 (6)where xi = r/Ri and ai and Ri have the same meaning as in Eq. (4).
(6)where xi = r/Ri and ai and Ri have the same meaning as in Eq. (4).
The stellar M/LR appears as a parameter in the fit to the kinematical data, adopting the deprojected light profile and certain forms for a possible DM halo. From the shape of the colour profile, one concludes that M/L as a population property is approximately constant out to a radius of 2′. At larger radii, the M/L may drop owing to a declining metallicity. However, this is only weakly constrained and any effect on the inner projected velocity dispersion would be completely degenerate with a dark halo.
The Sersic profile can be deprojected using an approximation given by Prugniel & Simien (1997)![\begin{eqnarray*} j(r)&=&j_1\tilde{j}(r/a_{\rm s}),\\ \tilde{j}(x)&\simeq& x^{-p}\mathrm{exp}(-x^{1/m}),\\ j_1&=&\left\lbrace\frac{\Gamma(2m)}{\Gamma[(3-p)m]}\right\rbrace\frac{I_0}{2a_{\rm s}},\\ p&\simeq& 1 - 0.6097/m + 0.05463/m^2, \end{eqnarray*}](/articles/aa/full_html/2012/02/aa16517-11/aa16517-11-eq107.png) where the latter equation comes from Lima Neto et al. (1999), Γ(x) is the Gamma function, and I0, as, and m refer to the Sersic parameters from Eq. (2). We also refer to Mamon & Łokas (2005b) for a compilation of the relevant formulae.
where the latter equation comes from Lima Neto et al. (1999), Γ(x) is the Gamma function, and I0, as, and m refer to the Sersic parameters from Eq. (2). We also refer to Mamon & Łokas (2005b) for a compilation of the relevant formulae.
Integrating the luminosity density, j(r), the enclosed luminosity is found. Lima Neto et al. (1999) give ![\begin{eqnarray} L_{\rm s}(r)&=&L_{\mathrm{tot}}\tilde{L}_{\rm s}(r/a_{\rm s}),\label{eq:sersic_lum}\\ \tilde{L}_{\rm s}(x)&=&\frac{\gamma[(3-p)m,x^{1/m}]}{\Gamma[(3-p)m]}, \end{eqnarray}](/articles/aa/full_html/2012/02/aa16517-11/aa16517-11-eq113.png) where γ is now the incomplete Gamma function and
where γ is now the incomplete Gamma function and 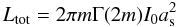 (9)is the total luminosity of the profile. For our double Sersic profile, the luminosity is simply the sum of the luminosity of both the inner and outer Sersic profiles.
(9)is the total luminosity of the profile. For our double Sersic profile, the luminosity is simply the sum of the luminosity of both the inner and outer Sersic profiles.
Since beyond ~55 kpc the double-β and Sersic profiles display the most distinct behaviors (cf. Fig. 3), we inspected the influence of these dissimilar extrapolations on their respective enclosed luminosities, which are directly related to the stellar mass through the M/L. Figure 7 considers the enclosed luminosities of both models normalized to the total luminosity of the double Sersic model given by Eq. (9). As expected from Fig. 3, the luminosities are very similar not only within the ~55 kpc where the galaxy light was directly measured, but well beyond. A ~10% difference in the total enclosed luminosity is reached only at 200 kpc. In practice, however, the extension of elliptical galaxies may be lower than this limit. In NGC 4636, for example, the globular cluster distribution is cut-off at about ~60 kpc (Dirsch et al. 2005). A similar behavior has been seen in M 87, the central galaxy of Virgo, where the planetary nebulae distribution show a truncation of the stellar halo at ~150 kpc (Doherty et al. 2009). Therefore, any differences in the extrapolations beyond 200 kpc are not relevant to a dynamical analysis of the galaxy.
Given the similarities between the light profiles and to avoid any uncertainties introduced by the approximations used in the Sersic profile deprojection (which are not present in the analytic form of the β profile deprojection), the Jeans analysis that we now describe was based on the stellar distribution given by the β model profile. In any case, the velocity dispersions shown in Fig. 8 were found to vary by less than 2 km s-1 at the most distant kinematic point, when the double Sersic model was used a basis of the stellar mass profile.
 |
Fig. 7 A comparsion between the enclosed luminosities of the double β profile (dashed blue line) and the double Sersic profile (red solid line), normalized to the double Sersic total luminosity. The arrow indicates the last spectroscopic point measured on the major axis. |
4.2. Jeans analysis
The basis of our modeling is the spherical Jeans equation, which is strictly valid only for infinite, non-rotating systems. Its solutions, when applied to real galaxies, may be considered as good approximations, but there is no guarantee that they correspond to physically correct distribution functions. Moreover, the potential and the orbital anisotropy are degenerate, although we refer to Hansen & Moore (2006) and the remarks below. On the positive side, this equation has an appealing simplicity, known anisotropies of elliptical galaxies in the inner regions are generally small (e.g. Gerhard et al. 2001; Cappellari et al. 2006) and one can use the higher moments of the velocity distribution as constraints of the anisotropy. Cappellari et al. (2006) also demonstrated that more sophisticated dynamical modeling does not reveal grossly different results. The main uncertainty probably does not arise from the modeling approach, but collectively from the distance uncertainty, the quality of the data, and the assumption of sphericity.
For convenience and clarity, we give in the following the basic formulae. The Jeans equation is (e.g. Binney & Tremaine 2008) ![\begin{equation} \frac{\mathrm{d}[j(r)\sigma_r^2(r)]}{\mathrm{d} r} + \frac{2\beta(r)}{r}j(r)\sigma_r^2(r)=-j(r)\frac{GM(r)}{r^2}, \end{equation}](/articles/aa/full_html/2012/02/aa16517-11/aa16517-11-eq116.png) (10)which relates the light distribution, j(r), and radial velocity dispersion, σr(r), with the underlying gravitational potential or enclosed total mass, M(r), and where
(10)which relates the light distribution, j(r), and radial velocity dispersion, σr(r), with the underlying gravitational potential or enclosed total mass, M(r), and where 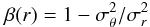 (11)is the anisotropy parameter, which indicates possible departures from pure isotropy in the form of radial (β > 0) or tangential (β < 0) orbits.
(11)is the anisotropy parameter, which indicates possible departures from pure isotropy in the form of radial (β > 0) or tangential (β < 0) orbits.
For a given light and mass distribution, and a constant anisotropy, the solution to the Jeans equation is 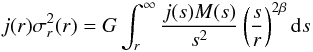 (12)(e.g. Mamon & Łokas 2005b, hereafter MŁ05), which is then projected to be compared with the velocity dispersion measurements
(12)(e.g. Mamon & Łokas 2005b, hereafter MŁ05), which is then projected to be compared with the velocity dispersion measurements ![\begin{equation} \label{eq:jeans3} \sigma_{\mathrm{LOS}}^2(R)=\frac{2}{I(R)}\left[\int_R^{\infty}\frac{j\sigma_r^2r\mathrm{d}r}{\sqrt{r^2-R^2}} - R^2\int_R^{\infty}\frac{\beta j\sigma_r^2\mathrm{d}r}{r\sqrt{r^2-R^2}}\right] \end{equation}](/articles/aa/full_html/2012/02/aa16517-11/aa16517-11-eq123.png) (13)(Binney & Mamon 1982). For the anisotropy profiles adopted in Sects. 4.4 and 4.5, Eqs. (12) and (13) can be combined to yield the single integral solution
(13)(Binney & Mamon 1982). For the anisotropy profiles adopted in Sects. 4.4 and 4.5, Eqs. (12) and (13) can be combined to yield the single integral solution 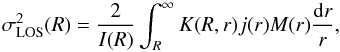 (14)where the kernels K for the different anisotropy models are provided in Appendix A2 of (Mamon & Łokas 2005b).
(14)where the kernels K for the different anisotropy models are provided in Appendix A2 of (Mamon & Łokas 2005b).
The accuracy of the models can be quantified by the use of a simple χ2 test 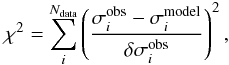 (15)where σobs is the measured velocity dispersion, σmodel is the predicted dispersion at the same radial distance, δσobs is the observational error associated with the dispersion measurement, and the sum is taken over all radial bins.
(15)where σobs is the measured velocity dispersion, σmodel is the predicted dispersion at the same radial distance, δσobs is the observational error associated with the dispersion measurement, and the sum is taken over all radial bins.
Under the spherical Jeans analysis, additional constraints on the dynamical behavior of the galaxy can be obtained by modeling the higher order moment of the velocity distribution which can be related to the Gauss-Hermite coefficient h4 (van der Marel & Franx 1993). For this, the higher order Jeans equations must be solved. This task can be achieved only if additional information about the distribution function is known. In particular, by assuming distribution functions of the form f(E,L) = fo(E)L − 2β with constant β, it is possible to reduce the two higher-order Jeans equation to only one. A more detailed discussion, as well as the relevant formulae can be seen in Łokas (2002) and Napolitano et al. (2009). Our results using this approach are presented and discussed in Sect. 4.6.
4.3. The velocity dispersion profile
To construct the radial dependence of the velocity dispersion profile, we averaged for a given radial bin the dispersion along the major and the minor axis (although the ellipticity is tiny) from Figs. 5 and 6. The dispersion values are symmetrical with respect to the galaxy center and are in agreement between the both axes when errors are considered. The bins are chosen in such a way that the inner region, where the S/N is highest, has the densest binning while the outer radii are covered with larger bins. The principal uncertainties are those in the mean values calculated by pPXF. Final values are listed in Table 4, which also lists the adopted h4 values. Their uncertainties are the standard deviations of the h4 values in the respective bins.
4.4. Models without DM
 |
Fig. 8 Dynamical models of NGC 7507. Black circles indicate in all panels the line-of-sight velocity dispersion. All models are given outside of 400 pc, where the luminosity model is unaffected by seeing. Top left: stars-only models. The black solid line is an isotropic model using M/LR = 3.13. This model is shown in all panels as a comparison. The red dotted line is the best-fit model for a constant anisotropy using β = 0.12, while the blue dashed line is a fully radial model (β = 1). The green dashed line is the model using the anisotropy as given in Eq. (16), while the green dot-dashed line is a model using the Osipkov-Merrit anisiotropy (Eq. (17)). The red solid line is a model with M/LR = 2, based on Tortora et al.’s stellar population analysis (see Sect. 5.1). Top right: MOND predictions using the “simple” and “standard” interpolation formulae. The dashed red area is an isotropic model, while the blue area indicates a fully radial model for the former interpolation. Bottom left: NFW models using c = 5 and c = 10. Parameters for each model are reported in Table 6. Bottom right: Logarithmic dark halo models. Using β = 0, β = 0.3, and MŁ anisotropy. Parameters for each model are given in Table 7. |
The simplest model is the one in which M(r) = M ⋆ (r) (i.e. no DM) and β = 0 (orbital isotropy). One can adopt the expected value for the M/L from an stellar populations analysis (which is a hypothetical value) or treat it as a free parameter in the Jeans equation solution, which is the procedure we chose here. This gives an upper limit to the stellar M/L. This model is shown as the black solid line in Fig. 8 (top left panel). It uses an M/LR = 3.13 and already gives a very good description of the dispersion profile with χ2 = 46.8 for 16 degrees of freedom, where the statistics is calculated outside 400 pc, which is the radius where the data are no longer affected by seeing.
Adopted velocity dispersion,σ, and h4 values and their respective uncertainties.
When the anisotropy was allowed to vary, we obtained almost the same M/LR of 3.11 and β = 0.12, which is a slightly better fit (red dotted line). Table 5 shows the parameters for different best-fit models. An unrealistic totally radial model (β = 1) is also shown in Fig. 8 as a comparison (blue dashed line).
From theoretical considerations (e.g. Abadi et al. 2006), elliptical galaxies are expected to have an anisotropy profile that is increasingly radially biased with growing radius. An analytical profile with this characteristic was introduced by MŁ05 as 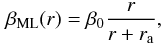 (16)with β0 ~ 0.5 and ra ~ 1.4Re when fitted to the merger simulations of Dekel et al. (2005). Another profile frequently used is the Osipkov-Merritt anisotropy model (Osipkov 1979; Merritt 1985),
(16)with β0 ~ 0.5 and ra ~ 1.4Re when fitted to the merger simulations of Dekel et al. (2005). Another profile frequently used is the Osipkov-Merritt anisotropy model (Osipkov 1979; Merritt 1985), 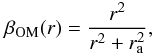 (17)where ra is a characteristic radius marking the transition to outer radially biased orbits in both cases. Since the data do not really constrain the value for ra, we fixed it to ra = 1.4 Re, using Re = 31″, from Faber et al. (1989). Even though our derived effective radius is significantly larger (see Sect. 3.1), we use this older estimation since it has been used in the previous studies of the galaxy, and also because it implies a faster transition to a radial behavior. The predictions from the Jeans equation using these anisotropies are shown in Fig. 8 (top left panel). The MŁ05 anisotropy gives a good description for the dispersion profile (green dashed line), but formally not better than the constant β = 0.12 model. It reaches a value of β = 0.33 at the outermost kinematic point. However, the Osipkov-Merritt anisotropy (green dash-dotted line) overpredicts the dispersion for the inner regions and underpredicts it for larger radii, making it less preferable as a realistic description within the context of this model.
(17)where ra is a characteristic radius marking the transition to outer radially biased orbits in both cases. Since the data do not really constrain the value for ra, we fixed it to ra = 1.4 Re, using Re = 31″, from Faber et al. (1989). Even though our derived effective radius is significantly larger (see Sect. 3.1), we use this older estimation since it has been used in the previous studies of the galaxy, and also because it implies a faster transition to a radial behavior. The predictions from the Jeans equation using these anisotropies are shown in Fig. 8 (top left panel). The MŁ05 anisotropy gives a good description for the dispersion profile (green dashed line), but formally not better than the constant β = 0.12 model. It reaches a value of β = 0.33 at the outermost kinematic point. However, the Osipkov-Merritt anisotropy (green dash-dotted line) overpredicts the dispersion for the inner regions and underpredicts it for larger radii, making it less preferable as a realistic description within the context of this model.
Comparison of different best-fit dynamical models without DM.
An interesting relation between anisotropy β and the logarithmic density slope α of a spheroidal system near equilibrium has emerged from DM simulations. Hansen & Moore (2006) found β(α) = 1 − 1.15 (1 + α/6), albeit with some scatter. This relation has also been analyzed by Mamon et al. (2006) for ellipticals formed in simulations of mergers of spirals consisting of stars, gas and DM. They found different results for the DM, but a quite similar relation for the stellar density distribution. If this were universal, the dynamical analysis of spherical systems would be greatly facilitated. We apply the above relation to NGC 7507 and calculate for our double-beta model (Eq. (4)) the logarithmic slope α = (r/j)dj(r)/dr. The resulting anisotropy profile shows a swift increase from isotropy at the center to β = 0.3 at around 500 pc, with a mild increase outwards. This behavior can be reasonably reproduced using the MŁ05 anisotropy profile with a small ra. In the context of a no-DM model, this anisotropy favors an even lower stellar M/L and underestimates the observed velocity dispersion at large radii, giving a poor fit to the data.
4.5. Including a dark halo
Even though the velocity dispersion profile up to ~90″ of NGC 7507 can satisfactorily be described by models without dark matter, the paradigm of galaxy formation requires the presence of dark halos. We therefore allow for a (cuspy) NFW profile (e.g. Navarro et al. 1996) and a (cored) logarithmic halo. In both cases we fix the stellar M/L to 3.01, therefore maximizing the contribution of the stellar component to the total mass budget (“maximum spheroid”, e.g. Weijmans et al. 2009), this is supported by the fact that the contribution of DM in the inner regions is thought to be close to negligible (e.g. Gerhard et al. 2001; Borriello et al. 2003; Mamon & Łokas 2005a).
Comparison of different best fitting dynamical models including NFW halos.
4.5.1. NFW models
The NFW profile is given by 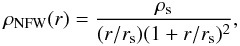 (18)where ρs and rs are a characteristic density and radius, respectively; the enclosed mass for this profile is given by
(18)where ρs and rs are a characteristic density and radius, respectively; the enclosed mass for this profile is given by 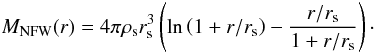 (19)We explored three models, an isotropic model, a model with a slight radial anisotropy (β = 0.3) and a model using the MŁ anisotropy with ra = 43″ as in Sect. 4.4. We excluded the possibility of tangential orbits beacuse they were inconsistent with the stars-only models. For each anisotropy, we used a set of concentrations, c = {1,1.25,1.5,...13} , which encompasses the range of concentrations found for low luminosity ellipticals (c ~ 5, Napolitano et al. 2008) and the ones found in simulations for halos of similar mass (c ~ 10, e.g. Bullock et al. 2001; Macciò et al. 2008). Concentrations are related to the characteristic density by
(19)We explored three models, an isotropic model, a model with a slight radial anisotropy (β = 0.3) and a model using the MŁ anisotropy with ra = 43″ as in Sect. 4.4. We excluded the possibility of tangential orbits beacuse they were inconsistent with the stars-only models. For each anisotropy, we used a set of concentrations, c = {1,1.25,1.5,...13} , which encompasses the range of concentrations found for low luminosity ellipticals (c ~ 5, Napolitano et al. 2008) and the ones found in simulations for halos of similar mass (c ~ 10, e.g. Bullock et al. 2001; Macciò et al. 2008). Concentrations are related to the characteristic density by 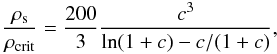 (20)where the critical density is ρcrit =
(20)where the critical density is ρcrit = 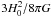 . We also set a grid of characteristic radii, rs = { 1,2,...,100 } kpc, and calculate the χ2 for each (c,rs) pair. The results can be seen in Fig. 9. 68%, 90% and 99% confidence levels correspond to Δχ2 = {2.30,4.61,9.21} (Avni 1976).
. We also set a grid of characteristic radii, rs = { 1,2,...,100 } kpc, and calculate the χ2 for each (c,rs) pair. The results can be seen in Fig. 9. 68%, 90% and 99% confidence levels correspond to Δχ2 = {2.30,4.61,9.21} (Avni 1976).
As seen in Fig. 9, we cannot constrain simultaneously c and rs, with the available data/modeling. Even though we have explored a generous range of parameters, a global minimum lies beyond the explored space. The minimum χ2 values for the isotropic and MŁ models are worse than the best-fit stars-only models, even though the models with an NFW profile include more free parameters. This is an indication that the data shows a preference for the stars-only models, or more exactly, that our assumed stellar M/LR is closer to the total M/L, which should be constant across the galaxy. The exception is the model with β = 0.3, which gives a significantly smaller χ2 than all of the no-DM models.
Since we cannot constrain simultaneously the values for c and rs, we explore the amount of DM in the NFW halos by selecting the cases c = 5 and c = 10. The NFW parameters of each halo and the assumed concentrations can be seen in Table 6. The velocity dispersion prediction for each of these models is depicted in Fig. 8 (bottom left panel).
 |
Fig. 9 χ2 for models including an NFW halo. Minimum χ2 for each model is indicated. Left panel: NFW halo and stars with isotropic distribution. Central panel: NFW halo plus stars with a radial anisotropy of β = 0.3. Right panel: NFW halo and stars following a MŁ anisotropy profile. |
The best-fit model is the one for c = 5 and β = 0.3, which gives a virial mass of 2.2 × 1011 M⊙. The c = 10 model for the same anisotropy gives a slightly worse fit and a significantly lower virial mass with 5.9 × 1010 M⊙. Even though the MŁ anisotropy should give a more realistic representation of the true orbital structure of elliptical galaxies, the mass which correspond to the best-fit scale radius is very low, although the 1 − σ level is broad with a maximum mass of 1.9 × 1010 M⊙ for c = 5. The Hansen & Moore (2006) anisotropy performs even more poorly, with even lower predicted masses and much larger χ2.
The fraction of DM within 1Re (using the value from Faber et al. 1989) is lower than 5% for all models. This number can be compared with the values found for galaxies of similar brightness studied by Weijmans et al. (2009): NGC 3379 with fDM(<Re) = 0.08 and NGC 821 with fDM(<Re) = 0.18. Even though this low value could be considered as the natural result of the minimal halo assumption, this is not exactly the case. If we were to drop this assumption and allow the stellar M/L to be a free parameter for the c = 5 and c = 10 NFW halos, we would find that the M/L diminishes at most to a value of 2.9, depending on the assumed anisotropy, reinforcing the prior assumption. DM fractions within 2Re can also be seen in Table 6.
4.5.2. Models with a logarithmic halo
Even though most, if not all, N-body simulations favor cuspy profiles, observations of dwarf and low surface brightness galaxies indicate the presence of constant density cores instead of r-1 cusps (see de Blok 2010, for a recent review). From the different types of cored profiles, we selected the logarithmic potential (Binney & Tremaine 2008), which has a density 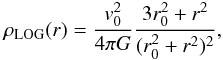 (21)and enclosed mass
(21)and enclosed mass 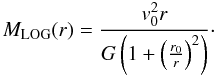 (22)The modeling procedure is similar to the one applied in the section. As for the NFW profiles, the stellar M/LR remains fixed at 3.01. A grid of parameters was then set with r0 = {1,2...80} kpc and v0 = {40,45...215} km s-1 and for each pair, the value of χ2 is calculated using Eq. (15) for the same three anisotropies as in the previous section; β = 0, β = 0.3, and β(r) following Eq. (16). The grid was later refined for the case β = 0. The best-fitting halo parameters for each studied case are given in Table 7.
(22)The modeling procedure is similar to the one applied in the section. As for the NFW profiles, the stellar M/LR remains fixed at 3.01. A grid of parameters was then set with r0 = {1,2...80} kpc and v0 = {40,45...215} km s-1 and for each pair, the value of χ2 is calculated using Eq. (15) for the same three anisotropies as in the previous section; β = 0, β = 0.3, and β(r) following Eq. (16). The grid was later refined for the case β = 0. The best-fitting halo parameters for each studied case are given in Table 7.
The isotropic case allows a light halo with a very small characteristic radius of only 25 pc. Assuming β = 0.3 the halo is much larger with r0 = 7 kpc and a circular velocity of 100 km s-1. This radial model provides a significantly tighter fit to the observed velocity dispersion. This halo is the one that gives the lowest χ2 amongst all models (with or without DM). The MŁ anisotropy allows a large range of possible halos, but giving a worse fit than the β = 0.3 case. As in the case of NFW halos, the amount of DM enclosed within one Re is minimal, again having values of less than 5% for all models. The velocity dispersion for these three best-fit models can be seen in Fig. 8 (bottom right panel).
4.6. The Gauss-Hermite parameter h4
Predictions for the Gauss-Hermite h4 profile for different models can be seen in Fig. 10, where we have followed the procedure of Łokas (2002) and related kurtosis and h4 using 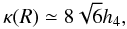 (23)(van der Marel & Franx 1993). We have considered the stars-only, NFW with c = 5 and 10, and the logarithmic cases withr isotropy and completely radial anisotropies. Although the velocity dispersion profiles are best reproduced with radial anisotropies using β = 0.3, we did not calculate their h4 predictions since they would lie between the two aforementioned models, without adding new information. As in the cases of the velocity dispersion profiles, since the light profile is affected by seeing, the model is not expected to reproduce the inner 400 pc.
(23)(van der Marel & Franx 1993). We have considered the stars-only, NFW with c = 5 and 10, and the logarithmic cases withr isotropy and completely radial anisotropies. Although the velocity dispersion profiles are best reproduced with radial anisotropies using β = 0.3, we did not calculate their h4 predictions since they would lie between the two aforementioned models, without adding new information. As in the cases of the velocity dispersion profiles, since the light profile is affected by seeing, the model is not expected to reproduce the inner 400 pc.
The measured h4 data are noisy (green circles) and all models systematically fail to reproduce its high values. We note that the K+00 data are equally noisy and reach similar high values (blue stars in Fig. 10). The difference is most evident in the inner 500 pc where the K+00 values are closer to zero and ours scatter around ~0.05. Although some systematic effect may be shifting our measurements to higher values, it can hardly be S/N (which is especially high at small radii) nor template mismatching (innermost spectra are very well-fitted using the comprehensive MILES stellar library). Perhaps the only conclusion that we can give is that the h4 data does not favor isotropic models, which predict slightly negative values for h4 (see Sect. 5.3 for an alternative explanation).
Comparison of different best-fit dynamical models using a logarithmic DM halo.
5. Discussion
5.1. Stellar M/L
The stellar M/L determines the amount of baryonic matter and thus, based on its difference from the total mass, also the fraction of dark matter. Our M/L-value is not quite consistent with what one would theoretically expect for an old, metal-rich population by comparison with published population synthesis models, but it is in agreement with literature values.
K+00 gives a central M/LB value of 5.9 for a distance of 26.9 Mpc. Since dynamically derived M/Ls are inversely proportional to distance, at our adopted distance of 23.2 Mpc this value transforms into M/LB = 6.8, which gives M/LR = 3.14 using (B − R) = 1.90 (Franx et al. 1989b) and (B − R)⊙ = 1.06 (Binney & Merrifield 1998), in excellent agreement with our value. Magorrian & Ballantyne (2001), based on kinematic data by Bertin et al. (1994), found M/LB ~ 7, somewhat higher than our value, but also in agreement considering their shorter distance (21 Mpc).
 |
Fig. 10 Kurtosis models for NGC 7507. Green circles represent our h4 measurements as given in Table 4. Blue stars are the measurements from K+00. Black, red, blue, and green lines represent the stars-only, NFW (c = 5), NFW (c = 10), and logarithmic models, with parameters described in the text, respectively. Solid lines are isotropic models, while dotted lines are fully radial models. |
The stellar M/Ls even of old elliptical galaxies are apparently not universal: Cappellari et al. (2006) find values in the range 1.5 ≲ M/LI ≲ 6.0. For NGC 7507, M/LR = 3.1 translates into M/LI = 2.42. If we only consider elliptical galaxies in the Cappellari et al. (2006) sample, that is, excluding S0 galaxies, this range would narrow to 2.3 ≲ M/LI ≲ 6.1, putting NGC 7507 among the ellipticals with the lowest M/L. This value, unless the metal abundance of NGC 7507 is distinctly subsolar, would indicate a somewhat younger galaxy, with an age around 8 Gyr for a solar abundance, which agrees with previous line-strength measurements of this galaxy (Trager et al. 1998; Ogando et al. 2008). This is unsurprising because a large fraction of isolated elliptical galaxies are known to be of younger age (Collobert et al. 2006; Reda et al. 2007), which is consistent also with simulations (Niemi et al. 2010). Tortora et al.’s (2009) stellar population models give a very similar age of 7.7 Gyr (Kroupa IMF), but a siginificantly different M/LR = 2. This value is in contradiction with the line strength analyses and with our dynamically derived M/L and would imply a huge DM content, even in the innermost parts of the galaxy (red solid line in Fig. 8, top left panel).
5.2. Dark matter?
That an isotropic model with no DM closely fits the observations nicely, does not imply that there is no DM. This situation was realized before in analyses where PNe were used as dynamical tracers (Romanowsky et al. 2003; Dekel et al. 2005, MŁ05). However, the relatively low stellar M/L-value of NGC 7507 is in line with the finding that, regardless of the situation at larger radii, the DM content in the inner region of elliptical galaxies is negligible (Gerhard et al. 2001; Mamon & Łokas 2005a; Cappellari et al. 2006). Within the framework of a spherical model, a possibility to host DM at larger radii is a radial anisotropy. It must then be a coincidence that the observed dispersion so closely follows the predictions of the photometric model under isotropy. This is a difference to the use of PNe as dynamical tracers, where the density profile of the parent population is notoriously uncertain.
Are the stellar orbits of NGC 7507 affected by a strong radial anisotropy? The comparison with the kurtosis profiles for a few models shows that a fully radial anisotropy of the stellar component can produce a consistently positive kurtosis of the observed order, although failing in the innermost regions. However, we say that with caution, since the kurtosis might also be influenced by rotation (Dekel et al. 2005).
NGC 7507 with a stellar mass of about 2 × 1011 M⊙ belongs to the most massive isolated elliptical galaxies in the simulations of Niemi et al. (2010). The dark halos in which they are embedded have predicted masses of the order of a few times 1012 M⊙ within their virial radii. Our halos from Table 6 are far from this mass, although we caution that the extrapolation to the virial radius might be uncertain (Mamon & Łokas 2005b).
5.3. Limitations of a spherical model
Even though the apparent spherical symmetry of the galaxy and the small amount of rotation give reasons to use our modeling approach, at the same time other observations may point to a more complex scenario. High h4 values could be signature of an undetected face-on disk or flattening along the line of sight (Magorrian 1999; Magorrian & Ballantyne 2001), which might also explain the failure to reproduce the h4 values when using the Łokas (2002) simplification. The second observed particularity is the rotation along the minor axis. Elliptical galaxies with this property are rare: Franx et al. (1989b) found that minor axis rotation was larger than major axis rotation in only 2 out of 22 galaxies in their sample. This behavior is a signature of triaxial galaxies (e.g. Binney 1985). Another sign of triaxiality comes from the outermost velocity along the major axis which shows a significant difference with the inner measurements. This change in the mean velocity corresponds to a sudden change in the ellipticity at the same radius (~100′′, Figs. 2 and 5).
5.4. MOND and the baryonic Tully-Fisher relation
Among the problems that MOND faces is how the Newtonian and MONDian regimes are linked. Taking this interpolation function as μ(x) = x/(1 + x) (known as “simple”, Famaey & Binney 2005), the MONDian circular velocity is 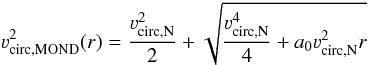 (24)(e.g. Richtler et al. 2008), where νcirc,N is the Newtonian circular velocity associated with the stellar component and
(24)(e.g. Richtler et al. 2008), where νcirc,N is the Newtonian circular velocity associated with the stellar component and 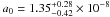 cm s-2 (Famaey et al. 2007) is the acceleration constant that separates the MOND and Newtonian realms. An alternative interpolation function, dubbed “standard”, is μ(x) = x/
cm s-2 (Famaey et al. 2007) is the acceleration constant that separates the MOND and Newtonian realms. An alternative interpolation function, dubbed “standard”, is μ(x) = x/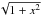 (Sanders & McGaugh 2002), for which the circular velocity is given by
(Sanders & McGaugh 2002), for which the circular velocity is given by 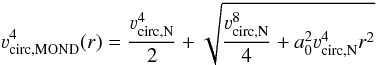 26(e.g. Samurović & Ćirković 2008). The masses associated with these circular velocities are introduced in Eq. (14) to obtain the MOND predictions for the projected velocity dispersion profile for the isotropic case, using in all cases M/L ⋆ ,R = 3. As seen in Fig. 8 (top right panel), the simple interpolation formula cannot explain the velocity dispersion profile under isotropy. The outermost measured points can only be explained under a totally radial model and only when the lowest allowed values for a0 are considered. The standard interpolation formula (green lines in the same plot) gives very similar predictions for the isotropic and radial cases for the outermost bins, and again favors a lower value for a0.
26(e.g. Samurović & Ćirković 2008). The masses associated with these circular velocities are introduced in Eq. (14) to obtain the MOND predictions for the projected velocity dispersion profile for the isotropic case, using in all cases M/L ⋆ ,R = 3. As seen in Fig. 8 (top right panel), the simple interpolation formula cannot explain the velocity dispersion profile under isotropy. The outermost measured points can only be explained under a totally radial model and only when the lowest allowed values for a0 are considered. The standard interpolation formula (green lines in the same plot) gives very similar predictions for the isotropic and radial cases for the outermost bins, and again favors a lower value for a0.
The barred spiral galaxy NGC 7513 is found at an angular distance of 18.2 arcmin from NGC 7507. In the MOND context, it is interesting to ask whether it could provide an external gravitational field which would modify the MOND phenomenology in NGC 7507. The mean of the published Tully-Fisher distances is 19.3 Mpc and thus places NGC 7513 with respect to NGC 7507 (23 Mpc) somewhat in the foreground and a separation of 4 Mpc would produce a very weak field. Adopting an inclination-corrected HI-line width of 275 km s-1 as the value for a constant MONDian rotation curve (Springob et al. 2007), the acceleration at NGC 7507 would be 6.3 × 10-13 m s-2. Assuming the same distance as for NGC 7507, the separation would be 123 kpc and the acceleration at NGC 7507 would be 2 × 10-11 m s-2. Therefore, an external field should not influence any of the MONDian dynamics of NGC 7507.
The baryonic Tully-Fisher relation (BTFR) of spiral galaxies relates circular velocity (which is a proxy for the total mass) to the baryonic content of the galaxy. This relation, which reads Mbar = 50 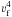 , where νf is the circular velocity in the flat part of the rotation curve, has been found to be correct over many orders of magnitude (McGaugh 2005; Trachternach et al. 2009). A tight relation between baryonic mass and circular velocities is not expected when DM is assumed to dominate the dynamics, but it finds a natural explanation under MOND (Sanders & McGaugh 2002). Similarly to spirals, early-type galaxiess have been found to follow a relation that is analogous to the Tully-Fisher relation (Gerhard et al. 2001; Magorrian & Ballantyne 2001), but since circular velocities up to a large radius are difficult to obtain, there is no surprise in finding that ellipticals follow a relation that is offset from the spiral BTFR, i.e. circular velocities are probably overestimated. For NGC 7507, we calculated the circular velocity at the outermost point with measured kinematics of 250 km s-1. Using McGaugh’s version of the BTFR, this implies a mass of 2 × 1011 M⊙. Using Eq. (6) with our preferred M/L value, we obtained 2.5 × 1011 M⊙, that is, NGC 7507 would lie somewhat above the BTFR for spirals; this appears inconsistent with previous results for other ellipticals (Gerhard et al. 2001), although consistent when all uncertainties are taken into account. We also note that the slope of 4 required by MOND remains a disputed value (see e.g. Gurovich et al. 2010).
, where νf is the circular velocity in the flat part of the rotation curve, has been found to be correct over many orders of magnitude (McGaugh 2005; Trachternach et al. 2009). A tight relation between baryonic mass and circular velocities is not expected when DM is assumed to dominate the dynamics, but it finds a natural explanation under MOND (Sanders & McGaugh 2002). Similarly to spirals, early-type galaxiess have been found to follow a relation that is analogous to the Tully-Fisher relation (Gerhard et al. 2001; Magorrian & Ballantyne 2001), but since circular velocities up to a large radius are difficult to obtain, there is no surprise in finding that ellipticals follow a relation that is offset from the spiral BTFR, i.e. circular velocities are probably overestimated. For NGC 7507, we calculated the circular velocity at the outermost point with measured kinematics of 250 km s-1. Using McGaugh’s version of the BTFR, this implies a mass of 2 × 1011 M⊙. Using Eq. (6) with our preferred M/L value, we obtained 2.5 × 1011 M⊙, that is, NGC 7507 would lie somewhat above the BTFR for spirals; this appears inconsistent with previous results for other ellipticals (Gerhard et al. 2001), although consistent when all uncertainties are taken into account. We also note that the slope of 4 required by MOND remains a disputed value (see e.g. Gurovich et al. 2010).
6. Summary and conclusions
We have obtained wide-field photometry in Kron-Cousins R and Washington C as well as new long-slit spectroscopy of the field elliptical NGC 7507 out to about ~90″, reaching farther out than previous studies.
We have measured almost no rotation along the major axis and significant rotation (Δν ~ 50 km s-1) along the minor axis (although the galaxy is almost perfectly circular). The velocity dispersion profile of the galaxy shows a rapid decline along both axes.
We have performed a spherical Jeans analysis to find the mass profile that most closely represents the projected velocity dispersion profile. When assuming isotropy, a radially constant M/LR ratio of 3.1 would be sufficient to reproduce the velocity dispersions. This value corresponds, if solar abundance is assumed, to an age in the range 8–10 Gyr. DM halos can be included in the isotropic case, but provide significantly poorer fits than the stars-only models. When we allowed for radial anisotropies and cored/cuspy dark halos, we were able to improve the fit to the velocity dispersion profile marginally. This contradicts the result od Kronawitter et al. (2000) and Gerhard et al. (2001) who found this galaxy to be one of the best examples for hosting a dark halo. It is however in line with the results of Magorrian & Ballantyne (2001) who also found no clear evidence of DM.
The most massive NFW halo, using β = 0.3 and a concentration parameter of 5, has a scale rs = 25 kpc, implying a virial mass of only 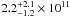 M⊙. Modified Newtonian dynamics (MOND), if applied straightforwardly, predicts velocity dispersions that are too high.
M⊙. Modified Newtonian dynamics (MOND), if applied straightforwardly, predicts velocity dispersions that are too high.
It appears that NGC 7507 is a very interesting case in the discussion of DM in elliptical galaxies. It remains to be seen whether non-spherical models based on an extended data set, perhaps including also PNe and/or globular clusters, would provide different results.
Online material
T1 CTIO/MOSAIC surface photometry of NGC 7507.
Major axis kinematics of NGC 7507.
Minor axis kinematics of NGC 7507.
Acknowledgments
We thank the referee, Dr. Gary Mamon, for a careful and insightful report. We thank Roberto Saglia for providing the kinematic measurements from Kronawitter et al. (2000) in electronic form. We thank Srdjan Samurović and Michael Hilker for making available their Linux compatible versions of R. van der Marel’s code; Michele Cappellari and Anne-Marie Weijmans for useful advice on the usage of pPXF. R.S. acknowledges support from a CONICYT doctoral fellowship and the ESO Studentship Program. T.R. acknowledges support from the Chilean Center for Astrophysics, FONDAP Nr. 15010003, and from FONDECYT project Nr. 1100620. L.P.B. acknowledges support from CONICET, Agencia Nacional de Promoción Científica y Tecnológica, and Universidad Nacional de La Plata (Argentina). A.J.R. was supported by National Science Foundation grants AST-0808099 and AST-0909237.
References
- Abadi, M. G., Navarro, J. F., & Steinmetz, M. 2006, MNRAS, 365, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y. 1976, ApJ, 210, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Bedregal, A. G., Aragón-Salamanca, A., Merrifield, M. R., & Milvang-Jensen, B. 2006, MNRAS, 371, 1912 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Beifiori, A., Maraston, C., Thomas, D., & Johansson, J. 2011, A&A, 531, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, G., Bertola, F., Buson, L. M., et al. 1994, A&A, 292, 381 [NASA ADS] [Google Scholar]
- Binney, J. 1985, MNRAS, 212, 767 [NASA ADS] [Google Scholar]
- Binney, J., & Mamon, G. A. 1982, MNRAS, 200, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Merrifield, M. 1998, Galactic Astronomy (Princeton University Press) [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, second edition (Princeton University Press) [Google Scholar]
- Borriello, A., Salucci, P., & Danese, L. 2003, MNRAS, 341, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Bacon, R., Bureau, M., et al. 2006, MNRAS, 366, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Collobert, M., Sarzi, M., Davies, R. L., Kuntschner, H., & Colless, M. 2006, MNRAS, 370, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G. 2010, Adv. Astron., 2010, 5 [Google Scholar]
- de Lorenzi, F., Gerhard, O., Coccato, L., et al. 2009, MNRAS, 395, 76 [NASA ADS] [CrossRef] [Google Scholar]
- de Souza, R. E., Gadotti, D. A., & dos Anjos, S. 2004, ApJS, 153, 411 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., & Corwin, J. R. 1976, in Second reference catalogue of bright galaxies (Austin: University of Texas Press), 0 [Google Scholar]
- Dekel, A., Stoehr, F., Mamon, G. A., et al. 2005, Nature, 437, 707 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dirsch, B., Richtler, T., Geisler, D., et al. 2003, AJ, 125, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Dirsch, B., Schuberth, Y., & Richtler, T. 2005, A&A, 433, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doherty, M., Arnaboldi, M., Das, P., et al. 2009, A&A, 502, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Douglas, N. G., Napolitano, N. R., Romanowsky, A. J., et al. 2007, ApJ, 664, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Wegner, G., Burstein, D., et al. 1989, ApJS, 69, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & Binney, J. 2005, MNRAS, 363, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., Gentile, G., Bruneton, J., & Zhao, H. 2007, Phys. Rev. D, 75, 063002 [NASA ADS] [CrossRef] [Google Scholar]
- Forestell, A. D., & Gebhardt, K. 2010, ApJ, 716, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Franx, M., Illingworth, G., & Heckman, T. 1989a, ApJ, 344, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Franx, M., Illingworth, G., & Heckman, T. 1989b, AJ, 98, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Geisler, D. 1996, AJ, 111, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O. E. 1993, MNRAS, 265, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O., Kronawitter, A., Saglia, R. P., & Bender, R. 2001, AJ, 121, 1936 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Hansen, L., Jorgensen, H. E., et al. 1994, A&AS, 104, 179 [NASA ADS] [Google Scholar]
- Graham, A. W., & Driver, S. P. 2005, PASA, 22, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Gurovich, S., Freeman, K., Jerjen, H., Staveley-Smith, L., & Puerari, I. 2010, AJ, 140, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, S. H., & Moore, B. 2006, New A, 11, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, J. B., Tonry, J. L., Barris, B. J., et al. 2003, ApJ, 583, 712 [Google Scholar]
- Kelson, D. D., Zabludoff, A. I., Williams, K. A., et al. 2002, ApJ, 576, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Kronawitter, A., Saglia, R. P., Gerhard, O., & Bender, R. 2000, A&AS, 144, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lauberts, A., & Valentijn, E. A. 1989, The surface photometry catalogue of the ESO-Uppsala galaxies [Google Scholar]
- Lima Neto, G. B., Gerbal, D., & Márquez, I. 1999, MNRAS, 309, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas, E. L. 2002, MNRAS, 333, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Macciò, A. V., Dutton, A. A., & van den Bosch, F. C. 2008, MNRAS, 391, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J. 1999, MNRAS, 302, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., & Ballantyne, D. 2001, MNRAS, 322, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., & Łokas, E. L. 2005a, MNRAS, 362, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., & Łokas, E. L. 2005b, MNRAS, 363, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., Łokas, E., Dekel, A., Stoehr, F., & Cox, T. J. 2006, in EAS Pub. Ser. 20, ed. G. A. Mamon, F. Combes, C. Deffayet, & B. Fort, 139 [Google Scholar]
- McGaugh, S. S. 2005, ApJ, 632, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez, R. H., Teodorescu, A. M., Kudritzki, R.-P., & Burkert, A. 2009, ApJ, 691, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 1985, MNRAS, 214, 25P [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Coccato, L., et al. 2008, in IAU Symp. 244, ed. J. Davies, & M. Disney, 289 [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Coccato, L., et al. 2009, MNRAS, 393, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Capaccioli, M., et al. 2010, MNRAS, 1835 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Niemi, S., Heinämäki, P., Nurmi, P., & Saar, E. 2010, MNRAS, 405, 477 [NASA ADS] [Google Scholar]
- Ogando, R. L. C., Maia, M. A. G., Pellegrini, P. S., & da Costa, L. N. 2008, AJ, 135, 2424 [NASA ADS] [CrossRef] [Google Scholar]
- Osipkov, L. P. 1979, Soviet Astron. Lett., 5, 42 [Google Scholar]
- Poulain, P., & Nieto, J.-L. 1994, A&AS, 103, 573 [NASA ADS] [Google Scholar]
- Proctor, R. N., Forbes, D. A., Romanowsky, A. J., et al. 2009, MNRAS, 398, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Prugniel, P., & Simien, F. 1997, A&A, 321, 111 [NASA ADS] [Google Scholar]
- Pu, S. B., Saglia, R. P., Fabricius, M. H., et al. 2010, A&A, 516, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reda, F. M., Proctor, R. N., Forbes, D. A., Hau, G. K. T., & Larsen, S. S. 2007, MNRAS, 377, 1772 [NASA ADS] [CrossRef] [Google Scholar]
- Richtler, T., Schuberth, Y., Hilker, M., et al. 2008, A&A, 478, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richtler, T., Salinas, R., Misgeld, I., et al. 2011, A&A, 531, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanowsky, A. J., Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 301, 1696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Romanowsky, A. J., Strader, J., Spitler, L. R., et al. 2009, AJ, 137, 4956 [NASA ADS] [CrossRef] [Google Scholar]
- Samurović, S., & Ćirković, M. M. 2008, A&A, 488, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samurović, S., & Danziger, I. J. 2005, MNRAS, 363, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H., & McGaugh, S. S. 2002, ARA&A, 40, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schuberth, Y., Richtler, T., Dirsch, B., et al. 2006, A&A, 459, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sersic, J. L. 1968, Atlas de galaxias australes, ed. J. L. Sersic [Google Scholar]
- Shapiro, K. L., Cappellari, M., de Zeeuw, T., et al. 2006, MNRAS, 370, 559 [NASA ADS] [Google Scholar]
- Springob, C. M., Masters, K. L., Haynes, M. P., Giovanelli, R., & Marinoni, C. 2007, ApJS, 172, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Statler, T. S., & Smecker-Hane, T. 1999, AJ, 117, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Tal, T., van Dokkum, P. G., Nelan, J., & Bezanson, R. 2009, AJ, 138, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Teodorescu, A. M., Méndez, R. H., Bernardi, F., Riffeser, A., & Kudritzki, R. P. 2010, ApJ, 721, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, J., Saglia, R. P., Bender, R., et al. 2007, MNRAS, 382, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Tortora, C., Napolitano, N. R., Romanowsky, A. J., Capaccioli, M., & Covone, G. 2009, MNRAS, 396, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Trachternach, C., de Blok, W. J. G., McGaugh, S. S., van der Hulst, J. M., & Dettmar, R. 2009, A&A, 505, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trager, S. C., Worthey, G., Faber, S. M., Burstein, D., & Gonzalez, J. J. 1998, ApJS, 116, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van der Marel, R. P. 1994, MNRAS, 270, 271 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., & Franx, M. 1993, ApJ, 407, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Weijmans, A.-M., Cappellari, M., Bacon, R., et al. 2009, MNRAS, 1006 [Google Scholar]
- Wu, X., Zhao, H., Famaey, B., et al. 2007, ApJ, 665, L101 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison between the different measurements of the velocity dispersion profile of the major axis of NGC 7507 as described in the text. |
| In the text | |
 |
Fig. 2 CTIO/MOSAIC surface photometry of NGC 7507. a) Ellipticity profile. b) C − R color profile. c) R surface brightness profile (black circles) and R surface photometry from Franx et al. (1989b) (filled red squares). The solid red line is the fit of a double β model to our data. Residuals can be seen in panel d). |
| In the text | |
 |
Fig. 3 Surface brightness profile of NGC 7507. The green dots indicate the R photometry in units of L⊙ pc-2. The dashed blue lines represent the two Sersic profiles, while the solid blue line is their sum. The red solid line represents the double β model. |
| In the text | |
 |
Fig. 4 C − R color image of NGC 7507 based on the short exposures. Image has been median smoothed in 3 × 3 pixel boxes. Image size is 2′ × 2′. |
| In the text | |
 |
Fig. 5 Major axis kinematics of NGC 7507, as extracted with pPXF (see text). a) Hermite coefficient h4 profile, b) h3 profile, both panels show a dashed line at the zero level for comparison, c) velocity dispersion. The horizontal error bars show the regions across which the spatial binning was done (shown only in this panel, but valid for all four). The vertical dashed strip indicates a gap between the detectors in which no measurements are possible, d) rotation profile. For all panels, open black circles are our data, red solid squares are from K+00, solid green circles are from Franx et al. (1989a), and blue open squares come from Bertin et al. (1994). |
| In the text | |
 |
Fig. 6 Minor axis kinematics of NGC 7507. The vertical dashed strips show the positions of the gaps between detectors and two interloping background galaxies, which were masked in the spatial binning process. Symbols are the same as in Fig. 5. |
| In the text | |
 |
Fig. 7 A comparsion between the enclosed luminosities of the double β profile (dashed blue line) and the double Sersic profile (red solid line), normalized to the double Sersic total luminosity. The arrow indicates the last spectroscopic point measured on the major axis. |
| In the text | |
 |
Fig. 8 Dynamical models of NGC 7507. Black circles indicate in all panels the line-of-sight velocity dispersion. All models are given outside of 400 pc, where the luminosity model is unaffected by seeing. Top left: stars-only models. The black solid line is an isotropic model using M/LR = 3.13. This model is shown in all panels as a comparison. The red dotted line is the best-fit model for a constant anisotropy using β = 0.12, while the blue dashed line is a fully radial model (β = 1). The green dashed line is the model using the anisotropy as given in Eq. (16), while the green dot-dashed line is a model using the Osipkov-Merrit anisiotropy (Eq. (17)). The red solid line is a model with M/LR = 2, based on Tortora et al.’s stellar population analysis (see Sect. 5.1). Top right: MOND predictions using the “simple” and “standard” interpolation formulae. The dashed red area is an isotropic model, while the blue area indicates a fully radial model for the former interpolation. Bottom left: NFW models using c = 5 and c = 10. Parameters for each model are reported in Table 6. Bottom right: Logarithmic dark halo models. Using β = 0, β = 0.3, and MŁ anisotropy. Parameters for each model are given in Table 7. |
| In the text | |
 |
Fig. 9 χ2 for models including an NFW halo. Minimum χ2 for each model is indicated. Left panel: NFW halo and stars with isotropic distribution. Central panel: NFW halo plus stars with a radial anisotropy of β = 0.3. Right panel: NFW halo and stars following a MŁ anisotropy profile. |
| In the text | |
 |
Fig. 10 Kurtosis models for NGC 7507. Green circles represent our h4 measurements as given in Table 4. Blue stars are the measurements from K+00. Black, red, blue, and green lines represent the stars-only, NFW (c = 5), NFW (c = 10), and logarithmic models, with parameters described in the text, respectively. Solid lines are isotropic models, while dotted lines are fully radial models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


