| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 12 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201117544 | |
| Published online | 04 January 2012 | |
Dielectronic recombination data for dynamic finite-density plasmas
XIV. The aluminum isoelectronic sequence
1
Department of PhysicsWestern Michigan University,
Kalamazoo,
MI
49008,
USA
2
Department of Physics, University of Strathclyde,
Glasgow
G4 0NG,
UK
e-mail: gorczyca@wmich.edu
Received:
22
June
2011
Accepted:
7
October
2011
Context. A comprehensive study of dielectronic recombination (DR) for the aluminum-like isoelectronic sequence has been completed.
Aims. Total and final-state resolved DR rate coefficients for the ground and metastable initial levels of 17 ions between Si ii and Zn xviii are presented.
Methods. Within an isolated-resonance, distorted-wave (IPIRDW) approximation, multiconfiguration Breit-Pauli (MCBP) calculations are carried out for the total and partial DR rate coefficients of Al-like ions. Both Δnc = 0 and Δnc = 1 core-excitations are included, using LS-coupled and intermediate-coupling (IC) schemes.
Results. The inaccuracies of earlier empirical data and/or LS-coupling calculations, particularly at lower temperatures characteristic of photoionized plasmas, is demonstrated by comparison with present, state-of-the-art IC DR rate coefficients. Fine-structure effects are found to increase the DR rate coefficient at low temperatures and decrease it at high temperatures, rendering earlier LS calculations incomplete. Good agreement is found between present IC results and experimental measurements.
Key words: plasmas / atomic processes / scattering / atomic data
© ESO, 2012
1. Introduction
Cosmic gases are ionized primarily via two mechanisms: collisional ionization and photoionization. The former process dominates within, for example, stars, supernova remnants, and interstellar and intergalactic media, while the latter is predominant in H ii regions, planetary nebulae, and active galactic nuclei. In collisionally ionized gas the ionization is primarily due to electron impact ionization, hence the ions are formed at temperatures kT corresponding to roughly half of their ionization potential (e.g., see Bryans et al. 2006). By contrast, in photoionized plasmas the ions are formed at substantially lower temperatures kT than the characteristic energies of the ionizing photons (Ferland et al. 1998; Kallman & Bautista 2001). Thus ionization balance is achieved over very different ranges in temperature in collisionally ionized and photoionized gases.
DR is the dominant electron-ion recombination process for most of the ions found in low density photoionized plasmas and low-to-medium density electron collisionally ionized plasmas (Arnaud & Raymond 1992; Arnaud & Rothenflug 1985; Kallman et al. 1996). Computer codes developed for modeling photoionized plasmas include CLOUDY (Ferland et al. 1998) and XSTAR (Kallman & Bautista 2001). For electron collisionally ionized plasmas the CHIANTI code (Landi et al. 2006), for instance, is used to model spectral emission while ADAS (Summers 2003) is used to carry-out spectral diagnostics, mainly for magnetic fusion plasmas. These modeling codes require accurate DR rate coefficients for calculating reliable ionization balance, thermal structure, and line emissions of cosmic plasmas. As an example, recent predictions of the collisional ionization equilibrium abundances of iron ions (Dere et al. 2009), using new DR rate coefficients computed by Badnell (2006b), found large differences from ionic fractions determined using the previously recommended DR data (Mazzotta et al. 1998), emphasizing the importance of using state-of-the-art results versus older, unreliable data.
Available data for the aluminum-like isoelectronic sequence.
In order to produce an up-to-date, reliable set of DR data for all ions relevant to the modeling of astrophysical and laboratory plasmas, Badnell et al. (2003) initiated a program to calculate accurate total and partial DR rate coefficients from both ground and metastable initial states of all ionization stages of all ions up through Zn. Partial final-state resolved rate coefficients are necessary for collisional–radiative modeling at densities found in magnetic fusion plasmas and some astrophysical sources such as the broad line region (BLR) of AGNs. Data for metastable initial states are necessary to model plasmas whose characteristic time-evolution is comparable with the lifetime of the metastables, i.e. the metastables are not in quasi-static equilibrium with the ground level. State-of-the-art MCBP calculations have been performed and data assembled for the hydrogenic (Badnell 2006a), helium-like (Bautista & Badnell 2007), lithium-like (Colgan et al. 2004), beryllium-like (Colgan et al. 2003), boron-like (Altun et al. 2004), carbon-like (Zatsarinny et al. 2004b), nitrogen-like (Mitnik & Badnell 2004), oxygen-like (Zatsarinny et al. 2003), fluorine-like (Zatsarinny et al. 2006), neon-like (Zatsarinny et al. 2004a), sodium-like (Altun et al. 2006), and magnesium-like (Altun et al. 2007) isoelectronic sequences; for the argon-like sequence, total DR rate coefficients from the ground state have also been computed (Nikolić et al. 2010). Radiative recombination (RR) rate coefficients have also been calculated by Badnell (2006d) for all isoelectronic sequences up to magnesium-like ions. However, no systematic, state-of-the-art calculations have been performed for the aluminum-like isoelectronic sequence, and yet these ions are also abundant in astrophysical plasmas. For example, lines of Si ii, Ar vi, and Ca viii have been observed with high-resolution by the Solar and Heliospheric Observatory (SoHO) (Curdt et al. 2001, 2004; Landi et al. 2004). Thus there is a need for an up-to-date, reliable database for this system. The purpose of the present paper is to report on a detailed investigation of DR for this sequence and the production of new, accurate DR rate coefficients for aluminum-like ions.
Radial scaling parameters used in the present study for Δnc = 0 core-excitations for the aluminum-like isoelectronic sequence.
2. Existing aluminum-like DR data
The aluminum-like DR rate coefficients that are presently being used as input for the
modeling codes such as CLOUDY, XSTAR, and CHIANTI have been taken from the recommended
database of Mazzotta et al. (1998), which is a
compilation of the most reliable DR data available at that time, with interpolation and/or
extrapolation of data to ionization stages for which no explicit calculations existed, as
summarized in Table 1. The first calculations of DR
rate coefficients for aluminum-like ions were carried out by Jacobs et al. (1977a,b, 1979, 1980) for
Si ii, S iv, Ca viii, Fe xiv, and Ni xvi
using an uncoupled angular momentum description of DR. In this simplified model, the
autoionization rates were obtained from the threshold values of the partial-wave
electron-impact excitation cross sections for the corresponding ions by means of the
quantum-defect theory relationship between these values. The excitation cross sections were
obtained in the distorted-wave approximation and only dipole 3s−3p and 3p−3d transitions
were included. In addition, radiative decay of autoionizing states was approximated as the
ionic core radiative decay rate. A single fitting formula for all temperatures
Tand all ionizations stages q
was then developed by Mewe et al. (1980) based in
part on the computed data for Fe xiv and Si ii by Jacobs et al. and in
part on the data of Ansari et al. (1970). However,
this q-scaling is based on the Burgess formula parameterization (Burgess 1965) and fails to account for the highly
non-hydrogenic behavior of the rate coefficient at low q. A more accurate
parameterization was produced by Shull &
Van Steenberg (1982) using a two-peak fit formula
 , where the
ci and
Ei were obtained from a least-squares fit
to the rate coefficients of Jacobs et al. for Si ii, S iv,
Ca viii, Fe xiv, and Ni xvi, and these parameters were then
interpolated to obtain similar fitting coefficients for Ar vi. Using the fits of
Shull & Van Steenberg (1982), a similar
parameterization was obtained by interpolation for P iii, Cl v,
K vii, Ti x, Cr xii, Mn xiii, and Co xv
(Landini & Monsignori Fossi 1991).
, where the
ci and
Ei were obtained from a least-squares fit
to the rate coefficients of Jacobs et al. for Si ii, S iv,
Ca viii, Fe xiv, and Ni xvi, and these parameters were then
interpolated to obtain similar fitting coefficients for Ar vi. Using the fits of
Shull & Van Steenberg (1982), a similar
parameterization was obtained by interpolation for P iii, Cl v,
K vii, Ti x, Cr xii, Mn xiii, and Co xv
(Landini & Monsignori Fossi 1991).
Explicit DR calculations for S iv were also performed within an LS-coupling, distorted-wave approximation by Badnell (1991), using AUTOSTRUCTURE (Badnell 1986, 1997), as is implemented in the present study, and by Al-Mulhem & Nasser (1992), using Cowan’s code (Cowan 1981), considering only the 3s → 3p excitations. Then a series of LSR-matrix calculations was performed for Si ii and S iv (Nahar & Pradhan 1995; Nahar 1996), and for Ar vi, Ca viii, and Fe xiv (Nahar 2000). DR rate coefficients for Si ii and S iv were also determined by Aldrovandi & Péquignot (1973) using the Burgess formula (Burgess 1965), and a low-resonance (i.e., low-temperature) rate coefficient was obtained by Nussbaumer & Storey (1986).
Such was the status of available aluminum-like DR rate coefficients when the database of Mazzotta et al. (1998) was compiled. In most cases, that data was ultimately derived from the LS calculations of Jacobs et al. (1977a,b, 1979, 1980), which were fit by Shull & Van Steenberg (1982) for even-numbered nuclei (and interpolated for Ar vi), and then interpolated for odd-numbered nuclei by Landini & Monsignori Fossi (1991) – see Table 1. (These data were also extrapolated to Cu xvii and Zn xviii by Mazzitelli & Mattioli 2002.) However, for Si ii and S iv, Mazzotta et al. (1998) chose to incorporate the R-matrix results of Nahar & Pradhan (1995) and Nahar (1996). All of the compiled results were thus based on simpler LS calculations that, as we will see, did not include all of the important physics required for aluminum-like ions, especially the effects of fine-structure splitting.
Since the compilation of Mazzotta et al. (1998), the only aluminum-like DR data produced has been, first, the configuration-averaged distorted-wave (CADW) results of Loch et al. (2007) for Ar vi, and, importantly, the storage ring experimental results of Schmidt et al. (2006) for Fe xiv, with accompanying calculations by Badnell (2006c). These latter calculations were performed using the multi-configuration Breit-Pauli code AUTOSTRUCTURE, including important configuration-interaction and fine-structure splitting effects, as was verified by the good agreement between experimental and theoretical DR rate coefficients. The purpose of the present study is to compute DR rate coefficients for the entire aluminum-like isoelectronic sequence using the same methodology as was implemented by Badnell (2006c), as described in the next section, and thus to create a new DR database for this isoelectronic sequence.
3. Theory
Since the more in-depth details of our calculations have already been described by Badnell et al. (2003), we only outline the main points here. DR calculations are performed with the AUTOSTRUCTURE code (Badnell 1986, 1997; Badnell & Pindzola 1989), a multi-configuration Breit-Pauli (MCBP) implementation within an independent processes and isolated resonance distorted-wave (IPIRDW) approximation. This code is based on lowest order perturbation theory, where both the electron-electron and electron-photon interactions are treated to first order. Energy levels and radiative and autoionization rates were calculated in LS- and IC-coupling (MCBP) approximations.
For the initial atomic structure, we follow the same methodology used in Badnell (2006c). A basis consisting of the 3s23p, 3s3p2, 3s23d, 3p3, 3s3p3d, 3p23d, 3s3d2, and 3p3d2 configurations was used to describe the aluminum target states. Optimized radial orbitals were determined by varying the scaling parameters λ3ℓ in model STO potentials (Burgess et al. 1989) and including the mass-velocity and Darwin corrections. The values of the radial scaling parameters for the 1s, 2s, and 2p closed-core orbitals were fixed at the default value of 1.0 whereas the λ3ℓ values were optimized and yielded the values listed in Table 2. Distorted wave calculations were performed to generate the continuum εℓ and bound nℓ (n > 3) orbitals. The (N + 1)-electron basis configurations were then constructed by coupling an εℓ or nℓ orbital to the N-electron target configurations. Autoionization and radiative rates (electric dipole) were determined from wave functions constructed using all such (N + 1)-electron configurations and then used to calculate the DR cross sections and rate coefficients for the desired aluminum-like ion.
The DR process for an arbitrary aluminum-like ion I, with a degree of
ionization q, for Δnc = 0 core excitation
(3s → 3p, 3s → 3d, and 3p → 3d) can be described as 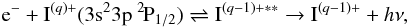 (1)where
the doubly-excited intermediate resonance states
I(q − 1) +∗∗ included are
3s23pnℓ, 3s3p2nℓ,
3s23dnℓ, 3p3nℓ,
3s3p3dnℓ, 3p23dnℓ,
3s3d2nℓ, and 3p3d2nℓ. Values for
the principal quantum number n were included up to n = 55,
and a quantum-defect approximation was used for higher values 56 ≤ n ≤ 1000
(Badnell et al. 2003), while the values for the
orbital quantum number were included up to ℓ ≤ 13. For
Δnc = 1, only 3 → 4
(3s → 4ℓ′,3p → 4ℓ′,
and 3d → 4ℓ′) core-excitations were considered, and we used
3s24ℓ′, 3s3p4ℓ′, and
3p24ℓ′ configurations (with
0 ≤ ℓ′ ≤ 3) in addition to those used for
Δnc = 0. These 20 configurations gave rise to 295 target
levels. Other values included were ℓ ≤ 6 and n ≤ 55, with
a quantum-defect approximation for higher n ≤ 1000.
(1)where
the doubly-excited intermediate resonance states
I(q − 1) +∗∗ included are
3s23pnℓ, 3s3p2nℓ,
3s23dnℓ, 3p3nℓ,
3s3p3dnℓ, 3p23dnℓ,
3s3d2nℓ, and 3p3d2nℓ. Values for
the principal quantum number n were included up to n = 55,
and a quantum-defect approximation was used for higher values 56 ≤ n ≤ 1000
(Badnell et al. 2003), while the values for the
orbital quantum number were included up to ℓ ≤ 13. For
Δnc = 1, only 3 → 4
(3s → 4ℓ′,3p → 4ℓ′,
and 3d → 4ℓ′) core-excitations were considered, and we used
3s24ℓ′, 3s3p4ℓ′, and
3p24ℓ′ configurations (with
0 ≤ ℓ′ ≤ 3) in addition to those used for
Δnc = 0. These 20 configurations gave rise to 295 target
levels. Other values included were ℓ ≤ 6 and n ≤ 55, with
a quantum-defect approximation for higher n ≤ 1000.
In the IPIRDW approximations, the partial DR rate coefficients
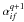 from an initial metastable level i into a final level f
are given by
from an initial metastable level i into a final level f
are given by 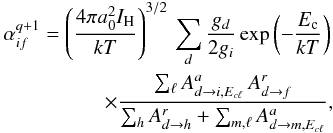 (2)where
gd is the statistical weight of the
(N + 1)-electron doubly-excited resonance state d,
gi is the statistical weight of the
N-electron target state and the autoionization
Aa and radiative
Ar rates are in inverse seconds. Here,
Ec is the energy of the continuum electron of angular momentum
ℓ, which is fixed by the position of the resonances, and
IH is the ionization potential energy of the hydrogen atom,
k is the Boltzmann constant, T is the electron
temperature, and
(2)where
gd is the statistical weight of the
(N + 1)-electron doubly-excited resonance state d,
gi is the statistical weight of the
N-electron target state and the autoionization
Aa and radiative
Ar rates are in inverse seconds. Here,
Ec is the energy of the continuum electron of angular momentum
ℓ, which is fixed by the position of the resonances, and
IH is the ionization potential energy of the hydrogen atom,
k is the Boltzmann constant, T is the electron
temperature, and  cm3. Partial DR rate coefficients from the ground and metastable states are
tabulated according to the ADAS (Summers 2003)
adf09 format.
cm3. Partial DR rate coefficients from the ground and metastable states are
tabulated according to the ADAS (Summers 2003)
adf09 format.
The total (Δnc = 0 plus Δnc = 1) DR
rate coefficients were fitted using the formula 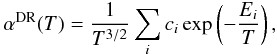 (3)where T
and Ei are in units of temperature (K) and the
rate coefficients αDR are in units of
cm3 s-1.
(3)where T
and Ei are in units of temperature (K) and the
rate coefficients αDR are in units of
cm3 s-1.
For our RR calculations, the same procedure used by Badnell (2006d) is employed here. Briefly, the aluminum-like targets were described by the eight configurations that were used in the DR calculations for the n = 3 complex, and capture to all nℓ up to n ≤ 1000 and ℓ ≤ 200 were included (with ℓ ≥ 4 treated hydrogenically).
 |
Fig. 1 Present Maxwellian-averaged DR and RR rate coefficients for Si ii-Ca viii ions (excluding S iv − see Fig. 4): red solid curve, present IC; blue solid curve, present LS; green solid curve, previous recommended compilation (Mazzotta et al. 1998); gray dashed curve, present RR rate coefficient; (a) black dashed curve, Burgess formula (Aldrovandi & Péquignot 1973); (b) black squares, LS (Jacobs et al. 1979); (c) black dash dotted curve, empirical formula (Mewe et al. 1980); (d) open circles, fitted data (Shull & Van Steenberg 1982); (e) red circles, extrapolated fits (Landini & Monsignori Fossi 1991); (f) magenta solid curve, LSR-matrix, RR + DR (Nahar & Pradhan 1995; Nahar 1996, 2000); (i) black dotted curve, low temperature data (Nussbaumer & Storey 1986); and (j) pink dotted curve, configuration-average distorted-wave results (Loch et al. 2007). |
 |
Fig. 2 Present Maxwellian-averaged DR and RR rate coefficients for Sc ix-Fe xiv ions: red solid curve, present IC; blue solid curve, present LS; green solid curve, previous recommended compilation (Mazzotta et al. 1998); gray dashed curve, present RR rate coefficient; (b) black squares, LS (Jacobs et al. 1979); (c) black dash dotted curve, empirical formula (Mewe et al. 1980); (d) open circles, fitted data (Shull & Van Steenberg 1982); (e) red circles, extrapolated fits (Landini & Monsignori Fossi 1991); (f) magenta solid curve, LSR-matrix, RR + DR (Nahar 2000); (g) black solid curve, IC AUTOSTRUCTURE (Badnell 2006c); and (l) blue dashed curve, experimental measurements (Schmidt et al. 2006). |
 |
Fig. 3 Present Maxwellian-averaged DR and RR rate coefficients for Co xv-Zn xviii ions: red solid curve, present IC; blue solid curve, present LS; green solid curve, previous recommended compilation (Mazzotta et al. 1998); gray dashed curve, present RR rate coefficient; (b) black squares, LS (Jacobs et al. 1979); (c) black dash dotted curve, empirical formula (Mewe et al. 1980); (d) open circles, fitted data (Shull & Van Steenberg 1982); (e) red circles, extrapolated fits (Landini & Monsignori Fossi 1991); and (k) blue circles, extrapolated fit (Mazzitelli & Mattioli 2002). |
The total RR rate coefficients were fitted using the formula (Verner & Ferland 1996) ![\begin{equation} \label{Eq:Fit:RR} \alpha^{{\rm RR}}(T) = A \, \sqrt{T_0/T} \, \left[ \left( 1 + \sqrt{T/T_{0}} \right)^{1-B} \left(1 + \sqrt{T/T_{1}} \right)^{1+B} \right]^{-1} , \end{equation}](/articles/aa/full_html/2012/01/aa17544-11/aa17544-11-eq99.png) (4)where, for low-charge ions,
we replace B by (Gu 2003)
(4)where, for low-charge ions,
we replace B by (Gu 2003)
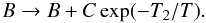 (5)Here,
T0,1,2 are in units of
temperature (K), the rate coefficients αRR(T)
are in units of cm3 s-1, A has units of
cm3 s-1, and B and C are
dimensionless. Partial RR rate coefficients are tabulated according to the ADAS (Summers 2003) adf48 format.
(5)Here,
T0,1,2 are in units of
temperature (K), the rate coefficients αRR(T)
are in units of cm3 s-1, A has units of
cm3 s-1, and B and C are
dimensionless. Partial RR rate coefficients are tabulated according to the ADAS (Summers 2003) adf48 format.
4. Results
Using AUTOSTRUCTURE as described above, we computed DR rate coefficients, in both LS-coupled and Breit-Pauli, intermediate-coupled (IC) approximations, for the entire aluminum-like isoelectronic sequence. These results are compared to all other available data in Figs. 1−4. Also indicated in these figures are the regions of maximum abundance in both photoionized and collisionally-ionized plasmas. The photoionized zones were calculated by us using CLOUDY (v08.00; Ferland et al. 1998), whereas the collisionally ionized zones were obtained based on the calculations of Bryans et al. (2009), assuming the fractional abundance of the target ions are 10% of their peak values in each case.
We first focus on the case of S iv, since several independent LS-coupled calculations have been reported for this ion. It is seen in an expanded view (see Fig. 4) that our present LS results are in excellent agreement with the earlier LS AUTOSTRUCTURE results of Badnell (1991), as is expected. These results are also in good agreement with those of Jacobs et al. (1979), and thus with the fitted curve of Shull & Van Steenberg (1982). We find fair agreement with the results of Al-Mulhem & Nasser (1992) up to about the peak of either rate coefficient; however, the high-temperature tail of the Al-Mulhem & Nasser (1992) results is appreciably lower than our present results, presumably due to their only including the 3s → 3p core excitations and neglecting the 3p → 3d excitations that are more important at higher energies.
Also shown are the LSR-matrix results (Nahar & Pradhan 1995; Nahar 1996, 2000) for the coherent sum of DR and RR; a DR rate coefficient was inferred from these and then used as data in the compilation of Mazzotta et al. (1998). Aside from the low-temperature difference due to their inclusion of RR (we show our present RR results for comparison), these R-matrix calculations yielded a peak rate coefficient that is significantly lower than all other LS calculation peaks – their peak is only 74% of our present LS peak. Although the reason for such a large discrepancy is unclear, it should be pointed out that the use of the R-matrix method for computing DR cross sections is problematic in that radiation damping effects, which were not included in the calculations of Nahar & Pradhan (1995); Nahar (1996, 2000), need to be considered, and, furthermore, sufficient resolution of resonances is required – see Gorczyca & Badnell (1997) and Gorczyca et al. (2002) for further discussions.
It can be seen that neither the Burgess formula results of Aldrovandi & Péquignot (1973) nor the parameterized Burgess-type expression of Mewe et al. (1980) correctly predict the quantitative behavior of the rate coefficient. Although the Mewe et al. (1980) results used some of the parameters in their fit from the results of Jacobs et al. (1979), other parameters in the fit were determined from Ansari et al. (1970), thereby leading to the large discrepancy seen between the Mewe et al. (1980) and Jacobs et al. (1979) results.
Also shown in Fig. 4 are the present IC results, which have taken into account additional fine-structure effects. It is seen that these results differ significantly from the present LS results: at lower temperatures, the IC results are higher than the LS results, whereas at higher temperatures, the IC results are lower than the LS results. In order to gain a better understanding of why relativistic (mainly spin-orbit-induced, fine-structure splitting) effects are important here for a low-charged system, we study the DR resonance features in closer detail. A comparison of the present LS and IC cross sections is shown in Fig. 5. In the low-energy region, it is seen that the additional fine-structure-split series e− + 3s23p(2P1/2) → 3s23p(2P3/2)nℓ, which is present in the IC calculation but not accounted for in the LS calculation, gives an appreciable contribution to the DR cross section below the 3s23p(2P3/2) threshold at 0.118 eV, thus explaining the enhancement of the IC rate coefficient at lower temperatures. Note also that these fine-structure resonances are not included in the simplified dipole model of Jacobs et al. (1977a,b, 1979, 1980).
 |
Fig. 4 DR rate coefficients of S iv: red solid curve, present IC; blue solid curve, present LS; green solid curve, previous recommended compilation (Mazzotta et al. 1998); gray dashed curve, present RR rate coefficient; (a) black dashed curve, Burgess formula (Aldrovandi & Péquignot 1973); (b) black squares, LS (Jacobs et al. 1979); (c) black dash dotted curve, empirical formula (Mewe et al. 1980); (d) open circles, fitted data (Shull & Van Steenberg 1982); (f) magenta solid curve, LSR-matrix, RR + DR (Nahar & Pradhan 1995; Nahar 1996, 2000); (g) black solid curve, LS AUTOSTRUCTURE (Badnell 1991); and (h) open stars, LS (Al-Mulhem & Nasser 1992). |
At higher energies near the strong, dipole-allowed 3s3p2 and 3s23d
thresholds, on the other hand, the IC threshold cross section is suppressed relative to the
LS cross section. Looking in greater detail at the
3s3p2(2P1/2,3/2)nℓ
Rydberg resonance behaviors as threshold is approached (see Fig. 6), it can be seen that there is a sudden drop-off in IC DR resonance strengths
for n ≥ 36 in both series. It is at this point that the resonances, after
having core radiatively decayed to the
3s23p(2P3/2)nℓ
states, subsequently autoionize and do not contribute to the DR process (Jacobs et al. 1977b). The entire process, dielectronic
capture, radiative decay, and subsequent autoionization, can be depicted as
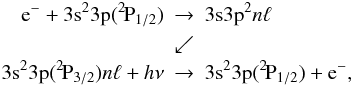 and
is responsible for the suppression of the DR rate coefficient at higher temperatures. Thus,
the proper treatment of
3s23p(2P1/2) − 3s23p(2P3/2)
fine-structure splitting leads to an additional Rydberg series at lower energies, thereby
increasing the low-temperature DR rate coefficient, but also leads to the subsequent
autoionization of radiatively-decayed states from the core-excited resonances at higher
energy, thereby decreasing the higher-temperature DR rate coefficient. We find that the
higher-temperature suppression is constant for all lower ionization stages as
αIC/αLS ≈ 0.8
until about Sc ix, when the
Δnc > 0 core excitations become more
prominent and gradually mask this Δnc = 0 suppression, tending
toward a reduced suppression of
αIC/αLS ≈ 0.9
at higher ionization stages.
and
is responsible for the suppression of the DR rate coefficient at higher temperatures. Thus,
the proper treatment of
3s23p(2P1/2) − 3s23p(2P3/2)
fine-structure splitting leads to an additional Rydberg series at lower energies, thereby
increasing the low-temperature DR rate coefficient, but also leads to the subsequent
autoionization of radiatively-decayed states from the core-excited resonances at higher
energy, thereby decreasing the higher-temperature DR rate coefficient. We find that the
higher-temperature suppression is constant for all lower ionization stages as
αIC/αLS ≈ 0.8
until about Sc ix, when the
Δnc > 0 core excitations become more
prominent and gradually mask this Δnc = 0 suppression, tending
toward a reduced suppression of
αIC/αLS ≈ 0.9
at higher ionization stages.
These trends are evident in Figs. 1−4, which show our present LS and IC results for the entire isoelectronic sequence. Also shown are all other available aluminum-like DR data. These comparisons emphasize, first and foremost, that essentially all of the earlier results do not account for the lower-temperature DR that is due to lower-lying resonances below the Rydberg limit. This becomes especially pronounced at the higher ionization stages. On the other hand, the high-temperature tail of the results based on the fits of Mewe et al. (1980), Shull & Van Steenberg (1982), or Landini & Monsignori Fossi (1991) tend to align more with our LS results at higher ionization stages (of course, fine-structure effects reduce this tail by about 10%, as previously discussed). It appears that the LS results of Jacobs et al. (1980) for Ca viii have included the effects of lower resonances, but the fit of Shull & Van Steenberg (1982) omitted this lower-temperature contribution. The CADW results of Loch et al. (2007) for Ar vi also predict a low-temperature rate coefficient in qualitative agreement with the present calculations; those calculations used the same IPIRDW approach, but neglected the term splitting of configurations, and, more importantly, did not include 3s → 3d contributions, hence the lower rate coefficient at high temperature.
The R-matrix calculations (Nahar & Pradhan 1995; Nahar 1996, 2000) do predict a low-temperature feature, but it is not clear how much of this is due solely to RR, which that unified method includes coherently along with DR (results from our present RR calculation are also shown for comparison). Furthermore, those R-matrix results are particularly troubling, especially at the lowest ionization stage of Si ii, for which their peak rate coefficient is almost an order of magnitude less than the present LS results (and the Burgess formula results of Aldrovandi & Péquignot 1973). Note for this lowest ionization stage, the results of Jacobs et al. (1977b) are only about one-third of the present LS results. These discrepancies could be due to the fact that, since electron correlation effects are strongest at the lowest ionization stage, it is here that the inaccuracies introduced by cruder theoretical approximations and/or implementations is expected to be most prominent.
 |
Fig. 5 DR cross section of S iv: red solid curve, IC results; blue solid curve, LS results. All results have been convoluted with a Gaussian distribution of width 0.1 eV (0.001 eV for the inset). |
Perhaps the most meaningful comparison of all aluminum-like ions is for Fe xiv, which not only has received considerable theoretical attention, due to its astrophysical importance, but the DR rate coefficient has also been measured experimentally at the Test Storage Ring (TSR) facility (Schmidt et al. 2006). For this ion, we see that our IC rate coefficient is in excellent agreement with the earlier IC AUTOSTRUCTURE results of Badnell (2006c), as expected, and these agree well with the experimental results at higher temperatures. Here the results of Jacobs et al. (1977a) are also in good agreement, and therefore so are the fitted results of Shull & Van Steenberg (1982); as discussed earlier, the parameterized results of Mewe et al. (1980) also are fairly reliable at higher ionization stages and higher temperatures. However, those earlier rate coefficients of Jacobs et al. (1977a), Shull & Van Steenberg (1982), and Mewe et al. (1980) do not consider low-temperature contributions. The R-matrix results (Nahar 2000) do indicate some contribution at lower temperatures, but the absolute rate coefficient, at all temperatures, is inexplicably at least a factor of three lower than our present results or experiment.
 |
Fig. 6 DR cross section of S iv for the e− + 3s23p(2P1/2) → 3s3p2(2P1/2,3/2)nℓ resonances in both IC and LS-coupling: red solid curve, the 3s3p2(2P1/2)nℓ IC series; blue solid curve, the 3s3p2(2P3/2)nℓ IC series; green solid curve, the 3s3p2(2P)nℓLS series. All series are convoluted with a FWHM Gaussian of 1.2 meV. |
The present or earlier IC Maxwellian rate coefficients for Fe xiv are substantially lower than the experimental results at lower temperature. In order to study this discrepancy in finer detail, we compare the two rate coefficients, in Fig. 7, at the experimental electron-cooler thermal distribution resolution, characterized by a transverse temperature of kT⊥ = 12 meV and a longitudinal temperature of kT∥ = 0.09 meV with respect to the ion beam direction (Dittner et al. 1986). Just above threshold, the theoretical rate coefficient is much lower than experiment. This is surely due to the slight inaccuracies in resonance energies; if a resonances occurs in the vicinity of threshold and the theoretical prediction for its position is in error by a small negative energy, than that resonance is erroneously not included in the DR cross section contribution – see Robicheaux et al. (2010) for a recent discussion. This is an inherent limitation in the current state of theoretical calculations for very low energies. However, there is also a theoretical underestimate in the rate coefficient at about 25 eV; this cannot be explained by slight inaccuracies in resonance positions, but might instead be due to configuration-interaction (CI) between different Rydberg series, which is not included in the present IPIRDW implementation. Indeed, it is seen that there very well could be strong mixing between the nearly-degenerate 3s3p2(2P)9ℓ and 3s23d(2D)10ℓ resonances, since overlapping resonances interact more strongly, and inclusion of this interaction could lead to an enhanced overall resonance strength; a recent study (Kwon & Savin 2011) has demonstrated this same type of interference effect.
 |
Fig. 7 Comparison of present IC (red solid curve) and experimental measurements (blue solid curve, Schmidt et al. 2006) DR rate coefficients for Fe xiv. |
At higher energies, as the Rydberg limits are approached, the experimental rate coefficient is found to be lower than the theoretical predictions. This is due to the electric field ionization of high Rydberg states, leading to a suppressed DR contribution. The experimental Maxwellian rate coefficient shown in Fig. 7 has therefore also included an estimated addition for high Rydberg states, computed using AUTOSTRUCTURE, and this inclusion gives a modified experimental rate coefficient that is slightly higher than theory for high temperatures.
 |
Fig. 8 Comparison between present IC results (red solid curve) and recommended compilation (green solid curve, Mazzotta et al. 1998) for the aluminum-like isoelectronic sequence. |
In comparing the present results to previous data, several conclusions can be reached. First and foremost, our present IC results are in good agreement with the only experimental results available – the TSR data for Fe xiv (Schmidt et al. 2006). Second, all previous LS rate coefficients for S iv were consistent with the present LS results except, inexplicably, the R-matrix results (Nahar & Pradhan 1995; Nahar 1996, 2000); similar R-matrix results for Si ii were almost an order of magnitude less than the present LS results. Third, the recommended compilation by Mazzotta et al. (1998) was ultimately based on the simplified-model results of Jacobs et al. (1977a,b, 1979, 1980), which were then fitted by Shull & Van Steenberg (1982) and Landini & Monsignori Fossi (1991), except in the case of Si ii and S iv, for which the anomalous R-matrix results (Nahar & Pradhan 1995; Nahar 1996, 2000) were used. Lastly, even the accurate LS calculations did not include the physical effects of fine-structure splitting, which give rise to an additional Rydberg series near threshold, thereby increasing the low-temperature DR rate coefficient, and also allow autoionization of higher-n (n > 35) radiatively decayed states, decreasing the high-temperature DR rate coefficient.
Fitting coefficients ci (in cm3 K3/2 s-1) and Ei (in K) for the total ground-state IC DR rate coefficients. Y(N) means Y × 10N.
The net effect of including all the correct physics in our present, state-of-the-art IC calculations is shown in Fig. 8. The present IC DR rate coefficients for the entire aluminum-like sequence is shown (lower curves correspond to lower ionization stage) compared to the compiled data of Mazzotta et al. (1998) – that which had been used to date in plasma modeling codes. It is most readily seen that the earlier data do not include any of the low-temperature contributions that become increasingly important as the ionization stage is increased. At higher-temperatures, there is still a large discrepancy, especially for the lowest-charged ions, where the earlier compiled rate coefficients are significantly weaker due to the poor LS results that were used. And even for higher ionization stages, where electron correlation becomes less important and the earlier LS results and/or scaled fits are more reliable, the high-temperature tail eventually exceeds the present results, due to the reautoionization phenomena that is not included in those LS results.
Total DR rate coefficients (Δnc = 0 + Δnc = 1) for the entire aluminum-like isoelectronic sequence are fitted using Eq. (3) and the DR fitting coefficients are listed in Table 3. These fits are accurate to better than 5% for all the Al-like isoelectronic sequence in the electron temperature range q2(10−107) K, where q is the charge of the recombining ion. The accuracy is better than 1% over the collisionally ionized range. On the other hand, our RR rate coefficients data for this isoelectronic sequence are fitted using Eqs. (4) and (5). The RR fitting coefficients are tabulated in Table 4. The fits are accurate to better than 1% over the temperature range q2(10−107) K.
Lastly, we have also included DR from metastable states in addition to the ground-state. Representative results for Mn xiii are shown in Fig. 9 for the first five levels. Not only are there enormous difference between results for the two LS terms, but there is a significant difference between DR from the two fine-structure-split 3s23p(2P1/2) and 3s23p(2P3/2) levels, especially at low temperature, since the m = 2 series no longer has a second fine-structure-split Rydberg series enhancement near threshold. These comparisons further emphasize the need for tabulation of DR data from ground and metastable states.
 |
Fig. 9 Maxwellian-averaged total DR (red solid curve) and RR (gray dashed curve) rate coefficients from the ground and metastable 3s23p(2P1/2,3/2) (m = 1,2) and 3s3p2(4P1/2,3/2,5/2) (m = 3−5) initial levels. |
5. Summary
We have carried-out systematic calculations of DR and RR rate coefficients for the aluminum-like isoelectronic sequence in a multi-configuration intermediate coupling Breit-Pauli approximation for all ions (Si ii-Zn xviii). All previous DR data for this isoelectronic sequence were either obtained by using empirical formulas or were performed in an LS-coupling or simplified framework and did not include all of the relevant physics. We find that, most importantly, the inclusion of fine-structure effects in our calculations led to an increased low-temperature DR rate coefficient, due to the additional fine-structure-split 3s23p(2P3/2)nl DR resonance series, and a decreased high-temperature DR rate coefficient, due to the subsequent reautoionization of fine-structure-excited radiative decay states, compared to all earlier LS-coupled calculations. As a result, the earlier recommended database (Mazzotta et al. 1998) contained DR rate coefficients that were unphysically low at lower-temperatures and unphysically high at higher temperatures. Furthermore, that database (Mazzotta et al. 1998) uses the R-matrix results of Nahar & Pradhan (1995) for Si ii which are inexplicably almost an order of magnitude lower than any other LS results.
Our present final IC results are benchmarked to the existing experimental data (Schmidt et al. 2006) for Fe xiv, showing overall good agreement for the total DR rate coefficient. However, our present IC rate coefficient, using the experimental energy distribution, is found to be less than the experimental rate coefficient at lower temperature, which we attribute to a theoretical uncertainty in the energy positions of near-threshold resonances (whether they are predicted to be above or below threshold). There is also a noticeable difference in the two rate coefficients at about 25 eV above threshold, which may be due to interference effects between neighboring Rydberg series that are not included in our calculations. Nevertheless, our Maxwellian-averaged DR rate coefficient is found to be within the experimental uncertainty of 20% for all temperatures of interest.
Lastly, we have also considered partial recombination and metastable-state processes. All of our computed data have been tabulated in ADAS format, and total DR and RR rate coefficients have been fitted, for plasma modeling use.
Acknowledgments
We would like to thank E. W. Schmidt for providing us with the experimental data. This work was funded in part by NASA APRA, NASA SHP SR&T, and STFC grants.
References
- Al-Mulhem, A., & Nasser, I. 1992, Phys. Rev. A, 46, 2945 [NASA ADS] [CrossRef] [Google Scholar]
- Aldrovandi, S. M. V., & Péquignot, D. 1973, A&A, 25, 137 [NASA ADS] [Google Scholar]
- Altun, Z., Yumak, A., Badnell, N. R., Colgan, J., & Pindzola, M. S. 2004, A&A, 420, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Altun, Z., Yumak, A., Badnell, N. R., Loch, S. D., & Pindzola, M. S. 2006, A&A, 447, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Altun, Z., Yumak, A., Yavuz, I., et al. 2007, A&A, 474, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ansari, S. M. R., Elwert, G., & Mücklich, P. 1970, Z. Naturforsch., 25a, 1781 [NASA ADS] [Google Scholar]
- Arnaud, M., & Raymond, J. 1992, ApJ, 398, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., & Rothenflug, R. 1985, A&AS, 60, 425 [NASA ADS] [Google Scholar]
- Badnell, N. R. 1986, J. Phys. B, 19, 3827 [Google Scholar]
- Badnell, N. R. 1991, ApJ, 379, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 1997, J. Phys. B, 30, 1 [Google Scholar]
- Badnell, N. R. 2006a, A&A, 447, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R. 2006b, ApJ, 651, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2006c, J. Phys. B, 39, 4825 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2006d, ApJS, 167, 334 [Google Scholar]
- Bautista, M. A., & Badnell, N. R. 2007, A&A, 466, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R., & Pindzola, M. S. 1989, Phys. Rev. A, 39, 1690 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., O’Mullane, M. G., Summers, H. P., et al. 2003, A&A, 406, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryans, P., Badnell, N. R., Gorczyca, T. W., et al. 2006, ApJS, 167, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Bryans, P., Landi, E., & Savin, D. W. 2009, ApJ, 691, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A. 1965, ApJ, 141, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A., Manson, H. E., & Tully, J. A. 1989, A&A, 217, 319 [NASA ADS] [Google Scholar]
- Colgan, J., Pindzola, M. S., Whiteford, A. D., & Badnell, N. R. 2003, A&A, 412, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colgan, J., Pindzola, M. S., & Badnell, N. R. 2004, A&A, 417, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra (Berkeley: University of California Press) [Google Scholar]
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curdt, W., Landi, E., & Feldman, U. 2004, A&A, 427, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dittner, P. F., Datz, S., Miller, P. D., Pepmiller, P. L., & Fou, C. M. 1986, Phys. Rev. A, 33, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Gorczyca, T. W., & Badnell, N. R. 1997, Phys. Rev. Lett., 79, 2783 [NASA ADS] [CrossRef] [Google Scholar]
- Gorczyca, T. W., Badnell, N. R., & Savin, D. W. 2002, Phys. Rev. A, 65, 062707 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2003, ApJ, 590, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, V. L., Davis, J., Kepple, P. C., & Blaha, M. 1977a, ApJ, 211, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, V. L., Davis, J., Kepple, P. C., & Blaha, M. 1977b, ApJ, 215, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, V. L., Davis, J., Rogerson, J. E., & Blaha, M. 1979, ApJ, 230, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, V. L., Davis, J., Rogerson, J. E., et al. 1980, ApJ, 239, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kallman, T. R., Liedahl, D., Osterheld, A., Goldstein, W., & Kahn, S. 1996, ApJ, 465, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Kwon, D.-H., & Savin, D. W. 2011, Phys. Rev. A, 83, 012701 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Storey, P. J., & Zeippen, C. J. 2004, ApJ, 607, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Landini, M., & Monsignori Fossi, B. C. M. 1991, A&AS, 91, 183 [NASA ADS] [Google Scholar]
- Loch, S. D., Abdel-Naby, S. A., Ballance, C. P., & Pindzola, M. S. 2007, Phys. Rev. A, 76, 022706 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzitelli, G., & Mattioli, M. 2002, At. Data Nucl. Data Tables, 82, 313 [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [Google Scholar]
- Mewe, R., Schrijver, J., & Sylwester, J. 1980, A&AS, 40, 323 [NASA ADS] [Google Scholar]
- Mitnik, D. M., & Badnell, N. R. 2004, A&A, 425, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nahar, S. N. 1996, ApJS, 106, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N. 2000, ApJS, 126, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N., & Pradhan, A. K. 1995, ApJ, 447, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Nikolić, D., Gorczyca, T. W., Korista, K. T., & Badnell, N. R. 2010, A&A, 516, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nussbaumer, H., & Storey, P. J. 1986, A&AS, 64, 545 [NASA ADS] [Google Scholar]
- Robicheaux, F., Loch, S. D., Pindzola, M. S., & Ballance, C. P. 2010, Phys. Rev. Lett., 105, 233201 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schmidt, E. W., Schippers, S., Müller, A., et al. 2006, ApJ, 641, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., & Van Steenberg, M. 1982, ApJS, 48, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, H. P. 2003, ADAS User Manual (v2.6), http://www.adas.ac.uk/manual.php [Google Scholar]
- Verner, D. A., & Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Korista, K. T., Badnell, N. R., & Savin, D. W. 2003, A&A, 412, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Korista, K., Badnell, N. R., & Savin, D. W. 2004a, A&A, 426, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Korista, K. T., Badnell, N. R., & Savin, D. W. 2004b, A&A, 417, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Fu, J., et al. 2006, A&A, 447, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Radial scaling parameters used in the present study for Δnc = 0 core-excitations for the aluminum-like isoelectronic sequence.
Fitting coefficients ci (in cm3 K3/2 s-1) and Ei (in K) for the total ground-state IC DR rate coefficients. Y(N) means Y × 10N.
All Figures
 |
Fig. 1 Present Maxwellian-averaged DR and RR rate coefficients for Si ii-Ca viii ions (excluding S iv − see Fig. 4): red solid curve, present IC; blue solid curve, present LS; green solid curve, previous recommended compilation (Mazzotta et al. 1998); gray dashed curve, present RR rate coefficient; (a) black dashed curve, Burgess formula (Aldrovandi & Péquignot 1973); (b) black squares, LS (Jacobs et al. 1979); (c) black dash dotted curve, empirical formula (Mewe et al. 1980); (d) open circles, fitted data (Shull & Van Steenberg 1982); (e) red circles, extrapolated fits (Landini & Monsignori Fossi 1991); (f) magenta solid curve, LSR-matrix, RR + DR (Nahar & Pradhan 1995; Nahar 1996, 2000); (i) black dotted curve, low temperature data (Nussbaumer & Storey 1986); and (j) pink dotted curve, configuration-average distorted-wave results (Loch et al. 2007). |
| In the text | |
 |
Fig. 2 Present Maxwellian-averaged DR and RR rate coefficients for Sc ix-Fe xiv ions: red solid curve, present IC; blue solid curve, present LS; green solid curve, previous recommended compilation (Mazzotta et al. 1998); gray dashed curve, present RR rate coefficient; (b) black squares, LS (Jacobs et al. 1979); (c) black dash dotted curve, empirical formula (Mewe et al. 1980); (d) open circles, fitted data (Shull & Van Steenberg 1982); (e) red circles, extrapolated fits (Landini & Monsignori Fossi 1991); (f) magenta solid curve, LSR-matrix, RR + DR (Nahar 2000); (g) black solid curve, IC AUTOSTRUCTURE (Badnell 2006c); and (l) blue dashed curve, experimental measurements (Schmidt et al. 2006). |
| In the text | |
 |
Fig. 3 Present Maxwellian-averaged DR and RR rate coefficients for Co xv-Zn xviii ions: red solid curve, present IC; blue solid curve, present LS; green solid curve, previous recommended compilation (Mazzotta et al. 1998); gray dashed curve, present RR rate coefficient; (b) black squares, LS (Jacobs et al. 1979); (c) black dash dotted curve, empirical formula (Mewe et al. 1980); (d) open circles, fitted data (Shull & Van Steenberg 1982); (e) red circles, extrapolated fits (Landini & Monsignori Fossi 1991); and (k) blue circles, extrapolated fit (Mazzitelli & Mattioli 2002). |
| In the text | |
 |
Fig. 4 DR rate coefficients of S iv: red solid curve, present IC; blue solid curve, present LS; green solid curve, previous recommended compilation (Mazzotta et al. 1998); gray dashed curve, present RR rate coefficient; (a) black dashed curve, Burgess formula (Aldrovandi & Péquignot 1973); (b) black squares, LS (Jacobs et al. 1979); (c) black dash dotted curve, empirical formula (Mewe et al. 1980); (d) open circles, fitted data (Shull & Van Steenberg 1982); (f) magenta solid curve, LSR-matrix, RR + DR (Nahar & Pradhan 1995; Nahar 1996, 2000); (g) black solid curve, LS AUTOSTRUCTURE (Badnell 1991); and (h) open stars, LS (Al-Mulhem & Nasser 1992). |
| In the text | |
 |
Fig. 5 DR cross section of S iv: red solid curve, IC results; blue solid curve, LS results. All results have been convoluted with a Gaussian distribution of width 0.1 eV (0.001 eV for the inset). |
| In the text | |
 |
Fig. 6 DR cross section of S iv for the e− + 3s23p(2P1/2) → 3s3p2(2P1/2,3/2)nℓ resonances in both IC and LS-coupling: red solid curve, the 3s3p2(2P1/2)nℓ IC series; blue solid curve, the 3s3p2(2P3/2)nℓ IC series; green solid curve, the 3s3p2(2P)nℓLS series. All series are convoluted with a FWHM Gaussian of 1.2 meV. |
| In the text | |
 |
Fig. 7 Comparison of present IC (red solid curve) and experimental measurements (blue solid curve, Schmidt et al. 2006) DR rate coefficients for Fe xiv. |
| In the text | |
 |
Fig. 8 Comparison between present IC results (red solid curve) and recommended compilation (green solid curve, Mazzotta et al. 1998) for the aluminum-like isoelectronic sequence. |
| In the text | |
 |
Fig. 9 Maxwellian-averaged total DR (red solid curve) and RR (gray dashed curve) rate coefficients from the ground and metastable 3s23p(2P1/2,3/2) (m = 1,2) and 3s3p2(4P1/2,3/2,5/2) (m = 3−5) initial levels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


