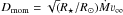| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201015818 | |
| Published online | 03 January 2012 | |
Predictions for mass-loss rates and terminal wind velocities of massive O-type stars
1 Astronomical Institute “Anton Pannekoek”, University of Amsterdam, Science Park 904, 1098 Amsterdam, The Netherlands
e-mail: lmuijres@gmail.com
2 Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland, UK
3 Astronomical Institute, Utrecht University, Princetonplein 5, 3584 CC Utrecht, The Netherlands
4 School of Physical and Geographical Sciences, Lennard-Jones Laboratories, Keele University, Staffordshire, ST5 5BG, UK
5 Argelander-Institut für Astronomie der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received: 24 September 2010
Accepted: 21 October 2011
Context. Mass loss from massive stars forms an important aspect of the evolution of massive stars, as well as for the enrichment of the surrounding interstellar medium.
Aims. Our goal is to predict accurate mass-loss rates and terminal wind velocities. These quantities can be compared to empirical values, thereby testing radiation-driven wind models. One specific topical issue is that of the so-called “weak-wind problem”, where empirically derived mass-loss rates and (modified) wind momenta fall orders of magnitude short of predicted values.
Methods. We employ an established Monte Carlo model and a recently suggested new line acceleration formalism to solve the wind dynamics more consistently.
Results. We provide a new grid of mass-loss rates and terminal wind velocities of O-type stars, and compare the values to empirical results. Our models fail to provide mass-loss rates for main-sequence stars below a luminosity of log(L/L⊙) = 5.2, where we appear to run into a fundamental limit. At luminosities below this critical value there is insufficient momentum transferred to the wind in the region below the sonic point in order to kick-start the acceleration of the flow. This problem occurs at almost the exact location of the onset of the weak-wind problem. For O dwarfs, the boundary between being able to start a wind, and failing to do so, is at spectral type O6/O6.5. The direct cause of this failure for O6.5 stars is a combination of the lower luminosity and a lack of Fe v lines at the base of the wind. This might indicate that – in addition to radiation pressure – another mechanism is required to provide the necessary driving to initiate the wind acceleration.
Conclusions. For stars more luminous than 105.2 L⊙, our new mass-loss rates are in excellent agreement with the mass-loss prescription by Vink et al. (2000, A&A, 362, 295) using our terminal wind velocities as input to this recipe. This implies that the main assumption entering the method of the Vink et al. prescriptions – i.e. that the momentum equation is not explicitly solved for – does not compromise the reliability of the Vink et al. results for this part of parameter space. Finally, our new models predict terminal velocities that are typically 35 and 45 percent larger than observed values. Such over-predictions are similar to those from (modified) CAK-theory.
Key words: radiative transfer / stars: mass-loss / stars: winds, outflows / stars: early-type / stars: massive
© ESO, 2012
1. Introduction
In this article, we present predictions for mass-loss rates and velocity structures for a grid of O-type stars, using two distinct methods for solving the wind dynamics.
Mass loss forms an integral aspect characterizing massive O-type stars. Because of their short lifetimes, massive stars are important tracers of star formation in galaxies. Furthermore, they enrich the interstellar medium with metals, both during their lives via stellar winds, as well as when they explode at the very end of their evolution. In order to build an evolutionary framework for massive stars, it is essential to map the mass-loss processes during the various evolutionary stages, as the exact rates of mass loss greatly influence the evolutionary tracks (e.g. Maeder 1981; Chiosi & Maeder 1986). The effects of mass loss on the evolutionary tracks are at least two-fold: first and foremost the stellar mass is reduced, and secondly, the rotational velocity is strongly affected, as the mass also carries away angular momentum (e.g. Langer 1998; Maeder & Meynet 2000).
For the continuous stellar winds from massive stars, the outflow is thought to be driven by the transfer of energy and momentum from the radiation field to the atmosphere through the absorption of photons in atomic transitions. The exact amount of momentum and energy transfer has been the subject of both theoretical and observational studies for many decades (Lucy & Solomon 1970; Castor et al. 1975; Pauldrach et al. 1986; Puls et al. 1996; de Koter et al. 1997; Vink et al. 1999; Krtička & Kubát 2004; Mokiem et al. 2007). For luminous O-type stars, with log(L/L⊙) > 5.2, the theoretical predictions of Vink et al. (2000) seem to be in reasonable agreement with empirical mass-loss rates provided that O-stars are only subject to modest amounts of wind clumping (with clump filling factors of only 5–10). However, for objects with luminosities log(L/L⊙) below approximately 5.2, a severe drop – by a factor of ~100 – in the empirically determined modified wind momentum (basically a multiplication of the mass-loss rate and the terminal velocity) has been revealed. This problem has in literature been referred to as “the weak-wind problem” (Puls et al. 1996; Martins et al. 2005b; Puls et al. 2008; Marcolino et al. 2009).
It deserves proper investigation simply because of the enormity of the effect. It is particularly important to find out whether the problem is caused by the mass-loss diagnostics or the predictions, as both are also applied to more luminous stars, where agreement between diagnostics and predictions has seemingly been achieved. But how certain can we be that this agreement is not a coincidence if we are aware of severe problems at lower luminosity?
Furthermore, we note that the oft-used mass-loss predictions of Vink et al. (2000) are semi-empirical, in the sense that empirical values for the wind velocity structure and terminal velocity are used as input to the modelling. In order to trust our overall knowledge of the mass-loss rates from O-type stars – at all masses and luminosities – it is pivotal to further scrutinize the Vink et al. (2000) assumptions, most notably that of the adopted wind dynamics.
Recently, Müller & Vink (2008) suggested a new parametrization of the line acceleration, expressing it as a function of radius rather than of the velocity gradient, as in Castor et al. (1975, henceforth CAK) theory. The implementation of this new formalism allows for local dynamical consistency, as one can determine the energy and momentum transfer at each location in the wind through the use of Monte Carlo simulations. Although the formalism was applied with three independent starting conditions that showed convergence to the same wind parameters, it has thus far only been applied to one object, that of an O5 dwarf.
For the adopted line force parameterization Müller & Vink identify an exact solution in case the medium is isothermal. We expand on this result by also accounting for a temperature stratification. To allow for such a study we employ the new line acceleration parameterization but solve for the wind dynamics consistently by applying a numerical method to solve for the momentum equation.
The purpose of our study is threefold: i) to solve the wind dynamics numerically, and compare the results to those of Müller & Vink (2008); ii) to compute a larger grid of dynamically derived O-star mass-loss rates and wind terminal velocities, and determine the accuracy of the predictions made by Vink et al. (2000); and iii) to utilize the grid in order to investigate the weak-wind problem.
Our paper is organized as follows. In Sect. 2, we start off describing the core of our method and the different methods to treat the wind equation. The results are presented in Sect. 3 and discussed in the Sect. 4. We end with the conclusions (Sect. 5).
2. Method
The method of de Koter et al. (1997) and Vink et al. (1999), applied to derive the mass-loss rates of O and early-B type stars (Vink et al. 2000, 2001), Luminous Blue Variable stars (Vink & de Koter 2002) and Wolf-Rayet stars (Vink & de Koter 2005), is an extension of a treatment developed by Abbott & Lucy (1985). It is based on an iteration cycle between the stellar atmosphere model isa-wind (de Koter et al. 1993) and a Monte Carlo simulation, mc-wind (de Koter et al. 1997), in which the energy per unit time ΔL that is extracted from the radiation field in interactions of photons with the gas, is computed. From this a mass-loss rate Ṁ is computed on the basis of which a new isa-wind model is constructed. The predicted mass loss is the one for which the input mass-loss rate of isa-wind equals the mass-loss rate computed by mc-wind.
As is consistently pointed out in the papers referred to above, the method does not address the equation of motion but uses a prescribed trans-sonic velocity structure. This implies that although in a global sense the method fulfills the constraint of energy conservation, it need not hold that the actual local forces acting on the gas are consistent with the force implied by the adopted velocity law. Müller & Vink (2008) relax on this assumption and present an improved treatment of the problem introducing a new way to parametrize the line force. We first discuss an approach presented by these authors, which we refer to as the “best-β method, as it allows to link to empirically derived estimates of the steepness of the velocity law (characterized by a parameter β, see below). In a second step, we present solutions that numerically solve the wind dynamics.
We first briefly introduce isa-wind in Sect. 2.1, emphasizing the treatment of the heuristic velocity law, and mc-wind in Sect. 2.2, focusing on the determination of the mass-loss rate using the global energy argument. In Sect. 2.3 we recapitulate the essentials of the parametrization of the line force by Müller & Vink and in Sect. 2.4 the principle of their best-β method. In the following subsection we introduce our hydrodynamical method. Finally, Sect. 2.6 is devoted to a discussion of the physical conditions at the sonic point.
2.1. The model atmosphere
The code isa-wind computes the structure, radiation field and ionization/excitation state of the gas of an outflowing stellar atmosphere in non local thermodynamic equilibrium (non-LTE), assuming radiative equilibrium. No artificial separation between the photosphere and wind is assumed. The temperature structure is treated somewhat simplified in that it results from initial LTE based Rosseland opacities (i.e. grey). The fact that the temperature structure is not affected by possible departures from the populations from their LTE state implies that the effect of line blanketing is not treated self-consistently, although non-LTE line blocking is taken into account. Radiation transfer in spectral lines is treated in the Sobolev approximation (Sobolev 1960).
The input stellar parameters are the luminosity L, the effective temperature Teff (specifying the radius R), the mass M and chemical abundances. The wind is described by the mass-loss rate Ṁ and a velocity structure, which are connected through the equation of mass continuity 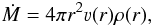 (1)where ρ(r) is the mass density and v(r) is the velocity at radius r. Outside the photosphere, the velocity structure is assumed to follow a β-law, i.e.
(1)where ρ(r) is the mass density and v(r) is the velocity at radius r. Outside the photosphere, the velocity structure is assumed to follow a β-law, i.e. 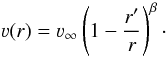 (2)The free parameter β is a measure of the velocity gradient. A low value of β implies that the velocity approaches the terminal flow velocity ν∞ relatively close to the star; for a large value this happens only further out in the wind. The β-law does not hold in the photosphere since the line force is not the dominant term in the equation of motion, but gravity and the acceleration due to the gas pressure gradient also contribute to the flow structure. The radius r′ is a smoothing parameter that is used to connect the β-law to the (quasi) hydrostatic photosphere and must assure that ν(r) and its spatial derivative are continuous at the point where one couples the photospheric velocity law to the β-law. The velocity structure in the photosphere is determined by solving the non-isothermal equation of motion, neglecting line radiation pressure and assuming that continuum radiation pressure is the result from Thomson scattering only. An inner boundary velocity (or density) is chosen, which may be used to tune the total Rosseland optical depth of the photosphere and wind (see below).
(2)The free parameter β is a measure of the velocity gradient. A low value of β implies that the velocity approaches the terminal flow velocity ν∞ relatively close to the star; for a large value this happens only further out in the wind. The β-law does not hold in the photosphere since the line force is not the dominant term in the equation of motion, but gravity and the acceleration due to the gas pressure gradient also contribute to the flow structure. The radius r′ is a smoothing parameter that is used to connect the β-law to the (quasi) hydrostatic photosphere and must assure that ν(r) and its spatial derivative are continuous at the point where one couples the photospheric velocity law to the β-law. The velocity structure in the photosphere is determined by solving the non-isothermal equation of motion, neglecting line radiation pressure and assuming that continuum radiation pressure is the result from Thomson scattering only. An inner boundary velocity (or density) is chosen, which may be used to tune the total Rosseland optical depth of the photosphere and wind (see below).
The wind is assumed to be homogeneous, i.e. the outflowing gas is not clumped (but see Muijres et al. 2011), and the terminal velocity is chosen to be 2.6 times the effective escape velocity from the stellar photosphere, which is in reasonable concordance with empirically determined terminal velocities of O-stars (Lamers et al. 1995; Kudritzki & Puls 2000). The base of the photosphere is positioned at a Rosseland optical depth of about 20–25 and the wind extends out to 20 R ⋆ .
2.2. The Monte Carlo method mc-wind
The code mc-wind uses the model atmosphere structure computed by isa-wind to determine the total amount of energy that is transferred from the radiation field to the wind – in interactions of photons with ions in the gas – by means of a Monte Carlo simulation of the trajectories of photon packets emitted at the base of the photosphere and escaping through the outer boundary of the model. Each photon can travel an optical depth weighted (random) distance to a point of interaction. This point is determined by taking into account all the opacity the photon encounters on its path, so it includes contributions from both lines and continua. At the point of interaction the type of interaction is determined, using proper weighing functions (Vink et al. 1999). The possible interactions are thermal absorption and emission, electron scattering and line scattering. The interaction is assumed to be coherent in the co-moving frame of the ion. In the observers frame, however, energy can be exchanged from the radiation field to the gas (or vice versa). It is traced which ion is involved in the interaction, such that, for instance, the contributions to the radiative force can be dissected and identified. This provides us with a powerful tool to study the nature of the line force at each location in the wind.
The radiative force per unit mass equals (Abbott & Lucy 1985): 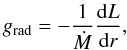 (3)where dL is the amount of energy lost by the radiation field in a layer of thickness dr.
(3)where dL is the amount of energy lost by the radiation field in a layer of thickness dr.
Once the total amount of energy transferred to the wind is known, the mass-loss rate that can be driven for the density and velocity structure of the adopted isa-wind model can be calculated. Neglecting enthalpy: 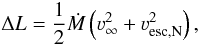 (4)where ΔL is the total amount of energy lost by the radiation field and
(4)where ΔL is the total amount of energy lost by the radiation field and 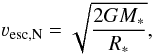 (5)is the Newtonian escape velocity from the stellar surface. G is the gravitational constant. A new isa-wind atmosphere, adopting the mass-loss rate as determined in mc-wind, is computed followed by a new Monte Carlo simulation. This procedure is repeated until the input mass-loss rate of mc-wind equals the output mass-loss rate. Although the mass-loss rate that is predicted in this way reflects that in a global sense the energy that is needed to drive the wind is indeed extracted from the radiation field, it does not mean that the input line force (implied by the velocity law) equals the output line force from the Monte Carlo simulation locally, i.e. the equation of motion of the wind is not solved.
(5)is the Newtonian escape velocity from the stellar surface. G is the gravitational constant. A new isa-wind atmosphere, adopting the mass-loss rate as determined in mc-wind, is computed followed by a new Monte Carlo simulation. This procedure is repeated until the input mass-loss rate of mc-wind equals the output mass-loss rate. Although the mass-loss rate that is predicted in this way reflects that in a global sense the energy that is needed to drive the wind is indeed extracted from the radiation field, it does not mean that the input line force (implied by the velocity law) equals the output line force from the Monte Carlo simulation locally, i.e. the equation of motion of the wind is not solved.
Here we improve on this situation using two methods. Both methods A and B require a parametrization of the line force predicted by mc-wind. We therefore first discuss this aspect.
2.3. Line force parametrization
Figure 1 shows the Monte-Carlo line force (blue crosses) as is produced in the first iteration step of a typical O3 V star (L = 105.83L⊙, Teff = 44 600 K and M = 58 M⊙). The Monte Carlo line force is determined in a statistical way and shows scatter. Given the delicate nature of the equation of motion it can not be used as such and must be represented by an appropriate analytical fit function. We adopt a parametrization of the line force as a function of radius, rather than of optical depth, as opted for by Castor et al. (1975). In Sect. 4.2 we show that this leads to a more accurate numerical representation of the line force, at least for the type of stars studied here. In doing so, we follow Müller & Vink (2008), who motivate 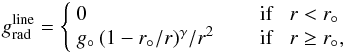 (6)where g°, r° , and γ are fit parameters to the Monte Carlo line force. This choice of the fit function, i.e. without any explicit dependency of the line force on the velocity gradient, implies that in our models the critical point is the sonic point. Figure 1 shows a typical result for this fit (black dotted curve). The deviations are (as mentioned) due to scatter in the simulation.
(6)where g°, r° , and γ are fit parameters to the Monte Carlo line force. This choice of the fit function, i.e. without any explicit dependency of the line force on the velocity gradient, implies that in our models the critical point is the sonic point. Figure 1 shows a typical result for this fit (black dotted curve). The deviations are (as mentioned) due to scatter in the simulation.
 |
Fig. 1 The line force (blue crosses) as predicted by mc-wind in the first iteration step. A fit (black dotted line) using Eq. (6) to represent the line force is overplotted. Note the modest scatter on the Monte Carlo results due to noise. |
2.4. Method A: Best-β solution
In this section, we use the line force representation Eq. (6) to determine – after making certain assumptions – an analytical solution of the velocity law in the outer part of the wind, following Müller & Vink (2008). This solution can be compared to the β-law (Eq. (2)) and used to derive ν∞ and the β value that is most representative. This is useful in comparing to the often applied β-law.
We aim to find a solution of the equation of motion 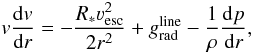 (7)where p is the gas pressure and
(7)where p is the gas pressure and 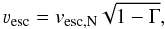 (8)is the effective surface escape velocity of the star. Γ is the continuum radiation pressure in units of the Newtonian gravitational acceleration. Sufficiently far from the photosphere this term is dominated by radiation pressure on free electrons, i.e. Γ = Γe, where Γe is essentially constant for early-type stars. Close to or in the photosphere, the acceleration due to free-free, bound-free and bound-bound processes may compete with electron scattering and should, in principle, be considered in Eq. (8). For our best-β solution, however, we assume a constant continuum acceleration, which we set to Γe. Substituting the equation of state for an ideal gas and using Eq. (1), the term (1/ρ) dp/dr can be written as:
(8)is the effective surface escape velocity of the star. Γ is the continuum radiation pressure in units of the Newtonian gravitational acceleration. Sufficiently far from the photosphere this term is dominated by radiation pressure on free electrons, i.e. Γ = Γe, where Γe is essentially constant for early-type stars. Close to or in the photosphere, the acceleration due to free-free, bound-free and bound-bound processes may compete with electron scattering and should, in principle, be considered in Eq. (8). For our best-β solution, however, we assume a constant continuum acceleration, which we set to Γe. Substituting the equation of state for an ideal gas and using Eq. (1), the term (1/ρ) dp/dr can be written as: 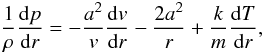 (9)where k is Boltzmann’s constant, m the mean particle mass and a(r) is the local sound speed, given by:
(9)where k is Boltzmann’s constant, m the mean particle mass and a(r) is the local sound speed, given by: 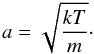 (10)We assume the wind to be isothermal, such that the sound speed is constant. The equation of motion can now be rewritten as
(10)We assume the wind to be isothermal, such that the sound speed is constant. The equation of motion can now be rewritten as 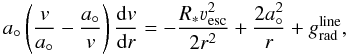 (11)where a° is the isothermal sound speed at the effective temperature of the star. Equation (11) is a critical point equation, where the left- and right-hand side vanish at the point v(rs) = a°, i.e. where rs is the radius of the sonic point. It yields several types of solutions. Müller & Vink (2008) show that for the isothermal case and a line force as described in Eq. (6), analytical expressions for all types of solutions of Eq. (11) can be constructed by means of the Lambert W function (as for a further discussion of the solution of Eq. (11) containing an additional centrifugal term, see Müller2001). Even for the interesting trans-sonic case of a stellar wind, the analytical solution has an intricate shape. However, a useful approximate wind solution for the velocity law can be constructed if the pressure related terms 2a2/r and a/v can be neglected. We note, however, that at the sonic point the contribution of the two pressure terms is non-negligible (Müller & Vink 2008). After some manipulation one finds that the approximate velocity law is given by:
(11)where a° is the isothermal sound speed at the effective temperature of the star. Equation (11) is a critical point equation, where the left- and right-hand side vanish at the point v(rs) = a°, i.e. where rs is the radius of the sonic point. It yields several types of solutions. Müller & Vink (2008) show that for the isothermal case and a line force as described in Eq. (6), analytical expressions for all types of solutions of Eq. (11) can be constructed by means of the Lambert W function (as for a further discussion of the solution of Eq. (11) containing an additional centrifugal term, see Müller2001). Even for the interesting trans-sonic case of a stellar wind, the analytical solution has an intricate shape. However, a useful approximate wind solution for the velocity law can be constructed if the pressure related terms 2a2/r and a/v can be neglected. We note, however, that at the sonic point the contribution of the two pressure terms is non-negligible (Müller & Vink 2008). After some manipulation one finds that the approximate velocity law is given by: 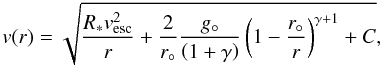 (12)where C is an integration constant. From this equation, the terminal wind velocity can be derived if the integration constant C can be determined. This can be done assuming that at radius r° the velocity approaches zero. This yields
(12)where C is an integration constant. From this equation, the terminal wind velocity can be derived if the integration constant C can be determined. This can be done assuming that at radius r° the velocity approaches zero. This yields 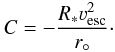 (13)In the limit r → ∞ we find that:
(13)In the limit r → ∞ we find that: 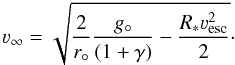 (14)The terminal velocity ν∞ can also be determined from the equation of motion. At the critical point, the left-hand and right-hand side of Eq. (11) both equal zero. Introducing ν∞ in relation to g° as expressed in Eq. (14), we find
(14)The terminal velocity ν∞ can also be determined from the equation of motion. At the critical point, the left-hand and right-hand side of Eq. (11) both equal zero. Introducing ν∞ in relation to g° as expressed in Eq. (14), we find ![\begin{equation} \label{eq:vinfnew} v_{\infty,{\rm new}} = \sqrt{\frac{2}{r_{\circ}} \left[ \left( \frac{r_{\rm s}}{r_{\rm s}-r_{\circ}} \right)^{\gamma} \frac{r_{\rm s}}{(1+\gamma)} \left( \frac{\vesc}{2} - 2 r_{\rm s} \right) - \vesc^2 \right]}. \end{equation}](/articles/aa/full_html/2012/01/aa15818-10/aa15818-10-eq53.png) (15)A direct comparison to the β-law can be made for the supersonic regime of the wind and results in
(15)A direct comparison to the β-law can be made for the supersonic regime of the wind and results in 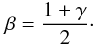 (16)Given the assumptions made in this derivation, this result is only approximately correct.
(16)Given the assumptions made in this derivation, this result is only approximately correct.
The procedure that is followed to obtain the best-β solution is that in each Monte Carlo simulation the values of g°, r°, and γ are determined by fitting the output line force. Using these values and the current value of the sonic point radius, Eqs. (14)–(16) are used to determine ν∞ and β. ν∞ derived from Eq. (15), the mass loss predicted in mc-wind, and the expression derived for β serve as input for a new isa-wind model. The two codes are iterated until convergence is achieved.
Following Müller & Vink (2008), we assume that convergence is achieved when the values for ν∞ derived from Eqs. (14) and (15) agree within 10 percent. This implies that our predicted terminal velocities have at least this uncertainty. Once the velocity convergence criterion is fulfilled all fit parameters and the values for Ṁ and the sonic point radius will be stable to within five to ten percent.
2.5. Method B: Hydrodynamic solution
The accuracy of the best-β solution hinges on the assumptions that the wind is isothermal and that the Eddington-factor Γ is constant (here taken to be equal to Γe). It may be expected that these assumptions have an impact on the velocity structure near the sonic point, which is where the mass-loss rate is set. To assess this impact and to improve on the physical treatment, we devise a numerical solution of the equation of motion (Eq. (11)) throughout the entire photosphere and wind, referred to as the hydrodynamic solution.
To this end we start our solution at the critical point ν = a and proceed both down-stream and up-stream using a 4th order Runge Kutta method with adaptive stepsize control (Press et al. 1992). Applying l’Hôpital’s rule (see e.g. Lamers & Cassinelli 1999) an expression can be devised to determine dv/dr at v(rs) = a. In order to determine the location of the sonic point rs we require 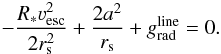 (17)The above equation is solved numerically.
(17)The above equation is solved numerically.
 |
Fig. 2 A comparison between the best-β and hydrodynamic velocity laws for an O3 V star. Here, the best-β velocity law is the one determined by using the fit-parameters of the hydrodynamic solution. The label “approx” in the left panel refers to the approximate velocity law, as given by Eq. (12). Three different radial regimes are plotted: full radial range (left panel); the region around the sonic point (middle panel) in which the location of the sonic point in the hydrodynamic solution is indicated with an arrow, and the photospheric region (right panel). Note that at high velocities both methods, as well as the approximate velocity law, yield very similar velocity stratifications. Near the sonic point the best-β velocity law is steeper than the hydrodynamic velocity law. Its sonic point is closer to the star. Given this difference, the right panel shows that in the photosphere where hydrostatic equilibrium controls the equation of motion, the shape of both velocity profiles is very similar. |
So far, the hydrodynamic solution assumes an iso-thermal medium. At the sonic point the temperature gradient is very small, therefore the location of rs can be reliably determined using Eq. (17), even if dT/dr would be taken into account. The neglect of the temperature gradient in the hydrodynamic solution in the region below the sonic point has a significant impact on the structure – for instance on the total (Rosseland) optical depth from the inner boundary to the sonic point. To solve this problem, we account for the temperature structure inward of the critical point. This requires an iterative procedure between the solution of the non-isothermal equation of motion 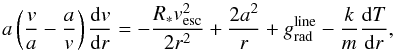 (18)and the temperature structure (see Sect. 2.1). After starting numerical integration of the velocity structure at the sonic point rs now determined by applying Eq. (17), but using the local value of the temperature at the sonic point) in the down-stream direction, we include the dT/dr term in Eq. (18). This implies that the location of the sonic point is not affected. In the up-stream direction the temperature gradient is negligible, and is ignored.
(18)and the temperature structure (see Sect. 2.1). After starting numerical integration of the velocity structure at the sonic point rs now determined by applying Eq. (17), but using the local value of the temperature at the sonic point) in the down-stream direction, we include the dT/dr term in Eq. (18). This implies that the location of the sonic point is not affected. In the up-stream direction the temperature gradient is negligible, and is ignored.
Figure 2 compares the best-β and hydrodynamic velocity laws for an O3 main sequence star. It shows that the best-β solution behaves very similar to the numerical velocity law. Note that if one zooms in on the location of the sonic point, one sees that for the best-β velocity structure rs is positioned slightly more inward, or, alternatively, that the velocity law is steeper in the lower part of the wind. In the best-β method, the absolute scaling of the velocity structure in the photosphere is based on the adopted velocity at the inner boundary of the model (see Sect. 2.1). Therefore, only the position of rs as predicted by the hydrodynamical method is physically meaningful, albeit in the context of the assumption Γ = Γe.
Once this iterative procedure has converged, and the non-LTE state of the gas is computed throughout the atmosphere, we iterate between isa-wind and mc-wind in the same manner as described in Sect. 2.4. Again, save for ν∞, the fit parameters converge on an accuracy of better than ten percent in a few iteration cycles. For ν∞ we are forced to adopt an accuracy of 20 percent. Our predicted terminal velocities have at least this uncertainty.
2.5.1. Remaining assumptions and uncertainties
In the hydrodynamic solution the contribution of bound-free and free-free opacity to the continuum radiation pressure is ignored (see Sect. 2.1). In the photosphere, the contribution of these processes to Γ is not negligible and may in fact be of the order of Γe.
We use the Sobolev approximation for line radiation transfer. The Sobolev approximation becomes ill-founded for small velocity gradients dv/dr or velocities lower than the sound speed. Pauldrach et al. (1986) showed that in the photosphere (where the velocity is very small) the line force is underestimated in the Sobolev approximation. Further out, in the region of the sonic point, the line optical depth is overestimated compared to co-moving frame values, implying an overestimate of the line force in this region and therefore an overestimate of the mass-loss rate.
In addition to the above two sources of uncertainty to the balance of forces at and below the sonic point is the quality of the fitting function Eq. (6) in this part of the wind, that may be uncertain by up to a factor of two. This is not expected to be a big problem deep in the photosphere, as both the fit function as well as the simulated Monte Carlo line force are small compared to the radiative force on free electrons, but at the sonic point it might play a role.
2.6. The line force at the sonic point: a test for the validity of the best-β method
The critical point of the equation of motion is the sonic point. A dissimilarity between the sonic point and the critical point may occur when the line force is represented by an explicit function of dv/dr, such as in CAK and modified-CAK theory (Pauldrach et al. 1986). Although these descriptions provide extremely valuable insights, they do make assumptions regarding the behavior of 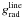 (see Sect. 4.2). The same applies for our method. Here we want to point out that Eq. (17) implies that – whatever the description of the line force – at the sonic point
(see Sect. 4.2). The same applies for our method. Here we want to point out that Eq. (17) implies that – whatever the description of the line force – at the sonic point 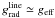 , as the pressure gradient terms 2a2/r and (k/m) dT/dr are small compared to the line force. This is characteristic for monotonic winds of early-type stars (see Feldmeier & Shlosman 2000, for non-monotonic flows). Here
, as the pressure gradient terms 2a2/r and (k/m) dT/dr are small compared to the line force. This is characteristic for monotonic winds of early-type stars (see Feldmeier & Shlosman 2000, for non-monotonic flows). Here 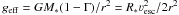 . This implies that for the velocity structure to be a physical solution it must be that at the sonic point
. This implies that for the velocity structure to be a physical solution it must be that at the sonic point 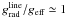 , as pointed out by e.g. Castor et al. (1975). We require from our best-β solutions, that this criterion is fulfilled. If
, as pointed out by e.g. Castor et al. (1975). We require from our best-β solutions, that this criterion is fulfilled. If 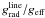 is not approximately equal to 1 at the sonic point, we interpret this as a failure of the wind to become trans-sonic due to a lack of line force at the location in the wind where it is essential. Dynamical effects might occur, such as fall back, that are beyond the topic of this paper. In any case, we interpret such solutions as cases in which the wind cannot be initiated by line driving alone. For the hydrodynamical solution a failure to fulfill the above requirement implies that we do not find a solution at all.
is not approximately equal to 1 at the sonic point, we interpret this as a failure of the wind to become trans-sonic due to a lack of line force at the location in the wind where it is essential. Dynamical effects might occur, such as fall back, that are beyond the topic of this paper. In any case, we interpret such solutions as cases in which the wind cannot be initiated by line driving alone. For the hydrodynamical solution a failure to fulfill the above requirement implies that we do not find a solution at all.
 |
Fig. 3 Predicted Ṁ, ν∞ and β for the main sequence stars. Best-β solutions are given in red and hydrodynamic solutions in green. For comparison, theoretical results by Vink et al. (2001) are provided in blue. |
3. Results
3.1. Grid
In order to study our predictions of the wind properties of O-type stars in a systematic manner, we define a grid of main sequence, giant and supergiant stars using the spectral calibration of Martins et al. (2005a) adopting theoretical effective temperature scales. This calibration is based on non-LTE models that take into account line blanketing effects and an outflowing stellar wind. We have applied solar abundances as derived by Anders & Grevesse (1989), consistent with the predictions of Vink et al. (2000). For all stars in the grid, we have derived the mass-loss rate, terminal velocity and β-parameter. The hydrodynamic solution does not feature a β, rather γ is the parameter that describes the slope of the velocity law. To better facilitate a comparison between the different methods we have applied Eq. (16) to convert γ into a β-value, referred to as βγ. The calculated grid is given in Table 1. The final column lists the mass-loss rate as predicted using the fitting formula of Vink et al. (2000) that assume a fixed value of β = 1, but for an input variable value of ν∞ = 2.6 νesc.
Figures 3–5 show wind properties as a function of effective temperature, for dwarfs, giants and supergiants respectively.
We present all the results of the best beta method, i.e. prior to applying the requirement defined in Sect. 2.6 that at the sonic point the acceleration due to the line force should approach the effective gravity. Having pointed this out, we first draw attention to the striking behavior in our best-β predictions of dwarfs. In the direction of decreasing temperature, the terminal flow velocity drastically increases for spectral types O6.5 or later. For giants the O7 star shows a similar behavior. We argue below that this behavior reflects the failure of the wind to become supersonic, therefore we interpret these solutions to be non-physical.
3.2. Early O-stars (spectral types O3 through O6)
Let us, however, first focus on stars of spectral type earlier than O6.5. The two methods give quite comparable results. The best-β method predicts Ṁ values that are higher by up to ~0.1 to 0.3 dex in all cases, i.e. dwarfs, giants and supergiants. The best-β terminal flow velocities are ~10 to 20 percent lower compared to the hydrodynamic solutions. These differences can be understood by focusing on the velocity structures near the sonic point. In the best-β solution the velocity law is steeper in the region near the sonic point, therefore the sonic point is closer to the photosphere. This leads to a higher mass-loss rate and lower terminal velocity. The absolute value of the terminal velocity and the ratio of ν∞ to the effective escape velocity as a function of temperature will be compared to observations in Sect. 4. Typical error bars on the ν∞ determination are 10 percent for the best-β solutions (see Sect. 2.4) and 20 percent for the exact solutions (see Sect. 2.5) due to Monte Carlo noise on the line force (see also Fig. 1).
The slope of the velocity law in the best-β solution increases slightly with luminosity class, from typically 0.85 in dwarfs, to 0.95 in giants, to 1.0 in supergiants. In the hydrodynamic models (method B) the βγ value is typically 0.05–0.10 lower than the corresponding best-β solution.
3.3. Late O-stars (spectral types O6.5 through O9.5)
Figures 3 and 4 show that for spectral type O6.5 the terminal velocity of dwarfs and giants suddenly peaks, relative to spectral type O6. We investigate this behavior in more detail in Fig. 6 in which the line force from the Monte Carlo simulation is plotted in the region around the sonic point for the best-β solutions of the dwarf O6 and O6.5 star. For the O6 star, the line force at the base of the wind (below the sonic point) rises steeply. At first the dominant contributors are iron lines, notably from Fe v. The ensemble of transitions mainly occur between excited states, although some are from meta-stable states that are relatively strongly populated. Further out, the iron contribution levels out (at ~30%) and other elements start to contribute to the force, such as carbon, nitrogen, sulfur, argon and nickel. The contribution of resonance lines of carbon and nitrogen at the sonic point amounts to ~20%. Note that at the sonic point the 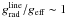 condition is nicely fulfilled for the O6 V.
condition is nicely fulfilled for the O6 V.
 |
Fig. 6 The Monte Carlo line force as a fraction of the effective gravity in the region around the sonic point for the best-β solution of the O6 V (top panel) and O6.5 V (bottom panel) stars. The contribution of iron is shown separately (blue dotted line). Note that in the case of the O6.5 star the line acceleration does not balance the effective gravity at the sonic point. This is interpreted as a failure to support a line driven wind. |
Model parameters, following Martins et al. (2005a), and predicted wind properties for dwarfs, giants and supergiants.
For the O6.5 star this is not the case. Here the line force at the base of the wind (below the sonic point) rises only gradually. The difference with the O6 V star is that in this region iron is mainly in the form of Fe iv, which for this particular spectral flux distribution is less efficient in absorbing stellar flux than are Fe v lines1. Therefore the velocity structure will be shallower, limiting the potential of other elements in contributing to the force. As a result the sonic point starts to shift out to larger radii, and we find that at the sonic point the cumulative line acceleration is some 40% less than the effective gravity. We therefore interpret this outcome as a failure of the wind to become supersonic at rs and do not consider it to be a physical solution.
The best-β solutions where we clearly encounter this problem have brackets placed around the predicted wind properties as listed in Table 1. These include all the dwarf stars of spectral type O6.5 or later. They are to be considered non-physical.
The supergiants do not suffer from this problem. In all cases the 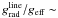 1 was reached at the sonic point and we consider them physical solutions. The terminal velocities for the O6.5 I to O9.5 I scatter by about 20%, with a small hint that here also the O6.5 star has a higher ν∞. The latter occurs because elements such as silicon, iron and sulfur add to the line force in the outer wind along with the normal contribution of carbon, nitrogen and oxygen.
1 was reached at the sonic point and we consider them physical solutions. The terminal velocities for the O6.5 I to O9.5 I scatter by about 20%, with a small hint that here also the O6.5 star has a higher ν∞. The latter occurs because elements such as silicon, iron and sulfur add to the line force in the outer wind along with the normal contribution of carbon, nitrogen and oxygen.
The value of β for the late spectral types increases to 1.05 from 1.0 for earlier spectral types. The βγ values associated to the hydrodynamic solutions increase marginally compared to that in early-O stars.
4. Discussion
In discussing our results we first compare with previous theoretical predictions for mass-loss rates and terminal velocities in Sects. 4.1 and 4.2. We compare to observations in Sect. 4.3.
 |
Fig. 7 The wind energy as a function of the effective temperature for dwarfs (left panel), giants (middle panel) and supergiants (right panel). The best-β method is given by the red squares, the hydrodynamic method by the green circles and the Vink et al.-recipe by the blue triangles. Note that the kinetic energy in the wind is almost equal for all three methods. The mass-loss rate and terminal velocity for the three methods vary. |
4.1. Comparison to Vink et al. mass-loss recipe
The Monte Carlo method by de Koter et al. (1997) as summarized in Sect. 2 has been used by Vink et al. (2000, 2001) to compute a grid of mass-loss rates for O-type stars from which a fitting formula has been derived that provides Ṁ as a function of luminosity, effective temperature, mass and the ratio of the terminal velocity over the effective escape velocity, i.e. ν∞/νesc. This mass loss prescription is widely used in stellar evolution predictions (see e.g. Meynet & Maeder 2003; Palacios et al. 2005; Limongi & Chieffi 2006; Eldridge & Vink 2006; Brott et al. 2009; Vink et al. 2010).
For the spectral range that is investigated here the canonical value, based on empirical findings, for the ratio of terminal velocity over escape velocity is 2.6. To compare to the Vink et al. (2000) results, we calculated the mass-loss rate of our grid of stars using their prescription, that assumes β = 1. The results are given in the last column of Table 1. Figure 7 shows the total energy that is extracted from the radiation field and that is transferred to the stellar wind for all three methods: best-β, hydrodynamic and Vink et al. prescription. All three methods yield similar, but not identical results in the regime where the best-β and hydrodynamical method provide physical solutions. In terms of mass loss rates, we find that the predictions with the best-β and hydrodynamical method are on average about 0.2 to 0.3 dex lower than Vink et al., again with the clear exception of the stars for which we fail to drive a stellar wind. As suggested by the similar wind energies the terminal velocities predicted by our best-β and hydrodynamical method turn out to be higher than adopted by Vink et al.. We discuss these ν∞ in more detail in Sect. 4.3 as well as the reason why Vink et al. are able to predict Ṁ values for late O-type dwarfs and giants, where we fail.
We emphasize that if the Vink et al. prescription is used assuming the terminal velocities predicted by our best-β or hydrodynamical method, wherever these yield physical solutions, the mass loss rates agree to within ~ 0.1 dex.
4.2. Comparison to (modified) CAK-theory
Since Lucy & Solomon (1970) it is generally accepted that the winds of massive stars are driven by the transfer of momentum (and energy) from the radiation field to the atmospheric gas, and that atomic transitions play a pivotal role in this process. Castor et al. (1975) describe the force associated to atomic transitions by introducing a force multiplier 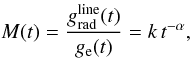 (19)where k and α are fitting parameters and t is an optical depth like parameter given by:
(19)where k and α are fitting parameters and t is an optical depth like parameter given by: 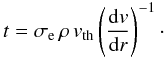 (20)Here ρ is the density, vth the thermal velocity of carbon ions at the effective temperature of the star (Pauldrach et al. 1986) and σe the mass scattering coefficient of the free electrons. This parametrization of the line force is based on the expression of the force multiplier for a single spectral line,
(20)Here ρ is the density, vth the thermal velocity of carbon ions at the effective temperature of the star (Pauldrach et al. 1986) and σe the mass scattering coefficient of the free electrons. This parametrization of the line force is based on the expression of the force multiplier for a single spectral line, ![\begin{equation} \label{eq:cakline} M_{\rm line}(t) = \frac{\Delta\nu_{\rm D} \,F_{\nu}}{F} \frac{1}{t} \left[ 1-\exp{(\eta t)} \right], \end{equation}](/articles/aa/full_html/2012/01/aa15818-10/aa15818-10-eq95.png) (21)where ΔνD is the Doppler shift of the frequency of the spectral line due to the thermal velocity of the particles in the wind, Fν is the flux at frequency ν, F the total flux and η is the ratio of line opacity to electron scattering opacity. Note that for optically thin lines Mline(t) becomes independent of t, whilst for optically thick lines Mline(t) ∝ t. The cumulative effect of an ensemble of lines of various strengths is then expressed by Eq. (19). The constant α in this expression is a measure of the ratio of line acceleration from optically thick lines only to the total line acceleration and k is related to the overall (line)strength of the ensemble of lines. See Puls et al. (2000) for a more in depth discussion on the CAK line force. It is assumed that α and k are constants throughout the wind (but see Kudritzki 2002). The effects of changes in the ionization structure of the wind are modeled by multiplying expression 19 by the term (ne/W)δ, introduced by Abbott (1982). ne is the electron number density, W the dilution factor and δ is a constant.
(21)where ΔνD is the Doppler shift of the frequency of the spectral line due to the thermal velocity of the particles in the wind, Fν is the flux at frequency ν, F the total flux and η is the ratio of line opacity to electron scattering opacity. Note that for optically thin lines Mline(t) becomes independent of t, whilst for optically thick lines Mline(t) ∝ t. The cumulative effect of an ensemble of lines of various strengths is then expressed by Eq. (19). The constant α in this expression is a measure of the ratio of line acceleration from optically thick lines only to the total line acceleration and k is related to the overall (line)strength of the ensemble of lines. See Puls et al. (2000) for a more in depth discussion on the CAK line force. It is assumed that α and k are constants throughout the wind (but see Kudritzki 2002). The effects of changes in the ionization structure of the wind are modeled by multiplying expression 19 by the term (ne/W)δ, introduced by Abbott (1982). ne is the electron number density, W the dilution factor and δ is a constant.
The parametrization of the line force as given by Eq. (19) leads to an analytical expression for Ṁ and ν∞ as a function of the fitting parameters k and α and the stellar parameters. These expressions are given by Castor et al. (1975). Pauldrach et al. (1986) extend these expressions to account for the finite size of the stellar disk.
To allow for a comparison with Abbott’s results for the behavior of the force multiplier as a function of t, we ignore the effect of ne/W. We calculated the force multiplier of the simulated line force, i.e. Eq. (6), at all our radius grid points and determined the corresponding value t. Typically, the optical depth like parameter ranges from t = 10-5 to large t. At large t the line force can be neglected compared to the continuum radiation force. Following Abbott (1982), we do not consider these large t points in this discussion but we focus on the range t < 10-0.5.
 |
Fig. 8 Top panel: the logarithm of the force multiplier M(t) for the hydrodynamic solution of our O3 V model (red plusses) as a function of the optical depth like parameter t; our fit function Eq. (6) to this data (green line) and the CAK fit function Eq. (19) to this data (blue line). Bottom panel: the force multiplier as a function of radius r for the same star. Note that the CAK force multiplier is smaller than ours for large radii, resulting in a lower predicted ν∞. |
Figure 8 compares the behavior of the force multiplier for our best-β solution of the O3 V star. Note that our Monte Carlo solution shows that M(t) can not be fully described by a strict power law, as assumed in (modified) CAK, or equivalently, α is not independent of t (Vink 2000). Two causes can be pointed out (see e.g. Puls 1987; Schaerer & de Koter 1997): i) the presence of a diffuse field due to multiple scatterings; ii) a complex behavior of radial stratification of the excitation and ionization, specifically near the sonic point. Here the wind accelerates rapidly, which causes a sudden steep drop in the electron density. As a result, elements which happen to have two dominant ionization stages (near rs) may temporarily re-ionize.
The introduction of a δ-dependence of the CAK force multiplier in Eq. (19), by adding the term (ne/W)δ, does not improve the fit to the Monte Carlo line force. This extended CAK description describes a plane through the three dimensional space spanned by the logarithms of t, ne/W and M(t), while the Monte Carlo line force follows a curved line through this space and is thus not confined to that plane.
Our fitting function, Eq. (6), nicely captures the curved behavior of the line force in the supersonic part of the flow2.
Using the force multipliers k and α as derived from the Monte Carlo line force we can compute the CAK mass loss and terminal velocity (Castor et al. 1975). The ṀCAK values derived from these k and α are typically 0.0 to 0.3 dex higher than our best-β results and our hydrodynamic solutions. A comparison of the terminal velocities is not meaningful since the slope in the supersonic part of the wind is not represented well by α. Therefore, the velocities derived with our k and α are on the order of the escape velocity. If we compare to the modified CAK terminal velocities, following (Pauldrach et al. 1986), we note that they are slightly lower than the velocities we derive (see also Sect. 4.3.1).
4.3. Comparison with observations
In this section, we compare our results to observations. We first compare predicted and empirical terminal velocities. Given that we find that for stars more luminous than 105.2 L⊙ our mass-loss rates agree well with the Vink et al. prescription – which has been extensively scrutinized (see e.g. Repolust et al. 2004) – we focus the comparison of empirical and predicted mass-loss rates on lower luminosity stars, for which a “weak-wind problem” has been identified.
4.3.1. Terminal velocities
Several studies have been devoted to measuring the terminal velocities of early-type stars. Summarizing the work by Howarth & Prinja (1989); Prinja et al. (1990); Lamers et al. (1995); Howarth et al. (1997); Puls et al. (1996), and Kudritzki et al. (1999), Kudritzki & Puls (2000) derive that the average value of empirically determined terminal velocities for stars hotter than 21 000 K is ν∞ = 2.65 νesc. The quoted accuracy of this mean value is roughly 20 percent. The ν∞ values are “measured” from the maximum blue-shifted absorption vmax in resonance lines of ions such as C iv, N v and Si iv, located in the ultraviolet part of the spectrum. These measurements are prone to systematic uncertainties, that have been extensive discussed in the literature (see for instance the above references). They may work in both directions. Effects that may cause the terminal velocity to be higher than vmax are measurements from lines that are not saturated in the outer wind (where for all practical purposes ν∞ is reached) or from ions that recombine in the outer wind. The former may be expected for stars with weak winds, the latter is more likely to occur in very dense winds. Effects that may cause ν∞ to be smaller than vmax may be the presence of turbulence in the outflow or the presence of strong atmospheric absorption at wavelengths slightly bluer than the wavelength corresponding to the terminal velocity, mistakenly contributed to absorption in the resonance line. Given the possible occurrence of these systematic effects, the uncertainty in the terminal velocity may be 10–15 percent for supergiants, and substantially larger than 20 percent for dwarfs. The error in the ratio ν∞/νesc also includes uncertainties in νesc. The largest contribution to this error comes from uncertainties in the stellar masses, that have been derived from a comparison to tracks of stellar evolution. It seems realistic to adopt a 30–40 percent uncertainty in the empirical values of ν∞/νesc rather than the 20 percent; quoted at the beginning of this section.
Although Kudritzki & Puls (2000) (and also Lamers et al.1995) conclude that the ratio ν∞/νesc is constant for O-type stars, the results of Howarth & Prinja (1989) show this ratio to decrease with temperature, from about 3.5 at 31 500 K to about 2.4 at 43 500 K. A luminosity class dependence of ν∞/νesc has to our knowledge not yet been reported.
 |
Fig. 9 Predictions of the ratio of terminal velocity over effective escape velocity at the surface for both the best-β (in red) and hydrodynamic method (in green) as a function of effective temperature. The blue circles denote the data from Lamers et al. (1995) and the black triangles show the empirical values from Howarth & Prinja (1989) in which ν∞ is determined from the ultraviolet P-Cygni profiles. |
Figure 9 shows our predictions of ν∞/νesc plotted against temperature. Different symbol types denote best-β, hydrodynamic results and empirical values from Howarth & Prinja (1989) and Lamers et al. (1995). As discussed in Sects. 2.4 and 2.5 our predictions of ν∞ have individual random error bars of 10 to 20 percent
In all cases, our predictions result in terminal velocities that are larger than observed. For the main sequence O3-O6 stars the mean predicted ratio is 3.1 for the best-β method and 3.6 for the hydrodynamical method. This is 17% and 36% higher than the observed mean value of 2.65. For giants the discrepancies are respectively 30% and 44%. For the supergiants the largest discrepancies are found. Using all O stars, the best-β method over-predicts the ratio by 54%. The hydrodynamical method yields values that are on average 60% higher. The discrepancy between theory and observations thus seems to increase from dwarfs to giants to supergiants. Given the uncertainties, the over-prediction for the dwarfs may not be significant.
The predictions show a tentative trend of a decreasing ν∞/νesc with temperature. As pointed out, recent empirical studies do not recover this behavior. Interestingly, this type of trend appears to be visible in the study by Howarth & Prinja (1989). Their trend is plotted in Fig. 9, featuring a slope that is comparable to the slope of our predictions. However, given the uncertainties in the current empirical estimates of ν∞, we do not feel that this can be applied to (further) scrutinize the theory.
Larger predicted terminal velocities are also reported by Lamers et al. (1995). In their sample, dominated by supergiants, a comparison to CAK models yields over-predictions by about 33 percent, so slightly less compared to what we find. The reason for the over-predicted ν∞ values is unclear. Possible explanations (for part of the problem) include, i) overestimated corrections for the effect of turbulence (see above); ii) a clumped and porous outer wind, hampering the acceleration of the flow in this part of the outflow from reaching as high a terminal velocity as predicted here and in (modified) CAK (see Muijres et al. 2011); or iii) a systematic over-estimate of stellar masses. A systematic discrepancy between masses of galactic stars derived from comparing their positions in the Hertzsprung-Russell diagram to evolutionary tracks and masses calculated from the spectroscopically determined gravity was reported by e.g. Herrero et al. (1992, but see Weidner & Vink 2010. Improvements in both the model atmospheres and fitting procedure seem to have reduced, but possibly not yet eliminated, the size of this discrepancy (Repolust et al. 2004; Mokiem et al. 2005).
Unfortunately, progress in resolving the differences in predicted and empirical ν∞/νesc ratios quite strongly depends on our knowledge of stellar masses. Hopefully, detailed studies of very large populations, such as the VLT-FLAMES Survey of massive stars (Evans et al. 2005) and the VLT-FLAMES Tarantula Survey (Evans et al. 2011) may help resolve this issue.
4.3.2. Mass loss rates: the weak-wind problem
Relatively recent, analysis of appreciable samples of galactic stars using sophisticated model atmospheres has revealed a mismatch, possibly as high as a factor of 100, between empirically derived mass-loss rates and theoretical predictions for stars less luminous than about 105.2 L⊙ (see e.g. Martins et al. 2005b; Mokiem et al. 2007; Marcolino et al. 2009, and Fig. 10). As mass loss scales with some power of the luminosity, this problem occurs below a critical mass-flux and is termed the “weak-wind” problem (for a recent review, see Puls et al. 2008). Proposed explanations address deficiencies in determining the empirical mass-loss rates as well as in mass-loss predictions. Regarding empirical Ṁ determinations it should be realized that only UV resonance lines can be used as a diagnostic in the weak-wind regime, whilst in the (lets call it the) strong wind regime Hα and, in the Galactic case, radio-fluxes may also be used. The ions that produce the UV resonance profiles, such as C iv, N v and Si iv, often represent minor ionization species. The ionization continua of these species border the soft X-ray regime and therefore wind material may be susceptible to (non-thermal) processes producing soft X-ray emission, such as shocks or magnetic mechanisms (Martins et al. 2005b).
From a theoretical viewpoint, potential causes of the weak-wind problem include the decoupling of the major driving ions (the metals) from the bulk of the plasma at low densities, when Coulomb coupling fails, and the subsequent ionic runaway (Springmann & Pauldrach 1992; Babel 1995, 1996; Krtička & Kubát 2000; Owocki & Puls 2002; Krtička et al. 2003); the shadowing of wind-driving lines by photospheric lines (Babel 1996), and the neglect of curvature terms in the velocity field (Puls et al. 1998; Owocki & Puls 1999).
The results presented in this paper point to a cause for the weak winds related to the predictions of mass loss. This potential cause was quantitatively explored by Lucy (2010), who pointed out that the global dynamical constraint imposed by Vink et al. (2000) and recapped in Sect. 2.2 (notably Eq. (4)) need not guarantee that the derived mass-loss rates are consistent with stationary trans-sonic flows. Here we have shown that although this assumption by Vink et al. (2000) is allowed for stars with luminosities above 105.2 L⊙, it is not for lower luminosities. This luminosity limit for galactic O stars agrees with the empirical limit at ~105.2 L⊙ to within 0.1 dex in log L. The physical cause of the different Ṁ regimes (weak and strong winds) is a lack of line acceleration at the base of the wind. In main sequence stars, a contribution of Fe v lines is present in O6 stars and is missing in the (lower luminosity and cooler) O6.5 stars, where Fe iv is more dominant (see Sect. 3.3). The importance of the Fe v/iv ionization balance has been pointed out by Lucy (2010) and is confirmed by our results.
In one fundamental aspect our results differ from that of Lucy (2010). For the sample of low luminosity stars (i.e. less than 105.2 L⊙) investigated by Marcolino et al. (2009), Lucy (2010) predicts mass-loss rates that are about 1.4 dex lower than anticipated by Vink et al. (2000). The hydrodynamical method presented in this paper, which identifies the ability of the star to drive an outflow with a balance of the line force and the gravitational force at the sonic point, predicts that these stars do not have a wind at all. As it is clear form the presence of the shape of UV resonance lines that these stars do have stellar winds (with average mass loss rates that are 0.8 dex lower than Lucy’s predictions), our result suggests that either some other mechanism is driving the wind or is supplementing the line acceleration at the base of the wind. Which force (or forces) counterbalances gravity remains to be identified, but perhaps magnetic pressure, effects of turbulence, and/or pulsations may play a role.
We do point out that once material is accelerated, there is sufficient opacity available to further accelerate it to larger velocities. Interestingly, Martins et al. (2005b) report that for their sample of galactic weak-wind objects the average value of ν∞/νesc is rather close to unity, and not 2.65. Although they concede that given the low wind densities their ν∞ values may be lower limits, they point to a mechanism of X-ray heating proposed by Drew et al. (1994) that may perhaps explain these results. In the outer atmospheres of weak winds the cooling times can become quite long, such that heating of the material in for instance shocks may warm up the medium and strongly modify the ionization structure, in effect canceling the line force.
Modified CAK theory does not predict the weak-wind discontinuity. In this theory the adopted values for k and α are based on the input stellar spectrum, while the dilution and excitation/ionization changes throughout the wind are described by a fixed δ. Therefore, no self-consistent feedback between the wind properties and the line acceleration is accounted for. We note that in the predictions by Pauldrach et al. (2001) a change of slope of the modified wind momentum luminosity relation can be seen at a luminosity of about 105.2 L⊙. It is tentative to suggest that if Pauldrach et al. would have implemented the iterative procedure that we use, they might have identified a weak-wind regime on theoretical grounds.
 |
Fig. 10 The modified wind momentum |
5. Conclusions
We have presented new mass-loss rates and terminal wind velocities for a grid of massive O-type stars, improving the treatment of physics in the Monte Carlo method by Abbott & Lucy (1985) and de Koter et al. (1997) to predict wind properties of early-type stars. Two new types of solutions have been discussed. First, building on the work of Müller & Vink (2008), we present so-called best-β solutions in which one still assumes a β-type velocity law (see Eq. (2)) in the wind, but in which the terminal velocity and β are no longer adopted but constrained by requiring that they best fit the line force (distribution). Second, we abandon the β-type velocity structure and introduce numerical solutions of the wind stratification. Our main conclusions are:
-
1.
For stars more luminous than 105.2 L⊙ the best-β and hydrodynamical method yield β and ν∞ results in agreement with each other (within 5–20 percent), whilst the mass-loss rates agree within a factor of 2.
-
2.
Furthermore, both methods are in very good agreement with the mass-loss prescription by Vink et al. (2000) using our terminal velocities in their recipe. This implies that the main assumption entering the method on which the Vink et al. results are based – i.e. that the momentum equation is not solved explicitly – is not compromising their predicted Ṁ in this luminosity range. Terminal velocity is an input parameter to the Vink et al. recipe. If we apply the canonical value ν∞ = 2.6νesc, the discrepancy between our mass-loss rates and their mass-loss rates is of the order of 0.2,althoughoccasionally0.6dex.
-
3.
At luminosities ≲ 105.2 L⊙ our hydrodynamical method fails to produce an outflow because of a lack of line driving at the base of the wind. This critical luminosity coincides with the onset of the “weak-wind problem”.
-
4.
For O dwarfs the above luminosity criterion translates to a boundary between starting and failing to start a wind at O6/O6.5. The direct cause of the failure to start a wind in O6.5 V stars is the lower luminosity and the lack of Fe v lines at the base of the wind compared to O6 V stars.
-
5.
The fact that our hydrodynamical method fails to drive a wind at L ≲ 105.2 L⊙ may imply that some other mechanism is driving the weak winds or is supplementing the line acceleration at the base of the wind to help drive gas and initiate the wind.
-
6.
For stars more luminous than 105.2 L⊙ we predict, using the best-β and hydrodynamical method, terminal velocities that are typically 35 and 45 percent higher than observed. Such over-predictions are similar to what is seen in MCAK-theory (Lamers et al. 1995).
-
7.
We predict beta values in the range 0.85 to 1.05, with a trend that supergiants have slightly higher β values than dwarfs. This range of β values agrees very well with empirical results by Massa et al. (2003).
We note that a similar situation occurs at spectral type B1, where the relatively inefficient Fe iv lines are replaced by the more effective Fe iii lines (Vink et al. 1999).
We also compared our fitting formula to the output of the starting model of the iteration cycle of the O3 V star. This allows us to assess whether the iteration procedure perhaps forces the line force into the shape of Eq. (6). However, also the line force resulting from the first iteration cycle is well represented by our description, indicating that it is quite generic.
Acknowledgments
We would like to thank the referee Achim Feldmeier for constructive comments.
References
- Abbott, D. C. 1982, ApJ, 259, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Babel, J. 1995, A&A, 301, 823 [Google Scholar]
- Babel, J. 1996, A&A, 309, 867 [NASA ADS] [Google Scholar]
- Brott, I., Hunter, I., de Koter, A., et al. 2009, Comm. Asteroseismol., 158, 55 [NASA ADS] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Chiosi, C., & Maeder, A. 1986, ARA&A, 24, 329 [NASA ADS] [CrossRef] [Google Scholar]
- de Koter, A., Heap, S. R., & Hubeny, I. 1997, ApJ, 477, 792 [Google Scholar]
- de Koter, A., Schmutz, W., & Lamers, H. J. G. L. M. 1993, A&A, 277, 561 [NASA ADS] [Google Scholar]
- Drew, J. E., Hoare, M. G., & Denby, M. 1994, MNRAS, 266, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Vink, J. S. 2006, A&A, 452, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Smartt, S. J., Lee, J., et al. 2005, A&A, 437, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmeier, A., & Shlosman, I. 2000, ApJ, 532, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209 [NASA ADS] [Google Scholar]
- Howarth, I. D., & Prinja, R. K. 1989, ApJS, 69, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A. J., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Krtička, J., & Kubát, J. 2000, A&A, 359, 983 [NASA ADS] [Google Scholar]
- Krtička, J., & Kubát, J. 2004, A&A, 417, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., Owocki, S. P., Kubát, J., Galloway, R. K., & Brown, J. C. 2003, A&A, 402, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R. P. 2002, ApJ, 577, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P., Puls, J., Lennon, D. J., et al. 1999, A&A, 350, 970 [NASA ADS] [Google Scholar]
- Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to Stellar Winds (Introduction to Stellar Winds, ed. H. J. G. L. M. Lamers, & J. P. Cassinelli (Cambridge, UK: Cambridge University Press), 452 [Google Scholar]
- Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
- Limongi, M., & Chieffi, A. 2006, ApJ, 647, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 2010, A&A, 512, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1981, A&A, 99, 97 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Marcolino, W. L. F., Bouret, J., Martins, F., et al. 2009, A&A, 498, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005a, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., Hillier, D. J., et al. 2005b, A&A, 441, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massa, D., Fullerton, A. W., Sonneborn, G., & Hutchings, J. B. 2003, ApJ, 586, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mokiem, M. R., de Koter, A., Puls, J., et al. 2005, A&A, 441, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muijres, L. E., de Koter, A., Vink, J. S., et al. 2011, A&A, 526, A32 [Google Scholar]
- Müller, P. E. 2001, Ph.D. Thesis, Univ. of Heidelberg, Germany, http://www.ub.uni-heidelberg.de/archiv/1422 [Google Scholar]
- Müller, P. E., & Vink, J. S. 2008, A&A, 492, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owocki, S. P., & Puls, J. 1999, ApJ, 510, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Puls, J. 2002, ApJ, 568, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Palacios, A., Arnould, M., & Meynet, G. 2005, A&A, 443, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, ed. P. W. H., Teukolsky, S. A., Vetterling, & W. T. B. P. Flannery [Google Scholar]
- Prinja, R. K., Barlow, M. J., & Howarth, I. D. 1990, ApJ, 361, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J. 1987, A&A, 184, 227 [NASA ADS] [Google Scholar]
- Puls, J., Kudritzki, R., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS] [Google Scholar]
- Puls, J., Kudritzki, R., Santolaya-Rey, A. E., et al. 1998, in Properties of Hot Luminous Stars, ed. I. Howarth, ASP Conf. Ser., 131, 245 [Google Scholar]
- Puls, J., Springmann, U., & Lennon, M. 2000, A&AS, 141, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&A Rev., 16, 209 [Google Scholar]
- Repolust, T., Puls, J., & Herrero, A. 2004, A&A, 415, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., & de Koter, A. 1997, A&A, 322, 598 [NASA ADS] [Google Scholar]
- Sobolev, V. V. 1960, Moving envelopes of stars, ed. V. V. Sobolev [Google Scholar]
- Springmann, U. W. E., & Pauldrach, A. W. A. 1992, A&A, 262, 515 [NASA ADS] [Google Scholar]
- Vink, J. S. 2000, Ph.D. Thesis, Universiteit Utrecht [Google Scholar]
- Vink, J. S., & de Koter, A. 2002, A&A, 393, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 1999, A&A, 350, 181 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Brott, I., Gräfener, G., et al. 2010, A&A, 512, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidner, C., & Vink, J. S. 2010, A&A, 524, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Model parameters, following Martins et al. (2005a), and predicted wind properties for dwarfs, giants and supergiants.
All Figures
 |
Fig. 1 The line force (blue crosses) as predicted by mc-wind in the first iteration step. A fit (black dotted line) using Eq. (6) to represent the line force is overplotted. Note the modest scatter on the Monte Carlo results due to noise. |
| In the text | |
 |
Fig. 2 A comparison between the best-β and hydrodynamic velocity laws for an O3 V star. Here, the best-β velocity law is the one determined by using the fit-parameters of the hydrodynamic solution. The label “approx” in the left panel refers to the approximate velocity law, as given by Eq. (12). Three different radial regimes are plotted: full radial range (left panel); the region around the sonic point (middle panel) in which the location of the sonic point in the hydrodynamic solution is indicated with an arrow, and the photospheric region (right panel). Note that at high velocities both methods, as well as the approximate velocity law, yield very similar velocity stratifications. Near the sonic point the best-β velocity law is steeper than the hydrodynamic velocity law. Its sonic point is closer to the star. Given this difference, the right panel shows that in the photosphere where hydrostatic equilibrium controls the equation of motion, the shape of both velocity profiles is very similar. |
| In the text | |
 |
Fig. 3 Predicted Ṁ, ν∞ and β for the main sequence stars. Best-β solutions are given in red and hydrodynamic solutions in green. For comparison, theoretical results by Vink et al. (2001) are provided in blue. |
| In the text | |
 |
Fig. 4 Predicted Ṁ, ν∞ and β for giants. Colors have the same meaning as in Fig. 3. |
| In the text | |
 |
Fig. 5 Predicted Ṁ, ν∞ and β for supergiants. Colors have the same meaning as in Fig. 3. |
| In the text | |
 |
Fig. 6 The Monte Carlo line force as a fraction of the effective gravity in the region around the sonic point for the best-β solution of the O6 V (top panel) and O6.5 V (bottom panel) stars. The contribution of iron is shown separately (blue dotted line). Note that in the case of the O6.5 star the line acceleration does not balance the effective gravity at the sonic point. This is interpreted as a failure to support a line driven wind. |
| In the text | |
 |
Fig. 7 The wind energy as a function of the effective temperature for dwarfs (left panel), giants (middle panel) and supergiants (right panel). The best-β method is given by the red squares, the hydrodynamic method by the green circles and the Vink et al.-recipe by the blue triangles. Note that the kinetic energy in the wind is almost equal for all three methods. The mass-loss rate and terminal velocity for the three methods vary. |
| In the text | |
 |
Fig. 8 Top panel: the logarithm of the force multiplier M(t) for the hydrodynamic solution of our O3 V model (red plusses) as a function of the optical depth like parameter t; our fit function Eq. (6) to this data (green line) and the CAK fit function Eq. (19) to this data (blue line). Bottom panel: the force multiplier as a function of radius r for the same star. Note that the CAK force multiplier is smaller than ours for large radii, resulting in a lower predicted ν∞. |
| In the text | |
 |
Fig. 9 Predictions of the ratio of terminal velocity over effective escape velocity at the surface for both the best-β (in red) and hydrodynamic method (in green) as a function of effective temperature. The blue circles denote the data from Lamers et al. (1995) and the black triangles show the empirical values from Howarth & Prinja (1989) in which ν∞ is determined from the ultraviolet P-Cygni profiles. |
| In the text | |
 |
Fig. 10 The modified wind momentum |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.