| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201118024 | |
| Published online | 19 December 2011 | |
Compression of matter in the center of accreting neutron stars
1 N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
e-mail: bejger@camk.edu.pl; jlz@camk.edu.pl; haensel@camk.edu.pl;
2 LUTh, UMR 8102 du CNRS, Observatoire de Paris, 92195 Meudon Cedex, France
e-mail: morgane.fortin@obspm.fr
Received: 5 September 2011
Accepted: 26 October 2011
Aims. To estimate the feasibility of dense-matter phase transition, we studied the evolution of the central density as well as the baryon chemical potential of accreting neutron stars. We compared the thin-disk accretion with and without the magnetic field torque with the spin-down scenario for a selection of recent equations of state.
Methods. We compared the prevalent (in the recycled-pulsar context) Keplerian thin-disk model, in which the matter is accreted from the marginally-stable circular orbit, with the recent magnetic-torque model that takes into account the influence of stellar magnetic field on the effective inner boundary of the disk. Calculations were performed using a multi-domain spectral methods code in the framework of General Relativity. We considered three equations of state consistent with the recently measured mass of PSR J1614-2230, 1.97 ± 0.04 M⊙ (one of them softened by the appearance of hyperons).
Results. If there is no magnetic torque and efficient angular momentum transfer from the disk to the star, substantial central compression is limited to the region of initial stellar masses close to the maximum mass. Outside the maximum mass vicinity, accretion-induced central compression is significant only if the angular momentum transfer is inefficient. Accounting for the magnetic field effectively decreases the efficiency of angular momentum transfer and implies a significant central compression.
Conclusions. An efficient angular momentum transfer from a thin disk onto a non-magnetized neutron star does not provide a good mechanism for the central compression and possible phase transition. Substantial central compression is possible for a broad range of masses of slowly-rotating initial configurations for magnetized neutron stars. Accretion-induced central compression is particularly strong for stiff equation of state with a high-density softening.
Key words: stars: neutron / accretion, accretion disks / magnetic fields / pulsars: general / dense matter
© ESO, 2011
1. Introduction
Neutron stars (NSs) are detected in binary systems by X- and γ-ray observatories because of the immense amounts of radiation released in the process of accretion of matter falling from a companion star onto the NS surface. Because the stellar mass increases during accretion, it is usually assumed that the density in the center of the star increases as well, and that a sufficient increase of mass may result in a phase transition (the details of which are not yet fully known). It is expected that a phase transition in the NS core might cause observable astrophysical phenomena, such as star-quakes, spin clustering, gravitational wave emission and therefore serve, it is hoped, as a testbed for the quantum chromodynamics (QCD) phase diagram (Cheng & Dai 1998; Glendenning & Weber 2001; Blaschke et al. 2001; Zdunik et al. 2005; Blaschke et al. 2008; Xu & Liang 2009 and references therein).
We aim to show with three recent equations of state (EOSs) of NS cores, that the central baryon number density, nc, and the baryon chemical potential, μc, may change in a non-trivial way while the star gains in mass and simultaneously increases its rotation rate during accretion. In particular, we will study whether, and if so, to what extent, the evolution of nc and μc depends on the EOS of dense matter. Our considered EOSs are consistent with the recently-measured mass of PSR J1614-2230, 1.97 ± 0.04 M⊙ (Demorest et al. 2010). Complementary questions that may be asked are (a) how does the actual efficiency of the angular-momentum transfer and the stellar magnetic field coupling to the disk affect the final rapidly-rotating NS configuration; and (b) how does the accretion-induced evolution depend on the mass of the initially slowly rotating configuration. Thus far, the formation of millisecond pulsars was most often modeled following the classical paper of Cook et al. (1994) who assumed the stellar magnetic field is sufficiently weak that it does not influence the accretion flow significantly; consequently, one assumed B = 0 and the accretion from the marginally-stable circular orbit (of radius rms). Notable exceptions were Possenti et al. (1999), Burderi et al. (1999), Blaschke et al. (2001), Colpi et al. (2001), and Blaschke et al. (2008), who used simple models of magnetic torque acting in the NS-accretion-disk system (Ghosh & Lamb 1979, see also Ghosh & Lamb 1991).
Here we compare the results obtained using the B = 0 approach with those employing the recent effective magnetic-torque model of Kluźniak & Rappaport (2007), used recently by Bejger et al. (2011) to study the formation of a millisecond pulsar PSR 1903+0327. The details of magnetic-field decay during the accretion-driven evolution phase of an NS’ life are still far from being understood in spite of theoretical and observational efforts in recent years (see Sect. 4 of Bejger et al. 2011 for a brief summary). Hence, we employ the simplest possible description of the magnetic-field decay that was shown to be consistent with at least a subclass of observed accreting NSs (Shibazaki et al. 1989) – this approach allows us to study the qualitative features of the influence of disk accretion on the behavior of the NS central parameters.
The text is organized in the following way. Section 2 gives a short description of the methods used to obtain the accreting NS tracks. The results are presented in Sect. 3. Section 4 contains our summary and conclusions.
2. Methods and models
We simulated the spin evolution of NSs caused by the thin-disk accretion without a magnetic field and compared it with the results for the magnetic-torque model of Kluźniak & Rappaport (2007). Because the original Newtonian magnetic-torque model was insufficient in extreme cases of rapidly-rotating, massive and compact NSs, we additionally employed the modification by Bejger et al. (2011), which takes into account the relativistic effects caused by the existence of the marginally-stable circular orbit (recalled briefly in the Appendix). We considered three recent EOSs – APR EOS by Akmal et al. (1998), DH EOS by Douchin & Haensel (2001) and BM EOS from a set of non-linear relativistic mean field models of Bednarek & Mańka (2009)1. The first two EOSs assume nucleon NS cores, while the BM EOS has a characteristic high-density softening associated with appearance of hyperons. Constructing an EOS yielding Mmax > 1.97 M⊙ in spite of the hyperon softening is not an easy task, therefore it deserves some additional explanations. The crucial feature of our BM EOS is a repulsive contribution to the pressure coming from the quartic terms in the vector meson fields in the Lagrangian (Bednarek & Mańka 2009). We emphasize, that the BM model reproduces semi-empirical nuclear-matter data as well as the semi-empirical estimates of the potential wells of hyperons in the nuclear matter, coming from hypernuclear data, involving hypernuclei and Σ − -atoms, as well as the strength of the Λ − Λ attraction in the ΛΛ-hypernuclei (Bednarek & Mańka 2009). Neutron-star configurations were obtained with the numerical library LORENE2, using the implementation of the Bonazzola et al. (1993) formalism for axi-symmetric and rigidly-rotating stars (rotstar code).
2.1. Magnetic torque neglected
Assuming that the magnetic field is not disturbing the Keplerian thin accretion disk structure, one usually considers the spin-up scenario in which the angular momentum is transferred from the disk to the NS via accretion from the marginally-stable circular orbit (Cook et al. 1994; Zdunik et al. 2002). In this process, an infall of a particle of baryon mass dMb and specific orbital angular momentum lms leads to a new quasi-stationary stellar configuration of baryon mass Mb + dMb and angular momentum J + dJ, according to 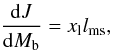 (1)where the parameter xl ( ≤ 1) quantifies our lack of knowledge of the fraction of angular momentum that is transferred to the star by an infalling particle; recent numerical simulations suggest that the value of xl is close to unity (see, e.g., Beckwith et al. 2008; Shafee et al. 2008).
(1)where the parameter xl ( ≤ 1) quantifies our lack of knowledge of the fraction of angular momentum that is transferred to the star by an infalling particle; recent numerical simulations suggest that the value of xl is close to unity (see, e.g., Beckwith et al. 2008; Shafee et al. 2008).
2.2. Magnetic torque included
If the magnetic field does affect the accretion flow, the B = 0 model ceases to be correct. To calculate the increase of the total stellar angular momentum J in this case, one must modify the Eq. (1) to incorporate the fact that the disk now terminates at some r0 > rms, depending on the value of magnetic field. We use the prescription of Kluźniak & Rappaport (2007), which gives the following evolution equation: ![\begin{equation} \frac{{\rm d}J}{{\rm d}M_{\rm b}}= l(r_0) -\frac{\mu^2}{9r_0^3 {\dot M}_{\rm b}} \left[3-2\left(\frac{r_{\rm cor}}{r_0}\right)^{3/2}\right], \label{eq:acc_mag} \end{equation}](/articles/aa/full_html/2011/12/aa18024-11/aa18024-11-eq21.png) (2)where μ = BR3 is the dipole magnetic moment of an NS (assumed to be parallel to J), rcor is the corotation radius and Ṁb denotes the mean accretion rate; for a detailed description of the parameters and modifications in obtaining r0, related to the relativistic marginally-stable circular orbit, see the appendix and Bejger et al. (2011).
(2)where μ = BR3 is the dipole magnetic moment of an NS (assumed to be parallel to J), rcor is the corotation radius and Ṁb denotes the mean accretion rate; for a detailed description of the parameters and modifications in obtaining r0, related to the relativistic marginally-stable circular orbit, see the appendix and Bejger et al. (2011).
A complete evolution model of a magnetized NS accreting from a disk needs a formula for the accretion-induced surface magnetic field decay. Because the theoretical state-of-the-art of this subject is quite complicated and far from being complete (see Sect. 4 of Bejger et al. 2011 for a brief summary), we used the simplest, but observationally-motivated decay law proposed by Shibazaki et al. (1989; see also Taam & van den Heuvel 1986; van den Heuvel & Bitzaraki 1995) and assumed that B decreases as a function of accreted mass ΔM only: B = Bi/(1 + ΔM/mB), where mB = 10-4 M⊙. We also tested other available forms of decay law (exponential-like formula used recently by Osłowski et al. 2011 in the context of population-synthesis studies, and the quadratic modification of Shibazaki et al. law) and conclude that this choice has no qualitative influence on the results.
3. Results
To estimate the feasibility of dense-matter phase transitions, we examined the compression of matter in the cores of accreting NSs by measuring the increase of the central baryon number density nc as well as the central baryon chemical potential μc = (pc + ec)/nc (pc and ec are the pressure and mass-energy density, respectively). Furthermore, we compared the results for spin-up-induced central compression with the isolated NS spin-down results.
3.1. Magnetic torque neglected
For B = 0 the features of accretion-driven evolution of nc and μc are qualitatively similar for all investigated EOSs.
 |
Fig. 1 Evolution of the central baryon number density nc in the disk-accretion spin-up as well as the spin-down scenario, shown for the spin frequency f–central baryon density nc plane (DH EOS, B = 0). |
 |
Fig. 2 Accretion tracks of the gravitational mass–central baryon number density, M − nc, plane. Magnetic field tracks were obtained for Ṁb = 10-9 M⊙/yr. The shaded region contains configurations for which the stellar equatorial radius Req is larger than rms (DH EOS). |
We will thus illustrate these features using the DH EOS and begin with the comparison of spin-up (with the most efficient angular momentum transfer xl = 1) and spin-down–induced increase of nc pictured in Fig. 1 in the spin-frequency-central density plot; the configurations are allowed to span the whole frequency range from the initially non-rotating stars up to the mass-shedding limit (or the axi-symmetric perturbation instability limit). Evidently, the spin-down allows for a higher nc increase than the xl = 1 accretion spin-up. To investigate this feature, Fig. 2 shows the behavior of the gravitational mass M as a function of nc.
 |
Fig. 3 Maximum central density nc,f attainable for a given evolutionary track compared to the initial nc,i, both plotted as functions of the gravitational mass of the initial non-rotating configuration, Mi. Upper panel: spin-up scenario. The reference line nc,i is the static sequence. Lower panel: spin-down scenario. The reference nc,i line is the mass-shedding limit, to be compared with nc,f of static configurations (DH EOS). |
For an astrophysically-motivated range of NS initial masses, Mi = 1.2 − 1.6 M⊙, the xl = 1 accretion never leads to a substantial central compression; moreover, the maximal central compression is attained for moderate spin periods, followed by a decrease of nc. On the contrary, lowering the efficiency of angular momentum transfer to e.g. xl = 0.5 allows for a substantial nc increase. A detailed summary and comparison between various types of tracks is included in Fig. 3, where the initial and final nc is plotted as a function of the initial stellar mass Mi for both spin-up (upper panel) and spin-down (lower panel). The nearly horizontal line for xl = 0.5 in the upper panel denotes the instability limit. Based on these data we conclude that to achieve a significant nc increase in an astrophysically-sound evolutionary process one should consider
-
an initial mass of the configuration quite close to the value of thestatic-star maximum mass in case ofxl = 1,
-
or a value of xl significantly lower than 1 (dotted lines in Figs. 2 and 3),
-
a more efficient mechanism, such as the spin-down of an isolated NS – constant Mb track leads to a higher increase of nc than thin-disk accretion, as shown in Fig. 1 and the lower panel of Fig. 3.
Results for the chemical potential μc for the DH EOS are plotted in Fig. 4; results for APR and BM EOSs are presented in Figs. 5 and 6.
3.2. Magnetic torque included
An inclusion of the magnetic torque acting in the NS-disk system changes the results significantly, as Fig. 2 shows. As an example, we used the “canonical case” of the initial magnetic field Bi = 1012 G and the average accretion rate Ṁb = 10-9 M⊙/yr (dashed lines; dots denote the decaying magnetic field for the initial mass Mi = 1.4 M⊙). Overall, the magnetic-torque results resemble those for a reduced efficiency of the angular momentum transfer, xl = 0.5. Including the magnetic field substantially increases nc and μc for an astrophysically interesting range of initial masses, Mi = 1.2 − 1.6 M⊙ (Figs. 3 and 4 for the DH EOS, and Figs. 5 and 6 for APR and BM EOSs). The nearly horizontal line segments in the upper panels of Figs. 3 and 5 correspond to the axisymmetric instability limit – it is reached by configurations that were not spun up to the mass-shedding limit; lowering the mass accretion rate results in an extended instability limit line toward smaller initial masses. In addition to the maximum attainable compression, the results for a predefined amount of accreted mass (ΔM = 0.1 M⊙, ΔM = 0.25 M⊙) are plotted for comparison in Fig. 3.
For the DH EOS and Mi = 1.4 M⊙, accretion of about 0.25 M⊙ implies (nc,f − nc,i)/nc,i ≈ 0.2. This should be compared with very small (of a few percent) compression for B = 0 and xl = 1 case. Including the magnetic torque is therefore crucial for accretion-induced compression in the core of an NS with initial mass ~1.4 M⊙. Note also a fairly strong effect of the EOS stiffness below approximately three nuclear densities, as well as its high-density behavior. As seen for example in Fig. 5, for our fixed magnetic dissipation evolution model, a stiff BM EOS with a high-density hyperon softening predicts a fractional increase of nc by about 120% at Mi = 1.4 M⊙, while μc increases by ~500 MeV. The overall picture obtained for magnetized stars, with Mi = 1.2−1.6 M⊙, is therefore essentially different from the B = 0 one.
 |
Fig. 4 Gravitational mass of the initially non-rotating configuration, Mi as a function of the maximum attainable central baryon chemical potential μc,f for a given evolutionary track compared to the initial μc,i. Lines are denoted analogously to Fig. 3. Left panel: spin-up scenario. Right panel: spin-down scenario (DH EOS). |
4. Conclusions
We have studied the influence of two thin-disk accretion models – with and without the involvement of magnetic field – on the evolution of the central density and chemical potential in accreting NSs. For B = 0 accretion from the marginally-stable circular orbit leads to a negligible central compression (a few per cent) for astrophysically-relevant initial configurations (slowly-rotating stars with Mi = 1.2−1.6 M⊙) and maximally-efficient angular momentum transfer (xl = 1 in Eq. (1), a value currently favored by numerical simulations). Consequently, this mechanism does not seem viable to trigger a dense-matter phase transition. Substantial central compression could be obtained for xl smaller than unity, or in a different evolutionary process (e.g., spin-down). Including the magnetic torque changes the outcome profoundly, but for a typical initial magnetic field, Bi ≃ 1012 G and accretion rate Ṁb = 10-9 M⊙ one is able to produce massive, weakly-magnetized (B ≃ 108 G) millisecond pulsars with a sizable (even as large as 100%) central compression, thus probing much higher densities, which in turn may trigger a phase transition. Even such a low final value of B still influences the accretion process and should be accounted for; only lowering it even more, to ≃ 107 G, essentially allows for the recovery of the B = 0 results.
Note also a quite impressive dependence of the NS spin-up evolution on the very presence of the magnetic-field. The magnetic torque substantially decreases the spin-up efficiency, as the comparison with the xl = 1 and xl = 0.5 results show – in other words, spinning-up with magnetic field requires more accreted mass to reach a desired spin frequency. A considerable subset of “magnetic-torque” tracks ends at the axisymmetric instability limit (i.e., nearly horizontal lines in Figs. 3 and 5), while the vast majority of the xl = 1 tracks can reach the mass-shedding limit. This result correlates with the EOS stiffness and is most pronounced for the BM EOS, softened by the existence of hyperons; potentially, it may help in the understanding of a puzzling non-detection of submillisecond pulsars, as well as assist in the studies of formation of stellar-mass BHs and their mass function.
 |
Fig. 5 Increase of the central baryon number density nc as a function of the initial gravitational mass Mi for the APR and BM EOSs. Notations as in Fig. 3. |
 |
Fig. 6 initial gravitational mass Mi as a function of intial and maximal central chemical potentials, μc for the APR and BM EOSs. Notations as in Fig. 4. |
We have restricted ourselves to the EOSs of hadronic matter. A phase transition to quark matter softens the high-density EOS, so that reaching Mmax > 1.97 M⊙ requires some tuning of both hadronic and the quark-matter model. An approach based on an effective model of the QCD of quark matter used recently by Bonanno & Sedrakian (2011) indicates that the vector repulsion in quark matter should be sufficiently strong to reach Mmax > 1.97 M⊙ (we recall that vector-meson repulsion in hadronic matter is also crucial for our BM EOS model). In any case, the maximum mass of NSs with quark cores (so-called hybrid stars) turns out to be very close to that reached at the central density equal to the deconfinement density (Bonanno & Sedrakian 2011).
Our results were obtained using three specific EOSs of dense matter, an effective magnetic torque model in the pulsar–accretion disk system, and a simplistic description of accretion-induced magnetic-field dissipation. We believe, however, that in a qualitative sense these results posses a general validity.
Acknowledgments
This work was partially supported by the Polish MNiSW research grant no. N N203 512838, LEA Astrophysics Poland-France (Astro-PF) and ESF Research Networking CompStar programmes. M.B. acknowledges the Marie Curie Fellowship within the 7th European Community Framework Programme (ERG-2007-224793).
References
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, K., Hawley, J. F., & Krolik, J. H. 2008, MNRAS, 390, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, I., & Manka, R. 2009, J. Phys. G: Nucl. Part. Phys., 36, 095201 [Google Scholar]
- Bejger, M., Zdunik, J. L., & Haensel, P. 2010, A&A, 520, 16 [Google Scholar]
- Bejger, M., Fortin, M., Haensel, P., & Zdunik, J. L. 2011, A&A, in press [arXiv:1106.2432] [Google Scholar]
- Blaschke, D., Grigorian, H., & Poghosyan, G. 2001, Physics of Neutron Star Interiors, 578, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Blaschke, D., Poghosyan, G., & Grigorian, H. 2008, AIPC, 1068, 191 [NASA ADS] [Google Scholar]
- Bonanno, L., & Sedrakian, A. 2011, A&A, in press, Doi: 10.1051/0004-6361/201117832 [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marc, J. A. 1993, A&A, 278, 42 [Google Scholar]
- Burderi, L., Possenti, A., Colpi, M., et al. 1999, ApJ, 519, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., & Dai, Z. G. 1998, ApJ, 492, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M., Possenti, A., Popov, S., & Pizzolato, F. 2001, Physics of neutron star interiors, ed. D. Blaschke, A. Sedrakian, & N. K. Glendenning (Springer, LNP 578), 440 [Google Scholar]
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A., 1994, ApJ, 423, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Demorest, P. B., Pennucci, T., et al. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A& A, 380, 151 [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, P., & Lamb, F. K., 1979, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1991, Neutron Stars: Theory and Observations, ed. J. Ventura, & D. Pines (Dordrecht: Kluwer) 363 [Google Scholar]
- Glendenning, N. K., & Weber, F. 2001, ApJ, 559, L119, Physics of Neutron Star Interiors, 578, 305 [Google Scholar]
- van den Heuvel, E. P. J., & Bitzaraki, O. 1995, A&A, 297, L41 [NASA ADS] [Google Scholar]
- Kluźniak, W., & Rappaport, S. 2007, ApJ, 671, 1990 [NASA ADS] [CrossRef] [Google Scholar]
- Lavagetto, G., Burderi, L., D’Antona, F., et al. 2004, MNRAS, 348, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Osłowski, S., Bulik, T., Gondek-Rosińska, D., & Belczyński, K., 2011, MNRAS, 413, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Possenti, A., Colpi, M., Geppert, U., et al. 1999, ApJS, 125, 463 [Google Scholar]
- Shafee, R., McKinney, J. C., Narayan, R., et al. 2008, ApJ, 687, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Shibazaki, N., Murakami, T., Shaham, J., & Nomoto, K. 1989, Nature, 342, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., & van den Heuvel, E. P. J. 1986, ApJ, 305, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, R., & Liang, E. 2009, Science in China G: Phys. Astron., 52, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L., Haensel, P., & Gourgoulhon, E. 2002, A&A, 381, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdunik, J. L., Haensel, P., & Bejger, M. 2005, A&A, 441, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Calculation of the inner-boundary radius of the accretion disk
To simplify the calculation of the specific orbital angular momentum l at every step of spin-up evolution, we used the Bejger et al. (2010) result: the Keplerian orbital frequency of a particle in the thin disk at a radius r0 is well-approximated by the “Schwarzschildian/Newtonian” formula 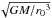 . This ansatz yields a surprisingly accurate determination of l for r0 ≃ rms for a broad range of stellar masses and spin frequencies up to the mass-shedding limit.
. This ansatz yields a surprisingly accurate determination of l for r0 ≃ rms for a broad range of stellar masses and spin frequencies up to the mass-shedding limit.
 |
Fig. A.1 Difference (in km) between the real value of rms and the value |
Here we show that this approximate approach allows for a reasonably accurate determination of the rms as well. It corresponds to the dl/dr = 0 condition; the inner-edge of an accretion disk r0 is a solution of 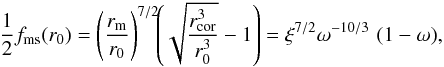 (A.1)
(A.1)
where rcor is the corotation radius, 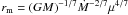 is the magnetospheric radius and ξ = rm/rcor. Function fms introduced by Bejger et al. (2011; reducing to fms ≡ 1 in the Eq. (17) of Kluźniak & Rappaport 2007) ensures a proper behavior of the torque near rms
is the magnetospheric radius and ξ = rm/rcor. Function fms introduced by Bejger et al. (2011; reducing to fms ≡ 1 in the Eq. (17) of Kluźniak & Rappaport 2007) ensures a proper behavior of the torque near rms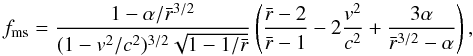 (A.2)with
(A.2)with 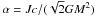 ,
, 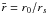 and rs = 2GM/c2 denoting the Schwarzschild radius. Marginally stable circular orbit radius rms is then a solution of equation fms(rms) = 0. Figure A.1 shows, using the example of the DH EOS (other EOSs we tested yield similar results) the comparison of the rms calculated exactly from integrals of motion with the approximate value
and rs = 2GM/c2 denoting the Schwarzschild radius. Marginally stable circular orbit radius rms is then a solution of equation fms(rms) = 0. Figure A.1 shows, using the example of the DH EOS (other EOSs we tested yield similar results) the comparison of the rms calculated exactly from integrals of motion with the approximate value 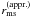 , obtained by means of Eq. (A.2). For almost all configurations the difference is less than 0.6 km (for rms < R we adopt rms = R), and the regions where
, obtained by means of Eq. (A.2). For almost all configurations the difference is less than 0.6 km (for rms < R we adopt rms = R), and the regions where 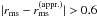 km are small and well-confined near high-mass and mass-shedding, submillisecond rotation.
km are small and well-confined near high-mass and mass-shedding, submillisecond rotation.
All Figures
 |
Fig. 1 Evolution of the central baryon number density nc in the disk-accretion spin-up as well as the spin-down scenario, shown for the spin frequency f–central baryon density nc plane (DH EOS, B = 0). |
| In the text | |
 |
Fig. 2 Accretion tracks of the gravitational mass–central baryon number density, M − nc, plane. Magnetic field tracks were obtained for Ṁb = 10-9 M⊙/yr. The shaded region contains configurations for which the stellar equatorial radius Req is larger than rms (DH EOS). |
| In the text | |
 |
Fig. 3 Maximum central density nc,f attainable for a given evolutionary track compared to the initial nc,i, both plotted as functions of the gravitational mass of the initial non-rotating configuration, Mi. Upper panel: spin-up scenario. The reference line nc,i is the static sequence. Lower panel: spin-down scenario. The reference nc,i line is the mass-shedding limit, to be compared with nc,f of static configurations (DH EOS). |
| In the text | |
 |
Fig. 4 Gravitational mass of the initially non-rotating configuration, Mi as a function of the maximum attainable central baryon chemical potential μc,f for a given evolutionary track compared to the initial μc,i. Lines are denoted analogously to Fig. 3. Left panel: spin-up scenario. Right panel: spin-down scenario (DH EOS). |
| In the text | |
 |
Fig. 5 Increase of the central baryon number density nc as a function of the initial gravitational mass Mi for the APR and BM EOSs. Notations as in Fig. 3. |
| In the text | |
 |
Fig. 6 initial gravitational mass Mi as a function of intial and maximal central chemical potentials, μc for the APR and BM EOSs. Notations as in Fig. 4. |
| In the text | |
 |
Fig. A.1 Difference (in km) between the real value of rms and the value |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


