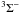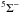| Issue |
A&A
Volume 535, November 2011
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201117584 | |
| Published online | 22 November 2011 | |
Atomic data for neutron-capture elements
III. Charge transfer rate coefficients for low-charge ions of Ge, Se, Br, Kr, Rb, and Xe⋆
1
Michigan State University, Department of Physics and Astronomy, 3248 Biomedical Physical Sciences, East Lansing, MI 48824-2320, USA
e-mail: sterling@pa.msu.edu
2
Department of Physics and Astronomy and the Center for Simulational Physics, University of Georgia, Athens, GA 30602-2451, USA
e-mail: stancil@physast.uga.edu
Received: 28 June 2011
Accepted: 12 August 2011
We present total and final-state resolved charge transfer (CT) rate coefficients for low-charge Ge, Se, Br, Kr, Rb, and Xe ions reacting with neutral hydrogen over the temperature range 102–106 K. Each of these elements has been detected in ionized astrophysical nebulae, particularly planetary nebulae. CT rate coefficients are a key ingredient for the ionization equilibrium solutions needed to determine total elemental abundances from those of the observed ions. A multi-channel Landau Zener approach was used to compute rate coefficients for projectile ions with charges q = 2–5, and for singly-charged ions the Demkov approximation was utilized. Our results for five-times ionized species are lower limits, due to the incompleteness of level energies in the NIST database. In addition, we computed rate coefficients for charge transfer ionization reactions between the neutral species of the above six elements and ionized hydrogen. The resulting total and state-resolved CT rate coefficients are tabulated and available at the CDS. In tandem with our concurrent investigations of other important atomic processes in photoionized nebulae, this work will enable robust investigations of neutron-capture element abundances and nucleosynthesis via nebular spectroscopy.
Key words: atomic data / atomic processes / HII regions / nuclear reactions, nucleosynthesis, abundances / stars: evolution / planetary nebulae: general
Tables 4 and 5 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/535/A117
© ESO, 2011
1. Introduction
The detection of n-capture elements (atomic number Z > 30) in ionized astrophysical nebulae has underscored the need for atomic data required to accurately solve for the ionization equilibrium of these species. Trans-iron element emission lines have been detected in objects ranging from planetary nebulae (e.g., Zhang et al. 2005; Sharpee et al. 2007; Sterling et al. 2007; Sterling & Dinerstein 2008; Sterling et al. 2009; Otsuka et al. 2010, 2011) to H II regions (e.g., Baldwin et al. 2000; Blum & McGregor 2008, and references therein), and the interstellar medium of other galaxies (Vanzi et al. 2008). Determinations of their abundances have important implications for the production and chemical evolution of n-capture nuclides in the Universe (e.g., Busso et al. 1999; Sneden et al. 2008; Sterling & Dinerstein 2008). Se, Kr, and Xe are the most widely detected n-capture elements in ionized nebulae (e.g, Dinerstein 2001; Sharpee et al. 2007; Sterling & Dinerstein 2008; Sterling et al. 2009), but other trans-iron elements have also been detected in nebular spectra, including Ge (Sterling et al. 2002; Sterling & Dinerstein 2003), Br, and Rb (Péquignot & Baluteau 1994; Zhang et al. 2005; Sharpee et al. 2007; Sterling et al. 2009).
Due to the limited number of detectable n-capture element ions in individual nebulae, it is necessary to convert abundances of the observed ions to elemental abundances by correcting for unobserved ionization stages. Numerical simulations of ionized nebulae present a robust and accurate method of deriving such ionization corrections, provided that accurate data for atomic processes affecting the ionization equilibrium of the modeled elements are available. Since n-capture element emission lines have been detected primarily in photoionized nebulae, the most important atomic data required for ionization balance determinations are photoionization cross sections and rate coefficients for radiative recombination, dielectronic recombination, and charge transfer (CT). Unfortunately, these data are poorly if at all known for ions of trans-iron elements.
This paper is the third in a series presenting theoretical atomic data determinations relevant to nebular ionization balance solutions for low-charge n-capture element ions. In the first two (Sterling & Witthoeft 2011; Sterling 2011), we furnished multi-configuration Breit-Pauli distorted-wave photoionization cross sections and radiative and dielectronic recombination rate coefficients for Se and Kr ions.
To address the need for CT data for low-charge ions of n-capture elements, we present calculations based on the Landau-Zener (LZ) and Demkov approximations. We consider reactions of the form 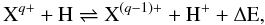 (1)with q = 1–5 and X = Ge, Se, Br, Kr, Rb, and Xe. The forward reaction, CT recombination (in terms of the projectile Xq+), is exothermic for these elements when q ≥ 2, and the reverse reaction for multiply-charged systems is generally unimportant at the temperatures of photoionized nebulae (near 104 K). On the other hand, of these elements only Kr has a higher ionization potential than H, and hence CT recombination is endoergic for singly-ionized Ge, Se, Br, Rb, and Xe. We therefore provide rate coefficients for both CT recombination of singly-charged ions and CT ionization of neutral species.
(1)with q = 1–5 and X = Ge, Se, Br, Kr, Rb, and Xe. The forward reaction, CT recombination (in terms of the projectile Xq+), is exothermic for these elements when q ≥ 2, and the reverse reaction for multiply-charged systems is generally unimportant at the temperatures of photoionized nebulae (near 104 K). On the other hand, of these elements only Kr has a higher ionization potential than H, and hence CT recombination is endoergic for singly-ionized Ge, Se, Br, Rb, and Xe. We therefore provide rate coefficients for both CT recombination of singly-charged ions and CT ionization of neutral species.
Our LZ calculations are multi-channel, in the sense that several exit channels for the X(q−1)+ system are simultaneously considered. This avoids the problem of overestimating cross sections when adding two-channel cross sections of the same molecular symmetry (Butler & Dalgarno 1980b; Kingdon 1995). For singly-ionized atoms, CT usually cannot be treated in the LZ approximation, and hence we utilize the Demkov approximation to determine rate coefficients for those systems.
LZ calculations are generally accurate to within a factor of three for systems (and final channels) with large rate coefficients ( ≳ 10-9 cm3 s-1; Butler & Dalgarno 1980b; Kingdon & Ferland 1996), but can be less accurate when the rate coefficient is small (though in that case, CT often is much less important than radiative and dielectronic recombination). The quantum mechanical molecular-orbital close-coupling (QMOCC) approach (e.g., Kimura & Lane 1989; Zygelman et al. 1992; Wang et al. 2004) is the most accurate theoretical method for determining CT rate coefficients at the temperatures of interest. However, given the time- and computationally-intensive nature of such calculations, we have chosen to first render LZ calculations for these systems. We will test the sensitivity of abundance determinations to uncertainties in the CT rate coefficients (assumed to be roughly a factor of three) through numerical simulations of ionized nebulae. Those systems which are most critical for ionization equilibrium solutions are targets for further investigation with QMOCC methods.
The structure of this paper is as follows. In Sect. 2, we discuss the details and methodology of our calculations. We present the resulting total and final-state resolved CT rate coefficients in Sect. 3, and summarize our investigation in Sect. 4.
2. Calculations and methodology
2.1. Multi-channel Landau Zener calculations
For projectiles with charge q = 2–5, we compute CT rate coefficients in the multi-channel Landau-Zener (MCLZ) approximation, based on the formalism of Butler & Dalgarno (1980b) and Janev et al. (1983) with the low-energy modifications of Chang & Pritchard (1979).
While CT is a quasi-molecular problem, the basic details of the interaction can be understood from consideration of the initial channel (in which both the projectile Xq+ and target H are assumed to be in their ground states), the final channels (which can include ground and excited states of X(q−1)+), and the interaction between them. As the atoms approach each other, if the ionization potential of X(q−1)+ exceeds that of H (as is the case for q = 2–5 for all elements we consider), CT is exoergic and the diabatic potential curves can cross at an internuclear distance Rx. The CT reaction is usually driven by a radial coupling that connects initial and final channels corresponding to the same molecular symmetry of XHq+. Adiabatic potential curves of molecular states with the same symmetry cannot cross, and Rx corresponds to the radius at which the adiabatic potentials most closely approach (the “avoided crossing” distance).
In the LZ approximation, charge exchange is assumed to be localized at the internuclear distance Rx, with the probability of exchange given by 2p(1 − p), where p = e − w and ![\begin{equation} w = \frac{\pi ^2 [\Delta U(R_{\mathrm{x}})]^2}{hv\left[ \frac{\rm d}{{\rm d}r} (H_{11} - H_{22}) \right]_{R_{\mathrm{x}}}}\cdot \label{wdef} \end{equation}](/articles/aa/full_html/2011/11/aa17584-11/aa17584-11-eq17.png) (2)In this equation, v is the relative radial velocity of the projectile and target, H11 and H22 are the incoming and outgoing diabatic potentials, and ΔU(Rx) is the separation of the adiabatic potentials at Rx. The cross section at energy E is
(2)In this equation, v is the relative radial velocity of the projectile and target, H11 and H22 are the incoming and outgoing diabatic potentials, and ΔU(Rx) is the separation of the adiabatic potentials at Rx. The cross section at energy E is 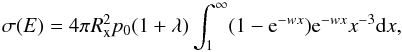 (3)where λ = [H11(∞) − H11(Rx)] /Ei (Butler & Dalgarno 1980b). The approach probability p0 is determined from the orbital and spin angular momenta of the initial and final states, which can form gif = (2Li + 1)(2Si + 1)(2Lf + 1)(2Sf + 1) molecular states, and the spin S and orbital angular momentum projection quantum number Λ′ of the molecular state (Herzberg 1952; Dalgarno et al. 1990):
(3)where λ = [H11(∞) − H11(Rx)] /Ei (Butler & Dalgarno 1980b). The approach probability p0 is determined from the orbital and spin angular momenta of the initial and final states, which can form gif = (2Li + 1)(2Si + 1)(2Lf + 1)(2Sf + 1) molecular states, and the spin S and orbital angular momentum projection quantum number Λ′ of the molecular state (Herzberg 1952; Dalgarno et al. 1990): 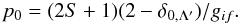 (4)The above describes a two-channel LZ interaction. In MCLZ calculations, several capture channels are considered simultaneously, each with a unique value of Rx, as the projectile approaches the target. In this case, for N final channels the probability for capture into a state n is given by (Janev et al. 1983)
(4)The above describes a two-channel LZ interaction. In MCLZ calculations, several capture channels are considered simultaneously, each with a unique value of Rx, as the projectile approaches the target. In this case, for N final channels the probability for capture into a state n is given by (Janev et al. 1983) ![\begin{eqnarray} P_n &=& p_1p_2\dots p_n(1-p_n)\Big[1+(p_{n+1}p_{n+2}\dots p_N)^2 \nonumber \\ & &+ (p_{n+1}p_{n+2}\dots p_{N-1})^2(1-p_N)^2+\dots \nonumber \\ & & +p_{n+1}^2(1-p_{n+2})^2+(1-p_{n+1})^2\Big]. \label{mclzprob} \end{eqnarray}](/articles/aa/full_html/2011/11/aa17584-11/aa17584-11-eq32.png) (5)LZ calculations require estimates of the incoming and outgoing potentials, the avoided crossing distance Rx, and the energy separation of the adiabatic potentials at Rx. We use approximations for these quantities from Butler & Dalgarno (1980b) as follows. In atomic units1, the incoming potential is
(5)LZ calculations require estimates of the incoming and outgoing potentials, the avoided crossing distance Rx, and the energy separation of the adiabatic potentials at Rx. We use approximations for these quantities from Butler & Dalgarno (1980b) as follows. In atomic units1, the incoming potential is 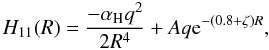 (6)where αH is the polarizability of H, R the internuclear distance, and ζ is the exponent of a single orbital wavefunction ( − 1.0 for H targets). Typically set to 25, A was reduced in some cases to yield physically reasonable behavior in the potential, which occasionally was spurious in the repulsive core (this generally only occurs when Rx ≲ 4.5–5 a0, in which case the rate coefficient is usually small at photoionized plasma temperatures). The outgoing potential is given by
(6)where αH is the polarizability of H, R the internuclear distance, and ζ is the exponent of a single orbital wavefunction ( − 1.0 for H targets). Typically set to 25, A was reduced in some cases to yield physically reasonable behavior in the potential, which occasionally was spurious in the repulsive core (this generally only occurs when Rx ≲ 4.5–5 a0, in which case the rate coefficient is usually small at photoionized plasma temperatures). The outgoing potential is given by 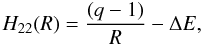 (7)where ΔE = IP(Xq+) – IP(H) – Eexc is the energy defect, IP is the ionization potential of the indicated system, and Eexc is the excitation energy of the final X(q−1)+ state.
(7)where ΔE = IP(Xq+) – IP(H) – Eexc is the energy defect, IP is the ionization potential of the indicated system, and Eexc is the excitation energy of the final X(q−1)+ state.
The avoided crossing distances Rx are determined by equating Eqs. (6) and (7). In Fig. 1, we illustrate the diabatic potentials and Rx values for the final channels of the case Xq+ = Kr3+. Note that we ignore fine structure in our calculations.
 |
Fig. 1 Incoming diabatic potential H11 for Kr3+ + H (thick solid line), and diabatic potentials H22 for six exit channels of Kr2+ + H+ + ΔE corresponding to |
The final piece of necessary information, ΔU(Rx), is perhaps the greatest uncertainty in LZ calculations, as the formula provided by Butler & Dalgarno (1980b) is an empirical fit to a small number of quantal calculations. The value of ΔU(Rx) depends on whether the electron capture process is type I (the H 1s electron is transferred without affecting the core electrons of the projectile) or type II (electron capture is accompanied by the excitation of a core electron). The formulae of Butler & Dalgarno (1980b) for these two scenarios are:  where β = 2IP(H) = 1.0 in atomic units. The potential for type II reactions is reduced relative to their type I counterparts due to the rearrangement of the core electrons.
where β = 2IP(H) = 1.0 in atomic units. The potential for type II reactions is reduced relative to their type I counterparts due to the rearrangement of the core electrons.
Once the quantities H11, H22, Rx, and ΔU(Rx) are determined, then the cross section for each final channel can be determined from Eq. (3), as illustrated for Xq + = Kr3+ in Fig. 2. These are integrated over a Maxwellian velocity distribution to derive final-state resolved rate coefficients.
 |
Fig. 2 Total (thick solid curve) and final-state resolved cross sections for CT recombination of Kr3+. Energies are given in eV/u, where u is the atomic mass unit. |
2.2. Demkov calculations
In the case of singly-charged ions (q = 1 in Eq. (1)), the LZ approximation cannot be applied since the final channels do not have Coulomb potentials (hence there are no avoided crossings). The reaction proceeds through radial coupling connecting molecular states with the same symmetry as in the LZ calculations, but the coupling is not localized and can be represented with an exponential form. This type of interaction can be described by the Demkov approximation (Demkov 1964; Olson 1972; Swartz 1994).
The reaction is assumed to occur at an interaction distance that we label Rx due to its analogous nature to the avoided crossing distance in LZ calculations. Rx is given by equating ΔU(R) with (Swartz 1994) 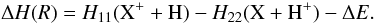 (10)For the potential H11(X + H + ), the polarizability term (see Eq. (6)) should include a quadrupole term in addition to the dipole polarizability if X is not an S ground term (Gentry & Giese 1977):
(10)For the potential H11(X + H + ), the polarizability term (see Eq. (6)) should include a quadrupole term in addition to the dipole polarizability if X is not an S ground term (Gentry & Giese 1977): 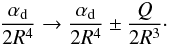 (11)To determine ΔH(R) for each element, static average electric dipole polarizabilities were taken from Lide (2002) and quadrupole matrix elements from Tables 2 and 3 of Froese Fischer (1977).
(11)To determine ΔH(R) for each element, static average electric dipole polarizabilities were taken from Lide (2002) and quadrupole matrix elements from Tables 2 and 3 of Froese Fischer (1977).
The transition probability for the reaction is p = e − w with (Demkov 1964; Swartz 1994) ![\begin{equation} w = \left[ 1 + \mathrm{exp}\left( \frac{2\pi^2\Delta U(R_{\mathrm{x}})}{h\alpha v} \right) \right]^{-1}, \label{demkovw} \end{equation}](/articles/aa/full_html/2011/11/aa17584-11/aa17584-11-eq61.png) (12)where h is Planck’s constant and α is the polarizability of the neutral species X. Defining
(12)where h is Planck’s constant and α is the polarizability of the neutral species X. Defining 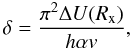 (13)the cross section at energy E is
(13)the cross section at energy E is 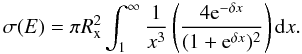 (14)We compute two-channel cross sections, which can be added to determine the total cross section. While this addition can lead to overestimated total cross sections (see Sect. 2.1), only Se and Br have more than one exoergic final channel, and their cross sections are typically small in the relevant temperature range. As for the MCLZ calculations, the cross sections are integrated over a Maxwellian velocity distribution to derive rate coefficients.
(14)We compute two-channel cross sections, which can be added to determine the total cross section. While this addition can lead to overestimated total cross sections (see Sect. 2.1), only Se and Br have more than one exoergic final channel, and their cross sections are typically small in the relevant temperature range. As for the MCLZ calculations, the cross sections are integrated over a Maxwellian velocity distribution to derive rate coefficients.
3. Results
In Table 1, we provide information for the exit channels of our MCLZ and Demkov calculations, including energy defects ΔE, avoided crossing distances (or interaction distances, for singly-charged ions) Rx, and the energy separation ΔU of the adiabatic curves at Rx. These parameters were used to compute the CT cross section for each final channel. In addition, we list the molecular symmetries common to the initial and final channels and whether the reaction is type I or type II. When a final state can connect to the initial state via more than one molecular symmetry, the cross sections for each symmetry were added to determine the state-specific cross section. The state-resolved cross sections were added to determine the total CT cross section, and rate coefficients determined by integrating over a Maxwellian velocity distribution.
Details of MCLZ and Demkov calculations.
Total charge transfer recombination rate coefficients (cm3 s-1) for the reactions Xq+ + H → X(q−1)+ + H+ + δE.
The total CT recombination rate coefficients of each ion are given in Table 2 as functions of temperature, and are illustrated in Fig. 3. We note that for q = 5, highly-excited Rydberg states can be favorable exit channels, but the reported level energies in NIST for X4+ ions are incomplete at those energies. Thus, CT into those highly-excited states could not be computed, and as a result the rate coefficients for q = 5 are lower limits. As seen in Fig. 3, the computed q = 5 rate coefficients are smaller than those for q = 4 with the exception of Ge5+. Since CT rate coefficients generally increase with charge for q ≥ 3, we recommend that q = 4 CT rate coefficients be used as rough estimates for Se, Br, Kr, Rb, and Xe q ≥ 5 ions.
 |
Fig. 3 Total rate coefficients for CT recombination of X+ (dash-dot-dot-dot-dash curves), X2+ (dash-dot-dash curves), X3+ (dotted curves), X4+ (solid curves), and X5+ (dashed curves), where X is the element indicated in each panel. The q = 5 rate coefficients are lower limits due to incomplete experimental energy level measurements. Note that the Rb+ rate coefficient is below 10-14 cm3 s-1 over the plotted temperature range. |
When the radial coupling CT rate coefficient from our MCLZ and Demkov calculations is sufficiently small, CT can proceed via other coupling mechanisms. Two such examples are radiative CT and spin-orbit (SO) coupling. For radiative CT, the canonical rate coefficient is taken to be 10-14 cm3 s-1 (Butler et al. 1977). This value is uncertain by at least an order of magnitude (Butler et al. 1977; Stancil & Zygelman 1996), but given the small rate coefficient, CT is unlikely to be an important recombination mechanism compared to radiative or dielectronic recombination when radiative CT dominates radial coupling. The rate coefficients listed in the tables are the maximum of the radially-coupled and radiative CT rate coefficients (thus, all values of 1.00E-14 indicate that radiative CT dominates radially-coupled CT). For some exit channels, radiative CT dominates radial coupling at all temperatures from 102–106 K. States with such small rate coefficients tend to be associated with small or large avoided crossing distances (Rx ≲ 5 a0, Rx ≳ 15–20 a0). For some singly- and doubly-charged ions, the only exothermic exit channel(s) has a very small rate coefficient dominated by radiative CT.
Spin-orbit coupling is not as well understood as the radial or radiative mechanisms. Rate coefficients for SO-coupled CT reactions can range from 10-17–10-12 cm3 s-1 (Butler & Dalgarno 1979, 1980a; Pradhan & Dalgarno 1994; Stancil 2001), though detailed calculations are very few and to our knowledge exist only for singly-charged ions. Because of this, we consider SO coupling only for CT recombination of singly-charged ions and CT ionization of neutral species. For small radial coupling CT rate coefficients (≤10-12 cm3 s-1), we adopt 10-12 cm3 s-1, which is the largest computed rate coefficient for SO coupling (Pradhan & Dalgarno 1994), as an upper limit to the rate coefficient. This estimate provides a much smaller, but more robust upper limit than estimates based on the Langevin model (Stancil 2001).
However, SO coupling is not relevant for all of the singly-ionized species we consider, since it only connects initial and final states of different molecular symmetries for which radial and rotational coupling are forbidden. For CT recombination of Rb+ (and the reverse reaction), the entrance and exit channels correspond to 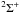 molecular states, and SO coupling therefore plays no role. In the case of Kr+ and Xe+, for which there is only one exothermic exit channel, the diabatic potentials for the triplet exit channels do not cross the potential curve of the singlet entrance channel, and hence SO coupling is unlikely to be important for these reactions. We therefore adopt the SO coupling upper limit to the rate coefficients only for singly-ionized Ge, Se, and Br.
molecular states, and SO coupling therefore plays no role. In the case of Kr+ and Xe+, for which there is only one exothermic exit channel, the diabatic potentials for the triplet exit channels do not cross the potential curve of the singlet entrance channel, and hence SO coupling is unlikely to be important for these reactions. We therefore adopt the SO coupling upper limit to the rate coefficients only for singly-ionized Ge, Se, and Br.
CT ionization is exothermic for the neutrals of the elements we consider, with the exception of Kr. We provide rate coefficients for these systems in Table 3, and depict them in Fig. 4. As for CT recombination, we adopt the largest of the rate coefficients associated with the radial, radiative, and (when important) SO mechanisms.
Total charge transfer ionization rate coefficients (cm3 s-1) for the reactions X0 + H+ → X+ + H + δE.
 |
Fig. 4 Total rate coefficients for CT ionization of the indicated neutral species. |
The CT recombination rate coefficients for singly-ionized species were computed from the CT ionization rate coefficients via detailed balance: 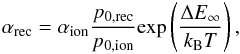 (15)where αrec,ion are the rate coefficients for CT recombination and ionization, respectively, p0,rec,ion are the approach probabilities corresponding to the molecular symmetries involved in the recombination and ionization reactions, ΔE∞ is the asymptotic energy defect, and kB the Boltzmann constant. We note that Eq. (15) was applied only to state-resolved rate coefficients. In the case of Kr, for which CT recombination of singly-charged ions is exothermic, the CT ionization rate coefficients were computed in an analogous manner. For neutral Kr, the energy defect is very small (corresponding to 4700 K), and hence the CT ionization reaction can operate efficiently in photoionized nebulae. CT recombination of singly-charged ions is less important at photoionized temperatures for the other elements (see Fig. 3), as the lowest energy defect is that of Xe (corresponding to 17 000 K).
(15)where αrec,ion are the rate coefficients for CT recombination and ionization, respectively, p0,rec,ion are the approach probabilities corresponding to the molecular symmetries involved in the recombination and ionization reactions, ΔE∞ is the asymptotic energy defect, and kB the Boltzmann constant. We note that Eq. (15) was applied only to state-resolved rate coefficients. In the case of Kr, for which CT recombination of singly-charged ions is exothermic, the CT ionization rate coefficients were computed in an analogous manner. For neutral Kr, the energy defect is very small (corresponding to 4700 K), and hence the CT ionization reaction can operate efficiently in photoionized nebulae. CT recombination of singly-charged ions is less important at photoionized temperatures for the other elements (see Fig. 3), as the lowest energy defect is that of Xe (corresponding to 17 000 K).
State-resolved rate coefficients are important for understanding the emission line spectra of photoionized nebulae, since CT populates excited states from which emission lines can be measured (e.g., Kingdon & Ferland 1996). We therefore provide final-state resolved rate coefficients for CT recombination in Table 4 and for CT ionization in Table 5 (both available at the CDS).
The derived abundances of Se and Kr have explicitly been shown to be sensitive to uncertainties in CT rate coefficients (Sterling et al. 2007), and other trans-iron elements are expected to be similarly sensitive. Unfortunately, it is not possible to ascertain robust uncertainties for CT rate coefficients computed with the LZ or Demkov approximations without accompanying QMOCC calculations. Butler & Dalgarno (1980b) found that their LZ rate coefficients agreed with quantal calculations to within a factor of three for ions of light elements with large CT rate coefficients, but that the disagreement could exceed an order of magnitude in the case of systems with small rate coefficients. No such comparison is possible for the heavy ions we have investigated, since QMOCC computations are not available for any of these systems. Our forthcoming study of the sensitivity of n-capture abundance determinations to atomic data uncertainties, using Monte Carlo simulations with photoionization modeling codes, will help to identify the ions that most urgently require QMOCC determinations of CT rate coefficients.
4. Summary
We have presented CT recombination rate coefficients for the first five ionization stages of the n-capture elements Ge, Se, Br, Kr, Rb, and Xe reacting with neutral hydrogen. A multi-channel Landau-Zener approach was employed for multiply-charged ions, while the Demkov approximation was used for singly-charged species. We note that the computed rate coefficients for q = 5 are lower limits, due to the incompleteness of energy listings in the NIST database. Because of that, we recommend that the four-times ionized recombination rate coefficients be used for q ≥ 5, with the exception of Ge5+. For reactions between the neutral species of these elements and H+, we computed CT ionization rate coefficients. Total rate coefficients are given over the range of temperatures 102–106 K in Tables 2 and 3, while final-state resolved rate coefficients are presented in Tables 4 and 5 (available at the CDS). In addition, all rate coefficients can be obtained at http://www.pa.msu.edu/astro/atomicdata/charge_transfer/. In tandem with our concurrent investigations into the photoionization and radiative and dielectronic recombination properties of n-capture elements (e.g., Sterling & Witthoeft 2011; Sterling 2011), these CT rate coefficient determinations will enable the abundances of n-capture elements to be reliably determined in ionized astrophysical nebulae. Such studies bear significant implications for n-capture nucleosynthesis, the structure and internal mixing of evolved stars, and the chemical evolution of trans-iron elements in the Universe.
Acknowledgments
N. C. Sterling gratefully acknowledges support from an NSF Astronomy and Astrophysics Postdoctoral Fellowship under award AST-0901432 and from NASA grant 06-APRA206-0049. The work of P. C. Stancil was partially supported by NASA grant NNX09AC46G.
References
- Baldwin, J. A., Verner, E. M., Verner, D. A., et al. 2000, ApJS, 129, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, R. D., & McGregor, P. J. 2008, AJ, 135, 1708 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, S. E., & Dalgarno, A. 1979, ApJ, 234, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, S. E., & Dalgarno, A. 1980a, A&A, 85, 144 [NASA ADS] [Google Scholar]
- Butler, S. E., & Dalgarno, A. 1980b, ApJ, 241, 838 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, S. E., Guberman, S. L., & Dalgarno, A. 1977, Phys. Rev. A, 16, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, A. M., & Pritchard, D. E. 1979, J. Chem. Phys., 70, 4524 [NASA ADS] [CrossRef] [Google Scholar]
- Dalgarno, A., Du, M. L., & You, J. H. 1990, ApJ, 349, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Demkov, Y. N. 1964, Sov. Phys.-JETP, 18, 138 [Google Scholar]
- Dinerstein, H. L. 2001, ApJ, 550, L223 [Google Scholar]
- Froese Fischer, C. 1977, The Hartree-Fock Method for Atoms: A Numerical Approach (New York: Wiley) [Google Scholar]
- Gentry, W. R., & Giese, C. F. 1977, J. Chem. Phys., 67, 2355 [NASA ADS] [CrossRef] [Google Scholar]
- Herzberg, G. 1952, Spectra of Diatomic Molecules (New York: Van Nostrand), 318 [Google Scholar]
- Janev, R. K., Belic, D. S., & Bransden, B. J. 1983, Phys. Rev. A, 28, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, M., & Lane, N. F. 1989, Ad. At. Mol. Opt. Phys., 26, 79 [Google Scholar]
- Kingdon, J. B. 1995, MNRAS, 274, 425 [NASA ADS] [Google Scholar]
- Kingdon, J. B., & Ferland, G. J. 1996, ApJS, 106, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Lide, D. R. 2002, CRC Handbook of chemistry and physics: a ready-reference book of chemical and physical data (Boca Raton: CRC Press) [Google Scholar]
- Olson, R. E. 1972, Phys. Rev. A, 6, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Otsuka, M., Tajitsu, A., Hyung, S., & Izumiura, H. 2010, ApJ, 723, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Otsuka, M., Meixner, M., Riebel, D., et al. 2011, ApJ, 729, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Péquignot, D., & Baluteau, J. P. 1994, A&A, 283, 593 [NASA ADS] [Google Scholar]
- Pradhan, A., & Dalgarno, A. 1994, Phys. Rev. A, 49, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Sharpee, B., Zhang, Y., Williams, R., et al. 2007, ApJ, 659, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stancil, P. C. 2001, in Spectroscopic Challenges of Photoionized Plasmas, ed. G. J. Ferland, & D. W. Savin, ASP Conf. Ser., 247, 3 [Google Scholar]
- Stancil, P. C., & Zygelman, B. 1996, ApJ, 472, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Sterling, N. C. 2011, A&A, 533, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sterling, N. C., & Dinerstein, H. L. 2003, Rev. Mex. Astron. Ser. Conf., 18, 133 [NASA ADS] [Google Scholar]
- Sterling, N. C., & Dinerstein, H. L. 2008, ApJS, 174, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Sterling, N. C., & Witthoeft, M. C. 2011, A&A, 529, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sterling, N. C., Dinerstein, H. L., & Bowers, C. W. 2002, ApJ, 578, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Sterling, N. C., Dinerstein, H. L., & Kallman, T. R. 2007, ApJS, 169, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Sterling, N. C., Dinerstein, H. L., Hwang, S., et al. 2009, PASA, 26, 339 [NASA ADS] [Google Scholar]
- Swartz, D. A. 1994, ApJ, 428, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzi, L., Cresci, G., Telles, E., & Melnick, J. 2008, A&A, 486, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J. G., Stancil, P. C., Turner, A. R., & Cooper, D. L. 2004, Phys. Rev. A, 69, 062702 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Liu, X.-W., Luo, S.-G., Péquignot, D., & Barlow, M. J. 2005, A&A, 442, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zygelman, B., Cooper, D. L., Ford, M. J., et al. 1992, Phys. Rev. A, 46, 3846 [Google Scholar]
All Tables
Total charge transfer recombination rate coefficients (cm3 s-1) for the reactions Xq+ + H → X(q−1)+ + H+ + δE.
Total charge transfer ionization rate coefficients (cm3 s-1) for the reactions X0 + H+ → X+ + H + δE.
All Figures
 |
Fig. 1 Incoming diabatic potential H11 for Kr3+ + H (thick solid line), and diabatic potentials H22 for six exit channels of Kr2+ + H+ + ΔE corresponding to |
| In the text | |
 |
Fig. 2 Total (thick solid curve) and final-state resolved cross sections for CT recombination of Kr3+. Energies are given in eV/u, where u is the atomic mass unit. |
| In the text | |
 |
Fig. 3 Total rate coefficients for CT recombination of X+ (dash-dot-dot-dot-dash curves), X2+ (dash-dot-dash curves), X3+ (dotted curves), X4+ (solid curves), and X5+ (dashed curves), where X is the element indicated in each panel. The q = 5 rate coefficients are lower limits due to incomplete experimental energy level measurements. Note that the Rb+ rate coefficient is below 10-14 cm3 s-1 over the plotted temperature range. |
| In the text | |
 |
Fig. 4 Total rate coefficients for CT ionization of the indicated neutral species. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.