| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201117890 | |
| Published online | 18 October 2011 | |
Letter to the Editor
Intermittent turbulent dynamo at very low and high magnetic Prandtl numbers⋆
1
CNRS, Institut d’Astrophysique Spatiale, UMR 8617, 91405 Orsay, France
e-mail: eric.buchlin@ias.u-psud.fr
2
Univ Paris Sud, Institut d’Astrophysique Spatiale, UMR 8617, 91405 Orsay, France
Received: 16 August 2011
Accepted: 20 September 2011
Context. Direct numerical simulations of plasmas have shown that the dynamo effect is efficient even at low Prandtl numbers, i.e., the critical magnetic Reynolds number Rmc that is necessary for a dynamo to be efficient becomes smaller than the hydrodynamic Reynolds number Re when Re → ∞.
Aims. We test the conjecture that Rmc tends to a finite value when Re → ∞, and we study the behavior of the dynamo growth factor γ at very low and high magnetic Prandtl numbers.
Methods. We use local and nonlocal shell models of magnetohydrodynamic (MHD) turbulence with parameters covering a much wider range of Reynolds numbers than direct numerical simulations, that is of astrophysical relevance.
Results. We confirm that Rmc tends to a finite value when Re → ∞. As Rm → ∞, the limit to the dynamo growth factor γ in the kinematic regime follows Reβ, and, similarly, the limit for Re → ∞ of γ behaves like Rmβ′, with β ≈ β′ ≈ 0.4.
Conclusions. Our comparison with a phenomenology based on an intermittent small-scale turbulent dynamo, together with the differences between the growth rates in the different local and nonlocal models, indicate that nonlocal terms contribute weakly to the dynamo effect.
Key words: dynamo / magnetohydrodynamics (MHD) / turbulence
Figures 5 and 6 are available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
The magnetic Prandtl number Pm (the ratio of the kinematic viscosity ν to the magnetic diffusivity η) is one of the non-dimensional parameters that control the properties of plasma. This ratio translates to Pm = Rm/Re, where Re and Rm are the hydrodynamic and the magnetic Reynolds numbers respectively, and this means in particular that it is an important parameter influencing the properties of turbulence in a plasma. Its value is large in hot, rarefied plasmas such as the interstellar or intracluster medium and the solar wind, and it is small in cool and dense plasmas as in planets and the Sun’s convective zone, which is at the origin of the solar magnetic field.
Iskakov et al. (2007) and Schekochihin et al. (2007) demonstrated with direct numerical simulations that the turbulent dynamo is effective even for small Pm, but the minimum Prandtl number that they were able to use was limited by the resolution of the simulation to 0.070 (with eighth-order hyperviscosity). Owing to this limitation, they cannot tell for sure whether the critical magnetic Reynolds number Rmc tends to a finite value when the hydrodynamic Reynolds number Re tends to infinity (their maximum Re is 6200). Large-scale dynamos at Pm down to 10-3 have also been obtained by Brandenburg (2009). However, the range of Pm that is relevant to astrophysics is even wider.
Shell models of magnetohydrodynamical (MHD) turbulence allow us to go much beyond these limits, up to Re ≈ 1012 and Pm ≈ 10 ± 12 in this paper. They are dynamical models of the nonlinear interactions between fields on different scales and have been developed for the study of turbulence in various frameworks such as hydrodynamics (Gledzer 1973), MHD (Gloaguen et al. 1985; Yamada & Ohkitani 1987), reduced MHD (Nigro et al. 2004; Buchlin & Velli 2007), Hall-MHD (Galtier & Buchlin 2007), and MHD with a global rotation rate (Perrone et al. 2011). A review of shell models can be found in Biferale (2003) and in the book by Bohr et al. (2005).
The simplification that they provide, making them complementary to direct numerical simulations (that are limited by the resolution one can afford), has allowed numerous results to be obtained. MHD shell models have been proven to display dynamo action (Gloaguen et al. 1985; Frick & Sokoloff 1998; Sahoo et al. 2010), including magnetic field reversals (Perrone et al. 2011). They have in particular been used by Stepanov & Plunian (2006) for the dynamo at low Pm, and later by the same authors (Stepanov & Plunian 2008) to propose a phenomenology of the turbulent dynamo at both low and high Pm (using nonlocal shell models: Plunian & Stepanov 2007).
In this paper, we use local and nonlocal shell models to derive properties of the dynamo over a very wide range of Reynolds and Prandtl numbers, extending the results of Iskakov et al. (2007) and Stepanov & Plunian (2006).
2. Model equations and numerical set up
In shell models, the Fourier space for the fields of MHD is divided in concentric shells of radii kn = λn (λ is the separation factor between shells), and the fields in each of these shells are represented by the complex scalars un for the velocity field and 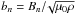 for the magnetic field (ρ is the density of the plasma, bn has the dimension of a velocity). The nonlinear terms of incompressible MHD, a convolution in Fourier space, are written in the following symmetric form when expressed as a function of the Elsässer variables
for the magnetic field (ρ is the density of the plasma, bn has the dimension of a velocity). The nonlinear terms of incompressible MHD, a convolution in Fourier space, are written in the following symmetric form when expressed as a function of the Elsässer variables 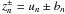
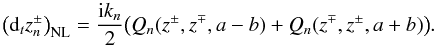 (1)In general, the coefficients of the nonlinear terms are determined by the conservation of quantities representing the invariants of incompressible MHD in three dimensions (3D), namely the energy, cross helicity, and magnetic helicity.
(1)In general, the coefficients of the nonlinear terms are determined by the conservation of quantities representing the invariants of incompressible MHD in three dimensions (3D), namely the energy, cross helicity, and magnetic helicity.
In the local “GOY” shell model (Giuliani & Carbone 1998; Stepanov & Plunian 2006), the nonlinear terms are limited to quasi-local interactions between three consecutive shells 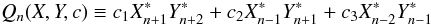 (2)with c = a ± b and
(2)with c = a ± b and 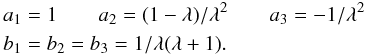 In the nonlocal “Sabra” model (Plunian & Stepanov 2007; Stepanov & Plunian 2008), where the hypothesis of quasi-local interactions is released,
In the nonlocal “Sabra” model (Plunian & Stepanov 2007; Stepanov & Plunian 2008), where the hypothesis of quasi-local interactions is released, 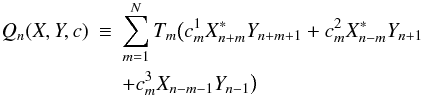 (3)with the coefficients
(3)with the coefficients 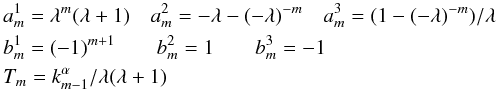 and where N is the number of shells used in the computation. The α exponent in Tm controls the strength of long-range (in Fourier space) nonlinear interactions: following Stepanov & Plunian (2008), we use α = −1 for strong nonlocal interactions, and α = −5/2 for weak nonlocal interactions; α = −∞ would correspond to no nonlocal interactions, i.e., to a local model.
and where N is the number of shells used in the computation. The α exponent in Tm controls the strength of long-range (in Fourier space) nonlinear interactions: following Stepanov & Plunian (2008), we use α = −1 for strong nonlocal interactions, and α = −5/2 for weak nonlocal interactions; α = −∞ would correspond to no nonlocal interactions, i.e., to a local model.
The forcing fn is a solution of a stochastic Langevin equation and is applied to the two first modes n = 0 and 1 of the velocity only, and the dissipation is modeled by Laplacian diffusivity coefficients ν (viscosity) and η (magnetic diffusivity).
The equations for all three models (local GOY model, weakly and strongly nonlocal Sabra models) are solved numerically using a third-order Runge-Kutta scheme for the nonlinear and forcing terms, and a first-order implicit scheme for the dissipation. The time step is adaptive and is set to the smallest time scale of the nonlinear terms, with a security factor of 5. We use λ = 2, and the initial condition for the velocity field is 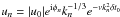 , where | u0 | = 10-1, δt0 = 10-3, and φn are independent random phases. After one large eddy turnover time t1 with no magnetic field (the shell-model equations reduce to hydrodynamic shell-model equations), we introduce an initial magnetic field
, where | u0 | = 10-1, δt0 = 10-3, and φn are independent random phases. After one large eddy turnover time t1 with no magnetic field (the shell-model equations reduce to hydrodynamic shell-model equations), we introduce an initial magnetic field 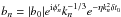 , where | b0 | = 10-10 and
, where | b0 | = 10-10 and 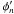 are also independent random phases: the cross helicity is close to zero, and the Lorentz force (scaling as k2ub) is negligible. The initial conditions for both u (at t = 0) and b (at t = t1) correspond to power-law energy spectra with a slope − 5/3 cut by the equivalent of the dissipation during the duration δt0.
are also independent random phases: the cross helicity is close to zero, and the Lorentz force (scaling as k2ub) is negligible. The initial conditions for both u (at t = 0) and b (at t = t1) correspond to power-law energy spectra with a slope − 5/3 cut by the equivalent of the dissipation during the duration δt0.
Each model is run with a wide range of parameters ν and η from 10-12 to 1 (6281 independent runs of each model). Such a range of parameters is only made possible thanks to the simplifications operated in the shell models.
Every ten time steps, we compute the kinetic energy 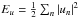 , from which we evaluate the hydrodynamic and magnetic Reynolds numbers by
, from which we evaluate the hydrodynamic and magnetic Reynolds numbers by 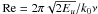 and
and 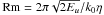 . We also evaluate the growth rate γ of the magnetic energy
. We also evaluate the growth rate γ of the magnetic energy 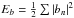 from the local slope of lnEb(t). We stop this analysis when Eb becomes greater than 10-4Eu, i.e., restricting ourselves to the kinematic regime of the dynamo. In this way, we get a large set of (Re,Rm,γ) triplets, from which statistics can be evaluated.
from the local slope of lnEb(t). We stop this analysis when Eb becomes greater than 10-4Eu, i.e., restricting ourselves to the kinematic regime of the dynamo. In this way, we get a large set of (Re,Rm,γ) triplets, from which statistics can be evaluated.
3. Results
Growth rate as a function of Reynold numbers.
 |
Fig. 1 Growth rate γ as a function of the Reynolds numbers Re and Rm (note that the color scale is different for positive and negative values of γ), in the case of the weakly nonlocal Sabra model (α = −5/2). The stability curve, corresponding to the γ = 0 level line, is overplotted. The dashed rectangle corresponds to the range of parameters explored by the direct numerical simulations of Iskakov et al. (2007); the green triangles indicate the initial Reynolds numbers used in Fig. 4; the dotted line is where Pm = 1. |
In Fig. 1, we plot the average of γ in bins of (Re,Rm) for the weakly nonlocal model (α = −5/2). We see that the dynamo is effective (γ > 0) for higher values of Rm. The level line γ = 0 represents the stability curve Rmc(Re) of the dynamo; a striking feature is that it is almost independent of Re and that it seems to have a finite limit when Re → ∞. This is a feature that has been noted by Iskakov et al. (2007) up to Re ≈ 3600, and here we confirm this result up to values of Re ≈ 1012. In addition, at low Re, we also recover the decrease in the stability curve.
The three different models (see also Figs. 5 and 6 online) have the same general behavior and the numerical results that we obtain for Rmc, summarized in Table 1 are almost indistinguishable. One can note however that the stability curves Rmc(Re) are shifted upwards (Fig. 2) and that the limit of Rmc as Re → ∞ slightly increases (Table 1) when the range of nonlocal interactions decreases. This implies that nonlocal interactions increase the efficiency of the dynamo, even at small Pm where these nonlocal interactions are expected to be weak.
 |
Fig. 2 Stability curves Rmc(Re) for the local (plain line), weakly nonlocal (dashes), and strongly nonlocal (dots) models, and from Iskakov et al. (2007) (diamonds). |
Numerical values obtained for the three models.
Growth rates at a given kinetic or magnetic Reynold number.
 |
Fig. 3 Logarithm of the growth rate γ (when positive) as a function of the magnetic Prandtl number Pm for different magnetic Reynolds numbers Rm (curves are labeled with log Rm), for the weakly nonlocal model. Inset: the limit γ∞ of γ for Re → ∞ and a power-law fit (plain line). |
The curves γ(Pm) for different Rm are plotted in Fig. 3; the plot variables are the same as in Fig. 1 of Iskakov et al. (2007). These curves correspond to horizontal cuts in Fig. 1, with inverted abscissa and with a shift by log Rm to the left. They confirm two results of Iskakov et al. (2007) for the growth rate at a given Rm, again over a much wider range of parameters: (1) for a given Rm, the growth rate γ reaches a limit1l(Rm) ≡ limγ(Re,Rm) for Re → ∞ (i.e., Pm → 0, the saturation of γ starting for Pm slightly greater than 1); and (2) for any sufficiently large magnetic Reynolds number (Rm ≳ 250), this limit l(Rm) is positive.
Similarly, vertical cuts in Fig. 1 (not shown) demonstrate that for a given Reynolds number Re, the growth rate γ reaches a limit l′(Re) ≡ limγ(Re,Rm) for Rm → ∞, i.e., for Pm → ∞. Again, the saturation of γ starts for Pm slightly greater than 1; this asymmetry with respect to Pm = 1 can be seen in Fig. 1 as a shift between the dotted line (Pm = 1) and the “crest line” of the representation of γ(Re,Rm), and to our knowledge this shift has not been noted before.
Asymptotic behavior of the limits of the growth rate.
We determine the limit l(Rm) as defined before by taking the average of γ on the three leftmost data points of each curve of Fig. 3, with the condition that a limit has been reached. The inset of Fig. 3 shows that l(Rm) is a power law of Rm: its slope β is obtained by a linear fit log l ~ βlog Rm, and the results for all three models are given in Table 1. Similarly, l′(Re) is a power law of Re, and its slope β′ (also given in Table 1) is obtained by the linear fit log l′ ~ β′log Re.
Values of β and β′ are in the range [0.33,0.43 ] . These values for β and β′, which could not be determined by the direct numerical simulations of Iskakov et al. (2007), seem to favor a dynamo driven by small-scale motions (an exponent 1/2 is expected) over an outer-scale, or mean-field, dynamo (an exponent of 0 is expected). Assuming that | u(ℓ) | ~ ℓζ1 (i.e., ζ1 is the exponent of the first structure function of the velocity field), a small-scale dynamo phenomenology (e.g., Stepanov & Plunian 2008) can indeed be summarized as follows:
-
ForPm ≪ 1, the scale on which the magnetic field grows the fastest is the resistive scale ℓη ~ Rm − 1/(1 + ζ1), which lies within the inertial range of the velocity spectrum. The growth rate is the inverse turnover time at this scale, i.e., γ = uℓη/ℓη ~ Rm(1 − ζ1)/(1 + ζ1), giving β = (1 − ζ1)/(1 + ζ1).
-
Similarly, for Pm ≫ 1, the scale on which the magnetic field grows the fastest is the viscous scale ℓν ~ Re − 1/(1 + ζ1), where resistive dissipation is negligible. The growth rate is then γ = uℓν/ℓν ~ Re(1 − ζ1)/(1 + ζ1), giving β′ = (1 − ζ1)/(1 + ζ1) = β.
With no intermittency, ζ1 = 1/3 and we recover β = β′ = 1/2 for the small-scale dynamo, as mentioned before. With hydrodynamic turbulence intermittency2, the She & Leveque (1994) phenomenology provides the value ζ1 = 1/9 + 2(1 − (2/3)1/3) ≈ 0.364 and then the small-scale dynamo phenomenology gives β = β′ ≈ 0.466, in agreement with the numerical result of Stepanov & Plunian (2008).
In our simulations, the values we obtain for ζ1 (shown in Table 1 and computed from ten independent runs with ν = η = 10-10) are closer to the She & Leveque 1994 value than to one-third (no intermittency), although both are within 3-σ error bars. The small-scale dynamo phenomenology then yields the values for β and β′ given as βphenom.(ζ1) in Table 1. This prediction and the simulation values are lower in the case of the strongly nonlocal model, as a consequence of the higher value of ζ1 in this case.
The values for β and β′ are systematically lower than the βphenom. predictions, but they are still mostly consistent with them. They are also lower than the numerical result of Stepanov & Plunian (2008). The difference from the prediction might be caused, at least for the nonlocal models, by a contribution of the outer-scale dynamo to the growth of the magnetic field, while the difference from the numerical results of Stepanov & Plunian (2008) may come from the different averaging process3.
Magnetic energy spectra.
The difference, however small, between local and nonlocal models is surprising if one considers that nonlocal interactions in wavenumber space are expected to become important at large Pm. However, for all values of Pm, the evolution of magnetic spectra is consistent with mainly local transfers from kinetic to magnetic energy, and so does not require important nonlocal transfers:
-
1.
ForPm = 1 (ν = η = 10-3 or 10-10 in Fig. 4), magnetic energy grows first on scales corresponding to the end of the inertial range of the kinetic energy spectrum, close to the dissipation range, at a speed depending on Reynolds numbers.
-
2.
For Pm ≪ 1 (ν = 10-10 and η = 10-3 in Fig. 4), the wavenumber range where magnetic energy can grow is limited by the magnetic diffusivity scale.
-
3.
For Pm ≫ 1 (ν = 10-3 and η = 10-10 in Fig. 4), the range where magnetic energy can grow is limited by the viscous scale, showing that transfers from the kinetic to the magnetic energy are still mainly local (despite the inclusion of nonlocal terms in the model).
We note that the scales on which the magnetic energy grows most are consistent, at both small and large Pm, with the scales used above to compute the magnetic energy growth rate in the small-scale dynamo phenomenology.
4. Conclusion
We have computed the growth rate γ of the magnetic field in the kinematic regime of a dynamo as a function of the Reynolds numbers Re and Rm, with, thanks to shell models, a much wider range of parameters than previous studies using direct numerical simulations. This wider parameter range is of astrophysical relevance and brings a new perspective to results from direct numerical simulations; it allows us to answer some important outstanding questions about the kinematic regime of the dynamo, assuming of course that results from shell models remain valid for the general MHD equations.
We confirm that the critical magnetic Reynolds number Rmc tends to a finite value at large Reynolds numbers Re. Furthermore, the growth rate γ tends to a finite value l(Rm) when Re tends to infinity, and we find a scaling l(Rm) ~ Rmβ with β ≈ 0.4. Similarly, γ tends to a finite value l′(Re) ~ Reβ′ when Rm tends to infinity, with β′ ≈ 0.4. Both limits l(Rm) and l′(Re) are attained for Rm ≳ Re.
 |
Fig. 4 Evolution of the spectra (compensated by k5/3) of kinetic energy (black) and magnetic energy (blue), for different sets of initial Reynolds numbers (Re,Rm) (shown as green triangles in Fig. 1), for the weakly nonlocal Sabra model. The spectra are averaged over ten independent runs and are plotted at time intervals shown as Δt in the plot titles. The different shades are a guide for understanding the direction of time (from black to gray and from dark to light blue, cycling every five spectra). |
These scalings can be explained by an intermittent, mainly small-scale dynamo. Furthermore, our results imply that nonlocal interactions (in Fourier space) play a role in the kinematic dynamo, although a limited one. This behavior is consistent with results on the locality of nonlinear interactions in MHD systems: in Alexakis et al. (2005), Mininni et al. (2005) (direct numerical simulations), and Plunian & Stepanov (2007) (shell models), nonlocal interactions are significant but are mostly confined to a wavenumber range that is relatively small compared to the wavenumber separation factor between shells that interact in shell models.
Online material
This limit is noted γ∞(Rm) in Iskakov et al. (2007), but we need to use a different notation because of the other limit that we introduce.
A MHD model such as Politano & Pouquet (1995) would not be relevant to the kinematic regime of the dynamo (low magnetic field).
Acknowledgments
Financial support from STFC (UK), CNES and CNRS (France) is acknowledged. I thank the referee for his useful comments. This work has benefited from discussions with P. Démoulin, S. Fauve, S. Galtier, F. Plunian, M. Proctor, and A. Schekochihin, in particular at the 2009 workshop “Frontiers in Dynamo Theory” in Paris, and from the work of K. Olivier during an internship in Orsay.
References
- Alexakis, A., Mininni, P. D., & Pouquet, A. 2005, Phys. Rev. E, 72, 046301 [Google Scholar]
- Biferale, L. 2003, Ann. Rev. Fluid Mech., 35, 441 [Google Scholar]
- Bohr, T., Jensen, M. H., Paladin, G., & Vulpiani, A. 2005, Dynamical Systems Approach to Turbulence (Cambridge University Press) [Google Scholar]
- Brandenburg, A. 2009, ApJ, 697, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Buchlin, E., & Velli, M. 2007, ApJ, 662, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Frick, P., & Sokoloff, D. 1998, Phys. Rev. E, 57, 4155 [NASA ADS] [CrossRef] [Google Scholar]
- Galtier, S., & Buchlin, E. 2007, ApJ, 656, 560 [Google Scholar]
- Giuliani, P., & Carbone, V. 1998, Europhys. Lett., 43, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gledzer, E. B. 1973, Sov. Phys. Dokl., 18, 216 [NASA ADS] [Google Scholar]
- Gloaguen, C., Léorat, J., Pouquet, A., & Grappin, R. 1985, Physica D, 17, 154 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Iskakov, A. B., Schekochihin, A. A., Cowley, S. C., McWilliams, J. C., & Proctor, M. R. E. 2007, Phys. Rev. Lett., 98, 208501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mininni, P., Alexakis, A., & Pouquet, A. 2005, Phys. Rev. E, 72, 046302 [NASA ADS] [CrossRef] [Google Scholar]
- Nigro, G., Malara, F., Carbone, V., & Veltri, P. 2004, Phys. Rev. Lett., 92, 194501 [NASA ADS] [CrossRef] [Google Scholar]
- Perrone, D., Nigro, G., & Veltri, P. 2011, ApJ, 735, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Plunian, F., & Stepanov, R. 2007, New J. Phys., 9, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Politano, H., & Pouquet, A. 1995, Phys. Rev. E, 52, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Sahoo, G., Mitra, D., & Pandit, R. 2010, Phys. Rev. E, 81, 036317 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Iskakov, A. B., Cowley, S. C., et al. 2007, New J. Phys., 9, 300 [Google Scholar]
- She, Z. S., & Leveque, E. 1994, Phys. Rev. Lett., 72, 336 [Google Scholar]
- Stepanov, R., & Plunian, F. 2006, J. Turbulence, 7, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, R., & Plunian, F. 2008, ApJ, 680, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, M., & Ohkitani, K. 1987, J. Phys. Soc. Japan, 56, 4210 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Growth rate γ as a function of the Reynolds numbers Re and Rm (note that the color scale is different for positive and negative values of γ), in the case of the weakly nonlocal Sabra model (α = −5/2). The stability curve, corresponding to the γ = 0 level line, is overplotted. The dashed rectangle corresponds to the range of parameters explored by the direct numerical simulations of Iskakov et al. (2007); the green triangles indicate the initial Reynolds numbers used in Fig. 4; the dotted line is where Pm = 1. |
| In the text | |
 |
Fig. 2 Stability curves Rmc(Re) for the local (plain line), weakly nonlocal (dashes), and strongly nonlocal (dots) models, and from Iskakov et al. (2007) (diamonds). |
| In the text | |
 |
Fig. 3 Logarithm of the growth rate γ (when positive) as a function of the magnetic Prandtl number Pm for different magnetic Reynolds numbers Rm (curves are labeled with log Rm), for the weakly nonlocal model. Inset: the limit γ∞ of γ for Re → ∞ and a power-law fit (plain line). |
| In the text | |
 |
Fig. 4 Evolution of the spectra (compensated by k5/3) of kinetic energy (black) and magnetic energy (blue), for different sets of initial Reynolds numbers (Re,Rm) (shown as green triangles in Fig. 1), for the weakly nonlocal Sabra model. The spectra are averaged over ten independent runs and are plotted at time intervals shown as Δt in the plot titles. The different shades are a guide for understanding the direction of time (from black to gray and from dark to light blue, cycling every five spectra). |
| In the text | |
 |
Fig. 5 Same as Fig. 1 for the local GOY model. |
| In the text | |
 |
Fig. 6 Same as Fig. 1 for the strongly nonlocal (α = −1) Sabra model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


