| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201117093 | |
| Published online | 04 October 2011 | |
Multiple populations in ω Centauri: a cluster analysis of spectroscopic data
1
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
e-mail: raffaele.gratton@oapd.inaf.it
2
Department of Physics and Astronomy, University of California, Los Angeles, 430 Portola Plaza, Box 951547, Los Angeles, CA 90095-1547, USA
e-mail: cijohnson@astro.ucla.edu
3
Department of Astronomy, Indiana University, Swain West 319, 727 East Third Street, Bloomington, IN 47405-7105, USA
e-mail: catyp@astro.indiana.edu
Received: 16 April 2011
Accepted: 21 May 2011
ω Centauri, the largest globular cluster of the Milky Way, is composed of several stellar populations, which can be seen in both photometry and spectroscopy. The history of how these different populations assembled will allow us to reconstruct the evolution of this complex object. In particular, understanding the detailed chemical evolution will be particularly illuminating. However, this is not easy because of the errors intrinsic to abundance determinations. We performed a statistical cluster analysis on the large data set of accurate abundances recently provided for about 800 red giant branch stars. We find that stars in ω Cen divide into three main groups. The metal-poor group includes about a third of the total. It shows a moderate O-Na anticorrelation, and similar to other clusters, the O-poor second generation stars are more centrally concentrated than the O-rich first generation ones. This whole population is La-poor, with a pattern of abundances for n-capture elements that is very close to a scaled r-process one. The metal-intermediate group includes the majority of the cluster stars. This is a much more complex population, with an internal spread in the abundances of most elements. It shows an extreme O-Na anticorrelation, with a very numerous population of extremely O-poor and He-rich second generation stars. This second generation is very centrally concentrated. This whole population is La-rich, with a pattern of the abundances of n-capture elements that shows a strong contribution by the s-process. The spread in metallicity within this metal-intermediate population is not very large, and we can attribute it either to non-uniformities of an originally very extended star-forming region, or to some ability to retain a fraction of the ejecta of the core-collapse SNe that exploded first, or both. As previously noticed, the metal-rich group has an Na-O correlation rather than anticorrelation. There is evidence for the contribution of both massive stars ending their life as core-collapse SNe, and intermediate/low mass stars, producing the s-capture elements. Kinematics of this population suggests that it formed within the cluster rather than being accreted.
Key words: stars: abundances / stars: evolution / stars: Population II / globular clusters: individual: omega Centauri
© ESO, 2011
1. Introduction
It has recently become evident that globular clusters, hitherto considered as simple stellar populations, are actually made of multiple stellar populations (see Gratton et al. 2001, 2004). Evidence includes both photometry (Bedin et al. 2004; Piotto et al. 2007) as well as spectroscopy (Gratton et al. 2001; Carretta et al. 2009a,b, 2010a). Most globular clusters host only a small number of stellar populations, differing in their content of light elements, typically described by anticorrelations among C and N, Na and O, Mg and Al, and likely He (Bedin et al. 2004; Carretta et al. 2009a; Gratton et al. 2010), while the abundances of Fe-peak elements do not show any spread (Carretta et al. 2009c). But in a few, generally massive globular clusters, different populations differ in the abundances of virtually all elements. In many respects, these objects can be considered as intermediate between globular clusters and ultra compact dwarf galaxies (see, e.g., Forbes & Kroupa 2011; and Norris & Kannappan 2011). Examples include M 54 (Carretta et al. 2010b), M 22 (Marino et al. 2009), NGC 1851 (Lee et al. 2009; Carretta et al. 2010d) and ω Cen. This last, which is the brightest and most massive Milky Way cluster, represents the most extreme case of such variations.
The presence of multiple populations in ω Centauri was discovered almost half a century ago by Woolley (1966). Various studies provided evidence for the large spread in metallicity within this cluster: among many others, we cite Freeman & Rodgers (1975), Butler et al. (1978), Cohen (1981), Norris & Da Costa (1995a,b), Suntzeff & Kraft (1996), and Smith et al. (2000). All these studies found a predominance of metal-poor stars ([Fe/H] < −1.5), with a tail up to fairly high metallicities ([Fe/H] ~ −1). More recently, Pancino et al. (2000) discussed the presence of a group of metal-rich stars on the red of the main red giant branch (RGB), which they called RGB-a (for anomalous), and a metallicity [Fe/H] > −1. Perhaps the most surprising discovery, however, was the splitting of the main sequence (Bedin et al. 2004) into at least two (and possibly more) separate sequences, and the fact that the red sequence is clearly more numerous than the blue one. This lead to the suspicion that the blue sequence is much more He-rich (Norris 2004), which was soon confirmed by the spectroscopic analysis by Piotto et al. (2005), showing that the blue main-sequence is more metal-rich than the red one, just the opposite of what is expected if the splitting were to be attributed simply to a metal abundance difference.
Clearly, many different populations are present in ω Cen: multiple populations are found in the RGB (Sollima et al. 2005a), subgiant branch and main sequence (Bellini et al. 2010). Early attempts to reconstruct the history of these populations met with severe problems. For instance, various authors proposed age-metallicity relations for ω Cen by combining photometric and spectroscopic observations of subgiant-branch stars (see, e.g., Sollima et al. 2005b; Stanford et al. 2006; Villanova et al. 2007), but the results contradicted each other, likely because these studies neglected the large variations in He content present among different groups of stars. However, reconstructing the early history of globular clusters from photometry alone is very difficult, because the long time elapsed since the cluster formation renders the differences caused by age subtle and easily masked by other effects (He and heavy-element variations). Some clarification might then possibly come from the chemistry, exploiting the fact that different elements are produced by stars in different mass ranges, and hence on different timescales. Thanks to the use of multi-fibre instruments, very extensive high-resolution spectroscopic studies of several hundred red giants are now available (Johnson & Pilachowski 2010; Marino et al. 2011). These studies provide several interesting observations. For instance, while a clear Na-O anticorrelation is present among metal-poor stars, overabundances of both Na and O are obtained for the most metal-rich ones (those on the RGB-a of Pancino et al. 2000). In addition, the Na-O anticorrelation is present in stars over a large range in metallicity and its extension possibly increases with metallicity. This is not easy to reconcile with the typically very narrow metal distribution of other clusters. Finally, the abundances of the n-capture elements mainly produced by the s-process clearly rise with metallicity (Norris & Da Costa 1995; Smith et al. 2000; Pancino 2003; Johnson & Pilachowski 2010; Marino et al. 2011). The production of s-process elements is usually thought to occur in small-mass asymptotic giant branch (AGB) stars, and on a much longer timescale than that considered for the evolution of the stars responsible of the Na-O anticorrelation from fast rotating massive stars (Decressin et al. 2007) or massive AGB stars undergoing hot bottom burning (Ventura et al. 2001). As discussed by Marino et al. (2011), there is a timescale problem to be solved.
In addition, Carretta et al. (2010a) proposed that ω Cen might be similar to M 54, a GC whose position is coincident with the nucleus of the Sagittarius dwarf spheroidal (dSph) galaxy. The authors noticed that when this galaxy will be dispersed as a consequence of its tidal interaction with the Milky Way, some part of the stars in the field of the dSph – themselves much more metal-rich than M 54 – would probably remain locked within M 54. The red giants would then appear as an anomalous red giant branch, in analogy with the RGB-a of ω Cen. Whether this is the correct explanation of the RGB-a of ω Cen remains to be verified. This might possibly be obtained by a chemical abundance analysis of the RGB-a stars. For instance, if this interpretation were correct, we should expect that the RGB-a stars be poor in α-elements, because this is the typical signature observed in metal-rich stars in dSph.
Part of the analysis problems possibly arise from the difficulties of clearly separating the different populations of ω Cen. While progress is being made to understand the separation of the different populations on the main sequence, the separation of the populations on the RGB remains difficult. Detailed abundances for many elements can help to differentiate the RGB populations and understand their origins. To explain their results, Marino et al. (2011) proposed a subdivision of their RGB sample into different metallicity bins, but realized that some stars could be assigned to incorrect bins owing to errors in metallicity. They attempted to correct for these errors, but their corrections were not based on robust, objective criteria. In this paper, we will re-examine this question with a more objective approach, that is with grouping algorithms that are usually adopted in statistical analysis. These methods are applied to the sample by Johnson & Pilachowski (2010), which is about three times more numerous than that considered by Marino et al. (2011) but has similar error bars. We will show that a few groups naturally arise from the data themselves. These groups, derived from chemical properties, also have different broad band colours. The properties of these groups nicely correspond to the main populations found in other evolutionary phases (e.g. the main sequence). We also briefly discuss dynamical properties for these groups. We think that the division into groups will allow significant progress in future modelling of the formation of this cluster.
2. Input data
The data we considered in our analysis are those produced by Johnson & Pilachowski (2010), who provided abundances for eleven elements (Fe, O, Na, Al, Si, Ca, Sc, Ti, Ni, La, and Eu) in 855 stars. In addition to the elemental abundances, we have coordinates (and hence distance from cluster centre), radial velocities and photometry (BV from van Loon et al. 2007; and JHK from 2MASS, Skrutskie et al. 2006).
The main objective of our analysis is to find “natural groups” from this data set, which can help in the interpretation of the evolution of ω Cen. Group analysis usually requires several parameters to be known for all the members of the input populations. Owing to availability of data, not all elements were measured in all stars, a fact that should be taken into account in our analysis. Furthermore, while error bars for individual elements can be significant with respect to the overall scatter throughout the cluster, clearly there is some redundancy among the input data, because various elements can be grouped together according to their similar nucleosynthesis. For instance, abundances of the Fe-peak elements Sc and Ni (not available for many stars) do not really add much to what is obtained using Fe alone. We then considered in our analysis the following four quantities:
-
The Fe abundance [Fe/H], which is assumed to be representativeof the overall metallicity. We will see below that this quantity iswell correlated with the colour of stars along the RGB,as expected. Fe may be producedby both core collapse and thermonuclear supernovae.
-
The ratio between the Na and O abundances [Na/O]. This ratio is representative of the location of stars along the Na-O anticorrelation, and is likely correlated with the He abundance, although this relation is presumably not linear (see, e.g., Gratton et al. 2010)
-
The average of the elements Si, Ca, and Ti, all mainly produced by α-capture reactions in massive stars, later exploding as core-collapse SNe. Use of an average of these three elements has two advantages: first, it reduces the number of stars for which data are not available; second, it reduces star-to-star scatter. In practice, we used this [α/Fe] ratio. This might be either a measure of the relative contribution of core-collapse and thermonuclear SNe, or (more likely in the case of ω Cen, see below) of the weights to be given to the contribution by stars of different masses among the core-collapse SNe.
-
The abundance of La, which is an n-capture element that in the Sun is mainly produced by the s-process.
These data are available for 797 stars, which is more than 93% of the total sample observed by Johnson & Pilachowski (2010). A cluster analysis for this sample is then expected to be representative at least for the major populations in ω Cen. Most of the 70 stars excluded from this analysis lack La abundances (57 stars); the remaining ones lack either O or Na abundances (or both). Missing stars tend to be located farther from the cluster centre (average distance of 7.8 ± 0.5 arcmin, with respect to an average value of 6.30 ± 0.16 arcmin for the stars included in the sample). This is probably why they have on average a higher [O/Fe] value (0.37 ± 0.02 vs. 0.12 ± 0.01) (see Sect. 5.2). However, their Na abundance is not smaller than for the stars of our sample (0.25 ± 0.04 vs. 0.16 ± 0.01), and the Na-O anticorrelation is poorly defined for these stars – likely because of larger than average errors. The excluded stars have on average an [Fe/H] slightly lower than for those stars included in the sample ([Fe/H] = −1.69 ± 0.03 vs. −1.60 ± 0.01). It is then likely that most of the stars excluded belong to groups #4 an #5 cited below, although they are probably distributed among all groups. Three of the excluded stars (45 485, 4715, and especially 45 358) have large La, as well as Na and Al abundances. No O abundance determination is available for these stars, all of them being metal rich ([Fe/H] > −1.1)
Of course, it would be important to use additional data in our classification, but unfortunately, these are available only for a minority of the stars. For instance, Al abundances help to better clarify the p-capture mechanisms responsible for the Na-O anticorrelation. Al abundances have been estimated by Johnson et al. (2008, 2009, 2010) for 311 stars of our sample. In addition, Eu abundances would be very helpful to better understand the nature of the n-capture processes that are relevant for ω Cen. However, Eu abundances are available for only 184 of these 797 stars. We deem reduction of our sample to only those stars with Al or Eu abundances too much of a limitation. On the other hand, we will discuss in Sects. 3.3 and 3.4 both Al and Eu abundances for the groups we will derive from our analysis.
3. Analysis and results
In our analysis we used the R statistical package (R Development Core Team 2011). R is a system for statistical computation and graphics, freely available on-line1. Several algorithms for cluster analysis are available within R. Our results are based on the k-means algorithm (Steinhaus 1956; MacQueen 1967), although in Sect. 4 we will briefly discuss results obtained with other clustering algorithms. k-means clustering is a method of cluster analysis that aims to partition n observations into k-clusters in which each observation belongs to the cluster with the nearest mean. Given a set of observations (x1, x2, ..., xn), where each observation is a d-dimensional real vector, k-means clustering distributes the n observations into k sets (k = n) S = { S1,S2,...,Sk } so as to minimize the within-cluster sum of squares W: 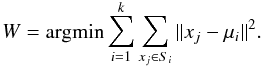 (1)Practically, there are various algorithms used to find this minimum. Within the R-package, the algorithm of Hartigan & Wong (1979) is used by default. The Hartigan & Wong algorithm generally performs better than other k-means algorithms.
(1)Practically, there are various algorithms used to find this minimum. Within the R-package, the algorithm of Hartigan & Wong (1979) is used by default. The Hartigan & Wong algorithm generally performs better than other k-means algorithms.
Two key features of k-means are:
-
Euclidean distance is used as a metric and variance is used as ameasure of cluster scatter. The various parameters used might betransformed before computing these distances to weight themadequately. A sensible choice is to normalize themto the observational errors. These are quite similar for thedifferent quantities we considered (see Johnson & Pilachowski2010), so that we skipped this step in our analysis.
-
The number of clusters k is an input parameter: an inappropriate choice of k may yield poor results. That is why, when performing k-means, it is important to run diagnostic checks for determining the number of clusters in the data set.
A key limitation of k-means is its cluster model. The concept is based on spherical clusters that are separable in a way so that the mean value converges towards the cluster centre. The clusters are expected to be of similar population, so that the assignment to the nearest cluster centre is the correct assignment. When the clusters have very different sizes, this may result in a poor assignation of members to clusters. However, in the present case, we expect that with an appropriate choice of the number of groups k, most of the scatter within one cluster is caused by observational errors, which are similar for the different clusters. We then considered the assumption of similar size for the different clusters acceptable. Of course, this does not mean that occasionally an assignation of some member (that is star) to a particular cluster is questionable.
Main group parameters.
In general, there is a strong inter-relation between the results of a cluster analysis provided by k-means and those provided by the principal component analysis. It is then useful to review the role played by the different parameters considered in our analysis in this perspective. On the whole, [α/Fe], which has a very small intrinsic scatter, comparable to observational errors, plays a minor role, and its inclusion in the analysis does not change the group identification significantly. The other three parameters considered in Sect. 2 are much more significant, but because there is a strong positive correlation between [Fe/H] and [La/Fe], the plane of the two principal components is very close to the [Na/O] vs. [La/H] plane. Then a subdivision of stars into different clusters may be well visualized in this plane, and we will use these two quantities as a proxy of the first two principal components.
 |
Fig. 1 Assignation of stars to the different groups in our k-means analysis in the [La/H] vs. [Na/O] plane. This plane roughly corresponds to that of the second and first component in a principal component analysis. Different colours are for stars of the different groups: green: group #1; red: group #2a; yellow: group #2b; violet: group #3; blue: group #4; black: group #5; cyan: group #6. |
As mentioned above, a critical assumption in the k-means analysis is the number of clusters. In our analysis, we started by considering a small number of clusters (k = 3). In this case, we found assignation of stars to the different clusters to be only driven by their [Na/O] value, which is the quantity exhibiting the largest scatter, and as mentioned above is close to the first principal component in our data. This result is of limited interest. We then increased k, looking for a combination that would distinguish between groups with a different metallicity (actually [La/H], roughly the second principal component), because we expect this to be a major parameter for the distinction in several populations within ω Cen. Because the run of [Na/O] is very extended among metal-rich stars, and guided by the result we obtained with k = 3, we deemed that three groups might be required for this metal abundance range, while perhaps two groups might be enough for the more metal-poor stars, where the [Na/O] values are apparently less scattered. Indeed, an analysis with k = 5 separates stars among both first and second principal components. However, the separation along the second component appeared much cleaner with six groups (see Fig. 1).
As we will see in the discussion, there are many appealing features in this subdivision; however, a first exploration of the results shows that one of the clusters (#2) is likely the results of the combination of two groups of stars, with quite different characteristics. We therefore performed a k-means analysis of this group alone, and divided it into two further groups, which we called #2a and #2b. Thus, at the end, our analysis is based on seven groups2. The main characteristics of the different groups are summarized in Table 1. Briefly:
-
Two groups are made of metal-poor stars, either O-rich(group #4, blue in all figures) or O-intermediate(group #6, turquoise). The[Fe/H] value is very similar, and all these stars areLa-poor. Together, these two groups have280 stars, that is 35% ofthe sample.
-
Four groups are made of stars of intermediate metallicity. They are, in order of increasing [Na/O]: group #5 (dark green), #1 (bright green), #3 (magenta), and #2a (red). This order also roughly corresponds to increasing [Fe/H] values (with an inversion between the two first groups). All these stars are La-rich. In total, these groups have 470 stars, that is 59% of the sample.
-
Finally, one group (#2b, yellow) is made of metal-rich stars. These are both Na and O-rich, and also La-rich. This group is made of 47 stars, that is 6% of the sample.
The properties of these different groups will be examined in more detail in the rest of this section.
 |
Fig. 2 V − (B − V) (left panel) and V − (V − K) (right panel) colour − magnitude diagrams for the observed stars in ω Cen. Different colours are for stars of the different groups (see Fig. 1). |
 |
Fig. 3 V − (B − V) colour–magnitude diagram for the observed stars in ω Cen. Metal-poor groups (#4 and #6) are in the left panel, metal-intermediate ones (#1, #2a, #3, #5) in the right one. Different colours are for stars of the different groups (see Fig. 1). |
3.1. Colour–magnitude diagram
Figure 2 shows the (V,B − V) and the (V,V − K) colour − magnitude diagrams for the stars observed in ω Cen. Stars assigned to the different groups are plotted with different colours. From this diagram, it is clear that the stars assigned to the metal-poor groups (#4 and #6, blue and cyan respectively) are on the blue side of the RGB, while those assigned to the metal-rich group (#2b, yellow) are on the red side. This last group can then be readily identified with the RGB-a sequence of Pancino et al. (2000). The metal-poor groups define a tight sequence, with no obvious segregation between the two groups, which indeed have very similar mean [Fe/H] and only differ in their [Na/O] ratio. This is most clearly shown in Fig. 3, where we separately plotted the (V,B − V) diagrams for the metal-poor groups (left panel) and for those of intermediate metallicity (right panel).
From these figures the presence of a correlation between colours along the RGB and stellar metallicity is apparent, as expected from evolutionary models. We may quantify this dependence to produce a metallicity index that depends on the colours of the stars along the RGB. The usefulness of this index will be discussed below. In order to define it, we started by fitting a cubic polynomial through the RGB of the two metal-poor groups. We then measured the (B − V) offset Δ(B − V) between each star and this reference sequence. Finally, we fitted a bilinear relation between [Fe/H] (dependent variable), and Δ(B − V) and V (independent variables). The best-fit parameters from this relation allow us to have a parameter for each star that we call [m/H], which on average is identical to [Fe/H], but which obviously can be different from it for each individual star (and even for each group). The average value of [m/H] for each group is also listed in Table 1.
 |
Fig. 4 Comparison between iron abundances from spectroscopy [Fe/H] and metal abundances derived from colours along the RGB ([m/H]). Different colours are for stars of the different groups (see Fig. 1). Results for all stars are plotted in panel a); panel b) is is only for metal-poor stars; panel c) is only for metal-intermediate stars; and panel d) is only for metal-rich stars. |
 |
Fig. 5 [α/H] vs. metal abundances derived from colours along the RGB ([m/H]). Different colours are for stars of the different groups (see Fig. 1). Results for all stars are plotted in panel a); panel b) is is only for metal-poor stars; panel c) is only for metal-intermediate stars; and panel d) is only for metal-rich stars. |
Figure 4 shows the correlation between [m/H] and [Fe/H] for the whole sample as well as separately for the metal-poor, metal-intermediate, and metal-rich groups. Of course, there is a good overall agreement between [m/H] and [Fe/H], the linear correlation coefficient being r = 0.58, whose significance is extremely high given the size of the sample (797 stars). An even better correlation is obtained with [α/H] (r = 0.64; see Fig. 5), while the correlations are markedly poorer with, e.g., [Na/H] or [O/H]. This confirms that [m/H] is a good proxy for a combination of [Fe/H] and [α/H] (these two quantities are extremely well correlated each other, with r = 0.90).
We notice when examining the results for the individual groups that while there is still a good correlation between [m/H] and [Fe/H] for the groups of intermediate metallicity, this correlation is much less obvious for the other groups. In particular, for the metal-poor group the hint for a correlation is only given by a dozen points (less than 5% of the total population of these groups) at a fairly high metallicity. The metallicity range appears very narrow for the remaining stars. We then suspect that this group is essentially monometallic, the observed spreads in [Fe/H] and [m/H] being only caused by observational errors, save for very few contaminants that are probably assigned erroneously to this group because of a low measured value of [La/Fe]. In addition, this plot suggests that for this group there is only a limited contamination from AGB stars (which should manifest as objects with low [m/H] for their [Fe/H], being bluer than RGB stars). Indeed, some stars scatter in this region of the plot, but they are very few.
As mentioned above, there is an obvious correlation between [Fe/H] and [m/H] for the intermediate metallicity groups. This suggests that there is a real spread in metallicity among these groups. However, a closer look reveals that the slope of the relation between [Fe/H] and [m/H] is significantly smaller than unity, that is, [Fe/H] varies much more than [m/H]. In addition, average [m/H] values for the different metal intermediate groups (which differ in their [Na/O] value, that is, their location along the Na/O anticorrelation) also differ much less than what is observed for [Fe/H]. We will return to this very interesting point below. We also note that a few points scattered below the bulk of the points in this plot may be interpreted as AGB contaminants.
Finally, there is some correlation between [Fe/H] and [m/H] for the metal-rich group as well, suggesting that also in this case there is some real spread in metallicity. Our data are not good enough to conclude if there is a continuous spread or rather two or more discrete values (as suggested by Johnson & Pilachowski 2010). A more accurate analysis of these stars might establish this interesting point.
Abundances of α-elements.
3.2. Abundances of α-elements
The results we obtained for the α-elements can be summarized as follows (see Table 2 for the abundances of the individual elements). The two most metal-poor groups have the same value of [α/Fe] = 0.20 ± 0.01, within the small statistical error bars. Systematic errors are probably much larger than these tiny statistical errors. The [Si/Fe] overabundances (on average, 0.25 dex for these two groups) are slightly larger than those obtained for Ca and Ti (0.24 and 0.12 dex), with almost negligible differences between groups #4 and #6. On the whole, we cannot avoid to notice that the α-excess is quite modest, with respect to typical values found in halo stars, and more similar to those found in dwarf spheroidals at this metallicity.
On the other hand, the intermediate metallicity groups not only provide on average higher α-excess, but [α/Fe] seems to be correlated with Na abundances and anti-correlated with O ones. Most of this trend is caused by the inclusion of Si among the elements used to estimate α/Fe, because there may be some leakage in the Mg-Al cycle producing Si (see Yong et al. 2005; and Carretta et al. 2009b). This is clearly present among this group of stars, as also discussed by Johnson & Pilachowski (2010). The average values of α/Fe for the Fe-intermediate groups are higher than what can be expected from this effect alone. This may be seen, e.g., by comparing the O-rich group #5 with respect to the Fe-poor, O-rich group #4 (0.27 ± 0.01 vs. 0.20 ± 0.01), or by comparing the average overabundances of Ca (0.33 vs. 0.24) and Ti (0.20 vs. 0.12). This suggests that the difference between the Fe abundances of the metal-poor and metal-intermediate groups (only 0.17 dex) is to be attributed to core-collapse and not thermonuclear SNe.
Similarly, the high [α/Fe] value obtained for the metal rich group #2b may only be explained by core-collapse SNe contribution. This result has been already discussed in Johnson & Pilachowski (2010). For this group, there is a correlation between the O and α-element overabundances.
 |
Fig. 6 Na-O anticorrelation for stars in ω Cen. Panel a): all stars; panel b): metal-poor groups (#4 and #6); panel c): metal-intermediate groups (#1, #2a, #3, and #5); panel d): metal rich group (#2b). Different colours are for stars of the different groups (see Fig. 1). |
3.3. Na-O and Al-O anticorrelations in different stellar populations of ω Cen
Figure 6 shows the Na-O anticorrelation for ω Cen, with different symbols for stars attributed to the different groups, as well as the same anticorrelation for the metal-poor, metal-intermediate, and metal-rich groups. As already noticed (see Carretta et al. 2010a; Johnson & Pilachowski 2010; Marino et al. 2011), the run of Na with O is very different in the various metal abundance ranges. These differences are even cleaner when using the results of our cluster analysis. We grouped our data according to the metallicity of the clusters, and plotted the Na-O anticorrelation separately for metal-poor (#4 and #6, blue and cyan, respectively), metal intermediate (#1, #3, #5 and #2a, green, violet, black, and red, respectively), and metal rich (#2b, yellow) groups. The differences in the Na-O anticorrelation between these three groups are very clear.
The Na-O anticorrelation is quite modest among the metal-poor groups, which include 280 stars (35% of the total): the interquartile of [Na/O] IQR(Na/O) is only 0.53 for this group. When compared to those observed in other globular clusters, this low value is similar to that found for 47 Tuc, M3 or M92. Group #4 (blue) can be identified with the P-star class and group #6 (cyan) with the I-star class of Carretta et al. (2009a). If this interpretation is correct, P-stars are the majority of this group (53 ± 4%), a value slightly higher than that of NGC 2808. Al abundances are available for 114 stars of these groups (69 in group #4, and 45 in group #6). Al abundances are correlated with those of Na, albeit with some scatter. Panel a of Fig. 7 shows the Al-O anticorrelation for these two groups. There is a clear trend for O-rich stars to be Al-poor, and viz. for O-poor stars. On average, group #4 has [Al/Fe] = 0.43 ± 0.04, while group #6 has [Al/Fe] = 0.71 ± 0.05. However, the star-to-star variations in Al abundances within the metal-poor groups are not as large as those observed for Na.
On the other hand, the Na-O anticorrelation is very extended among the metal intermediate groups, which include 470 stars (59% of the total), with IQR(Na/O) = 1.10. This value is higher than those of almost all other globular clusters, the only possible comparison being M54 (Carretta et al. 2010a). If we identify cluster #5 with the P-stars among this group, they make up 34 ± 3% of the total. This is distinctly less than the fraction of P-stars within the metal-poor groups. Also, groups #3 and #2a (in total, 176 stars, that is 37 ± 3%) can be identified with the E-population. Such a large fraction of E-stars is not observed in any other globular cluster. These groups also exhibit a clear Al-O anticorrelation (see panel b of Fig. 7), the average [Al/Fe] ratio steadily increasing between different clusters with decreasing O abundance (note that Al abundance is available for 32 stars of the the most extreme #2b group, red): [Al/Fe] = 0.45 ± 0.04, 0.84 ± 0.12, 1.05 ± 0.04, with 67, 30, and 49 stars for groups #5 (black), #1 (green), and #3 (violet), respectively. The largest scatter for group #1 agrees well with its intermediate character. While not extreme, the Al-O anticorrelation is quite conspicuous over these groups, however.
 |
Fig. 7 Al-O anticorrelation for stars in ω Cen. Panel a): all stars; panel b): metal-poor groups (#4 and #6); panel c): metal-intermediate groups (#1, #2a, #3, and #5); panel d): metal rich group (#2b). Different colours are for stars of the different groups (see Fig. 1). |
Finally, the metal-rich group #2a (yellow) shows a very clear correlation between Na and O. This result was already noticed by Johnson & Pilachowski (2010) and Marino et al. (2011), but it is even clearer from our cluster analysis. The Al abundances are available for only a few stars, with a possible hint for a correlation with both Na and O abundances (see panel c of Fig. 6). This is clearly different from what is observed even in most metal-rich globular clusters, like NGC 6388 and NGC 6441, which have metallicities comparable or even higher than that of this population of ω Cen (Gratton et al. 2007; Carretta et al. 2007).
These differences clearly signal a very different nucleosynthesis in the three groups. The presence of a correlation, rather than anticorrelation, between Na and O in the most metal-rich group is clearly distinct from what is observed in other globular clusters and indicates a different class of polluters, possibly related to a prolonged phase of formation. While less obvious, the different form of the Na-O and Al-O anticorrelation seen among the metal-poor and metal-intermediate groups indicates a less extreme modification and resembles the pair M4-NGC 2808 discussed in Carretta et al. (2009a). It suggests a different range in mass within the class of the polluters responsible for the observed abundance pattern that is typically observed in globular clusters.
 |
Fig. 8 Run of [La/Fe] against [Eu/Fe] for stars in ω Cen. Different colours are for stars of the different groups (see Fig. 1). Overimposed are the lines corresponding to a pure solar scaled r- (solid line) and s-contributions (dashed line). |
3.4. The n-capture elements
As mentioned in Sect. 1, n-capture elements are one of the basic ingredients of the ω Cen puzzle. In our analysis, we consider two such elements: La, which in the Sun is mainly produced by the s-process, and Eu, which in the Sun is almost entirely produced by the r-process. La belongs to the second peak of the s-process: very likely, it is produced essentially by the main component, which is thought to be active in AGB stars of fairly low mass (M < 3 M⊙). Because these stars have a very long lifetime (longer than several 108 yr), the large rise in La abundances observed between the two most metal-poor groups and the other groups strongly suggest a corresponding large age difference.
Our cluster analysis only reinforces this concept. The two most metal-poor groups, essentially distinguished by the [Na/O] value, share the same [La/Fe] = −0.17. Within this group there is no evidence for contribution by low-mass stars. These two groups also have the same Eu abundances ([Eu/Fe] ~ 0.2), within the errors. The La/Fe ratio is very close to that expected for a solar-scaled r-process (see Fig. 8). On the other hand, all other groups, while they have an [Eu/Fe] similar to that observed for the metal-poor group (again suggesting that heavy elements are enriched by core-collapse, and not thermonuclear SNe), are La-rich. The [La/Fe] values are quite uniform, with a small increasing trend with metallicity. The comparison of [Eu/La] abundances with solar scaled r- and s-contributions clearly indicate that La is produced by some kind of s-process.
Hence, either the s-process active in ω Cen is not the main component that is usually invoked to explain the s-production of elements like La, or there should be a substantial age difference of several 108 yrs between the formation of the metal-poor and of the other components of ω Cen. As discussed in Marino et al. (2011), it is not easy to avoid the main component as the major s-process active in ω Cen, so that the first hypothesis at present lacks any theoretical support.
A way to express this substantial age difference is to think of ω Cen as made in at least two (and probably more) clearly distinct episodes of star formation, the first one producing a large – but not exceptional – metal-poor globular cluster, with the typical abundance pattern observed for this class of objects (no variation in α-, Fe-peak, and n-capture elements, and with the usual Na-O and Mg-Al anticorrelations); and at least a second larger one, occurring later, which produces a much more complex abundance pattern, similar to that observed in M54. In addition, a third population is present (the RGB-a), with very peculiar characters, clearly distinct from those typical of globular clusters.
4. Comparison with other clustering algorithms
One of the main limitations of cluster analysis is the difficulty to define the robustness of the group subdivision obtained with one particular algorithm. For this reason, it is generally useful to compare results obtained with different cluster algorithms. To test our results, we considered two of them, available within the R-package: PAM (partitioning around medoids) and FANNY (fuzzy analysis).
PAM is described in chap. 3 of Kaufman & Rousseeuw (1990). Similarly to k-means, PAM is a partitioning method, but it uses medoids3, that is, real objects, to represent the clusters, rather than average values used by k-means. Practically, these algorithms select k-representative objects arbitrarily. For each pair of non-selected object h and selected object i, the total swapping cost TCih is calculated. For each pair of i and h, if TCih < 0, i is replaced by h. Each non-selected object is then assigned to the most similar representative object and the last two steps are repeated until there is no change. Briefly, PAM starts from an initial set of medoids and iteratively replaces one of the medoids by one of the non-medoids if it improves the total distance of the resulting clustering. PAM is more robust than k-means in the presence of noise and outliers because a medoid is less influenced by outliers or other extreme values than a mean. However, our sample contains no obvious outlier, so this should not be too much of a worry in the present case.
FANNY is a fuzzy clustering algorithm. In fuzzy clustering, each point has a degree of belonging to clusters, as in fuzzy logic, rather than belonging completely to just one cluster (as in crisp logic); thus, points on the edge of a cluster may be in the cluster to a lesser degree than points in the centre of cluster. The membership of observation i to cluster v is denoted by u(i,v). The memberships are non negative, and for a fixed observation i, they sum to 1. The particular method FANNY stems from chap. 4 of Kaufman & Rousseeuw (1990). FANNY aims to minimize the objective function: 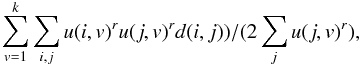 (2)where n is the number of observations, k is the number of clusters, r is the membership exponent and d(i,j) is the dissimilarity between observations i and j. Note that r → 1 gives increasingly crisper clusterings, whereas r → ∞ leads to complete fuzziness. After some trials, we adopted r = 1.5 for the present application, which produces groups of comparable sizes.
(2)where n is the number of observations, k is the number of clusters, r is the membership exponent and d(i,j) is the dissimilarity between observations i and j. Note that r → 1 gives increasingly crisper clusterings, whereas r → ∞ leads to complete fuzziness. After some trials, we adopted r = 1.5 for the present application, which produces groups of comparable sizes.
Table 3 gives the matrices of correspondences between groups defined by k-means, and those obtained with these two other algorithms. In each analysis, we set the number of groups at 6. Not surprisingly, there is a very good correspondence between the groups found by k-means and PAM: indeed, once the groups found by the two algorithms are properly ordered, the matrix of the correspondences is almost diagonal. The only significant deviations from a pure diagonal occur because about a third of the stars of the k-means group #3 (the moderately O-rich stars of intermediate metallicity) are combined with the O-rich, metal-rich stars of k-means group #2 into the PAM group #4; and because about a fourth of the stars of k-means group #6 (metal-poor, moderately O-poor stars) are combined with the stars of k-means group #4 (metal-poor, O-rich stars) into PAM group #6.
The correspondence between k-means and FANNY is also quite satisfactory, with a fairly diagonal matrix once proper identification of groups is made. In this case the largest deviations from linearity are that roughly half of the metal-intermediate, moderately O-poor stars of k-means group #1 are combined with the metal-poor, moderately O-poor stars of k-means group #6, into the FANNY group #3. Also, a consistent number of stars of k-means group #6 are combined with the metal-poor, O-rich stars of k-means group #4 into FANNY group #6; and a similar amount of stars of the same group are combined with the metal-intermediate, moderately O-poor stars of k-means group #1, into FANNY group #1.
We conclude that comparisons between different clustering methods suggest that the objective subdivision in groups considered in this paper, while in some case uncertain for individual stars, is on the whole quite robust. In particular, we deem that the agreement between completely different clustering methods (based either on hard, e.g. PAM/k-means, or soft partitioning, as FANNY) strongly supports our analysis.
Matrices of correspondences between clustering according different algorithms.
5. Discussion
5.1. Comparison between chemical groups and sequences on the colour–magnitude diagram
We next consider the matching of the different groups identified from our cluster analysis based on chemical composition to the different sequences found on the colour-magnitude diagrams (see Pancino et al. 2000; Piotto et al. 2005; Bellini et al. 2010). This procedure is much easier for those sequences identified on the RGB, because we can directly identify our stars in the colour magnitude diagram. From this first method, we can immediately identify our #2b group (yellow) with the RGB-a sequence (Pancino et al. 2000; Sollima et al. 2005a). In our sample, this group includes roughly 6% of the stars. While this value is similar to those found in other analyses (see, e.g., Bellini et al. 2009; and Marino et al. 2011), it is likely somewhat underestimated when compared to the fraction of, e.g., main-sequence stars in the corresponding sequence, because we are working with a magnitude-limited sample, and RGB-a stars are typically fainter in visual colours. Recently, Bellini et al. (2010) were able to follow this branch down to the main sequence. Their data suggests that this population is He-rich, a fact that could not be derived from RGB alone.
Determination of Y for star of the intermediate metallicity groups.
A very interesting discovery in ω Cen is the presence of a quite well populated blue main sequence (B-MS), which makes up roughly a quarter of the cluster (Bedin et al. 2004). Piotto et al. (2005) has found that this B-MS is more metal-rich than the red main-sequence (R-MS: [Fe/H] = −1.2 ± 0.2 vs. [Fe/H] = −1.6 ± 0.2), which can only be explained if it is also much more He-rich (Y > 0.35 vs. the canonical Big Bang value of Y ~ 0.25 for the R-MS), as originally suspected on the basis of star counts by Norris (2004). While it is conceivable that both B-MS and R-MS include several subpopulations (see Bellini et al. 2010), we will consider them as unique groups for the present discussion. For many reasons, we expect that the B-MS is related to stars that are very poor in O (and rich in Na; see discussion in Johnson & Pilachowski 2010). This has been beautifully confirmed for NGC 2808 by direct observation of stars in the different sequences by Bragaglia et al. (2010b). We can then tentatively identify the most O-poor groups #3 (violet) and #2a (red) as the progeny of the B-MS, and by subtraction, the remaining groups should be the progeny of the R-MS. This identification is confirmed by several circumstantial facts:
-
In total, we assigned 176 stars to these two groups. This makes up afraction of 22 ± 2% of the total, which is very similar to the fraction of main-sequence stars in the B-MS. It is actually slightly lower, but this can be easily attributed to the different areas of the cluster sampled by HST photometry and by the present spectroscopy.
-
Both groups belong to the intermediate-metallicity group of ω Cen. On average, they have [Fe/H] = −1.46, to be compared with a value of [Fe/H] = −1.70 that is obtained for the groups identified with the R-MS. This difference is similar within the errors to that obtained for main-sequence stars by Piotto et al. (2005).
-
Groups #2b (yellow) and #3 (violet) are much more centrally concentrated than the remaining metal-poor and metal-intermediate groups of ω Cen. This is analogous to the case of the main sequence, where the B-MS is much more centrally concentrated than the R-MS (Sollima et al. 2007; Bellini et al. 2009).
-
Dupree et al. (2011) showed that the intermediate-metallicity, Na/Al-rich (and thus O-poor) stars had strong He-detections (from the chromospheric line at 10 800 Å) compared to the Na/Al-poor stars; their sample is small, but it supports our results.
If we then adopt groups #3 (violet) and #2a (red) as the progeny of the B-MS population, it turns out that the R-MS should itself include at least two different metallicity components (a metal-poor and a metal-intermediate one), and each of them should have an O-rich and a moderately O-poor population (P and I components, following the Carretta et al. 2009a, nomenclature). We might then expect that a suitable combination of filters should be able to split the R-MS of ω Cen into at least four components (and probably more, see below), provided sufficiently accurate photometry is available. This prediction should be compared with the results obtained by Bellini et al. (2010).
On the other hand, the B-MS should be more homogeneous because it lacks the metal-poor component. However, it still likely has a spread both in O-deficiency (and then potentially in helium) and in metallicity (see next subsection).
5.2. Are groups intrinsically homogeneous?
The metal-poor groups.
We obtain a low dispersion in [Fe/H] and [m/H] for these two groups and a very similar average value. The narrow range of both [Fe/H] and [m/H] suggests that residuals about the mean are caused by random errors of measurement. These two groups also have very similar abundances of all elements except for Na and O, with low scatter. There is therefore no reason to think of a real spread in metallicity among these two groups.
Metal intermediate groups.
The dispersion in [Fe/H] and [m/H] is higher for the four intermediate groups, and the two quantities are correlated, suggesting a real dispersion in metallicity. Even more interestingly, there is a possible trend of [Fe/H] values with decreasing [Na/O], a similar but much less pronounced trend appearing also in [m/H]. This might be interpreted in terms of a variation in the helium content, similar to what is observed in NGC 2808 (Bragaglia et al. 2010a). To discuss this point, we first notice that a variation of Y has two effects on the metal abundance determinations:
-
The temperature of the RGB rises with Y by some dT/dY = 500 (D’Antona et al. 2002). Because d(B − V)/dT ~ 0.0008, we have d(B − V)/dY = 0.4. On the other hand d[m/H]/d(B − V) = 1.4, hence: dY/d[m/H] ~ −1.8.
-
The [Fe/H] value rises because the hydrogen content X decreases when the helium content Y increases, that is, X ~ 1 − Y decreases (neglecting the small metallicity term Z). The effect is roughly dY/d[Fe/H] ~ 1.5.
The offset of Y can then be derived by comparing the offsets in [Fe/H] with [m/H] between the different groups. Note that the effect of raising Y on [Fe/H] and [m/H] have opposite signs, so that dY/(d [Fe/H] − d [m/H]) ~ 0.82. Let us now consider the four intermediate metallicity groups of ω Cen (see Table 4). Column 6 of this table gives the difference between the values of [Fe/H] and [m/H] obtained for the different groups. The difference between groups #5 (black) and #1 (green) is small, significant at only about the 1 sigma level (simply considering the dispersion of data for individual stars). That is: the difference in Y between these two groups is not significant. We will then combine these two groups, and assume that they have the same Y = 0.25 value (the cosmological one). We then estimate the Y value of groups #3 (violet) and #2a (red) using the relations given above. While this derivation is quite rough, this He excess agrees very well with estimates based on the colour of MS stars. We note that groups #3 and #2a might be combined (with a weighted mean of Y = 0.349 ± 0.013), to correspond to the b-MS of ω Cen. As discussed in the previous section, there are several reasons for this identification. Here we add the most important one: they appear to have similar He abundance. Note that the difference in the Y value for the MSs of ω Cen found in Piotto et al. (2005) might have been overestimated because the impact of a variation of Y on [Fe/H] determinations was neglected. Consequently, the difference in metallicity between the B-MS and R-MS may actually be a bit smaller than previously thought (although still within the error bars of Piotto et al. 2005).
Metal-rich group.
Group #2a displays a quite large spread in metallicity and correlated [Fe/H] and [m/H] values (see panel d of Fig. 4). This indicates a real spread in metallicity. There are some hints that points in panel d of Fig. 4 are concentrated into two subgroups, possibly suggesting the existence of two distinct populations, one with [Fe/H] ~ −1, and the other more metal-rich, with [Fe/H] ~ −0.7. This has also been suggested by the metallicity distribution function discussed by Johnson & Pilachowski (2010). More accurate estimates of [Fe/H] are needed to confirm this hint.
 |
Fig. 9 Cumulative fraction versus log distance plots. Different colours are for stars of the different groups (see Fig. 1). Panel a): metal-poor groups only (#4 and #6); panel b): metal-intermediate groups only (#1, #2a, #3, and #5); panel c): all groups. Different colours are for stars of the different groups. |
5.3. Concentration and kinematics of the groups
Among the various properties of the groups identified by our cluster analysis, it is interesting to study the radial density distributions of the various populations. ω Cen has a half-light two-body relaxation time comparable to its age (~12 Gyr: see Harris 2010). The relative distribution of stars reflect then the initial conditions.
Panel c of Fig. 9 shows the cumulative fraction versus log distance plots. Examining this figure, we find that the O-rich groups #4 (blue) and #5 (black) exhibit a nearly identical distribution; all other groups appear more centrally concentrated. This makes sense because the other groups are more O-poor than groups #4 and #5, and there appears to be a general correlation between central concentration and O-deficiency among globular clusters (see Norris & Freeman 1979; Kravtsov et al. 2010; Carretta et al. 2010c; Lardo et al. 2011; Nataf et al. 2011); the higher central concentration of the He-rich populations in ω Cen was already noticed by Sollima et al. (2007) and Bellini et al. (2009). It also appears that groups #1 (green) and #3 (violet) are quite similar in their spatial distribution, while group #2a (red) is clearly more centrally concentrated than the other populations; this is not surprising because these are the most O-poor stars. All these results are confirmed by Kolmogorov-Smirnov tests (see Table 5). We interpret this result as an indication that the second-generation stars (I component) of the metal-poor group are more centrally concentrated than the first generation (P component) stars. This agrees with the radial distribution of the P and I components found in many monometallic globular clusters by Carretta et al. (2009a).
Panel a of Fig. 9 shows the metal-poor only plot. There is a very significant difference between the radial distributions of groups #4 (blue) and #6 (cyan), as confirmed by the Kolmogorov-Smirnov test, which yields a probability of 1.7 × 10-4 that the two groups are extracted from parent populations with the same radial distributions.
Panel b of Fig. 9 shows the same plot, but this time for the intermediate metallicity groups only. It appears that groups #1 (green) and #3 (violet) are very similar in their spatial distribution, while group #2a (O-poor, red) is clearly more centrally concentrated than the other populations, the opposite holds for group #5 (O-rich, black). Clearly, there is a correlation between the degree of O-depletion and radial concentration; the O-rich stars are more evenly distributed and the most O-poor stars are the most centrally concentrated; the “gradient” is wonderfully illustrated in this plot. The Kolmogorov-Smirnov tests of Table 5 confirm the significance of these findings.
Results of Kolmogorov-Smirnov test of consistency between radial distributions of different groups.
 |
Fig. 10 Radial velocity vs. position along the major axis of ω Cen. Panel a): metal-poor groups (#4 and #6); panel b): metal-intermediate groups (#1, #2a, #3, and #5); panel c): metal rich group (#2b). Different colours are for stars of the different groups (see Fig. 1). |
Concerning kinematics, it is well known that ω Cen has a quite conspicuous rotation (Merritt et al. 1997; Norris et al. 1997; Sollima et al. 2005b; Reijns et al. 2006; Pancino et al. 2007), where the rotation axis appears to be close to the minor axis projected on sky. Radial velocities are available for all stars in our sample, either from Reijns et al. (2006) or from measurements on the spectra gathered by Johnson & Pilachowski (2010). Average values and standard deviations about the mean for the individual groups of our analysis are listed in the last column of Table 1. Figure 10 shows the rotation curves we obtain for the various populations. There is no large difference between the rotation curves for the various populations, although data are not adequate for the #2b group (yellow). However, this last group is peculiar because apparently it is kinematically cooler than the other components, with a rms spread of radial velocities of only 9.1 km s-1 (while values for the other components are in the range 13 − 15 km s-1: see Table 1).
6. Conclusions
ω Cen is a complex cluster composed of several populations. These populations differ in many different characteristics (helium, metallicity, abundances of light elements, central concentration, etc.), and probably originated in different episodes of star formation, although it is also possible that some of the observed differences might simply be caused by poor mixing in very extended star-forming regions. Disentangling different populations is a first step in trying to reconstruct this puzzle.
Trying to put this on objective basis, we performed a classical cluster analysis on the extensive spectroscopic data recently obtained by Johnson & Pilachowski (2010). We used the popular k-means algorithm, but we also found similar results with other algorithms, which use different approaches, so that we deem the main conclusions to be quite robust.
Our group analysis suggests that stars in ω Cen might be divided into three main groups, which likely have a different history:
-
A metal-poor group, which includes about a third of the total. Thisis the simplest population, appearing to be itself quitehomogeneous in the abundances of most elements, and lookingquite similar to a typical globular cluster. It shows amoderate O-Na anticorrelation, and similar to other cases, theO-poor second generation stars are more centrally concentratedthan the O-rich first generation ones. This whole population isLa-poor, with a pattern of abundances for n-capture elements that isvery close to a scaled r-process one.
-
A metal-intermediate group, which includes the majority of the cluster stars. This is a much more complex population, with an internal spread in the abundances of most elements. It shows an extreme O-Na anticorrelation, with a very numerous population of extremely O-poor and He-rich second-generation stars. This second generation is very centrally concentrated. The whole population is La-rich, with a pattern of the abundances of n-capture elements that shows a strong contribution by the s-process. We tentatively suggest that this population stems from a very large episode of star formation that occurred several hundred million years later than the episode responsible for the metal-poor group within the same dwarf galaxy. The composition difference between the metal-poor and the metal-intermediate populations might be attributed to the chemical evolution within this galaxy, where most (but not all) of the products of core-collapse SNe of the earlier populations were lost, while virtually all products of the intermediate mass stars that have evolved in this lapse were retained. The spread in metallicity within this metal-intermediate population is not very large, and we might attribute it either to non uniformities of an originally very extended star-forming region, or to some ability to retain a fraction of the ejecta of the core collapse SNe that exploded first, or both. The first hypothesis is favoured by the existence of a correlation between s-process and Fe-peak element abundances, which is more easily explained if primordial. This second episode might have been coincident in space with the earlier one, as seems to happen in nuclear star clusters (see e.g. Böker 2008). Alternatively, we might think that the metal-poor and metal-intermediate populations formed as separate clusters within a single dwarf galaxy, and have later merged after migration towards the centre of this galaxy caused by dynamical friction (see Bellazzini et al. 2008; Johnson & Pilachowski 2010; Agarwal & Milosavljevi 2011).
-
A metal-rich group. This is perhaps the most mysterious group. The presence of a Na-O correlation, rather than anticorrelation, clearly separates this population from globular clusters. In particular, we notice that a Na-O anticorrelation is present even in most metal-rich globular clusters (Gratton et al. 2007; Carretta et al. 2007), indicating that the high metallicity is not the reason of the difference between the composition of this group and that typical of globular clusters. Rather, the range of mass of the stars responsible for the metal-enrichment should be different. We suggest that stars over a much wider range of masses than typical for globular clusters must be considered: there is evidence for the contribution of both massive stars ending their life as core-collapse SNe, and intermediate/small mass stars, producing n-capture elements through the s-process. On the other hand, there is no evidence for a contribution by SN Ia. While, following Carretta et al. (2010a), we were tempted to interpret this group as stars of the host galaxy captured by the cluster (like the “nuclear” population seen in M54, which shares the composition of the Sagittarius dwarf galaxy), its composition is very different from that typically observed in dwarf spheroidals. In particular, it shows the typical excess of α-elements seen in globular clusters, while the metal-rich stars in dwarf spheroidals invariably have a relative deficiency of α-elements with respect to Fe. Furthermore, this population is more centrally concentrated than some of the other components and is much more kinematically cool, which is unexpected for a captured population and looks more consistent with further episodes of star formation within a nuclear cluster. Incidentally, we note that the lack of a sizeable “dwarf spheroidal”-like population in ω Cen is itself a fact that must be explained by scenarios of formation for this intriguing cluster.
It should be noticed that if we had adopted seven groups at start of our analysis, the subdivision would have been almost identical to those obtained with the six-group analysis, but the most metal and La-poor stars would have been divided into three groups with decreasing [O/Na] values, rather than two. This is different from the subdivision of group #2, adopted throughout this paper. Our approach provides a better insight into the properties of ω Cen. However, clearly there is some arbitrariness in the way we performed our cluster analysis.
Acknowledgments
This research has been funded by PRIN MIUR 20075TP5K9, and by PRIN INAF “Formation and Early Evolution of Massive Star Clusters”. This material uses work supported by the National Science Foundation under award No. AST-1003201 to CIJ. C.A.P. gratefully acknowledges support from the Daniel Kirkwood Research Fund at Indiana University.
References
- Agarwal, M., & Milosavljevi, M. 2011, ApJ, 729, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Ibata, R. A., Chapman, S. C., et al. 2008, AJ, 136, 1174 [Google Scholar]
- Bellini, A., Piotto, G., Bedin, L. R., et al. 2009, A&A, 507, 1393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellini, A., Bedin, L.R., Piotto, G., et al. 2010, AJ, 140, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Böker, T. 2008, ApJ, 672, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Carretta, E., Gratton, R. G., et al. 2010a, A&A, 519, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bragaglia, A., Carretta, E., Gratton, R.G., et al. 2010b, ApJ, 720, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, F., Dickens, R. J., & Epps, E. 1978, ApJ, 225, 148 [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007, A&A, 464, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009b, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., D’Orazi, V., & Lucatello, S. 2009c, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., et al. 2010a, ApJ, 714, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., et al. 2010b, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., D’Orazi, V., Lucatello, S., & Gratton, R. G. 2010c, A&A, 519, A71 [Google Scholar]
- Carretta, E., Gratton, R. G., Lucatello, S., et al. 2010d, ApJ, 727, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G. 1981, ApJ, 247, 869 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, A., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Maynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupree, A. K., Strader, J., & Smith, G. H. 2011, ApJ, 728, 155 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Forbes, D., & Kroupa, P. 2011, PASA, 28, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C., & Rodgers, A. W. 1975, ApJ, 201, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, E., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2007, A&A, 464, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D’Orazi, V. 2010, A&A, 517, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 2010 [arXiv:1012:3224] [Google Scholar]
- Hartigan, J. A., & Wong, M. A. 1979, Appl. Stat., 28, 100 [CrossRef] [Google Scholar]
- Johnson, C. I., & Pilachowski, C. A. 2010, ApJ, 722, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Pilachowski, C. A., Simmerer, J., & Schwenk, D. 2008, ApJ, 681, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Pilachowski, C. A., Rich, M. R., & Fulbright, J. P. 2009, ApJ, 698, 2048 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, V., Alcaino, G., Marconi, G., & Alvarado, F. 2010, A&A, 512, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufman, L., & Rousseeuw, P. J. 1990, Finding Groups in Data: an Introduction to Cluster Analysis (John Wiley & Sons) [Google Scholar]
- Lardo, C., Bellazzini, M., Pancino, E., et al. 2011, A&A, 525, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, J.-W., Kang, Y.-W., Lee, J., & Lee, Y.-W. 2009, Nature, 462, 480 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- MacQueen, J. B. 1967, Mathematical Statistics and Probability (University of California Press), 281 [Google Scholar]
- Marino, A. F., Milone, A. P., Piotto, G., et al. 2009, A&A, 505, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, A. F., Milone, A. P., Piotto, G., et al. 2011, ApJ, 731, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., Meylan, G., & Mayor, M. 1997, AJ, 114, 1074 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Gould, A., Pinsonneault, M. H., & Stetson, P. B. 2011, ApJ, 736, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E. 2004, ApJ, 612, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., & Da Costa, G. S. 1995a, ApJ, 441, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., & Da Costa, G. S. 1995b, ApJ, 447, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J., & Freeman, K. C. 1979, ApJ, 230, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, M. A., & Kannappan, S. J. 2011, MNRAS, 414, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Freeman, K. C., Mayor, M., & Seitzer, P. 1997, ApJ, 487, L187 [NASA ADS] [CrossRef] [Google Scholar]
- Pancino, E. 2003, Ph.D. Thesis, Un. Bologna [Google Scholar]
- Pancino, E., Ferraro, F. R., Bellazzini, M., Piotto, G., & Zoccali, M. 2000, ApJ, 534, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Pancino, E., Galfo, A., Bellazzini, M., & Ferraro, F. R. 2007, ApJ, 661, L51 [Google Scholar]
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- R Development Core Team 2011, R: A language and environment for statistical computing, Vienna, Asutria, ISBN 3-900051-07-0 [Google Scholar]
- Reijns, R. A., Seitzer, P., Arnold, R., et al. 2006, A&A, 445, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., Suntzeff, N. B., Cunha, K., et al. 2000, AJ, 119, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhaus, H. 1956, Bull. Acad. Polon. Sci., 4, 801 [Google Scholar]
- Sollima, A., Ferraro, F. R., Pancino, E., & Bellazzini, M. 2005a, MNRAS, 357, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A., Pancino, E., Ferraro, F. R., et al. 2005b, ApJ, 634, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A., Ferraro, F. R., Bellazzini, M., et al. 2007, ApJ, 654, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Stanford, L. M., Da Costa, G. S., Norris, J. E., & Cannon, R. D. 2006, ApJ, 647, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Suntzeff, N. B., & Kraft, R. P. 1996, AJ, 111, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T., van Leeuwen, F., Smalley, B., et al. 2007, MNRAS, 382, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Piotto, G., King, I. R., et al. 2007, ApJ, 663, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Woolley, R. V. D. R. 1966, R. Obs. Ann., 2, 1 [Google Scholar]
- Yong, D., Grundahl, F., Nissen, P. E., Jensen, H. R., & Lambert, D. L. 2005, A&A, 438, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Results of Kolmogorov-Smirnov test of consistency between radial distributions of different groups.
All Figures
 |
Fig. 1 Assignation of stars to the different groups in our k-means analysis in the [La/H] vs. [Na/O] plane. This plane roughly corresponds to that of the second and first component in a principal component analysis. Different colours are for stars of the different groups: green: group #1; red: group #2a; yellow: group #2b; violet: group #3; blue: group #4; black: group #5; cyan: group #6. |
| In the text | |
 |
Fig. 2 V − (B − V) (left panel) and V − (V − K) (right panel) colour − magnitude diagrams for the observed stars in ω Cen. Different colours are for stars of the different groups (see Fig. 1). |
| In the text | |
 |
Fig. 3 V − (B − V) colour–magnitude diagram for the observed stars in ω Cen. Metal-poor groups (#4 and #6) are in the left panel, metal-intermediate ones (#1, #2a, #3, #5) in the right one. Different colours are for stars of the different groups (see Fig. 1). |
| In the text | |
 |
Fig. 4 Comparison between iron abundances from spectroscopy [Fe/H] and metal abundances derived from colours along the RGB ([m/H]). Different colours are for stars of the different groups (see Fig. 1). Results for all stars are plotted in panel a); panel b) is is only for metal-poor stars; panel c) is only for metal-intermediate stars; and panel d) is only for metal-rich stars. |
| In the text | |
 |
Fig. 5 [α/H] vs. metal abundances derived from colours along the RGB ([m/H]). Different colours are for stars of the different groups (see Fig. 1). Results for all stars are plotted in panel a); panel b) is is only for metal-poor stars; panel c) is only for metal-intermediate stars; and panel d) is only for metal-rich stars. |
| In the text | |
 |
Fig. 6 Na-O anticorrelation for stars in ω Cen. Panel a): all stars; panel b): metal-poor groups (#4 and #6); panel c): metal-intermediate groups (#1, #2a, #3, and #5); panel d): metal rich group (#2b). Different colours are for stars of the different groups (see Fig. 1). |
| In the text | |
 |
Fig. 7 Al-O anticorrelation for stars in ω Cen. Panel a): all stars; panel b): metal-poor groups (#4 and #6); panel c): metal-intermediate groups (#1, #2a, #3, and #5); panel d): metal rich group (#2b). Different colours are for stars of the different groups (see Fig. 1). |
| In the text | |
 |
Fig. 8 Run of [La/Fe] against [Eu/Fe] for stars in ω Cen. Different colours are for stars of the different groups (see Fig. 1). Overimposed are the lines corresponding to a pure solar scaled r- (solid line) and s-contributions (dashed line). |
| In the text | |
 |
Fig. 9 Cumulative fraction versus log distance plots. Different colours are for stars of the different groups (see Fig. 1). Panel a): metal-poor groups only (#4 and #6); panel b): metal-intermediate groups only (#1, #2a, #3, and #5); panel c): all groups. Different colours are for stars of the different groups. |
| In the text | |
 |
Fig. 10 Radial velocity vs. position along the major axis of ω Cen. Panel a): metal-poor groups (#4 and #6); panel b): metal-intermediate groups (#1, #2a, #3, and #5); panel c): metal rich group (#2b). Different colours are for stars of the different groups (see Fig. 1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


