| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117354 | |
| Published online | 19 September 2011 | |
A deep search for H2D+ in protoplanetary disks⋆
Perspectives for ALMA
1
MPIfR, Auf dem
Hügel 69, 53121
Bonn,
Germany
e-mail: echapill@mpifr-bonn.mpg.de; bparise@mpifr-bonn.mpg.de; fjdu@mpifr-bonn.mpg.de
2
Université de Bordeaux, Observatoire Aquitain des Sciences de
l’Univers, 2 rue de
l’Observatoire, BP
89, 33271
Floirac, France
3
CNRS/INSU – UMR5804, Laboratoire d’Astrophysique de Bordeaux,
2 rue de l’Observatoire,
BP 89, 33271
Floirac, France
e-mail: guilloteau@obs.u-bordeaux1.fr
Received:
27
May
2011
Accepted:
6
July
2011
Context. The structure in density and temperature of protoplanetary disks surrounding low-mass stars is not well known yet. The protoplanetary disks’ midplane are expected to be very cold and thus depleted in molecules in gas phase, especially CO. Recent observations of molecules at very low apparent temperatures (~6 K) challenge this current picture of the protoplanetary disk structures.
Aims. We aim at constraining the physical conditions and, in particular, the gas-phase CO abundance in the midplane of protoplanetary disks.
Methods. The light molecule H2D+ is a tracer of cold and CO-depleted environment. It is therefore a good candidate for exploring the disks midplanes. We performed a deep search for H2D+ in the two well-known disks surrounding TW Hya and DM Tau using the APEX and JCMT telescopes. The analysis of the observations was done with DISKFIT, a radiative transfer code dedicated to disks. In addition, we used a chemical model describing deuterium chemistry to infer the implications of our observations on the level of CO depletion and on the ionization rate in the disk midplane.
Results. The ortho-H2D+ (11,0−11,1) line at 372 GHz was not detected. Although our limit is three times better than previous observations, comparison with the chemical modeling indicates that it is still insufficient for putting useful constraints on the CO abundance in the disk midplane.
Conclusions. Even with ALMA, the detection of H2D+ may not be straightforward, and H2D+ may not be sensitive enough to trace the protoplanetary disks midplane.
Key words: circumstellar matter / protoplanetary disks / radio lines: stars
Based on observations carried out with the Atacama Pathfinder Experiment and the James Clerk Maxwell Telescope. APEX is a collaboration between the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory. The JCMT is operated by the Joint Astronomy Centre on behalf of the Science and Technology Facilities Council of the United Kingdom, the Netherlands Organisation for Scientific Research, and the National Research Council of Canada.
© ESO, 2011
1. Introduction
Planetary systems are believed to be formed in the latest stages of protostellar evolution within protoplanetary disks. The details of this process are, however, not known. Constraining the physical and chemical structure in disks during their evolution is required to get more insight into this question.
Current models predict that protoplanetary disks consist of three typical layers. They are, going from the surface to the midplane of the disk: 1) the outer layer, a PDR directly illuminated by the stellar UV; 2) a warm molecular zone, where the UV is sufficiently attenuated to allow formation of molecules; and 3) a cold midplane where temperature is low and most molecules are expected to be frozen on dust grains (Bergin et al. 2007). All static chemical models published so far produce similar results (e.g. Aikawa & Nomura 2006; Semenov et al. 2005). The chemistry is dominated by two main processes: molecular freeze-out onto grains in the cold midplane and photodissociation in the upper layers (enhanced by grain growth that allows the UV field to penetrate deeper into the disk). This simple picture has, however, not yet been constrained by observations, and some puzzles still remain. In particular, very cold C2H, CN and CO (≤ 15 K, i.e. below the evaporation temperature) have been detected in the DM Tau disk (Dartois et al. 2003; Piétu et al. 2007; Henning et al. 2010; Chapillon et al. 2011), pointing out that some process may lead to cold gas-phase molecules in the disk midplane. Radial and vertical mixing is usually invoked to explain partial molecular replenishment of the cold disk midplane from the higher warm layer (Semenov et al. 2006; Aikawa 2007). Such an explanation is not fully satisfactory with respect to the current chemical results (see for example Hersant et al. 2009). Observations of a chemical tracer of cold regions are thus needed.
Source coordinates (J2000) and properties.
H2D+ is a very promising molecule for tracing the disk midplane
because it is probably the only remaining observable species in a cold medium, where
molecules are frozen onto grains. H2D+ is exclusively formed in the
gas phase at low temperatures (T < 20−30 K). Moreover, CO (and other
heavy species like N2) is a very efficient destroyer of
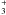 and H2D+. High
abundances of H2D+ can thus only build up in depleted environments.
The ortho-H2D+ (11,0 − 11,1) line, hereafter
o-H2D+, is commonly detected towards cold and dense prestellar
cores, see for instance Caselli et al. (2008).
Observation of o-H2D+ has also been proposed by Ceccarelli et al. (2004) as a way to measure the midplane ionization,
since H2D+ may be the dominant ion in that region.
and H2D+. High
abundances of H2D+ can thus only build up in depleted environments.
The ortho-H2D+ (11,0 − 11,1) line, hereafter
o-H2D+, is commonly detected towards cold and dense prestellar
cores, see for instance Caselli et al. (2008).
Observation of o-H2D+ has also been proposed by Ceccarelli et al. (2004) as a way to measure the midplane ionization,
since H2D+ may be the dominant ion in that region.
Until now, no firm detection of o-H2D+ in protoplanetary disks has been definitively secured. A tentative detection on DM Tau obtained with the CSO was claimed by Ceccarelli et al. (2004) and later challenged by the SMA observations of Qi et al. (2008). Using a line profile appropriate for the DM Tau disk, Guilloteau et al. (2006) showed that the Ceccarelli et al. (2004) data only indicates a 2σ tentative detection. There are only upper limits in TW Hya (Ceccarelli et al. 2004; Thi et al. 2004; Qi et al. 2008) obtained with the JCMT and the SMA.
The paper is organized as follows. The observations are presented in Sect. 2, and upper limits for the o-H2D+ column densities are derived in Sect. 3. The implications for the level of CO depletion and ionization in the disk midplane are discussed in Sect. 4. The feasibility of ALMA observations are discussed in Sect. 5, and we summarize our study in Sect. 6.
2. Observations
We searched for o-H2D+ in two well-studied, nearby or large protoplanetary disks. Their properties are summarized in Table 1. TW Hya is the nearest observable T-Tauri star, located only at 56 pc from the Sun and surrounded by a rather small disk of about 200 AU of radius. It is the only protoplanetary disk where molecules have been studied in some systematic way because of its proximity (Qi et al. 2008). The disk is viewed nearly face-on. DM Tau is a well known TTauri star of 0.5 M⊙ surrounded by a large and massive molecular disk (Guilloteau & Dutrey 1994, 1998; Öberg et al. 2010). Dartois et al. (2003) and Piétu et al. (2007) have performed high-resolution multitransition, multi-isotope studies of CO, and demonstrated the existence of a vertical temperature gradient in the disk, as well as the presence of cold gas-phase CO.
We retrieved observations of o-H2D+ toward DM Tau from the JCMT
archive. The o-H2D+ line at 372.421 GHz was observed, together with
L1544 in January 2007 with the multibeam receiver HARP and the ACSIS backend with a
resolution of 0.03 km s-1. The source was centered on the pixel at the tracking
center (H10). DM Tau was observed during about 10.75 h on source, with a system temperature
of 605 K on average leading to an rms of 44 mK ( ) at a resolution of 0.03 km s-1.
) at a resolution of 0.03 km s-1.
Using the APEX telescope, we observed the o-H2D+ at 372.421 GHz
toward TW Hya during 3.8 h on source in July and September 2010 with the new FLASH 345
receiver. The dual-polarization receiver FLASH operates a two-SB SIS mixer provided by IRAM
(Maier et al. 2005). The July and September
observations were carried out with different backends, respectively leading to spectral
resolutions of 0.15 km s-1 and 0.06 km s-1. Data were resampled to a
spectral resolution of 0.20 km s-1. Since no planet was visible, the focus was
checked by line pointing on RAFGL 5254 and IRAS 07454-7112. Pointing was done toward the
same calibrators. The rms noise is 18 mK ( ) obtained after removing a constant baseline
to the data at 0.2 km s-1 of resolution.
) obtained after removing a constant baseline
to the data at 0.2 km s-1 of resolution.
We did not detect any o-H2D+ emission in any of the sources. Assuming a Jansky-to-Kelvin (S/TA) conversion factor of 30 for the JCMT1 and 41 for APEX2, and presuming that the total linewidths are 2 km s-1 for DM Tau and 1 km s-1 for TW Hya, we derived a 1σ noise level on the integrated line of 0.32 Jy km s-1 for DM Tau and 0.33 Jy km s-1 for TW Hya. We converted to flux density as the sources are unresolved.
Previous observations by Ceccarelli et al. (2004), Thi et al. (2004), and Qi et al. (2008) give a 1σ rms of 1.2 Jy km s-1 for TW Hya and 0.88 Jy km s-1 for DM Tau (assuming an S/TMB conversion factor of 55 Jy/K for the CSO telescope). Our limits on the integrated intensities are therefore 3.3 times better for DM Tau and 3.6 times better for TW Hya.
3. Results
To derive upper limits on the o-H2D+ column density from these non-detections taking the disk structure into account, we used DISKFIT, a radiative transfer code optimized for disks (Piétu et al. 2007; Pavlyuchenkov et al. 2007). This code fits a parametric model to the data and the best model is determined by a minimization process. Disks can be reasonably described by a parametric model where all primary quantities are power-law functions of the radius (see Dutrey et al. 1994; Piétu et al. 2007): surface density Σ(r) = Σ0(r/R0)−p, temperature T(r) = T0(r/R0)−q, velocity v(r) = V0(r/R0)−v, and scale height H(r) = H0(r/R0)−h which controls the vertical density structure. The temperature is a simple power law of the radius, and no vertical gradient is taken into account. In the peculiar case of nondetection, all parameters except the value of Σ0 are fixed. The surface density of o-H2D+ at the reference radius (noted Σ0) is then derived under the LTE hypothesis (valid for densities >105 cm-3 see Parise et al. 2011,Fig. 5a). This parametric approach limits the number of assumptions on the disk structure. Table 2 presents the resulting o-H2D+ column densities distributions for several models.
For the two sources, parameters such as position, inclination, and position angle are fixed according to previous CO observations (Piétu et al. 2007; Hughes et al. 2008). Two values are adopted for the exponent of the column density distribution p = 0 (i.e. flat distribution) and p = −1 (i.e. surface density linearly increasing with radius) to match the results of chemical modeling (see Willacy 2007, and this work).
Given the uncertainties on the disks’ thermal structure, we derived the o-H2D+ column density assuming a low (case L) and high (case H) temperature. For DM Tau, a useful upper limit can be derivedfrom the 12CO measurement with T100 = 30 K and q = 0.6. This is an upper limit because the 12CO emission is optically thick enough to mainly trace the upper layers of the disks. Less abundant isotopologues, which sample deeper in the disk, as well as other molecules (HCO+, C2H, CN, and HCN, see Piétu et al. 2007; Henning et al. 2010; Chapillon et al. 2011) give lower values (T100 ~ 10−15, q ~ 0−0.4). The law 15 × (r/100)-0.4 is adopted for the cold case. For TW Hya, the two temperature cases considered here (T100 = 40 K,q = 0.2 and T100 = 30 K,q = 0.5) correspond to the two temperature solutions of Hughes et al. (2008).
The results also depend on the external radius. In the p = 0 case, Rout is chosen in agreement with CO observations (i.e. 720 AU for DM Tau and 200 AU for TW Hya). When the o-H2D+ column density increases with the radius (p = −1), the flux is dominated by the outer disk, we adopted a radius of 550 AU for DM Tau in that case. This assumption is in accordance with the “tapered edge” model (see Discussion).
o-H2D+column densities.
The derived 3 σ upper limits on the o-H2D+ column density at 100 AU is about 1012 cm-2 (see Table 2). That is ~4 times lower than the previous estimation of 4.5 ± 0.9 × 1012 cm-2 by Ceccarelli et al. (2004) on DM Tau. To make a more direct comparison, the value of Σ100 was also derived by adopting the same disk parameters as Ceccarelli et al. (2004) (T100 = 10 K, q = 0 and p = 0). In that case we find Σ100 = 1.3 × 1012 cm-2, so a factor 3 lower.
Qi et al. (2008) have derived a 3σ upper limit of 5.1 × 1012 cm-2 on TW Hya. Our upper limit is a factor ~5 lower, but because their adopted thermal structure is not given, we cannot fit the same disk model to our data.
4. Discussion
Disk structure adopted for the chemical modeling.
Our deep integrations show that o-H2D+ emission, if any, is actually much fainter than previously thought. In this section, we discuss the implications of our nondetections on the amount of CO remaining in gas phase in the disks midplane.
To derive a lower limit on the CO abundance in the disk midplane, we made use of the time-dependent chemical code dedicated to deuterium chemistry presented in Parise et al. (2011) and calculated the o-H2D+ abundance on a grid of densities and temperatures, over several hypotheses on the local CO abundance, grain growth, and ionization rate. Using a realistic density and temperature profile for the disk, we then compute the resulting column density of o-H2D+, and compare it to the one derived from observations. We also derived the emission lines profiles for each of those disk chemical models using the radiative transfer code DISKFIT under LTE.
The chemical model was first developed to describe the deuterium chemistry at work in cold
prestellar cores (Parise et al. 2011). This code
takes all different spin states of the different molecules and ions into account. In
particular, ortho and para H2, 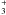 and isotopologues are considered separately,
with up-to-date reaction rates from Hugo et al.
(2009) and recombination rates for all ions of Pagani et al. (2009). A simple chemistry of CO and N2 is also included.
The reactions are all in gas phase except the formation of H2, HD, and
D2 on grains. The code is time-dependent, and the developement of deuterium
fractionation has been shown to be limited by the ortho-H2 to para-H2
conversion timescale (Pagani et al. 2009). In the
midplane of protoplanetary disks, we expect that this conversion has already happened
efficiently, so we used the steady-state abundances reached at long times.
and isotopologues are considered separately,
with up-to-date reaction rates from Hugo et al.
(2009) and recombination rates for all ions of Pagani et al. (2009). A simple chemistry of CO and N2 is also included.
The reactions are all in gas phase except the formation of H2, HD, and
D2 on grains. The code is time-dependent, and the developement of deuterium
fractionation has been shown to be limited by the ortho-H2 to para-H2
conversion timescale (Pagani et al. 2009). In the
midplane of protoplanetary disks, we expect that this conversion has already happened
efficiently, so we used the steady-state abundances reached at long times.
We obtained the o-H2D+ abundance relative to H2 as a function of density and temperature. We ran the code for several values of the CO abundance (x[CO] = 0,10-6,10-5,10-4). We also varied the effective grain size (a = 0.1,1 and 10 μm). The abundance of H2D+ should also depend on the ionization, so we varied the cosmic rays ionization rate (ξ = 1 × 10-17,3 × 10-17 and 1 × 10-16 s-1). The UV field is neglected, which should not be a problem since H2D+ will, in any case, be predominantly in the dense regions.
To estimate the o-H2D+ column densities resulting from the chemical simulations we need a model of the disk H2 density and temperature. For the surface density we adopted two different models:
-
the simple model where the H2 surfacedensity is described by a power law
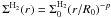 , truncated at a given radius
(Rout), hereafter Model 1;
, truncated at a given radius
(Rout), hereafter Model 1; -
and a model where the H2 surface density is an exponentially tapered power law, as would result from viscous spreading of the disk
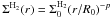 , hereafter Model 2 (see also Hughes et al. 2008).
, hereafter Model 2 (see also Hughes et al. 2008).
We adopted the same temperature law as previously, without vertical gradient. Parameters are summarized in Table 3. To derive local densities, we further assumed hydrostatic equilibrium.
For DM Tau, the disk parameters mainly come from the analysis performed by Piétu et al. (2007). The density models are derived from the continuum observations of Guilloteau et al. (2011). Model 1 is arbitrarily extended up to an external radius of 700 AU (in agreement with CO emission).
For TW Hya, the parameters are derived from Hughes et al. (2008). Their “cold” case applies to the density Model 1 and the “hot” case to Model 2.
The disks are expected to have vertical temperature gradients, which we ignore in this simple modeling. As a consequence, the abundance of o-H2D+ above the midplane is underestimated (see for instance Asensio Ramos et al. 2007, Fig. 1). Nevertheless, because the H2 density above the midplane is significantly lower, the contribution of this additional layer to the total o-H2D+ column density is negligible (see Figs. 6 and 7 of Willacy 2007). For DM Tau, the two adopted temperature profiles represent two extreme cases, one only considering the low midplane temperature, the other using the higher values sampled by 12CO at 1−2 scale heights.
 |
Fig. 1 o-H2D+ spectrum in DM Tau. The dashed line indicates the systemic velocity. The resolution is 0.17 km s-1. |
 |
Fig. 2 o-H2D+ spectrum in TW Hya. The dashed line indicates the systemic velocity. The resolution is 0.20 km s-1. |
The top panel of Fig. 3 presents the distribution of the o-H2D+ column density for DM Tau, Model 2 case L, and the standard value of the cosmic ray ionization ξ = 3 × 10-17 s-1. All models with CO depletion show a region of high column density at R = 40−50 AU (low-temperature case) or R = 150−200 AU (high-temperature case). In each case, this corresponds to a kinetic temperature around 20 K. These models also display a region of low o-H2D+ column density for T ~ 15 K. This is caused by the rapid evolution of the ortho/para ratio of H2D+ with temperature in this range (the ratio o/p decreases by a factor of 3 between 20 K and 15 K for a density of 106 cm-3, and x(CO) = 10-6). This effect has already been shown in previous works, see Flower et al. (2004, their Fig. 6) and Sipilä et al. (2010, their Fig. 4. Apart from that feature (which is much more pronounced for x[CO] = 0), the o-H2D+ column density increases with the radius in Model 1 (in qualitative agreement with Willacy 2007). In Model 2 this increase is tapered off by the exponential fall in the H2 surface density. For DM Tau, the o-H2D+column density peaks around R = 550 AU, where it reaches 1013 cm-2. Because the disk of TW Hya is small (Rout ~ 200 AU), the temperature is high in the whole disk, and, as a consequence the o-H2D+ column density is low regardless of the CO abundance (column density below 1012 cm-2 if we exclude the high ionization case), and the models are not constraining. The predicted integrated spectra, for each of the models are computed using DISKFIT. The bottom panel of Fig. 3 presents the predicted spectra together with observational data for DM Tau, Model 2 case L, and the standard value of the cosmic ray ionization. The predicted o-H2D+ line fluxes for DM Tau are presented in Table 4 and Fig. 4. The integrated line flux seems to vary roughly like ξ0.5 and a-0.5. The dependency over the CO abundance is more complicated.
 |
Fig. 3 Results from the chemical modeling for DM Tau, case L, Model 2 and ξ = 3 × 10-17s-1. Top: predicted o-H2D+ column densities as a function of radius for several values of grain size: a = 0.1 μm (black); 1 (red) and 10 (blue); and CO abundance: x[CO] = 10-6 (thin lines) 10-5 (medium) and 10-4 (thick). The green lines correspond to the best 3σ upper limits derived from observations with p = 0 and p = −1. Bottom: observed spectrum (green) and predicted line profiles (same color and thickness convention). |
 |
Fig. 4 o-H2D+ predicted flux as a function of CO abundance (left), cosmic ray (middle), and grain size (right) for DM Tau. Grain size: a = 0.1 μm (black); 1 (red) and 10 (blue). Cosmic ray ionization rate: ξ = 1 × 10-17 (triangle), 3 × 10-17 (square), and 1 × 10-16 s-1 (octagon). CO abundance: x[CO] = 10-6 (open marker) 10-5 (filled marker), and 10-4 (cross). The green line corresponds to our 3σ limit derived from observations. The dashed lines illustrate the dependencies. |
Predicted o-H2D+ line fluxes (mJy km s-1) for DM Tau.
From Fig. 4 one can see that the current upper limits are not very stringent on the disk parameters unless the ionization rate is very high. At best only the models with small grains, CO depleted by a factor 100 and ξ > 3 × 10-17 s-1 are excluded in the DM Tau case. With a CO depletion of order 10 or so, any grain size would fit the current data. The chemical models are not constraining for TW Hya.
Compared to the earlier study of Ceccarelli & Dominik (2005), which did not consider the ortho and para H2D+ separately, our chemical model including all spin-dependent reaction rates predicts column densities on average five to ten times weaker. Accordingly, as the o-H2D+ line emission is mostly optically thin, except for the highest column densities (above a few 1012 cm-2), we predict flux densities three to five times lower than Asensio Ramos et al. (2007).
5. Implications for ALMA
In this section, we discuss the feasibility of observational improvements compared to the present work, using the ALMA interferometer. Figure 3 demonstrates that an increase in flux sensitivity by at the very least a factor of 10 (the emission being optically thin) compared to the present observations is required to secure a convincing detection of H2D+ (in the framework of the chemical models of Sect. 4). An even higher sensitivity would be required to disentangle the different models. The current upper limits, obtained with single dishes of 12−15 m diameter and integration times five to ten hours, show that only larger instruments can expect to detect H2D+. ALMA is the most promising: in single-dish mode, the fifty 12-m antennas will bring a gain of seven in sensitivity compared to APEX (assuming similar receiver performances). However, in interferometric mode, even in its compact configuration, the angular resolution of the main array will be around 1′′, so that the sources will be highly resolved. In such cases, the brightness sensitivity becomes the relevant parameter. In the beam of the current instruments, the observed discs are diluted by about a factor three to four, as the APEX beam size is 14′′ compared to an outer disk diameter around 7−8′′. However, the aperture filling factor of ALMA is only about 40%, compared to the filled aperture for APEX. In a similar integration time and assuming similar noise performance, the ALMA brightness sensitivity should therefore enable us to reach a detection level of column densities only two times lower than the current level in each ALMA synthesized beam. Further spatial smoothing would improve the sensitivity to extended structure, but only moderately, as this implies degrading the weight of the longest baselines. Using the ALMA compact array (ACA) may be more appropriate: the collecting area of the 12 7-m antennas is four times that of APEX, so accounting for an effective filling factor around 30−40% also leads to similar brightness sensitivities to those for the 12-m antennas compact configuration.
While detailed predictions will require proper knowledge of the ALMA performances at the difficult frequency of 372.4 GHz, these simple considerations show that o-H2D+ is unlikely to become a major “workhorse” for studying e.g., the kinematics of disks.
6. Conclusion
-
We have improved the sensitivity to o-H2D+ by afactor 3 over previous observations. Noo-H2D+ was detected, contradicting previoustentative detections.
-
With our chemical model, TW Hya is, in any case, too warm or not dense enough to provide detectable o-H2D+ at the current sensitivity.
-
The limit on DM Tau is incompatible with very high CO depletion (x [CO] < 10-6) and small grains (0.1 μm). However, it is not diskriminant with more reasonable values of the grain sizes and/or CO abundances.
-
Much more sensitive observations will be required to obtain significant constraints. Even with the powerful ALMA interferometer, it will be extremely difficult to reach a sensitivity that will allow constraining the ionization level and the amount of CO in the disk midplanes by means of the observation of o-H2D+.
Acknowledgments
We acknowledge Anne Dutrey for many fruitful discussions. Remo Tilanus kindly provided us with the JCMT data. E.C., B.P. and F.D. are supported by the Deutsche Forschungsgemeinschaft (DFG) under the Emmy Noether project PA 1692/1-1. S.G. acknowledges financial support by the French program PCMI from CNRS/INSU.
References
- Aikawa, Y. 2007, ApJ, 656, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Aikawa, Y., & Nomura, H. 2006, ApJ, 642, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- AsensioRamos, A., Ceccarelli, C., & Elitzur, M. 2007, A&A, 471, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., Aikawa, Y., Blake, G. A., & van Dishoeck, E. F. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 751 [Google Scholar]
- Caselli, P., Vastel, C., Ceccarelli, C., et al. 2008, A&A, 492, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., & Dominik, C. 2005, A&A, 440, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Dominik, C., Lefloch, B., Caselli, P., & Caux, E. 2004, ApJ, 607, L51 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chapillon, E., Guilloteau, S., Dutrey, A., Piétu, V., & Guélin, M. 2011, A&A, submitted [Google Scholar]
- Dartois, E., Dutrey, A., & Guilloteau, S. 2003, A&A, 399, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutrey, A., Guilloteau, S., & Simon, M. 1994, A&A, 286, 149 [NASA ADS] [Google Scholar]
- Dutrey, A., Guilloteau, S., & Guelin, M. 1997, A&A, 317, L55 [NASA ADS] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2004, A&A, 427, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilloteau, S., & Dutrey, A. 1994, A&A, 291, L23 [NASA ADS] [Google Scholar]
- Guilloteau, S., & Dutrey, A. 1998, A&A, 339, 467 [NASA ADS] [Google Scholar]
- Guilloteau, S., Piétu, V., Dutrey, A., & Guélin, M. 2006, A&A, 448, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henning, T., Semenov, D., Guilloteau, S., et al. 2010, ApJ, 714, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Hersant, F., Wakelam, V., Dutrey, A., Guilloteau, S., & Herbst, E. 2009, A&A, 493, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hughes, A. M., Wilner, D. J., Qi, C., & Hogerheijde, M. R. 2008, ApJ, 678, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Hugo, E., Asvany, O., & Schlemmer, S. 2009, J. Chem. Phys., 130, 164302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maier, D., Barbier, A., Lazareff, B., & Schuster, K. F. 2005, in Sixteenth International Symposium on Space Terahertz Technology, 428 [Google Scholar]
- Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2010, ApJ, 720, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Belloche, A., Du, F., Güsten, R., & Menten, K. M. 2011, A&A, 526, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlyuchenkov, Y., Semenov, D., Henning, T., et al. 2007, ApJ, 669, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Piétu, V., Dutrey, A., & Guilloteau, S. 2007, A&A, 467, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qi, C., Wilner, D. J., Aikawa, Y., Blake, G. A., & Hogerheijde, M. R. 2008, ApJ, 681, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Pavlyuchenkov, Y., Schreyer, K., et al. 2005, ApJ, 621, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Wiebe, D., & Henning, T. 2006, ApJ, 647, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Sipilä, O., Hugo, E., Harju, J., et al. 2010, A&A, 509, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thi, W., van Zadelhoff, G., & van Dishoeck, E. F. 2004, A&A, 425, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willacy, K. 2007, ApJ, 660, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Wilner, D. J., Ho, P. T. P., Kastner, J. H., & Rodríguez, L. F. 2000, ApJ, 534, L101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 o-H2D+ spectrum in DM Tau. The dashed line indicates the systemic velocity. The resolution is 0.17 km s-1. |
| In the text | |
 |
Fig. 2 o-H2D+ spectrum in TW Hya. The dashed line indicates the systemic velocity. The resolution is 0.20 km s-1. |
| In the text | |
 |
Fig. 3 Results from the chemical modeling for DM Tau, case L, Model 2 and ξ = 3 × 10-17s-1. Top: predicted o-H2D+ column densities as a function of radius for several values of grain size: a = 0.1 μm (black); 1 (red) and 10 (blue); and CO abundance: x[CO] = 10-6 (thin lines) 10-5 (medium) and 10-4 (thick). The green lines correspond to the best 3σ upper limits derived from observations with p = 0 and p = −1. Bottom: observed spectrum (green) and predicted line profiles (same color and thickness convention). |
| In the text | |
 |
Fig. 4 o-H2D+ predicted flux as a function of CO abundance (left), cosmic ray (middle), and grain size (right) for DM Tau. Grain size: a = 0.1 μm (black); 1 (red) and 10 (blue). Cosmic ray ionization rate: ξ = 1 × 10-17 (triangle), 3 × 10-17 (square), and 1 × 10-16 s-1 (octagon). CO abundance: x[CO] = 10-6 (open marker) 10-5 (filled marker), and 10-4 (cross). The green line corresponds to our 3σ limit derived from observations. The dashed lines illustrate the dependencies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


